Abstract
Neurons in the medial superior olive (MSO) process sound localization cues through binaural coincidence detection, in which excitatory synaptic inputs from each ear are segregated onto different branches of a bipolar dendritic structure and sum at the soma and axon with submillisecond time resolution. Although synaptic timing and dynamics critically shape this remarkable computation, synaptic interactions with intrinsic ion channels have received less attention. Using paired somatic and dendritic patch-clamp recordings in gerbil brainstem slices together with compartmental modeling, we show that activation of Kv1 channels by dendritic EPSPs accelerates membrane repolarization in a voltage-dependent manner and actively improves the time resolution of synaptic integration. We demonstrate that a somatically biased gradient of Kv1 channels underlies the degree of compensation for passive cable filtering during propagation of EPSPs in dendrites. Thus both the spatial distribution and properties of Kv1 channels play a key role in preserving binaural synaptic timing.
The temporal relationship between excitatory synaptic input and action potential output is critical for sensory encoding as well as for the induction of some forms of synaptic plasticity 1,2. However, in the majority of neurons where excitatory inputs sum in the dendritic arbor, the relative timing of synaptic input is subject to distortions both in time and amplitude as a result of dendritic cable filtering 3,4. The computational challenge of maintaining fine temporal resolution in the face of dendritic distortions is especially acute in neurons of the medial superior olive (MSO) where phase-locked auditory information from the two ears is first integrated. Principal neurons of the MSO encode microsecond differences in the arrival time of sounds to the two ears (interaural time differences, or ITDs) through systematic variations in the rate of action potential output. Rate-encoded ITDs are a critical cue used by birds and mammals for localizing sounds along the horizontal plane 5–7.
At the cellular level, discrimination of ITDs in mammals involves the spatial and temporal summation of time-locked glutamatergic excitation and glycinergic inhibition in MSO principal neurons. Intriguingly, excitatory synaptic inputs from spherical bushy cells of the cochlear nucleus are segregated onto different branches of bipolar dendritic arbors 8. The axon, where action potential initiation occurs, emerges from the soma or proximal dendrite 9,10. While computational models have been used to predict that this synaptic input segregation in MSO neurons and their avian analogs may improve the fidelity of binaural coincidence detection 11–14, to date there has been almost no experimental data regarding the dendritic properties of these cells, and thus the role of the dendrites in shaping binaural coincidence detection is unclear.
To understand how MSO dendrites influence synaptic coincidence detection, we have combined simultaneous dendritic and somatic current-clamp recordings, both whole-cell and excised patch voltage-clamp recordings and computational modeling to explore how the properties of MSO dendrites influence binaural coincidence detection and temporal coding. Our results show that dendritic EPSPs activate a somatically biased population of low voltage activated K+ channels (KLVA), which accelerate membrane repolarization. The presence of KLVA approximately doubles the temporal resolution of binaural coincidence detection as compared to a passive leak conductance of the same density, and imposes a uniform somatic time course of EPSPs propagating from disparate dendritic locations. Thus, both the biophysical properties and spatial distribution of KLVA are critical determinants of the high resolution of binaural coincidence detection in the MSO.
Results
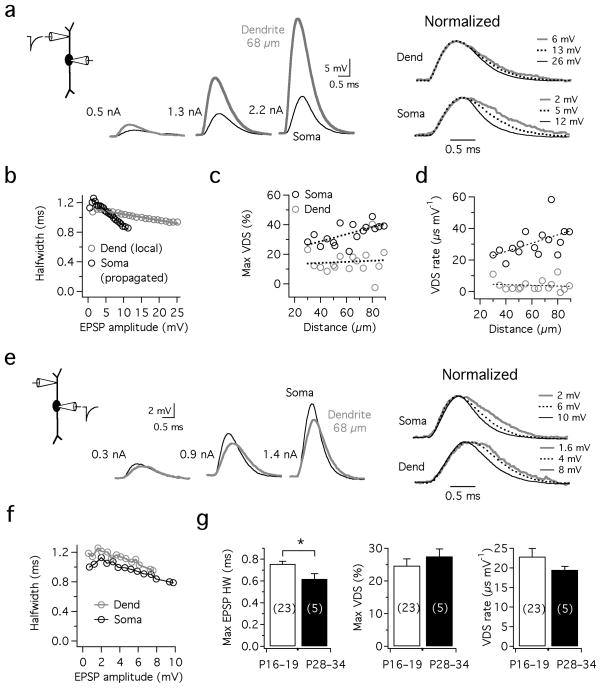
MSO principal cells were identified in brainstem slices by the bipolar morphology of their dendrites when viewed under infrared DIC optics 9, as well as the characteristic onset (single spike) firing pattern and unusually low input resistance these cells exhibit electrophysiologically (avg. 12.0±0.69 MΩ for P16–19 gerbils; n=20). To examine how EPSPs are shaped as they propagate from known locations in the dendrites to the soma, we made simultaneous somatic and dendritic current clamp recordings and injected simulated synaptic currents (sEPSCs; see Methods) into the dendrites and varied current amplitude to elicit depolarizations encompassing the entire subthreshold voltage range (Fig. 1a). These sEPSPs showed marked attenuation following propagation to the soma, which was proportional to the recording distance. In all recordings, one of the most striking features of sEPSPs was the voltage dependence of their shape. As the amplitude of sEPSPs increased, their halfwidth (sEPSP duration measured at half amplitude) progressively declined in both the dendrite and soma, contrary to what would be observed in a passive system where EPSP halfwidth is independent of amplitude (Fig. 1a,b). We define the maximum voltage-dependent sharpening, or VDS, as the percentage decrease in halfwidth (HW) observed in a family of sEPSPs spanning the subthreshold voltage range, from ~1–2 mV to just below spike threshold ([(HWmin epsp − HWmax epsp )/HWmin epsp ]*100%). The maximum VDS differed at the two recording locations. The average maximum VDS was 35% at the soma but only 15% in the dendrites, despite the fact that the dendrites received far greater depolarizations (Fig. 1c). Since VDS is sensitive to the magnitude of the subthreshold voltage range, which varied across cells from 8–19 mV, for each family of sEPSPs VDS was normalized with respect to the sEPSP amplitude (the VDS rate: maximum Δ halfwidth/maximum Δ amplitude; Fig. 1d). VDS rates averaged 31.0 μs/mV at the soma, but were only 3.9 μs/mV at the site of sEPSC injection in the dendrites (30–90 μm, n=16). Both the rate and magnitude of VDS in the dendrites were insensitive to the site of dendritic sEPSC injection, whereas for propagated sEPSPs measured at the soma VDS tended to increase proportionally with sEPSC injection distance (Fig. 1c). Presumably, the voltage-dependent mechanism responsible for EPSP sharpening is more effectively recruited by the large dendritic EPSPs that are necessary for the production of comparable somatic sEPSP amplitudes.
Figure 1. Propagation of simulated EPSPs from the dendrites to the soma in MSO neurons.
a. Simultaneous recording from the soma (black) and dendrite (gray; 68 μm from the soma) in response to injection of dendritic sEPSCs of 3 increasing amplitudes (0.2, 0.8, and 2.2 nA). The sEPSPs in a are shown normalized at the right, revealing a systematic decrease in sEPSP halfwidth with increasing amplitude. b. Plot of halfwidth vs. sEPSP amplitude for the cell shown in a, revealing a steeper voltage-dependent sharpening (VDS) of sEPSPs at the soma vs. the dendrite. c. Population data shows that the maximum degree of VDS was more prominent at the soma than in the dendrites. There was a trend for stronger VDS at both recording sites with increasing distance from the soma (0.06%/μm dendrite, 0.20%/μm soma; n=16). d. The rate of VDS over the subthreshold voltage range is higher at the soma than in the dendrite. Fits: dendrite, 0.02±0.05μs/mV*μm; soma, 0.26±0.12 μs/mV*μm. e,f. In the same cell as in a and b, attenuation of backpropagating sEPSPs was far less pronounced than during forward propagation from the dendrites to the soma. Note the prominent VDS observed in normalized traces with somatic sEPSC injection (e, right). g. VDS is insensitive to developmental stage. Despite a significant decline in EPSP duration (minimum halfwidth, measured just below spike threshold; p=0.03), VDS magnitude and rate in electrophysiologically mature animals (P28–34) was not significantly different from younger animals (P16–19; p=0.43 and p=0.21 for magnitude and rate respectively).
The results above indicate that the mechanism underlying the shortening of sEPSP duration is particularly prominent in the perisomatic region. Accordingly, when sEPSCs were injected into the soma in the same population of cells, a prominent voltage dependence of sEPSP duration was also observed at the soma even in the absence of strong dendritic depolarization (25% maximal sharpening over the 12 mV average subthreshold voltage range at the soma; n=17; Fig. 1e,f). In these responses, there was also a striking asymmetry in the attenuation of sEPSPs propagating towards the soma relative to those backpropagating into the distal dendrites (e.g. 1e vs. 1a). Further refinement of backpropagating sEPSP duration in the dendrites was detected, but was relatively subtle (Fig. 1f). Finally, given that the intrinsic electrical properties of MSO principal cells are known to undergo developmental changes up to ~3 postnatal weeks 9, we measured VDS in MSO neurons recorded from gerbils between P28–34. Although sEPSP halfwidths were narrower in older vs. younger neurons (0.62±0.04 ms vs. 0.76±0.02 ms, n=5 and 23 respectively, p=0.03), VDS rate and maximum magnitude were not significantly different between the two age ranges (Fig. 1g; p=0.43 and 0.21 for max VDS and VDS rate). Thus, VDS appears relatively insensitive to developmental stage.
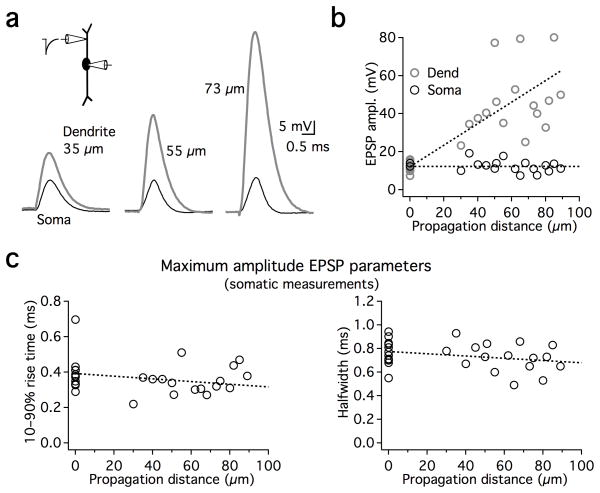
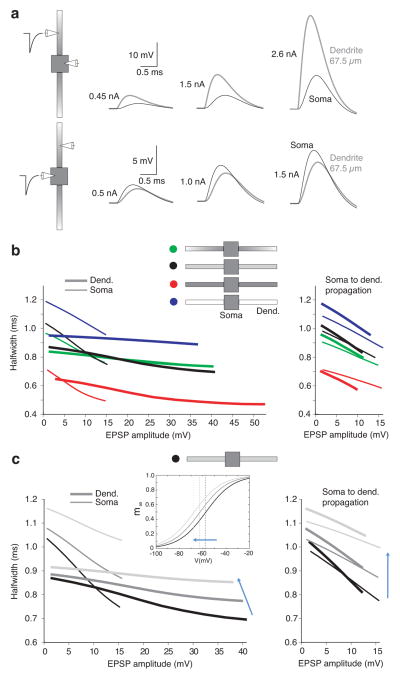
To understand how EPSP shape is controlled as a function of distance in the dendrites, we compared the somatic shape of the maximal subthreshold sEPSPs that had been introduced either in the soma itself (in dual somatic recordings; n=12), or in different locations along the dendrites (n=16; Fig. 2). In the examples shown in Fig. 2a, comparable somatic depolarizations required progressively larger dendritic sEPSPs in order to overcome the large attenuation observed during propagation in MSO dendrites. However, somatic sEPSPs appeared relatively uniform in rise time and duration despite their different spatial origins (Fig. 2c). These results suggest that VDS compensates for EPSP broadening from passive cable properties of the dendrite, which would be expected to prolong both the rise time and the decay of sEPSPs originating from more distal dendritic locations.
Figure 2. The shape of EPSPs is stable regardless of propagation distance.
a. sEPSPs from different dual dendritic and somatic recordings elicited with sEPSCs adjusted to be just below action potential threshold. Increasing dendritic depolarizations are required as a function of distance in order to produce just subthreshold somatic sEPSPs of comparable amplitude and shape. Amplitude of current injections: 2.3, 3.2, and 2.8 nA for dendritic recordings 35, 55, and 73 μm from the soma respectively. b. Group data from all paired recordings, showing dendritic responses (gray circles) and somatic responses (black circles). Points at 0 μm: sEPSP responses to somatic current injection were obtained using dual somatic recordings to prevent distortions of shape due to series resistance. c. Rise time and halfwidth of maximal subthreshold sEPSPs (recorded at the soma) as a function of the sEPSC dendritic location. sEPSPs at the soma propagating from different dendritic locations are of comparable rise time and duration as those elicited locally at the soma. Linear fits to the data show a slight negative trend with increasing distance from the soma (dotted lines). Linear fits both exhibit slopes of −0.001 ms/μm and are constrained to pass through the average somatic responses at 0 μm (rise time: 0.39 ms, halfwidth: 0.77 ms).
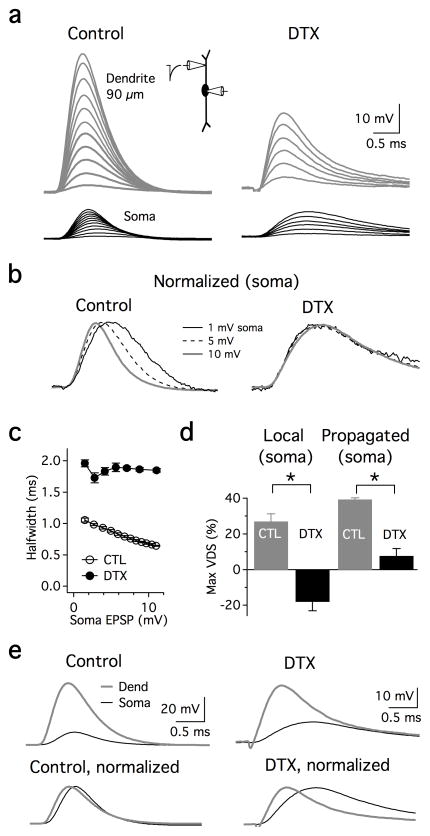
A candidate mechanism that could contribute to VDS is a fast-activating, KLVA conductance that has been described in several auditory and non-auditory neurons, including principal cells of the MSO. These K+ channels are composed of subunits from the Kv1 subfamily, and have been shown to influence membrane excitability in the subthreshold voltage range 9,15. To test whether these channels are capable of influencing the repolarization of propagating EPSPs in the MSO, we examined the effects of α-dendrotoxin (DTX), a potent blocker of Kv1.1, 1.2, 1.3, and 1.6 subunits, on subthreshold EPSP shape in the soma and dendrites. Bath application of 100 nM DTX produced dramatic changes in the intrinsic properties of MSO cells. VDS was strongly affected by DTX. When maximal subthreshold somatic sEPSPs were generated via dendritic sites 55–90 μm away (“propagated” sEPSPs), VDS was largely eliminated (from 39% to 8% in the presence of DTX; Fig. 3a–c; n=4). When sEPSPs were both generated and measured at the soma in dual recordings (“local” sEPSCs), KLVA blockade not only eliminated VDS, but in some cells induced a voltage-dependent broadening (27% to −18% average VDS, n=5, Fig. 3d). The latter effect reflects the activation of voltage-gated sodium channels by sEPSPs that is normally masked by K+ channel activation16. The effects of DTX on EPSPs were partially the result of changes in resting conductances. In the presence of DTX, the resting potential depolarized by ~3 mV (−61.7±1.4 to −58.4±1.3 mV; p=0.007), and the input resistance measured at the soma increased by ~3 fold (11.4±1.3 MΩ to 36.2±4.2 MΩ; p=0.0003, n=7), indicating that KLVA contributes to the resting conductance of MSO principal neurons. The increase in input resistance also decreased the somatic current required to generate action potentials by 3.3 fold (2,060±921 pA to 620±277 pA, n=5). Finally, blockade of KLVA strongly affected the cable filtering properties of MSO dendrites (Fig. 3e). Simulated EPSPs propagating from the distal dendrites (55–90 μm) to the soma were sharpened by 19% in normal ACSF (0.79±0.10 ms dendrite vs 0.61±0.05 ms soma, n=4) but were broadened by 92% when DTX was added (1.25±0.14 ms dendrite vs. 2.36±0.40 ms soma). These results indicate that DTX-sensitive K+ channels are critical for reducing the temporal broadening of synaptic excitation that would otherwise occur if the dendrites were passive.
Figure 3. A DTX-sensitive conductance mediates EPSP sharpening.
a. Simultaneous dendritic (gray) and somatic (black) voltage responses to sEPSCs recorded in control ACSF and in the presence of 100 nM α-DTX. sEPSCs were injected in the lateral dendrite 90 μm from the soma (0.2–2.2 nA, 0.2 nA increment). In DTX, sEPSP attenuation is sharply reduced, and both the rise time and duration of the response is increased. sEPSC: 0.2–1.2 nA, 0.2 nA increment. b. Normalized traces of 3 selected sEPSPs in a, showing VDS over the subthreshold voltage range. sEPSPs of identical amplitude show no VDS in DTX (right). c. In the neuron shown in a, DTX eliminated VDS and increased sEPSP halfwidth by ~2 fold. Points are the average of 5 traces. d. Group data showing VDS at the soma in response to somatic sEPSCs (“Local”, n=5), or in the dendrite 55–90 μm away (“Propagated”, n=4). Local sEPSPs at the soma were generated and measured using different pipettes in dual recordings. Maximum VDS (max VDS) was expressed for EPSP halfwidth in control ACSF (gray bars) as well as in the presence of DTX (black bars). Negative and positive values reflect a relative broadening and sharpening, respectively. Asterisks: significant differences between control and DTX conditions (paired 2-tailed t-test; p=0.0004 and p=0.0002 for local and propagated EPSPs) e. DTX slowed the rise time and increased the duration of sEPSPs during propagation from the dendrites to the soma, 90 μm away (same cell as in a–c). Control: 2200 pA; DTX: 1200 pA.
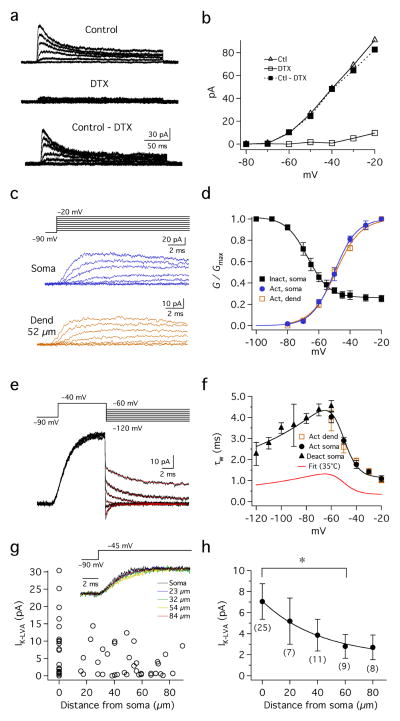
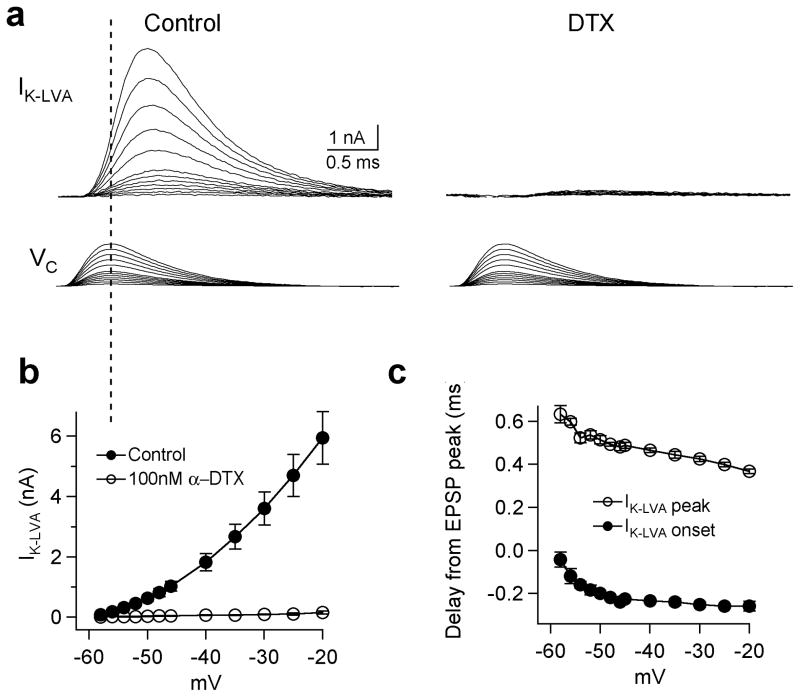
To directly observe the DTX-sensitive currents we made voltage-clamp recordings of pharmacologically isolated K+ currents in outside-out patches pulled from both the soma and dendrites of MSO principal cells (25°C). These procedures allowed us to record the voltage sensitivity and activation kinetics of these currents under conditions of high spatial and temporal voltage control. Patches were held at −90 mV to remove inactivation, and then stepped to voltages between −80 and −20 mV in 10 mV increments (Fig. 4a–c). These step commands evoked fast activating, slowly inactivating currents at voltages positive to −70 mV. Outward currents exhibited both inactivating and non-inactivating components, both of which were extensively blocked in the presence of 100 nM DTX (77±8% blockade at −40 mV, n=6; Fig. 4a, b). The half-activation voltage was similar for both somatic and dendritic patches (−49.0±1.5 mV, slope 7.4±0.7 mV; −48.8±1.4 mV, slope 8.1±0.4; Fig. 4c,d). Steady-state inactivation of KLVA current (IK-LVA) was tested in somatic patches with prepulses between −100 mV and −20 mV for 1.5 s followed by a test pulse to −45 mV for 200 ms (Suppl. Fig. 1). The inactivating component of IK-LVA comprised 74% of the total current and showed a half-inactivation voltage of −67.1±1.5 mV, with a slope factor of −6.2±0.5 mV (Fig. 4d, black squares; n=6). IK-LVA in both the soma and dendrite displayed fast, nearly identical activation kinetics: when corrected for an experimentally measured temperature coefficient (Q10) of 3.3, activation time constants decreased from 1.32 to 0.33 ms between −60 and −20 mV (Fig. 4c,f). Deactivation of IK-LVA following brief voltage steps in somatic patches was also rapid, ranging from 1.37 to 0.69 between −60 and −120 mV (Fig. 4e,f). Finally, we examined the somatodendritic distribution of IK-LVA in outside-out patches pulled either from the soma or dendrites up to 90 μm away (Fig. 4g,h). In response to steps from −90 to −45 mV, IK-LVA kinetics were similar in patches all along the soma and dendrites (Fig. 4g, inset). However, current amplitude was on average lower in the dendrites relative to the soma (Fig. 4h). The average amplitude of IK-LVA declined systematically as a function of distance along the dendrites. IK-LVA averaged 7.06±1.7 pA at the soma and decreased to 2.7±1.18 pA in the dendrites up to 90 μm in the dendrites (n=24, soma, n=37 dendrite; 20 μm bins; Fig. 4h). Thus, IK-LVA is available for activation by EPSPs throughout MSO neurons, but its density is biased significantly toward the soma and proximal dendrites.
Figure 4.
Characterization IK-LVA in outside-out patches. a,b. Pharmacologically isolated IK-LVA during voltage clamp. Steps: −90 mV to potentials between −80 to −20 mV, 10 mV increments). Outward currents resistant to 100 nM α-DTX (middle) were subtracted from Control (top), yielding the DTX-sensitive current (bottom). c. Kinetic similarity of DTX-sensitive currents recorded at the soma and dendrites. Steps same as in a. d. Activation and steady-state inactivation of IK-LVA. The peak conductance of DTX-sensitive K+ channels in the soma (blue) and dendrites (brown) elicited by steps between −80 and −20 mV from −90 mV. Steady state inactivation of somatic IK-LVA: peak conductances from voltage steps to −45 mV from a −90 mV holding potential after 1.5 s prepulses between −120 and −30 mV (see Suppl. Fig. 1; n=6). e. Deactivation of IK-LVA. Prepulses (−90 to −40 mV for 10 ms) followed by tail currents elicited between −60 and −120 mV. Fits were made to tails 300 μs to 15 ms after the step (see Methods). f. Activation and deactivation rates (τw) vs. voltage for somatic patches (blue circles and triangles respectively). Activation rates are shown for dendritic patches (brown). Fits to τw at 25°C were made according to f(V)=0.28*(100.0/(6.0*exp((V+60.0)/6.34)+24.0*exp(− (V+60.0)/63.53))+1.23, also shown adjusted to 35°C using an experimentally measured Q10 of 3.3 (red). g. Distribution of IK-LVA in the soma and dendrites. Inset: normalized peak currents from different locations have similar kinetics. h. Average current amplitude at the soma and dendrite (20 μm bins) decreased with a length constant of 42 μm (single exponential fit). Dendritic currents in the 60 μm bin were significantly different from those at the soma (*; p= 0.41, 0.06, 0.03 and 0.06 for bins 20–80 μm, respectively; Wilcoxon signed rank test, unequal sample variances).
To examine more directly the temporal relationship between EPSPs and the K+ currents they activate, we isolated IK-LVA in whole-cell recordings from MSO principal neurons at near-physiological temperature (35°C; see Methods), and delivered simulated EPSP commands (sEPSPs) scaled to produce depolarizations traversing the voltage range above −60 mV (Fig. 5a,b; peak amplitudes between −58 and −20 mV in 2 or 5 mV increments; see Methods). In these experiments, a larger fraction of the current was sensitive to bath application of 100 nM DTX as compared to responses to steps in outside-out patches (87–97% block between −60 and −20 mV, not shown), possibly because the sEPSP commands were too brief to effectively activate slower, non-DTX sensitive currents. At all voltages, sEPSP commands elicited fast and transient outward currents whose peaks trailed the sEPSP peaks by between 0.63 to 0.37 ms, depending on stimulus amplitude (Fig. 5c). The earliest discernable current (the “onset”, defined as the earliest outward current exceeding 3 standard deviations above the noise floor of the recording) preceded the peak of the sEPSP command by only 0.04 to 0.26 ms. The above results show that IK-LVA possesses the appropriate properties to account for the voltage-dependence and temporal dynamics of EPSP sharpening in MSO neurons. Interestingly, in whole-cell recordings, when the voltage-dependence of KLVA was examined at 35°C using pharmacological subtractions, the half-activation voltage measured with single boltzmann fits was 11 mV more positive than that recorded in outside-out patches (Suppl. Fig. 2), a shift possibly reflecting changes in the intracellular milieu and channel properties caused by patch excision that have been well documented (e.g. see ref. 17). However, channel kinetics were similar between currents measured in whole-cell recordings and excised patches when the latter were corrected for their difference in temperature. As detailed below, successful reproduction of VDS in model MSO neurons required IK-LVA activation to exhibit a voltage-dependence closer to whole-cell, and not excised patch parameters.
Figure 5. Relative timing of IK-LVA and simulated EPSP in whole-cell recordings at 35°C.
a. IK-LVA elicited by sEPSP voltage commands of amplitudes over the voltage range dominated by DTX-sensitive currents. sEPSP commands were delivered from the presumed resting membrane potential of −60 mV (see methods for leak subtraction). The peak EPSP amplitudes were scaled between 2 and 40 mV with 2 or 5 mV intervals, corresponding to peak voltages between −58 and −20 mV. b. Sensitivity of outward currents to 100 nM α-DTX (n=6). c. The time difference between the simulated EPSP peak and IK-LVA onset (closed circle) and peak (open circle) is plotted as a function of peak membrane potential.
To better understand how EPSP sharpening is influenced by cell morphology and input location, we constructed an idealized compartmental model that describes the subthreshold nonlinear dynamics of MSO principal neurons. The neuron model consists of a soma (a cylinder: 20 μm long and 20 μm in diameter) and two unbranched dendrites (150 μm long and 3.5 μm uniform diameter) in a bipolar configuration. The intrinsic properties were modeled after ref. 24 with two modifications: first, the density of IK-LVA and hyperpolarization-activated cation current (Ih) provided the majority of the resting conductance, and second, the densities were adjusted to maintain a resting potential of −60 mV with a membrane time constant of 600 μs (see Methods and Suppl. Fig. 4). A lower density of dendritic vs. somatic IK-LVA was required to reproduce the pattern of VDS observed with forward propagating and backpropagating EPSPs. Models exhibiting either a uniform lower dendritic density of IK-LVA (“step-gradient” model) or an exponentially declining gradient of dendritic IK-LVA (“exponential” model) produced both the sensitive VDS at the soma as well as the relatively modest VDS observed during EPSP propagation into the dendrites (Fig. 6a,b, black and green lines respectively). When a uniform density of IK-LVA was employed throughout the soma and dendrites, VDS for backpropagating EPSPs was more pronounced in the dendrites than at the soma, contrary to experimental observations (red lines in Fig. 6b right vs 1b,f). Finally, in models where dendritic IK-LVA was replaced with a passive leak current (thus preserving the resting potential and time constant), VDS shifted to longer durations by ~200 μs. All models exhibited relatively modest VDS at their dendritic input sites as compared to the soma (Fig. 6b, left, purple lines), a consequence of the relatively lower membrane surface area in the dendrites.
Figure 6. VDS for dendritic and somatic EPSC injection in a compartmental model of the MSO.
a. Schematic of dual recordings in the multicompartment model. Injection of EPSCs either in the dendrite 67.5 μm from the soma (top row) or at the soma itself (bottom row). Somatic EPSP halfwidth decreases as depolarization increases for both stimulus locations. b. VDS dependence on the spatial distribution of KLVA. VDS at the soma and at 67.5 μm in the dendrites (thin and thick lines), in response to either dendritic or somatic EPSCs (left and right graphs respectively). Four different IK-LVA density distributions are compared: green, exponential-gradient in dendritic IK-LVA density based on experimental data (see Fig. 4f,g); black, step-gradient model; red, uniform IK-LVA density; blue, active soma and passive dendrites with GK-LVA in dendrites frozen at its resting value. The step-gradient model and exponential-gradient model best reproduce experimental data in Fig. 1. c. Step-gradient model showing the dependence of VDS on the position of the IK-LVA activation function. Left and right-hand graphs display dendritic and somatic sites of current injection, respectively. left, inset, Activation functions [(m∞)4 ] exhibit the same slopes but different voltages of half activation: black, V1/2,m= −58 mV (as in whole cell data); med gray, V1/2,m= −63 mV; light gray, V1/2,m= −68 mV (as in outside-outside patch data). V1/2,m values correspond to single Boltzmann fits of maximal conductance adjusted to give the same resting conductance and potential for soma and dendrite in all three cases (see Suppl. Fig. 6). Best match to the VDS data is obtained with V1/2,m= −58 mV.
The relationship between the resting potential and IK-LVA activation characteristics was a critical determinant of the maximum magnitude of VDS. In models we observed the closest match with experimental VDS when IK-LVA exhibited voltage dependence close to what we observed in whole-cell experiments. With shallower activation functions, VDS was not as large as that observed experimentally (Suppl. Fig. 5). Shifts in IK-LVA activation to progressively more negative voltages (such as the range observed in outside-out patches) resulted in a proportionally greater resting activation of the channel but also led to a sharply reduced VDS of sEPSPs (Fig. 6c; see also Suppl. Fig. 6 to see how total gK-LVA was varied in the face of changing activation functions to maintain the same resting conductance across models). These results suggest that the whole-cell configuration more closely maintains the native state of IK-LVA and is used in the model in subsequent simulations.
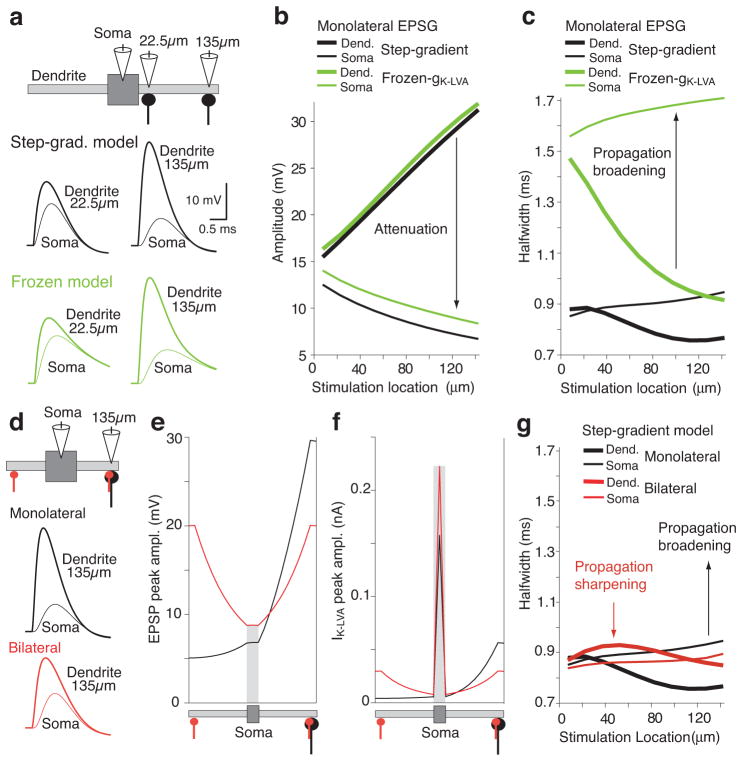
Additional insight about how IK-LVA shapes EPSPs spatially was obtained with the model by simulating the responses to transient synaptic conductances of constant amplitude (EPSGs) injected at different dendritic locations. To further highlight the dynamic and nonlinear aspects of IK-LVA activation, comparison simulations were done with the channel converted into a static conductance (“frozen gK-LVA”; Fig. 7). Increasingly larger local depolarizations were found for inputs more distant from the relatively large capacitance and current sink of the soma (thick lines, Fig. 7a,b). With either active or frozen gK-LVA, EPSPs at the soma exhibited progressively stronger attenuation as their stimulation distance increased. However, active gK-LVA strongly regulated the duration of EPSPs all along the dendrite (Fig. 7a,c). In the model with frozen gK-LVA, local dendritic EPSP duration decreased as synapse location moved distally, due to the bipolar dendritic geometry (e.g., EPSPs at the terminus of the dendrite will be briefer in a longer dendrite because depolarizing currents spread away comparatively faster). However, the relatively brief distal dendritic EPSPs broadened up to ~800 μs after propagation to soma, due to passive cable filtering along the length of the dendrite. In models with active gK-LVA, the temporal broadening of EPSP duration that occurred with passive cable filtering was strongly reduced due to the active repolarization of propagating EPSPs, particularly in the proximal dendrites and soma where channel density is the greatest (for comparison with experimental data of Fig. 2, see Suppl. Fig. 7).
Figure 7.
Spatial effects of voltage-dependent sharpening in an MSO neuron model. a. Effect of IK-LVA on EPSPs propagating through dendrites compared in models with active and passive gK-LVA (Step-grad-model and frozen model; black and green traces, respectively). Responses shown from two synaptic locations. b. Dendritic and somatic EPSP amplitudes (thick and thin lines) as a function of dendritic EPSC location. Attenuation of the EPSP amplitude from stimulation location to soma as predicted by cable theory. Models color coded as in a. c. Duration (halfwidth) of the dendritic and somatic EPSPs in b. EPSPs broadened for most of the synaptic locations in both models as predicted by cable theory. IK-LVA generates more attenuation but also decreases EPSP broadening during propagation to the soma. d. Comparison of voltage dependent sharpening between monolateral and bilateral synaptic inputs 135 μm from the soma. Top, monolateral and bilateral configuration: conductance in monolateral case is double that of each bilateral synaptic input. Bottom, time courses for selected locations for monolateral and bilateral stimulation configurations. e. Peak EPSP amplitude during propagation from the synaptic location to the soma. Stimulation at 135μm from the soma edge for monolateral and bilateral cases. f. Peak IK-LVA amplitude induced by EPSPs traveling from the stimulation location to the soma. g. EPSP halfwidths for EPSPs recorded locally at the injection site in the dendrites (thick lines) and after propagation to the soma (thin lines). EPSPs broadened during propagation to the soma for most monolateral locations, but sharpened for most bilateral locations.
The input location invariance of somatic EPSP duration was particularly striking during bilateral synaptic stimulation, a configuration that more closely resembles in vivo conditions during binaural hearing (Fig. 7d–g). In the bilateral configuration, each dendritic conductance was half the amplitude of those in monolateral simulations (red and black lines, respectively), thus representing the same number of activated synapses. Despite the fact that the dendrite(s) received the largest depolarization in these simulations, the largest recruitment of IK-LVA occurred at the soma, due to its greater IK-LVA density and membrane surface area (Fig. 7f). Relatively stronger recruitment of somatic IK-LVA occurred in the bilateral condition. Even though the input dendrite was more depolarized in the monolateral case, the opposite dendrite acted as a current sink, leading to less somatic depolarization. For the bilateral case, axial synaptic current from each dendrite meets at the soma, cancels, and eliminates effective current spread into the opposite dendrite. Accordingly, bilaterally evoked somatic EPSPs exhibited shorter durations than monolateral EPSPs and showed less spatial dependence in duration as well (Fig. 7g, thin red vs. black lines).
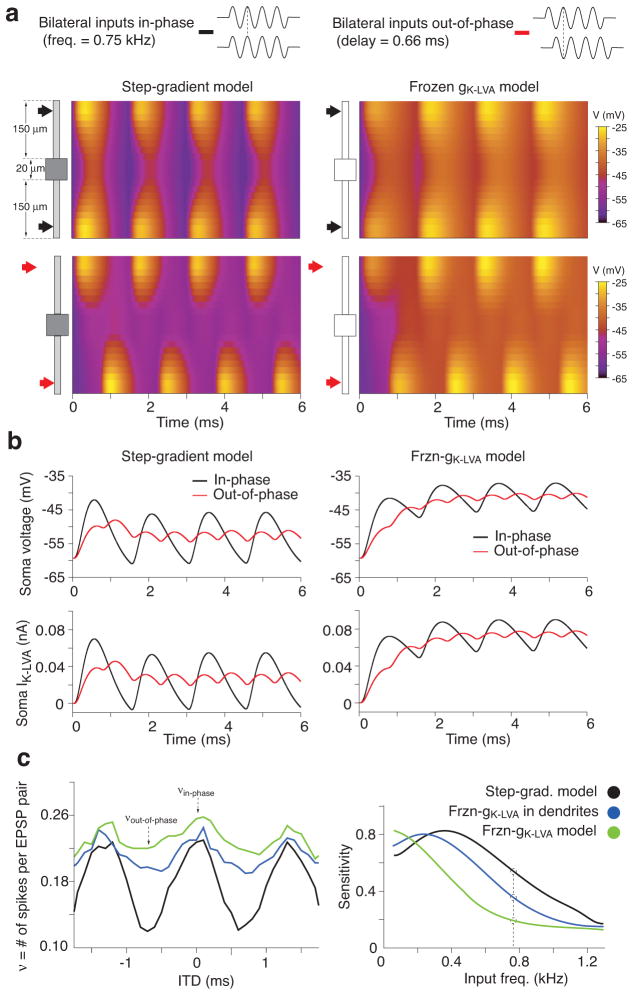
The spatiotemporal influence of IK-LVA on synaptic integration strongly enhanced the sensitivity of MSO neuron models to the submillisecond phase of excitatory inputs during high frequency repetitive stimulation. Fig. 8a shows comparisons between two models containing identical step-gradients of active or frozen gK-LVA (left and right panels, respectively) to either in-phase or out-of-phase bilateral excitatory inputs. The inputs delivered were short trains of synaptic conductances at 750 Hz (10 cycles with a period of ~1.3 ms). At such short inter-stimulus intervals, the onset of ongoing EPSPs would be in close temporal register with activated IK-LVA. Compared to the active model, the frozen model showed an increase in temporal summation with reduced phase sensitivity at the soma for bilateral inputs (Fig. 8b, top panels) and also less spatial attenuation of ongoing EPSPs throughout the cell (Fig. 8a). Active gK-LVA far more effectively interacts with the temporal dynamics of each phase of somatic voltage changes, whereas frozen gK-LVA functioned effectively as a leak current under the same stimulus conditions (Fig. 8b, bottom panels). When the model is elaborated to include an axon (with spike-generator conductances as in ref. 24; see Methods and Supp. Figs. 8 and 9) the ITD responsiveness reflects the EPSP sharpening for trains of binaural inputs (Fig. 8c left panel). When gK-LVA in the dendrites (purple curve) or in the whole neuron (green curve) is frozen, temporal summation increases in the case of out-of-phase ITD inputs (as it is shown in Fig. 8b top panels), increasing the number of spikes per bilateral EPSP input pairs. We define ITD sensitivity as the modulation index: (νin– phase −νout –of – phase )/(νin– phase + νout –of – phase ), where ν is firing frequency. Sensitivity degrades as more of gK-LVA is frozen (Fig. 8c, right panel). Increasing input frequency decreases ITD sensitivity in all three cases due to the fact that temporal summation increased firing for out-of-phase stimulation and saturated firing frequency for in-phase stimulation (see Suppl. Figs. 9,10). Thus, active gK-LVA in the soma and dendrites improves ITD sensitivity over a larger input frequency range. These results underscore the fact that IK-LVA controls the length of EPSP duration and therefore the time window of binaural coincidence detection at high frequencies not only through its passive contribution to the low input resistance but also its voltage dependency.
Figure 8. Spatio-temporal dynamics of membrane potential and IK-LVA for bilateral ITD-like distal inputs (750 Hz).
a. Top: Spatial profile of voltage along the soma and dendrites (ordinate) advancing in time for for in-phase inputs. Color code indicates voltage. Model: step-gradient configuration for active (left) and frozen gK-LVA (right). Bottom: Spatio-temporal voltage evolution for out-of-phase inputs. Active IK-LVA sharpens voltage time courses, especially proximally. b. Somatic voltage and IK-LVA (top and bottom) time courses for in-phase (black) and out-of-phase (red) bilateral inputs. Left column, step-gradient model with active gK-LVA. Right column, frozen gK-LVA model, with IK-LVA behaving as a leak current. c. ITD tuning curves and sensitivity function for three different spiking models (see Methods and Suppl. Fig 8): step-gradient model (black curves), frozen gK-LVA in dendrites (blue curve) and frozen gK-LVA in the whole cell (green curves). Left, ITD tuning curve for bilateral inputs at 750 Hz computed as ν: the number of spikes per EPSP-pair. For inputs at 750 Hz the ratio of νin-phase over νout-of-phase for a model with frozen IK-LVA is small, poorly discriminating different ITDs. The difference in number of spikes between in-phase inputs versus out-of-phase inputs increases as the amount of active IK-LVA in the model increases (from green to blue to black curve). Right, sensitivity functions for different input frequencies in the MSO neurons’ physiological range. The step-gradient model with a distribution of IK-LVA like that found in-vitro shows higher sensitivity for a broader range of input frequencies.
Discussion
Voltage transients propagating along passive dendrites suffer distortions in amplitude, rise time, and duration. These distortions likely would be problematic for neurons that use temporal coding strategies, as the location of the synapse itself would influence the timing of synaptic inputs at the soma and axon, and ultimately degrade the precision and reliability of action potential signaling. The encoding of sound localization cues by MSO neurons represents one of the most striking examples of this paradox in the nervous system. Modulation of firing rate with changes in azimuthal sound location requires an ability to resolve time differences in the arrival of binaural inputs on the order of tens of microseconds, far shorter than the membrane time constant (~250 μs for adult animals) 9. Here, we demonstrate an essential role of both the biophysical properties and spatial distribution of Kv1 channels in compensating for these passive cable distortions using electrophysiological approaches and compartmental modeling.
Molecular basis for IK-LVA
We have shown a critical role for IK-LVA in improving the time resolution of excitatory summation. In MSO principal neurons, channel activation occurred near −65 mV, negative to the average resting potential of −58 mV. The majority of K+ current at voltages negative to −30 mV was blocked by 100 nM α-DTX, a toxin that binds with high affinity to channels that possess Kv1.1, Kv1.2, Kv1.3 and Kv1.6 subunits 18–20. The negative activation range of the channel together with the sensitivity to dendrotoxin-K 9,15 is consistent with a heteromeric channel containing Kv1.1 subunits. We observed a small α-DTX insensitive component of low voltage-activated outward current, consistent with physiological and behavioral studies showing that non-Kv1.1 containing channels also influence auditory temporal coding 21,22. The kinetics of IK-LVA we describe in MSO neurons are considerably faster than those of homomeric Kv1 channels 18,23, and resemble Kv1 channel kinetics described in bushy cells of the mammalian cochlear nucleus 24, cells which also encode auditory information with high temporal precision.
Synaptic sharpening by IK-LVA
Kv1 channels are expressed widely throughout the central nervous system 25,26, where these channels provide a strong influence on both the current threshold for action potential initiation as well as the shape of the waveform itself 27–30. Due to their activation in the subthreshold voltage range, Kv1 channels have been shown to damp dendritic excitability as well as delay the onset to firing 31–33. Our present results show that in MSO principal neurons, IK-LVA is sufficiently rapid to actively truncate the time course of synaptic excitation on a submillisecond time scale. Three features of IK-LVA were critical for producing effective VDS in compartmental models. First, a steep voltage dependence of channel activation was important for the generation of significant outward currents over the relatively limited (~12 mV) subthreshold voltage range of MSO neurons. Second, VDS was maximal in the compartmental model when we used the half-activation voltage obtained from whole-cell recordings, and not outside-out patches. Models with more negative ranges of channel activation increased the resting conductance but exhibited comparatively little VDS. Third, the rapid kinetics of channel activation critically influenced the time course of excitation in the MSO. In whole-cell recordings, IK-LVA accelerated the repolarization of sEPSPs, reducing the duration of dendritically propagated sEPSPs by as much as 46% (35% on average). It is important to consider that both leak and hyperpolarization-activated cation channels are also major components of the high intrinsic resolution of binaural coincidence detectors in birds and mammals, but their contribution to the overall resting conductance is static over the time scale of individual synaptic events 34. Along with KLVA, these channels provide a fast overall response characteristic to MSO neurons, which is actively truncated by the additional recruitment of IK-LVA during excitation.
Kv1 channels have long been known to play especially strong roles in controlling the excitability and firing precision of neurons in auditory brainstem pathways concerned with temporal coding in both birds and mammals 35–40. As in the MSO, Kv1 channels in these neurons contribute substantially to the resting conductance, increasing the speed of membrane voltage changes, increasing the current required for action potential generation, and suppressing repetitive firing 41–43. The present study, however, demonstrates that in the MSO the contribution of Kv1 channels to the resting membrane properties is, by itself, insufficient to provide the submillisecond temporal resolution required for ITD encoding. In models in which IK-LVA was replaced with a passive leak current the time course of excitation approximately doubled, which degraded the distinction between in-phase and out-of-phase bilateral excitation especially at high frequencies (e.g., Fig. 8). Thus, while it has been previously recognized that the activation of Kv1 channels is important for creating a narrow time window for action potential firing 15,41–44, the present results highlight a far more dynamic role of Kv1 channels in defining the window over which binaural coincidence detection takes place.
Somato-dendritic distribution of IK-LVA
Our study is the first to examine how IK-LVA acts spatially in the dendrites for the control of synaptic timing in the auditory system. We show directly that Kv1 channels are expressed in both the soma and dendrites, but their density is biased toward the soma. As EPSPs propagate along the dendrites of MSO principal neurons, passive cable filtering delays the rise time of EPSPs and increases their duration. However, as these events invade the proximal dendrites and soma, they differentially activate greater IK-LVA near the soma, due to the higher density of channels as well as the greater membrane surface area relative to the dendrites. In addition, the capacitive load of the soma prolongs excitation, resulting in more temporal overlap between IK-LVA and the EPSP. The perisomatic activation of IK-LVA was particularly robust during bilateral stimulation, where slower, dendritically filtered EPSPs more efficiently recruited IK-LVA proximally in opposing dendrites. Conversely, in the far distal dendrites where cable properties dictated faster local EPSP time courses, we observed little effect of IK-LVA-mediated EPSP sharpening even during strong depolarizations. Thus, the somatically-biased distribution of IK-LVA compensates for dendritic cable filtering, and preserves the time course of submillisecond synaptic potentials occurring over disparate regions of the dendrites, effectively setting an upper limit on the duration of excitation.
Functional implications for ITD encoding in vivo
Extensive debate regarding models of ITD encoding revolves around whether the ITD sensitivity of MSO neurons is determined by the relative delays of excitatory binaural inputs (the Jeffress model) 45, or by the timing/and or magnitude of glycinergic inhibition (the Grothe/McAlpine model) 46,47. The role of IK-LVA in shaping synaptic timing would be expected to impact all models of ITD detection, as the reduction of EPSP duration by IK-LVA would increase the requirement for temporal proximity of binaural excitatory inputs and reduce width of the ITD tuning curve, enabling a “place code” to exist in the case of a Jeffress-type mechanism. The width of excitatory tuning would influence a “slope code” scenario that features inhibition as well (Grothe/McAlpine model). However, the interactions of IK-LVA with mixed inhibitory and excitatory synaptic potentials will likely be a more complicated function of their relative magnitudes and temporal patterns, neither of which has been described yet in MSO neurons in vivo. The location of the resting potential at the foot of the activation curve of IK-LVA will render the effects of this current highly sensitive to the effects of summating inhibition as well as neuromodulators that affect resting conductances. More generally, our results predict that IK-LVA will play an important role in reducing firing to inappropriately timed excitation and enhancing the ability of MSO neurons to compute ITDs at higher frequencies.
Methods
All experimental procedures followed the guidelines of the National Institutes of Health and were approved by the Institutional Animal Care and Use Committee at the University of Texas at Austin.
Slice preparation
Mongolian gerbils (Meriones unguiculatus) from P16–19 were obtained either from Charles River Laboratories (Wilmington, Mass.), or from an in-house colony. All work was approved by the Institute In a small subset of experiments, older gerbils were used (P28–P35). Gerbils were anesthetized with halothane, decapitated, and their brains were removed in artificial cerebrospinal fluid (ACSF) at 32°C, and saturated with 95%/5% oxygen/carbon dioxide. ACSF contained (in mM): 125 NaCl, 2.5 KCl, 2 CaCl2, 20 NaHCO3, 1.25 NaH2PO4, 25 glucose; pH 7.4 with NaOH. Horizontal brainstem slices 200 μm thick were cut with an oscillating tissue slicer (Leica VT1000S, Leica, Germany) at 32°C. Slices were incubated at 35°C in oxygenated ACSF for at least 30 minutes, and held at room temperature thereafter. For recording, slices were transferred to a recording chamber and constantly superfused with oxygenated ACSF at ~4 mL/min. and held at 35±0.1°C unless indicated otherwise.
Current-clamp electrophysiology
For recording, slices were visualized at 160x using infrared differential interference contrast microscopy in conjunction with a Newvicon tube camera system (NC-70; Dage-MTI). Both dendritic and somatic current-clamp recordings were made with thick-walled borosilicate glass pipettes (1.65 O.D), pulled to resistances of 3–4 MΩ (somatic electrodes) or 6–11 MΩ (dendritic electrodes). The pipette solution consisted of (in mM): 115 K+ gluconate, 20 KCl, 10 sodium phosphocreatine, 0.5 EGTA, 4 MgATP, 0.3 NaGTP; pH 7.3 with KOH. Dual current-clamp recordings were made with a pair of amplifiers with a fast voltage-follower circuit (BVC-700, Dagan, Minneapolis, MN), and signals were low-pass filtered at 5 kHz, digitized, and transferred to a Macintosh Power PC via an Instructech ITC-18 interface (sampling rate 50 kHz). Data acquisition was controlled by custom macros programmed in IGOR-Pro (WaveMetrics, Inc., Lake Oswego, OR).
Analysis
Measurements of dendritic distances were made relative to the center of the soma. Recordings were accepted for analysis if the series resistance in the dendrites and soma remained below 50 MΩ and 15 MΩ, respectively. In addition, dual somatic recordings were used to confirm that the time course of the current injection was not affected by the range of series resistances encountered in these experiments. Drugs and toxins were bath applied. Group data reflect the average ± standard error of the mean. Unless specified otherwise, a 2-tailed Student’s t-test with equal variance assumption was used for statistical comparisons, with a significance criterion of 0.05.
Voltage clamp electrophysiology
Dendritic and somatic outside-out patches were obtained at 25°C using an Axopatch 200B amplifier (Molecular Devices). The internal solution was the same as used in the whole-cell current clamp experiments. Pipettes had 5–7 MΩ open tip resistances. Patches were held at −90 mV and currents were elicited by voltage steps to between −80 and −20 mV (corrected for a 10 mV junction potential). Potassium currents were pharmacologically isolated with bath application of a control solution consisting of 1μM TTX, 200μM CoCl, 50μM ZD7288, and 1mM TEA to block voltage-gated sodium, calcium, Ih and high voltage-activate K+ currents. To further isolate channels containing Kv1 subunits, currents obtained in control experiments were subtracted from currents produced after 100 nM α-DTX was applied to the patch at ~0.4 psi via a flow pipe of 100 μm diameter (microfil, WPI). In order to prevent DTX from contaminating the solution bathing the slice, the flow pipe was housed inside the lumen of a glass capillary that siphoned extracellular solution from the bath. Patches were then guided inside the lumen of the siphon in front of the DTX flow pipe. Traces were low-pass filtered online at 2–5 kHz, and measurements were made from the average of 1–4 repititions. The data were fit with a Boltzmann equation of the form f(V) = 1/(1+exp((V1/2−V)/k)), where V1/2 is the half-maximal voltage, and k is the slope factor. To measure steady-state inactivation, brief prepulses (−90 to −40 mV for 10 ms) were delivered to patches, and peak tail currents were measured between −60 and −120 mV. Fits were made to tails 300 μs to 15 ms after the step using the equation f(t)=[A ± B exp(−t/τw)]4.
Measurements from outside-out patches of IK-LVA density were carried out in the control solution stated above. Steps were delivered from a holding potential of −80 to −45 mV, below the activation of high voltage-activated K+ channels (activation ~ −30 mV, data not shown). Traces represent the average of 10–70 trials. To maintain patch uniformity pipette resistances were restricted between 8–9 MΩ (outer diameter of ~ 1.8 μm at 160x magnification). There was no significant correlation between tip resistance and IK-LVA magnitude (Suppl. Fig. 3). Online pipette capacitance compensation was employed, and leak subtraction was performed using a P/-4 subtraction protocol.
In experiments measuring IK-LVA in response to sEPSPs (Fig. 5), whole-cell voltage clamp protocols were carried out at near physiological temperatures (35°C) in the control solution stated above. In addition CNQX (10 μM) and strychnine (1 μM) were added to the bath in order to decrease fast glutamatergic and glycinergic currents. IK-LVA was elicited with EPSP voltage commands between 2 and 40 mV from −60 mV, the average resting potential of MSO neurons. EPSP commands were taken from the average evoked EPSP (~2mV) in a cell that exhibited the average EPSP halfwidth of P17 gerbils (0.64 ms). All traces represent averages of 3–6 trials and were low-pass filtered at 5 kHz. Capacitance neutralization and >75% series resistance compensation were employed. Pipettes were wrapped with Parafilm to reduce pipette capacitance. Leak subtraction was performed offline using a P/–4 protocol. However, the leak pulses were elicited from a holding potential of −80 mV, outside of the activation range of IK-LVA but still within the linear portion of the I–V relationship (when Ih was blocked pharmacologically). To minimize noise 20 traces of leak current were averaged before subtraction.
Modeling
An idealized compartmental model of an MSO neuron was developed that exhibits the characteristic bipolar dendritic architecture of these cells. The neuron model has a soma (area, AS) and two unbranched dendrites of uniform diameter, d (3.5 μm), and of length, l (150 μm). The current balance equations in the non-spiking regime take the form, for each dendrite (0 ≤ x ≤ l):
and, e.g. for the somatic compartment:
The subscripts S, 1, and 2 refer to the soma and each of the two dendrites (for simplicity, we dropped the subscripts in the cable equation and for the gating variables in the soma); Ri is the axial resistivity (200 Ω cm) and Cm is the membrane capacitance (0.9 μF/cm2 ). The dendrites V have sealed distal ends: . The values for the maximal conductance densities Gx and x reversal potentials Vx are given below. The inwardly rectifying cationic conductance, Gh, was modeled as a static leak, as channel gating kinetics are at least ten times slower than the time course of EPSPs in MSO neurons (S. Khurana and N.L. Golding, Soc. Neurosci. Abstr. 467.15, 2007). The dynamics for the gating variables (activation, m, and inactivation, h) of IK-LVA satisfy:
where
m∞ (V) = 1/[1 + exp((V−V1/2, m )/km )], h∞(V) = (1 − ζ)/[1 + exp((V − V1/2,h )/kh)] + ζ, τm (V) = 21.5/[6 exp((V + 60)/7) + 24 exp(−(V + 60)/50.6] + 0.35, and τh (V) = 170/[5 exp((V + 60)/10) + exp(−(V + 70)/8] + 10.7. The values for parameters (in mV: V1/2,m =−57.34, km = 11.7, V1/2,h =−67, kh = 6.16; ζ= 0.27; and expressions for τm (V ) and τh (V) were obtained using Neurofit 48 based on our outside-out patch voltage-clamp recordings; functional expressions for τm(V ) and τh(V ) were then fit by using a least squares method. We used m4 for conductance activation of IK-LVA, the lowest power that provided a good fit to the data. The voltage dependence of gating from outside-out patch data was shifted by about 10 mV in the depolarizing direction (see Figs. 4d, 6b and Suppl. Fig. 6). While this description was used in our model simulations, a power of 1 was used to describe the channel activation curves in Fig. 4d, in order to provide a more intuitive description of the channel V1/2 and aid comparisons to other studies. Maximal conductances were constrained to maintain a resting potential of ~ −60 mV and a somatic membrane time constant of ~0.6 ms, both average values for MSO neurons from 17–18 day old gerbils 9. In addition, we adjusted the dendritic maximal conductances (for step-gradient and exponential-gradient distributions) in order to match the average VDS recorded experimentally in both the soma and dendrites > 50 μm from the soma (n=13). We found that VDS properties were well described if we chose a dendritic membrane time constant of 1.6 ms. Satisfying all of the above requirements proved difficult, and required a precise balance between IK-LVA and Ih. Furthermore, VDS was highly sensitive to both the voltage dependence and kinetics of IK-LVA. As a confirmatory and independent check on our model we simulated the response to an EPSP-like clamp at the soma (cf, Fig. 5) and found good agreement of the IK-LVA transients from the model and from the experimental recordings (Suppl. Fig. 4 shows the comparisons in the V-IK-LVA plane). The parameter values that we used are as follows (conductances in mS/cm2). For the soma: Gleak,S =0.3, GK-LVA,S =17, Gh,S=0.86, and for the dendrites in the case of uniform density model. For the dendrites in the step-gradient model: Gleak = 0.3, GK-LVA = 0.18, Gh = 0.38. For the dendrites in the exponential-gradient model: Gleak = 0.3, GK-LVA = 17 [0.6 exp(−x/74)+0.05]; Gh = 1.8 [0.6.exp(−x/74)+0.05]. In all cases: Vleak = −60 mV, VK = −106 mV, and Vh = −43 mV. With these conductance values and cable architecture, our neuron model has input resistance, Rinput ≈ 11.4 MΩ (from the soma), and dendritic space constant λD = 280 μm for the step-gradient and frozen cases.
The input Isyn was specified as a depolarizing current injection (double exponential function with τrise= 0.22 ms and τdecay= 0.43 ms) or as a conductance-based excitatory input, Gsyn (x, t)(V − Vsyn), with Gsyn as an alpha function with τsyn=0.2 ms and Vsyn= 0 mV).
For the compartmental implementation we used 10 equally sized compartments for each dendrite, while the soma was represented as a cylinder (diameter, 20 μm and length, 20 μm) using 3 equally sized compartments (e.g., ref. 49, Chapters 2, 3). Our computer code was written in the C programming language. The differential equations of the model were integrated numerically using the fourth-order Runge–Kutta method (see ref. 49, Chapter 14), using a time step of 0.0025 ms.
The spiking model, schematized in Suppl. Fig. 8, was constructed from the multi-compartment model of bipolar dendrites and a soma (explained above) by adding a 5-compartment initial segment of uniform diameter, d (2 μm), and of length, l (25 μm), and a 5-compartment uniform diameter axon d (1 μm), and of length, l (100 μm). GK-LVA and Gh are frozen for the initial segment and axon, and thus any VDS in the spiking model is generated at the dendrite and soma compartments. The only active currents in the initial segment and axon were the high threshold activated potassium current (IK-HT) and sodium current (INa) obtained from ref. 24. Since spike identification is not problematic in the axon, spike counting for ITD tuning curves was done at the first node of the axon (light blue time course on Suppl. Fig. 8).
In order to create realistic ITD curves we injected trains of conductance-based inputs into the middle compartment of each dendrite with different delays. Bilateral input trains (ten EPSP pairings with Gaussian noise on the amplitudes, maintaining constant total-EPSG amplitude and peak EPSG timing cycle to cycle) triggered spikes with different probabilities dependent on the relative delay of bilateral EPSPs invading the axonal spike generation region (Suppl. Fig. 9). Forty trials were generated for each ITD with ten cycles of bilateral simulation per trial. The standard deviations for the number of spikes were computed in order to see the variability on spike count for each of the neuron model configurations (thin lines on the ITD tuning curves on Suppl. Figs. 9 and 10).
Supplementary Material
Acknowledgments
We thank Drs. Dan Johnston and Alex Reyes for their comments on a previous version of the manuscript. This work was supported by grants from the NIH (DC006877 to N.L.G. and DC008543 to J.R.), as well as Ruth Kirschstein NRSAs to P.J.M and L.L.S.
Footnotes
Author Contributions
P.J.M. performed all voltage-clamp experiments characterizing IK-LVA in patches and whole cells. N.L.G. conducted dual somatic and dendritic current-clamp recordings. L.L.S. performed some of the experiments from older animals and also made some of the initial observations on voltage-dependent sharpening. P.E.J. performed all of the simulations. N.L.G. and J.R. helped design and supervise experiments and simulations, respectively. N.L.G. wrote the manuscript, with contributions from P.J.M., P.E.J., and J.R.
Bibliography
- 1.Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule. Annu Rev Neurosci. 2008;31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
- 2.Mauk MD, Buonomano DV. The neural basis of temporal processing. Annu Rev Neurosci. 2004;27:307–340. doi: 10.1146/annurev.neuro.27.070203.144247. [DOI] [PubMed] [Google Scholar]
- 3.Rinzel J, Rall W. Transient response in a dendritic neuron model for current injected at one branch. Biophys J. 1974;14:759–790. doi: 10.1016/S0006-3495(74)85948-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Segev I, London M. Untangling dendrites with quantitative models. Science. 2000;290:744–750. doi: 10.1126/science.290.5492.744. [DOI] [PubMed] [Google Scholar]
- 5.Carr CE. Processing of Temporal Information in the Brain. Annual Reviews in Neuroscience. 1993;16:223–243. doi: 10.1146/annurev.ne.16.030193.001255. [DOI] [PubMed] [Google Scholar]
- 6.Grothe B. Sensory systems: New roles for synaptic inhibition in sound localization. Nat Rev Neurosci. 2003;4:540–550. doi: 10.1038/nrn1136. [DOI] [PubMed] [Google Scholar]
- 7.Joris P, Yin T. A matter of time: internal delays in binaural processing. Trends in Neurosciences. 2007;30:70–78. doi: 10.1016/j.tins.2006.12.004. [DOI] [PubMed] [Google Scholar]
- 8.Stotler WA. An experimental study of the cells and connections of the superior olivary complex of the cat. J Comp Neurol. 1953;98:401–431. doi: 10.1002/cne.900980303. [DOI] [PubMed] [Google Scholar]
- 9.Scott LL, Mathews PJ, Golding NL. Posthearing developmental refinement of temporal processing in principal neurons of the medial superior olive. J Neurosci. 2005;25:7887–7895. doi: 10.1523/JNEUROSCI.1016-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Scott LL, Hage TA, Golding NL. Weak action potential backpropagation is associated with high-frequency axonal firing capability in principal neurons of the gerbil medial superior olive. J Physiol. 2007;583:647–661. doi: 10.1113/jphysiol.2007.136366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Agmon-Snir H, Carr CE, Rinzel J. The role of dendrites in auditory coincidence detection. Nature. 1998;393:268–272. doi: 10.1038/30505. [DOI] [PubMed] [Google Scholar]
- 12.Dasika VK, White JA, Colburn HS. Simple models show the general advantages of dendrites in coincidence detection. J Neurophysiol. 2007;97:3449–3459. doi: 10.1152/jn.00669.2005. [DOI] [PubMed] [Google Scholar]
- 13.Grau-Serrat V, Carr CE, Simon JZ. Modeling coincidence detection in nucleus laminaris. Biological cybernetics. 2003;89:388–396. doi: 10.1007/s00422-003-0444-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhou Y, Carney LH, Colburn HS. A model for interaural time difference sensitivity in the medial superior olive: interaction of excitatory and inhibitory synaptic inputs, channel dynamics, and cellular morphology. J Neurosci. 2005;25:3046–3058. doi: 10.1523/JNEUROSCI.3064-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Svirskis G, Kotak V, Sanes DH, Rinzel J. Enhancement of signal-to-noise ratio and phase locking for small inputs by a low-threshold outward current in auditory neurons. J Neurosci. 2002;22:11019–11025. doi: 10.1523/JNEUROSCI.22-24-11019.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Scott LL, Mathews PJ, Golding NL. Perisomatic voltage-gated sodium channels actively maintain linear synaptic integration in principal neurons of the medial superior olive. J Neurosci. 2010;30:2051–2062. doi: 10.1523/JNEUROSCI.2385-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Martina M, Vida I, Jonas P. Distal initiation and active propagation of action potentials in interneuron dendrites. Science. 2000;287:295–300. doi: 10.1126/science.287.5451.295. [DOI] [PubMed] [Google Scholar]
- 18.Grissmer S, Nguyen AN, Aiyar J, Hanson DC, et al. Pharmacological characterization of five cloned voltage-gated K+ channels, types Kv1.1, 1.2, 1.3, 1.5, and 3.1, stably expressed in mammalian cell lines. Mol Pharmacol. 1994;45:1227–1234. [PubMed] [Google Scholar]
- 19.Hopkins WF, Allen ML, Houamed KM, Tempel BL. Properties of voltage-gated K+ currents expressed in Xenopus oocytes by mKv1.1, mKv1.2 and their heteromultimers as revealed by mutagenesis of the dendrotoxin-binding site in mKv1.1. Pflugers Arch. 1994;428:382–390. doi: 10.1007/BF00724522. [DOI] [PubMed] [Google Scholar]
- 20.Stühmer W, Ruppersberg JP, Schröter KH, Sakmann B, et al. Molecular basis of functional diversity of voltage-gated potassium channels in mammalian brain. EMBO J. 1989;8:3235–3244. doi: 10.1002/j.1460-2075.1989.tb08483.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Allen PD, Schmuck N, Ison JR, Walton JP. Kv1.1 channel subunits are not necessary for high temporal acuity in behavioral and electrophysiological gap detection. Hear Res. 2008;246:52–58. doi: 10.1016/j.heares.2008.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brew HM, Hallows JL, Tempel BL. Hyperexcitability and reduced low threshold potassium currents in auditory neurons of mice lacking the channel subunit Kv1.1. J Physiol (Lond) 2003;548:1–20. doi: 10.1113/jphysiol.2002.035568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sokolov MV, Shamotienko O, Dhochartaigh SN, Sack JT, Dolly JO. Concatemers of brain Kv1 channel alpha subunits that give similar K+ currents yield pharmacologically distinguishable heteromers. Neuropharmacology. 2007;53:272–282. doi: 10.1016/j.neuropharm.2007.05.008. [DOI] [PubMed] [Google Scholar]
- 24.Rothman JS, Manis PB. Kinetic analyses of three distinct potassium conductances in ventral cochlear nucleus neurons. J Neurophysiol. 2003;89:3083–3096. doi: 10.1152/jn.00126.2002. [DOI] [PubMed] [Google Scholar]
- 25.Sheng M, Tsaur ML, Jan YN, Jan LY. Contrasting subcellular localization of the Kv1.2 K+ channel subunit in different neurons of rat brain. J Neurosci. 1994;14:2408–2417. doi: 10.1523/JNEUROSCI.14-04-02408.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang H, Kunkel DD, Schwartzkroin PA, Tempel BL. Localization of Kv1.1 and Kv1.2, two K channel proteins, to synaptic terminals, somata, and dendrites in the mouse brain. J Neurosci. 1994;14:4588–4599. doi: 10.1523/JNEUROSCI.14-08-04588.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bekkers JM, Delaney AJ. Modulation of excitability by alpha-dendrotoxin-sensitive potassium channels in neocortical pyramidal neurons. J Neurosci. 2001;21:6553–6560. doi: 10.1523/JNEUROSCI.21-17-06553.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goldberg EM, Clark BD, Zagha E, Nahmani M, et al. K+ channels at the axon initial segment dampen near-threshold excitability of neocortical fast-spiking GABAergic interneurons. Neuron. 2008;58:387–400. doi: 10.1016/j.neuron.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kole MH, Letzkus JJ, Stuart GJ. Axon initial segment Kv1 channels control axonal action potential waveform and synaptic efficacy. Neuron. 2007;55:633–647. doi: 10.1016/j.neuron.2007.07.031. [DOI] [PubMed] [Google Scholar]
- 30.Shu Y, Yu Y, Yang J, McCormick DA. Selective control of cortical axonal spikes by a slowly inactivating K+ current. Proc Natl Acad Sci USA. 2007;104:11453–11458. doi: 10.1073/pnas.0702041104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mckay B. Kv1 K+ Channels Control Purkinje Cell Output to Facilitate Postsynaptic Rebound Discharge in Deep Cerebellar Neurons. J Neurosci. 2005;25:1481–1492. doi: 10.1523/JNEUROSCI.3523-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Metz AE, Spruston N, Martina M. Dendritic D-type potassium currents inhibit the spike afterdepolarization in rat hippocampal CA1 pyramidal neurons. J Physiol (Lond) 2007;581:175–187. doi: 10.1113/jphysiol.2006.127068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Storm JF. Temporal integration by a slowly inactivating K+ current in hippocampal neurons. Nature. 1988;336:379–381. doi: 10.1038/336379a0. [DOI] [PubMed] [Google Scholar]
- 34.Yamada R. Hyperpolarization-Activated Cyclic Nucleotide-Gated Cation Channels Regulate Auditory Coincidence Detection in Nucleus Laminaris of the Chick. J Neurosci. 2005;25:8867–8877. doi: 10.1523/JNEUROSCI.2541-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ashida G, Abe K, Funabiki K, Konishi M. Passive Soma Facilitates Submillisecond Coincidence Detection in the Owl’s Auditory System. J Neurophysiol. 2007;97:2267–2282. doi: 10.1152/jn.00399.2006. [DOI] [PubMed] [Google Scholar]
- 36.Barnes-Davies M, Barker MC, Osmani F, Forsythe ID. Kv1 currents mediate a gradient of principal neuron excitability across the tonotopic axis in the rat lateral superior olive. Eur J Neurosci. 2004;19:325–333. doi: 10.1111/j.0953-816x.2003.03133.x. [DOI] [PubMed] [Google Scholar]
- 37.Brew HM, Forsythe ID. Two voltage-dependent K+ conductances with complementary functions in postsynaptic integration at a central auditory synapse. J Neurosci. 1995;15:8011–8022. doi: 10.1523/JNEUROSCI.15-12-08011.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Oertel D, Bal R, Gardner SM, Smith PH, Joris PX. Detection of synchrony in the activity of auditory nerve fibers by octopus cells of the mammalian cochlear nucleus. Proc Natl Acad Sci U S A. 2000;97:11773–11779. doi: 10.1073/pnas.97.22.11773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Reyes AD, Rubel EW, Spain WJ. Membrane properties underlying the firing of neurons in the avian cochlear nucleus. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rothman JS, Manis PB. The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J Neurophysiol. 2003;89:3097–3113. doi: 10.1152/jn.00127.2002. [DOI] [PubMed] [Google Scholar]
- 41.Ferragamo MJ, Oertel D. Octopus cells of the mammalian ventral cochlear nucleus sense the rate of depolarization. J Neurophysiol. 2002;87:2262–2270. doi: 10.1152/jn.00587.2001. [DOI] [PubMed] [Google Scholar]
- 42.Rathouz M, Trussell L. Characterization of outward currents in neurons of the avian nucleus magnocellularis. J Neurophysiol. 1998;80:2824–2835. doi: 10.1152/jn.1998.80.6.2824. [DOI] [PubMed] [Google Scholar]
- 43.Svirskis G, Kotak V, Sanes DH, Rinzel J. Sodium along with low-threshold potassium currents enhance coincidence detection of subthreshold noisy signals in MSO neurons. J Neurophysiol. 2004;91:2465–2473. doi: 10.1152/jn.00717.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.McGinley MJ, Oertel D. Rate thresholds determine the precision of temporal integration in principal cells of the ventral cochlear nucleus. Hear Res. 2006;216–217:52–63. doi: 10.1016/j.heares.2006.02.006. [DOI] [PubMed] [Google Scholar]
- 45.Jeffress LA. A place theory of sound localization. J Comp Physiol Psychol. 1948;41:35–39. doi: 10.1037/h0061495. [DOI] [PubMed] [Google Scholar]
- 46.Brand A, Behrend O, Marquardt T, McAlpine D, Grothe B. Precise inhibition is essential for microsecond interaural time difference coding. Nature. 2002;417:543–547. doi: 10.1038/417543a. [DOI] [PubMed] [Google Scholar]
- 47.McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nat Neurosci. 2001;4:396–401. doi: 10.1038/86049. [DOI] [PubMed] [Google Scholar]
- 48.Willms AR. NEUROFIT: software for fitting Hodgkin-Huxley models to voltage-clamp data. J Neurosci Methods. 2002;121:139–150. doi: 10.1016/s0165-0270(02)00227-3. [DOI] [PubMed] [Google Scholar]
- 49.Koch C, Segev I. Methods in Neuronal Modeling: From Ions to Networks. MIT Press; 1998. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.