Large-scale motions in the adenylate kinase solution ensemble: coarse-grained simulations and comparison with solution X-ray scattering

Abstract

While coarse-grained (CG) simulations provide an efficient approach to identify small- and large-scale motions important to protein conformational transitions, coupling with appropriate experimental validation is essential. Here, by comparing small-angle X-ray scattering (SAXS) predictions from CG simulation ensembles of adenylate kinase (AK) with a range of energetic parameters, we demonstrate that AK is flexible in solution in the absence of ligand and that a small population of the closed form exists without ligand. In addition, by analyzing variation of scattering patterns within CG simulation ensembles, we reveal that rigid-body motion of the LID domain corresponds to a dominant scattering feature. Thus, we have developed a novel approach for three-dimensional structural interpretation of SAXS data. Finally, we demonstrate that the agreement between predicted and experimental SAXS can be improved by increasing the simulation temperature or by computationally mutating selected residues to glycine, both of which perturb LID rigid-body flexibility.

Introduction

Many recent works have provided evidence that not just the average structure, but also motions or “dynamics” around this structure, are important to protein functions including catalytic rate control [1-4], macromolecular recognition [5], and/or allosteric regulation [6-9]. For therapeutic and engineering applications, it is important to understand physical allosteric mechanisms in specific proteins [10]. Recent studies have been building evidence to support the hypothesis that evolution has selected well-defined motions in allosteric proteins. For example, motions in apo-proteins tend to parallel closure pathways associated with ligand binding [11-13]. In many cases the bound conformation has a substantial minority population in the absence of ligand [5, 14], though this “population shift” behavior does not necessarily indicate that the conformational transition precedes ligand binding in the presence of ligand [15-17]. For simulation of conformational transitions, coarse-grained (CG) models provide a useful first approximation for capturing gross motional features, possibly because such features are primarily determined by structural topology [18-20]. They are also a useful approach to simulate large-scale conformational transitions without constraints so that many different reaction coordinates can be simultaneously assessed [16, 21]. However, due to the approximations inherent in CG simulations, it is important to validate these models with experiments. While detailed testing requires high-resolution experiments like NMR HSQC [22] and relaxation [23], hydrogen exchange [24], these methods can be less sensitive to large-scale global motions. Thus, techniques that provide even low-resolution validation of these motions are important adjuncts.

For example, small-angle X-ray scattering (SAXS) provides a useful approach to assess the flexibility (motional amplitude) of rigid bodies in different allosteric states. Specifically, since SAXS is the Fourier transform of the interatomic distance distribution, scattering can be predicted from structural coordinates using the Debye formula [25, 26] and compared to the experiment. While calculating average scattering from ensembles of full-atom structures [25, 26] is prohibitively costly, scattering can be estimated accurately at low angles from large ensembles of coarse-grained structures through the use of effective residue structure factors [27]. Specifically, the Debye formula is applied to the atoms within residues and averaged over different conformations from known crystal structures. With this approximation, hundreds of C_α-scale conformations can be analyzed per hour on an 8-core AMD computer.

Although SAXS does not provide three-dimensional structural information due to orientational averaging, simulations can be used to refine the structural interpretation of SAXS data. Here, we show that while experimental SAXS curves can guide optimization of simulation conditions to approximate a given solution ensemble, these curves can be structurally interpreted with more detail by calculating correlations between predicted scattering and various structural properties over a large ensemble of structures.

Here, we apply this approach to the allosteric-like protein adenylate kinase (AK), which recycles AMP to ADP by phosphorylating it with ATP. Crystal structures of apo and bound AK show that upon substrate binding, two small domains (LID and NMP) close over the larger CORE domain. The substrates ATP and AMP bind at the CORE-LID and CORE-NMP interfaces, respectively, and the two predominant states are open (O) and closed (C) [28]. NMR experiments have shown that the thermophilic adenylate kinase from Aquifex aeolicus (AKthermo) exhibits an opening rate six-times-slower than that of E. coli AK (AKmeso), thereby limiting the catalytic turnover rate at room temperature [3]. This conformational gating of a chemical reaction is analogous to allostery.

Recently, we have performed CG conformational transition (double-well Gō) simulations of AKmeso, AKthermo, and high-temperature and mutational variations of each protein [16, 29]. These simulations showed that LID rigid-body flexibility is higher in AKmeso, and that in AKthermo, such flexibility can be increased to that of AKmeso by mutating some key hinge prolines to glycine [29]. We also found that the glycine mutants increased flexibility of some key hinges and destabilized parts of the contact network (e.g. various interactions involving the CORE-LID connector helices).

Here, we investigate several key questions. First, while X-ray crystallography provides detailed information about selected conformations of AK in the absence and presence of ligand, SAXS data can be used to estimate the extent of Cartesian fluctuations within the solution structural ensemble. To estimate this global flexibility for AKmeso, we compare experimental curves to those calculated from CG simulation ensembles of AKmeso. We show the relation between predicted scattering and varying strengths of interresidue interactions, which modulates the global flexibility. Second, to identify possible population shifts, we fit SAXS curves measured in both the absence and the presence of ligand to linear combinations of predicted scattering from the O and C state simulations. Such a population-based approach has previously been demonstrated in prediction of SAXS data through CG simulations of Hck tyrosine kinase [30].

Third, to structurally interpret the scattering data, we calculate the correlation between predicted scattering and various structural metrics over large simulation ensembles as a function of (q = 2π/d), where d is the Bragg spacing. These metrics include CORE-LID and CORE-NMP center of mass distances, which reflect rigid-body motions, and root mean square deviations (rmsds) of the flexible LID and NMP domains to the closed crystal structure, which reflect the compactness of these domains. These correlations can also suggest explanations for how differences in predicted scattering between simulations arise from differences in the structural properties of the simulation ensembles. To expand upon the connection between scattering and global flexibility, we predict scattering from AK simulations at a range of nominal temperatures. Finally, to isolate the effects of individual structural features upon the scattering curve, we perform computational glycine mutations [29] designed to selectively perturb individual features.

Results and Discussion

Simulation and scattering calculation approach

To generate ensembles from which to predict scattering in O and C states, we perform 150-ns single-well Gō simulations based on Karanicolas-Brooks potentials [31, 32]. These potentials include sequence-specific dihedral and contact energies, which compared to “vanilla” Gō potentials enable characterization of important small-scale motions and performing computational mutants. Since we are interested in ground-state O and C properties, rather than the conformational transition mechanism described in our prior AK Gō models [16, 29], we simulate O and C separately rather than unify them into a double-well potential. In addition, as in our previous simulations [16, 29], we simulate ligand binding to the closed state by adding selected ligand-mediated interactions to the C-state contact potentials.

We calibrate the simulated flexibility of AK by varying the contact energy scale (S_con), by which we scale the Karanicolas/Brooks [31, 32] energies to compensate for extra backbone conformational entropy induced by the generic bond angle potential [33]. For our O/C conformational transition simulations, we calibrated S_con to 2.5 so that the C simulation averaged about 2.0 Å C_α rmsd with respect to the closed crystal structure (rms_C) [16] to reproduce prior atomistic simulations of AK [34]. This significantly exceeded the S_con of 1.7 that used in double-well Gō simulations of smaller conformational transitions [33, 35]). This high S_con of 2.5 may best approximate the behavior of AK in vivo, where crowding from other biomolecules reduces the population of expanded structures [36]. However, since SAXS is measured in more dilute solution, we simulated AK with S_con between 1.5 and 2.5 to optimize the computational / experimental fit.

For each Fast-SAXS prediction, we randomly select an ensemble of 1000 structures from the 150-ns simulation. In addition, as described in the methods, we augment Fast-SAXS [27] to include CG ligand atoms for “ligand-bound” structures for which the rmsd of AMP and/or ATP binding sites from the C crystal structure is small. For experimental data, we compare to Bacillus globisporus AK since scattering data is not available for E. coli AK in all relevant states. SAXS patterns from E. coli and B. globisporus AKs correspond closely under conditions where data from both species are available (data not shown). This is not surprising since their two sequences are 51% identical and the closed crystal structures differ by only 1.08 Å rmsd according to the MultiProt structural alignment server [37] (203/214 residues aligned).

Estimating flexibility in solution

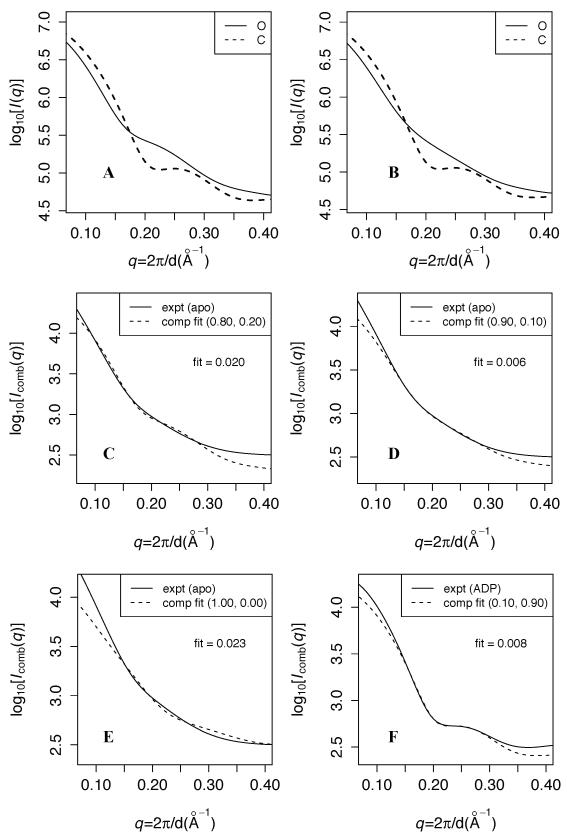
Figure 1A shows that at S_con = 2.5, the C simulation predicts a more curved profile than the O simulation, especially near q ~ 0.22, which is consistent with C being more ordered than O as expected. Figure 1B shows that with S_con = 1.9, the predicted O scattering profile is substantially less inflected near q ~ 0.22 than at S_con = 2.5. Conversely, the predicted C curves are similar for ensembles generated using the two S_con, both exhibiting a small dip near q ~ 0.22.

Figure 1. Experimental vs. predicted SAXS curves at different contact energy scales.

A and B: Predicted scattering at contact energy scales (S_con) of 2.5 and 1.9, respectively. The solid (dashed) line indicates the prediction from the O (C) simulation. For each calculation, predicted scattering (I(q)) is averaged over 1000 randomly selected structures from the corresponding simulation ensemble, and log₁₀[I_avg(q)] is plotted. C, D, and E: fits of log₁₀(I_comb) at S_con = 2.5, 1.9, and 1.5, respectively, to the apo experimental data over 0.14 < q < 0.3. I_comb is the optimal linear combination of predicted O and C scattering to fit the data; the weights (w_O,w_C) are indicated in parentheses. “fit” in each panel indicates the root mean square deviation between experimental and fitted computational data over that q range. F: fit of log₁₀(I_comb) at S_con = 1.9 to the ADP-bound experimental data.

Panels C-E compare fits of predicted scattering from simulation ensembles at different S_con to experimental scattering measured under apo (ligand-free) conditions. Since both apo and liganded conditions may comprise a mixed population of O and C [34, 38], according to the conformational selection hypothesis, we fit to the data varying linear combinations of the predicted open and closed scattering as follows:

$$I_{comb}=w_O{I}_O+w_C{I}_C,$$

where w_O and w_C are the respective weights of predicted scattering intensity from O and C simulations. We fit log₁₀[I_comb] to experiment using linear regression over the range 0.14 < q < 0.3, and the w_O/C with the lowest R² are used to calculate I_comb. As detailed in the methods, we choose this q range because the largest difference in curve shapes between the apo experiment and the S_con = 2.5 simulation occurs in this region. We optimize w_O/C to a precision of 0.05, as detailed in the methods. Since R² values are always 0.99 or above, for clarity, we report the fit (denoted F) as the root mean square deviation between experimental and fitted computational data over this q interval.

Table I and Figure 1D show that the optimal fit over 0.14 < q < 0.3 occurs for S_con = 1.9 with w_O = 90%, and a change of only ± 0.2 in S_con significantly increases F. Figure 1C shows that at S_con = 2.5, the predicted scattering is more strongly inflected at q ~ 0.22 than the experimental data, while at S_con = 1.5 (panel E), the predicted scattering curve is substantially shallower. This provides a measure of the impact of the strength of interresidue interactions on the intrinsic flexibility of the system – and the corresponding sharpness of features in the scattering pattern. We also note that the S_con = 2.5 O simulation produces a slightly better fit at low angles ( q < 0.14) than the S_con = 1.9 O simulation. Panel F shows the fit of I_comb at S_con = 1.9 to experimental data collected in the presence of substrate ADP. A 10% population of O flattens the small dip predicted at q ~ 0.22 (panel B), producing a very small F. This is biochemically consistent with the conformational equilibrium required for catalytic cycling. By contrast to the apo experimental data, Table I shows that a broad range of S_con, especially between 1.7 and 2.1, produces small F to the ADP data, and F ≤ 0.01 is achieved at all S_con.

Table I. fit of scaled computational to experimental data over 0.14 < q < 0.3.

Simulation	wO	fit to apo data	wC	fit to ADP data
wt-1.5	1.00	2.34	1.00	0.53
wt-1.7	1.00	1.04	0.95	0.78
wt-1.9	0.90	0.56	0.90	0.80
wt-2.1	0.90	1.51	0.85	0.74
wt-2.5	0.80	2.04	0.90	0.99
375K	0.90	1.27	0.85	0.73
413K	1.00	0.64	0.90	0.86
450K	1.00	1.43	0.95	0.85
+7G	0.85	0.79	0.85	0.99
+3G	0.90	0.90	0.90	1.12
A8G	0.85	1.14	0.85	0.82
E161G	0.80	2.14	0.85	0.71
V121G	0.85	1.86	0.85	0.75
V148+T149G	0.85	2.23	0.80	0.76

w_O indicates the optimal weight of the O scattering predictions for fitting to the apo data, and w_C indicates the optimal weight of the C scattering predictions for fitting to the ADP data. The fits to apo and ADP are calculated as the root mean square deviation between experimental and fitted computational data over the interval 0.14 < q < 0.30, divided by 0.01 here for simplicity.

Given that any closed structures present in the absence of ligand are by definition unbound, we recalculated I_comb based on the C simulation prediction excluding implicit ligand atoms and refitted this I_comb to the apo data. Figure S1 shows that surprisingly, at both S_con = 2.5 and S_con = 1.9 (panels A and B, respectively), F slightly worsens relative to the original I_comb calculation for which I_C includes ligand. This suggests that closed-like conformations sampled without ligand differ slightly from the bound closed conformation, most likely because without ligand, the bound C conformation would have a large cavity.

Table S1 shows the values of several key structural metrics in these simulations. r_CM,core-lid and r_CM,core-nmp, the average CORE-LID and CORE-NMP center of mass distances, respectively, are measures of rigid-body motions. rms_lid and rms_nmp, the C_α rms deviations of LID and NMP domains relative to the closed crystal structure, are measures of domain unfolding. For O simulations, the ensemble-average r_CM,core-lid and rms_lid are strongly anticorrelated with S_con, whereas ensemble-average r_CM,core-nmp and rms_nmp are considerably less sensitive. For the C simulations, none of these variables is very sensitive to S_con. The optimal S_con = 1.9 corresponds to r_CM,core-lid = 34.4 Å and rms_lid = 3.5 Å in the O simulation. These values are 2.5 Å and 1.9 Å higher, respectively, than the corresponding values for the S_con = 2.5 simulation.

In addition, Figure S2 shows I_comb fits to SAXS data collected in the presence of inhibitor and bisubstrate analog AP₅A, which by bridging the ATP and AMP sites with two extra phosphates should maximize the population of C. I_comb matches this experiment even better than the ADP experiment, especially for q < 0.14; however, a higher w_O (15%) is unexpectedly required. Including additional long-distance ligand-mediated interactions between AMP- and ATP-binding site residues does not reduce the w_O required (data not shown). This suggests that the extra phosphates of AP₅A may either destabilize the closed state (allowing a higher population of an open conformation) or prevent complete closure of the LID and NMP domains.

Beyond q ~ 0.3, I_comb captures the shape of the experimental curve but systematically underestimates the intensity for each experimental condition (data not shown). Previous works have demonstrated a similar q limit to the accuracy of Fast-SAXS [27, 30]. This results in part from is imprecision in CG residue positions (at the C_α) and from limitations in the construction of effective residue scattering factors. Beyond q = 0.3, all-atom models are likely required to produce accurate predictions of scattering. However, the correspondence of shapes in the predicted and observed patterns supports the notion that the conformational distribution from the simulation is meaningfully accurate.

Correlation of scattering curves with structural parameters

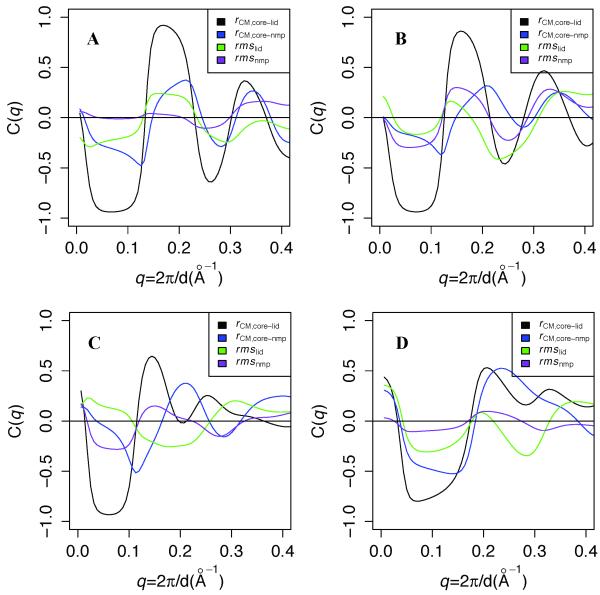
The observation that r_CM,core-lid and rms_lid are the structural properties with the highest sensitivity to S_con (Table S1) suggests that these features are important to determining the shape of the scattering curves. To better quantify the relationship between scattering and the three-dimensional structure, we calculate the correlation between the structural metrics in Table S1 and the scattering patterns. For a given simulation, we calculate the “ensemble correlation” of predicted intensity with a given structural property:

$$C\left(q\right)=\text{corr}({\log }_{10}I(q,s),D\left(s\right)),$$

where C(q) is the ensemble correlation, I(q,s) is the predicted scattering intensity for conformation s from the ensemble at a given q, and D(s) is the value of a given structural metric for conformation s.

Figure 2A shows the results of these calculations. The predicted scattering is strongly correlated with r_CM,core-lid and weakly to r_CM,core-nmp up to q ~ 0.35 in the O simulation at S_con = 2.5. At S_con = 1.9 (panel B), the anticorrelation to r_CM,core-lid at q ~ 0.25 weakens slightly, but anticorrelation with rms_lid correspondingly increases. Reducing S_con to 1.5 (panel C) significantly reduces the correlation to r_CM,core-lid for 0.12 < q < 0.22 and eliminates it beyond 0.22. Panel D shows that for the C simulation at S_con = 1.9, predicted scattering is moderately correlated with both r_CM,core-lid and r_CM,core-nmp up to q ~ 0.25. rms_nmp is not significantly correlated with predicted scattering in any simulation ensemble. Finally, while all the correlations should converge to 0 at q = 0, where scattering depends only on the number of electrons in the system, small deviations from this condition in all panels likely result from differences in the number of explicit waters added to each ensemble structure by Fast-SAXS [27].

Figure 2. Ensemble correlation of scattering with various Cartesian structural metrics.

A, B, and C plot ensemble correlation C(q) between predicted scattering and several structural metrics in O simulations at S_con = 2.5, 1.9, and 1.5, respectively, and panel D shows C(q) for the C simulation at S_con = 1.9. r_CM,core-lid and r_CM,core-nmp denote center of mass distances between the CORE domain and the LID and NMP domains, respectively, and rms_lid and rms_nmp denote the C_α root mean square deviations of LID and NMP, respectively, to the closed crystal structure. C(q) is calculated for each Cartesian metric for each simulation as described in the results.

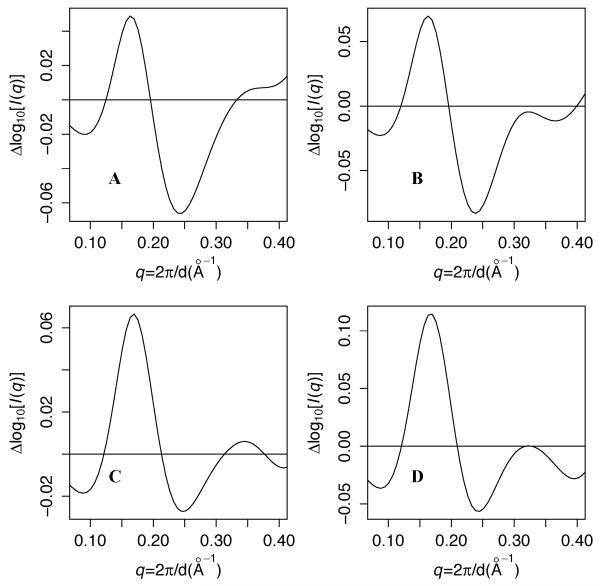
These correlation curves suggest an interpretation of the differences in predicted scattering between the simulations at S_con = 2.5 and S_con = 1.9. Figure 3A shows that relative to the simulation at S_con = 2.5, the simulation at S_con = 1.9 predicts higher scattering intensity between 0.12 < q < 0.20 and lower intensity for 0.20 < q < 0.32. These differences are qualitatively consistent with the higher r_CM,core-lid at S_con = 1.9, coupled with the positive correlation between scattering and r_CM,core-lid for 0.12 < q < 0.22 and with the anticorrelation with r_CM,core-lid for 0.12 < q < 0.22 (and for the S_con = 1.9 simulation, also with rms_lid). In other words, these results suggest that under apo conditions, most of the differences in scattering among the simulations arise from differences in LID rigid-body flexibility.

Figure 3. Differences in predicted scattering vs. the wild type simulation at S_con = 2.5.

A: S_con = 1.9 wild-type simulation. B: wild-type simulation at 413K. C: +7G simulation. D: +3G simulation. All simulations use S_con = 2.5 and T=300K unless otherwise specified.

Temperature variation

To better understand the connection between SAXS and global flexibility, we predict scattering from AK simulations with S_con = 2.5 at a range of temperatures. This test is also important because of the artificial nature of temperature in coarse-grained molecular dynamics. Previously, we showed that increasing the Gō simulation temperature of thermophilic Aquifex aeolicus AK (AKthermo) from 300K to 375K shifts its LID rigid-body flexibility toward that of the more flexible AKmeso [29]. Figure S3A shows that at S_con = 2.5, increasing the AKmeso simulation temperature from 300K to 375K partially dampens the inflection at q ~ 0.22. Panel B shows that at 413K, this inflection disappears, and F is comparable to that predicted from the S_con = 1.9 simulation at 300K. At 450K, the fit worsens (Table I). Interestingly, r_CM,core-lid in the 413K simulation is nearly identical to that obtained in the S_con = 1.9 simulation at 300K (Table S1). Figure 3B shows that heating to 413K alters scattering similarly to decreasing S_con from 2.5 to 1.9. In addition, Figure S4B shows that the 413K simulation produces a similar correlation function for r_CM,core-lid as the O simulation at S_con = 1.9. These observed similarities between the S_con = 1.9 simulation at 300K and the S_con = 2.5 simulation at 413K further strengthen our inference that the apo solution ensemble of AK makes significant excursions from the crystal structure.

Furthermore, the results for these two similar simulations show that agreement with a particular experiment can be highly sensitive to simulation parameters that affect flexibility. For CG simulations, this suggests that the simulations be performed under a variety of (de)stabilizing conditions to compare to a particular experiment. For example, a rigid simulation might best predict functional properties in the crystalline state and/or in vivo where crowding may narrow the conformational equilibrium [36]; a flexible simulation might be more appropriate for predicting a protein’s behavior under dilute conditions such as those under which these SAXS data was measured.

Computational mutations

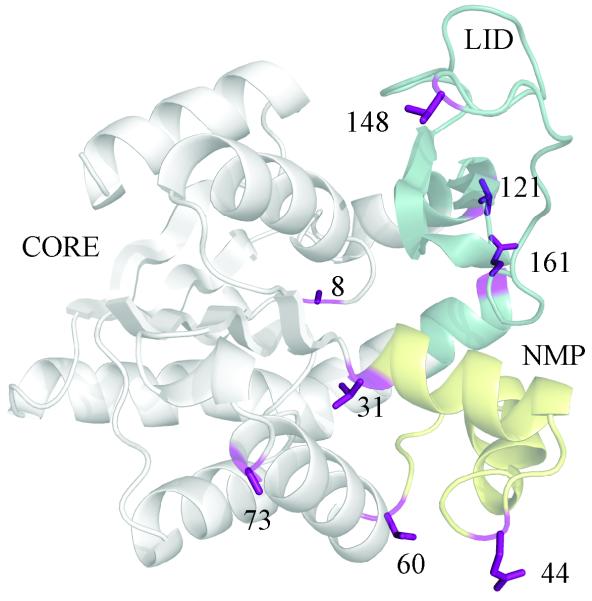
To further assess the importance of structural metrics suggested by Table S1 and Figure 2 to be important to the scattering profile, we perform computational mutations designed to selectively perturb individual features, as described in detail in the methods and our previous work [29]. Figure 4 indicates the locations of the sites that are tested individually and/or in combination. Previously, we showed that computationally mutating key hinge prolines to glycine in thermophilic Aquifex aeolicus AK (the +7G mutant) produces AKmeso-like LID rigid-body flexibility, while mutating the prolines to their AKmeso counterparts causes only mild changes [29]. Surprisingly, the most strongly perturbing mutation characterized was P8G in the CORE. This residue interacts with the CORE-LID connector helices but is ~ 15 Å from the primary CORE-LID hinge residues (122 and 155). The P155G mutant within the hinge had a significantly smaller effect.

Figure 4. Locations of mutant sites tested.

The mutant sites tested are indicated on the closed structure of E. coli AK (1AKE). +7G mutates positions 8,44,60,73,148,149, and 161 to glycine, and +3G mutates positions 8, 121, and 161 to glycine. Position 149 is omitted for clarity.

Table I shows that I_comb for the AKmeso+7G mutant [29] fits the apo experiment better than the wild-type simulation at S_con = 2.5. The +3G mutant, in which we mutate position 8 and both CORE-LID hinge residues (V121 and E161 in AKmeso numbers) to glycine, improves the fit slightly less. Figure S3C shows that +7G fits slightly better at small angles than +3G, but panel D shows that +3G requires a smaller w_C to optimize F. Table I shows that of 5 key positions mutated in +7G and/or +3G, only A8G approaches the F achieved by +3G and +7G, while V121G has a small effect. Figure S4C-D show that surprisingly, the correlation functions for r_CM,core-lid for +7G and +3G O simulations more closely resemble those of the wild-type simulation at S_con = 2.5 than at S_con = 1.9. Figure 3C-D shows that by contrast to the S_con = 1.9 simulation at 300K and the S_con = 2.5 simulation at 413K, the +7G and +3G mutants at S_con = 2.5 improve F more by increasing intensity over 0.12 < q < 0.22 than by decreasing it for 0.22 < q < 0.32. This difference is expected because unlike the S_con = 1.9 and heated simulations, which are expected to globally increase flexibility, these mutant simulations are expected to perturb the ensemble differently by loosening selected degrees of freedom. Table S1 shows that +7G increases the average r_CM,core-lid in the O ensemble by 2.0 Å while increasing rms_lid by a smaller amount than does reducing S_con from 2.5 to 1.9. This, plus the observation that the internal LID glycine mutant (V148G+T149G) produces a similar rms_lid as +7G but does not improve F, further strengthens our hypothesis that r_CM,core-lid is more important than rms_lid for the fit to experiment.

The correspondence between the excellent fit to the apo experiment and an average r_CM,core-lid of about 34 Å that occurs for the S_con = 1.9 O simulation at 300K, the simulation at S_con = 2.5 and T = 413K, and the +7G simulation demonstrates the offsetting effects of increasing interaction strength and temperature. It may also explain why the fit for +3G, which has an r_CM,core-lid of 35.7 Å, is slightly poorer than for these 3 conditions but still better than that at S_con = 1.7. Furthermore, the modest change of r_CM,core-lid caused by A8G alone appears to correspond with its modest improvement of F, while the E161G and V121G mutants had little or no effect upon either the fit or the ensemble-average r_CM,core-lid.

The picture presented by the +7G, +3G, and A8G simulations is consistent not only with the experimental apo curve, but also with the small w_C predicted under apo conditions by the population shift hypothesis [5, 14] and observed by single-molecule FRET experiments [38]. Thus, it is plausible that the experimental apo scattering data reflects a protein with well-folded domains but high-amplitude rigid-body motions.

Conclusions

By comparing SAXS data with predictions from coarse-grained simulation ensembles of AK with varying energy scales for interresidue interactions, we demonstrate that AK is flexible in solution in the absence of ligand. Incorporating a small population of the closed form into SAXS predictions in the absence of ligand improves the fit to the apo experiments, which supports the population shift hypothesis. Similar linear combination fits to substrate- and inhibitor-bound experimental curves support the presence of a small population of O with ligand present. In addition, the ensemble correlations between predicted scattering and various structural metrics as a function of q argue that LID rigid-body motional amplitude contributes strongly to the shape of the scattering curves. Conformational fluctuations within LID and/or NMP may be below the resolution limit of this coarse-grained approach. Furthermore, at a high contact energy scale, increasing the simulation temperature to 413K, which perturbs flexibility throughout the protein, improves the fit to the unbound experimental data. Computationally mutating key hinge and/or loop residues to glycine, which selectively enhances LID rigid-body motions, similarly improves the unbound fit. The similar effects of these two contrasting perturbations upon predicted scattering further support the distinct importance of LID rigid-body motions for explaining the observed scattering. Finally, our results show that combining SAXS and CG simulations provides a unique approach to defining the structural ensemble of a protein under a variety of experimental conditions. This strengthens SAXS as a probe not only the global flexibility but also specific degrees of freedom that may have high biological importance.

Supplementary Material

02

Figure S1: Effect of including apo-C in the fit to apo experiment A and B: fits of log₁₀(I_comb) at S_con = 2.5 and 1.9, respectively, where I_comb is calculated without CG ligand atoms included in the I_C calculation.

03

Figure S2: Observed with inhibitor and predicted scattering A and B indicate fits of predicted scattering from simulations with S_con of 2.5 and 1.9, respectively, to SAXS data collected in the presence of inhibitor and bisubstrate analog AP₅A.

04

Figure S3: Experimental and predicted SAXS curves for thermal perturbations and mutants A and B: Linear combination fits of O and C simulations at 375K and 413K, respectively, to the apo experimental data over 0.14 < q < 0.3. C and D: corresponding fits for the +7G and +3G O simulations, respectively, at 300K. All these simulations use S_con = 2.5.

05

Figure S4: Correlation of scattering with various Cartesian metrics for thermal perturbations and mutants Panels A-D correspond to the simulations shown in Figure S3. Ensemble correlations are calculated as for Figure 2.

06

Figure S5: Computed CG scattering factors for adenosine, ribose rings and phosphates of ATP and AMP Adenosine is indicated by ado_ATP/AMP, ribose rings by rib_ATP/AMP, and phosphates by P_α-γ and P_ε

07

Figure S6: Predicted scattering for the bound crystal structure (1AKE) without (black) and with (blue) ligand included in the calculation

08

Figure S7: Differences in predicted scattering between O and C simulations A: S_con = 2.5; B: S_con = 1.9.

Highlights.

• We compared predicted scattering from coarse-grained adenylate kinase simulations to experiments

• A flexible simulation fits the unliganded experiment best

• Both with and without substrates, a small population of the alternate state improves the computational / experimental fit

• The scattering curves are highly dependent on rigid-body motions of the mobile LID domain

• Computational perturbations of temperature and the sequence improve the fit to experiment

APPENDIX

Methods

Simulations

Simulations are carried out with the molecular dynamics program CHARMM [39, 40] for 10 million 1.5-fs time steps for a total of 150 ns apiece. For sampling ground-state (O and C) conformational ensembles, this time length is adequate even though a longer length of 750 ns was required to collect a statistically adequate number of transitions in double-well models [16].

As described in our previous work [29], computational mutants were performed in PyMOL and a short local minimization of residues near the mutant sites was performed with GROMACS 4.5 [41] before building new double-well Gō potentials [31, 32] with the new sequence.

SAXS data

All data were collected at the BioCAT undulator beamline (18ID) [42] at the Advanced Photon Source using methods described in detail previously [43]. Data were collected at AK concentrations of both 11 and 22 mg/mL; here we fit the computations to the 22 mg/mL data since this produces a closer fit than the 11 mg/mL data, possibly due do an increase in the folded population by crowding and/or self-chaperoning.

Augmented Fast-SAXS

To apply Fast-SAXS [27] to a ligand-binding protein such as AK, it is important to calculate coarse-grained (CG) structure factors for the ligand, especially in this case where the ligands contain strongly scattering phosphorus atoms. To avoid the problem of conformational averaging for AK’s ligands ATP and AMP, we calculate these structure factors for approximately rigid subgroups (adenosine, ribose, and each phosphate). We ignore bridging phosphates to reflect the scattering contributions of the natural substrates.

First, we derived atomic scattering factors for phosphorus with Cromer-Mann coefficients [44] and corrected for excluded solvent volume as in equation 3 of Yang et al. [27]. For the rigid subgroups, we calculated CG scattering factors according to equation 5 of Yang et al. [27] (Figure S5). For comparison, F_CG at q = 0 is typically ~ 10 for small and/or hydrophobic residues and ~23 for large polar residues like arginine and histidine [27]; thus, the substantial scattering contribution of phosphates (P_α-γ, P_ε) is expected. We initially tested this algorithm on the closed crystal structure (Figure S6). This shows that ligand substantially alters predicted scattering in the range of 0.14 < q < 0.3. Given the absence of a dip in the ADP-bound experimental curve at q ~ 0.22 (Figure 1F), the ligand addition substantially improves the fit.

Predicting scattering from simulation structures is more challenging because unlike the protein residues, ligand residues are represented implicitly by ligand-mediated interactions. To approximate explicit CG ligand coordinates for calculating scattering, we first identify “ligand-bound” structures for which the rmsd of AMP and/or ATP binding site residues from the closed crystal structure is small. We use rmsd cutoffs of 1.3 Å for the AMP binding site and 1.75 Å for the larger ATP binding site. We treat AMP and ATP binding sites separately. We then add CG ligand atoms to these bound structures by transforming the ligand coordinates from the crystal structure into the reference frame of the binding-site residues from the simulation structure.

Computational / experimental comparison

Figure S7 shows that at S_con values of both 2.5 and 1.9, the magnitude of difference between O and C simulations is maximal at q ~ 0.12 and q ~ 0.22, and crosses or approaches zero at q ~ 0.18 and q ~ 0.30. Based on high sensitivity of predicted scattering to S_con in this q region (Figure 1), we choose 0.14 < q < 0.3 as the range of q for which to fit simulation to experiment. For reference, we also fitted the simulations at different S_con to experiment over the broader range 0.10 < q < 0.3. While the relationship between in F and S_con is the same, the sensitivity to S_con is reduced, especially in thermally perturbed simulations. This suggests that the optimal linear regression fit is not constant with q and that thus, fits over smaller q ranges are more informative about the conformational dynamics.