The high spontaneous mutation rate: Is it a health risk?

Abstract

The human mutation rate for base substitutions is much higher in males than in females and increases with paternal age. This effect is mainly, if not entirely, due to the large number of cell divisions in the male germ line. The mutation-rate increase is considerably greater than expected if the mutation rate were simply proportional to the number of cell divisions. In contrast, those mutations that are small deletions or rearrangements do not show the paternal age effect. The observed increase with the age of the father in the incidence of children with different dominant mutations is variable, presumably the result of different mixtures of base substitutions and deletions. In Drosophila, the rate of mutations causing minor deleterious effects is estimated to be about one new mutation per zygote. Because of a larger number of genes and a much larger amount of DNA, the human rate is presumably higher. Recently, the Drosophila data have been reanalyzed and the mutation-rate estimate questioned, but I believe that the totality of evidence supports the original conclusion. The most reasonable way in which a species can cope with a high mutation rate is by quasi-truncation selection, whereby a number of mutant genes are eliminated by one “genetic death.”

My topic is mutation. Mutation is the ultimate source of variability on which natural selection acts; for neutral changes it is the driving force. Without mutation, evolution would be impossible. My concern, however, is not with mutation as a cause of evolution, but rather as a factor in current and future human welfare. Since most mutations, if they have any effect at all, are harmful, the overall impact of the mutation process must be deleterious. And it is this deleterious effect that I want to discuss.

The ideas that I am presenting are not new. Some go back to early in the century, but the evidence has been strengthened in recent times. In this review, I shall draw on the work of many who have contributed to this history.

This lecture is dedicated to three heroes. The first is Wilhelm Weinberg, a busy German physician and obstetrician—42 years of practice and more than 3,500 births—who somehow found time to invent all manner of clever tricks for studying heredity in that recalcitrant species, Homo sapiens. He was the first to suggest that the mutation rate might be a function of paternal age (1). The second hero is J. B. S. Haldane, an eccentric polymath with an enormous number and an incredible diversity of accomplishments. He was one of the first to measure a human mutation rate and was the first to notice a sex difference in the rate (2). The third is H. J. Muller, who made mutation an experimental subject by devising an objective way of measuring it and showing that ionizing radiation is mutagenic. In the later years of his life, Muller spent much of his energy, physical and emotional, in a crusade against unnecessary human exposure to radiation. Interestingly, he gave little attention to what is surely much more important, chemical mutagens. The main reason is that when he was still active there were no known mutagens that were not highly toxic; mustard gas is an example. Had he known of relatively harmless compounds that are highly mutagenic, he would surely have extended his crusade to environmental chemicals. Curiously, although Muller emphasized the high rate of spontaneous mutation, he did not include it in his crusade, mainly, I think, because he saw no feasible way to reduce it (3).

The Nature of Mutations

It is convenient to divide mutations into three main groups: (i) gain or loss of one or more chromosomes; (ii) rearrangement, gain, or loss of parts of chromosomes as a result of chromosome breakage; (iii) changes in individual genes or small regions of DNA. The first two are customarily called chromosome mutations, the third, gene mutations. Of course the categories overlap, and there are other kinds of changes that I have omitted. My concern today is with the third group, gene mutation. The mutational change can be, and often is, an individual nucleotide substitution. It may also be the gain, loss, or rearrangement of a group of nucleotides within or close to a gene. Classical genetics could not distinguish among these, but molecular techniques can, and, as I shall show later, the distinction is important.

The most important properties of gene mutations, for the purposes of this talk, are: First, to repeat, if they have an observable effect they are almost always harmful. Second, most of the changes are not in the genes, but in the great bulk of so-called “junk” DNA, most of which has no known function. Many of these changes are effectively neutral. Third, most mutations have very minor effects, if any. We usually think of a mutation as an eye color change, a conspicuous disease, or some other phenotypic change that is sharp and striking, and indeed these are the kinds of mutations that have been most useful for classical genetic analysis. But diverse experiments in various species, especially Drosophila, show that the typical mutation is very mild. It usually has no overt effect, but shows up as a small decrease in viability or fertility, usually detected only statistically. Fourth, that the effect may be minor does not mean that it is unimportant. A dominant mutation producing a very large effect, perhaps lethal, affects only a small number of individuals before it is eliminated from the population by death or failure to reproduce. If it has a mild effect, it persists longer and affects a correspondingly greater number. So, because they are more numerous, mild mutations in the long run can have as great an effect on fitness as drastic ones.

Mutation Rates in Males and Females

The first evidence for a sex difference in mutation rates came from Haldane, who studied the severe X-linked bleeding disease, hemophilia (2). A male with the disease gets the mutant gene from his mother. This can happen in two ways: (i) the mother carries the mutant gene on one of her X chromosomes, but because the gene is recessive she is normal, or (ii) the mutation occurs in a germ cell of the mother. Haldane showed that if the mutation rate is the same in both sexes, two-thirds of affected sons come from heterozygous (carrier) mothers. He discovered that almost all of the affected sons had carrier mothers, so the mutation must have occurred in an earlier generation. Thus, most mutations must occur in males, such as the maternal grandfather. Haldane’s analysis was very clever, but not fully convincing, partly because of the elaborate calculations required and partly because identification of carrier women through an increased clotting time was sometimes ambiguous (4). Nevertheless, his conclusion was correct and subsequent work has supported it (5).

Another severe X-chromosomal disease, Lesch–Nyhan syndrome, is a severe defect in purine metabolism. It, like hemophilia, has a much higher male than female mutation rate (6). In contrast, another tragic X-linked disease, Duchenne-type muscular dystrophy, does not have a striking sex difference in mutation rate (5). I shall return to a discussion of why this gene should differ from the other two.

In classical genetics, there was no way to determine whether a mutation occurred in the mother or the father, except for X-linked genes. Molecular biology has changed this, and the results are dramatic. In a study of multiple endocrine neoplasia Type B (MEN2B), the investigators were able to determine the parent of origin in 25 de novo cases (7). All 25 of the mutations occurred in the father. A study of multiple endocrine neoplasia Type A (MEN2A) revealed 10 new cases, again all of paternal origin (8). A still more extreme example is Apert syndrome (achrocephalosyndactyly). Fifty-seven new mutations were identified, and again all were paternal (9). This is a total of 92 new mutations, all paternal. So it looks as if, for some classes of mutations, almost all occur in the male.

A much higher male than female mutation rate offers a ready explanation for the near-absence of affected males for severe (lethal or sterilizing) dominant X-linked disorders. This is precisely what is expected with a high male mutation rate (10). Since affected males would come almost entirely from heterozygous mothers, and such females do not reproduce, none or very few affected sons are expected. This seems a more attractive hypothesis than the ad hoc explanation usually invoked, prenatal lethality of all affected males, which seems unlikely for all 13 such diseases.

Classical hemophilia provides another example, but with a different mechanism (11). Almost one-half of the cases are caused by an X chromosome inversion. For some reason, the inversions happen entirely in males, or almost so. It is possible that, in the absence of a pairing partner in male meiosis, the X chromosome loops on itself to produce an inversion. Whether this is an isolated instance or an example of a more general mechanism remains to be seen.

There is additional evidence from a surprising source, molecular evolution. We know that the rate of evolution of a neutral allele is simply its mutation rate (12). The Y chromosome is found exclusively in males, whereas the autosomes occur equally in both sexes. Therefore, if almost all mutations occur in males the rate of evolution of a neutral locus on the Y chromosome should be about twice as high as that of an autosomal locus. A comparison in human ancestry of a pseudogene (argininosuccinate synthetase), with one copy on the Y chromosome and another on chromosome 7, showed that evolution in the Y chromosome was 2.2 times as fast (13). There are numerous uncertainties in such a study, but it adds support to the high male mutation rate hypothesis. A more extensive study of evolution in introns showed that in the higher primates, including humans, the estimated male/female ratio is 5.06, with 95% confidence limits 3.24 and 8.79 (14).

Paternal Age Effect

How can we account for a higher mutation rate in males than in females? The most obvious explanation lies in the much greater number of cell divisions in the male germ line than in the female germ line. In the female the germ cell divisions stop by the time of birth and meiosis is completed only when an egg matures. In the male, cell divisions are continuous and many divisions have occurred before a sperm is produced. If mutation is associated with cell division, as if mutations were replication errors, we should expect a much higher mutation rate in males than in females.

This makes the strong prediction that the mutation rate should increase with the age of the father, since the older the man, the more cell divisions have occurred. On the other hand, there should be no age effect in females.

Let me interject at this point that there is a well-known maternal age effect for traits that are caused by errors in chromosome transmission. The kind of accident that leads to a child with an extra chromosome is strongly associated with the mother’s age (15). There may be a slight paternal age effect, but the far more striking effect is maternal. My concern, however, is with gene mutations which, when those with small effects are considered, are much more frequent.

I mentioned earlier Weinberg’s suggestion that mutations should be associated with paternal age (1). He was unable to test the idea, and it lay dormant for many years. It is now, however, well established that a number of human inherited traits are associated with the father’s age at the time of birth (or conception) of the affected child.

The procedure consisted of identifying children with dominantly inherited diseases whose parents were normal. Then, having ascertained such trios, the age of the parents was determined. In the classical literature (4), four conditions showed such an effect: achondroplasia, Apert syndrome, myositis ossificans, and Marfan syndrome. The average age of fathers at the time of birth of an affected child was 6.1 years greater than that of fathers of normal children in the same population. There was also a smaller maternal age increase, 3.8 years, mainly, if not entirely, because of the correlation of ages of husbands and wives. Maternal age and birth order showed no significant effect independent of paternal age (16).

Another test of the hypothesis is to examine the age of maternal grandfathers of males with severe X-chromosomal diseases. The fathers of five daughters heterozygous for Lesch–Nyhan disease, whose mothers were normal homozygotes, were about 7 years older than the population average; the standard error is of course very large (6).

Recently, a paternal age effect for heart defects has been reported (17). Pooling ventricular and atrial septal defects with patent ductus, the investigators found a small but significant increase in the fathers’ ages. This was a case-controlled study, with smoking controlled and maternal age regressed out. About 5% of the incidence over age 35 is attributable to father’s age. This suggests that a small fraction of these congenital defects is due to dominant mutations. It also suggests a strategy: examine families in which the fathers of affected children are unusually old. A linkage and molecular analysis might lead to the discovery of a gene predisposing to heart defects.

A study of birth and death records of European royal families suggests that daughters of old fathers have a slightly shortened life span (18). This is consistent with mutations on the X chromosome playing a small, but significant role in longevity. If confirmed, this will add to the evidence that mutation is one factor in aging.

Huntington disease is caused by an excess number of CAG repeats. The larger the number of repeats, the earlier the onset. Paternally derived cases have a larger increase over the parent value than maternally derived cases (19). The discrepancy may be the consequence of the greater number of cell divisions in the male germ line. Demonstrating a paternal age effect is complicated by the limitation of reproduction at older ages because of the severity of the disease.

Nonlinearity of the Paternal Age Effect

Let us now examine the number of cell divisions ancestral to a sperm produced by a father of a specified age. The necessary data are summarized by Vogel and Rathenberg (4). In the female, the number of divisions from zygote to egg is estimated to be 24. The male is more complicated. Until the age of puberty, X_p, taken to be 13 years (X_p = 13), there are 36 divisions (N_p = 36). Afterward, there are 23 divisions per year (ΔN = 23). Thus, the number of cell divisions prior to sperm production in a man of age X is

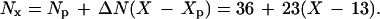At age 20 the number of cell divisions is about 200, at age 30 it is 430, and at age 45, 770.

We can use these numbers to estimate the average increase in paternal age associated with an affected child, assuming that the number of mutations is proportional to the number of cell divisions. The calculations depend on the variance of fathers’ ages, which is about 50, and lead to an expected increase of 2.7 years (20, 21). Although there are uncertainties, they are not sufficient to account for the great discrepancy between the expected paternal age increase, 2.7 years, and that observed, about 6 years. Clearly, the hypothesis that the number of mutations is proportional to the number of cell divisions is out.

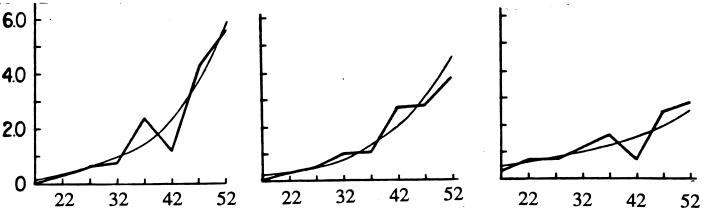
The data are consistent with a power function of age; the best fit involves a cubic term. A somewhat different and more sophisticated analysis by Risch et al. (22) leads to a similar conclusion. The nonlinear effect is apparent for Apert syndrome and achondroplasia in Fig. 1.

Figure 1.

Relative frequency of affected children of normal parents (ordinate) as a function of paternal age (abscissa). (Left) Apert syndrome, n = 111. (Center) Achondroplasia, n = 152. (Right) Neurofibromatosis, n = 243. From ref. 22.

I don’t find this nonlinear effect at all surprising. Everything gets worse with age, so I fully expect fidelity of replication, efficiency of editing, and error correction to deteriorate with age. For a man of age 20, the male mutation rate is about 8 times the female rate. With a linear increase, in a man at age 30, the ratio is 430/24 = 18, at age 45 it is 770/24 = 32. With nonlinearity, these ratios are much larger, some 30-fold at age 30 and as much as two orders of magnitude at age 40. Examples such as MEN2A, MEN2B, and Apert syndrome, in which a total of 92 new mutations were all paternal, are therefore not so surprising. Whatever selective forces reduced the mutation rate in our distant past, at a time when most reproduction must have been very early, were not effective for older males.

I conclude that for a number of diseases the mutation rate increases with age and at a rate much faster than linear. This suggests that the greatest mutational health hazard in the human population at present is fertile old males. If males reproduced shortly after puberty (or the equivalent result were attained by early collection of sperm and cold storage for later use) the mutation rate could be greatly reduced. (I am not advocating this. For one thing, until many more diseases are studied, the generality of the conclusion is not established. Furthermore, one does not lightly suggest such socially disruptive procedures, even if there were a well-established health benefit.)

Why Do Some Mutations Not Show a Paternal Age Effect?

Fig. 1 shows a much reduced paternal age effect for neurofibromatosis. Similarly, X-linked Duchenne muscular dystrophy shows no significant sex difference or grandparental age effect (5). Why should these two diseases be different?

Achondroplasia, which shows a striking paternal age effect (Fig. 1), is mainly, if not entirely, due to a base substitution. In 16 cases examined (23), all of the mutations were changes from glycine to arginine at a specific site; 15 were GGG ⇒ AGG transitions, the other was GGG ⇒ CGG. These all involve a CpG dinucleotide. Presumably, mutations occur elsewhere in the gene but do not produce the phenotype. Similarly, the 57 paternal mutations in Apert syndrome all involved C ⇒ G transversions at two adjacent sites (9).

The genes for Duchenne muscular dystrophy and neurofibromatosis are both enormous, with many introns. One muscular dystrophy study reported that of 198 mutations, 62% were deletions or duplications (24). The 38% point mutations were almost entirely from sperm, whereas the deletions came from both parents; in fact, the data suggest a higher female rate, but the confidence limits are large. The data for neurofibromatosis are similar (25). About two-thirds are deletions and one-third are base substitutions. Again, base substitutions are largely paternal, whereas deletions are more often maternal.

The slight paternal age effect for neurofibromatosis (Fig. 1) is presumably due to a mixture of a minority of base substitutions with a strong paternal age effect and a majority of chromosome mishaps with no such effect.

This immediately suggests a hypothesis: point mutations are somehow associated with the replication process; they show a much higher mutation rate in males and a large increase with paternal age. Mutations due to small chromosomal changes are not specifically associated with replication, at least not correlated to the number of replications. Perhaps they happen at a particular time, such as meiosis; in any case, they do not seem to happen repeatedly during germ cell proliferation.

Of course, there are exceptions. S. S. Sommer (personal communication) has studied extensively the X-linked, hemophilia-like trait, factor IX. Transitions show the expected excess of paternal mutations, whereas deletions show a female excess. Curiously, GC ⇒ AT transitions are more frequent in females and are usually associated with somatic mosaicism. The data suggest an increased maternal age for transversions. The numbers are small, and it will be interesting to see if the finding is confirmed. If so, are there other loci with similar effects or is this an isolated example?

In their extensive and detailed study, Risch et al. (22) classified the syndromes into two groups. The first, with a large paternal age effect, includes acrodysostosis, achondroplasia, Apert syndrome, basal cell nevus, cleidocranial dysostosis, Crouzon syndrome, fibrodysplasia ossificans progressiva, Marfan syndrome, oculodentodigital syndrome, Pfeiffer syndrome, Progeria, and Waardenburg syndrome. The second group, with little age effect, includes multiple exostoses, neurofibromatosis, retinoblastoma, Sotos syndrome, and Treacher–Collins syndrome. Thus, roughly two-thirds of these conditions appear to be strongly cell division dependent and the rest only slightly so. Presumably, these differences reflect different proportions of base substitutions and deletions.

Imprinting and Other Possibilities

Some workers (26, 27) have invoked imprinting to explain the higher male mutation rate. Imprinting is known to be sex dependent, so they suggest that faulty imprinting may be responsible for the high male mutation rate. Imprinting or methylation may “mark” the chromosome in some way, making it more mutable. The detailed mechanism is not clear.

This is a possible hypothesis, but I think there are strong arguments against it as the major explanation of the sex and paternal age effect. One is that the imprinting hypothesis, although it is consistent with a sex effect, does not predict an age effect, whereas the cell division hypothesis does. Furthermore, somatic mutations where imprinting is not involved show a mutation accumulation with age, and therefore with number of cell divisions. Somatic mutations of glycophorin A (the MN blood group locus) increase at a rate of about 3% per year (28). Finally, the imprinting hypothesis would predict a striking sex difference in the mouse, which has imprinting, but does not have the large number of cell divisions characteristic of the human male. Russell and Russell (29) give 7.7 × 10⁻⁶ and 3.2 × 10⁻⁶ for the spontaneous mutation rate per locus in males and females, respectively. These rates are uncertain, particularly the female rate, but it is clear that there is no such large sex difference as is found for most human genes.

For these reasons, I prefer the cell division hypothesis as the major explanation of a high ratio of male-to-female mutation rates and the paternal age effect. Yet this may not be the whole story. There are some unexplained minor discrepancies in the sex ratio, possible irregularities in X inactivation, and perhaps distortion of segregation ratios (26, 27). So we can’t rule out at least some minor effects from causes other than the number of cell divisions.

There is much to be done. One job is to confirm or reject the hypothesis that base substitutions are cell division dependent, whereas small cytogenetic changes are not. Many more diseases should be studied to test the generalizations that I have made from a rather small number. Much of what I have discussed has depended on classical methods, but molecular studies of parent of origin and, presumably soon, direct analyses of spermatozoa should be very revealing. Also, are paternal inversions, such as are reported for some cases of hemophilia, and paternal expansion of repeated elements, as in Huntington disease, major causative factors or only minor players in the larger drama? Finally, what fraction of base substitutions occur at hot spots? Are these more or less related to paternal age than other mutations?

The Total Mutation Rate

The analysis so far has demonstrated the relative importance of sex and paternal age differences in mutation rates, but it says nothing about the absolute values. There is very little information about the human genomic mutation rate. Rates for some genes have been measured, but one cannot be sure as to how representative these are and uncertainty about the number of genes and the importance of extragenic mutations discourages simply multiplying the average rate by the gene number. Furthermore, the mutations of greatest frequency are those with very minor effects, which are difficult to study by any existing methods. So I shall turn to Drosophila for information about the genomic rate.

The Genomic Mutation Rate in Drosophila

Some years ago, H. J. Muller suggested two procedures for greatly increasing the number of mutations detected and, hence, amplifying the power of the test procedure. One was to measure all the mutations on a chromosome rather than individual loci, thus enriching the power by three orders of magnitude. This was accomplished by using special chromosomes with marker genes and crossover suppressors, so that a chromosome could be made homozygous and the effects of recessive mutations brought out. The viability of these homozygotes can be measured by comparison with other genotypes segregating in the same culture. Sometimes the new mutations were lethal, so that this class of flies was missing. Much more often, however, there was simply a small reduction in the numbers of this class, indicating mutations with minor effects on viability.

The second enriching procedure was to sequester a chromosome by keeping it continually heterozygous for many generations. After this time, it could be made homozygous and its viability compared in the same culture with a tester chromosome from a standard laboratory stock. In this way, the total effect of the accumulated recessive mutations could be assessed. The experiments were designed to minimize selection during the accumulation process by using only a single male each generation and growing the flies under optimum conditions of Drosophila husbandry (30).

Yet, the reduction of viability when chromosomes with accumulated mutations are made homozygous doesn’t give the answer we want. The frequency and effect of the mutations are confounded. The decreased viability could be caused by many mutations with very small effects or a smaller number with correspondingly larger effects. To make this distinction, a suggestion by Bateman (31) was employed. This used the fact that as the number of mutations increases the variance from culture to culture increases. This of course means replicating the accumulation lines many times.

The first person with sufficient time, patience, and courage to undertake such an experiment was the late Terumi Mukai in Japan (32). The mutations were mostly very mild in their effects, causing a viability reduction of 2–3%. Some full lethal mutations also occurred, but they were readily detected and much fewer in number. The method of analysis necessarily means that the mutation-rate estimate is a minimum, for the smaller the effect the more likely the mutant is to go undetected. Mukai’s minimum estimate suggested a mutation rate of about one new mutation per zygote, much higher than had been previously thought. I found this result hard to believe and arranged for Mukai to redo the experiments in my laboratory, which he did with three replications (30). One more experiment was done later by Ohnishi (33). For the details of the experiments and statistical analysis, see ref. 30. Each of the three experiments involved millions of flies.

The results are summarized in Table 1. Not surprisingly, since they are based on variances whose estimates are quite unstable, the mutation rate estimates differ widely, from 0.29 to 1.48 per zygote. The rate of mutation for lethals and others with drastic effects is about 0.03, so the number of mildly deleterious mutations is from 10 to 50 times larger. The average mutation frequency per zygote, giving equal weight to each of the three experiments, is 0.65. This is a minimum estimate, since it assumes (quite unrealistically) that the minor viability mutants are equal in effect. If the distribution of viability effects is exponential, the estimate is twice as high (30). This suggests that the average fly carries about one new mutant gene with a minor deleterious effect, and perhaps more.

Table 1.

Minimum mutation rate and average reduction of homozygous viability per mutant in three experiments done at different times

Experiment	m (×103)	V (×105)	Σμ/chrom	s̄	Σμ/zygote
Mukai (1964)	3.80	10.26	0.141	0.027	0.71
Mukai (1972)	3.64	4.47	0.296	0.012	1.48
	4.41	11.67	0.167	0.026	0.84
	4.88	22.87	0.104	0.047	0.53
Ohnishi (1977)	1.72	5.08	0.058	0.030	0.29

For explanation of calculations see ref. 30. The mutation rate per zygote is five times that per (second) chromosome. m, decrease in viability per generation of mutant accumulation; V, variance in viability decrease; Σμ, mutation rate (minimum); s̄, mean viability decrease per mutant (maximum). Σμ/chrom ≥ m²/V; s̄ ≤ V/m. 

For many years these results were either ignored or accepted uncritically, but recently the data have been reanalyzed and subjected to the waves of higher criticism. Keightley (34) has argued that the true mutation rate is much lower than estimated. He suggests two explanations: that the tester chromosomes improved in viability during the experiments and that the sequestered chromosomes contained active transposable elements. My view is that neither explanation is likely to be correct. The tester chromosome was from a long-established laboratory strain and the viability would have had to change in a uniform way during each of three independent experiments. The sequestered chromosome showed no signs of active transposition (e.g., sterility or increased lethal rate). Furthermore, in a later experiment in which transposable elements were known to be active (35), the estimated mutation rate was more than 10 times higher. So I continue to believe that the data reported in Table 1 are essentially correct and will take one mutation per zygote as a typical rate.

The human species has considerably more genes than Drosophila and far more DNA. Mutation rates per generation for individual loci are roughly comparable in man and Drosophila, so it is likely that the genomic mutation rate in humans is considerably higher. Evolution rates for presumed neutral base substitutions, when multiplied by the number of bases in the genome, suggest tens of new mutations per individual; 100 or more has been suggested (36). But how many of these are in nonactive DNA regions and presumably neutral is unknown. I shall assume, for discussion, that the human mutation rate is at least as high as the Drosophila estimates. If, as Keightley argues, it turns out that the estimates are much too high, that will be good news; but I shall stay with the more pessimistic assumption.

Persistence of Mutations in the Population

As mentioned earlier, most mutations—if they have effects large enough to be detected phenotypically—are deleterious. This means that they occur and persist in the population until they are removed by natural selection. The greater the average deleterious effect of the mutation, the shorter time it will persist before being eliminated. A recessive mutation may remain hidden in the population for a very long time, since it can be eliminated only when homozygous. In both flies and people, recessive mutations may persist for thousands of generations. But the evidence is strong that the great majority of mutations are partially dominant, so that heterozygotes show some decrease in fitness. Heterozygotes are far more numerous than homozygotes, in the ratio 2p(1 − p) to p², where p is the (usually very small) frequency of the mutant gene. Therefore, a small amount of selection against heterozygotes is more important from the standpoint of mutant elimination than a large amount of selection in homozygotes.

We can assess the mean number of generations that a mutant gene persists by extracting chromosomes from natural populations and making them homozygous (37). The reduced viability of homozygotes from natural populations should be greater than that from those with one generation of mutation accumulation by a factor equal to the number of generations the average mutant gene persists in the population. When chromosomes from a natural population are made homozygous, using chromosomes with crossover-suppressing inversions and marker genes, the reduced viability per chromosome due to minor viability mutants is about 0.12 (38). Dividing this by the values of m in Table 1 gives ratios ranging from 25 to 70. Thus, the average mutant gene persists in the population for some 25–70 generations.

Other kinds of experiments give persistence values of 33–167 (39) and 50–100 generations (40). For further discussion, I shall assume a value of 80. The value is uncertain, but I emphasize that, despite the uncertainty, the value is much too small to be consistent with complete recessivity of the mutations; the population kinetics of “recessive” mutations is dominated by their effects in heterozygotes because of partial dominance.

Mutations and Population Fitness

Haldane (41) announced a principle that has had an enormous influence in assessing the impact of deleterious mutations on the population. He noted that the mean reduction in fitness from partially dominant mutations at the i-th locus is twice the mutation rate at that locus, 2 μ_i. Assume a mutation rate of 0.5 per gamete or 1.0 per zygote. If the loci act independently, the mean fitness, compared with a mutant-free individual, is the product of (1 − 2 μ_i) over all loci or, approximately e^−2Σμ = e⁻¹ = 0.37. If the mutation rate is twice as high, as seems likely, the mean fitness is reduced to 0.14 of the mutation-free value. Muller (3) made essentially the same point. In his words, each mutation leads ultimately to one “genetic death,” since each mutation can be eliminated only by death or failure to reproduce.

This seems like a large mutation load, even for flies, and would surely be an excessive load for the human population. Furthermore, it is likely that our total mutation rate is greater than that of flies. So, we have a problem.

There is a way out, however. In stating his genetic death principle, Muller (42) stated, “For each mutation, then, a genetic death—except in so far as, by judicious choosing, several mutations may be picked off in the same victim.” Thus, natural selection, acting in a way that seems reasonable for both fly and human populations can indeed pick off several mutations at once.

I might add that such an efficient way of removal of mutations at small cost is strictly a consequence of sexual reproduction. An asexual species must either have a much lower mutation rate or suffer a large number of genetic deaths (43, 44). But, how is elimination of groups of mutations in sexual species accomplished?

Truncation Selection

Animal and plant breeders have long known that the most efficient form of selection is “truncation selection.” As applied to our problem, this implies that all individuals with more than a certain number of mutations are eliminated from the population. This is shown in Fig. 2.

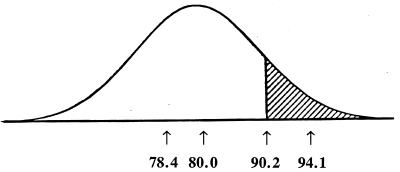
Figure 2.

Truncation selection. All of the individuals to the right of the truncation point (those in the shaded area) are eliminated by pre-reproductive death or failure to reproduce. In this example, 10% are eliminated and 90% contribute to the next generation. From left to right, the numbers along the abscissa are the mean number of mutations per individual in the selected group, in the population before selection, at the truncation point, and in the group eliminated by selection.

Let me illustrate the consequences of truncation selection with a simple numerical example, using what seem to me to be reasonable values. I’ll assume a mutation rate of one per zygote per generation and a mean persistence of 80 generations. Thus, the average fly carries 80 mutations. Assume that the population is truncated so that 10% are selectively eliminated—the 10% with the largest number of mutations. The distribution of random mutations is roughly Poisson. Actually, the variance is a little less than Poisson for the following reason. Each generation of selection reduces the variance, mainly by generating linkage disequilibrium. This is partially, but not completely, restored by recombination and mutation (ref. 45, p. 154).

A Poisson distribution with a mean of 80 is essentially normal, so I shall assume a normal distribution with a standard deviation of 8. The mean number of mutations in individuals in the selected group deviates from the population mean by x = zσ/p, where z is the ordinate at the truncation point, σ is the standard deviation, and p is the proportion saved (ref. 46, p. 192). Thus, the mean number of mutations per individual in the selected group is 80 − (0.1755)(8)/0.9 = 80 − 1.56 = 78.44. Similarly, the mean number per individual in the eliminated group is 80 + 14.1 = 94.1 (Fig. 2). Thus, the individuals that reproduce and are represented in the next generation have 1.56 fewer mutations than the unselected population. This is more than enough to balance one new mutation per generation.

I have used arbitrary numbers, but I believe they are realistic for Drosophila. They illustrate the point that truncation selection of rather small intensity is very effective in eliminating mutations. If the mutant genes act independently, 80 mutations, each causing a fitness reduction of 1/80, would reduce the population fitness to e⁻¹ = 0.37. Thus, 10% elimination by truncation removes more mutations than 63% independent elimination.

Quasi-Truncation Selection

Of course, natural selection in either flies or people does not line up individuals and remove all of those with more than a certain number of mutations. The unreality of this model kept me for many years from considering this as a way in which the population deals with a high mutation rate. Then, thanks to a suggestion from Milkman (47), Kimura and I worked out the consequences of what I shall call “quasi-truncation selection” (48).

Instead of an abrupt cutoff at 10%, consider that the probability of selective elimination increases gradually over a range of numbers of mutations. This turns out to be almost as good. If the range of gradual change is two standard deviations, the process of mutation elimination is about 87% as efficient as sharp truncation (48). I believe that, although strict truncation is totally unrealistic, quasi-truncation selection is reasonable. So if 10% truncation selection reduces the number of mutations by 1.56 per generation, quasi-truncation selection of the same intensity would reduce the number by (0.87)(1.56), or 1.36—still enough to balance one new deleterious mutation per generation.

I conclude that for flies, and very likely for human populations in the past, mildly harmful mutations were balanced by quasi-truncation selection. Since people have more genes and a great deal more DNA than Drosophila, this form of selection seems to me to be the most likely mechanism by which the population could survive and prosper, despite a high mutation rate.

Until recent times, the size of the human population grew at an extremely slow rate. With the population largely density regulated, something like quasi-truncation selection seems likely. There was a high reproduction rate with a death rate such that only about two children per couple survive to reproduce. Despite the largely random nature of accidental and environmental deaths, those individuals with the smallest number of mutations enjoyed a greater chance of being among the survivors and quasi-truncation selection could operate.

The Current Human Population

However efficient natural selection was in eliminating harmful mutations in the past, it is no longer so in much of the world. In the wealthy nations, natural selection for differential mortality is greatly reduced. A newborn infant now has a large probability of surviving past the reproducing years. There are fertility differences, to be sure, but they are clearly not distributed in such a way as to eliminate mutations efficiently. Except for pre-natal mortality, natural selection for effective mutation removal has been greatly reduced.

It seems clear that for the past few centuries harmful mutations have been accumulating. Why don’t we notice this? If we are like Drosophila, the decrease in viability from mutation accumulation is some 1 or 2% per generation. This is more than compensated for by much more rapid environmental improvements, which are keeping well ahead of any decreased efficiency of selection. How long can we keep this up? Perhaps for a long time, but only if there remains a social order that permits steady environmental improvements. If war or famine force our descendants to return to a stone-age life they will have to contend with all the problems that their stone-age ancestors had plus mutations that have accumulated in the meantime.

We have seen that quasi-truncation selection can efficiently remove harmful mutations, and the average fitness reduction can be made quite small. This, plus environmental improvements, means that average survival and fertility are only slightly impaired by mutation. Yet, those 80 mutations in a fly—and whatever the number is in the human species—must surely have deleterious effects that don’t show up in a life table (or as effects on fitness). How many headaches, stomach upsets, depressed periods, and such things that make life less pleasant, but don’t reduce viability or fertility, would be eliminated if our mutation rate had been lower? I suspect the number is substantial.

If the human mutation rate were to drop to zero, we would probably not notice it except for the absence of some of the most loathsome dominant diseases. Loss of variability would not be a problem for a very long time. The genetic variance in the population is enough to satisfy the dreams of even the most wild-eyed eugenist. If we could reduce the mutation rate to zero (without important side effects, of course) I would be for it. If some centuries in the future new mutations are needed, we shall certainly know how to produce them.

I do regard mutation accumulation as a problem. It is something like the population bomb, but it has a much longer fuse. We can expect molecular techniques to increase greatly the chance of early detection of mutations with large effects. But there is less reason for optimism about the ability to deal with the much more numerous mutations with very mild effects. But this is a problem with a long time scale; the characteristic time is some 50–100 generations, which cautions us against advocating any precipitate action. We can take time to learn more.

Meanwhile, we have more immediate problems: global warming, loss of habitat, water depletion, food shortages, war, terrorism, and especially increase of the world population. If we don’t somehow reduce the global birth rate to a sustainable level commensurate with economic viability, we won’t have the luxury of worrying about the mutation problem.