Constrained Mixture Models as Tools for Testing Competing Hypotheses in Arterial Biomechanics: A Brief Survey

Abstract

Hypothesis testing via numerical models has emerged as a powerful tool which permits the verification of theoretical frameworks against canonical experimental and clinical observations. Cleverly designed computational experiments also inspire new methodologies by elucidating important biological processes and restricting parametric spaces. Constrained mixture models of arterial growth and remodeling (G&R) can facilitate the design of computational experiments which can bypass technical limitations in the laboratory, by considering illustrative special cases. The resulting data may then inform the design of focused experimental techniques and the development of improved theories. This work is a survey of computational hypothesis-testing studies, which exploit the unique abilities offered by the constrained mixture theory of arterial G&R. Specifically, we explore the core hypotheses integrated in these models, review their basic mathematical conceptualizations, and recapitulate their most salient and illuminating findings. We then assess how a decade’s worth of constrained mixture models have contributed to a lucid, emerging picture of G&R mechanisms.

1 Introduction

Arteries possess a set of mechanisms by which they accomplish several crucial tasks. They must deliver an unfaltering supply of oxygenated blood to the distal vasculature, not only under conditions of acute changes in metabolic demand, but also during diseased states and under varying degrees of irreversible, aging-related damage to key constituents. This organ system must also ensure that blood, being pumped cyclically by the heart, perfuses the distal beds at a nearly constant flowrate. These requirements must be met with as little energy expenditure as possible. Also, the arterial system must endure on the order of a billion cardiac cycles. Perhaps the most extraordinary aspect of the arterial system is that it meets all of its diverse demands through what appears to be a set of common (though complex and still mostly unelucidated) chemomechanobiological mechanisms, which work complementarily (Humphrey, 2008). It follows that an enhanced understanding of these mechanisms would yield improved insights into a wide variety of arterial behaviors in health and disease. The associated complexities, however, pose several formidable conceptual and methodological challenges.

Hypothesis testing is a widely-appreciated feature of the scientific method, and since the work by Popper (1959), more attention has been given to the importance of formulating hypotheses which may potentially be falsified. Of course, by rejecting the null hypothesis, one may gain additional confidence in the validity of a hypothesis. Numerical experiments, as with experiments in the laboratory, should be designed so as to facilitate the rejection of a hypothesis or null hypothesis. Thus, hypothesis testing is also a useful for verifying increasingly complex computational models of biological systems (Anderson et al., 2007). We therefore seek frameworks which permit the transformation of questions and conjectures into testable hypotheses.

Clearly, there exists great motivation to develop theories of arterial growth and remodeling (G&R). Several frameworks have been proposed for modeling G&R of soft tissues, with applications in cardiovascular mechanics (Kuhl and Holzapfel, 2007; Rachev et al., 1998; Rodriguez et al., 1994; Skalak, 1981; Taber, 1998), but they focus more on the consequences of G&R, rather than the fundamental mechanisms which drive G&R. Humphrey and Rajagopal (2002) introduced a framework based on mixture theory and motivated it, in large part, by the ability to investigate G&R’s governing principles via the testing of competing hypotheses. Humphrey and Rajagopal also posited that such theoretical and computational studies would catalyze the clarification of complex mechanisms and the narrowing of parametric spaces, while simultaneously motivating increasingly sophisticated experimental techniques, thus yielding more detailed and complete empirical observations. Over the course of a decade, this framework has proven useful for elucidating the processes and trends associated with arterial G&R. The resulting numerical experiments predict trends and behaviors which may then be compared to experimental observations.

Other theories of arterial G&R exist and may be used to test various postulated mechanisms which yield expected or observed behaviors. Driessen et al. (2004) demonstrate a computational model and its predictions based on the hypothesis that synthesizing cells align and turnover fibrillar collagen in response to evolving principal stretches. Similarly, Hariton et al. (2007) test the hypothesis that principal stresses govern fiber alignment and compared their predicted results to observed and expected behaviors. These models make different assumptions about tissue homeostasis, and they compute homeostatic fiber alignment distributions accordingly. Watton et al. (2004) also note that their model can be used to test hypotheses concerning fiber alignment. Subsequent works investigate the effects of altering the model’s various assumptions and thereby compare competing hypotheses; for a comprehensive review see Watton et al. (2011). As can be seen, arterial G&R hypothesis testing is by no means limited to any particular theoretical framework. However, we restrict our attention to constrained mixture models to emphasize their particular strengths.

2 Hypotheses in Arterial G&R

Constrained mixture models of arterial growth and remodeling have, in common, three fundamental hypotheses (Valentín and Humphrey, 2009). These hypotheses are important not only individually; their combined, complementary effects are pivotal determinants of the expected behavior of arteries which must adapt in response to events such as injury, disease or evolving metabolic demands. Constrained mixture models put forward these hypothesized mechanisms as means by which arteries preserve or approach optimal behavior under changing conditions.

2.1 Hypothesis I: Constitutive turnover

The first fundamental hypothesis (hypothesis I) relates to the degree and manner of constitutive turnover: that synthesizing cells respond to their evolving chemomechanical environment, in part, by incorporating new material and removing old material from the extracellular matrix and via cell proliferation and apoptosis. From this hypothesis we follow two associated sub-hypotheses. The first (hypothesis I-a) is that synthesizing cells produce new structurally-significant (i.e., load-bearing) proteins at individually varying rates in response to local chemomechanics. Similarly, existing constituents may be degraded as functions of their loading histories over the course of their lifespans. Turnover rates of arterial constituents have been observed to vary in response to changing mechanical and chemical cues (Dooley et al., 2007; Leung et al., 1976; Li et al., 1998; Rizvi and Myers, 1997). In the context of a theoretical hypothesis, Fung (1991) proposed a simple conceptual mathematical relation: that the rate of volumetric growth is a function of a scalar measure of stress,¹ though this concept dates back at least to Thoma (1893). Volumetric changes (i.e., growth or atrophy) are clear consequences of these hypothesized behaviors. However, relative changes in mass fractions of multiple constituents, which alter the artery’s composition and mechanical responses, may more appropriately be categorized as remodeling (Humphrey and Rajagopal, 2002).

A second sub-hypothesis (hypothesis I-b) is that fibrillar proteins, such as collagen and smooth muscle, are deposited in preferred directions and that synthesizing cells have the ability to remodel the extracellular matrix by altering these directions in response to evolving local environmental conditions. Typically, directions of principal stresses or stretches are used to define the directions of fiber alignment. For example, Driessen et al. (2004) and Hariton et al. (2007) posit that synthesizing cells endow favorable biological functions or behaviors by affecting local anisotropy. The same concept can motivate similar hypotheses in arterial G&R models, which may then be tested by comparing predicted responses in evolved arteries.

2.2 Hypothesis II: Depositional prestretches

The second cardinal hypothesis is that newly produced constituents are deposited under a state of prestretch. Mounting evidence suggests that synthesizing cells are not only capable of depositing material in varying quantities and, in the case of fibrillar collagen, different directions, but that they can also endow newly secreted material with a mechanical prestretch (Kozel et al., 2006; Wagenseil and Mecham, 2007). Also implied in this hypothesis are other related phenomena, such as spatial variations in prestretches, for which there are at least two main motivations: a gradient of prestretches for elastin, which is proposed to result from differential deposition and cross-linking over specific temporal intervals during development (Langille, 1996; Stenmark and Mecham, 1997), and the related results of effective prestretches as a result of varying constituent mass fractions (e.g., retraction lengths, opening angles), with each constituent possessing a potentially unique prestretch (Dobrin et al., 1975, 1990; Fung, 1991). This concept is thus closely interwoven with the hypothesis of evolving mass fractions and fiber directions, with interesting complementary effects.

2.3 Hypothesis III: Vasoactivity

The third, and perhaps the most well-studied and appreciated fundamental hypothesis, is that of the central role of smooth muscle contractility. In an application of deductive physiology, Murray (1926) proposed that the body minimizes metabolic costs by maintaining an optimal volume of blood. It was later recognized that his conclusions implied a constancy of luminal shear stress, which arteries actively adjust their caliber to maintain (Rodbard, 1975; Zamir, 1977). Price et al. (1981) identified two distinct mechanisms governing smooth muscle activity. The first mechanism is a consequence of actin-myosin fiber overlap (Guyton and Hall, 1997), which permits smooth muscle to develop peak forces at an optimal length. The second mechanism is a chemical dosage-response; biochemical constrictors and dilators (e.g., endothelin-1, acetylcholine, and others) modulate the active force developed for a given active muscle fiber length. A well-known instance of this phenomenon is the increase in caliber in response to upregulation of the vasodilator nitric oxide by endothelial cells, when subjected to increased flow-induced shear stresses.

Through these mechanisms, active smooth muscle permits arteries to quickly accommodate changes in blood flow – to dilate in response to increased blood flow and to constrict for decreased flows. Smooth muscle achieves its role via a latching mechanism, which minimizes metabolic costs associated with maintaining caliber, yet allows rapid adaptation to altered hemodynamic conditions (Guyton and Hall, 1997). In addition to accommodating temporary changes in blood flow (e.g., a brief interval of elevated physical exertion), smooth muscle will shift its vasoactive response under conditions of sustained hemodynamic changes (Bai et al., 2004), thereby resetting the artery’s caliber.

3 Mathematical Formulation

We now provide a general conceptual overview for how these foundational hypotheses may be cast into mathematical forms. Baek and Humphrey (2010) discuss further details pertaining to computational considerations. For quasi-static conditions, and neglecting body forces, the balance of linear momentum, at any growth and remodeling time s, requires that

$$\text{div }\mathit{\sigma }(s)=\mathbf{0}.$$ (1)

In arterial mechanics, the Cauchy stress tensor is

$$\mathit{\sigma }(s)=\frac{1}{\text{det }\mathbf{F}(s)}\mathbf{F}(s)\frac{\partial W(s)}{\partial \mathbf{F}{(s)}^{\mathrm{T}}}+{\mathit{\sigma }}_{\text{act}}(s),$$ (2)

where F(s) is the deformation gradient tensor, W(s) is the stored-energy function for the entire mixture, and σ_act(s) is a tensor describing the active contribution by smooth muscle, in the current configuration.

For the case of a biological tissue composed of multiple families of constituents, with each constituent, in turn, having multiple generations of continuously-replaced cohorts, Baek et al. (2005) generalized the kinematics of the constrained mixture and introduced notation which permits the tracking of unique natural (stress-free) configurations for each cohort of material. We adopt their notation and define the motions of each cohort to be

$${\mathbf{F}}_{n(\tau )}^k(s)=\mathbf{F}(s){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^k(\tau ),$$ (3)

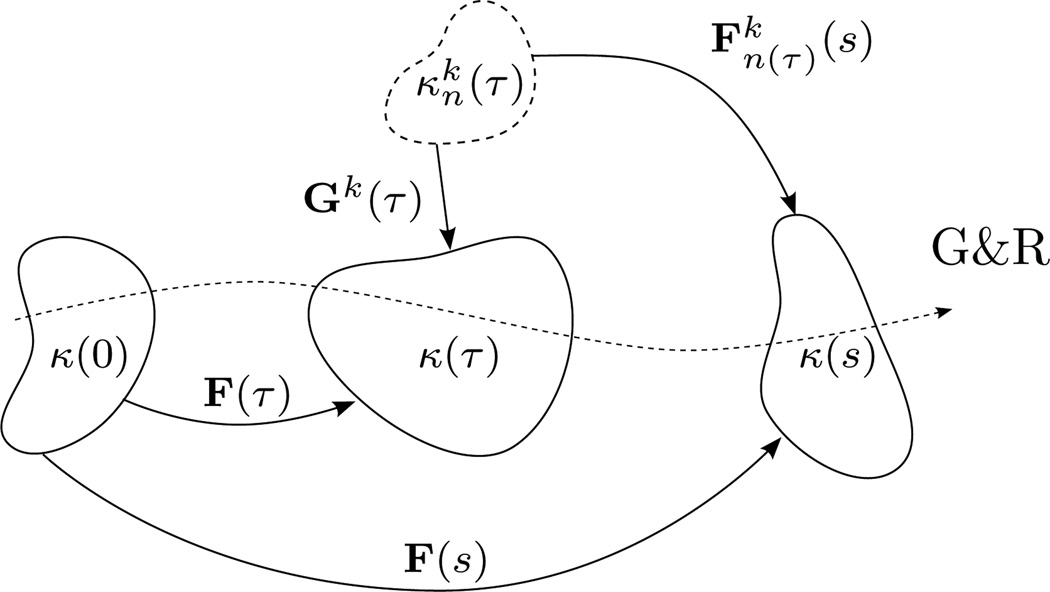
where G^k(τ) is a tensor describing the state of prestretch for the k^th structurally-significant constituent, which is incorporated into the mixture at deposition time τ, and F(τ) and F(s) are deformation gradient tensors describing the motions from the reference configuration at G&R time 0 to the configurations at the time of deposition τ and the current time s, respectively. Figure 1 illustrates these configurations and motions. Equation (3) thus intimately couples the concepts of material being continuously replaced under a state of prestretch (hypotheses I and II). Also stipulated in equation (3) is the condition that all constituents, once incorporated into the mixture, are constrained to move together.

Figure 1.

Schema of G&R in a constrained mixture of multiple prestretched constituents. The k^th newly produced constituent, with natural (unstressed) configuration ${\kappa }_n^k(\tau )$, is incorporated into the in vivo configuration κ(τ) under a state of prestretch G^k(τ) at deposition time τ ∈ [0, s]. Deformation gradients F(τ) and F(s) describe motions from the reference configuration κ(0) (an original and known in vivo state) to κ(τ) and the current in vivo configuration κ(s), respectively.

Having described the kinematics, we may now focus on the evolving mass densities and elastic stored energies, as related to hypothesis I-a. The total mass density (calculated with respect to a reference unit volume) can be written as

$$\rho (s)={\displaystyle \sum _k}\left[{\rho }^k(0)Q^k(s)+{\displaystyle \underset{0}{\overset{s}{\int }}}{m}^k(\tau )q^k(s,\tau )\mathrm{d}\tau \right],$$ (4)

where ρ^k(0) is an original mass density for the k^th constituent, Q^k (s) is the related survival fraction, m^k(τ) is the rate of mass-density production at the time of deposition τ, and q^k(s, τ) is the fraction of material deposited at time τ that survives to the current time s. Equation (4) can then be used to generalize the rule-of-mixtures and derive the total elastic stored-energy function

$$W(s)={\displaystyle \sum _k}\left[\frac{{\rho }^k(0)}{\rho (s)}{Q}^k(s){Ŵ}^k\left({\mathbf{F}}_{n(0)}^k(s)\right)+{\displaystyle \underset{0}{\overset{s}{\int }}}\frac{m^k(\tau )}{\rho (s)}{q}^k(s,\tau ){Ŵ}^k\left({\mathbf{F}}_{n(\tau )}^k(s)\right)\mathrm{d}\tau \right],$$ (5)

where Ŵ^k (·) is the deformation-dependent stored-energy contribution for a specific cohort of family k, which can be of any appropriate functional form.

Physiologically motivated relations for the kinetics of mass turnover may be conceptualized as

$$m^k(\tau )=m_0^k{f}_{\text{prod}}(\mathrm{\Delta }\sigma (\tau ),\mathrm{\Delta }C(\tau )),$$ (6)

where $m_0^k$ is a basal rate of mass-density production, which recovers tissue maintenance under homeostatic conditions, and f_prod(·) is a function of local chemomechanical conditions (changes in stress Δ σ(τ) and biochemical stimuli Δ C(τ)) with the restriction f_prod (Δ σ(τ) = 0,Δ C(τ) = 0) ≡ 1. Further restrictions, such as direct proportionality to both arguments, may be imposed to test various hypotheses regarding mechanobiological responses of synthesizing cells. The survival fractions Q^k(s) and q^k(s, τ) may also take different forms as functions of time or more complex functions of loading histories. The only constraints on the survival fractions are that they be either constant or monotonically decreasing in time, with Q^k(s), q^k(s, τ) ∈ [0, 1].

Recalling hypothesis I-b, we may define the direction of alignment of a newly-deposited fiber, in general, as a vector-valued function

$${\mathbf{m}}^k(\tau )=𝔣(\mathbf{A}(\tau )),$$ (7)

where A(τ) is a second-order tensor related to the local mechanical environment (e.g., a tensoral measure of stress or strain). Some possible functions 𝔣(·) include the eigenvectors of an appropriate stress or strain tensor.

We may model the active contribution to the Cauchy stress as the product of two functions: a scalar-valued function with units of stress, and a tensor-valued function, which contextualizes the scalar value in the current (spatial) configuration. The active contribution can then be written as

$${\mathit{\sigma }}_{\text{act}}(s)=f_{\text{act}}({\lambda }_{\text{act}}(s),C(s))𝔤(s),$$ (8)

where the scalar-valued function f_act(·), representing both mechanisms in hypothesis III, is a function of the active muscle length λ_act(s) and chemical constrictors C(s), and 𝔤(s) is a structural tensor. Specific functional forms for active muscle stress have been proposed by Rachev and Hayashi (1999) and Murtada et al. (2010, 2012).

4 Survey of Works

4.1 Physiological motivations and basic behaviors

In addition to suggesting that arteries respond to instantaneous changes in wall shear stress, Rodbard (1975) proposed that arteries respond to sustained alterations in blood flow through a two-step process. The first step is a rapid vasoactive response which tends to restore wall shear stress (Kamiya and Togawa, 1980); the second step is a more delayed process of entrenchment, by which the artery adjusts its structural composition (Dajnowiec and Langille, 2007). Luminal wall shear stress is thus a vital mechanical stimulus. Furthermore, it appears that arteries remodel to maintain a homeostatic mean circumferential stress (Wolinsky, 1970). Noting the relationships between inner radius, wall thickness, shear stress, and mean circumferential stress, Humphrey and Rajagopal (2003) proposed testing Rodbard’s hypothesis, as driven by luminal wall shear stress and circumferential stress. This section describes several works which, with increasing sophistication, apply these concepts within membrane models.

Using Humphrey and Rajagopal’s idea of coupling Rodbard’s hypothesis with mean intramural stresses, Gleason et al. (2004) test competing hypotheses concerning the role of the replacement of prestretched constituents in carotid arteries for cases of a sustained alteration in blood flow. Assuming instantaneous and complete vasodilation, the authors prescribe an inner radius corresponding to that which preserves the homeostatic shear stress for a 33% step increase in flow, and they compute the evolving thickness which satisfies radial equilibrium as the artery’s composition evolves. Specifically, this work compares the consequences of permitting constant turnover for all arterial constituents (i.e., collagen, muscle, and elastin) to those of disallowing turnover of elastin (hypothesis I-a). This second case is motivated by the observation that arterial elastin is deposited perinatally, with little or no subsequent synthesis (Davis, 1995). Although the authors emphasize that this work is intended primarily as an illustrative exposition of the framework, the model predicts an incomplete or ‘suboptimal’ state for the case of no elastin turnover, which does not preserve the artery’s original behavior and is consistent with experimental observations. The model predicts that the artery which experiences turnover for all constituents does recover original behavior.

Within the context of hypertension, Gleason and Humphrey (2004) employ a similar model wherein the inner radius is prescribed to be constant, and the thickness is then computed to satisfy radial equilibrium for a 33% increase in transmural pressure. Again, the model investigates predicted behaviors for the case of full turnover of all three major load-bearing constituents and compares them to the case for which elastin does not turn over. In the case of all constituents being replaced, the model predicted G&R which yields thickening, as expected for the case of increased transmural pressure, and preserved mechanical behavior. That is, growth and remodeling occurred by maintaining constant the relative amounts of all constituents. Also, the artery retains no permanent memory of a preferred geometry as endowed by permanent elastin. In contrast, for the case of no elastin turnover, the model again predicts ‘suboptimal’ remodeling wherein the mechanical response is not preserved. These predictions, as in the previous work (Gleason et al., 2004), suggest that, in reality, constituent turnover is likely restricted to collagen and smooth muscle, since we know that arteries under hypertensive conditions become markedly stiffer.

Gleason and Humphrey (2004) also compare predicted results based on various hypothesized cases for mass kinetics. The results demonstrate that kinetic functions can have profound effects on the rates of evolution for geometry and final constitutive behavior. Subsequent works also consider the effects of increased axial stretch (Gleason and Humphrey, 2005a) and combined hemodynamic perturbations (Gleason and Humphrey, 2005b). An interesting feature of these models is the use of gamma distribution function to describe depositional prestretches for newly-deposited material (hypothesis II). This assumption illustrates the natural ability of testing hypothesized prestretch behavior within constrained mixture models.

Due to the dearth of data for constituent kinetics at the time publication, the above series of works consider only kinetic functions of non-dimensional time. Also, kinetics are assumed to be independent of mechanical or chemical stimuli. These limitations are addressed by Humphrey et al. (2007) and Baek et al. (2007), who present a set of hypotheses relating to cerebral vasospasm and a corresponding computational model. A notable feature of this implementation is that arterial caliber and thickness are free to evolve as functions of transmural pressure, vasoactivity, and arterial composition. Also, mass kinetics are taken as linear functions of both the mean circumferential stress and constrictor concentrations. Survival fractions are functions of both time and cohort-specific tension histories. Furthermore, mass kinetics are functions of actual time. These refined assumptions and abilities facilitate improved flexibility in hypothesis testing.

In addition to predicting realistic time courses for the onset and eventual resolution of vasospasm, the model by Baek et al. (2007) predicts evolving geometry and passive behavior as consequences of complex emerging phenomena. Kinetic relations are also investigated parametrically, facilitating the identification of realistic values for kinetic constants. Consistent with clinical observations, the results suggest that the onset of vasospasm is a chemo-dominated process, with the role of chemical kinetics overwhelming any countering mechanical feedbacks. In contrast, resolution of vasospasm is likely an intramural stress-driven process, wherein the rate at which the artery attains a normal inner radius depends primarily on the circumferential stress, driving turnover of collagen and muscle. This work illustrates the importance of considering the coupled effects of each of the individually important hypotheses; it also shows that the constrained mixture framework can be readily amended to suit specific conditions of interest (i.e., to model specific, acute pathologies using appropriate hypotheses).

Adopting the basic framework put forth by Baek et al. (2007), Valentín et al. (2009) investigate the interrelated effects of the three fundamental hypotheses in response to changes in flow and transmural pressure. The work revisits Rodbard’s concept of two-phased responses in arterial adaptations and shows that the complementary effects of the hypothesized fundamental mechanisms can yield expected geometries, time courses, and mechanical behaviors in response to corresponding changes in flow and pressure. Cardamone et al. (2010) extend this model to allow mass-density production to also be a function of short-term loading over the cardiac cycle. Figueroa et al. (2009), using a novel fluid-solid-growth (FSG) model, compare results assuming cases of G&R mediated by (i) intramural stresses and (ii) by a combination of intramural and local wall shear stresses. The predicted results suggest that arterial models should account for the combined effects of intramural and local flow-induced shear stresses. As in earlier works, these models emphasize the need to consider the effects of hypothesized mechanisms in unison, rather than individually; shear-induced alterations in chemicals, evolving intramural stresses, and varying mass kinetics are linked via positive and negative feedbacks, with the net result being complex, emergent behavior.

4.2 Intracranial aneurysms

Baek et al. (2005) apply the constrained mixture model within a finite element framework to investigate dominant modes of G&R in intracranial saccular aneurysms and propose stress-mediated collagen production rate functions which depend on the total mass and synthesizing cell density. Elastin and smooth muscle activity are not considered, due to the lack of either constituent in collagenous saccular aneurysms. Survival fractions are prescribed as sigmoidal functions of cohort lifespan. These physiologically-motivated functional forms also require prescribed ‘gain’ parameters K_g which scale constituent production rates to the change in a local scalar measure of stress. In response to an initial loss of mass, the model predicts a race or ‘competition’ between the rate of the incorporation of collagen into the matrix and the aneurysm’s rate of radial expansion. For different values of the gain parameter K_g, the model can predict well-controlled, bounded expansion, wherein the aneurysmal wall thickens rapidly enough to impart a protective effect and arrest aneurysmal growth. Alternatively, the model can also predict steadily increasing, unbounded growth for cases in which the deposition of material is not occurring at a rate sufficiently high to counter unrelenting aneurysmal expansion. Kroon and Holzapfel (2007) describe a similar model, whereby collagen turnover is driven by a scalar measure of stretch. As in Baek et al. (2005), their work demonstrates the ability to predict stable cerebral aneurysm evolution. In light of the fact that the majority of cerebral saccular aneurysms do remain stable, these models suggests a restricted range of kinetic values; they illustrate the framework’s utility in helping to identify important physiologically-motivated parameters.

In an effort to elucidate the effects of evolving fiber orientations (hypothesis I-b) in aneurysmal growth, Baek et al. (2006) consider 3 hypotheses regarding fiber alignment. Again, the authors draw conclusions based on which cases predict stable or unbounded behavior; they essentially specify equation (7) as functions of directions of principal stresses and stretches. The authors test each hypothesis by determining if the model can predict bounded G&R behavior, which is observed in a majority of cerebral aneurysms. Perhaps surprisingly, the model does not predict stable aneurysmal growth for the case in which new fibers are deposited preferentially along the direction of maximum principal stress. Rather, only for the cases in which fiber alignment is dictated by the lesser principal stress or greater principal stretch does the model predict lesion stabilization.

4.3 The use of null hypotheses

The previously described works have shown themselves to be useful for testing of competing hypotheses regarding specific aspects of the three fundamental hypotheses. It was not until later that these hypotheses of arterial G&R were themselves posed as null-hypotheses and tested more rigorously. Valentín and Humphrey (2009) consider a subset of hypotheses I, II, and III, while prescribing the orientations of new fibers to be constant, which is likely a reasonable first approximation for axisymmetric arterial G&R. These hypotheses are tested by letting the model predict G&R trends in the absence of one or more of the three hypotheses, essentially recasting each of the hypotheses as null hypotheses: that the model can predict stable, realistic trends in the absence of one or more of these fundamental mechanisms.

Interestingly, although the model can predict stable trends (i.e., bounded growth) for cases in which a single fundamental mechanism is omitted, the resulting artery is severely limited in its ability to respond to changing hemodynamic conditions and its ability to adapt over time to altered pressure; the simulated artery cannot behave in the manner described by Rodbard (1975). In addition, the model predicts that the artery cannot maintain stable long-term G&R trends when lacking constituent-level prestretches and vasoactivity and only a quasi-stable G&R equilibrium when mass production rates are fixed and the artery lacks a vasoactive response. This work not only shows the individual importance of each central hypothesis; it also demonstrates the complementary effects of these mechanisms and emphasizes, as have prior models, that these mechanisms cannot be studied in isolation.

4.4 Advancement beyond the membrane assumption

The utility of membrane models to elucidate arterial G&R behavior notwithstanding, they do not permit modeling of thick-walled arteries. Fortunately, several thick-walled formulations have recently been presented. The first such work, put forth by Alford et al. (2008), employs a hybrid model combining some aspects of kinematic growth and the constrained mixture theory and tested hypotheses related to mass kinetics (hypothesis I-a). The authors provide a rich set of results with ample comparison to experimental data. Of particular interest here are the predicted effects of varying radial distributions of elastin mass fractions, motivated by observed variations in opening angles and axial retraction lengths along the length of the rat aorta (Liu and Fung, 1988). This model not only predicts realistic opening angles before G&R; it also predicts evolving opening angles comparable to experimental observations, for cases of a simulated 50% increase in transmural pressure. A key conclusion is that the permanence of elastin plays a central role in the artery’s ability to achieve stable, compensatory states (what Gleason and colleagues refer to as suboptimal states).

Although they did not focus specifically on G&R, Cardamone et al. (2009) compare predicted results based on different hypotheses concerning spatial prestretch distributions for elastin (hypotheses I-a and II). The authors motivate their hypotheses with observations of elastin deposition during perinatal growth: that changing rates of elastin production in early developmental intervals, during which arteries grow rapidly (Bendeck and Langille, 1991; Bendeck et al., 1994), result in corresponding gradients in elastin prestretch. Following perinatal development, elastin deposition ceases (Langille, 1996; Stenmark and Mecham, 1997), and the artery continues to grow with its now permanent elastin retaining a ‘memory’ via growth-induced prestretches. This work presents several results showing the predicted effects of various hypothesized modes of elastin deposition during development (e.g., stress fields in relevant configurations, opening angles, etc.) and compares them to experimental and previous theoretical works. Figure 2 describes the geometries involved, and figure 3 shows the effects of elastin prestretch distributions on axial retraction lengths and opening angles. However, perhaps the most important conceptual aspect of this work is that it does suggest an alternate interpretation, via prestretches, by which the intramural mechanical state may be inferred from well-known opening angle measurements. Namely, this approach does not require the assumption of a unstressed (as opposed to an unloaded) configuration for the artery; it merely requires postulating the homeostatic constituent mass fractions and prestretch distributions within the in vivo configuration.

Figure 2.

Schema of the current in vivo loaded configuration, denoted by κ(s), and the excised unloaded (β₁) and radially cut (β₂) configurations. F₁ describes motions from a current loaded in vivo state to the excised unloaded state, and F₂ describes motions following the introduction of a radial, stress-relieving cut. Variables l and L represent the axial lengths of the artery in the in vivo and excised, unloaded states, respectively. The opening angle is Φ₀. The shaded annular region (representing a non-free surface) reminds the reader that κ(s) is an axially tethered, unexcised configuration.

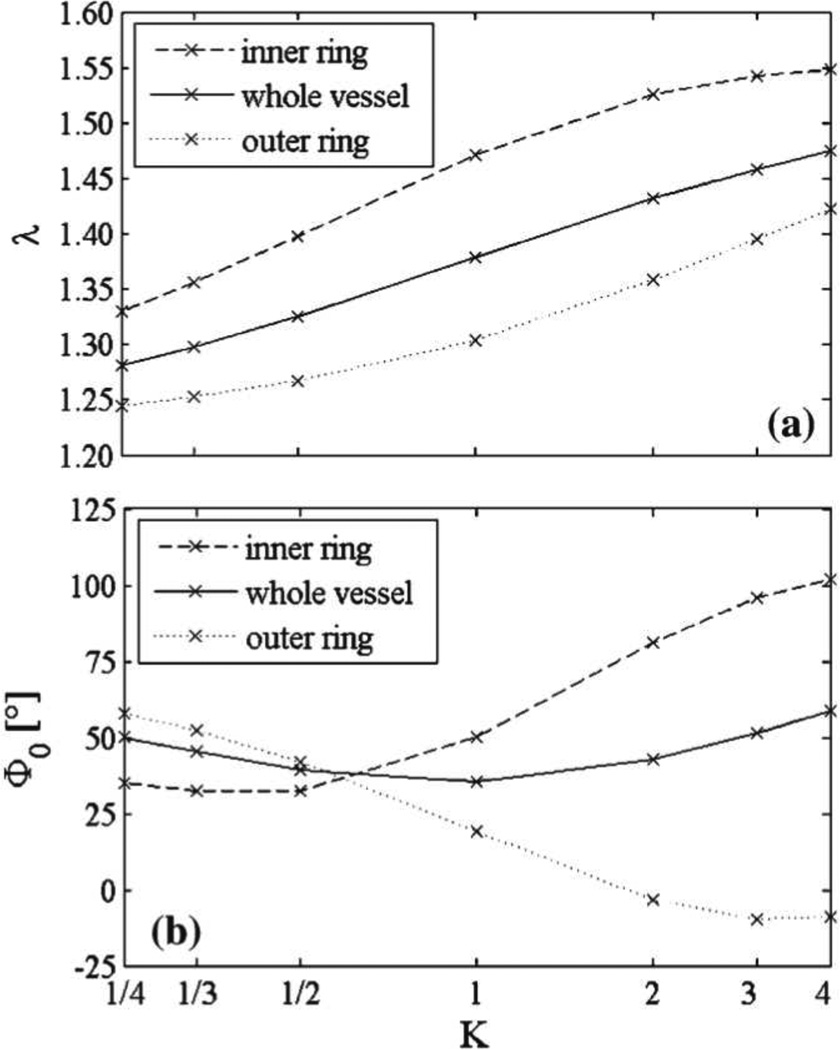
Figure 3.

Results from Cardamone et al. (2009), illustrating the effects of elastin prestretch distribution on the inverse axial retraction ratio λ = l/L, panel (a), and opening angle Φ₀, panel (b), for the inner and outer sectors of a basilar artery; see figure 2 for more information. Here, parameter K represents different hypothesized prestretch distributions corresponding to varied sequences of elastin secretion and cross-linking during arterial development. These results demonstrate the potentially strong influence of constituent prestretches on measurable geometric quantities (reproduced from Cardamone et al., 2009).

One limitation of the work by Cardamone et al. (2009), notwithstanding its ability to predict realistic opening angles, is that the model considered only a single layer and cannot account for the potentially important effects of the strong constitutive – and thus mechanical – discontinuities present in arteries possessing a clear boundary (in the form of a well-defined external elastic lamina) between the dissimilar media and adventitia. Nonetheless, the authors clearly illustrate the importance of constitutive behavior, in the form of prestretch, as a function of radial position in arteries and that these types of hypotheses can be tested numerically and the predictions compared to observations.

Combining ideas from the aforementioned thick-walled models, Karšaj et al. (2010) and Karšaj and Humphrey (2011) present thick-walled models of uniform growth, driven by mean intramural stresses and wall shear stresses. These models are able to predict expected behaviors for canonical cases of arterial growth and remodeling (i.e., evolving compositions and geometric responses to alterations in pressure and flow, as in Gleason and Humphrey, 2005b; Valentín et al., 2009). The authors go on to compare the predicted evolving opening angles and axial retractions as functions of elastin prestretch distribution, thereby extending the concepts of Cardamone et al. (2009) into the realm of time-dependent G&R. In a similar model, Wan et al. (2010) present a thick-walled model of growth within a single-layered artery. Their model predicts reasonable trends for evolving geometries and intramural Cauchy stress distributions, although their trends are expressed in non-dimensionalized time. As in Gleason and Humphrey (2005a), local homeostatic prestretches are calculated with pre-determined distribution functions (in lieu of using a convolution integral as in equation (4)).

Employing a novel theoretical interpretation based on a constrained mixture, Machyshyn et al. (2010) present a finite element model for fusiform aortic aneurysms. They hypothesize stretch-driven relations for hypotheses I-a and I-b (but first order kinetics for degradation) and are able to predict the evolutions of a ‘healthy’ state and of a fusiform aneurysm. The model, however, does not account for smooth muscle contractility. This limitation obviously precludes the consideration of active stresses in response to altered inner radii, but the model can still predict bounded growth (cf. Baek et al., 2005, 2006). As a consequence of the specific framework, the model first computes recruitment stretches (cf. Watton et al., 2004) rather than by prescribing prestretches a priori. Interestingly, the model predicts homeostatic recruitment stretches (which are roughly analogous to prestretches) of ~1.15–1.25 for a healthy aorta, which are considerably higher than the depositional prestretch values for collagen of 10% or less used in most other constrained mixture models.

Valentín et al. (2011) test hypotheses regarding aging within the context of a multilayered model of the human abdominal aorta. As in most other models, they posit that elastin is only produced during development, and that it irreversibly degrades over long time spans (decades). The authors extend the concept of homeostatic states by proposing that the media and adventitia possess unique homeostatic mass fractions and kinetics, depending on local, rather than mean intramural stresses. In other words, synthesizing cells express layer-specific phenotypes whereby they work to maintain mass fractions and kinetics constant through each layer. The model also permits active and passive mechanical constants to change with age. Maximum smooth muscle activity is proportional to the amount of remaining elastin (further coupling hypotheses I and III), and collagen cross-linking increases with age, as a result of glycation (as a result of diabetes, for example). Similar to the work of Baek et al. (2006), the model can predict both bounded and unbounded growth, depending on the degree of increased collagenous stiffening. For sufficiently high collagenous stiffening, the model predicts a reversal of radial expansion, which suggests that glycation-induced cross linking may confer a protective effect on the aged aorta, at the expense of a greatly stiffened aorta.

Having built upon the intuition and restricted parameter spaces garnered from simpler models, thick-walled constrained mixture models facilitate investigation of arterial mechanics in sophisticated and fundamentally novel ways. Thick-walled models allow more detailed inferences of intramural composition, anisotropy and non-homogeneity. Most obviously, they provide the ability to test hypotheses regarding spatial distributions of arterial constituents. The predicted results are compared to experimental observations of opening angles and other measures (Holzapfel and Ogden, 2010). By proposing and numerically testing hypotheses and comparing predicted results to experimental and clinical observations, several groups have been able to elucidate mechanisms and processes that are likely responsible for the remarkable properties of large arteries.

5 Discussion

The constrained mixture framework has proved to be a useful theoretical apparatus by which to investigate phenomena governing arterial growth and remodeling. In particular, it readily facilitates the testing of multiple competing hypotheses involving what are likely fundamental arterial behaviors. Specialized models may be constructed to test hypotheses suitable for specific conditions and pathologies of interest. Moreover, the framework’s advantages are not merely incidental; they exist precisely because this theoretical system was conceived with those abilities in mind. Indeed, the framework itself is based on three well-tested hypotheses, motivated by diverse observations and arguments deduced from first principles of biological optimization.

In this brief survey, we recapitulate how constrained mixture models, within varied focused contexts, have been employed to examine salient aspects of ubiquitous arterial G&R processes: rates of constituent deposition and removal; alignment or re-arrangement of fibrillar constituents; effects of constituent-level prestretches; and the roles of vasomotor activity in normalcy and disease. By evaluating a series of pertinent hypotheses, each model offers unique insights on these distinct fundamental behaviors and their interactions, which are plausibly operative to some degree in all healthy arteries but may become compromised or absent under pathological conditions.

The models briefly described here can predict canonical arterial behaviors, consistent with the findings of Rodbard and others, whereby arteries can adapt in response to perturbations in luminal blood flow and transmural pressure. By intentionally omitting realistic behaviors (or by permitting unrealistic behavior) the models can predict suboptimal adaptations in response to altered hemodynamic conditions, or they can predict unrealistic adaptations that fully preserve healthy arterial behaviors. The potentially dominating effects of various kinetic parameters have also been demonstrated by parametric comparisons of predicted G&R trends and trajectories. Sophisticated fluid-solid-growthmodels have also applied these concepts to more general conditions.

Models of aneurysmal G&R, by omitting key constituents and behaviors (such as elastin and smooth muscle contractility) can predict stable lesion development via compensatory adjustments in the turnover and orientations of prestretched collagen in compromised states of G&R. Thick-walled models facilitate the testing of hypotheses involving the sequence of elastin deposition in development and resulting prestretch/residual stress distributions. Such applications of the constrained mixture framework also allow for more detailed investigations of G&R processes in large arteries and the effects of local chemomechanical stimuli on differential growth. Finally, null hypothesis testing has shown that only by including all of these behaviors can arterial models of G&R reproduce expected behaviors and trends, such as arterial homeostasis.

Successful modeling of arterial G&R under general conditions remains a distant goal. As theoretical and experimental tools continue to improve, however, we can more reasonably expect to attain enhanced predictive capabilities for specific cases. Though clinical observations and experiments in the laboratory will remain the standards against which we should compare numerical models, computational experiments can be executed at far lower cost, both in terms of time and funding. Numerics also permit researchers to overcome practical technical limitations such as tissue viability, as in the case of long-term ex vivo studies. To date, progressively improving constrained mixture models, each successively building upon findings and intuitions gleaned from previous works, have contributed to an emerging and increasingly coherent perspective on the processes involved in arterial growth and remodeling.