Tools of the trade: psychophysiological interactions and functional connectivity

Abstract

Psychophysiological interactions (PPIs) analysis is a method for investigating task-specific changes in the relationship between activity in different brain areas, using functional magnetic resonance imaging (fMRI) data. Specifically, PPI analyses identify voxels in which activity is more related to activity in a seed region of interest (seed ROI) in a given psychological context, such as during attention or in the presence of emotive stimuli. In this tutorial, we aim to give a simple conceptual explanation of how PPI analysis works, in order to assist readers in planning and interpreting their own PPI experiments.

Typically, in an fMRI experiment, researchers are interested in the activity of individual brain areas—for example which brain areas increase their activity during a behavioural task. Yet a major strength of functional imaging as a method is that it allows researchers to observe activity in networks of areas simultaneously and therefore as well as investigating functional localization (which areas are active during a task) it is possible to use functional imaging to probe functional interactions between brain areas. Using functional imaging data, researchers can investigate not only which individual brain areas are involved in a task, but also how information flows between brain areas (Stephan, 2004; Friston, 2011; Smith et al.., 2012) and how functional areas can change their connectivity to participate in different networks at different times (Smith et al.., 2012), or under different behavioural circumstances (Cacioppo and Decety, 2011).

This tutorial concerns one particular type of functional connectivity analysis (arguable the most popular technique in the literature at present): psychophysiological interactions (PPI) analysis. PPIs analysis concerns task-specific increases in the relationship between different brain areas’ activity (Friston et al.., 1997). PPI is a measure of what is generally referred to as functional connectivity—a statistical dependence between activity in between brain areas. Functional connectivity analysis in general may concern relationships between brain regions in any context, including when the brain is at rest (Biswal et al.., 1995); other techniques for functional connectivity analysis include Dynamic Causal Modelling [DCM (Friston et al.., 2003)], independent components analysis [ICA (Hyvarinen, 1999)] and Granger causality (Granger, 1969). Readers should be aware that each method aims to extract different types of connectivity information from the data and hence results from these different techniques are not equivalent; it is necessary to choose a technique which is effective for the particular experimental question and data type.

PPI is concerned with task-dependent functional connectivity analysis: the purpose of a PPI analysis is to determine which voxels in the brain increase their relationship with a seed region of interest in a given context, such as during a particular behavioural task. In other words, a PPI aims to identify regions whose activity depends on an interaction between psychological factors (the task) and physiological factors (the time course of a region of interest). A task-specific increase in the relationship between brain regions (a PPI effect) is suggestive of a task-specific increase in the exchange of information.

PPI analysis was originally proposed by Friston and colleagues in 1997, and has become more commonly used in recent years, perhaps as neuroscientists increasingly think about the brain in terms of networks and interactions between brain regions (Bullmore and Sporns, 2009; Deco et al.., 2011; Friston, 2011). PPI analysis can be implemented using any fMRI analysis package, and is particularly straightforward to carry out with SPM (http://www.fil.ion.ucl.ac.uk/spm/) FSL (http://www.fmrib.ox.ac.uk/fsl/), or AFNI (http://afni.nimh.nih.gov/sscc/gangc/CD-CorrAna.html) as these packages have PPI functions built into their graphical user interfaces.

In this tutorial, we provide a beginner’s guide to PPI in three parts. First, we explain the circumstances in which a PPI analysis might be used. Secondly, we explain conceptually how PPI analysis is implemented. Third, we discuss the interpretation of PPI results, including some comparison with resting-state functional connectivity analysis.

WHAT IS PPI FOR? A HYPOTHETICAL EXAMPLE¹

Imagine we had conducted an experiment in which participants navigated a route through a virtual reality maze, and this navigation condition was contrasted with a control condition in which the participants travelled passively through a similar maze. Now imagine when we analyse the data, we find that the prefrontal cortex and hippocampus were both more active during the navigation condition than during the passive control condition.

Faced with these results, we might come up with (at least) two possible interpretations: (i) the prefrontal cortex and hippocampus were both independently active in the navigation condition (say, because navigation requires planning, which involves the prefrontal cortex and because navigation requires spatial information, which is stored in the hippocampus). (ii) The prefrontal cortex and hippocampus work together interactively in navigation—perhaps some ‘top–down’ signal from the prefrontal cortex causes retrieval of information in the hippocampus, which is then passed back to the prefrontal cortex.

If the two active areas (hippocampus and prefrontal cortex) interact during navigation, we might reasonably expect their activity to be more strongly related during navigation than during the passive travel control. This is where PPI analysis is useful: for a given ‘seed’ region of interest, such as the hippocampus in this case, PPI analysis essentially tells us which voxels, across the whole brain, increase their relationship with (strength of regression on) that seed region during the task of interest. In the maze navigation task, we could use PPI to help distinguish between the two hypotheses above by asking which areas increased their relationship with the hippocampus during navigation as opposed to passive travel.

Incidentally, we should be clear from the outset that a standard PPI analysis does not make inferences about the direction of information flow, i.e. causality. PPI detects task-specific increases in the relationship between a seed region of interest and the rest of the brain, measured in terms of the strength of regression of activity in one region on another. However, there is no implication that the seed region is the driver rather than the driven area, or whether the connection is direct, rather than mediated by other areas.

HOW DOES A PPI ANALYSIS WORK?

In this section of the tutorial, we build up a strategy for analysing functional connectivity, as this is normally done in PPI analysis.

Identifying functionally connected brain regions

How do we go about looking for areas that interact with a brain area of interest, such the hippocampus in our maze experiment? The first principle underlying PPI is that if two areas are interacting, the level of activity in those areas will correlate over time—in other words, if activity in the two areas increases and decreases ‘in synch’ this suggests that activity in one area may be driven by activity in the other (although the direction of causality is unknown, as mentioned above). This relationship can be captured by performing a linear regression in which activity in the seed region is used to explain activity in other voxels across the brain.

The basic strategy for identifying a (non-task dependent, at this stage) relationship between a region of interest and the rest of the brain is as follows:

1. define a mask at your ‘seed’ region of interest (the hippocampus)—see Figure 1 for some comments about defining seed masks.

2. extract a representative time course of activity from that mask. This time course will be a vector containing a single value (e.g. the mean activity in the mask) for each time point (volume) in your fMRI data set. In FSL, the seed ROI time course is obtained using a command line tool called fslmeants; in SPM, there is a graphical interface for defining the region of interest, and time course extraction is then done automatically.

3. Having obtained a time course representing activity in the seed ROI, enter this time course as a regressor into a GLM analysis (a GLM or general linear model analysis is simply a ‘normal’ SPM or FEAT analysis, in which the regressors or explanatory variables typically represent blocks of a task). As with any GLM analysis, this will identify voxels where there is a significant effect such that activity is explained by a regressor or ‘explanatory variable’ (in this case, the seed ROI time course). The voxels that show a significant effect for the seed ROI time course are the ones that vary their activity ‘in synch’ with the hippocampus.

Fig. 1.

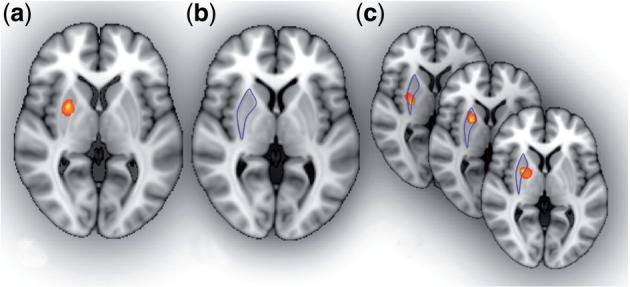
Defining the seed region of interest. PPI analysis investigates task-dependent relationships with activity in a seed mask. This seed mask may be defined in several ways. (a) A common approach is to select the voxels with the strongest task effect in a group analysis (e.g. the voxels most active during navigation). (b) Alternatively the mask may be defined anatomically, if there is a strong hypothesis about a particular anatomical region, and that region can be easily delineated on an anatomical scan (here we have selected the entire putamen). (c) We may define the region of interest individually for each participant. First we constrain our search to a volume of interest (here we use our anatomical putamen mask, but we could equally use a mask based on a group fMRI analysis). Then we select the voxels in each participant with the strongest task effect. This allows for inter-individual differences in functional anatomy and is probably the most sensitive approach. Note that in cases ‘a’ and ‘c’, we are selecting an ROI based on the results of our analysis. However, we need not be concerned about circularity in this case, because as long as we model the main effect of task when we run the PPI analysis, the PPI will only detect functional connectivity effects over and above (orthogonal to) the main effect of task.

Task-dependent effects

Using the analysis described so far, we would identify those voxels that correlate with the seed ROI in general. Indeed, identifying correlated voxels in this way is similar to the typical ‘seed based’ approaches for the analysis of resting-state functional connectivity. However, in PPI analysis we are interested in task-specific changes in the relationship between brain areas in functional connectivity. In other words, we are interested in the moderator effect of task context on interactions between brain regions (Baron and Kenny, 1986). Therefore a further manipulation is required.

Psychophysiological interactions

The aim of a PPI analysis is to identify task- or context-specific changes in the relationship between brain areas (or functional connectivity): for example, if two areas interact more in the context of a certain psychological task, activity in one areas should regress more strongly on activity in the other area during task blocks compared to during a control task or rest.

Consider the maze example again and imagine that when people navigate actively around the maze the hippocampus and the prefrontal cortex interact. In contrast, in the passive travel condition these two regions do not interact. Then we would expect the relationship between the two regions to be higher during the navigation condition than during the passive travel condition. In a psychophysiological interactions analysis, we particularly look for areas that have a stronger relationship with the seed ROI time course in one psychological context (e.g. task block) than another.

How do we identify task specific changes in functional connectivity? Instead of using the time course of the seed region in the GLM, we generate an ‘interaction regressor’ and use this instead. Generally speaking, the interaction (PPI) regressor will be the element-by-element product of the (mean-centred) task time course and the (demeaned) seed ROI time course (Figure 2). Voxels in which this PPI regressor is a good description of activity are those in which the seed region’s time course has a stronger relationship during the condition of interest (navigation) than it does during other conditions (passive travel).

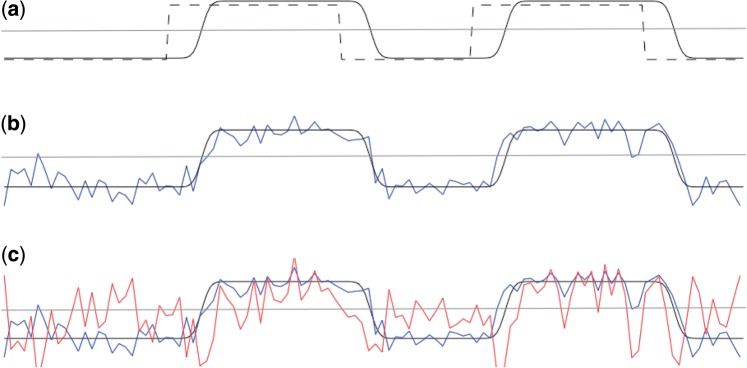
Fig. 2.

Generating a PPI regressor. (a) We start with a regressor representing the main effect of task (in this case, a block design) (dashed line), and convolve it with the HRF to get an HRF convolved task regressor (black line). The horizontal grey line is zero. (b) We extract a time course from our seed region of interest (blue line). If this region of interest was active during the task, the time course of activity from the seed region will be correlated with the HRF convolved task regressor. (c) We generate a PPI regressor (red line) as an element-by-element product of the HRF convolved task (black line) and seed ROI (blue line) regressors. Note that the PPI regressor is correlated with the seed region time course during task blocks, but anti-correlated with it during rest blocks. Consequently, voxels that are always correlated with the seed ROI (e.g. due to anatomical connections that are not task-relevant) will have an overall regression co-efficient of zero for the PPI regressor, but voxels which are more correlated with the seed ROI during task blocks than during rest will show a positive correlation with the PPI regressor.

It is possible to look at PPI effects for one seed region and multiple tasks, or multiple seed regions and one task, by creating multiple PPI regressors. Probably the simplest way to do this would be to create a PPI regressor for each task/seed region combination of interest, and set up the contrasts between these in the individual subjects’ analyses—then pass the results of these contrasts to a group-level analysis as one would for any group-level inference.

In contrast, if we consider simple correlations some brain regions will have a similar time course of activity to the seed region for reasons that are nothing to do with the experiment per se. For example, regions that are anatomically connected have correlated activity even during the resting state (Greicius et al.., 2009; Honey et al.., 2009). Regions that share neuro-modulatory influences or have common sensory input will all have correlated time courses regardless of what experiment you are doing. In contrast, in PPI we are only interested in relationships that change due to some manipulation we applied, for example, areas which interact during navigation but not during passive travel. Non-task specific, baseline interactions between brain areas (functional connectivity) should remain constant across conditions.

Co-variates of no interest

In PPI analysis, we are specifically looking for a change in functional connectivity due to a manipulation we ourselves have introduced (such as the psychological task). We therefore need to rule out a number of non-task-related explanations for the changes in the relationship between brain areas.

Following the approach described so far, we would have a GLM in which the regressor or explanatory variable is the interaction (PPI) term described above. This analysis tells us which regions are more correlated with the seed region during the task of interest than at other times, but there is a problem: because we generated the interaction term as the product of a task regressor and a seed ROI time course, regions in which there is an effect of task, or which are correlated with the seed ROI regardless of task, may also show up as being related to the interaction term.

To spell this out: we selected the (seed) region of interest on the basis that it was active in a certain contrast (in our example, navigation vs passive travel), and therefore we are pretty much certain to see a relationship with all the other areas that were active in that contrast in our original GLM analysis (because these also increase their activity during the navigation blocks). In other words, we will observe effects that are driven by a shared task input, which we knew before we even started the PPI analysis. Furthermore, voxels that have a similar time course to the seed region, even if this is not task related, will have a positive relationship with the interaction term—as described above, any voxels with anatomical connections to the seed region, or shared subcortical input, could show a non-task-specific effect.

To account for these confounds, we must include in our model the psychological and physiological time courses from which we derived the interaction term, as co-variates of no interest. We would therefore include all three time courses displayed in Figure 2c. This means that variance explained by the interaction term is only that over and above what is explained by the main effects of task and physiological correlation. This is the final PPI model.

Additional regressors

The co-variates of no interest described above (the task- and seed ROI regressors used to generate the PPI) should always be included to ‘model out’ baseline correlations. However, it is also advisable to include regressors that model any other known variance in your data, even if this is not correlated with the PPI. In any general linear model analysis, including PPI, the better your model describes your data, the lower the error variance—this makes the analysis more sensitive overall. Therefore, it is advisable to include regressors representing other task conditions, button presses, eye movements, errors, etc if you would normally include these in a model of your task for a typical (main effects) analysis.

Between-sessions PPI

In some fMRI designs, the effect of interest is not the effect of a task on brain activity, but the difference in size of that effect between two experimental sessions or two groups of participants. Say for example that in fMRI session 1, we get a group of participants to navigate around a maze they have never seen before. Then we take them out of the scanner and let them practice with the maze for a couple of hours. In fMRI session 2, they navigate around the maze again, but now the maze is familiar. We want to know whether there is a different spatial pattern of functional connectivity with the hippocampus before and after familiarization.

In this case, we have two slightly different options for PPI analysis depending on the question we want to ask.

1. If we only want to know which areas have greater functional connectivity with the hippocampus after the maze training, we can simply extract the time course from the hippocampus for each session, and enter this as a regressor together with all the regressors we would normally use to describe the task. Then in a higher level analysis, we identify voxels in which the variance explained by hippocampal activity increases in the second session (i.e. areas in which the Z-score for a regressor representing the time course of the hippocampal ROI increases). Essentially, in this case we are modelling the interaction between the effect of the seed ROI and session (pre-/post-training), rather than the interaction between the seed ROI and task blocks. Note that such an effect could be driven by changes in the kind of factors we normally model out by including the seed ROI time course as a regressor of no interest—for example, changes in anatomical connectivity. However, the approach is valid because a between-sessions effect could only be driven by a change in some factor, such as anatomical connectivity, which can be understood as the mechanism for the change in functional connectivity, and is therefore not a confound but a part of the effect of interest. In contrast, such between-sessions effects cannot be explained by a change in the response of the brain regions to the task itself, because even if the main effect of task has changed (say, the hippocampus and prefrontal cortex are both more active during the task after training), this effect will be captured by the task regressors for each session.

2. Using approach (a), we can conclude that functional connectivity has changed due to the between-sessions intervention, but not that this effect is task-specific. For example, after training people may be more inclined to recall spatial information, in general, even during passive travel or even during rest. Therefore, if we wish to conclude that the functional connectivity change is specific to a psychological context (e.g. that the hippocampus and prefrontal cortex interact more when navigating in a pre-trained maze, as opposed to simply saying HPC and PFC interact more after training in a maze) then it is necessary to do the full PPI analysis for each session as described for single session analysis, and compare the PPI effects in a higher level analysis.

Note that instead of between sessions, either of these approaches could be used to compare functional connectivity between groups of people—and the same considerations would apply when choosing method a or b. Approach (a) has been used, for example to compare carriers of genetic variations of a serotonin transporter (Heinz et al.., 2005), and to compare schizophrenic patients to healthy controls (Boksman et al.., 2005).

INTERPRETING FUNCTIONAL CONNECTIVITY IN PPI AND RESTING-STATE DATA

When PPI was proposed in 1997, the idea of using activity in one brain area to explain activity in another brain area was novel and surprising. In 2011, this idea will be familiar to many because it is the basis of resting-state connectivity studies (Biswal et al.., 1995; Deco et al.., 2011). We now know that a large proportion of activity in any brain area can be predicted by looking at activity in anatomically connected and/or functionally related brain areas. This is true even when the brain is at rest, i.e. not involved in any explicit task. At rest, the brain’s activity can be decomposed into a set of canonical spatial maps or ‘resting state networks’, which resemble functional networks commonly observed in task-based fMRI studies (Damoiseaux et al.., 2006; Smith et al.., 2009).

Resting-state fMRI is a powerful tool for investigating the brain, and is increasingly being used to contrast between groups of participants or to examine the effects of an intervention. Since both PPI and resting-state studies investigate ‘functional connectivity’, it seems worth reviewing the difference between the kinds of hypotheses which can be tested using PPI or resting-state data.

There is an important difference of interpretation between resting-state functional connectivity and functional connectivity as tested with PPI, and the two types of data should be regarded as complementary, not equivalent. In PPI, a functional connectivity effect is defined as a task-specific change in the relationship between two brain areas, over and above what can be explained by the shared main effects of task or by non-task dependent factors. In contrast, changes in resting-state networks’ activity may be driven either by changes in connectivity between the nodes of the network, or simply by changes in activity within the network, without changes in connectivity. In general in resting state, changes in connectivity cannot be distinguished from changes in activity because of two confounding factors.

Unconstrained mental activity

Consider our maze navigation example one more time. Say we give participants fMRI scans before and after familiarization with the maze, but in this case we use resting-state scans. Let us say we find an increased relationship between activity in the hippocampus and prefrontal cortex, in the ‘after’ scan. Is this because the prefrontal cortex and hippocampus are now working together to consolidate the participant’s mental map of the maze? Maybe, but remember the other possible hypothesis which motivated the PPI analysis at the very start of this tutorial: that prefrontal cortex and the hippocampus are both involved in maze navigation but do not interact. If, during the second resting-state scan, the participants are thinking about the maze task they have just done, this non-interaction hypothesis would also predict increased co-activation of the two areas. In other words, in the resting-state case, because we cannot model out the shared main effect of navigation (as this is unconstrained mental activity), we cannot distinguish between an increase in navigation-related cognition which causes co-activation of hippocampus and prefrontal cortex, and increase in functional connectivity so that one area is driving the other more strongly in the post-training state.

Changes in signal-to-noise ratio

There is a further difficulty in distinguishing changes in resting-state activity and connectivity, which was recently highlighted in a review by Friston (2011). As we shall see this difficulty does not apply in the case of PPI.

In the resting state, an increase in activity in either of two brain areas could produce a change in the observed functional connectivity between them, even if in fact there is no change in the extent to which one area activates the other at a neural level, simply due to an increase in SNR (signal-to-noise ratio). This is because what we are testing is how strongly the observed signal in one area depends on the observed signal in another area—but the observed signal measured with fMRI is a mixture of neural signal and observation noise. For example, say 5% of the variance in neural signal in one area (say, prefrontal cortex) is accounted for by activity in another area (say, hippocampus), but only 10% of the observed variance is due to neural signal. This means the observed effect size for the degree to which the hippocampus ROIs time course explains activity in prefrontal cortex is 0.5% (5% of 10%). Now, if, after the maze training, neural activity in the hippocampus doubles but external sources of noise (electrical noise, scanner noise) stay the same, then the PPI regressor will more closely reflect neural activity (rather than external sources of noise) and hence would account for a greater percentage of observed variance in other brain regions, even if correlations on the neural level remained the same. This apparent increase in ‘functional connectivity’ is simply due to the change in SNR in the seed region without any change in connectivity at all (Friston, 2011).

In the case of PPI, this problem is circumvented because we are explicitly modelling activity, separately from our model of connectivity. Recall that in the PPI analysis, we modelled both the main effect of the task and the seed ROI time course, as well as the PPI. The only change in SNR that could affect our PPI measure would be a task-specific one (because PPI is a measure of task-dependent changes in connectivity). But any task-dependent change in overall activity would be captured by the task regressor. Hence the ‘SNR issue’ does not apply for PPI.

A matter of interpretation

In view of the above comments, the reader might think that comparing resting-state data between groups is never useful. This is not the case. Whether a resting state or PPI approach is more appropriate depends very much on the research question.

In the case of resting-state data, both the issues of ‘uncontrolled mental activity’ and change in SNR are problematic if we wish to make an inference that functional connectivity has changed, over and above what can be explained by a change in the activity of individual brain areas, because in fact connectivity and activity cannot be separated. This is in contrast to a task-based PPI analysis in which the change in activity is under the control of the experimenter and can be modelled (by the task regressor). Therefore, if you wish to asses changes in connectivity, a PPI approach is required and you should refer to the section above on ‘between groups PPI’ to determine how to implement this. However, in many cases, changes in the brains’ resting patterns of activity (not necessarily connectivity) are exactly what researchers are interested in, and in that case, a resting-state approach may be more informative.

To illustrate the difference in interpretation, let us consider another fictional experiment. Say we are interested in the role of the amygdala in fear and anxiety and consider two different cases.

1. Fear of spiders: we hypothesize that in people who feel fear when they see spiders, functional connectivity between the visual cortex and the amygdala is stronger in the context of spiders. In this case, we are particularly interested in connectivity relating to a stimulus (the spider), so we need a task-based PPI study—for example, we take a group of spider-fearing subjects and show them pictures of spiders in the scanner, before and after phobia therapy. We conduct a PPI analysis using the amygdala as a seed region and the spider pictures as the psychological context, and compare the PPI effect before and after therapy. We find that activity in the amygdala is more strongly correlated with the spider-evoked visual activity before the therapy, than after.

2. Generalized anxiety: say we are interested in people who are generally more anxious and we think that their anxious state has something to do with the amygdala. We conduct resting-state scans on the patients before and after therapy for anxiety, and then analyse the data using a seed in the amygdala. We find that the network of areas correlating with the amygdala is reduced after the therapy. Now, given the confounds described above, this could be simply because the amygdala and other areas are active in anxious thoughts, and the patients are experiencing fewer anxious thoughts during the post-therapy scan. In other words, a change in unconstrained cognition has occurred. But this is exactly what the therapy aimed to achieve! Therefore a change in resting brain activity in a particular network is an interesting result, even though we cannot distinguish a change in activity from a change in connectivity in this case (and researchers should bear this point in mind when discussing their findings).

CAVEATS

Readers who are considering using PPI analysis should be aware of the following issues.

Deconvolution

PPI relies on modelling the interaction between a psychological context and brain activity. A problem arises because while the psychological context is measured in real time, brain activity is measured with a lag of ∼6 s and with temporal blurring, due to convolution with the haemodynamic response function. To combine the two time-series, both need to be convolved with the HRF, or both need to be expressed in terms of the underlying neural activity (deconvolved). The implementation of PPI in FSL uses the first approach while the implementation in SPM uses the second.

The main argument for attempting to deconvolve activity recorded from the seed ROI is that since we are interested in interactions on the neural level, PPI should operate on neural-like data (Gitelman et al.., 2003). The main argument against is that there is no deterministic way to deconvolve the HRF if its shapes is not known exactly. The only way to deconvolve two unknown signals is to use an algorithm, which tries to find the most plausible combination of neural signal and HRF to fit to the data. Therefore, there is no way of knowing if the deconvolution is really correct, and it may be just as valid to transform the psychological regressor with an assumed HRF. A further possibility would be to use a basis set for the HRF and hence produce a set of PPI regressors; however, interpretation of the results from such an analysis would be complicated by the need to distinguish the effect of similarity in HRF shape from scale of response; to our knowledge there is no literature exploring this approach.

In either case assumptions about the shape of the HRF is important. This is particularly so in the case of event-related designs, in which convolved regressors really reflect the shape of the HRF—in contrast, in a block design, almost any HRF will saturate to look a bit like a block.

(Lack of) power

PPI analyses tend to lack power and hence a high proportion of false negatives should be expected. In a PPI analysis, the psychological context, activity in a seed region and the interaction between them are all modelled. The interaction term (the PPI) is likely to have a similar time course to both the psychological and seed ROI time courses, because it was created by multiplying them together. General linear model analysis, as used in PPI and in fMRI analysis in general, detects variance that can be uniquely explained by one of the regressors in the model. This is problematic when two similar regressors are included in the model, because any variance which could be explained by both regressors is not assigned to either. Essentially, this means that the power to detect effects is lower for correlated regressors—as in PPI.

This characteristic of PPI designs is unavoidable, but researchers who perform PPI analyses should bear in mind that the chance of false negatives is rather high with this type of analysis (because the expected effect size would be much smaller than for an analysis of the main effect of task, etc).

Event-related designs

It may be particularly difficult to use PPI in experiments with event-related designs, for the two reasons just described: first, the shape of the HRF and assumptions about it are more important in the context of event-related designs. Secondly, as PPI analyses tend to lack power and event-related designs tend to have smaller effect sizes than block designs (due to a smaller proportion of the task time being spent in the condition of interest), spurious null results may be even more likely for PPIs in event-related designs that PPIs in block designs.

Spurious PPIs?

A PPI effect is a task-specific change in correlation between areas, which cannot be explained simply by a shared external driving force, such as the main effect of a task. To exclude these external effects, we model out the main effect of task. The success of this process depends on the assumption that we have been able to model all task related variance—but in practice this is unlikely to be the case because we make simplifying assumptions about the shape of neural responses, and we ignore unconstrained aspects of the participant’s behaviour.

For example, say that in the hypothetical maze–navigation experiment above, we modelled navigation using a block design (navigate/passive travel/rest are modelled as 30-s blocks). The use of a block design implies that the regions of interest are active fairly constantly at all times in the navigation condition, but this is probably not totally accurate. For example, what if in the navigation task, the prefrontal cortex and hippocampus (independently) are more activated when you turn a corner or reach a junction, and less active when you are moving down a straight section of the maze? Then their activity would actually look less like a 30-s block, and more like a spike every time a corner is encountered. This shared phasic activity causes a correlation between hippocampus and prefrontal cortex, during task blocks, over and above what is explained by our blocked model of task-driven activity. Such a correlation will be interpreted as a ‘PPI’ effect. This is problematic because un-modelled task-related variance is almost inevitably present in every experiment—other obvious sources would be variations in the participant’s level of attention, response to errors and learning effects. Furthermore, any non-linearities in the coupling between neural activity and the signal as measured by fMRI would not be modelled by the linear confound regressor for the task, and hence could possibly drive a spurious PPI effect. Users of PPI should bear these confounds in mind when interpreting their results.

SUMMARY

PPI analysis is a technique for investigating task-specific changes in functional connectivity, defined as task-specific changes in the relationship between brain areas. A task-specific increase in functional connectivity between areas is usually interpreted in terms of an increased flow of information between brain areas during that task. Task-based functional connectivity analysis therefore provides information about brain function, which is complementary to both task-based fMRI studies, which indicate which brain areas are involved in a task, and resting-state functional connectivity which investigates the brain’s intrinsic functional network architecture in the absence of external driving stimuli.

Detailed instructions on how to run PPI

Step by step instructions on how to run a PPI in FSL can be found on the corresponding author’s website: http://www.fmrib.ox.ac.uk/Members/joreilly/what-is-ppi. Instructions for running a PPI in SPM can be found in the SPM8 manual, www.fil.ion.ucl.ac.uk/spm/doc/manual.pdf

Conflict of Interest

None declared,