Extracellular Ca²⁺ Depletion Contributes to Fast Activity-Dependent Modulation of Synaptic Transmission in the Brain

Summary

Synaptic activation is associated with rapid changes in intracellular Ca²⁺, while the extracellular Ca²⁺ level is generally assumed to be constant. Here, using a novel optical method to measure changes in extracellular Ca²⁺ at high spatial and temporal resolution, we find that brief trains of synaptic transmission in hippocampal area CA1 induce transient depletion of extracellular Ca²⁺. We show that this depletion, which depends on postsynaptic NMDA receptor activation, decreases the Ca²⁺ available to enter individual presynaptic boutons of CA3 pyramidal cells. This in turn reduces the probability of consecutive synaptic releases at CA3–CA1 synapses and therefore contributes to short-term paired-pulse depression of minimal responses. This activity-dependent depletion of extracellular Ca²⁺ represents a novel form of fast retrograde synaptic signaling that can modulate glutamatergic information transfer in the brain.

Introduction

At most glutamatergic synapses, transmission involves a rapid flux of Ca²⁺ from the synaptic cleft into pre- and postsynaptic structures, both through voltage-gated channels and via ionotropic receptors. Because exocytosis has a steep and supralinear dependence on Ca²⁺ influx (Dodge and Rahamimoff, 1967; Goda and Stevens, 1994; Kamiya and Zucker, 1994), even modest extracellular Ca²⁺ depletion could have a profound effect on transmission. Such an effect would have far-reaching implications for synaptic communication in the brain (Brown et al., 1995; Egelman and Montague, 1998). Activity-dependent decreases in extracellular Ca²⁺ can be detected using ion-selective recording techniques, but these require very intense and prolonged trains of stimuli (Nicholson et al., 1978; Krnjevic et al., 1982; Mody and Heinemann, 1986). Although it has not been possible to measure fast transients of extracellular Ca²⁺ on a scale compatible with activation of individual synapses, useful insights have come from biophysical modeling. Simulations based on analytical considerations (Vassilev et al., 1997) or detailed compartmental models of the synaptic environment (Egelman and Montague, 1998, 1999; Rusakov et al., 1999; King et al., 2001; Rusakov, 2001) suggest that rapid, activity-dependent shifts in extracellular Ca²⁺ concentration, [Ca²⁺]_o, could occur following a single presynaptic action potential.

Initial experimental evidence for partial Ca²⁺ depletion in the synaptic cleft has emerged from recent electrophysiological studies of giant synapses. First, in calyxtype synapses in the auditory brainstem, fast Ca²⁺ influx was decreased following a prolonged (~100 ms) depolarization of the pre- or postsynaptic membrane, which was attributed to Ca²⁺ depletion in the cleft (Borst and Sakmann, 1999). Second, in the chick ciliary ganglion, the postdepolarization tail current in the presynaptic terminal was increased when the postsynaptic cell was removed, leaving the terminal exposed to the external medium (Stanley, 2000). However, there has been no experimental evidence that such depletion occurs at common types of central synapses, let alone that it has any functional consequences for fast synaptic transmission under physiological conditions. Here, using a novel optical method that allows extracellular Ca²⁺ transients to be detected at high resolution, we show that brief trains of stimuli evoke significant depletion of extracellular Ca²⁺. Furthermore, we show that this phenomenon depends in large part on activation of postsynaptic NMDA receptors (NMDARs). We then detect an effect of interfering with postsynaptic NMDARs on presynaptic Ca²⁺ influx in individual axonal boutons and demonstrate the consequences for activity-dependent plasticity of minimal (mainly single quantum) synaptic responses. The results show that depletion of extracellular Ca²⁺ plays a far greater role in synaptic communication than previously suspected, providing a retrograde signal of postsynaptic activation and contributing to limit the rate of anterograde information transfer.

Results

Measuring Extracellular Ca²⁺ with a Fluorescent Probe

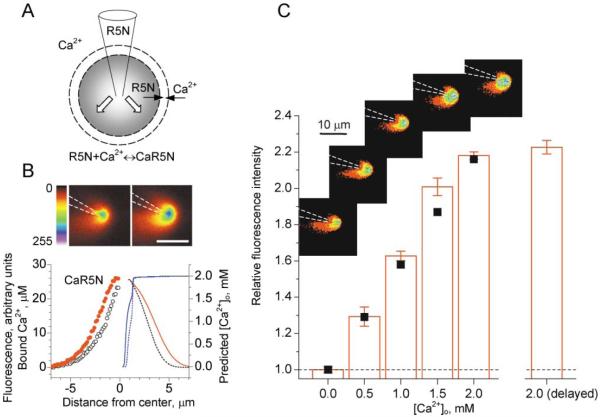
It has not previously been possible to detect external Ca²⁺ transients in the synaptic neuropil with extracellular fluorescent indicators, mainly because physiological concentrations of Ca²⁺_o (1–3 mM) will saturate all known indicators. Lowering the external Ca²⁺ below the saturation level is not useful at central synapses because of the profound resulting reduction in transmitter release probability (see below). To overcome this difficulty, we devised a simple dynamic probe, wherein an impermeant low-affinity Ca²⁺ indicator is delivered locally to the extracellular space via a pressurized patch pipette. When the Ca²⁺ indicator is ejected from the pipette into a Ca²⁺-containing medium (Figure 1A), its level will decrease as it diffuses away, and, simultaneously, the ratio of bound to free indicator will increase. To test this principle, we ejected the Ca²⁺ indicator Rhod-5N (K_d = 320 μM; 3 mM diluted in Ca²⁺-free ACSF) continuously from a pipette positioned in Ca²⁺-containing ACSF. We imaged the Ca²⁺-dependent fluorescence in a focal plane passing through the pipette tip, using two-photon excitation (Figure 1B), at two fixed values of the applied pressure (5 kPa and 10 kPa). To establish the biophysical mechanisms that could explain the observed fluorescence profiles, we simulated diffusion, binding, and unbinding of Ca²⁺ ions and Rhod-5N molecules using a multicompartmental model (Rusakov, 2001). This included parameters to describe the continuous ejection flux and three diffusing components: free Ca²⁺, free indicator, and Ca²⁺-bound indicator (see Experimental Procedures for details). Simulations predicted that the level of free Ca²⁺ should rapidly decrease toward the pipette tip (blue lines in Figure 1B). Importantly, the simulated profile of bound Ca²⁺ (red solid line in Figure 1B) could be matched with the experimental fluorescence profile (red circles in Figure 1B) using a single adjustable parameter in the model, the ejection flux rate. Decreasing this parameter 2-fold yielded a reasonable agreement with the experimentally observed change in the fluorescence profile (black dotted line, black open circles, Figure 1B); this reflects the prediction that the pressure in the probe should be roughly proportional to the efflux rate (in the laminar flow approximation). These data show that the biophysical model can satisfactorily explain the operation of the probe. To test the probe’s sensitivity to Ca²⁺, we measured average fluorescence within a 5 μm circle centered at the pipette tip while changing the Ca²⁺ concentration in the bath (insets in Figure 1C). A summary of these experiments is plotted in Figure 1C (columns) showing that the probe is responsive to [Ca²⁺]_o over the range 0–2 mM, with a sensitivity of ~2% per 100 μM. When we simulated this experiment by varying free Ca²⁺ in our computer model, the corresponding average level of bound Ca²⁺ near the pipette tip (square symbols in Figure 1C) matched the experimental dependence (bars in Figure 1C).

Figure 1. Extracellular Fluorescence Probe.

(A) Pressure application of Ca²⁺ indicator Rhod-5N (R5N; K_d = 0.32 mM) through a pipette results in a three-component diffusion-reaction in the extracellular space, as depicted; white arrows indicate the ejection flux drag; dashed circles illustrate a concentric shell within which diffusion, binding, and unbinding of Rhod-5N molecules and Ca²⁺ ions are calculated by the model explicitly.

(B) (Upper panels) Fluorescence profile near the probe pipette (3 mM Rhod-5N in Ca²⁺-free ACSF) obtained at two values of applied pressure (+5 kPa and +10 kPa, respectively; [Ca²⁺ ]_o = 2 mM, λ_ex = 810 nm; average of ten frames; scale bar, 10 μm; increasing fluorescence intensity indicated by colors from red through yellow and green to blue). (Graph) Circles (left ordinate, relative units), fluorescence profiles near the pipette tip at 10 kPa (red solid) and 5 kPa (black open); red and black lines (left ordinate, μM), the respective profiles of bound Ca²⁺ predicted by a multicompartmental model (see Experimental Procedures); to fit the experimental curve, the single unknown/adjustable parameter, the peak ejection rate through the pipette tip, was set at 0.50 m/s (red) and then changed to 0.25 m/s (black) to test the model prediction. Blue lines (solid and dotted, right ordinate), predicted free Ca²⁺ level at the same model settings.

(C) (Insets) Fluorescence profiles near the probe tip (average of ten frames 30 s apart; false colors as above) throughout one experiment at different [Ca²⁺]_o levels, as shown. Graph columns, mean brightness within a 5 μm circle around the pipette tip (average of n = 3 experiments); values are normalized with respect to the baseline level and corrected for focus drift over 20 frames (10 min). The final value [“2.0 mM (delayed)”] was obtained 20 min after the last increase of Ca²⁺. Black squares, level of bound Ca²⁺ near the pipette tip (relative values), as predicted by the diffusion model, with parameters as in (B); the two lowest computed values (at [Ca²⁺]₀ = 0 and 0.5 mM) were normalized with respect to the experimental fluorescence values. Scale bars, SEM.

Synaptic Responses Induce Extracellular Ca²⁺ Depletion

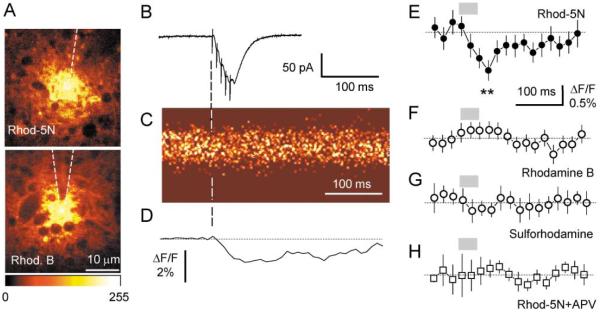
We placed the same probe 50–100 μm deep in an acute hippocampal slice (CA1 stratum radiatum). Fluorescence near the tip arises from the extracellular space; cytosolic compartments appear dark (Figure 2A). We then applied five electric stimuli (at 100 Hz) to the stratum radiatum in area CA1 200–500 μm from the probe and recorded either EPSCs from a CA1 pyramidal cell (whole-cell mode, see Figure 2B) or field EPSPs, in the vicinity of the probe. Fluorescence near the probe tip was imaged, simultaneously with electrophysiological recording, in line scan mode with 2 ms resolution, as illustrated in Figures 2B and 2C. These experiments revealed a small (up to 2% in individual experiments, e.g., Figure 2D) but significant decrease in Ca²⁺-dependent fluorescence. The average fractional change in fluorescence (ΔF/F) 45–55 ms after the first stimulus was −0.87 ± 0.21% (mean ± SEM, p < 0.006, n = 11; Figure 2E). This decrease was small but robust and could be detected after the first stimulus (Figure 2D). It decayed with a time constant of 143 ± 42 ms (single exponent) after the last stimulus.

Figure 2. Detection of Extracellular Ca²⁺ Transient with Fluorescence Probe.

(A) Characteristic appearance of extracellular fluorescence near the probe tip ~80 μm deep into the CA1 stratum radiatum area of an acute hippocampal slice; with two-photon excitation at 810 nm. Fluorescence from Ca²⁺-sensitive (3 mM Rhod-5N, upper panel) and Ca²⁺-insensitive (3 mM Rhodamine B, lower panel) probes appears similar, with cytosolic compartments visible as dark lacunae; color bar shows fluorescence scale (arbitrary units).

(B–D) Five stimuli (100 Hz) applied to stratum radiatum elicited EPCSs in a CA1 pyramidal cell near the probe (trace in [B], recorded in whole-cell mode, V_m = −70mV) and a transient decrease in the Rhod-5N probe fluorescence (line scan image in [C]; individual experiment shown) with an amplitude of ~2% ΔF/F (trace in [D], average of ten scans; five points averaging).

(E–H) Average fluorescence transient detected by probe with Rhod-5N ([E], n = 11; asterisks, average fractional fluorescence change, ΔF/F, 45–55 ms after the first stimulus: −0.87% ± 0.21%, p < 0.006), Rhodamine B ([F], n = 9), sulforhodamine ([G], n = 8), and Rhod-5N in the presence of 25 μM D-APV ([H], n = 9). Gray segments indicate application of five stimuli; dotted line, baseline; scale bars, SEM.

To test whether any extraneous optical effects of electric stimulation (e.g., changes in light scattering due to volume fluctuations) contributed to this fluorescence signal, we repeated these experiments using Rhodamine B and sulphorhodamine, respectively, highly lipophilic and nonlipophilic Ca²⁺-insensitive fluorophores with spectral properties similar to Rhod-5N. No significant response was seen with either fluorophore (Figures 2F and 2G; the small residual wave, which was similar for all control experiments, may reflect stimulus-evoked volume fluctuations). A possible artifact due to extracellular pH shift (i.e., an expected small, synaptically evoked alkaline shift of ~0.01 pH unit [Krishtal et al., 1987]) can also be discounted, since at pH > 5 Rhodamine-type fluorophores are relatively insensitive to pH changes (Kojima et al., 2001). Given the probe calibration reference (Figure 1C; see also Experimental Procedures), the observed ~1% decrease in fluorescence could be interpreted as a transient mean decrease in [Ca²⁺]_o over the sensed volume in the range of 40–50 μM.

What are the main Ca²⁺ sinks that might underlie this transient? Multicompartmental models of perisynaptic Ca²⁺ depletion (Egelman and Montague, 1999; Rusakov, 2001) suggest that the postsynaptic sinks driven by activation NMDARs could serve as a major contributor to any prolonged change in [Ca²⁺]_o. Indeed, when we applied D-2-amino-5-phosphonopentanoic acid (D-APV), a selective blocker of NMDARs, the fluorescent transient was reduced by >80% (average ΔF/F at 45–55 ms after the first stimulus: −0.13% ± 0.15%, p < 0.016 compared to ΔF/F at 45–55 ms without APV, n = 8; Figure 2H).

We conducted similar experiments in cultured hippocampal slices with a different Ca²⁺-sensitive indicator, Calcium Orange 5N (K_d = 20 μM), using fast confocal imaging (30–60 frames/s). These gave similar results: the average ΔF/F over 30–60 ms postonset was −0.87% ± 0.29%, (p < 0.016, n = 6); the control series with Rhodamine B showed no detectable response (average ΔF/F: −0.06% ± 0.21%, n = 5; see Experimental Procedures for details).

Could such a small fluctuation in [Ca²⁺]_o have any physiological significance? Because the detected signal reflects a volume-average change in the Ca²⁺-dependent fluorescence, it will underestimate local changes in [Ca²⁺]_o. Common sense suggests, and detailed biophysical modeling predicts, that Ca²⁺ depletion should be more profound in the vicinity of open Ca²⁺ sinks, e.g., within the synaptic cleft (King et al., 2001; Rusakov, 2001). These small volumes (an average synaptic cleft in CA1 occupies 6–8 × 10⁻⁴ μm³, assuming synaptic cleft width of ~20 nm and postsynaptic density area of 0.03–0.04 μm² [Schikorski and Stevens, 1997; Rusakov et al., 1998; Shepherd and Harris, 1998]) are below the optical resolution of laser scanning microscopy, where the fluorescence signal is integrated over a minimum tissue volume of ~0.1 μm³. Furthermore, such “hotspots” of depletion are likely to represent only a small fraction of the tissue volume: only ~2% of the extracellular space can be attributed to synaptic clefts in the hippocampus (Rusakov et al., 1998). Because the estimated change in average [Ca²⁺]_o is 40–50 μM, this finding could be interpreted as an almost total depletion of Ca²⁺ (i.e., to levels similar to intracellular) at all active synapses in the area (but see below). Alternatively, it could reflect a more moderate and/or heterogeneous depletion over a larger volume.

Activation of NMDARs Reduces the Ca²⁺ Available to Enter Axonal Boutons

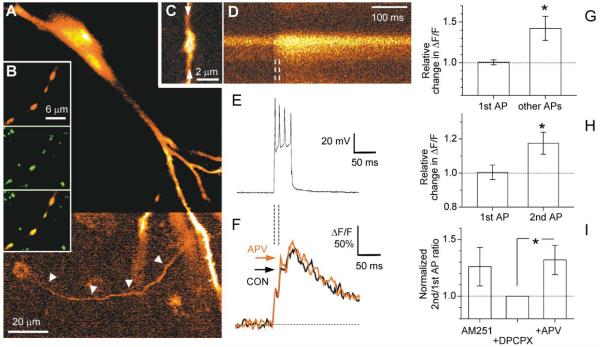
Ca²⁺ depletion should have extensive consequences for transmitter release: it should decrease the subsequent release probability by reducing the presynaptic action potential (AP)-evoked Ca²⁺ influx. We asked, therefore, whether we could facilitate Ca²⁺ influx into axonal terminals during repetitive spikes by blocking the putative Ca²⁺ sinks at these synapses, which we identified as NMDAR-mediated conductances (see above). To test this possibility, we recorded AP-evoked Ca²⁺ transients in axon boutons of CA3 pyramidal cells using fast confocal imaging. In cultured hippocampal slices, CA3 cells were impaled with a sharp electrode filled with a mixture of fluorescent Ca²⁺-sensitive indicators to increase the concentration-sensitive range of responses (see Experimental Procedures). The axon was followed (Figure 3A) into the stratum radiatum area, where synaptic boutons were clearly distinguishable as discrete varicosities (Figure 3B), as previously described (Emptage et al., 2001). In some instances, the morphological identification of the boutons was confirmed by coinjection of fixable tracers and, at the end of the experiment, by immunohistochemical labeling of the synaptic vesicle-associated protein synaptophysin (Figure 3B; also see Experimental Procedures). Brief trains of APs were elicited by injecting a 75 ms depolarizing current via the intracellular electrode, and the fluorescent Ca²⁺-indicator responses were compared before and after application of 25 μM D-APV. The average number of APs per train remained unchanged in D-APV (4.8 ± 0.6 and 4.6 ± 0.4 before and after application, respectively; n = 11), with 9–15 ms intervals between spikes in both conditions.

Figure 3. The Effect of NMDAR Blockade on Fast, Action Potential-Evoked Ca²⁺ Transients in Presynaptic Boutons.

(A) CA3 pyramidal cell in a cultured hippocampal slice, filled with fluorescent Ca²⁺ indicator by intracellular injection and imaged by confocal microscopy (488 nm excitation, see Experimental Procedures); color look-up table for the lower half of the image was adjusted to render the axon visible (arrowheads).

(B) (Upper panel) Axon segment with four varicosities (2% Cascade blue-biocytin labeling); (middle panel) the same segment labeled for synaptophysin immunoreactivity (SY38 antibody/Cy2-labeled IgG); (lower panel) overlay of the two upper images, with precise colocalization indicating that the varicosities are synaptic terminals; see Experimental Procedures for details.

(C) Axonal bouton (CA3 pyramidal cell, acute slice) imaged using Alexa Fluor 594 coinjected with Ca²⁺ indicator Fluo-4 (two-photon excitation at 810 nm); arrows, trajectory of the line scan in (D).

(D and E) Line scan of the Ca²⁺ indicator fluorescence transient ([D], average of ten traces; increasing fluorescence intensity indicated by colors from red through yellow to white) evoked by the brief train of action potentials shown in the simultaneous whole-cell current clamp recording (E).

(F) Average fluorescence (ΔF/F) in line scans (average of ten traces) of the bouton illustrated in (C) and (D), before (black line, CON) and after (red line, APV) application of 25 μM D-APV; arrows indicate peak fluorescence responses to the second spike.

(G) Average changes (relative to control) in AP-evoked bouton Ca²⁺ fluorescence monitored in hippocampal slice cultures, following application of 25 μM D-APV. 1st AP, average change in ΔF/F corresponding to the 1st spike (+0.5% ± 3.0%, n = 11; integrated over 0–10 ms after stimulus onset); Other APs, average change in the ratio between ΔF/F integrated over 10–100 ms after stimulus onset and ΔF/F integrated over 0–10 ms after stimulus onset (+42% ± 15%, p < 0.024, n = 11); single-photon excitation at 488 nm.

(H) Average changes in AP-evoked bouton Ca²⁺ fluorescence monitored in acute hippocampal slices, following application of 25 μM D-APV. 1st AP, average change in ΔF/F corresponding to the 1st spike (+0.4% ± 4.3%, integrated over 0–8 ms after the 1st spike onset; n = 10); 2nd AP, average change in the ratio between ΔF/F signals corresponding to the 2nd spike (integrated over 0–20 ms after the 2nd spike onset) and 1st spikes (+17% ± 6%, p < 0.022, n = 10); two-photon excitation at 810 nm.

(I) Blockade of adenosine and cannabinoid receptors does not affect NMDAR-dependent changes in Ca²⁺ transients. In acute slices incubated with 2 μM AM251, further incubation with 2 μM DPCPX reduces (insignificantly) the 2nd/1st ΔF/F (change −20% ± 14%, n = 6; see text), while the effect of APV remains (change +32% ± 14%, p < 0.05, n = 7). Dotted line, baseline level; scale bars, SEM.

These experiments were intended to test the hypothesis that blocking NMDAR-dependent Ca²⁺ sinks would reduce extracellular Ca²⁺ depletion following the first successful release, thereby enhancing Ca²⁺ influx into the bouton during the second and/or subsequent spikes. Because fluorescence transients in response to individual spikes in the train could not be easily distinguished in these recordings, we divided the entire fluorescence response into an “initial ΔF/F” (integrated over 0–10 ms interval after stimulus onset) and a “delayed ΔF/F” signal (integrated over 10–100 ms poststimulus). Since the interspike intervals were longer than 8–9 ms, the initial ΔF/F reflected the Ca²⁺ response to the first spike only. To test our hypothesis, we therefore calculated the ratio between the delayed and initial ΔF/F, with and without D-APV.

Similar experiments were carried out in acute slices where CA3 cells were held in a current clamp, whole-cell mode and filled with two fluorescent indicators, one to detect Ca²⁺ transients (0.2 mM Fluo-4) and one to trace axon morphology (40 μM Alexa Fluor 594). Both indicators were excited in two-photon mode and their emitted fluorescence separated at ~560 nm by a dichroic mirror. Individual axonal boutons (Figure 3C) were imaged (Figure 3D) while a brief train of APs was generated by a 50 ms depolarizing current (Figure 3E). In these experiments, the fluorescence responses to the first and second APs were often readily discernable, as illustrated in Figures 3D–3F. We therefore tested our hypothesis by calculating the ratio between the ΔF/F amplitudes in response to the second and first APs, with and without D-APV.

A statistical summary of the results is depicted in Figures 3G and 3H. It shows that D-APV increases the “delayed-to-initial” ΔF/F ratio by 42% ± 15%, (p < 0.024, n = 11) in cultured slices and the “second-to-first” ΔF/F ratio by 17% ± 6% (p < 0.022, n = 10) in acute slices. At the same time, the Ca²⁺-dependent response to the first spike was not affected in either preparation (average change in ΔF/F: +0.5% ± 3.0% and +0.4% ± 4.3%, respectively). We also tested whether these phenomena could be explained by the inhibitory presynaptic actions of endogenous retrograde messengers, such as adenosine or cannabinoids, which might be released postsynaptically in an NMDA- or depolarization-dependent manner (Manzoni et al., 1994; Wilson and Nicoll, 2001). In slices preincubated with the CB1 antagonist AM251 (Wilson and Nicoll, 2001), the adenosine receptor antagonist DCPCX (2 μM) did not reduce the APV-dependent increase in the second-to-first ΔF/F ratio (Figure 3I; change +32% ± 14%, p < 0.05, n = 7). (Figure 3I also illustrates that the average second-to-first ratio was reduced, albeit insignificantly, in DCPCX compared to baseline; this reduction could be the consequence of the increased probability of the first synaptic releases, which is expected to occur in DCPCX [Manzoni et al., 1994].) These data indicate that blocking NMDAR activation during a single synaptic release can facilitate Ca²⁺ influx into the presynaptic terminal during subsequent action potentials, at least within a short (10 ms or less) time period.

Synaptically Evoked Ca²⁺ Depletion Reduces the Probability of Subsequent Transmitter Release

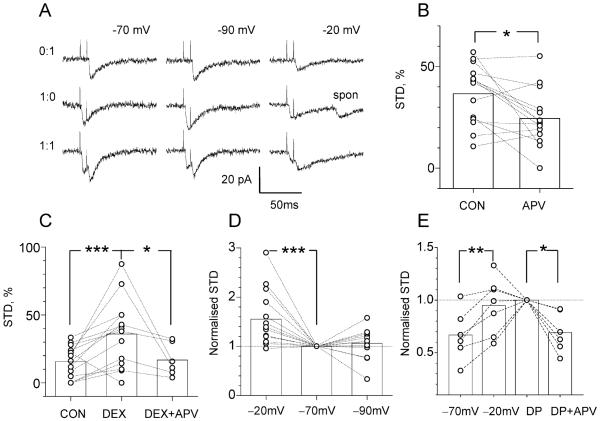
If there is significant extracellular Ca²⁺ depletion for some period after glutamate release, the probability that a second action potential during that period will evoke transmitter release should be reduced as a consequence of the diminished presynaptic Ca²⁺ influx. It is known that the release probability at individual stratum radiatum synapses in acute hippocampal slices is reduced for ~20 ms following a single successful release (Stevens and Wang, 1995). Although this phenomenon, here termed short-term depression (STD), has classically been attributed to the temporary depletion of readily releasable synaptic vesicles (Thies, 1965; Stevens and Tsujimoto, 1995; Stevens and Wesseling, 1999), other contributing mechanisms have not been ruled out (Dobrunz et al., 1997; Bellingham and Walmsley, 1999). The results of the experiments just described (Figures 1-3) suggest that synaptically evoked extracellular Ca²⁺ depletion could contribute to STD. To test this, we recorded from CA1 pyramidal cells in whole-cell mode and applied paired stimuli (8 ms interstimulus interval) under minimal stimulation conditions according to the criteria of Stevens and Wang (1995). The observed unitary (mostly single quantum) responses appeared identical to small spontaneous events and could be unambiguously discriminated from failures (see traces in Figure 4A); the interpulse interval was chosen to be the shortest at which two subsequent unitary EPSCs could be readily distinguished. In this experiment, calculating the success rates for either of the two responses over many trials allowed direct assessment of the underlying release probabilities.

Figure 4. Short-Term Paired-Pulse Depression Involves Postsynaptic NMDA Receptors, in a Voltage-Dependent Manner.

(A) Examples of single quantum EPSCs elicited by minimal stimulation with two stimuli 8 ms apart, at holding voltage of −70mV, −90mV, and −20mV, as indicated, in the same cell; three characteristic types (0:1, 1:0, 1:1) of successful response are shown (double failure, 0:0, response is not shown); spon, spontaneous EPSC that appears identical to the minimal evoked EPSC.

(B) APV decreases STD (see Experimental Procedures) by 26% ± 11% (p < 0.012, n = 14; cultured slices), with no effect on the baseline release probability (p_r: 0.44 ± 0.04 and 0.42 ± 0.04, respectively).

(C) Dextran increases STD by 137% ± 41% (p < 0.01, n = 14; acute slices), with no effect on the baseline release probability (p_r: 0.48 ± 0.04, 0.48 ± 0.05, and 0.42 ± 0.06, respectively); the effect of dextran is reversed by addition of APV (p < 0.024, n = 6; acute slices).

(D) Changing the holding voltage from −70mV to −20mV increases STD by 55.4% ± 15.0% (p < 0.005, n = 14; acute slices), whereas a change from −70mV to −90mV has no effect (change 6.0% ± 8.5%, n = 13; acute slices); data are normalized with respect to the baseline STD (at −70mV) in each cell. Throughout the experiments, the STD occurred against a background of baseline paired-pulse facilitation, with the absolute probability ratio “2nd EPSC/1st EPSC” of 1.42 ± 0.11 (series in [B]), 1.85 ± 0.19 (C), and 1.42 ± 0.14 (D).

(E) Activation of presynaptic adenosine or cannabinoid receptors does not affect NMDAR-dependent STD. In acute slices (preincubated in 2 μM AM251), increase in STD from −70mV to −20mV (change +39% ± 11%, p < 0.008, n = 6) is not reversed by incubation in 2 μM DPCPX (DP; change +14% ± 13%, n = 7) but is reversed by application of APV (DP + APV; change −31% ± 8%, p < 0.05, n = 6).

As expected, the absolute probability of the second successful EPSCs was consistently higher (1.5 to 2.0 times) than that of the first, which is a common consequence of the residual Ca²⁺ that persists within the terminal following the first spike (Kamiya and Zucker, 1994; Carter et al., 2002). Yet the probability of the second EPSC was significantly reduced when the first EPSC was successfully generated, which has been attributed to the occurrence of STD at these synapses (Stevens and Wang, 1995). We assessed this STD simply by calculating the proportion (relative probability) of second EPSC failures among all trials where the first EPSC was successful, as detailed in the Experimental Procedures. We then used this estimate to investigate whether blockade of the main Ca²⁺ sinks (NMDAR-driven conductances) would affect STD. Results of such experiments in cultured slices are shown in Figure 4B and demonstrate a 26% ± 11% reduction in STD in the presence of D-APV (p < 0.012, n = 14), with no significant effect of D-APV on the baseline release probability (p_r: 0.44 ± 0.04 and 0.42 ± 0.04, respectively). These results suggest that single activation of a single synapse is capable of inducing an NMDAR-dependent, transient Ca²⁺ depletion in the cleft. That a single synaptic release could activate NMDARs under conditions of voltage clamp (V_m = −70mV) and 1 mM Mg²⁺ was surprising, suggesting a significant soma-dendrite voltage drop in these cells. When we reviewed our recordings in these cultured slice preparations, however, it appeared that in more than 25% of the cases, the recorded trials were discarded because CA1 pyramidal cells actually fired action potentials in response to a minimal stimulus (data not shown). This indicates that, indeed, even a single synaptic activation in these cultured slices could produce a local depolarization sufficient to activate NMDARs. Because such strong depolarization had not been reported in acute slices, we carried out two other sets of experiments to assess the role of Ca²⁺ depletion in the latter preparations.

First, we lowered extracellular diffusivity by adding 5% dextran (40 kDa) to the superfusate, as described previously (Min et al., 1998; Perrais and Ropert, 2000), which reduces the water self-diffusion coefficient (measured with nuclear magnetic resonance) by 20%–25% (Watanabe et al., 1996) without any effects on the hippocampal slice morphology (Newman et al., 1995). Our hypothesis was that retarding extracellular diffusion should both increase activation of synaptic receptors (Min et al., 1998; Rusakov and Kullmann, 1998) and deepen any consequent extracellular Ca²⁺ depletion per se (Egelman and Montague, 1999; Rusakov, 2001), resulting in greater STD. These experiments (Figure 4C) demonstrated that dextran increased STD by 137% ± 41% (p < 0.004, n = 14); this increase was effectively reversed by D-APV (p < 0.024, n = 6; Figure 4E). Again, neither dextran nor D-APV had any significant effects on the baseline release probability (p_r, control: 0.48 ± 0.04, dextran: 0.48 ± 0.05, D-APV: 0.42 ± 0.06), thus ruling out any changes in presynaptic excitability during these manipulations. These data were therefore consistent with the hypothesis that retarded diffusion enhances the effects of NMDAR-dependent synaptically evoked extracellular Ca²⁺ depletion.

It remained uncertain, however, whether such depletion phenomena could be observed in acute slices under baseline conditions, i.e., without dextran. To establish this, we tested whether STD is affected when the postsynaptic voltage changes from −70mV to −20mV or to −90mV, which should, respectively, either relieve or enhance the Mg²⁺ block of NMDARs. As illustrated in Figure 4A, recorded minimal EPSCs lasted much longer at −20mV compared to −70mV, reflecting an enhanced contribution of NMDARs to the synaptic current. The summary of these paired-pulse experiments is depicted in Figure 4D, showing that depolarization of the postsynaptic cell increased STD by 55.4% ± 15.0% (p < 0.01, n = 14). This phenomenon cannot be readily accounted for by presynaptic mechanisms of vesicle release but is consistent with enhanced transient Ca²⁺ depletion in the synaptic cleft due to postsynaptic sinks. Similarly, the increased STD cannot be explained by the reduced signal-to-noise ratio for EPSCs recorded at −20mV, because the latter would overestimate the proportion of successful pairs of EPSCs versus successful single events (two superimposed EPSCs are more discernable from the noise than one) and therefore underestimate, rather than overestimate, the extent of STD at V_m = −20mV. In contrast, changing the holding voltage from −70mV to −90mV had no effect on STD (average change +6.0% ± 8.5%, n = 13, Figure 4D). This shows that, to obtain a Ca²⁺ depletion effect, the postsynaptic membrane must be, at least locally and transiently, depolarized. In control experiments (Figure 4E), preincubation of slices in AM251 (see above) did not eliminate the depolarization-dependent increase in STD, and subsequent application of DPCPX did not reverse this increase either: the increase, however, was successfully reversed by application of D-APV (Figure 4E). These data argue against a contributing role of the potential retrograde messengers, cannabinoids and adenosine, in the NMDAR-dependent STD component.

Discussion

The main results of this study are as follows. First, postsynaptic responses at CA3–CA1 synapses induce transient depletion of extracellular Ca²⁺; this phenomenon is NMDAR dependent. Second, NMDAR blockade increases the Ca²⁺ available to enter axonal boutons of CA3 pyramidal cells. Finally, interference with postsynaptic NMDARs affects the probability of consecutive synaptic releases at CA3–CA1 synapses, indicating a role for Ca²⁺ depletion in short-term synaptic plasticity.

How long could this Ca²⁺ depletion remain significant in the cleft? Our imaging data (Figure 2) show a Ca²⁺-dependent extracellular fluorescence transient that lasts tens of milliseconds. However, the integrated fluorescence, as discussed above, does not distinguish between hot spots of significant depletion near Ca²⁺ sinks and a small decrement of [Ca²⁺]_o that may decay slowly, over a larger tissue area, when the sinks are closing (Rusakov, 2001). Previous fast Ca²⁺ imaging in axonal boutons of neocortical pyramidal cells has shown that the fluorescence transient evoked by an AP remains remarkably stable during long trains of stimuli at frequencies up to 75 Hz, implying that any intracleft Ca²⁺ depletion at these synapses is not functionally significant beyond ~14 ms (Koester and Sakmann, 1998). However, at a stimulation frequency of 100 Hz, the later spikes generated a fluorescence transient which was ~80% of the initial amplitude (Koester and Sakmann, 1998). This result is consistent with our observation that D-APV facilitates the fluorescence response to the second spike by ~14% when the interspike interval is in the range of 9–10 ms (Figure 3E). A similar conclusion could be drawn from a study where STD in superior colliculus synapses, monitored by field EPSP recordings under conditions of low stimulus intensity, was apparently reduced by application of D-APV at interpulse intervals of 10 ms but not 40 ms or longer (Platt and Withington, 1997). On the other hand, it has been shown that hyperpolarizing the postsynaptic cell increases paired-pulse facilitation of the pharmacologically isolated NMDA (but not of the isolated AMPA) component of EPSCs at interpulse intervals of 25 ms or more (Clark et al., 1994), and recent reports attribute a similar phenomenon to positive ephaptic feedback at these synapses (Berretta et al., 2000). Although these findings are in principle compatible with our STD data (Figure 4), any role of Ca²⁺ depletion in STD at longer interpulse intervals requires further investigation. Also, the present finding that STD was not affected by changing the holding voltage from −70mV to −90mV (Figure 4D) is consistent with the view that, under conditions of voltage clamp at −70mV or lower in acute slices, the main contributor to STD of minimal responses is depletion of a readily releasable synaptic vesicle pool (Stevens and Wang, 1995). The role of Ca²⁺ depletion, however, is likely to become substantial whenever the local depolarization transient at the postsynaptic cell (e.g., due to multiquantal synaptic input or to a dendritic spike) allows activation of NMDAR-dependent Ca²⁺ sinks. At least in cultured slice preparations, such depolarization occurs even with minimal stimulation (Figure 4B and Emptage et al., 1999).

How large could the NMDAR-dependent Ca²⁺ depletion be within the synaptic cleft? Although this cannot be directly determined from the extracellular Ca²⁺ measurements (Figure 2), as discussed above, our results provide two independent parameters that might be relevant for such estimates: the reduction in presynaptic Ca²⁺ influx (Figure 3) and the increase in STD (Figure 4) following application of D-APV. According to a classical view, synaptic release of neurotransmitter increases with the fourth power of external Ca²⁺ concentration (Dodge and Rahamimoff, 1967). A similar relationship appears to hold for internal Ca²⁺ concentration and release (Zucker, 1996). Assuming that the fluorescence responses to individual spikes recorded here (Figures 3D–3F) are roughly proportional to the underlying increases in intracellular Ca²⁺ (Maravall et al., 2000), the average 17% increase in Ca²⁺ response to the second spike in D-APV (Figure 3H) should correspond to a 1.17⁴ = 1.87-fold increase in the success rates of the second EPSC. Our STD results (Figure 4D) indicate that in fact a 1.55-fold increase in STD has occurred after the Mg²⁺ block of NMDARs has been relieved by depolarization. Given that the STD increase in the latter result could be underestimated (see above), the consistency between changes in internal Ca²⁺ and STD is not unreasonable. The 17% increase in the Ca²⁺ transient in D-APV also suggests a (1–100/117) = 15% underlying decrement in the intracleft Ca²⁺ under normal conditions (Zucker, 1996), which is ~0.3 mM for the baseline of 2 mM. This value must be “diluted” six to eight times to match the estimated amplitude of the space-averaged [Ca²⁺]_o transient of 40–50 μM (Figure 2; see above), suggesting therefore that activated Ca²⁺ sinks in our experiments are localized to 10%–15% of the extracellular volume. Given that there are probably at least as many NMDARs and voltage-driven Ca²⁺ channels outside the cleft (in total) as inside, this value appears quite plausible. At the same time, the decay constant of the observed fluorescence transient (~143 ms, Figure 2E) is consistent with the decay properties of the simulated volume-average extracellular Ca²⁺ transient that should follow a fast wave of Ca²⁺ influx (Rusakov, 2001).

Is it possible to detect Ca²⁺ depletion using direct bath application of Rhod-5N? Simple calculations (see equation in Experimental Procedures) show that, to approach the sensitivity of the pipette probe (~1% ΔF/F for 2% depletion, see Figure 1), [Ca²⁺]_o should be reduced to 0.3–0.4 mM. However, when we lowered external Ca²⁺ to 0.4 mM (and Mg²⁺ to 0.1 mM), the evoked synaptic responses were dramatically reduced, which is explained by a sharp decrease in the release probability in low Ca²⁺. With a stimulation strength increased several-fold to match baseline responses, it was possible to detect an ~1% ΔF/F depletion signal (averaged over 11 recording sites; data not shown) using 25 μM Rhod-5N in the bath. Although this result is consistent with our probe measurements (Figure 2), this approach does not appear useable under physiological conditions (normal Ca²⁺/Mg²⁺).

Is there any alternative explanation for our results? Activation of presynaptic metabotropic glutamate receptors could in principle reduce the second release probability following a successful first release (Baskys and Malenka, 1991), but such effects would be independent of activation of postsynaptic NMDARs or postsynaptic depolarization. Although presynaptic NMDARs have recently been observed at a variety of synapses, they would, if present, be expected to have effects inconsistent with those described here, because the reported phenomena indicate either an NMDA-dependent enhancement of synaptic release (Liu et al., 1997; Cochilla and Alford, 1999) or no effect on release probability per se (Casado et al., 2000). In fact, since NMDARs are Ca²⁺ permeable, blockade of presynaptic NMDARs would decrease the presynaptic Ca²⁺ influx that follows the initial Ca²⁺ rise in the terminal, whereas we observed the opposite (Figure 3). We also note that the critical role of NMDAR activation in Ca²⁺ depletion does not preclude the possible involvement of voltage-gated Ca²⁺ channels or other downstream effectors. Activation of NMDARs is dependent on local depolarization due to AMPA receptor activation, and it would therefore be reasonable to consider both receptor types as important contributors to the synaptically evoked Ca²⁺ depletion.

If such extracellular Ca²⁺ depletion is common, it will influence the efficiency with which information is transmitted through a network, simply by constraining the frequency response of glutamatergic synapses. It is also possible that the brief but substantial activity-dependent Ca²⁺ depletion could contribute to synaptic plasticity, by affecting endogenous [Ca²⁺]_o sensors (Brown et al., 1995) or by modulating adhesion properties of Ca²⁺-dependent molecules such as cadherins that may bind synaptic elements (Tamura et al., 1998).

Finally, this study introduces a novel optical method to measure changes in extracellular Ca²⁺ at high spatial and temporal resolution. This method is based on a simple principle: changes in extracellular Ca²⁺ must interfere with a dynamic equilibrium that results from local injection of a fluorescent Ca²⁺ indicator. We believe that this dynamic equilibrium principle could be used to monitor other ions, in other tissues.

Experimental Procedures

Preparation and Electrophysiology

Experiments were carried out either in 3- to 4-week-old organotypic cultures of hippocampal slices (prepared from 8-day-old male Wistar rat pups) as previously described (Yamamoto et al., 1989; Stoppini et al., 1991), with addition of B27 supplements (Emptage et al., 1999), or 350 μm thick acute hippocampal slices from 1-month-old male Wistar rats. Preparations were perfused with ACSF (containing [in mM] NaCl, 120; KCl, 3; MgSO₄, 1; CaCl₂, 2.5; NaH₂PO₄, 1.2; NaHCO₃, 23; glucose, 11; Trolox, 1; picrotoxin, 0.1) and bubbled with 95%O₂/5%CO₂. In confocal imaging experiments, CA3 pyramidal cells in cultures were impaled with a sharp micropipette (100–120 MΩ) tip-filled with Ca²⁺ indicators, as specified below, and back-filled with 3 M K acetate. In whole-cell experiments, patch pipettes (2.5–7 MΩ) contained (in mM) Cs gluconate, 117.5; CsCl, 17.5; EGTA, 0.2; NaCl, 8; Mg-ATP, 2; GTP, 0.3; QX314-Br, 5; HEPES, 10 (pH 7.2, 295 mOsm), unless otherwise specified. Extracellular field recordings were carried out using either a sharp pipette filled with 3 M NaCl or a patch pipette filled with ACSF. Stimuli (100 μs square pulses) were applied to stratum radiatum fibers via bipolar tungsten electrodes. Electrophysiological data were collected using either A/DVANCE software (McKellar Designs, Vancouver) or LabView (National Instruments) interface (kindly provided by D. Kullmann) and analyzed offline.

Fast Laser Scanning Imaging

We used either a modified Bio-Rad MRC1000 confocal scanhead on a Zeiss Axioskop (argon laser excitation at 488 nm; NIMR) or a modified Bio-Rad Radiance 2000 on an Olympus BW50 microscope (two-photon excitation at 810 nm via a fs Ti-Sapphire MaiTai laser, SpectraPhysics; 700SP emission filter; Institute of Neurology–UCL) with a 60× N.A. 0.9 water-immersion objective. Extracellular probe experiments were conducted in acute slices unless otherwise specified; a stimulating electrode was placed in area CA1 stratum radiatum, and either EPSCs from CA1 pyramidal cells or field EPSPs from stratum radiatum were recorded in response to five stimuli at 100 Hz. Once a stable response was achieved, the probe micropipette (tip 2–3 μm) filled with either Rhod-5N, Rhodamine B, or sulphorhodamine (3 mM in Ca²⁺-free ACSF) was lowered into the stratum radiatum, 50–80 μm beneath the slice surface, between the stimulating and recording electrodes. Positive air pressure (+1–10 kPa) was adjusted and kept constant to achieve a steady fluorescence profile; when, within 10–15 min, pressure was released, fluorescence decayed to baseline in several seconds; the distance from the recording electrode was 30–50 μm, to ensure that pressure adjustment/release had no effect on synaptic responses. The probe was kept in the tissue for <15 min, to minimize fluorescent indicator uptake. The laser scanning line was positioned across the pipette tip, and 10 to 12 line scans (256 pixels across, 2 ms per line, triggered 150 ms before the first stimulus onset) were obtained at ~30 s intervals at each stage of the experiment. To optimize performance of the probe and reduce indicator uptake, these experiments were conducted at 25°C.

Fast presynaptic Ca²⁺ influx in CA3 pyramidal cell presynaptic boutons was imaged in cultured slices using ordinary confocal microscopy or in acute slices using two-photon excitation microscopy. In cultures (single-photon excitation at 488 nm), sharp electrodes were tip filled with 200 μM Oregon green BAPTA-1 (OGB1) + 1 mM OGB2 + 1 mM OGB5N in 100 mM K acetate (the mixture of Ca²⁺ indicators with different affinities was used to cover the wide range of Ca²⁺ responses); a 500LP emission filter was used for confocal imaging. In acute slices (two-photon excitation at 810 nm), 200 μM Fluo-4 and 20 or 40 μM Alexa Fluor 594 (ratio established empirically to minimize bleedthrough) were added to the pipette solution (K methanesulfonate-based); an HP560 dichroic mirror separated emission from Alexa Fluor 594 and Fluo-4 for simultaneous dual channel imaging of morphology and Ca²⁺ signals, respectively. Because, as we have shown previously (Emptage et al., 1999), different boutons of the same axon may exhibit distinct physiological properties, we normally recorded from one to three axonal boutons in each cell (Figures 3G, 3H, and 3I represent, respectively, 11 boutons in five cells, 10 boutons in five cells, and 7 boutons in four cells). Ten to thirty control trials (500–600 ms long) were recorded, 10–30 s apart, after which D-APV (25 μM) was washed in and recordings resumed 3–5 min later. Pixel size of 70 nm and 2 ms per scan line was used; experiments were conducted at 33°C–35°C. Fluorescence transients were analyzed offline using NIH-Image and Origin 6.0 (MicroCal). Photobleaching was corrected for by fitting the baseline fluorescence with linear or single exponential regression. All dyes were obtained from Molecular Probes.

Fluorescence Probe: Underlying Biophysics

To simulate this complex diffusion-reaction, we used a multicompartmental model consisting of N thin concentric shells (thickness δR), in exact correspondence with the numerical formulation described in detail earlier for the glutamate diffusion binding model (Rusakov and Kullmann, 1998; Rusakov, 2001). Two main modifications of the existing model were implemented. First, all three components of the diffusion-reaction, free Ca²⁺, free Rhod-5N, and bound Ca²⁺/Rhod-5N, were mobile, with diffusion coefficients of 0.75 μm²/ms, 0.3 μm²/ms, and 0.3 μm²/ms, respectively (Nicholson and Rice, 1987; Sabatini and Regehr, 1998). Consequently, for the ith diffusing component (i = 1, 2, 3), diffusion flux j_i through each shell interface was computed as j_i = −D_iδC_i/δR (Fick’s 1st law), where δC_i is the concentration difference between the adjacent shells; binding and unbinding of Rhod-5N molecules and Ca²⁺ ions were computed explicitly in each compartment at each time step, using a straightforward finite-difference scheme (Rusakov, 2001); the level of Rhod-5N was clamped at 3 mM within the pipette radius (1 μm), and the level of free Ca²⁺ was clamped at 2 mM (unless specified otherwise) at 10 μm from the tip. Our simulations were carried out at N = 100, δR = 0.1 μm; the model was initiated at 2 mM of free Ca²⁺ (and no indicator) throughout the space, and the equilibrated profiles were plotted t = 1000 ms later (in 3 × 10⁶ time steps). The binding and unbinding rates for Ca²⁺/Rhod-5N were set at 10⁴ M⁻¹ms⁻¹ and 3.9 ms⁻¹, respectively, in correspondence with the binding constant obtained for similar Ca²⁺ indicators (Ellis-Davies et al., 1996) and K_d = 320 μM. As a second modification, we set an ejection flow from the pipette tip, defined simply as the stationary radial flux Q(R ) = Q₀R²₀/R² (where Q₀ is the peak flow parameter at the tip, and Q is calculated outside the tip radius R₀) that drags all diffusion components outwardly radially; in each shell (and for each ith mobile component), this drag evoked mass transfer ∂C_i/∂t = QδC_i/δR. The unknown parameter of the model was the peak flow at the pipette tip Q₀, which was adjusted to match the experimental fluorescence profile and the predicted profile of bound Ca²⁺ (see Figure 1; fluorescence inside the probe, in Ca²⁺-free ACSF, was indistinguishable from the background). In the tissue, the extracellular space occupies fraction α (15%–20%) of the volume. Quantitatively, this implies a 1/α-fold increase in the diffusion source strength (Q₀), while the resulting concentrations should be scaled down by the same factor (Nicholson and Phillips, 1981; Rusakov, 2001); this “flattening” of the probe fluorescence profile in the tissue could be readily observed. Simulations with the model also showed that Q₀ was the overriding parameter (compared to diffusivity or k_on for Ca²⁺-indicator binding) that shaped the fluorescence profile: a 2-fold decrease in the diffusivity of all three diffusional components (e.g., to reflect tortuosity) produced negligible changes in the fluorescence profile sensitivity to external Ca²⁺. Given these relationships, the probe calibration in free solution (Figure 1C) was used as a reference for the in vitro estimates of changes in [Ca²⁺]_o: direct calibration within the tissue was less reliable due to the gradual uptake of indicator by cells.

To assess Ca²⁺ sensitivity of Rhod-5N applied directly to the bath medium, the bound Ca²⁺ concentration [CaRhod] was calculated from a quadratic equation (derived from the kinetic equilibrium):

$${\left[\mathrm{CaRhod}\right]}^2-({\left[\mathrm{Rhod}\right]}_{\text{tot}}+{\left({\mathrm{Ca}}^{2+}\right)}_{\text{tot}}+K_{\text{d}})\left[\mathrm{CaRhod}\right]+{\left[\mathrm{Rhod}\right]}_{\text{tot}}{\left[{\mathrm{Ca}}^{2+}\right]}_{\text{tot}}=0$$

where K_d = 0.32 mM, and [Rhod]_tot and [Ca²⁺]_tot are the known total concentrations of Rhod-5N and Ca²⁺ in the bath.

Immunohistochemistry

To establish that visualized axonal varicosities were indeed synaptic boutons, intracellular electrodes were filled with 2% Cascade blue-biocytin (Molecular Probes) in addition to the Ca²⁺ indicators. At the end of the experiment, the slice cultures were fixed by immersion in 3% para/0.1% glutaraldehyde in PBS (pH 7.4) for 20 min. After washing in PBS, the cultures were permeabilized with 0.1% saponin in PBS for 20 min and preincubated for 30 min in PBS with 1% bovine serum albumin and 10% (v/v) fetal calf serum (“dilution and blocking medium” [DBM]). Cultures were then incubated for 24 hr with monoclonal anti-synaptophysin antibody (SY38, Boehringer Mannheim; 1:100 in DBM), washed 3 × 15 min in PBS, and incubated with Cy3-labeled streptavidin (Sigma, 1:200 in DBM) to detect biocytin-filled axons and Cy2-labeled donkey anti-mouse IgG (Jackson ImmunoResearch, 1:200 in DBM) to detect synaptophysin immunoreactivity. All procedures were carried out at 4°C, except washes, which were at room temperature. After further washing (2 × 15 min in PBS), preparations were embedded in Mowiol in 1:1 PBS:glycerol, coverslipped, and imaged by simultaneous two-channel confocal microscopy, using BioRad A1 and A2 filter blocks for standard fluorescein and rhodamine double labeling with bleed-through correction.

Paired-Pulse Experiments

Evoked EPSCs were recorded in CA1 pyramidal cells held in a whole-cell voltage-clamp mode (at −70mV unless indicated otherwise),and the strength of stimuli applied to stratum radiatum fibers was lowered until the response probability was reduced to <0.5 without changes in the response amplitude (mainly single quantum responses, <20 pA). Fifty to 150 trials, at 8–10 s intervals, were recorded in each stage of the experiment; 5% dextran solution (40 kDa, Sigma) was rendered iso-osmotic by adding 6% water to the ACSF; R_s (8–22 MΩ) was monitored throughout. Given the notations P(0:0), P(0:1), P(1:0), and P(1:1) for the probabilities of the corresponding combinations of successful paired responses, as shown in Figure 4A, the short-term depression (STD) component was estimated as P(1:0)/{P(1:0) + P(1:1)}. This STD estimate is insensitive to failures (0:0 trials) that may arise from failure to initiate action potentials. Correspondingly, the baseline release probability was estimated as P(1:0) + P(1:1), and the background paired-pulse facilitation was {P(0:1) + P(1:1)}/{P(1:0) + P(1:1)}. In experiments with two or three holding voltages (−20mV, −70mV, and −90mV), the voltage was systematically changed every 30 to 40 sweeps. The paired-pulse experiments were conducted on cultures and acute slices, as indicated, at 33°C-35°C.