Simulation of fusion-mediated nanoemulsion interactions with model lipid bilayers

Abstract

Perfluorocarbon-based nanoemulsion particles have become promising platforms for the delivery of therapeutic and diagnostic agents to specific target cells in a non-invasive manner. A “contact-facilitated” delivery mechanism has been proposed wherein the emulsifying phospholipid monolayer on the nanoemulsion surface contacts and forms a lipid complex with the outer monolayer of target cell plasma membrane, allowing cargo to diffuse to the surface of target cell. While this mechanism is supported by experimental evidence, its molecular details are unknown. The present study develops a coarse-grained model of nanoemulsion particles that are compatible with the MARTINI force field. Simulations using this coarse-grained model have demonstrated multiple fusion events between the particles and a model vesicular lipid bilayer. The fusion proceeds in the following sequence: dehydration at the interface, close apposition of the particles, protrusion of hydrophobic molecules to the particle surface, transient lipid complex formation, absorption of nanoemulsion into the liposome. The initial monolayer disruption acts as a rate-limiting step and is strongly influenced by particle size as well as by the presence of phospholipids supporting negative spontaneous curvature. The core-forming perfluorocarbons play critical roles in initiating the fusion process by facilitating protrusion of hydrophobic moieties into the interface between the two particles. This study directly supports the hypothesized nanoemulsion delivery mechanism and provides the underlying molecular details that enable engineering of nanoemulsions for a variety of medical applications.

Introduction

Nanoscale particles, of 200 to 300 nm in diameter, have been developed to sequester loaded cargo until a specific target, recognized by the targeting surface ligands, is reached. The delivery of therapeutic agents including drugs, imaging agents, and macromolecules using nanoscale particles has advantages over conventional small molecule treatment. Delivery using nanoscale particles prevents premature degradation of the therapeutic agents, concentrates the agents at a specific target tissue or cell type, and aids agents in crossing through biological barriers such as the epithelium, endothelium, and plasma membrane [1]. Nanoparticle design must be precisely tailored to deliver each particular agent to its appropriate destination. To achieve efficient delivery to subcellular organelles, the scientific community must understand the molecular mechanisms of how nanoparticles interact with plasma membranes.

Phagocytosis and endocytosis are the most common internalization mechanisms for nanoparticles such as liposomes and polymer-based nanoparticles [1]. However, these internalization mechanisms involve lysosomal degradation that attenuates therapeutic efficiency and as such are not suited for the delivery of therapeutic biomolecules. Alternative strategies have been developed where cargo molecules are directly inserted into the cytoplasmic space through transient pores in the plasma membrane. Direct insertion methods include the conjugation of therapeutic cargo to cell-penetrating peptides [2, 3], electroporation [4, 5], and therapeutic ultrasound with microbubbles [6–8]. However, all of these methods have the potential to cause cell damage by disrupting the plasma membrane [3, 5, 9–11].

Another delivery mechanism is provided by perfluorocarbon-based nanoemulsion particles (PFC-NEPs) which are stabilized by an emulsifying phospholipid monolayer. The so called “contact-facilitated” delivery mechanism of PFC-NEPs involves neither lysosomal pathways nor substantial perturbations of the membrane. This delivery mechanism is hypothesized to start with the formation of a hemifusion complex between the monolayer of PFC-NEP and the outer monolayer of target cell plasma membrane. Cargo molecules then diffuse to the plasma membrane through the hemifusion complex and are finally internalized by lipid raft mediated endocytosis [11–14]. The contact-facilitated delivery mechanism is particularly useful for the delivery of biomolecules that are highly susceptible to enzymatic reactions. However, the molecular details of this mechanism are as yet undetermined due to experimental difficulties of structure determination of small, fluid, and highly heterogeneous systems.

Molecular dynamics simulations have been widely used to determine membrane structures at both atomistic [15–18] and coarse-grained levels [19–22]. Atomistic simulations are useful for collecting accurate structural details but are often too costly for examining larger-scale membrane behavior such as self-assembly of lipids into bilayers or vesicles, bilayer phase changes, domain formation, pore formation, and membrane fusion. Therefore, coarse-grained models have been extensively used to simulate these mesoscopic phenomena [19–22]. Proposed membrane fusion mechanisms involving a hemifusion stalk [23] have been demonstrated by the appearance of proposed intermediate structures in coarse-grained simulations [24, 25]. Furthermore, such simulations have identified important molecular-scale structural motifs, such as splayed lipids in inducing membrane fusion [26, 27]. Over the last few years, coarse-grained simulations have been adopted to model atomistic structures of biological emulsions such as low density lipoproteins and high density lipoproteins that support these simulations to model nanoemulsion particles and their interaction with bilayer [28–30].

This research focuses on an initial step of the contact-facilitated delivery mechanism [14], where two monolayers form a hemifusion complex which resembles the hemifusion stalk [31]. Coarse-grained molecular dynamics simulations have been used to directly observe hemifusion complex formation between a PFC based nanoemulsion particle and a liposome that models a target cell. These simulations were also used to test the dependence of nanoparticle-liposome fusion on particle size and lipid composition in order to identify important structural (physico-chemical) features of the particles required for optimization of fusion.

Methods

Development of a coarse-grained PFOB model

To simplify a model system, the MARTINI force field usually maps four atoms into a coarse-grained bead, or interaction site. The MARTINI force field contains four main types of interaction sites: polar (P), non-polar (N), apolar (C), and charged (Q). These main types are subdivided into 18 different subtypes based on their hydrogen bonding capability and level of polarity. Within the 18 different subtypes, 10 different levels of van der Waals interaction potentials are defined: super-attractive, attractive, almost-attractive, semi-attractive, intermediate, almost-intermediate, semi-repulsive, almost-repulsive, repulsive, and super-repulsive [32]. These potentials were obtained by varying the Lennard-Jones energetic well-depth parameter ε from 2.0 to 5.6 kJ/mol with a size parameter σ of 0.47 nm. The only exception is the super-repulsive potential where the size parameter is increased (σ = 0.62 nm) to preserve the strongly unfavorable interaction between charged (Q) and apolar (C) interaction sites. Despite its simplicity, the MARTINI force field has been widely and successfully used to simulate mesoscopic phenomena including membrane fusion, pore formation, self-assembly, and domain formation. Furthermore, the MARTINI force field is easy to implement and is transferable for other small molecules. These issues motivated the development of a coarse-grained model of a perfluorocarbon molecule, perfluorooctylbromide (PFOB), in accordance with the MARTINI force field (see Table 1).

Table 1.

PFOB coarse-grained force field parameters.

Bond stretching parameters
Bond	Force constant (kb, kJ mol−1 nm−2)	Equilibrium bond distance (r0, nm)
CB-CB	1250	0.5
Angle bending parameters
Angle	Force constant (kϑ, kJ mol−1 rad−2)	Equilibrium angle (θ0, radians)
CB-CB-CB	25	π
Lennard-Jones parameters for non-bonded interactions
Atom type	σ (nm)	ε (kJ mol−1)
CB	0.5	3.5
Partial charges and masses
Atom name	Charge (eC)	Mass (amu)
BRC	−0.11	179.92
CBM	0.09	150.02
CBE	0.02	169.02

PFOB was modeled by three interaction sites, named as follows: BRC (BrCF₂CF₂CF₂-), CBM (-CF₂-CF₂-CF₂-), and CBE (-CF₂-CF₂-CF₃) such that the coarse-grained model was a linear 3-particle system, BRC-CBM-CBE. Bond length was determined based on the Lennard-Jones (LJ) size parameters and bending angle was determined based on the existing MARTINI representation of the CG lipid aliphatic chain. To accelerate computation, the MARTINI force field normally uses the same mass for all interaction sites and ignores partial charges [32]. However, to preserve the asymmetric nature of PFOB, true mass and partial charges were used for each site in the force field development and simulations, as discussed in the Discussion section. These three sites were modeled by a new interaction site type, CB, which was developed in this work to preserve the stronger hydrophobic character of perfluorocarbons as compared with hydrocarbons. The initial guess for the LJ parameters (σ = 0.47 nm and ε = 3.5 kJ mol⁻¹) was taken from the polar interaction site type C1 of the MARTINI force field [32]. These parameters were then systematically varied starting from the initial guess to reproduce the density and heat of vaporization of liquid PFOB [33–36]. The final optimized CB parameters were σ= 0.5 nm and ε = 3.5 kJ mol⁻¹.

To describe the interaction of PFOB with other molecules such as lipids and water, the LJ parameters between CB and other interaction sites were prepared using the constant size parameter of σ= 0.5 nm and different well depth parameters (ε) based on the parameterized level of attractiveness between the two sites. The slightly greater than standard σ value imposes less favorable interaction level for all pairs than the corresponding pairs with the apolar (C) site. The super-repulsive potential between a charged (Q) and CB was treated as in the MARTINI force field, using a σ value of 0.62 nm.

Force field descriptions for other molecular components

PFOB was modeled by the new coarse-grained parameters described above. Two different phospholipids were used in the simulations: 1-palmitoyl-2-oleolyl-phosphatidylcholine (POPC), and 1-palmitoyl-2-oleolyl-phosphatidylethanolamine (POPE). The parameters for these lipids and water molecules were taken from the standard MARTINI force field [37]. Recently, the MARTINI force field changed the interaction between the charged sites (Q) and apolar sites (C) from repulsive in previous versions to super-repulsive. This change was made to prevent the penetration of ionic sites (Q) through the bilayers [37]. However, this modification also strongly inhibits membrane fusion events that require the protrusion of lipid tails out of the membrane. These events are inhibited in the new force field because of the stronger super-repulsive interaction between apolar lipid tails and the charged head group sites (the choline and the phosphate group) [26]. Therefore, for the current study, interaction values between the charged sites of lipid head group and the lipid tails were reduced from the super-repulsive value to their former repulsive parameters to enable the protrusion of hydrophobic tails in the simulated fusion process. Without this reduction, fusion is inhibited for these lipidic systems, preventing the observation of fusion events on the timescale of available simulation durations [26].

Generation of PFOB-NEP particles and liposomes

To generate a PFOB-NEP droplet, varying numbers of phospholipids, PFOB, and water molecules were randomly mixed in an initial box with dimensions 25.3 nm × 25.3 nm × 25.3 nm. A water shell of 5 nm in thickness surrounded this mixture in all directions so that the hydrophobic molecules were isolated inside the simulation box and would not form a lamellar phase with their periodic images. The system sizes and compositions that were successful in forming an intact PFOB-NEP are listed in Table 2. This initial simulation was extended, following the procedure below, until a PFOB-NEP droplet was formed.

Table 2.

Properties of particles tested for fusion. See Figure 1 for geometry definitions.

Liposomes
Name	# POPC	# POPE	PC:PE ratio	r0 radius (nm)	rc radius (nm)	2zp (nm)
L1	709	710	1:1	8.4	6.2	4.2
L2	504	506	1:1	7.4	5.2	4.0

PFOB-NEPs
Name	# PFOB	# POPC	# POPE	PC:PE ratio	r0 radius (nm)	rc radius (nm)
N1	1000	169	170	1:1	6.4	4.4
N2	1000	203	136	3:2	6.4	4.4
N3	1000	237	102	7:3	6.4	4.4
N4	1000	271	68	4:1	6.4	4.4

The protocol of Marrink et al. [21] was used to form the liposome: a small patch was taken from a large bilayer and put in a simulation box. Water molecules were then added into the box so that the small bilayer would be solvated in all directions. The composition of each of these pre-liposome formulations is listed in Table 2. The mean dimensions of the resulting simulation box were 26.5 nm × 26.5 nm × 26.5 nm along the x, y and z directions. This initial simulation was extended, following the procedure below, until a unilamellar liposome was formed.

Molecular dynamics simulations for particle formation and analyses of trajectories were performed with GROMACS version 4.0 [38]. As the first step in the simulations, an energy minimization was performed using a steepest descent method and the system was then gradually heated from 50 K to 303 K through a series of short molecular dynamics (MD) simulations. After these temperature equilibration steps, production simulations were run until the spherical PFOB-NEP and liposomes were formed. A distance cutoff of 1.2 nm was used for non-bonded interactions in combination with a standard shift function in which both the energy and force go to zero at the cutoff distance. The LJ potential is shifted smoothly from 0.9 nm to the cutoff distance of 1.2 nm and the electrostatic potential is shifted from 0.0 nm to the cutoff distance of 1.2 nm. The simulation was performed in an isobaric-isothermal ensemble (NpT) with the Berendsen pressure coupling scheme with a coupling time of 4 ps. The simulation temperature was 303 K via the Berendsen coupling scheme with the coupling time of 0.4 ps [39]. Time steps of 20 fs were used in production simulations.

Liposome:PFOB-NEP fusion simulations

The geometry of each particle tested for fusion is provided in Table 2. To start the fusion simulation, two spherical particles were placed together with less than 1 nm distance between their closest lipids and surrounded by water, as shown in Figure 1. Following the bilayer fusion procedure of Kasson et al.,[24, 40] two lipids, one from each particle, were selected to be connected by an intermediate water site which formed an artificial chemical linker between the water and the phosphate sites of each lipid with an equilibrium length of 0.5 nm. A series of short simulations were performed to gradually reduce the initial linker bond length to the equilibrium length as described below. A list of liposome:PFOB-NEP fusion pairs is provided in Table 4. Five independent replica simulations were run for each fusion pair to enhance sampling efficiency and improve simulation statistics.

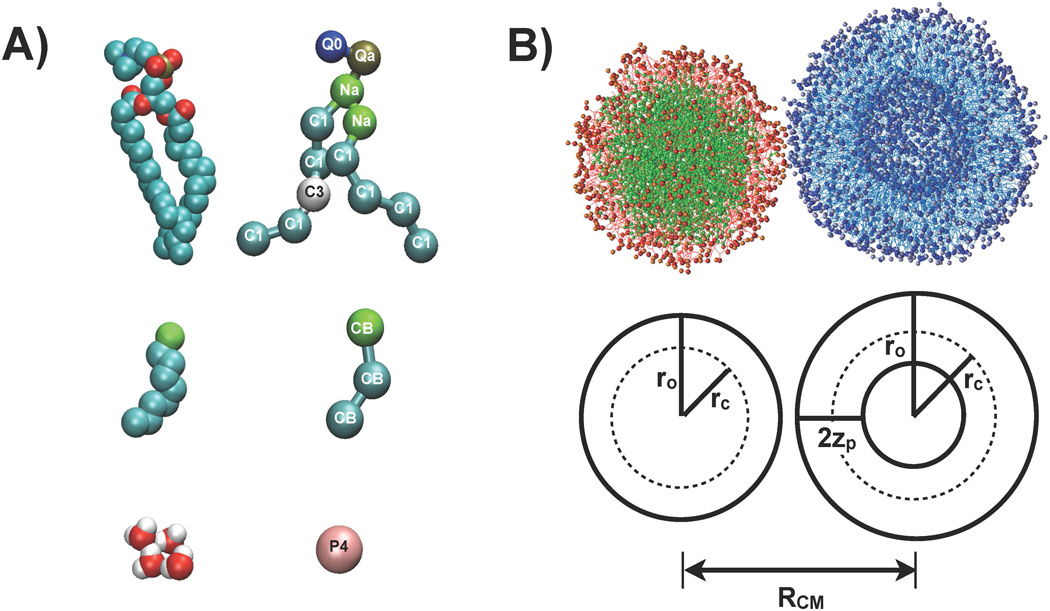
Figure 1.

The structure of a linked NEP and liposome and the structures of molecules contained in the system. A) The structures of phospholipid (POPC), perfluorooctylbromide (PFOB) and water molecules, from top to bottom, presented at an atomistic (left) and coarse-grained (right) level. The type is shown for each coarse-grained site. The CB type was specifically developed to model PFOB. B) The initial structure of a fusion simulation, with a PFOB-NEP and a liposome held in close contact through artificial links. PFOB is shown in green and enclosing phospholipids are shown in red. The lipids constituting the liposome are shown in blue. The geometry of the two particles is defined in the bottom panel. R_CM is the distance between the center of mass of each particle. r_o is the distance of phosphate group from the center of mass of each particle and r_c is the distance of lipid termini. 2z_p is the distance between phosphate group of the outer and inner monolayer.

Table 4.

Summary of fusion simulations. The fusion initiation modes are denoted by letter with descriptions in Figure 7 and the text.

Liposome-liposome fusion simulations
Name	Simulation size (# sites)	Simulation length (ns)	Fusion lag time (ns)	Initiation mode
L1-L1	225000	4000	--	--
L2-L2	214353	35000	--	--
Liposome-NEP fusion simulations
Name	Simulation size (# sites)	Simulation length (ns)	Fusion lag time (ns)	Initiation mode
L1-N1-1	219757	1080	366	C
L1-N1-2	219757	3030	2533	B
L1-N1-3	219757	1150	584	A
L1-N1-4	219757	1449	1210	D
L1-N1-5	219757	730	484	D
L2-N1-1	214441	770	217	D
L2-N1-2	214441	1790	1427	D
L2-N1-3	214441	1200	160	D
L2-N1-4	214441	1183	994	D
L2-N1-5	214441	410	183	D
L2-N2-1	212623	710	199	C
L2-N2-2	212623	730	615	D
L2-N2-3	212623	750	147	D
L2-N2-4	212623	410	82	D
L2-N2-5	212623	806	436	D
L2-N3-1	212623	1720	1138	C
L2-N3-2	212623	1510	961	C
L2-N3-3	212623	700	425	B
L2-N3-4	212623	616	350	D
L2-N3-5	212623	3270	3050	B
L2-N4-1	212623	2000	1576	B
L2-N4-2	212623	4300a	4000	--
L2-N4-3	212623	3500	2770	C
L2-N4-4	212623	1974	1512	B
L2-N4-5	212623	4300b	--	--

^aThis simulation system underwent anomalous fusion with a periodic image, as discussed in the text.

^bThis simulation system did not undergo fusion.

The same energy minimization and temperature equilibration steps were repeated by applying the simulation parameters described above for particle generation. After temperature equilibration, a series of short simulations of 1 ns length were performed while decreasing the artificial linker length by 0.2 nm after each simulation until the equilibrium length of 0.5 nm was achieved. These short simulations were followed by production simulations, each of which was performed for at most 4 µs. However, if a fusion complex was formed between the two particles before the 4 µs time limit, the simulation was stopped.

Results

Evaluation of the new coarse-grained PFOB model

To determine the bulk thermodynamic parameters including density and heat of vaporization, a simulation containing 559 PFOB molecules and a simulation of a single PFOB (at the equilibrium box size) was carried out for 100 ns at 298 K. These two simulations were used to compute the PFOB heat of vaporization as described previously [41]. As summarized in Table 3, the resulting PFOB density was 1.954 kg L⁻¹ and the heat of vaporization was 44.66 kJ mol⁻¹, values that are in reasonable agreement with the experimental results of 1.925 kg L⁻¹ for density and 42.67 kJ mol⁻¹ for heat of vaporization [33–36].

Table 3.

Bulk properties of liquid PFOB. The references for each experimental bulk property are Riess et al. [33] and Andre et al. [34] for density (ρ); Riess et al. [33], Gregor et al. [35], Faithful et al. [36] for heat of vaporization (Δ_vapH), Song et al. [57] for the solvation free energy of CF₄ in liquid n-hexane (Δ_solvG).

Property	Experimental value	Atomistic simulation result	Coarse-grained simulation result
ρ (kg L−1)	1.925 ± 0.007	1.891 ± 0.001	1.954 ± 0.001
ΔvapH (kJ mol−1)	43 ± 1	41.1 ± 0.3	44.660 ± 0.007
ΔsolvG (kJ mol−1)	2.056	2.00 ± 0.02	--

Additionally, the phase separation of PFOB in water was tested in the absence and in the presence of an emulsifying POPC monolayer. The results were compared to the structures from previous atomistic simulations [41]. The density profiles showed good agreement between the coarse-grained and atomistic simulations, further supporting the utility and applicability of the new coarse-grained model (Figure 2 and Supporting Movie 3).

Figure 2.

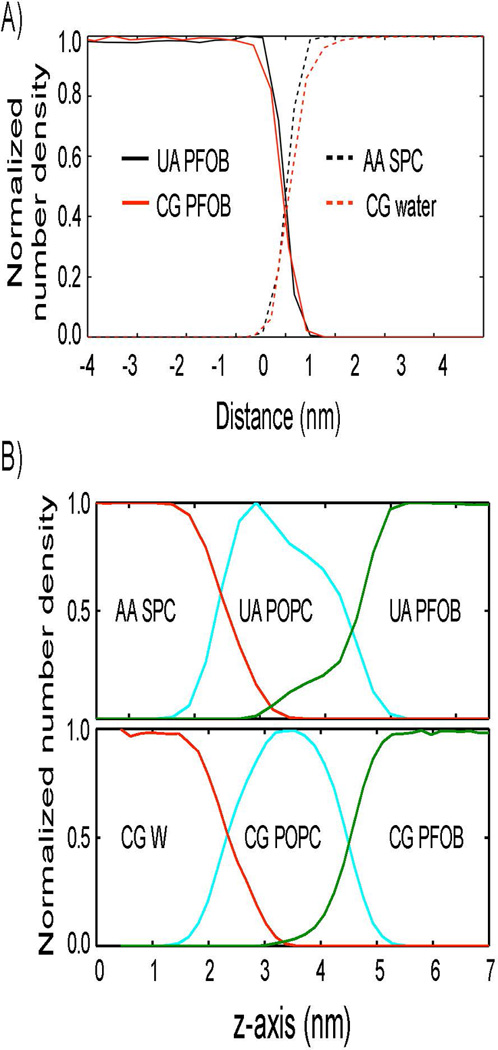
Interface structure comparison between atomistic and coarse-grained simulations A) in the absence and B) in the presence of an emulsifying phospholipid monolayer. A) The normalized number density profiles of water are shown in dotted red (coarse-grained) and black (atomistic) lines along the interface normal direction. Those of PFOB are shown in solid red (coarse-grained) and black (atomistic) lines. B) The top panel presents the normalized number density profiles of water (red), POPC monolayer (cyan), and PFOB (green) that were determined from an atomistic simulation. The bottom panel presents the same data that were determined from a coarse-grained simulation.

Spontaneous formation of liposomes and PFOB-NEP particles

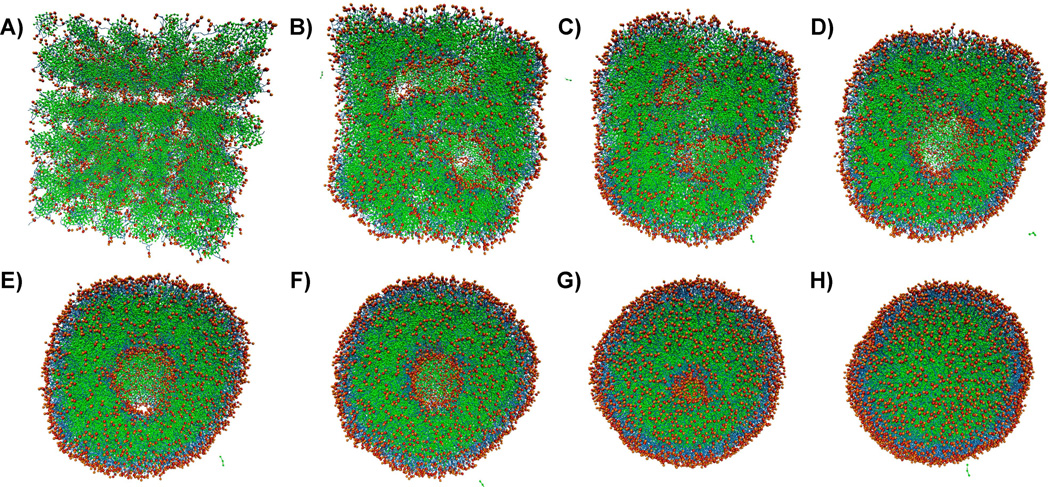
Systems of randomly dispersed PFOB-NEP components were prepared as described above. From these random starting structures, the emulsion formed rapidly: even after accounting for the approximately 4-fold faster time scale of the CG model [37], formation occurs in less than a few hundred nanoseconds. As shown in Figure 3 and Supporting Movie 1, PFOB molecules aggregated while amphipathic phospholipids were expelled to the surface of the growing PFOB particles. This process progressed in several phases and eventually resulted in small monolayer PFOB particles which merged and became a single continuous entity in a toroidal shape. The toroidal hole gradually decreased and PFOB molecules took a spherical shape with phospholipids covering the surface. The structure of the complete PFOB-NEP was defined by its outer radius r_o, which is the distance between the center of mass and the peak of phosphate group density, and r_c, which is the distance between the center of mass and the peak of terminal methyl carbon sites (see Figure 1). Incomplete PFOB-NEPs containing a water droplet inside the emulsion were occasionally observed. The water droplet was also enclosed by a phospholipid monolayer and, even after significant further simulation (close to 1 µs), it did not disappear. These structures would form when the system contained surplus lipids compared to the amount of PFOB. Therefore, when this was observed, new simulations were run with reduced numbers of phospholipids to obtain complete PFOB-NEPs.

Figure 3.

Spontaneous emulsion formation. Snapshots were taken at every 1.5 ns along the trajectory for the first 6 images (A–F). G was taken at 13.5 ns and H was taken at 22 ns, by which time the PFOB-NEP formation was complete. PFOB is shown in green, lipid tails in blue, and lipid polar head groups in red and orange. Water particles are omitted for clarity. An animation of this process is provided in Supporting Movie 1.

In addition to the emulsions, liposomes were spontaneously generated from the structures described above [21]. The L2 liposome (see Table 2) used in the simulation was the smallest that could be formed spontaneously from the starting planar bilayer structures: smaller initial structures failed to form liposomes, presumably due to the high curvature stress (data not shown). In addition to the parameters r_o and r_c, defined above, the structure of a liposome also characterized by 2p_z, which is the distance between two phosphate density peaks (see Figure 1).

Liposome:PFOB-NEP fusion

To characterize the fusion between PFOB-NEPs and liposomes prepared by the new coarse-grained simulations, particle size and lipid composition were varied. The tested liposome sizes were 8.4 nm and 7.4 nm in radius (r_o). The lipid composition of PFOB-NEP varied from 20 to 50 mol % of POPE with the remainder POPC. The tested combinations of size and composition with relevant characteristics of each fusion process are summarized in Table 4. An example fusion event is shown as an animation in Supporting Movie 2.

Fusion between the liposome and the PFOB-NEP particle was observed in all simulations except one (L2-N4-5) within the simulation time limit of 4 µs. An abnormal fusion event was observed in the L2-N4-2 simulation where a PFOB-NEP spontaneously fused with the periodic image of the linked liposome and subsequent fusion processes were hindered because of the periodic constraints. For this reason, L2-N4-2 fusion simulation was not further analyzed. All other fusion events followed the process presented in Figure 4. These fusion processes started with the merging of the two monolayers followed by PFOB molecules quickly moving into the inter-monolayer space of the fused liposome. The lipids from the PFOB-NEP were mixed into the outer monolayer of the liposome while the PFOB became evenly distributed in the inter-monolayer space. As a result of the fusion, the two particles were integrated into a single liposome with its 2p_z distance increased by ~2 nm (see Supporting Figure S2).

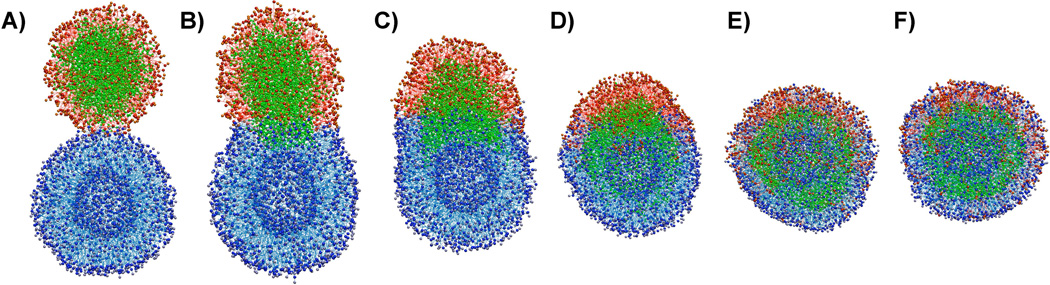
Figure 4.

Structural changes over the course of fusion. The snapshots are chosen at different time points to show the structural changes over the course of fusion event. Corresponding time points are defined in the following Figure 5A. PFOB is shown in green, the lipids enclosing the PFOB core in red, and the lipids forming the liposome in blue. An animation of this process is provided in Supporting Movie 2.

The distance between the center of mass of each particle is denoted by R_CM and defined in Figure 1. Figure 5A shows example R_CM profiles during a fusion event: R_CM fluctuates at a mean value that is equivalent to the sum of the two particle radii for a certain lag time then it drastically decreases. A fusion initiation was determined by the onset of drastic decay in R_CM – this period was designated as A. While the lag time for fusion initiation varied as summarized in Table 4, the subsequent changes in R_CM were fast and indistinguishable among different fusion events (see Figure 5B). The factors that lead to different fusion initiation are discussed below.

Figure 5.

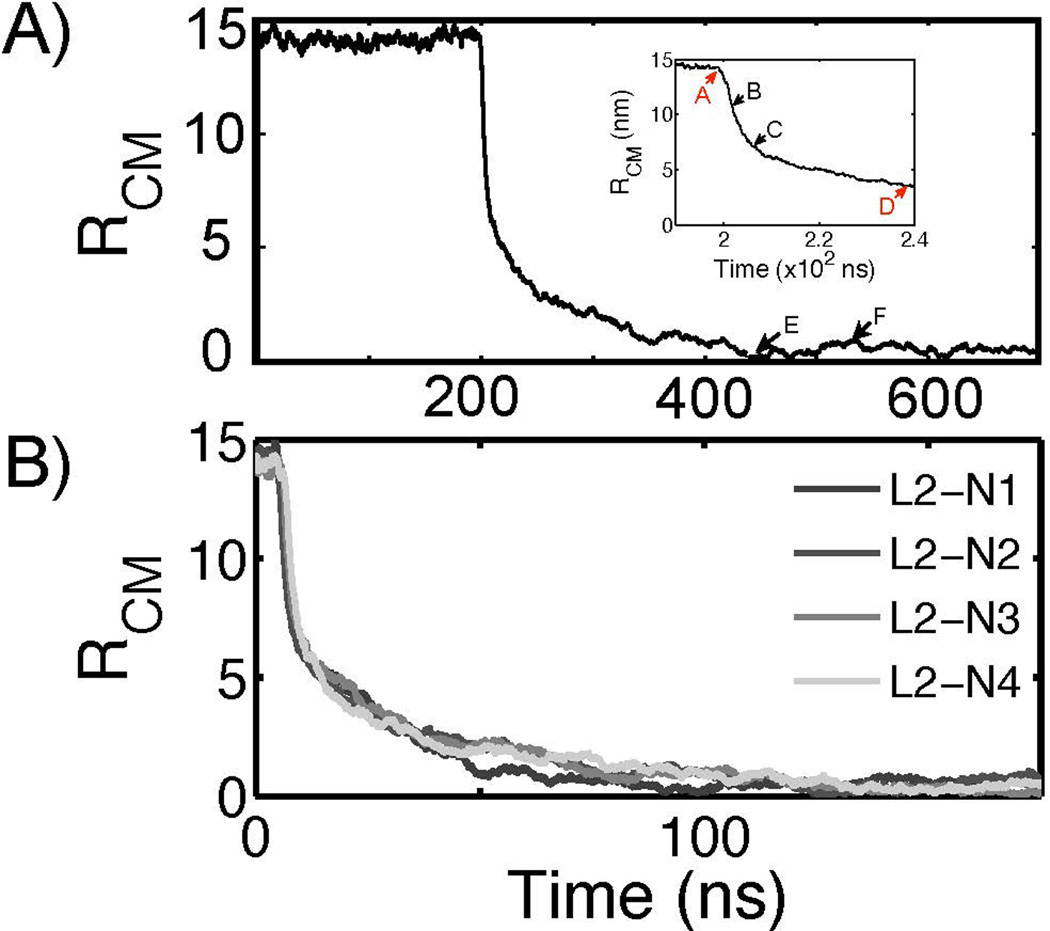
A reaction coordinate used to analyze the fusion process. A) The evolution of R_CM, the distance between the center of mass of each particle, is plotted as a function of time. Once the fusion is initiated, R_CM rapidly decreases to zero. The inset figure shows the four points (A, B, C, and D) based on the R_CM metric. A is when R_CM starts to drastically decrease, B is when R_CM is decreased by 25%, C by 50%, and D by 75%. E and F are arbitrarily chosen to show the structures after fusion event is completed. The corresponding structures at each time point are shown in Figure 4. This example R_CM profile is obtained from the fusion simulation L2-N2-1. B) The profiles of R_CM of four different fusion simulations are superimposed after aligned such that that the time point A of each profile overlaps. This figure shows that the subsequent steps after fusion is initiated are kinetically indistinguishable.

To understand the role of the liposome and nanoemulsion components in initiating fusion, the molecular composition of the interface between the two particles was assessed. To determine the composition, the whole system was transformed by a translation and rotation so that the molecular axis connecting the center of mass of each particle was on the z-axis. Next, the system was divided into thin slabs of 0.1 nm in thickness along the z-axis. To locate the slab at the interface, the number of lipid sites (CG beads) was counted for each slab. The contact interface was identified as the position with the lowest lipid density within the slab. [27]

To determine whether initiation of fusion was accompanied by dehydration at the contact interface, the number of water sites at the interface was counted. For this counting, a distance cutoff of 3 nm from the z-axis was applied so that fluctuations in bulk water would not obscure behavior at the fusion site. Figure 6 shows the changes in the number of waters between the monolayers at the fusion site. The number of waters between the monolayers dropped from 19 ± 4 to < 1 when fusion started. This drastic decrease in the number of waters suggested that the hydrophobic exposure described in the next section is dependent upon dehydration at the interface.

Figure 6.

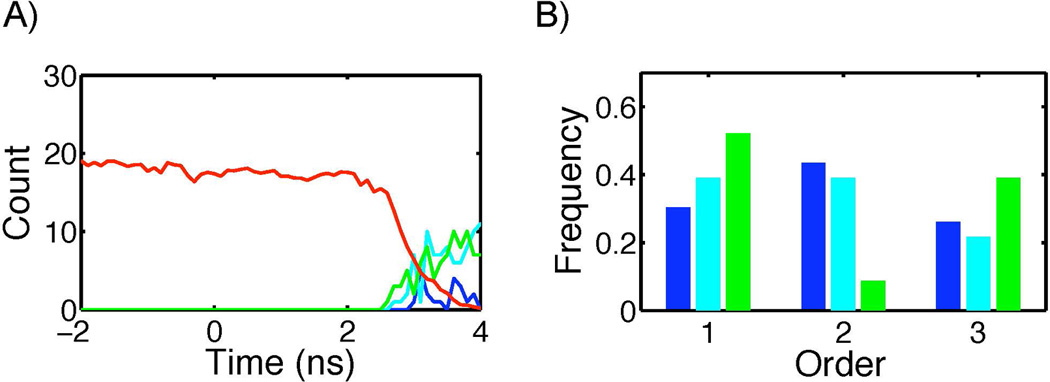
Changes in molecular composition at the interface. A) The evolution of the number of water (red) and each hydrophobic moiety (blue: lipid tails of liposome, cyan: lipid tails of PFOB-NEP, green:PFOB) at the interface is plotted with the fusion initiation point (A in Figure 5A) set at zero in time. This particular profile was obtained from the fusion simulation L2-N4-1. B) The frequencies to observe the hydrophobic moieties at the interface first, second, and third was plotted with the same color code used in A.

As shown in Figure 6A, the appearance of the hydrophobic moieties followed dehydration at the interface. Exposure of hydrophobic moieties to the membrane surface is known to be a rate limiting step of membrane fusion [26]. To explore the participation of hydrophobic molecules in initiating fusion, the appearance of lipid tails and PFOB was assessed by counting the CG beads of each molecule at the interface. The lipids of the PFOB-NEP and the liposome were evaluated separately. The sequence of hydrophobic moiety appearance differed between fusion events. Figure 6B shows the frequency with which each hydrophobic moiety appeared first, second, and third at the surface. PFOB was most frequently observed as the first hydrophobic moiety at the interface followed by the lipid tails of the PFOB-NEP. Additional details of fusion are presented in Supporting Information Figure S1.

Using this analysis, 23 fusion events were categorized into four distinct modes (labeled A–D in subsequent discussion) by the order of exposure of hydrophobic groups. For this classification, hydrophobic exposure events were considered to be simultaneous if they occurred within 0.3 ns of each other, thus setting a lower time limit for the mechanistic analysis. The modes assigned to each fusion simulation are presented in Table 4 and example structures of each mode are shown in Figure 7. In mode A, which was observed only in one fusion event (L1-N1-3), PFOBs first appeared at the interface with the exposure of lipid tails following after 0.4 ns. In mode B, observed in 5 fusion events (L1-N1-2, L1-N1-4, L2-N3-3, L2-N3-5, L2-N4-1, and L2-N4-4), PFOB and lipid tails from the PFOB-NEP first appeared at the interface, followed by the appearance of liposome lipid tails after 0.3 to 0.5 ns. In mode C, observed in 4 fusion events (L1-N1-1, L2-N2-1, L2-N3-1, and L2-N3-2), lipid tails from both PFOB-NEP and liposome were first observed at the interface while the appearance of PFOB was delayed by 0.5 to 0.9 ns. Finally, in mode D, which included the remaining 13 fusion events, all three hydrophobic moieties appeared at the interface simultaneously.

Figure 7.

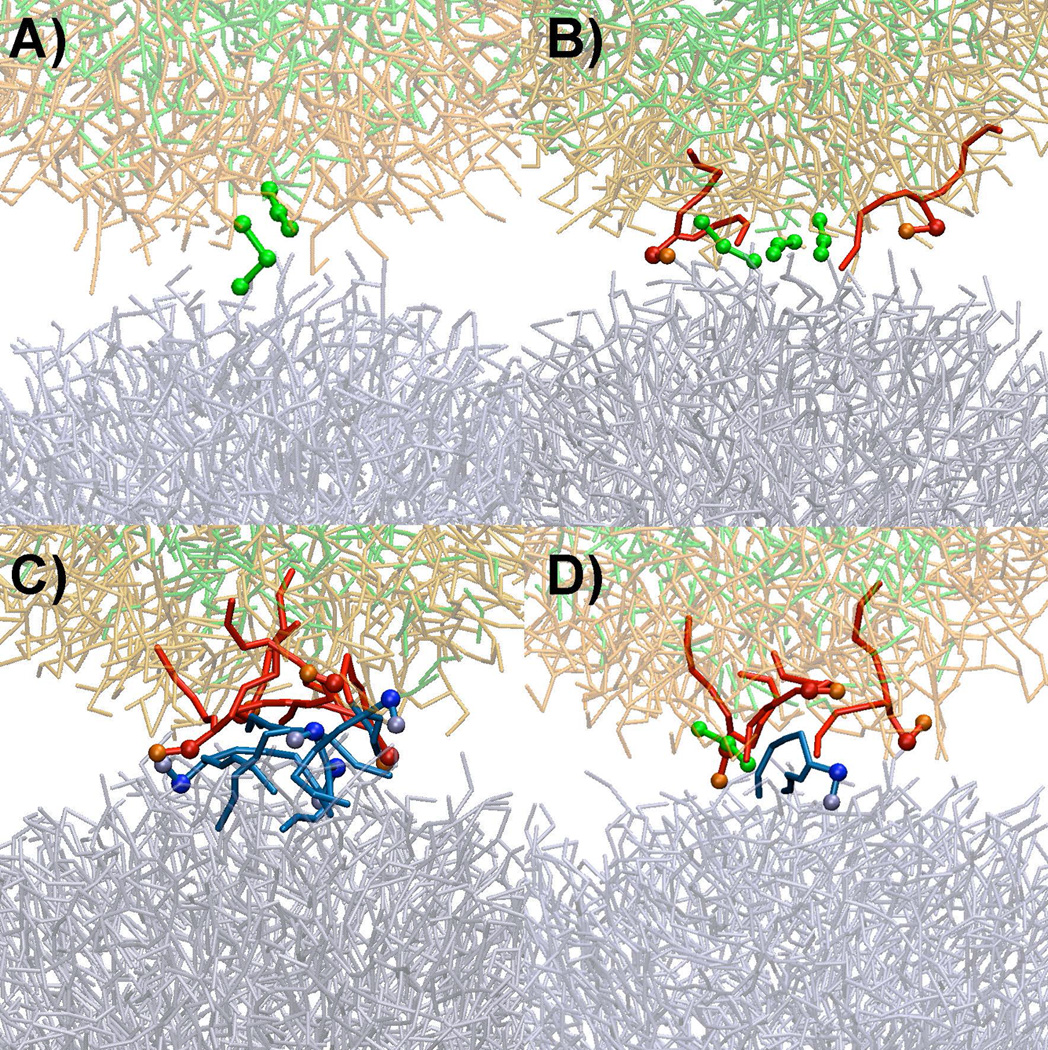
Different fusion initiation modes. A) Primary action of PFOB prior to the protrusion of lipids. B) Protrusion of PFOB-NEP lipid in conjunction with PFOB molecules (solid red) C) Protrusion of lipids in the absence of PFOB molecules. D) Interaction among three molecules. Lipids and PFOBs that directly involved in the initial monolayer disruption are depicted in darker colors and thicker sticks and additional balls while the rest of the molecules are shown in thinner sticks and faint colors. PFOBs are shown in green and light green colors with the enclosing phospholipids in red and orange colors. The phospholipids of the liposomes are shown in blue and light blue.

Dependence of fusion lag-time on lipid composition

The fusion lag time dependency on lipid composition was examined while the particle size was kept constant. To test the influence of negative intrinsic curvature, the fraction of POPE was decreased from 50 to 20 mol %. Figure 8B indicates that the fraction of POPE was negatively correlated with the lag time. The lag time differences of L2-N4 from L2-N1 and L2-N2 were statistically significant at a 95% confidence level. A similar analysis of fusion rate on particle size (Figure 8A) was performed and but the results were not statistically significant at a 95% confidence level.

Figure 8.

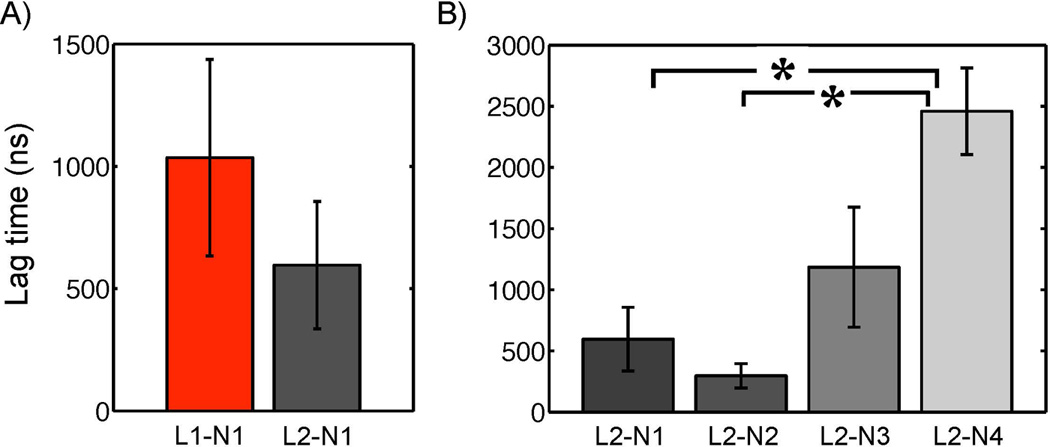
Fusion dependence on particle size and lipid composition. A) The lag times for the fusion initiation are compared among fusion simulations that differ in comprising particle size at a constant lipid composition of POPC:POPE=1:1. B) The lag times are compared among the fusion events between a liposome and various PFOB-NEPs that contained different amounts of POPE from 50 to 20 mol % with similar particle sizes. The differences of the designated pairs are statistically significant at a 95 % confidence level.

Order parameter dependence on particle size and lipid composition

Order parameters of lipid tails were examined to determine if particle size and different lipid composition affected the flexibility of lipid tail conformation in the NEP as addressed for liposomes [42]. The deuterium order parameters S_CD were computed with the following relation [43]:

$$S_{\mathit{\text{CD}}}=\frac{2}{3}{S}_{\mathit{\text{xx}}}+\frac{1}{3}{S}_{\mathit{\text{yy}}}$$

where S_ij is an element of an order parameter tensor S and is defined by

$$S_{\mathit{\text{ij}}}=\frac{1}{2}(3\text{cos}{\theta }_i\text{cos}{\theta }_j-{\delta }_{\mathit{\text{ij}}})$$

for i, j = x, y, z, where θ_i is the angle between the ith molecular axis and the sphere normal that is defined by a vector from a center of mass of the particle to the phosphate group of each lipid. The angular bracket implies averaging over time and molecules. The molecular axes are defined per CG bead along the tail. For the nth bead (C_n), the z axis was defined by a vector from C_n−1 to C_n+1, the y axis by a vector perpendicular to z and in the plane formed by C_n−1, C_n, and C_n+1, and the x axis by a vector perpendicular to y and z.

The deuterium order parameters were computed for each CG bead along the lipid tails of the liposome (L1, L2) and the PFOB-NEP (N1, N2, N3, N4) and are shown in Figure 9. The order parameters of palmitoyl (left) and oleoyl chain (right) are plotted separately. It was observed that greater particle sizes were positively correlated with greater order parameters, which indicated that conformational freedom was reduced as the particle size increased. Even though decreasing the POPE fraction did not affect the tail order substantially, the order parameters of oleoyl chain (C₂ and C₃), were significantly greater in the particles containing reduced amount of POPE as shown in Figure 10.

Figure 9.

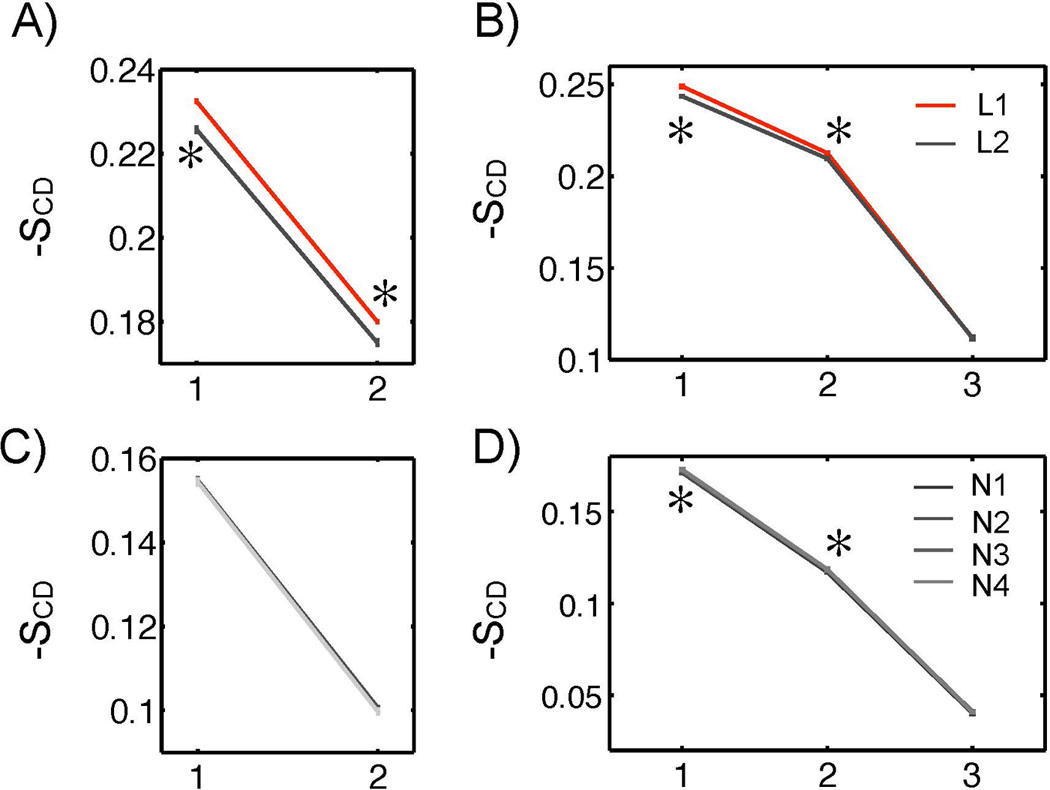
Lipid tail order parameters of liposomes and PFOB-NEPs. The lipid tail orders of sn-1 palmitoyl chain (A) and sn-2 oleoyl chain (B) of liposomes are plotted. The lipid tail orders of sn-1 palmitoyl chain (C) and sn-2 oleoyl chain (D) of PFOB-NEPs are plotted. The differences of the designated pairs are statistically significant at a 95% confidence level.

Figure 10.

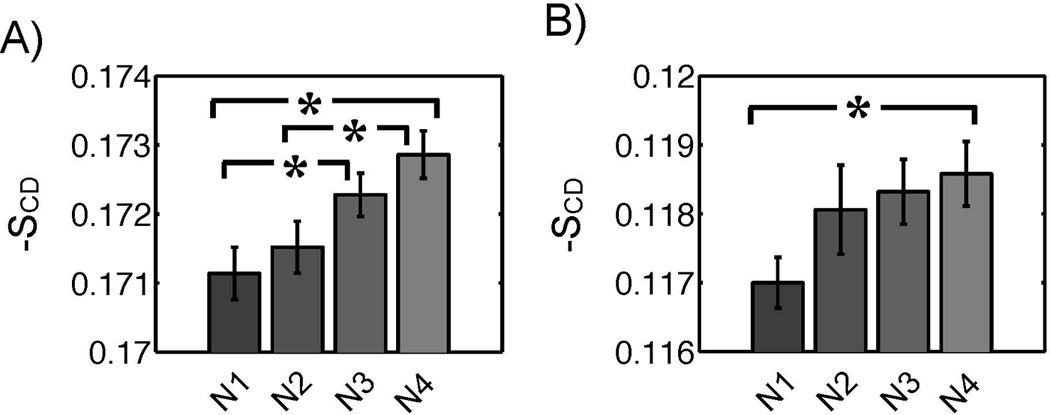
Statistically significant differences in tail orders among PFOB-NEPs. A) The tail orders at the C₂ position (A) and C₃ position of the oleoyl chain are plotted. The differences of the designated pairs are statistically significant at a 95% confidence level.

Discussion

To better understand the “contact-facilitated” delivery mechanism proposed for NEP-membrane interactions, force field parameters were developed at a coarse-grained level, generated spherical PFOB nanoemulsions and liposomes using equilibrium simulations, and ran fusion simulations after physically linking a PFOB-NEP and a liposome. 24 fusion events were observed across different combinations of PFOB-NEPs and liposomes, which strongly supports the contact-facilitated delivery mechanism. To the best of our knowledge, this is the first demonstration of fusion between liposomes and nanoemulsion particles enclosed by a phospholipid monolayer. This process shared some features with the well-established fusion process between two bilayers but also exhibited distinctive features that are discussed below.

Force field parameters

The newly developed coarse-grained PFOB model was able to reproduce bulk thermodynamic properties of PFOB in reasonable agreement with experimental observations. The emulsion-solvent interfacial structures determined with the coarse-grained model showed good agreement with the structure determined by atomistic simulations both in the absence and presence of an emulsifying phospholipid monolayer. Additionally, the spontaneous formation of PFOB emulsion droplets enclosed by a phospholipid monolayer starting from random mixtures of PFOB, phospholipids, and water further supported the validity of this new model. Even though non-zero partial charges were assigned to the three interaction sites to preserve the asymmetric nature of PFOB, PFOB behaved symmetrically without showing preferential orientation near the PFC-NEP surface (data not shown) as observed in atomistic simulations [44]. The small partial charges were not influential under these simplified simulation conditions. Hence, in the future, simulation performance of PFOB-NEPs could be improved by excluding these charges with no penalty to the simulation accuracy.

System configurations and approximations

To observe fusion events within the limit of available computing resources, a few constraints were imposed on the system configuration.

First, small particles were used, which has been common for vesicle fusion simulations [21, 24, 27, 40, 45]. Small size can both speed up the simulation and facilitate fusion between membranes due to pronounced curvature. While the smallest liposome size of ~15 nm in diameter corresponded to the minimum liposome size feasible in experiments [46], the smallest PFOB-NEP size ~13 nm in diameter was far below the experimentally-observed minimum PFC-NEP size of ~50 nm in diameter [47]. These small sized particles emphasized the effect of local curvature on the surface PFC-NEPs and target cell membranes to initiate fusion. Indeed, it was recently reported that synaptotagmin fusion protein could induce high local positive curvature and reduce the energy required to initiate membrane fusion [48, 49].

Second, the lipid:PFOB molecule ratios for PFOB-NEP formation were determined empirically under the condition that initial random mixtures of certain ratio would not form water droplets inside the emulsions. This condition could have resulted in dilute lipid packing on the surface that may affect the fusion event. Therefore, future studies should introduce lipids in water so that they spontaneously inserted into the preformed NEP surface to overcome this limitation.

Third, the NEP and liposome particles were placed close together and were connected by an artificial linker that maintained the initial close proximity between the two particles. Such linkage was necessary because spontaneous apposition of the two particles is a rare event beyond the current timescales of molecular simulation. Such encounter is entropically disfavored and energetically hindered due to electrostatic repulsion and dehydration penalties but can be facilitated by additional molecules such as ligand-receptor interactions [50]; e.g., to target cell-specific surface molecules [51]. In this work, these ligand-receptor interactions were mimicked by an artificial linker, as used in many recent fusion simulations [24, 27, 40].

Mechanisms for NEP-liposome complex formation

The 23 successful fusion events revealed four different modes for the disruption of the monolayers, as shown in Figure 7 and listed in Table 4. Three of the modes (A, B, and D) showed that PFOB played a primary role in initiating membrane disruption and lipid complex formation. In mode A, PFOB leaked prior to the reorientation of lipids into the interface and subsequently triggered membrane disruption. In modes B and D, PFOB also facilitated the reorientation and protrusion of lipid tails by solvating the hydrophobic tails exposed to surface. However, the boundaries between these modes were somewhat indistinct and, in any mode, the interplay between phospholipids and PFOBs was prevalent. This again emphasizes the critical role of PFOB in the initiation of fusion.

The “contact-facilitated” delivery mechanism originally hypothesized that the NEP and liposome particles would stay intact with a hemifusion complex spanning the gap and providing a continuous hydrophobic surface between the two particles [14]. This hypothesis was based on experimental observations [9, 12, 50, 52, 53] as well as on the lipophobic properties of PFOB that suggested it would maintain the emulsion core even after a hemifusion stalk formed. In contrast to this hypothesis, these simulations showed that hemifusion complexes are very short-lived, quickly expanding radially to allow the massive flow of PFOB into the intermonolayer space, finally leading to the complete absorption of PFOB-NEP into the apposed liposome.

There are a few possible reasons for this difference between simulation and experiment. First, the small particle sizes used in the simulations generate high curvature strain and surface tension that strongly drives the system to minimize the surface area for a given volume. In these simulations, disappearance of the hemifusion stalk through complete absorption is a likely mechanism to maximize such reduction in curvature and surface area. Such high curvature stress is much less likely when particles of larger, and more realistic, sizes are used. Second, the current systems are pure and lack proteins. The flow of PFOB from the NEP into the liposome separates the two monolayers and thickens the membrane. In plasma membranes containing high fractions of transmembrane protein, thickening of membrane would not be as energetically favorable because of increased hydrophobic mismatches with membrane proteins [54]. Finally, these simulations used a single flexible linker to keep the two particles in close proximity while the close apposition of PFC-NEPs to their target cells are mediated by multivalent ligand-receptor interactions with multiple copies of homing liands on PFC-NEP surface [55]. Such multivalent ligand-receptor interactions should keep PFC-NEPs from being absorbed into the target cells and thus further support the stability of the hemifusion stalk.

Fusion dependence on lipid composition

Lipids of negative spontaneous curvature are known to facilitate membrane fusion between the two outer monolayers because they can accommodate the highly negative curvature that occurs during hemifusion stalk formation [56]. This dependency was observed in the fusion simulations: lower fractions of POPE (~20 mol %) prolonged the lag time for the initiation of fusion compared to the PFOB-NEPs containing higher POPE fractions (50 and 40 mol %). The lag time trend with POPE fraction was statistically significant. In particular fusion was not observed between L2 and N4 in one simulation (L2-N4-5) with a low fraction of POPE molecules, until the simulation reached the 4 µs maximum time limit of available computing resources. Correlated increases in order parameters with increasing liposome size and decreasing POPE proportion help to explain the cause of the prolonged lag time, which is further discussed below.

Correlation of lipid tail order with fusion mechanism and rate

As expected, lipids were more ordered in the larger liposome (L1) than in the smaller one (L2). On the other hand, even though the area per head group was the same among PFOB-NEPs (N1 through N4), the higher fraction of POPE caused the lipid tails to become more disordered.

The lag time prolongation was more strongly correlated with increased tail order of PFOB-NEPs (4.1-fold longer) rather than to tail order of the liposome (1.7-fold longer). This observation suggests that membrane disruption in the PFOB-NEP monolayer may act as a rate-limiting step which, in turn, triggers liposome outer monolayer disruption. This speculation is supported by the fact that the hydrophobic moieties of the PFOB-NEP, including lipid tails and PFOB, were more frequently found as the first molecule at the NEP-liposome interface – rather than the lipid tails of liposome.

Conclusions

This paper presents a new coarse-grained PFOB model that preserves the thermodynamic properties of pure PFOBs as well as the phase separation in water due to its strong hydrophobicity. The validity of the model was also confirmed by the spontaneous emulsion formations starting from randomly mixed initial structures.

The reported simulations using this new CG model directly showed that fusion could occur between the monolayer of PFOB-NEP and the outer monolayer of liposome. This observation strongly supports the “contact-facilitated” delivery mechanism, which was hypothesized to proceed by forming an intermediate structure similar to the hemifusion stalk. Indeed, this fusion event between a PFOB-NEP and a liposome shared many aspects in common with the fusion mechanisms for two bilayers. The NEP-liposome fusion showed a similar dependence on the particle size and lipid composition: smaller sizes of higher negative-curvature lipid content resulted in faster fusion. Fusion was initiated by forming a hemifusion complex made of hydrophobic moieties protruded to the surface. Initial membrane disruption and hemifusion complex formation were the rate-limiting steps while subsequent steps occurred very quickly and barely differed among the observed fusion events.

This fusion process between a PFOB-NEP and a liposome has several distinctive features. It appeared that freely mobile PFOB molecules played critical roles in facilitating the fusion process. PFOB enhanced the protrusion of hydrophobic moieties from the PFOB-NEP to the interface region by solvating lipid tails. Finally it was observed that the flow of PFOB into the inter-monolayer space of the apposed liposome led to the complete absorption of a PFOB-NEP into the connected liposome.

This work has laid a foundation for new studies to understand the delivery mechanism of cargo molecules to target cell through membrane fusion. Systematic analysis to test the fusion dependency on particle size and lipid dependency as well as core-forming perfluorocarbon molecules would help to better characterize the mechanisms and to aid in the rational design of particles for optimal delivery.