Imputing and Predicting Quantitative Genetic Interactions in Epistatic MAPs

Abstract

Mapping epistatic (or genetic) interactions has emerged as an important network biology approach for establishing functional relationships among genes and proteins. Epistasis networks are complementary to physical protein interaction networks, providing valuable insight into both the function of individual genes and the overall wiring of the cell. A high-throughput method termed “epistatic mini array profiles” (E-MAPs) was recently developed in yeast to quantify alleviating or aggravating interactions between gene pairs. The typical output of an E-MAP experiment is a large symmetric matrix of interaction scores. One problem with this data is the large amount of missing values – interactions that cannot be measured during the high-throughput process or whose measurements were discarded due to quality filtering steps. These missing values can reduce the effectiveness of some data analysis techniques and prevent the use of others. Here, we discuss one solution to this problem, imputation using nearest neighbors, and give practical examples of the use of a freely available implementation of this method.

1. Introduction

1.1. Epistatic Mini Array Profiles

Genetic interactions are identified when mutations in multiple genes produce a phenotype which differs from what is expected based on individual mutations in each gene. Recently, high-throughput assays have been developed for the acquisition of large amounts of pairwise genetic interaction data in model organisms. Epistatic mini array profiles (E-MAPs) are one such approach capable of quantitatively measuring the strength of pairwise genetic interactions in yeast. The procedure supports the identification of both positive (alleviating) and negative (aggravating) interactions between genes, assignments that are extremely valuable in interpreting the biological basis of the epistatic relationships (1).

An E-MAP is most commonly represented in the form of a symmetric matrix with real-valued entries indicating the type and strength of interaction between each pair of genes under consideration. These scores are calculated based on the divergence in growth of yeast strains with two disrupted genes from the expected growth rate. Typically, a normalization process is applied to the interaction scores so that positive matrix entries denote an alleviating interaction, negative matrix entries denote an aggravating interaction, and values close to zero indicate the probable absence of an interaction between two genes, i.e., they function in independent pathways in the cell. Full details of the experimental procedure and the normalization process are described in Collins et al. (2).

The standard analysis technique applied to the E-MAP score matrix is agglomerative hierarchical clustering using the the Cluster tool (3). This type of analysis often provides insight into the underlying biology. For example, subsets of genes with similar interaction profiles may signify complexes of proteins involved in common biological processes.

One common characteristic of E-MAPs is the high proportion of missing entries that they contain (up to ~35%). Missing entries correspond to pairs of genes for whom interaction strengths could not be measured during the high-throughput process or those that were subsequently filtered due to unreliability. These missing values can reduce the effectiveness of downstream analysis, e.g., introducing instability in clustering (4), and prevent the use of others, e.g., matrix factorization techniques such as SVD and PCA. As each genetic interaction implies a functional relationship between gene pairs, individual interactions themselves can provide valuable biological insight. Consequently, there is a need for imputation techniques to “fill in the blanks.”

1.2. Imputation

A growing body of work focuses on the prediction of genetic interactions, but to date the emphasis has largely been on the prediction of binary links, i.e., synthetic lethality. These methods have had some success by integrating diverse biological data (5) or by focusing on network topology of the underlying protein interaction network (6, 7). Additionally, methods have been developed for predicting synthetic lethality using only the graph of synthetic lethal interactions (8, 9).

Recently, Ulitsky et al. (10) and Ryan et al. (11) have addressed the problem of imputing quantitative genetic interactions within E-MAPs, with both groups adopting related approaches.

Ryan et al. noted the similarities between E-MAP and gene expression datasets and adapted techniques originally developed for gene expression to work with the symmetric pairwise data found in E-MAPs. The goal in both cases is to construct a complete dataset by imputing quantitative measurements in order to improve the subsequent data analysis. Additionally, both E-MAPs and gene expression datasets display coherence among genes. For gene expression data, this is considered to be indicative of co-regulation while for E-MAPs, it is indicative of co-complex or pathway membership. An example of this coherence is shown in Fig. 1.

Fig. 1.

An example of coherence taken from the Chromosome Biology E-MAP. Members of the Swr1 complex display similar interaction profiles, and as a result are clustered together.

A number of gene expression imputation techniques were adapted to work with E-MAP data, including variations of the K nearest neighbors algorithm (12), local least squares (13), and Bayesian Principal Components Analysis (14). The performance of these techniques was assessed on a number of different datasets (including two different species) using a number of different metrics. Symmetric nearest neighbor-based approaches offered consistently accurate imputations in a tractable manner, and we focus here on one such approach – weighted symmetric nearest neighbors (wNN).

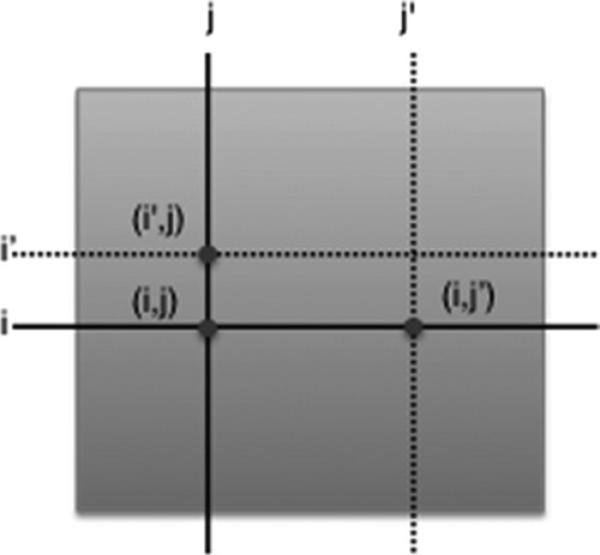
Nearest neighbor imputation is a simple strategy that uses genes with similar interaction profiles to impute missing values. Standard imputation algorithms based on nearest neighbors involve imputing values in feature-based asymmetric datasets (e.g., gene expression datasets). Ryan et al. proposed a simple modification to this approach designed to handle symmetric data. For each missing interaction (i, j ), find the K nearest neighbor(s) for both gene i and gene j. Then, find the values for the interaction of i with j 's neighbors and j with i's neighbors. These values are averaged to provide an imputed value for the missing entry (i, j). An illustration of this approach is shown in Fig. 2.

Fig. 2.

Symmetric nearest neighbors with K = 1. To estimate the missing value (i, j), the values given by (i′, j) and (i, j′) would be combined.

One issue with standard nearest neighbor-based approaches is that the accuracy of the method is very dependent on the choice of the parameter K. This can be alleviated by weighting the contribution of the neighbors based on their similarity to the query gene so that more similar genes make a greater contribution to the imputation. The degree of the contribution can be controlled by the choice of the weighting system. Ryan et al. employed the following weighting system (originally described in (15)), which ensures that closer neighbors are considerably more influential than more distant neighbors. Given a value r denoting the Pearson correlation between a gene i and its neighbor i′, the weight w(i, i ′) is calculated as follows:

$$w(i,i^{\prime })={\left(\frac{r^2}{1-r^2+\epsilon }\right)}^2.$$

A benefit of this weighting system (determined empirically) is that once the choice of neighbors is sufficiently high (K > 20), adding additional neighbors does not have a significant negative impact on the accuracy of the imputation. Near-optimal performance was obtained in all tested datasets with K = 50, so this is the default for the implementation we discuss.

Ulitsky et al. used the nearest neighbors as the basis for a more advanced approach – performing a linear regression over 167 features, including nearest neighbors, interactions between neighbors, and diverse genomic information (e.g., protein–protein interactions, shared phenotypes, Gene Ontology terms). However, they noted that this additional information offered only a marginal improvement to the accuracy of imputation and that its absence would not seriously affect imputation.

Although the E-MAP approach was developed for the budding yeast Saccharomyces cerivisiae (16), it has recently been extended to the fission yeast Schizosaccharomyces pombe (17). An analogous technique has also been developed for Escherichia coli (18) while related approaches exist for other organisms (e.g., Caenorhabditis elegans (19)). The additional genomic data available for these organisms is more limited than that for S. cerivisiae. The method we describe here, the wNN method of Ryan et al., does not rely on the availability of external data, a factor that may be important as the range of epistasis studies increases. Furthermore, the implementation is freely available.

1.3. Assessing the Accuracy of Imputation

While methods for assessing the accuracy of imputation are primarily of interest to those developing imputation methods, they should also be of concern to those applying the results. No imputation method performs equally well on all datasets, so for each new data-set it is worth estimating the accuracy of imputation prior to analyzing the results.

We introduce in the methods section an implementation of K fold cross validation, a simple tool for estimating the accuracy of imputation on a given E-MAP. It works as follows – the measured interactions are randomly partitioned into ten equally sized sets (or folds). Imputation is then performed ten times – with the interactions from onefold hidden in each run. We can then compare the imputations for these artificially introduced missing values with their actual measured interactions.

The program uses two metrics for assessing the accuracy of imputation – Pearson's correlation and the Normalized Root Mean Squared Error (NRMSE). Pearson's correlation has a scale of –1 to 1, and a higher correlation indicates a more accurate imputation.

NRMSE is defined as follows:

$$\mathrm{NRMSE}=\sqrt{\frac{\text{mean}\left[{(i{j}_{\text{answer}}-i{j}_{\text{guess}})}^2\right]}{\text{variance}\left[i{j}_{\text{answer}}\right]}},$$

where ij_answer denotes the set of known values and ij_guess denotes the corresponding set of imputed values. This is designed so that estimating the dataset mean results in an NRMSE of 1 and more accurate imputation results in a lower score.

1.4. Benefits of Imputation

There are two primary reasons for imputation – to improve downstream analysis, such as clustering, and to identify individual interactions which may be worth testing experimentally. Ryan et al. gave an example of how imputation could improve the use of average linkage hierarchical clustering, the standard analysis applied to E-MAPs. They identified clusters which had a statistically signifi-cant overlap with a known protein complex before and after imputation. They noted that after imputation in one E-MAP, a number of complexes were found with higher precision while in another E-MAP, an extra complex was identified.

Previous studies have used protein complexes as a way of interpreting genetic interactions – either within or between protein complexes. Many complexes were found to be “monochromatic” – enriched with either predominantly alleviating or predominantly aggravating interactions. Ulitsky et al. showed how the number of such complexes was increased significantly after imputation, suggesting a further benefit of imputation prior to downstream analysis.

Both groups showed that gene pairs predicted to have a strong genetic interaction were enriched with annotations similar to those of measured interactions (e.g., shared phenotypes, shared biological process, protein–protein interactions). This is an indication that imputation can generate reliable predictions for epistatic interactions, and thus may be worth validating using smaller scale experiments.

2. Materials

An implementation of the symmetric nearest neighbors algorithm can be obtained from http://www.bioinformatics.org/emapimputation.

This implementation requires an installation of Python 2.x preinstalled on many operating systems and also available at http://www.python.org/download/.

The expected input to the program is a symmetric score matrix in tab-delimited plain text with the first row and column containing gene names (see Note 1). For those using the E-MAP toolbox for MATLAB (20), such a file can be created using the “export-ForCluster3_0” command. If the matrix is in Excel, the plain text matrix can be created by choosing “File” → “Save As” → “Tab Delimited Text.” For reference, an example matrix is included with the implementation.

It may also be beneficial to prefilter the matrix (see Note 2).

3. Methods

Here, we give examples of three different use cases for our imputation software – obtaining a complete matrix for further analysis, obtaining a list of strong interactions for small-scale follow-up, and estimating the accuracy of imputation.

1. To obtain a complete matrix as output, run the program using the following command:

   • python symmetricNN.py –i matrix_input.txt –o matrix_output.txt
   • This matrix can then be used as an input to other programs, e.g., the Cluster program (3) (see Note 3) or the R environment (21). Additional input parameters can be specified for this command, e.g., to adjust the number of neighbors used for imputation, but in practice they are rarely needed (see Note 4).
2. To obtain a ranked list of strong genetic interactions, use the following command:

   • python symmetricNN.py –i matrix_input.txt –r ranked_output.txt
   • The output of this command is a list of genetic interactions predicted to be strongly alleviating (score > 2) or strongly aggravating (score < –2.5). They are ranked according to the total weight of their neighbors – so pairs which were imputed using very similar neighbors are ranked higher than those with more distant neighbors. There is no direct interpretation to the weight column; however, the pairs at the top of the list can be considered a more reliable estimate, and thus a better candidate for a small-scale follow-up. Sample output is shown in Table 1.
3. The accuracy of imputation on a given dataset can be estimated using the following command:

   • python test_imputation.py –i matrix_input.txt
   • Note that this command takes approximately ten times longer to compute than standard imputation, as it is essentially performing the imputation ten times.
   • The output of this command is similar to the following:
   • Estimated correlation = 0.63
   • Estimated NRMSE = 0.77
   • Typically, for an E-MAP, the correlation is in the range 0.6–0.7 and the NRMSE is in the range 0.7–0.8.

Table 1.

Strong epistatic interactions ranked based on the weight calculated from their neighbors

Gene A	Gene B	Score	Weight
YJL004C	YJL024C	–7.08	53.61
YGL005C	YGR261C	–6.02	37.31
YBR288C	YGL005C	–6.33	35.31
YGL005C	YHL031C	–11.40	34.83
YLR039C	YLR056W	4.33	33.24