Structure Prediction of Loops with Fixed and Flexible Stems

Abstract

The prediction of loop structures is considered one of the main challenges in the protein folding problem. Regardless of the dependence of the overall algorithm on the protein data bank, the flexibility of loop regions dictates the need for special attention to their structures. In this article, we present algorithms for loop structure prediction with fixed stem and flexible stem geometry. In the flexible stem geometry problem, only the secondary structure of three stem residues on either side of the loop is known. In the fixed stem geometry problem, the structure of the three stem residues on either side of the loop is also known. Initial loop structures are generated using a probability database for the flexible stem geometry problem, and using torsion angle dynamics for the fixed stem geometry problem. Three rotamer optimization algorithms are introduced to alleviate steric clashes between the generated backbone structures and the side chain rotamers. The structures are optimized by energy minimization using an all atom force field. The optimized structures are clustered using a traveling salesman problem based clustering algorithm. The structures in the densest clusters are then utilized to refine dihedral angle bounds on all amino acids in the loop. The entire procedure is carried out for a number of iterations, leading to improved structure prediction and refined dihedral angle bounds. The algorithms presented in this article has been tested on 3190 loops from the PDBSelect25 data set and on targets from the recently concluded CASP9 community-wide experiment.

1 Introduction

Loops are seen to typically be shorter in length than the ordered secondary structure components of a protein and are extremely vital to proteins. The presence of loops permits the formation of the secondary structure topology of a protein. The amino acids in loop regions are important to the formation of β-hairpins.¹ Further, loops are typically exposed on the surface of the proteins, thus making them directly accessible to the outside environment of the protein. Loops provide a means for sheltering the hydrophobic core of the protein from the external solvent, especially in globular proteins. Loops have been key participants in active and binding sites on the protein.² Detailed reviews of loop structure prediction techniques have been presented elsewhere.^3–5

1.1 Challenges in Loop Structure Prediction

Since loops form the parts of the protein sequence that lie between secondary structures, they possess greater randomness and structural flexibility than the secondary structure components of the protein. Most successful methods for the prediction of secondary structure regions in a protein have employed the explicit or implicit use of the protein data bank.⁶ By observing and deriving patterns of sequential identity from previously existing proteins, successful predictions regarding the locations of secondary structure elements are made. The prediction of the arrangement of β-strands in a protein is also orderly, and follows a definite, albeit currently incomplete, set of rules. This permits the use of physical and database derived constraints which can be used to enhance the β-sheet topology prediction algorithm. The absence of an ordered structure in loops suggests that exclusively database driven techniques cannot be employed consistently for the prediction of loop regions in proteins. In addition, given their much increased exposure to the outside environment, loops are observed to have relatively fewer and inconsistent contacts with the remainder of the protein structure, thus making it significantly more challenging to predict their structure. Given the flexibility associated with loop structures, the problem has previously been described as a mini ab initio protein folding problem.⁷ Given the very weak correlation between sequence and structure in loop structures,⁸ the comparative modeling techniques widely used in protein structure prediction become unsuitable. Fold recognition techniques are based on the idea that folds of proteins are conserved much more than sequence. However, loop structures do not have any observable patterns which can be categorized into the standard “folds”. Further, one of the main outstanding challenges in fold recognition algorithms is the prediction of loop structures,^9,10 thus making the approach unsuitable for the prediction of the structure of loops. The consensus in the field of protein structure prediction has been to tackle the problem of loop structure prediction using first principles or knowledge-based approaches.^11–13

The main aim of the loop structure prediction stage is the determination of tight bounds on the backbone dihedral angles of the amino acids in the loop. The prediction of the experimentally favored structure of a loop is extremely challenging. Loops are the most flexible parts of proteins, and move constantly under interactions with the environment. Thus, the “exact” structure of a loop is very hard to determine, and what is observed in experimentally elucidated structures is a snapshot of the structure of the loop. For an optimization-driven approach towards predicting the final three-dimensional structure of a target protein, the provision of tight dihedral angle bounds on loop residues is very important.

1.2 Flexible stem and Fixed stem loop structure prediction

Most loop structure prediction algorithms can be broadly classified into flexible stem and fixed stem structure prediction algorithms based on the input to the algorithm. The fixed stem geometry problem assumes that the structure of flanking secondary structure elements to a given loop is known. Thus, the flanking secondary structure residues, or “stems” can be fixed to the experimentally determined structure, and the problem is narrowed down to one of determination of the structure of the intermediate loop. The flexible stem geometry problem does not assume the knowledge of the structure of the flanking secondary structure elements. The only information available to a flexible stem geometry problem is the identity of the type of secondary structures which flank the loop, that is, α-helix or β-strand. It can be seen that the flexible stem geometry problem is a more challenging version of the loop structure prediction problem. Recent work has demonstrated the differences in the challenges facing flexible stem and fixed stem loop structure prediction problems.¹⁴ In this work, the authors perturbed 6–12 residues away from their crystal conformation and placed all side chains in non-native, but low energy conformations. Even for such small perturbations, it was seen that the resulting regeneration problem was much more challenging than the loop reconstruction problem.

2 Background

Most successful methods for loop structure prediction followed a series of steps consisting of improved dihedral angle sampling, removal of steric clashes, energy minimization and clustering of predicted structures to identify the best representative structures from the predicted ensemble.

A large part of the recent success in dihedral angle sampling can be attributed to the improved computational resources available, allowing finer discretizations of the dihedral angle space available to amino acids. Additional computational resources have also permitted the generation of a larger number of initial structures, resulting in an improved coverage of the structural space. The common theme of dihedral angle sampling in loop structure prediction techniques is the generation of initial dihedral angles from a large database of known structures. Xiang et al. have applied this process to a test set of 553 loops, ranging between five and twelve amino acids.⁷ As the approach was developed for fixed-stem geometry problems, tighter dihedral angle distributions were used to generate the initial loop structures. Similarly, de Pristo et al. generate 1000 initial structures by sampling backbone dihedral angles from a large database of dihedral angles generated from known loop structures, by using varying degrees of coarseness.¹¹ Based on their analysis, it was concluded that smaller number of samples generated from a finer distribution outperform the generation of a large number of initial structures from a coarser distribution. In a varied implementation of the previous algorithm, elimination criteria based on minimum number of occurences in a bin were used to filter initial structures generated from a database-derived dihedral angle distribution.⁹ Further, coarser discretization of the dihedral angle plane was used as a means to discard conformers that were too similar to ones previously generated. A number of additional criteria have also been used to discard initial structures generated from probability distributions. One approach towards improving initial structure generation in fixed-stem geometry problems has been to reject the structure if it becomes apparent that side-chain atoms cannot be fit, or if a closure of the loop to the fixed stem residues is not possible.⁷ A recent approach has derived a pseudo potential to deduce the quality of an initial structure derived from a probabilistic database.¹⁵ The authors use a pareto optimal searching (POS) method to span the search space of a large number of contact potentials, to derive a diverse initial conformational ensemble. Choi and Deane have used environment specific scoring parameters to improve the sampling for their loop structure prediction algorithm, FREAD.¹⁶ By including parameters specific to the environment and flanking secondary structures, it was shown that the initial structures generated were superior, both in terms of steric clashes and in terms of proximity of dihedral angles to the native structure. Initial structures generated have been shown to be directly correlated with the quality of the database they are derived from.^17–19 The quality of the database includes parameters such as the number of loop structures, pairwise sequence similarity of the database, variation in loop lengths and experimental method used to derive the native structure of the protein. Given the lack of correlation between loop sequence and structural similarity, it is still believed that the most successful initial structure generation algorithms are based on ab initio methods.^13,20 The analysis of the interaction of any predicted initial loop structure to the rest of the protein is another useful criterion that has been used previously for the generation of loop structures from large databases.²¹ Near-native loop structures have been identified using initial structure generation and structure optimization using the all atom CHARMM force field.²² Two representative states for each alanine-like residue, and four representative states for glycine are used to generate the initial sampling of loop structures. In addition, interactions with the protein core have been included into the scoring function. A number of successful approaches presented in literature have combined database driven and ab initio initial structure generation procedures.²³ Recent methods have used energy based criteria to eliminate initial structures before carrying out local optimization.²⁴ The approach identifies and removes initial structures with low hydrophobic and hydrogen bonding interactions before implementing side chain and all atom optimization procedures to generate an ensemble of predicted loop structures. Recent work has shown a significant improvement in sampling and initial structure generation for very long loops, using the inclusion of dipeptide segment sampling and the OPLS-AA force field.²⁵

A number of energy functions have been used for the structure optimization stage of loop structure prediction algorithms. These include database derived force fields, as well as first principles based energy functions. Most first principles based energy functions are modified forms of the AMBER,²⁶ CHARMM²⁷ or ECEPP/3²⁸ force fields, with parameters modified to target the loop structure prediction problem. In addition, knowledge derived statistical potentials have been utilized for the problem of fixed stem loop structure prediction.^16,29 Terms representing energetic contributions due to solvation, steric clashes, hydrogen bonding and short and long range contacts have been seen to be included in knowledge derived force fields. Hierarchical methods, which incorporate all-atom physical potentials with explicit and implicit solvent models, have been presented for the case of fixed stem loop structure prediction.⁹ This algorithm applies a multiscale approach, starting from a coarse model which explicitly incorporates crystal packing, and refines the initial structures using all atom potentials. Other methods have incorporated corrective terms to account for discrepancies in the hydrophobic expressions found in all atom potentials.²⁴ In addition, energy functions have also been used to classify native from non-native loop structures in large ensembles.³⁰

The structure optimization stage of loop structure prediction algorithms requires the energy minimization of the initial structures previously derived. Many methods have been used to efficiently navigate the tertiary structure space of a target loop. The optimization algorithms that have been employed for the purposes of loop structure prediction include molecular dynamics,³¹ simulated annealing,³² torsion angle mechanics^33,34 and nonlinear optimization.¹³ In addition, a number of side chain optimization algorithms have been introduced to alleviate steric clashes between the randomly generated side chain and backbone of the initial loop structures. Most side chain optimization algorithms use a large database of known side chain angles.¹³ A combination of side chain dihedral angles for any amino acid is known as a rotational isomer, or rotamer, of the residue. A number of rotamer libraries have been presented, which document all observed combinations of side chain dihedral angles. Two of these rotamer libraries have been used in the loop structure prediction algorithms presented in this article. In addition, methods have been presented in literature which address the side chain optimization problem using detailed atomistic or knowledge based potentials, by incorporating additional effects like ionization and solvation,³⁵ where the dielectric constant of interaction between side chain atoms is allowed to vary as a function of the interacting residues to account for these effects.

The next section presents the derivation of dihedral angle propensities for the purposes of generation of initial structures. This is followed by a description of the generation of initial loop structures, combined with checks to ensure uniqueness of the generated structures. Three rotamer optimization steps are presented, which alleviate local steric clashes between the side chains and the backbone generated. This is followed by a description of the constrained non-linear optimization stage for loop structure prediction, and an overview of a traveling salesman based clustering algorithm for the identification of tighter bounds on the dihedral angles of loop residues.

3 Mathematical Model

In this section, the mathematical models for loop structure prediction using fixed stem and flexible stem geometry are presented. The two methods primarily differ in their approaches towards developing initial loop structures, since the input data for the flexible stem geometry problem does not include structural data. A three-stage rotamer optimization procedure is implemented, which aims at alleviating steric clashes between the backbone and the side chains of the amino acids of the loop. This is followed by constrained non-linear optimization of all loop structures using the full-atom ECEPP/3 potential. Optimized structures derived out of this stage are subjected to clustering to identify high quality structures from the predicted ensemble. These structures are used to refine the dihedral angle bounds on the loops, before carryout out the entire algorithm in an iterative process.

3.1 Derivation of Dihedral Angle Propensities

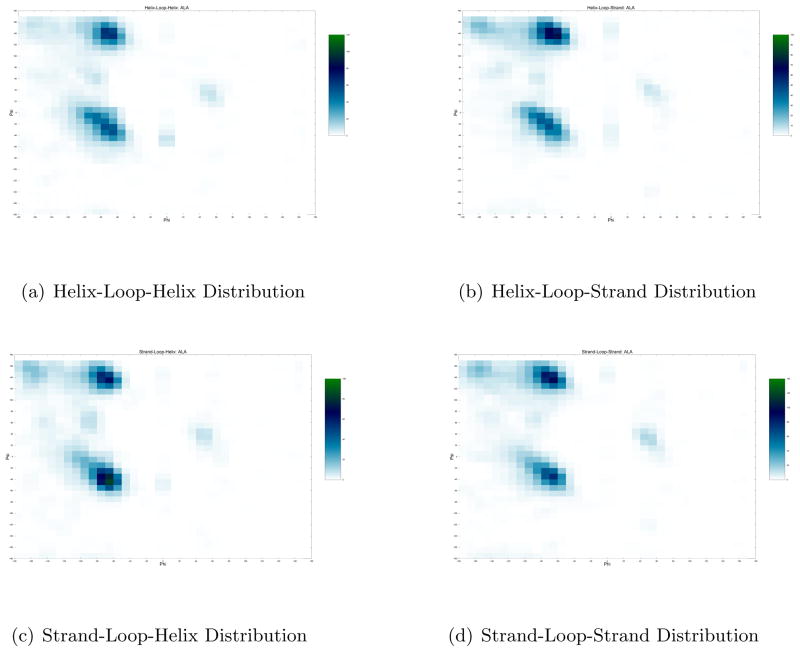
The generation of initial structures is a crucial step when local optimization techniques are employed. For the flexible stem geometry algorithm presented in this article, a large repository of structures from the PDBSelect25 data set was used as a library for generation of loop angle probability distributions. This data set contains 4092 single chain proteins, with pairwise sequence similarity below 25%. We collect loop segments between the lengths of 4 and 20 from this database, as longer lengths provide a very sparse distribution of amino acid dihedral angles. For each amino acid, we discretize the Ramachandran plot into a grid of size 10° X 10°. Based on the database of collected loop segments, we count the frequency of backbone dihedral angle occurences for each amino acid in each dihedral angle bin. A similar distribution is generated for each kind of loop, that is, separate distributions are generated from loops between helices, strands and any combination thereof. An example of the difference in dihedral angle distributions generated is shown in Fig 1. For any target loop, a set of 2000 initial structures are generated using these probability distributions. The process of generating initial structures is descibed as follows.

Figure 1.

Illustrative example of variation in distribution of Loop Residue Angles

3.3 Flexible Stem Geometry

For each amino acid in each type of loop, each discretized bin in the Ramachandran plot is assigned a number n_i that corresponds to the frequency of dihedral angle occurences observed. Hence the first, second and in general i^th bin can be represented by the numbers:

$$\begin{array}{r}{b}_1:1,\dots ,n_1\\ b_2:(n_1+1),\dots ,(n_1+n_2)\\ b_i:\sum _{j=1}^{i-1}{n}_j,\dots ,n_i+\sum _{j=1}^{i-1}{n}_j\end{array}$$ (1)

By generating a random number between 1 and Σ_j n_j, and identifying the bin it corresponds to, we can assign a backbone angle to an amino acid. However, since the initial dihedral angles of each amino acid are generated by unique distributions, possibilities of backbone steric clashes in the generated structure are high. In order to alleviate backbone steric clashes, we re-sample pairs of amino acids which are identified as having clashing backbones.

3.4 Fixed Stem Geometry

Prior to the implementation of the structure optimization algorithm in the fixed stem geometry problem, it is vital to get initial structures which fall into the feasible space of the optimization problem. Here, the feasible space of the problem is defined by the dihedral angle and distance bounds that can be derived from the experimental data of the stem residues flanking the loop. Various algorithms have been used for the problem of identifying structures which satisfy a sparse set of distance and dihedral angle constraints. For protein structure prediction problems, distance geometry algorithms like EMBED³⁶ and dgsol³⁷ have been used to produce feasible initial structures. In addition to distance geometry methods, a number of other algorithms like variable target methods³⁸ and molecular dynamics³⁹ have also been employed for this problem. A detailed review on algorithms for constrained protein structure determination is available elsewhere.⁴⁰

Initial structure generation in the fixed stem geometry problem is carried out through a torsion angle dynamics package, CYANA.⁴¹ By fixing the covalent bonds and bond angles to their mean values, the torsion angle dynamics package works in the dihedral angle space, thus reducing the number of variables drastically. Further, unlike target minimization, molecular dynamics allows itself the possibility of overcoming energy barriers, due to the presence of kinetic energy. Unlike classical molecular dynamics simulations, the torsion angle dynamics algorithms combine steric clashes-based energy terms and constraint-based penalties in a simplified target function. This allows for faster calculations, and results in the algorithm aiming to identify structures which are fairly low in energy, but are more importantly, feasible. Algorithmic implementation details of the initial point selection can be found elsewhere.⁴²

3.4.1 Uniqueness of Initial Structures

In order to ensure that initial structures generated are not very similar to each other, any new structure is required to be unique to each of its predecessors. Uniqueness is defined by the following equation

$$\sum _{i=1}^{N_{\mathit{dih}}}(({\phi }_{i,k}-{\phi }_{i,j})+({\psi }_{i,k}-{\psi }_{i,j}))\ge 5\forall j<k.$$ (2)

where φ_i,k and ψ_i,k refer to the backbone dihedral angles of amino acid i of loop conformer k. Here, N_dih represent all the dihedral angles of the loop. The index j runs over all loop conformers previously generated, while the index k refers to the new loop struture generated from the probability distribution. The equation requires that when comparing the new loop structure to its predecessors, at least one dihedral angle is found in a bin different to the previously generated structure.

3.5 Rotamer Optimization

Rotamer optimization is an important intermediate step in the loop structure prediction framework. Given an initial loop backbone, there is a very high likelihood that strong steric clashes exist between side chains of loop residues and the backbone of the loop. The objective of introducing a rotamer optimization step is to identify a better starting point for the full atom local optimization of the loop structure. It is also crucial to note that the rotamer optimization step is an intermediate stage used for steric clash removal only. Hence, a fast rotamer optimization algorithm essentially behaves as an efficient local minimization step.

Most successful rotamer optimization algorithms, especially for loop structure prediction, use rotamer libraries to carry out local energy minimization. Rotamer libraries consist of combinations of side chain angles observed in the database. The computational time required for a rotamer optimization algorithms depends on two factors: the energy function being considered and the size of the rotamer library being employed.^43,44 Hence, the aim is to devise rotamer optimization algorithms which use an energy function resembling an atomic force field and a search method that is exhaustive, while ensuring that the algorithm does not become computationally prohibitive.

Since the primary objective of the rotamer optimization step is the removal of steric clashes between the side chains, the use of an all atom force field may not be judicious. Further, the implementation of the rotamer optimization step is targeted towards removing steric clashes in the initial structures, without guarantees that the resulting side chains would remain fixed or feasible after the complete structure optimization. The use of an approximate energy function is the best tradeoff for the purposes of rotamer optimization. Most combinatorial rotamer optimization algorithms divide the energy of a conformation into two parts, given by the following equation:

$$min\sum _{(i,k),k\in R_i}{E}_{ik}^{\mathit{self}}+\sum _{(i,k),k\in R_i}\sum _{(j,l),j>i,l\in R_j}{E}_{\mathit{ikjl}}^{\mathit{pair}}.$$ (3)

Here $E_{ik}^{\mathit{self}}$ represents the contribution of the interaction of a rotamer with all fixed atoms during the rotamer optimization. In other words, the energy of interaction of movable atoms of the side chain of an amino acid i with all immovable atoms, including backbone atoms and C^β atoms, is expressed by this term. The second term ( $E_{\mathit{ijkl}}^{\mathit{pair}}$) represents the pair energy, and is a representation of the energy of interaction between rotamer k of residue i and rotamer l of residue j.

The efficiency of any rotamer optimization algorithm depends on the energy function, and can hence be signficantly improved by using an approximate energy function. The chosen energy function should closely resemble the all atom energy function it is derived from, while being computationally inexpensive. The energy function used in the rotamer optimization algorithms presented in this article is a piecewise linear approximation of the repulsive part of the Lennard Jones and hydrogen bonding potential terms in the ECEPP/3 force field. The repulsion terms are approximated by piece-wise linear functions that intersect the original expression at 2, 5, 10, 20, 50 and 100 kcal/mol. All energetic contributions above 100 kcal/mol are approximated by the last piecewise expression, while all energetic contributions less than 2kcal/mol are ignored.

In the loop structure prediction algorithms presented in this article, we have incorporated three rotamer optimization algorithms. The algorithmic details of the rotamer optimization steps have been presented previously.⁴² Here, the overview of the algorithms, along with changes made to the algorithms are presented.

3.5.1 Rotamer Optimization: FASTER

The first rotamer optimization algorithm, known as FASTER,⁴⁴ has been shown to produce nearly identical results to the global optimization dead end elimination algorithm, while being nearly 100–1000 times faster than it. The key steps of this rotamer optimization algorithm are:

1. Insert all backbone and C_β atoms onto a fixed grid. All backbone and C_β atoms are assumed to be immovable during the rotamer optimization step. This is to ensure that the rotamer optimization focuses only on identification of rotamer combinations which minimize the energy for the initial backbone generated using the probability distributions.

2. Load rotamers of each loop amino acid from the Penultimate library.⁴⁵

3. Pre-compute the self energy energy terms for each possible rotamer of each amino acid in the loop. In order to do this, we take each possible rotamer of any given amino acid, and evaluate the energy of the loop when this rotamer is used. This is possible since the self energy term is evaluated against all non-movable atoms of the loop. Similarly, we pre-compute the pair energies of combinations of rotamers of all amino acids in the loop. If the distance of a pair of rotamers is above a threshold, this computation is ignored.

4. Starting from the first amino acid of the loop, we iterate over all amino acids of the loop. For any amino acid, we iterate over all the possible rotamers of the amino acid. If the sum of the self and pair energy for any rotamer results in a total energy is better than the current energy, we replace this structure to be the current active structure. This structure is referred to as the Backbone determined minimum structure (BMEC). For each of the subsequent steps presented in this algorithm, the overview of the step is presented, and the reader is referred to the original work for details.⁴⁴

5. The first pass of the FASTER algorithm, called iterative batch relaxation (iBR), is split into 3 main steps. First, the total energy for all of the rotamers in each residue for the current configuration i is evaluated and stored. Next, the rotamer position k in each residue i that yields the minimum energy for the current loop configuration is saved. Finally, the total energy of the new conformation is calculated. This procedure is carried out until the energy of the loop configuration stabilizes or starts oscillating.

6. The next phase of FASTER is called the conditional iterative batch relaxation (ciBR). This step is similar to the previous step, except that the rotamer positions with lower energy are only accepted with an 80% probability. Ten iterations of ten optimization cycles each are performed and the lowest energy conformation is retained.

7. The final phase is the single-residue perturbation/relaxation (sPR) phase. This is a final iteration of the iBR phase, carried out by fixing the rotamer of one amino acid at a time and iterating over the remaining residues of the loop.

3.5.2 Rotamer Optimization: Cyclical Search Algorithm

The second rotamer optimization algorithm is a cyclic search method, and uses the enhanced rotamer library from Xiang and Honig.⁷ The main steps of the algorithm are presented below:

1. Insert all backbone and C_β atoms onto a fixed grid. All backbone and C_β atoms are assumed to be immovable during the rotamer optimization step.

2. Load rotamers of each loop amino acid from the Xiang and Honig library.⁷

3. Randomize the order in which amino acids would be visited by the algorithm. For each amino acid in this randomized list, we carry out the following steps.

4. Randomly rearrange the order of the residues to be visited by the rotamer optimization algorithm. For each residue i, the energy of the each rotamer k is evaluated using the approximate energy function. This includes the intra-chain and inter-chain interactions. In addition, the total ECEPP/3 energy of the original rotamer of the amino acid i is evaluated. If the approximate energy value of the new rotamer is within a cutoff value of the true ECEPP/3 energy of the original rotamer, the total ECEPP/3 energy of the new rotamer is evaluated. If this new energy is lower than the previous existing rotamer for this amino acid, we replace the rotamer of amino acid i with this new rotamer k.

5. This procedure is repeated until all amino acids of the loop have been addressed.

3.5.3 Rotamer Optimizaton: Random Rotamer Search

For the third phase of the rotamer optimization stage, we employ a procedure similar to the cyclic search algorithm presented in the previous section. However, instead of using the rotamer library by Xiang and Honig, we choose to restrict the rotamer search to the local neighborhood of the rotamers identified at this stage. It is assumed that the previous algorithms would bring the rotamers close to the local minima for the given fixed backbone. Hence, we create a rotamer library using a narrow Gaussian distribution around the current available rotamer. The mean of this distribution is the current rotamer itself, while a standard deviation of 10° is used. The aim of this step is to provide additional refinement to the rotamers in the neighborhood of the recorded value in the library. The algorithmic steps are outlined below.

1. Insert all backbone and C_β atoms onto a fixed grid. All backbone and C_β atoms are assumed to be immovable during the rotamer optimization step.

2. Load rotamers of each loop amino acid from a library of 50 rotamers created around the current existing rotamer, as explained previously.

3. Randomize the order in which amino acids would be visited by the algorithm.

4. For each amino acid visited, carry out the cyclical search algorithm presented in the previous section.

The advantage of using the three step procedure to rotamer optimization has been presented in literature,⁴² and a 35%–65% improvement in the energy of a structure at the end of the rotamer optimization steps is obtained.

3.6 Energy Minimization

Once the rotamer optimization step has been carried out, the loop structures are subjected to all atom energy minimization. The energy function used for this purpose is the all-atom ECEPP/3 potential, given by the expression

$$E_{\mathit{ECEPP}/3}=\sum _{(i,j)\in ES}\frac{q_i{q}_j}{r_{ij}}+\sum _{(i,j)\in NB}{F}_{ij}\frac{A_{ij}}{r_{ij}^{12}}-\frac{C_{ij}}{r_{ij}^6}+\sum _{(i,j)\in HB}\frac{A_{ij}^{\prime }}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^{10}}+\sum _{(k)\in \mathit{TOR}}\frac{E_{0,k}}{2}(1+c_{k}cos{n}_k{\theta }_k)$$ (4)

In Equation 4, r_ij represents the distance between a pair of atoms i and j, given that both the atoms fall into the set of atoms over which the summation is carried out. The parameter F_ij, which represents the relative impact of the repulsive part of the Lennard-Jones expression, is taken as 0.5 for 1 – 4 interactions, and 1.0 for 1 – 5 interactions. Non-bonding parameters such as A_ij, $A_{ij}^{\prime }$,B_ij and C_ij are atom pair dependent. The sets ES, NB and HB are defined over the set of pairs of atoms i and j that can have electrostatic, non-bonded and hydrogen bonding interactions, respectively. The set TOR runs over all torsion angles of the protein that can contribute to the last term of the expression.

The energy minimization problem can be represented as a constrained nonlinear programming problem. The constraints to the model are the backbone dihedral angle bounds. These bounds are refined at each stage, as is described in the next section. The Sequential Quadratic Programming (SQP) method is used via NPSOL.⁴⁶ This is attractive for protein structure prediction problems because it requires fewer evaluations of the objective function, which is computationally expensive.

3.7 Clustering

The main challenge behind the clustering step is the identification of a subset of predicted structures, which can be considered representative of the better structures of the ensemble. In the loop structure prediction framework, we address this challenge by implementing an iterative novel Traveling Salesman Problem (TSP) based clustering approach, known as ICON.⁴⁷ By considering each conformer generated from the ASTRO-FOLD 2.0 framework as a node on a traveling salesman path, we identify the globally optimal path through each of these nodes. Once the optimal path is determined, this path is partitioned into clusters such that the clusters minimize the global sum of intracluster differences in values. An overview of each of the steps of ICON is presented below, and the details can be found in literature.^47,48

With each conformer of the target loop as a node on the TSP path, we define binary variables y_i,i′ for any pair of nodes i and i′ as:

$$y_{i,i^{\prime }}=\{\begin{array}{lll}1\hfill & :\hfill & \text{if}\text{node}\text{i}’\text{immediately}\text{precedes}\text{node}\text{i}\hfill \\ 0\hfill & :\hfill & \text{otherwise}\hfill \end{array}$$ (5)

The objective function is then defined as:⁴⁹

$$min\sum _i\sum _{i^{\prime }}{y}_{i,i^{\prime }}{\phi }_{m_i,m_{i^{\prime }}}$$ (6)

where φ_mi,j,mi′,j is given by:

$$\phi (m_i,m_{i^{\prime }})=\sum _{j}min{(m_{i,j}-m_{i^{\prime },j},360-(m_{i,j}-m_{i^{\prime },j}))}^2$$ (7)

Here, the index j runs over all the pairs of (φ, ψ) angles of each amino acid of the target loop. Constraints which ensure that each node has exactly one node preceding and following it on the TSP path are implemented. In addition, efficient TSP solvers like Concorde⁵⁰ introduce additional cuts which eliminate circular tours and subtours. Once the optimal path through all conformers is determined, we propose an integer linear programming (ILP) model to determine the cluster boundaries for a given optimal ordering.⁴⁸ Since for any node on the TSP path, we know the immediate neighbors on the path, the aim is to simply determine the points on the TSP path where immediate neighbors on the path fall into separate clusters. This would be sufficient to identify the boundaries of clusters. In order to do this, we generate a distribution of φ_i,i+1 (where φ_i,i+1 are defined as in Equation 7). For any local window of x elements, we identify nodes where the neighbor distance falls below one standard deviation of the global average of this distribution. In addition, this distance would be the minimum in its local window, so as to ensure that we do not separate out elements that are very similar. By selecting local minima points of this distribution as cluster “seeds”, we now have the problem of placing the remaining “outlier” points with the cluster seed element immediately before or after them in the optimal TSP path. This has been modeled as an integer linear programming (ILP) model, with binary variables assigning the outlier points to either the cluster before or after them. The objective function includes terms which account for the fixed cost (distance between an outlier and the seed of the cluster) and variable cost (distance between two outliers both assigned to the same cluster seed). Constraints are introduced to ensure that there are no crossovers, i.e. for any pair of outliers i, i + 1, the assigned cluster of element i + 1 should be greater than or the same as that of element i. Details of the mathematical implementation of the model can be found elsewhere.⁴⁸ Subsequently, the cluster centroids for each cluster are identified by determining the cluster element with the minimum distance to all other elements of the cluster, with the distance being defined again as in Equation 7. Following this, we eliminate loosely bound clusters by analyzing cluster densities. All clusters with cluster densities greater than the median value are retained for future iterations. At the end of 10 iterations or when left with half the initial number of conformers, we re-rank the final list of cluster centroids using high resolution distance dependent force fields.^51,52 The lowest energy structures are identified as the structures nearest to the native.

3.8 Generation of improved bounds and iterative approach

Using the loop decoys in the top 10 clusters sorted by cluster density, we develop new backbone dihedral angle bounds for each amino acid in the loop. These new bounds replace previously existing bounds only if they are tighter. If this is not the case, we continue with the old bounds for the next iteration. Using the existing probability distribution, we re-generate initial structures for the next iteration of the loop structure prediction algorithm. However, if the initial backbone dihedral angles do not lie within the updated bounds, the value is rejected and the angle is re-generated from the probability distribution. The entire procedure consisting of rotamer optimization, all-atom energy minimization and clustering is repeated for five iterations.

At the end of the five iterations, the structures of the top 10 clusters sorted by cluster density are used to generate the final set of bounds that would be useful in the tertiary structure prediction of proteins.^42,53

4 Computational Results

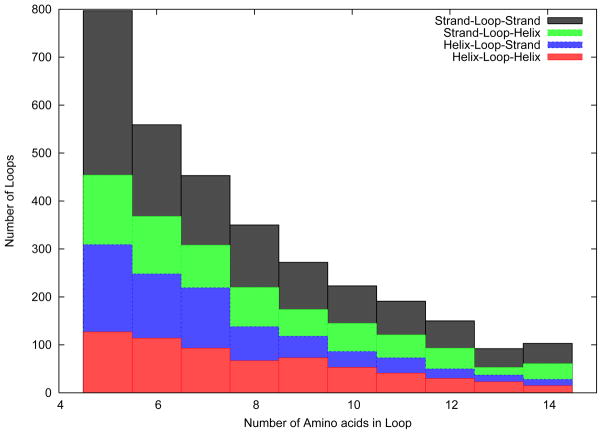
The loop structure prediction algorithm was tested on a large number of loops, ranging from five to fourteen amino acids in length. The distribution of the number of loops for each loop length is given in Figure 2. Three amino acids on either side of the loop were taken as the stem residues. This was done to ensure that the stem residues belonged to a secondary structure element, as the minimum number of amino acids in a helix and a strand are assumed to be four and three, respectively. As has been described previously, information regarding the type of secondary structure of the stem residues was available, while their structure was unknown to the algorithm. Figure 2 also shows the fraction of loops that were found in each kind of neighborhood (i.e., helices on both sides, strands on both sides or any combination thereof). As shown in the figure, loops belonging to all four classes have been included in the test set to avoid bias to any specific type of loop.

Figure 2.

Distribution of number and type of loops in the Loop Test Set

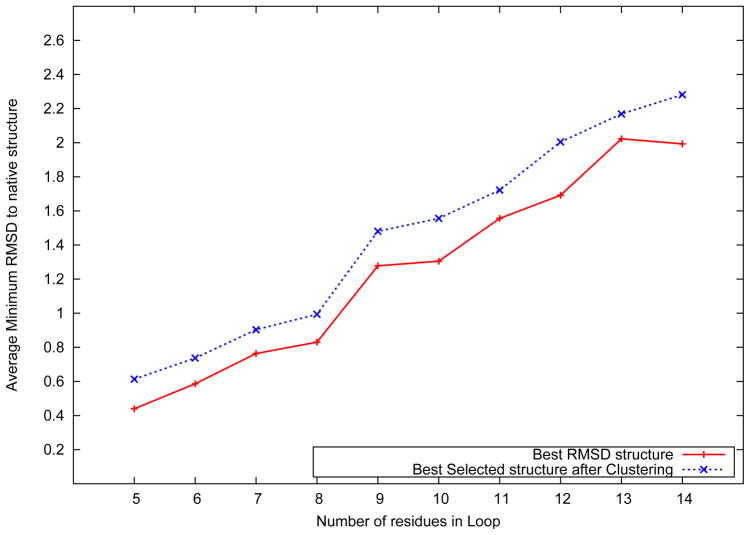
4.1 Fixed Stem Geometry

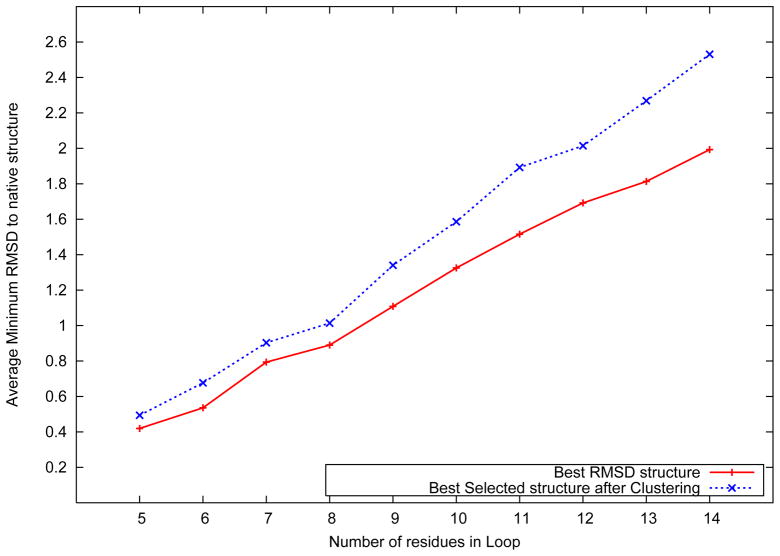
Figure 3 shows the distribution of the best predicted loop structure against the number of amino acids in the loop. As discussed previously, the input to the model included the sequence, secondary structure and structural information of the stem residues flanking the target loop. The best loop structure is defned to be the one with the lowest root mean squared deviation (RMSD) to the native structure. For each loop, the RMSD of the best structure in the predicted ensemble was evaluated, and the RMSD values were averaged across all loops of the same length.

Figure 3.

Average best structure RMSD distribution over loop length

Figure 3 also shows the average RMSD distribution of the best selected structure using the ICON clustering algorithm in the final stage of the algorithm. As shown in the figure, the algorithm achieves an average best structure RMSD of 0.42 Å for five residue loops. For loops with 14 amino acids, an average best structure RMSD of 1.99 Å was observed. In addition, the figure also shows the results of the clustering process in the final stage of the loop structure prediction algorithm. The clustering procedure is utilized in the final stage of the fixed stem loop structure prediction algorithm to identify a subset of five high quality structures from the predicted ensemble of loop structures. By utilizing a high resolution distance dependent force field,⁵¹ the algorithm identifies structures with an average RMSD of 0.49 Å for loops of length five, which rises up to 2.53 Å for loops of length fourteen.

4.2 Flexible Stem Geometry

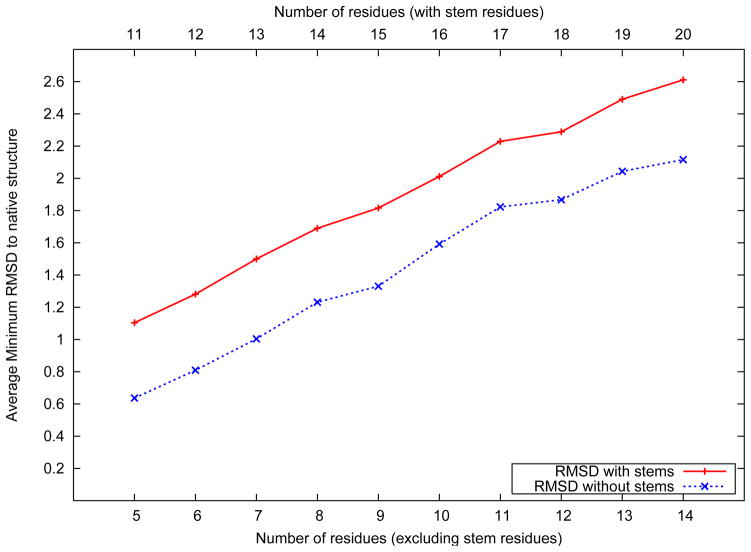
Figure 4 shows the distribution of the best predicted loop structure against the number of amino acids in the loop. The best loop structure is defned to be the one with the lowest root mean squared deviation (RMSD) to the native structure. For each loop, the RMSD of the best structure in the predicted ensemble was evaluated, and the RMSD values were averaged across all loops of the same length.

Figure 4.

Average best structure RMSD distribution over loop length

Figure 4 also shows the average RMSD distribution following the exclusion of the three stem residues attached to each loop. As shown in the figure, the algorithm achieves an average best structure RMSD of 0.63 Å for five residue loops (1.10 Å when including the stem residues). For loops as long as 14 residues, an average best structure RMSD of 2.12 Å without the stem residues, and 2.61 Å when they are included is observed. The average rank of the cluster which includes the best structure in the ensemble is 13.9. It is noteworthy that when the stem residues are included, a 14 residue loop structure prediction problem is equivalent to the ab initio prediction of the structure of a twenty amino acid peptide, with the knowledge of the type of secondary structure for three amino acids at either terminus.

Two additional observations can be made based on the results shown in Figure 4. First, we observe an almost consistent separation between the two lines representing the average best RMSD values with and without the stem residues, respectively. This suggests that the contribution of the stem residues to the RMSD is almost consistent across all loops. The stem residues of the loop are the only regions which are ordered, that is, have a secondary structure pattern associated. The dihedral angle bounds imposed on the stem residues are therefore much more stringent than their counterparts on the loop residues. Hence, the contribution of the stem residues to the RMSD would be expected to be lower and be consistent across different lengths of loops considered. Second, we observe an almost linear growth in the average best RMSD with respect to the loop length. The rate of growth of average best RMSD to the number of residues in the loop can be fit to an approximately straight line. With increasing number of amino acids in the loop, the tertiary structure space is expected to increase very nonlinearly. However, a combination of iteratively improving dihedral angle sampling, rotamer optimization, all atom energy minimization and near-native structure identification ensures that the RMSD of the best structure of the predicted ensemble continues to grow linearly. The RMSD of the best structure for each of the loops in the data set has been presented in the supplementary material.

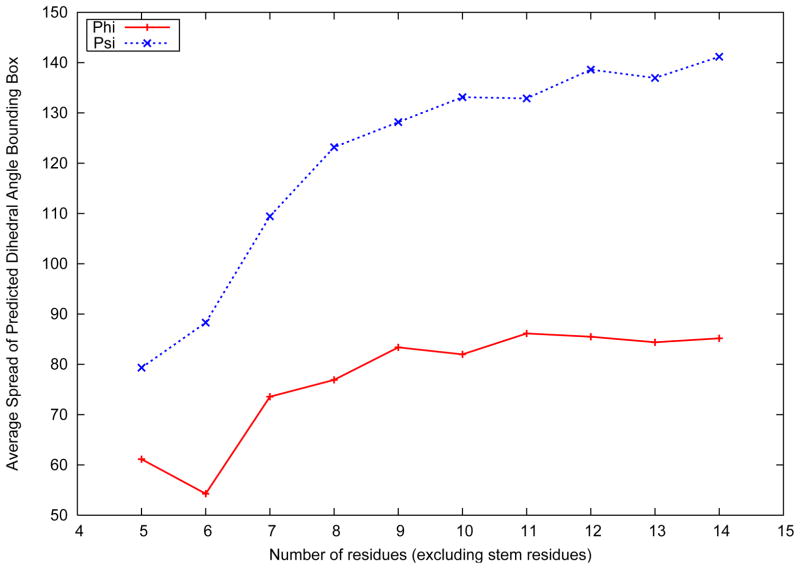
As discussed previously, the loop structure prediction algorithm is used to predict tight dihedral angle bounds on the backbone angles of the loop residues. Hence, while the prediction of low RMSD structures in the ensemble is encouraging, it is important that bounds generated on the backbone dihedral angles are as tight as possible. Figure 5 represents the width of the bounding box represented by the bounds on the backbone dihedral angles of the loop residues. The bounding box is defined as the difference between the upper and lower bounds on the dihedral angles of a loop.

Figure 5.

Average best structure RMSD distribution over loop length

As shown in Figure 5, the bounds predicted on the φ backbone dihedral angle are much tighter than the ones predicted on the ψ backbone angle. It has frequently been observed that the variation in φ is much smaller than the variation in the ψ dihedral angle, given that the φ values for the α-helical and β-strand residues are much closer than their corresponding values of the ψ dihedral angle.⁵⁴ For the φ dihedral angle, the lowest average bounding box width is 52° for loops of length six, and largest of 85° for loops of length eleven. For the ψ dihedral angle, corresponding values of 79° for loops of length five, and 138° for loops of length fourteen are observed. The bounding box width for both dihedral angles are seen to increase monotonically with loop length. With larger number of residues in a loop, the predicted loop structures are seen to span a wider range of RMSD values. The structures in the top clusters, which are used for the prediction of dihedral angle bounds tend to diverge, resulting in wider bounding box constraints on the dihedral angles. It is noteworthy that the bounding box range plateaus very early with the increase in number of amino acids in the loop. Beyond loops of length eleven, the average bounding box width for the backbone dihedral angles are seen to be almost constant. Given that the three dimensional search space expands significantly with increasing number of amino acids, the dihedral angle sampling, all atom optimization and clustering procedures in the loop structure prediction are seen to be successful in providing tight backbone dihedral angle bounds on all the residues of longer loops as well. Further, an average accuracy of 86.14% was seen for the bounding boxes of all amino acids in all loops. The accuracy of the bounding box was defined by:

$$\mathit{Accuracy}=\frac{\text{Number}\text{of}\text{dihedral}\text{angles}\text{within}\text{bounding}\text{region}}{\text{Total}\text{number}\text{of}\text{dihedral}\text{angles}}.$$ (8)

An analysis of the amino acids with erroneous predicted bounds shows that the average error in the prediction of the φ and ψ angles were 25.6° and 11.9°, respectively. The original bounds applied on each amino acid of the loop are derived from the PDB-Select25 data base. Since an iteration is counted only if the bounds on at least one amino acid are reduced by at least one bin, an iterative approach results in a reduction of bounds on the amino acids over each iteration. Hence, the final set of bounds are always tighter than the original bounds derived out of the PDBSelect25 data set. The error in the prediction of ψ angles is seen to be smaller, given that the average bounding box width is much larger. The error in prediction was calculated by evaluating the difference between the true dihedral angle and the closest predicted dihedral angle bound. Therefore, while the predicted bounds for more than 86% of loop amino acids include the true dihedral angle, the average error for the remaining residues are seen to be significantly smaller than the size of the Ramachandran plot itself.

4.3 Selected CASP9 targets

The loop structure prediction algorithms were applied to targets provided during the recently concluded CASP9 experiment. In order to define the loop regions of the protein, secondary structure prediction was first carried out to determine the regions of secondary structure in the protein. A mixed integer optimization based secondary structure prediction algorithm, CONCORD,⁵⁵ was used to determine the locations of α-helices and β-strands for any target protein.

4.3.1 Fixed Stem Geometry

Figure 6 shows the distribution of the best predicted loop structure against the number of amino acids in the loop for selected targets from the CASP9 experiment. For the purposes of the fixed stem geometry problem, we use the native secondary structure of the target protein. The structural data of the stem residues for any target loop was incorporated into the model in the form of distance and dihedral angle constraints. The number of loops for each loop length is shown in Table I.

Figure 6.

Average best structure RMSD distribution over loop length for CASP9 data set

Table I.

The number of loops for given loop lengths in the CASP9 data set

Loop Length	Number of Loops	Loop Length	Number of Loops
5	25	6	21
7	18	8	12
9	15	10	13
11	11	12	13
13	3	14	2

Figure 6 also shows the average RMSD distribution of the best structure and the selected structure using the ICON clustering algorithm in the final stage of the algorithm. As shown in the figure, the algorithm achieves an average best structure RMSD of 0.44 Å for five residue loops. For loops with 14 amino acids, an average best structure RMSD of 2.00 Å was observed. By utilizing the high resolution distance dependent force field,⁵¹ the algorithm identifies structures with an average RMSD of 0.61 Å for loops of length five, which rises up to 2.28 Å for loops of length fourteen.

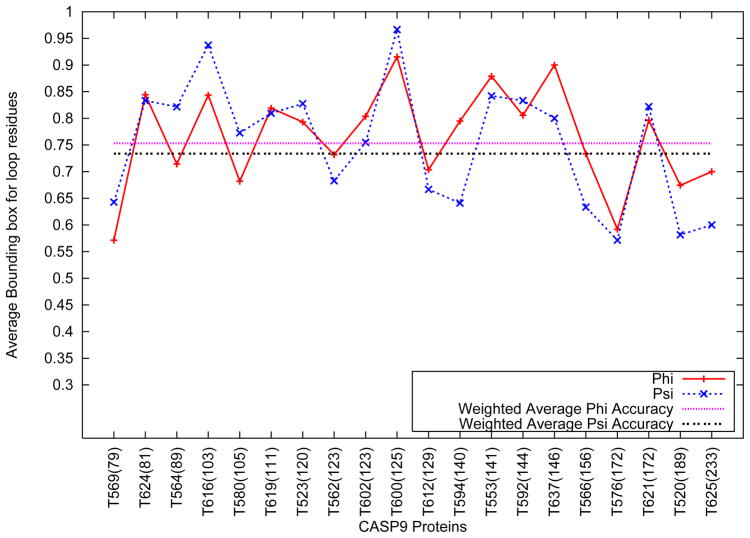
4.3.2 Flexible Stem Geometry

Figure 7 shows the variation in the accuracy of the bounding box for the backbone dihedral angles of the selected CASP9 targets. As shown in Figure 7, the weighted average φ and ψ accuracies were seen to be 75.9% and 73.8% respectively. The accuracy of the bounding boxes are seen to vary between 55% for T576 and 96.4% for T600.

Figure 7.

Average Accuracy of Loop Bounding Box for selected CASP9 targets

No correlation was observed between the length of the target protein and the accuracy of the bounding boxes. Table II shows the best RMSD structure derived out of the loop structure prediction algorithm, as compared to the Zhang-Server predictions for loops belonging to the subset of the proteins shown above with low sequence similarity to the protein data bank. As shown in the table, the average best RMSD of the structures of the loops considered are comparable to the average results observed in the PDBSelect25 data set. This further demonstrates that the loop structure prediction algorithm is not significantly affected by the similarity of a protein to the protein data bank. Similar results for all of the selected CASP targets are presented in Table II of the supplementary material.

Table II.

Comparison of average RMSD of CASP loop structures for low similarity proteins

Loop Length	Number of Loops	Lowest RMSD	RMSD (Zhang-Server)
5	5	1.21	1.24
6	4	1.31	1.39
7	3	1.46	1.45
8	2	1.63	1.67
9	1	1.72	1.73
10	2	2.01	1.99

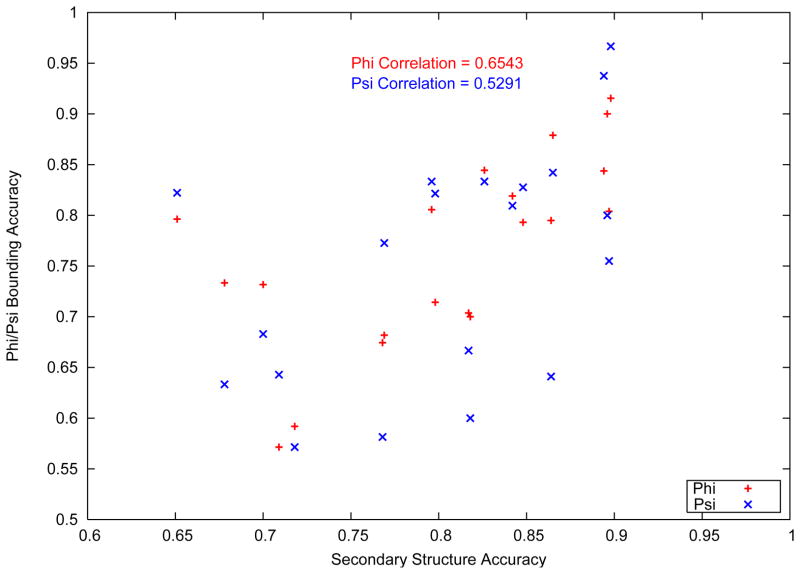
Other external factors were seen to affect the quality of bounding box predictions for the CASP9 targets. Figure 8 shows the variation of the bounding box accuracy with the accuracy in secondary structure prediction. The secondary structure accuracy is typically measured by the Q3 parameter, which evaluates the fraction of amino acids correctly assigned to one of three classes of secondary structure (helix, strand and coil).

Figure 8.

Variation of bounding box accuracy with Secondary structure accuracy

It is noteworthy that a positive correlation value of 0.6543 and 0.5291 (for φ and ψ respectively) was observed between the bounding box accuracy and the accuracy of the secondary structure prediction. The accuracy of the secondary structure prediction is a reflection of the length of loop, the type of loop ( i.e, the secondary structure elements on either side of the loop) and the residue types of the stem residues at the ends of the helix. Each of these parameters can affect the loop structure prediction process significantly. As discussed previously, the three dimensional search space expands exponentially with increasing amino acids in the loop sequence. The determination of the true length of the loop is crucial towards the loop structure prediction process. Similarly, in the description of the model, it was shown that separate probability distributions were created for loops depending on the secondary structure elements they are found between. Given that the distributions vary significantly, the initial structures, and therefore, the final predicted structures would be affected by accurate identification of the type of loop. Finally, the nature of the stem residues is vital since the side chain atoms of the stem residues affect the rotamer optimization of the loop residues. As the rotamer optimization is only carried out on the loop residues, the inclusion or exclusion of an amino acid in the loop can affect the output of the rotamer optimization stage.

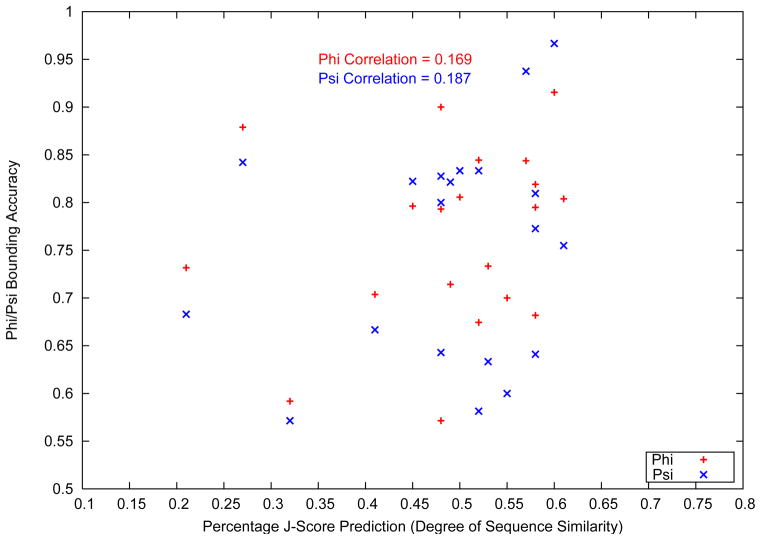
A separate study on the accuracy of the dihedral angle bounding boxes is presented in Figure 9. The figure shows the variation of the bounding box accuracy with the J-Score of target proteins.

Figure 9.

Variation of bounding box accuracy with J-Score

J-Score is a metric of the similarity of a target protein to the Protein Data Bank.⁶ The metric is evaluated by the 3-D Jury server,⁵⁶ using a multiple sequence alignment approach involving BLAST and PSI-BLAST.⁵⁷ As shown in Figure 9, a correlation study between the accuracy of the predicted loop dihedral angle bounding boxes and the J-Score of the target protein shows a very small correlation for both the φ and ψ backbone dihedral angles. A low correlation of the bounding box accuracy with the J-score of a protein indicates a low degree of dependence on the sequence similarity between a target protein and the protein data bank. Even though the initial structures are generated from a database derived probability distribution, the rotamer optimization and all atom physical potential based nonlinear optimization procedure ensure that the similarity of a target loop to the database has a minimal impact on the quality of prediction. Further, a lack of correlation between the J-score and bounding box accuracy is understandable given that the initial structures are not generated by using the loop structures of the top hits from the PSI-BLAST search. Homology modeling methods have been seen to have limited success in loop structure prediction, owing to the varied observed structures of loops with very similar sequences. The algorithm presented in this article is hence able to avoid the pitfalls of database driven loop structure prediction, even with the use of a probability distribution driven initial structure sampling procedure.

5 Conclusions

In this article, new iterative algorithms for loop structure prediction with flexible and fixed stems were introduced. The flexible stem geometry algorithm only requires the knowledge of the sequence and the secondary structure type of the three stem residues at each end of the loop, while the fixed stem geometry algorithm also requires structural information of the stem residues flanking the loop. Loop structure prediction is a critical intermediate step towards the tertiary structure prediction of proteins, as it provides tight dihedral angle bounds on the backbone dihedral angles of the residues in the loop regions of proteins. The flexible stem geometry algorithm employs an initial structure generation procedure based on a derived probability distribution. Initial structure generation in the fixed stem geometry algorithm is carried out using torsion angle dynamics. Three rotamer optimization procedures are incorporated to alleviate steric clashes between rotamers of the amino acids and the generated backbone of the loop. A full atom physics based energy function, ECEPP/3, is used to carry out nonlinear constrained optimization to collect predicted structures of the loop. A traveling salesman based clustering algorithm, ICON, is used to identify a subset of representative structures which are used to develop tight bounds on the backbone dihedral angles of the residues in the loop. The algorithms were applied on two data sets: a large number of loops from the PDBSelect25 data set, and loop regions of blind target proteins provided during the recently concluded CASP9 community-wide experiment. The algorithms were seen to predict high resolution structures for a large number of loops, and were able to derive tight dihedral angle bounds for amino acids in the loops. In the flexible stem geometry problem, a low degree of correlation was seen between the quality of the dihedral angle bounds and the similarity of a target protein to the Protein Data Bank, and hence the improved bounds on the dihedral angles do not depend on the J Score.

Figure 10.

Image for Table of Contents