A Generalized Form of Context-Dependent Psychophysiological Interactions (gPPI): A Comparison to Standard Approaches

Abstract

Functional MRI (fMRI) allows one to study task-related regional responses and task-dependent connectivity analysis using psychophysiological interaction (PPI) methods. The latter affords the additional opportunity to understand how brain regions interact in a task-dependent manner. The current implementation of PPI in Statistical Parametric Mapping (SPM8) is configured primarily to assess connectivity differences between two task conditions, when in practice fMRI tasks frequently employ more than two conditions. Here we evaluate how a generalized form of context-dependent PPI (gPPI; http://www.nitrc.org/projects/gppi), which is configured to automatically accommodate more than two task conditions in the same PPI model by spanning the entire experimental space, compares to the standard implementation in SPM8. These comparisons are made using both simulations and an empirical dataset. In the simulated dataset, we compare the interaction beta estimates to their expected values and model fit using the Akaike Information Criterion (AIC). We found that interaction beta estimates in gPPI were robust to different simulated data models, were not different from the expected beta value, and had better model fits than when using standard PPI (sPPI) methods. In the empirical dataset, we compare the model fit of the gPPI approach to sPPI. We found that the gPPI approach improved model fit compared to sPPI. There were several regions that became non-significant with gPPI. These regions all showed significantly better model fits with gPPI. Also, there were several regions where task-dependent connectivity was only detected using gPPI methods, also with improved model fit. Regions that were detected with all methods had more similar model fits. These results suggest that gPPI may have greater sensitivity and specificity than standard implementation in SPM. This notion is tempered slightly as there is no gold standard; however, data simulations with a known outcome support our conclusions about gPPI. In sum, the generalized form of context-dependent PPI approach has increased flexibility of statistical modeling, and potentially improves model fit, specificity to true negative findings, and sensitivity to true positive findings.

^*1. Introduction

Functional MRI allows one to study task-related regional brain responses and task-dependent connectivity analysis using psychophysiological interaction (PPI) methods. The latter affords the additional opportunity to understand how brain regions interact in a task-dependent manner (Chee et al., 2010; Dodel et al., 2005; Kim and Horwitz, 2008; Minnebusch et al., 2009; Schmitz and Johnson, 2006; Snijders et al., 2010). From 1998 to 2003 there were 81 studies citing Friston and colleagues initial paper describing psychophysiological interactions compared to 299 citations from 2004 to 2009 (Friston et al., 1997). Likewise, the important paper from Gitelman and colleagues, which enabled psychophysiological interactions to be applied to event-related designs by incorporating the hemodynamic response, has spurred a similar increase in citations, between 2004 and 2006 there were 29 citations compared to 57 citations from 2007 to 2009 (Gitelman et al., 2003). However, despite the increasing use of PPI and its potential role for advancing our knowledge regarding the functional integration of brain activity, the standard implementation in SPM8, where the psychophysiological term is formed by the interaction of neural activity and a difference vector of two tasks (e.g. A-B), has two major limitations. Currently, a single PPI can only identify regional effects related to differences between psychological contrasts and not similarities between contrasts. Second, the standard implementation described by Friston (1997) and Gitelman (2003), using a psychological vector of A or a psychological vector of A-B, does not span the space of all conditions and as such is potentially limited to simple experiments with only one or two conditions, respectively, or experiments that can be collapsed into two conditions for analysis. Here we utilize a generalization of the existing PPI methods that address these limitations (Higo et al., 2011; McLaren et al., 2008).

The initial framework for psychophysiological interactions was to identify regions that differ in connectivity by context or condition in block-designed fMRI studies (Friston et al., 1997; from here forward, we will refer to the modulation of connectivity by a psychological or behavioral context as “context-dependent connectivity”), thereby enabling inference regarding condition specific functional integration. However, in block or event-related task designs with two or more experimental conditions, one may be interested not only in condition-specific functional integration, but also where functional integration may be similar across conditions. When Gitelman et al. (2003) extended PPI to event-related designs by incorporating a deconvolution of the BOLD response step into forming the psychophysiological interaction, they started with the notion that psychophysiological interactions occur at the neural level, which results in a change in the BOLD signal, rather than at the level of BOLD signal, which is an indirect and downstream measure of neural activity. Since mathematically, the interaction of BOLD signal is not the same as the interaction of neural signal convolved with the canonical HRF, Gitelman and colleagues implemented a deconvolution step to arrive at an estimate of neural signal on which interaction analyses are performed (2003). In a study of simulated neural activity, the BOLD signal, and PPI, Kim and Horwitz concluded that PPI parameters are robust and generally agree with the underlying neural interactions (Kim and Horwitz, 2008). Their conclusion bolsters the use of PPI as non-invasive tool to investigate the dynamics of functional connectivity.

Both Gitelman et al. (2003) and Kim and Horwitz (2008) demonstrated the importance of properly modeling the underlying neural activity. However, the standard implementation of PPI in SPM8, using a psychological vector of A or a psychological vector of A-B, is still limited to models of only one or two conditions, respectively, or experiments that can be collapsed into two conditions for analysis, as only a single PPI regressor is created per first level analysis, when experiments often contain more than two conditions. For example, in an event-related design with two conditions, there are at least 3 discrete neuronal states defined by the experimenter: (i) activity during the processing of the stimulus for condition 1; (ii) activity during processing of the stimulus for condition 2; and (iii) activity while there is no stimulus being processed (e.g. “baseline” periods or null events). These states may all potentially differ from each other and collapsing two to test against the third is less desirable than modeling each condition separately as this leads to a model that does not span the full space of the conditions. The generalized form of context-dependent PPI (gPPI) spans the full space of the experimental design.

In this paper we describe the theoretical framework for the generalized form of context-dependent PPI (gPPI; Higo et al., 2011; McLaren et al., 2008). Following this description we use simulations to show, based on a gold standard, that gPPI consistently estimates psychophysiological interactions with greater accuracy. Additionally, we also use simulations to show that between-subject PPI effects can be both over and underestimated when gPPI is not utilized. Finally, we demonstrate some strengths of this approach using empirical data from an fMRI study of face recognition (Xu et al., 2009).

2. Materials And Methods

2.1. Statistics of PPI Approaches

The modeling of each condition independently is already standard practice when investigating fMRI activation patterns (Friston et al., 1995a; Friston et al., 1995b). The generalized form of context-dependent PPI (gPPI) applies this principle to PPI analysis and is available in the automated gPPI toolbox (http://www.nitrc.org/projects/gppi). The Statistical Parametric Mapping (SPM8; Wellcome Department of Imaging Neuroscience, University College London, UK) PPI (sPPI) approach and gPPI approach are both based on the same underlying concepts and use the following models (Friston et al., 1997; Gitelman et al., 2003):

$$Y_k=H\left(x_a\right)$$ (1)

$$Y_i{\left[H\left({x_a}^{\ast }{\mathrm{g}}_p\right)\right]}^{\ast }{\beta }_{\mathrm{i}}+\left[Y_{k}H\left({\mathrm{g}}_{\mathrm{p}}\right)\mathrm{G}\right]\ast {\beta }_{\mathrm{G}}+{\mathrm{e}}_{\mathrm{i}}$$ (2)

where H is the HRF in Toeplitz matrix form; Y_k is the BOLD signal observed in the seed region; x_a is the estimated neural activity from the BOLD signal in the seed region (Gitelman et al., 2003); Y_i is the BOLD signal observed at each voxel in the brain; β_i is a matrix of the beta estimates of the psychophysiological interaction terms; β_G is a matrix of the beta estimates of the seed region BOLD signal (Y_k), covariates of no interest (G), and task regressors that are the convolution of psychological vectors H(g_p); and e_i is a vector of the residuals of the model. In the sPPI approach, g_p is a vector formed by multiplying the condition ON times (onset times plus stimulus duration -- when the stimulus or psychological state is presented to the participant or when the participant experiences a defined psychological/experimental state) by a weighting vector (see Figure 5B of Gitelman et al., 2003). As of revision 3270 in SPM5, the weighting vector does not need to have a mean of zero as the psychological vector is no longer mean-centered before convolution (ftp://ftp.fil.ion.ucl.ac.uk/spm/spm5_updates/Updates_README.txt). This change removed the requirement of weighting the conditions based on the number of trials. In the gPPI approach, g_p is a matrix of N columns, where N is the number of conditions in the experiment and formed by separating the condition ON times into separate columns. This is the only difference between the two methods, but is sufficient to account for the different neuronal states in both the psychological regressors as well as the interaction regressors. Equation 2 is the general linear model for the PPI first-level statistics.

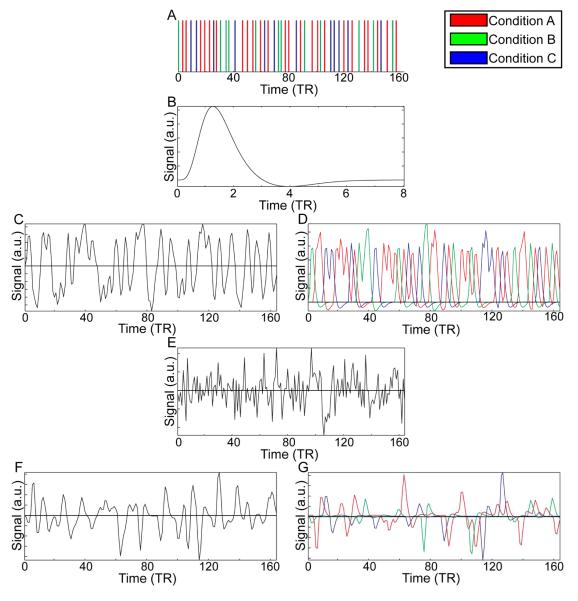
In figure 1 we graphically compare the standard PPI (sPPI) with the generalized form of context-dependent PPI (gPPI). In both sPPI and gPPI, the analyses start with identifying the condition ON times (figure 1A). In sPPI, the condition ON times for conditions A, B, and C are multiplied by a weighting vector (e.g. in this data [-1 1 1]) and are then convolved with the canonical hemodynamic response function (HRF; Figure 1B) to form the task regressor (Figure 1C). However, in gPPI, the condition ON times for conditions A, B, and C are separately convolved with the HRF (Figure 1B) for each condition to form a set of task regressors (Figure 1D). This step forms the task/psychological regressor(s) for the model (H(g_p) in equation 2). The latter is similar to the approach taken by Dodel and colleagues to address context-dependent connectivity (Dodel et al., 2005) by separately computing the correlations between regions for each condition. However, their method analyzes the correlations rather than the interaction of the neural signal and experimental conditions. Next, both sPPI and gPPI approaches extract the BOLD signal from an ROI and remove the effect of noise covariates, if any (matrix G, e.g. motion regressors). This adjusted signal is deconvolved (Figure 1E, matrix Y_k) to obtain an estimate the neural activity (Gitelman et al., 2003). In the sPPI approach, the estimated neural activity is multiplied by the product of condition ON times for conditions A, B, and C and the weighting vector (e.g. in this data [-1 1 1]) and then convolved with the HRF (Figure 1F). However, in the gPPI approach, the estimated neural activity is multiplied by the condition ON times for conditions A, B, and C separately and then convolved with the HRF (Figure 1G). The sPPI approach results in three vectors (Figure 1C,E,F), while the gPPI approach results in 2N+1 vectors (Figure 1D,E,G).

Figure 1. Exemplars of inputs and outputs of the sPPI and the gPPI approaches.

A: A vector of condition on times (A, B, C). B: SPM8 canonical hemodynamic response function (HRF). C: Psychological vector for GLM for the sPPI approach using [1 −1 −1] for A, B, and C, respectively, formed by multiplying the vector of condition ON times (A) by the weights and convolving the result with the canonical HRF. D: Psychological vectors for the GLM for the gPPI approach formed by separately convolving a vector of each conditions’ on times with the canonical HRF. E: Extracted BOLD signal from a region of interest for use in the GLM for both models as well as in the deconvolution process to estimate the neural response. F: Psychophysiological interaction vector for GLM for the sPPI approach using [1 −1 −1] for A, B, and C, respectively, formed by multiplying the condition on times (A) by the weights, then multiplying by the neural signal and convolving the with the canonical HRF. G: Psychophysiological interaction vectors for the GLM for the gPPI approach formed by separately multiplying a vector of each condition’s ON times with the neural signal and then convolving the canonical HRF.

The generalized form of context-dependent PPI is expandable to an infinite number of conditions, given enough trials and time points. This allows the analysis to span the entire space of experimental conditions, rather than partial models that only partially span the experimental space. However, as the number of conditions is increased, the number of regressors in the model is also increased, while the accuracy of the estimates is simultaneously decreased. Furthermore, methods that span the entire experimental space allow for psychophysiophysiological interactions to investigate how two regions interact to affect a third area where the effect may differ based on condition, although the interpretation becomes much more difficult with added terms.

While multi-condition PPI modeling is possible in FSL, the effect of spanning the entire experimental space compared to simple subtraction of two conditions as done in SPM8 has not been investigated. Additionally, the automated gPPI toolbox implements the technique of spanning the entire experimental space in the SPM8 framework, which may have the advantage over FSL by forming the psychophysiological interactions at the neural level given the deconvolution step described above (Gitelman et al., 2003).

2.2 Simulated Data

Simulated data were used to demonstrate the potential improvement in using gPPI over several other possible PPI models. The use of simulated data allows the generation of target voxels with a known psychophysiological interaction with the seed region without error. Thus, the models can be interpreted in the accuracy of the interaction estimate by comparing the estimate to the gold standard of the actual interaction value. If random noise is added to both the seed region and target voxels, then between-subject analyses can be use to evaluate the PPI effect across seed regions akin to a group analysis. If all models produce accurate estimates and have the same between-subject effects, then there is no advantage of using gPPI from a theoretical perspective.

Simulated data were generated with the following approach based on the gPPI framework: (1) create a seed region timecourse with known task effects by summing the products of the predicted HRF/task regressors and their weighting factors 1, 2, and 3 for conditions A, B, and C (when applicable), respectively (findings with other values were the same, but are not shown) and adding normally distributed random noise; (2) create psychophysiological interactions with the seed region for each condition by forming the PPI terms and multiplying them by a weighting factor; (3) create task effects by multiplying the predicted HRF/task regressors by weighting factors; (4) create a seed region term by multiplying the seed region timecourse from step 1 by a weighting factor; and (5) sum the psychophysiological interaction terms, along with the HRF/task responses for each condition, the connectivity with the seed region, and a constant. The weighting factors can be found in tables 1 and 2 and Supplement 1. These values are the gold standard solution of the PPI models.

Table 1.

Accuracy of Psychophysiological Interaction Estimates: 2 Conditions, No Fixation

Beta Weights for Simulated Data						Models
PPI A	PPI B	A	B	see d	consta nt	sPPI	sPPI+task s	sPPIplus	gPPI2
0.5	−0.5	0.5	−0.5	0.25	100	0.50 (0.50)	0.50 (0.50)	0.50 (0.50)	1.00 (1.00)
a	a-1	0.5	−0.5	0.25	100	0.00 (0.50)	0.03 (0.50)	0.50 (0.50)	1.00 (1.00)
0.5	−0.5	a	a-1	0.25	100	0.57 (0.50)	0.50 (0.50)	0.50 (0.50)	1.00 (1.00)
a	a-1	a	a-1	0.25	100	0.07 (0.50)	0.03 (0.50)	0.50 (0.50)	1.00 (1.00)
a	−a	0.5	−0.5	0.25	100	−0.14 (− 0.14)	−0.14 (− 0.14)	−0.14 (− 0.14)	−0.28 (− 0.28)
0.5	−0.5	a	a	0.25	100	0.50 (0.50)	0.50 (0.50)	0.50 (0.50)	1.00 (1.00)
a	− a	a	a	0.25	100	−0.14 (− 0.14)	−0.14 (− 0.14)	−0.14 (− 0.14)	−0.28 (− 0.28)

Beta weights were multipled by a design matrix with the following regressors: PPI for condition A, PPI for condition B, HRF task regressor for condition A, HRF task regressor for condition B, seed voxel timecourse, and a constant. All datasets used 100 different values for a. Values represent the mean estimated interaction weight of A-B (the mean expected value of the interaction of A-B). Bold values indicate models where the model did not capture the true interaction. a is random number generated from the randn function in MATLAB®, which generates random numbers with a mean of 0 and a variance of 1.

Table 2.

Accuracy of Psychophysiological Interaction Estimates: 3 Conditions, Fixation

Beta Weights for Simulated Data								Models
PPI A	PPI B	PPI C	A	B	C	see d	con stan t	sPPI	sPPI+t asks	sPPIpl us	gPPI2	gPPI3
a	a-1	0.00	a	a-1	0.00	0.25	100	0.441 (0.500)	0.487 (0.500)	0.500 (0.500)	1.000 (1.000)	1.000 (1.000)
a	a-1	0.5	a	a-1	0.5	0.25	100	0.259 (0.500)	0.297 (0.500)	0.313 (0.500)	0.625 (1.000)	1.000 (1.000)
a	a-1	a-0.5	a	a-1	a-0.5	0.25	100	0.663 (0.500)	0.719 (0.500)	0.729 (0.500)	1.457 (1.000)	1.000 (1.000)
0.5	−0.5	0	a	a-1	0	0.25	100	0.448 (0.500)	0.500 (0.500)	0.500 (0.500)	1.000 (1.000)	1.000 (1.000)
0.5	−0.5	0.5	a	a-1	0.5	0.25	100	0.267 (0.500)	0.310 (0.500)	0.313 (0.500)	0.625 (1.000)	1.000 (1.000)
0.5	−0.5	0	a	a-1	a-0.5	0.25	100	0.455 (0.500)	0.500 (0.500)	0.500 (0.500)	1.000 (1.000)	1.000 (1.000)
a	a-1	0	0.5	−0.5	0	0.25	100	0.493 (0.500)	0.487 (0.500)	0.500 (0.500)	1.000 (1.000)	1.000 (1.000)
a	a-1	0.5	0.5	−0.5	0.5	0.25	100	0.311 (0.500)	0.297 (0.500)	0.313 (0.500)	0.625 (1.000)	1.000 (1.000)
a	a-1	a-0.5	0.5	−0.5	0	0.25	100	0.708 (0.500)	0.719 (0.500)	0.729 (0.500)	1.457 (1.000)	1.000 (1.000)
a	a	0	a	a	0	0.25	100	−0.110 (-0.110)	−0.110 (-0.110)	−0.110 (-0.110)	−0.220 (−0.220)	−0.220 (−0.220)
a	a	0.5	a	a	0.5	0.25	100	−0.292 (−0.110)	−0.300 (−0.110)	−0.297 (−0.110)	−0.595 (−0.220)	−0.220 (−0.220)
0.5	−0.5	0	a	a	0	0.25	100	0.500 (0.500)	0.500 (0.500)	0.500 (0.500)	1.000 (1.000)	1.000 (1.000)
0.5	−0.5	0.5	a	a	0.5	0.25	100	0.318 (0.500)	0.310 (0.500)	0.313 (0.500)	0.625 (1.000)	1.000 (1.000)
a	a	0	0.5	−0.5	0	0.25	100	−0.110 (−0.110)	−0.110 (−0.110)	−0.110 (−0.110)	−0.22 (− 0.220)	−0.22 (− 0.220)
a	a	0.5	0.5	−0.5	0.5	0.25	100	−0.292 (−0.110)	−0.300 (−0.110)	−0.297 (−0.110)	−0.595 (−0.220)	−0.22 (− 0.220)
a	a	b	0.5	−0.5	0	0.25	100	−0.083 (−0.110)	−0.080 (−0.110)	−0.081 (−0.110)	−0.162 (−0.220)	−0.22 (− 0.220)
a	a	b	0.5	−0.5	0.5	0.25	100	−0.088 (−0.110)	−0.080 (−0.110)	−0.081 (−0.110)	−0.162 (−0.220)	−0.22 (− 0.220)

Beta weights were multipled by a design matrix with the following regressors: PPI for condition A, PPI for condition B, PPI for condition C, HRF task regressor for condition A, HRF task regressor for condition B, HRF task regressor for condition C, seed voxel timecourse, and a constant. All datasets used 100 different values for a. Values represent the mean estimated interaction weight of A-B (the mean expected value of the interaction of A-B). Bold values indicate models where the model did not capture the true interaction. a and b are random numbers generated from the randn function in MATLAB®, which generates random numbers with a mean of 0 and a variance of 1.

The following models were used to evaluate the generated psychophysiological interactions:

• (1)sPPI: PPI for condition A – condition B, task regressor for condition A – condition B, seed region timecourse, and a constant;
• (2a)sPPI+tasks: PPI for condition A – condition B, task regressor for condition A – condition B, task regressor for condition A, seed region timecourse, and a constant;
• (2b)sPPI+tasks: PPI for condition A – condition B, task regressor for condition A – condition B, task regressor for condition B, seed region timecourse, and a constant;
• (3)sPPIplus: PPI for condition A – condition B, PPI for condition A + condition B, task regressor for condition A – condition B, task regressor for condition A + condition B, seed region timecourse, and a constant; and
• (4)gPPI2: PPI for condition A, PPI for condition B, task regressor for condition A, task regressor for condition B, seed region timecourse, and a constant.

Only the sPPIplus and gPPI2 models span the entire experimental space and should produce equivalent results. Model 2a and 2b produce identical results and are reported as a single model in the results section.

For models with 3 conditions, a task regressor for condition C was added to models 2a, 2b, 3, and 4. Additionally, the following model was only evaluated with models with 3 conditions:

• (5)gPPI3: PPI for condition A, PPI for condition B, PPI for condition C, task regressor for condition A, task regressor for condition B, task regressor for condition C, seed region timecourse, and a constant.

In the 3 condition models, only gPPI3 spans the entire experimental space.

All of these models are full rank. Adding the missing task regressors to sPPI+tasks or sPPIplus models would make them rank deficient; however, since the contrasts being evaluated do not involve the task regressor terms, the contrast estimates and results do not change.

2.2.1 Simulated Data: Accuracy of Interaction Estimates

A number of different psychophysiological interactions and relationships of connectivity between different conditions were tested. Using a number of different psychophysiological interactions allows more general statements to be made about how each model could perform in PPI studies. The values used were aimed at investigating two scenerios: (1) the psychophysiological interaction (and task regressor) estimates of condition A and condition B are symmetric around 0 (e.g. if PPI for condition A is 1, then PPI for condition B must be −1) and (2) the interaction (and task regressor) estimates of condition A and condition B are not symmetric around 0 (e.g. if PPI for condition A is 1, then PPI for condition B can be any value except −1). As there is no empirical way to select the weighting factors, we used random numbers to test a range of interaction values. Simulated data was generated using the weighing factors in Tables 1 and 2. Importantly, the simulated data was generated without noise allowing the interpretation of accuracy to be made against the known interaction effect, or gold standard. 100 simulated datasets were generated for each model (Table 1 and 2).

2.2.2 Simulated Data: Model Fit

The next set of simulations evaluates how well each model fits the data in the presence of random noise. Additionally, we can test across seed regions, which would be akin to different subjects as the regions are independent, whether there is a significant PPI effect using a random effects between-subjects analysis. With a single group, this was tested with a one-sample t-test. Of particular interest are simulations where there is no PPI effect, or difference between the PPI for condition A and PPI of condition B, as a significant result would indicate a false positive finding.

For each model, 100 seed region timecourses were generated. For each seed region, 100 target voxels were created with normally distributed random noise added to them. The weighting factors for these models can be found in Supplement 1.

For each seed region, the PPI difference for condition A and condition B were averaged across the 100 target voxels. These means were entered into one-sample t-tests.

2.3. Empirical Data

2.3.1. Participants

Written informed consent was obtained from 74 participants healthy late middle-aged individuals (mean age 58.6 years, 20 males) after the procedures were fully explained. We conducted a recognition memory study and previously published the task effects (Xu et al., 2009) using a protocol approved by the University of Wisconsin Human Subjects Institutional Review Board that is in accordance with the Helsinki Declaration of 1975. Briefly, participants had to identify previously viewed (PV) and novel (N) neutral faces that were presented in a pseudorandom order in an event-related design. The PV faces were encoded during either a self-referential task (PV(self)) or a semantic task (PV(sem)). Thus, the study design yielded either 2 or 3 conditions depending on whether or not PV faces were collapsed across encoding condition. A full description of participants, acquisition, and tasks can be found in the Supplement.

2.3.2. Implementation of PPI Approaches

Both the sPPI and the gPPI approaches were used to evaluate context-dependent connectivity using a 6 mm radius sphere centered around the global maximum from the omnibus F-test of the PV>N contrast images, which was in ventral posterior cingulate cortex (PCC) at MNI coordinate −8, −62, 26 (Xu et al., 2009). These approaches were implemented in SPM8 using the automated gPPI toolbox with SPM.mat files (from SPM5) that produce identical results to those obtained through the SPM PPI GUI. While the present analysis is done in SPM8, the scripts are able to use SPM.mat files from both SPM2 and SPM5.

The sPPI approach had the following regressors: PPI for PV(self) + PPI for PV(sem) – PPI for N, task regressor for PV(self) + task regressor for PV(sem) – task regressor for N, seed region timecourse, and a constant. This only allows testing of PV>N.

The gPPI approach for 2 conditions (gPPI2) had the following regressors: PPI for PV(self) + PPI for PV(sem), PPI for N, task regressor for PV(self) + task regressor for PV(sem), task regressor for N, seed region timecourse, and a constant. This allows testing of PV>N, PV, and N.

The gPPI approach for three conditions (gPPI3) had the following regressors: PPI for PV(self), PPI for PV(sem), PPI for N, task regressor for PV(self), task regressor for PV(sem), task regressor for N, seed region timecourse, and a constant. This allows the testing of any combination of PV(self), PV(sem) and N conditions.

2.4. Model Comparisons with Akaike Information Criterion

The Akaike information criterion (AIC) finds the best model from a given set of models that explains the data with a minimum number of parameters by penalizing the addition of terms that don’t substantially lower the error of the model. Thus, AIC was used to operationally define which model (e.g. sPPI or gPPI2) provided a relative best fit of the data – with largest negative magnitude corresponding to best model fit to the data (Lindsey and Jones, 1998; Ludden et al., 1994). For each subject and method, the AIC was computed (Akaike, 1974) for each voxel and then compared using paired t-tests. In the context of SPM8, the following equation was used

$$AIC=2k+n\left[\log \left(\frac{RSS}{n}\right)\right]$$ (3)

where k is the number of regressors in the model, n is the number of time points, and RSS (residual sum of squares) is the degrees of freedom times the ResMS image from the model estimation process. This equation assumes that the residuals are normally distributed and have constant variance; it has previously been used in fMRI studies (den Dekker et al., 2009; Habeck et al., 2006).

In addition to testing whether the AIC was significantly lower between models, we also report the mean AIC decrease with gPPI2 compared to sPPI. A decrease of 10 can be interpreted as no evidence for choosing sPPI and has a probability of .67% that information is not lost in the sPPI model. A decrease between 4-7 can be interpreted as a little evidence for considering sPPI with a probability of between 13.53-3.02% that information is not lost in the sPPI model, respectively. A decrease of 1 or 2 provides substantial evidence for considering sPPI with a probability between 60.65-36.79% that no information is lost with the sPPI model (Burnham and Anderson, 2002).

Finally, we report the number of voxels that have at least a 1, 2, 4, 5, 7, or 10 unit decrease in AIC from sPPI to gPPI2 in at least 10, 20, 30, 40, 50, 60, or 70 subjects as a further gauge of the amount of improvement in gPPI2 (Table S6).

3. Results

3.1. Simulated Data: Accuracy of Interaction Estimates

Table 1 provides the psychophysiological interaction estimates from 4 different PPI models. In summary, whenever the psychophysiological interaction (and task regressor) estimates of condition A and condition B are symmetric around 0 (e.g. if PPI for condition A is 1, then PPI for condition B must be −1), then the estimates of the interaction are the same between sPPI and gPPI (after accounting for the fact that sPPI produces values half of gPPI due to the regressor amplitudes). Any variation from this leads to a deviation from the expected value and can result in interaction values that can either be higher (potentially false positives) or lower (potentially false negatives) than the expected value. This requirement can be relaxed to only include the interaction term if the task regressors span the space of all tasks (all models except sPPI),. The sPPIplus and gPPI2 estimates are always as expected. These results suggest that any experiment with at least 2 conditions that are modeled needs to use the gPPI framework or another model that spans the experimental space (e.g. sPPIplus) even if there are no fixation periods.

Table 2 provides the psychophysiological interaction estimates from 5 different PPI models. A similar pattern is found as with the 2 condition data. In summary, whenever the psychophysiological interaction (and task regressor) estimates of condition A and condition B are symmetric around 0 (e.g. if PPI for condition A is 1, then PPI for condition B must be −1) and condition C interaction and task regressor are 0, then the estimates of the interaction are the same for all models (after accounting for the fact that sPPI produces values half of gPPI due to the regressor amplitudes). Any variation from this leads to a deviation from the expected value and can result in interaction values that can either be higher (potentially false positives) or lower (potentially false negatives) than the expected value. If task regressors span the space of all tasks (all models except sPPI), then the requirements only apply to the PPI terms. If the PPI for condition C is not 0, then only gPPI3 can accurately estimate the PPI effect. Setting the PPI for condition C to a normally distributed random number allows the investigation of the correlation between the PPI A-PPI B and the value of PPI C. This correlation was 1, indicating that error in the model is related to the strength of the non-modeled PPI terms.

3.2. Simulated Data: Robustness of gPPI estimates and Model Fits

Estimated psychophysiological interaction magnitudes for each model, along with the standard error across seed regions, are presented in Table 3 for simulated data with 2 conditions. Based on the simulated data, the expected value of the interaction of condition A and B is from the sPPIplus model, with the exception of gPPI2, which is twice this value due to the amplitude of the regressors in the model for data with 2 conditions. Only models that span the entire space have values that match the expected values. When the PPI interaction effect is this great, all models were able to detect it; while smaller PPI differences were not detected (data not shown). However, in the absence of a PPI effect, the sPPI model detected an effect (e.g. false positive). The results of the model fits for this simulated data can be found in Table S1. gPPI2 usually had the greatest reduction in AIC and the reduction was at least 9, indicating very little evidence for choosing the sPPI model. Thus, sPPI potentially poorly estimates the interaction effect and poorly fits the data compared gPPI2. sPPIplus and gPPI are statistically identical because they both span the same experimental space and as such, any model that spans the entire experimental space will be identical to gPPI.

Table 3.

Robustness of PPI Estimates and Significance: 2 Conditions

	Models
Model Parameters	sPPI	sPPI+task s	sPPIplus	gPPI2	Single Condition
PPI Effect
1 Condition plus fixation	0.99 (0.01)	0.99 (0.01)	0.99 (0.01)	0.99 (0.01)	0.99 (0.01)
2 Conditions (A-B)	0.49 (0.01)	0.49 (0.01)	0.49 (0.01)	0.98 (0.02)	0.40 (0.01)
2 Conditions (effectively the same as 2 Conditions (A-B))	0.49 (0.01)	0.49 (0.01)	0.49 (0.01)	0.98 (0.02)	0.40 (0.01)
2 Conditions	0.88 (0.02)	0.88 (0.02)	0.49 (0.01)	0.98 (0.02)	1.00 (0.01)
2 Conditions plus fixation	0.71 (0.03)	0.58 (0.03)	0.51 (0.01)	1.02 (0.01)	1.91 (0.01)
No PPI Effect
2 Conditions plus fixation	0.15 (0.01)	0.01 (0.01)	0.01 (0.01)	0.02 (0.1)	0.06 (0.01)

Values are the mean and standard errors across seed voxels. For PPI Effect models, bold values indicate tests that were significant for A>B at p<0.05. For No PPI Effect models, bold values indicate tests that were significant for A-B~=0 at p<0.05.

Estimated psychophysiological interaction magnitudes for each model, along with the standard error across seed regions, are presented in Table 4 for simulated data with 3 conditions. Based on the simulated data, the expected value of the interaction of condition A and B is half the estimate from the gPPI3 model, except for gPPI2 where it is the same. Only models that span the entire space have values that match the expected values. With a smaller PPI effect, only gPPI3 consistently detects the effect based on one-sample t-tests. That is to say if the PPI effect is large enough, all models will detect it (data not shown); while more subtle PPI differences will only be detected with gPPI as shown here. Anytime the PPI for condition C is non-zero, the PPI effect was not detected (e.g. false negative) at this magnitude of difference between PPI for condition A and condition B. Additionally, in the absence of PPI for condition A and condition B being different, all models except gPPI3 detected an effect in at least one of the data simulations, which indicate that these models can potentially produce false positives. When the PPI for condition C was set to 0, only sPPI falsely detected a PPI effect, due to the design not spanning the entire task regressor space of 3 conditions. The results of the model fits for this simulated data can be found in Table S2. Models that span more of the experimental space had better model fits (larger decreases in AIC). Whenever the PPI for condition C was non-zero, then gPPI3 had the largest reduction in AIC and best model fit. The decreases for gPPI3 were always greater than 10 indicating very little evidence for choosing the sPPI model. Additionally, the decreases were more than 10 over that for models that spanned less than the entire experimental space depending on the value of the non-modeled PPI term indicating very little evidence for those models. Thus, models that do not span the entire experimental space potentially poorly estimate the interaction effect and poorly fit the data compared potentially leading to both false negatives and false positives.

Table 4.

Robustness of PPI Estimates and Significance: 3 Conditions, Fixation

	Models
Model Parameters	sPPI	sPPI+tasks	sPPIplus	gPPI2	gPPI3
PPI Effect
PPIA=1; PPIB=0.75; PPIC=0	0.15 (0.02)	0.12 (0.02)	0.12 (0.01)	0.24 (0.01)	0.25 (0.01)
PPIA=1; PPIB=0.75; PPIC=0.5	−0.02 (0.02)	−0.06 (0.02)	−0.06 (0.01)	−0.12 (0.02)	0.25 (0.01)
PPIA=0.125; PPIB=-0.125; PPIC=0	0.15 (0.01)	0.12 (0.01)	0.12 (0.01)	0.24 (0.01)	0.25 (0.01)
PPIA=0.125; PPIB=0.125; PPIC=0.5	−0.03 (0.01)	−0.06 (0.01)	−0.06 (0.01)	−0.13 (0.02)	0.25 (0.01)
No PPI Effect
PPIA=0;PPIB=0; PPIC=0	0.02 (0.01)	−0.01 (0.01)	−0.01 (0.01)	−0.01 (0.01)	0.00 (0.01)
PPIA=0;PPIB=0; PPIC=0.5	−0.16 (0.01)	−0.19 (0.01)	−0.19 (0.01)	−0.38 (0.02)	0.00 (0.01)
PPIA=0;PPIB=0; PPIC=−0.5	0.20 (0.01)	0.18 (0.01)	0.18 (0.01)	0.35 (0.01)	0.00 (0.01)

Values are the mean and standard errors across seed voxels. For PPI Effect models, bold values indicate tests that were significant for A>B at p<0.05. For No PPI Effect models, bold values indicate tests that were significant for A-B~=0 at p<0.05.

3.2. Empirical Data: Psychophysiological Interactions

The sPPI approach revealed 14 clusters at a p<0.01 in at least 50 edge-connected voxels showing greater connectivity to PV faces compared to N faces (Table S3, Figure S1, first row). The liberal threshold of p<0.01 uncorrected at the voxel level was chosen to illustrate the differences between approaches. No clusters were found for the opposite contrast. In gPPI2, there were ten significant clusters for the PV>N contrast (Table S4, Figure S1, middle row). The opposite contrast did not reveal any clusters. In gPPI3, there were 11 significant clusters for the PV>N contrast (Table S5, Figure S1, bottom row). Five clusters in sPPI did not have matching clusters in either gPPI approach. Several other clusters had minimal overlap with clusters in gPPI2 and gPPI3. One cluster in gPPI2 was not found in either sPPI or gPPI3. Two clusters were only found in gPPI3. The similarities between gPPI2 and gPPI3 suggests that the semantic and self-referential encoding conditions result in similar connectivity during recognition to these areas.

The observation that different approaches have different clusters does not imply that the interaction estimates between the three models are significantly different nor do we claim the values are different between models at the cluster level (Nieuwenhuis et al., 2011); however, since the goal is to identify which method is optimal at detecting psychophysiological interactions, their difference need not be significant.

3.2. Empirical Data: Model Fit Using the Akaike Information Criterion (AIC)

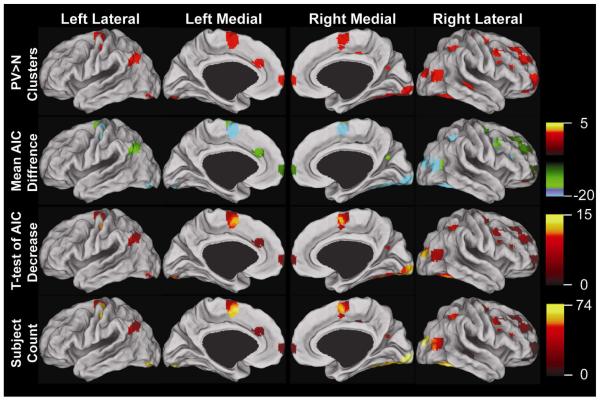
Comparison of AIC values between models revealed 1701 voxels where the AIC was significantly lower at a family-wise error corrected p-value of 0.05 in at least 20 contiguous voxels, within a mask of 3945 voxels form by the logical OR of the sPPI and gPPI2 results (Figure 2, top row), when using gPPI2 compared to using sPPI (Figure 2, third row). Areas that had significantly better model fits were primarily located in the supplementary motor area and posterior cortical areas, including the visual cortex. Using a more liberal threshold of p<0.01 in at least 50 contiguous voxels revealed a significant difference in 2501 voxels. No significant increases in AIC were found when comparing the gPPI2 to sPPI at either threshold. The extensive nature of improved model fits suggests that gPPI2 better represents the data.

Figure 2. Comparison on sPPI and gPPI approaches using the Akaike information criterion (AIC) on the PALS cortical surface (Van Essen, 2005).

Top row: mask of regions where either sPPI or gPPI revealed significant interaction effect for PV>N at p<.01 in at least 50 contiguous voxels. Second row: the mean AIC change from sPPI to gPPI. Third row:: significant clusters of decreased AIC values within the mask at threshold of a family-wise error corrected p-value of 0.05 in at least 20 contiguous voxels.. Bottom row: the number of subjects with a decrease of at least 7 in the AIC from sPPI to gPPI2.

Next we investigated the mean change in AIC for each cluster in each model (sPPI, gPPI2, and gPPI3) and report them in Tables S3-5. The mean AIC change in the voxels from the logical OR of the sPPI and gPPI2 are shown in Figure 2 (second row). In general, the larger the decrease in AIC in sPPI regions, the more likely the region wouldn’t be found with gPPI (potential false positives in sPPI). In the gPPI models, the larger the decrease from sPPI, the more likely the region was not found in sPPI (potential false negatives in sPPI).

An alternative way to look at AIC is to investigate the number of subjects that had a specified decrease at each voxel. The results are shown in Figure 2 (bottom row) for a decrease of 7 and Table S6 for decreases of 1, 2, 4, 5, 7, and 10. At a decrease of 7, a decrease that provides little evidence in support of choosing sPPI, there were 1737 out of 3945 voxels that had at least 30 of the 74 subjects with a decrease of at least this amount. At a decrease of 4, there were 2102 out of 3945 voxels that had at least 30 of the 74 subjects with a decrease of at least this amount. While not every subject has a significantly better model fit, a substantial number of participants have better model fits at the same location providing further evidence that gPPI is potentially better than sPPI.

Next we evaluated the relationship of PPI estimates and model fit. We extracted the mean contrast value (estimate of the interaction magnitude), mean AIC from 6mm spheres around two peaks from sPPI approach, and computed the t-statistics for the spheres (Table 5). The first peak selected was common to all three methods and was located in the right superior frontal gyrus at (18,56,6). The PV>N contrast values, after adjusting for the amplitude of the regressors, were not significantly different between the three models. Additionally, there was not a significant decrease in AIC values either. This suggests that the gPPI approaches and the sPPI approach are equivalent at this location. Next, we selected a peak that was found only in the sPPI results located in the right fusiform gyrus at (40,−56,−20) as an example of a potential false positive finding with sPPI. The contrast values were significantly lower for the gPPI2 and gPPI3 models using pair-wise t-tests. The AIC values were significantly lower indicating a better model fit with gPPI and the regional t-statistics did not indicate the contrast values were different than 0. Based on the model fit, this region is potentially a false positive in sPPI. However, since there is no gold standard with real data, we cannot know if this is absolutely a false positive or if the model could be further improved to detect a real effect.

Table 5.

Analysis of Model Fit and PPI Effects

		Models
Peak Voxel	Measure	sPPI	gPPI2	gPPI3
18,56,6	Contrast t-statistic	0.27 3.44	0.30 3.81	0.25 2.82
	AIC Change		−1.06	2.31*
40,−56,−20	Contrast t-statistic	0.38 2.94	0.10* 0.26	0.22* 1.62
	AIC Change		−61.9*	−59.4*

AIC, Akaike information criterion; PV, previously viewed items; N, novel items; Contrast estimates from sPPI were multiplied by 2 to scale them to be the same as gPPI.

^*Significantly different from SPM PPI Protocol using a paired t-test at p<0.05 (one-tailed).

3.3. Flexibility of the Generalized Form of Context-Dependent Psychophysiological Interactions

An important element to the use of gPPI is its flexibility. In the case of three conditions, there are at least four psychological states in the task described above (e.g. N, PV(self), PV(sem), when no face is being presented), which results in eight possible contrasts between conditions in the study (NvPV, NvPV(self), NvPV(sem), PV(self)vPV(sem), NvNone/Fixation, PVvNone/Fixation, PV(self)vNone/Fixation, and PV(sem)vNone/Fixation). Using the sPPI approach requires eight separate models that each potentially have suboptimal model fit, thereby increasing the possibility of false positives and negatives, while the gPPI approach requires only a single model that is a better fit to the data. Additionally, an estimate of PPI for each condition enables the comparison between conditions using contrasts within a single model. For example, single subject contrasts maps for a specific comparison may be computed and be used as input into a second-level one-sample t-test (e.g. PV>N, Figure S2). Estimates of PPI for each condition may also be directly tested using second-level paired t-tests or repeated-measure analysis of variances. Importantly, neither of these approaches requires new general linear models at the single subject level.

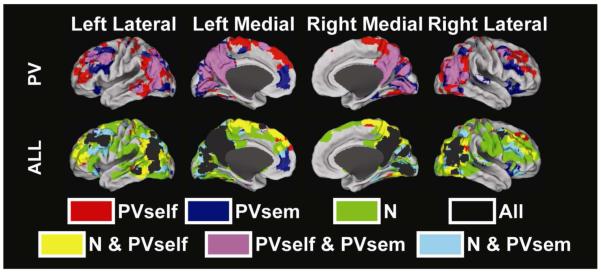
In creating estimates of PPI for each condition relative to baseline, conjunction maps can also be formed for different combinations of tasks to investigate similarities in connectivity. In Figure 3, we illustrate the conjunction, using a logical OR of PVself and PVsem maps each thresholded at FWE-corrected p<0.001 in at least 50 voxels. The maps show a number of regions that overlap including parts of the default-mode network. However, there are also qualitative differences between two conditions. We also illustrate the conjunction between PVself, PVsem, and N conditions using the same threshold (Figure 3 bottom).

Figure 3. Conjunction maps for the PV conditions and for all conditions projected onto the PALS cortical surface (Van Essen, 2005).

First row: logical OR between PVself and PVsem each thresholded at FWE-corrected p<0.01 in at least 50 contiguous voxels. Second row: logical OR between PVself, PVsem, and N each thresholded at FEW-corrected p<0.01 in at least 50 contiguous voxels.

4. Discussion

Psychophysiological interaction analyses not only provide information about functional integration of the brain, but they also elucidate the psychological or behavioral significance of such integration (Friston et al., 1997). Given the importance of such information regarding brain-behavior relationships, it is critical that PPI analysis methods properly model the experimental space and effects (Gitelman et al., 2003; Kim and Horwitz, 2008). We have presented data indicating that utilizing the generalized form of context-dependent PPI (gPPI) potentially reduces both false negatives and false positives, especially in experiments involving more than two conditions, using both simulated and real data.

Flexibility of statistical modeling is important in PPI methods given that many fMRI tasks incorporate more than two conditions to be contrasted. The gPPI approach improves experimenter flexibility in a number of ways. First, researchers can explore connectivity in individual conditions within their experiment. Second, researchers can explore the conjunction of connectivity across conditions. Finally, researchers do not need a separate model for comparisons of different interactions; rather a single model would allow for multiple contrasts that test the several possible interactions. While the example presented here only tested the effect of the gPPI approach on an event-related experiment, there is no reason to expect the conclusions to be different with a block design with more than two psychological states.

An ideal statistical estimate accurately models truly-existing patterns in population data. As one method of estimating the accuracy of the gPPI analysis methods, we compared the model fit (at the single subject level) of gPPI to sPPI methods. When we did a formal statistical comparison of the model-to-data fit of the sPPI versus gPPI (using AIC criterion), we found that the gPPI approach improved model fit compared to sPPI.

The accuracy of statistical methods also relies on the validity of the assumptions made by models used. Standard PPI methods in SPM8 assume that regional connectivity across conditions varies symmetrically around 0 (see section 3.1). This assumption does not affect context-dependent connectivity analyses of a task involving only two conditions, but this assumption would affect interpretation of PPI analysis of an fMRI task with more than two conditions (even if the third condition is a fixation cross “baseline”). Importantly, this assumption made by the standard SPM PPI method is not made in the gPPI approach introduced here. The gPPI approach spans all possible neurophsyiological relationships, thus does not make any assumptions of their inter-relationships between experimental conditions. The sPPIplus model, with PPI terms for for A-B and one for A+B, also spans the entire experimental space in the case of two conditions and baseline. This model produces the same results as gPPI under these circumstances. In sum, as long as the model spans the entire experimental space then the model will achieve the better fit.

We also provide evidence that gPPI may be more sensitive to true positive results than standard methods. Statistical comparison of results of gPPI versus sPPI methods showed several regions of context-dependent connectivity when only using gPPI methods. This result taken with evidence of improved model fit (according to AIC criterion) using gPPI suggests that this method may have greater sensitivity than standard methods. However, this interpretation is tempered by the lack of a true gold standard to which we can compare both methods. Despite the lack of a gold standard, the simulations support the conclusion that gPPI reduces the risk of false negatives.

While we have demonstrated several advantages of using gPPI over sPPI, there are still a number of caveats that need considered when interpreting the results. First, the results are only as good as the model and the design of the fMRI task being used. The failure to accurately model the neural state of the brain can lead to incorrect results (Visscher et al., 2003). With respect to PPI, it is critical to model all of the conditions independently. It is also important to keep in mind that all methodological concerns that influence the interpretation of fMRI studies also influence the interpretation of PPI results (e.g., choice of baseline condition; neurovascular coupling assumptions etc.). Thus, limits on interpretation of an fMRI task also limit more involved analysis of that same task. Second, the canonical hemodynamic response function used in the deconvolution step of PPI is assumed to be constant across voxels and individuals (Gitelman et al., 2003). As of yet, the choice of model for the deconvolution has not been investigated, despite different hemodynamic response functions being used in activation studies (Boynton et al., 1996). Future research should investigate the effect of different hemodynamic response functions, especially as PPI analysis methods are applied to patient populations that could have variable hemodynamic response due to changes in neurovascular coupling. Thirdly, psychophysiological analyses still require a sufficient number of trials and/or blocks. Based on the existing literature, at least 30 trials per condition should be used (Huettel and McCarthy, 2001). For example, the significance of either PV(sem) or PV(self) is potentially less than PV because the estimates are less reliable within each individual leading to greater variation between individuals. Finally, it is important to note that in SPM, the interaction is specific to the duration of events that were modeled at the first level. Despite these caveats, psychophysiological interactions have been demonstrated to have a physiological basis (Kim and Horwitz, 2008).

5. Conclusions

PPI analyses assess how the activity within brain networks is modulated by psychological states. The present study provides the theoretical framework for the generalized form of context-dependent PPI that enables the investigation of the brain’s functional integration and the psychological or behavioral significance of such integration. Importantly, we have presented evidence – comparing gPPI to the standard SPM PPI method using both simulated data and an empirical fMRI dataset – that the generalized form of context-dependent PPI approach spans the entire experimental space and that this approach may improve single-subject model-fit, specificity for true negatives, and sensitivity to true positive findings. Finally, gPPI is readily accessible through the automated gPPI toolbox.