A Convergent Functional Architecture of the Insula Emerges Across Imaging Modalities

Abstract

Empirical evidence increasingly supports the hypothesis that patterns of intrinsic functional connectivity (iFC) are sculpted by a history of evoked coactivation within distinct neuronal networks. This, together with evidence of strong correspondence among the networks defined by iFC and those delineated using a variety of other neuroimaging techniques, suggests a fundamental brain architecture detectable across multiple functional and structural imaging modalities. Here, we leverage this insight to examine the functional organization of the human insula. We parcellated the insula on the basis of three distinct neuroimaging modalities – task-evoked coactivation, intrinsic (i.e., task-independent) functional connectivity, and grey matter structural covariance. Clustering of these three different covariance-based measures revealed a convergent elemental organization of the insula that likely reflects a fundamental brain architecture governing both brain structure and function at multiple spatial scales. While not constrained to be hierarchical, our parcellation revealed a pseudo-hierarchical, multiscale organization that was consistent with previous clustering and meta-analytic studies of the insula. Finally, meta-analytic examination of the cognitive and behavioral domains associated with each of the insular clusters obtained elucidated the broad functional dissociations likely underlying the topography observed. To facilitate future investigations of insula function across healthy and pathological states, the insular parcels obtained here have been made freely available for download via http://fcon_1000.projects.nitrc.org, along with the analytic scripts used to perform the parcellations.

1. Introduction

Mounting evidence suggests that patterns of intrinsic functional connectivity (iFC), subtended by temporally correlated spontaneous fluctuations in the resting state fMRI (R-fMRI) signal, are sculpted by a history of task-evoked coactivation (Deco and Corbetta, 2011; Smith et al., 2009). A credible hypothesis for the neurophysiologic significance of iFC is thus that correlated intrinsic activity serves to maintain the integrity of neuronal networks supporting cognition and action, even in the absence of processing demands. Convergence among large-scale networks defined by iFC (intrinsic connectivity networks; ICNs) and those delineated using a plethora of modalities, including task-based coactivation (Smith et al., 2009; Toro et al., 2008), electrophysiological measures of neuronal activity (He et al., 2008; Keller et al., 2011), and static measures of brain structure (Mars et al., 2011a; Seeley et al., 2009) supports this hypothesis and suggests a fundamental brain architecture governing both structure and function.

Leveraging this insight, studies have demonstrated that data-driven clustering methods based on iFC measures can partition the brain into distinct functional systems, thus revealing its functional “building blocks” (e.g., Bellec et al., 2010; Craddock et al., In Press; Nelson et al., 2010a; Nelson et al., 2010b; Yeo et al., 2011). These studies have revealed much about the functional architecture of the brain at multiple spatial scales, from subregions and boundaries within specific functional areas to the organization of these areas into large-scale networks. This multiscale organization is consistent with the observation that many large-scale brain regions (e.g., prefrontal cortex) exhibit activation and connectivity profiles that evince both local functional heterogeneity as well as agglomerative or locally integrative functions (Duncan and Owen, 2000; Wilson et al., 2010). Data-driven iFC-based parcellation of functionally complex regions may therefore provide insights into this multiscale organization.

The insula constitutes one such region. Although its importance was long belied by its seclusion within the depths of the Sylvian fissure, the insula is now recognized as a nexus of sensory, somatic, interoceptive, cognitive and emotional processing, the integration of which may provide the neural substrate for human phenomenological experience (Craig, 2009a, b, 2011). Anatomically, the insula is positioned at the confluence of several neural pathways: besides being densely interconnected with itself, and with virtually all cortical association regions, it receives sensory, somesthetic and interoceptive inputs both from cortical areas and via the thalamus. It is also interconnected with the medial temporal lobe, amygdala, and basal ganglia (Augustine, 1996; Dum et al., 2009; Mesulam and Mufson, 1982b; Mufson and Mesulam, 1982).

Given this diverse connectivity, it is unsurprising that insular activation has been observed across a wide array of functional contexts, including sensory perception (from gustation and olfaction, to music perception; e.g., Molnar-Szakacs and Overy, 2006; Small, 2010; Small et al., 2003), vestibulo-proprioceptive processing, interoception (including satiety and craving; e.g., Critchley et al., 2004; Naqvi and Bechara, 2009), somesthesis (including nociception; e.g., Brooks et al., 2005; Starr et al., 2009), somatic control (including the regulation of cardioregulatory, vasomotor and visceromotor function; e.g., Cheung and Hachinski, 2000; Lerner et al., 2009; Shelley and Trimble, 2004), motor function (particularly speech; e.g., Ackermann and Riecker, 2010; Nestor et al., 2003), emotion (particularly empathy and disgust; e.g., Adolphs et al., 2003; Jabbi et al., 2007; Singer et al., 2009; Wicker et al., 2003), and cognition (including attention and language processing; e.g., Chee et al., 2004; Eckert et al., 2009; Nelson et al., 2010b; Steinbrink et al., 2009). Its implication across these myriad behavioral contexts has led to the suggestion that activation of the insula, in concert with activation of anterior cingulate cortex, likely subserves emergent integrative functions such as conscious awareness (Craig, 2009b; Medford and Critchley, 2010), salience detection (Seeley et al., 2007), task-set maintenance (Dosenbach et al., 2008; Dosenbach et al., 2007) or focal attention (Nelson et al., 2010a). Insula dysfunction across several clinical and psychiatric disorders involving impairments in somatic and social awareness, attention and emotion, such as autism (Di Martino et al., 2009a; Uddin and Menon, 2009), addiction (Goldstein et al., 2009), anxiety disorders (Paulus and Stein, 2006) and behavioral-variant fronto-temporal dementia (Seeley, 2010) further underscores the importance of this heterogeneous area to our understanding of brain function.

Efforts to delineate the organization of the insula have utilized a wide variety of techniques from electrical stimulation and neuropsychological studies of human patients (Cereda et al., 2002; Penfield and Faulk, 1955), to stereological and anatomical tracing studies of non-human primates (Mesulam and Mufson, 1982a, b; Mufson and Mesulam, 1982). Most recently, the dramatic upsurge in neuroimaging probes of the insula has prompted several studies specifically aimed at parcellating this region based on its structural and functional properties. Functional differentiation revealed by patterns of task-based activation, cytoarchitecture, structural connectivity (diffusion imaging-based) and intrinsic (i.e., task-independent or “resting state”) functional connectivity (iFC) has been described (Cauda et al., 2011; Deen et al., 2011; Kurth et al., 2010a; Kurth et al., 2010b; Nanetti et al., 2009; Nelson et al., 2010b). Here, we build on previous work by performing a network-based data-driven parcellation of the insula. We aimed to examine the extent to which parcellations are consistent across three distinct imaging modalities, namely, R-fMRI-based iFC, grey matter structural covariance and meta-analytic patterns of task-based coactivation. Grey matter structural covariance and task-based coactivation are two covariance-based methodological techniques that use structural (grey matter volume) and task-evoked functional data, respectively. Previous studies have demonstrated that the large-scale networks delineated using these approaches exhibit strong correspondence with those derived using iFC methods (Mennes et al., In Press; Seeley et al., 2009; Smith et al., 2009; Toro et al., 2008), suggesting that all three modalities capture similar properties of the brain’s functional organization.

We adopt a network-based voxel-wise clustering approach whereby individual insular voxels are grouped together if they exhibit similar whole-brain patterns of iFC, structural covariance or task-based coactivation. Further, we use a multi-site large-n dataset (www.nitrc.org/projects/fcon_1000) and the publicly available coactivation map analysis (Toro et al., 2008; http://coactivationmap.sourceforge.net) of the BrainMap database (Laird et al., 2005; http://brainmap.org). Despite the different methodological techniques and assumptions underlying these three modalities, we demonstrate strong cross-modal convergence in the parcellations obtained, at multiple spatial scales (i.e., from the relatively coarse scale of 2 clusters, to finer scales of ~9 clusters). That is, we show that the insula exhibits a multiscale organization that is embedded in shared (co-varying) patterns of activity and structure that likely reflect a history of functional interaction. This multiscale organization is consistent with work suggesting that the insula exhibits both subregional functional distinctions (functional heterogeneity) as well as emergent or integrative functions that span multiple subregions (e.g., Craig, 2011; Kurth et al., 2010b). Given the implication of the insula across several clinical and psychiatric disorders, including autism and addiction (Di Martino et al., 2009a; Naqvi and Bechara, 2009), delineating these connectivity-based functional building blocks of the insula will inform investigations of the role of this enigmatic area in both normal and pathological brain states.

2. Material and Methods

2.1. Analysis Overview

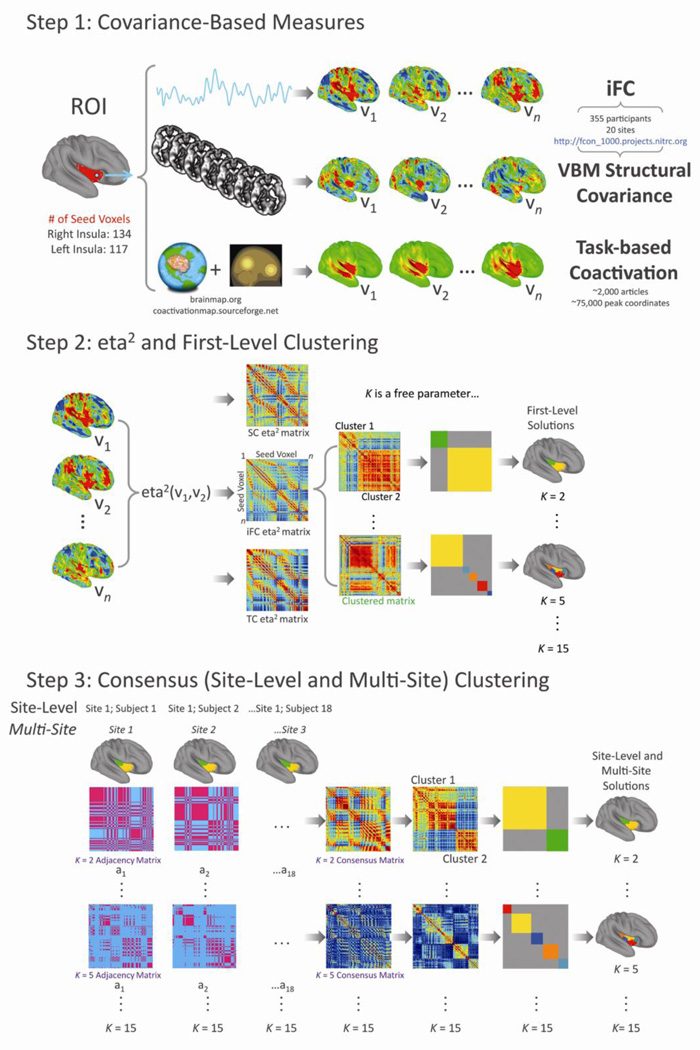
Figure 1 provides a schematic of the data analysis stream. Briefly, processing comprised the following steps:

• Step 1. For each voxel within ROIs encompassing the right (134 voxels) and left (117 voxels) insula (MNI152 4mm³ space), we computed voxel-wise maps of (1) Pearson correlation-based intrinsic functional connectivity (iFC) for an equal sampling of participants from each of 20 data collection sites included in the 1000 Functional Connectomes Project (http://fcon_1000.projects.nitrc.org), (2) whole-brain grey-matter inter-subject structural covariance computed using the same participants from the same 20 data collection sites, and (3) phi-correlation task-based coactivation (Toro et al., 2008; http://coactivationmap.sourceforge.net) across >75,000 peak coordinates from ~2000 articles currently available in the BrainMap database (Laird et al., 2005; http://brainmap.org).

• Step 2. Separately for each of the 3 data types, we used eta² to quantify the similarity between all possible pairings of the covariance maps associated with each of the 117 voxels in the left insula (i.e., ((117*117)−117)/2=6786 pairs) and separately, the 134 voxels in the right insula (8911 pairs). We then used spectral clustering to partition the insula into groups (clusters) of voxels such that intra-cluster similarity was maximized and inter-cluster similarity was minimized. We derived clustering solutions for K = 2,…,15.

• Step 3. For the iFC data, we were able to apply a consensus clustering approach (Bellec et al., 2010; Kelly et al., 2010; van den Heuvel et al., 2008) to identify the most stable clustering solutions across subjects within each data collection site (site-level solutions) and then across the 20 data collection sites (multi-site solutions). For structural covariance, which is a group-level, rather than participant-level measure, we were able to perform consensus clustering across the 20 data collection sites only (multi-site solutions). For the task-based coactivation data, only one set of clustering solutions could be calculated (as there was only one set of coactivation maps). Subsequent to identifying the final set of clustering solutions for each data type, we sought to identify the clustering solutions that exhibited the strongest convergence (similarity) across the three data types (image modalities). We also used two metrics to quantify the pair-wise similarity between the solutions identified for each modality, and selected those exhibiting the strongest cross-modality correspondence as the best or optimal solutions.

Figure 1. Analysis schematic.

Step 1: Covariance-Based Measures. Starting with ROIs comprising the right (134 voxels) and left (117 voxels) insula, per the Harvard-Oxford atlas that accompanies FSL (25% probability, resampled to 4×4×4mm voxels), we computed whole-brain intrinsic functional connectivity (iFC), grey-matter structural covariance, and task-based coactivation, for each voxel (v₁,…,v_n) within each ROI (n=134 for the right insula; n=117 for the left insula). Step 2: eta² and First-Level Clustering. For each covariance measure we used eta² to quantify the similarity between every pair of covariance maps, producing a set of 134×134 matrices containing 8911 unique eta² values ranging between 0 and 1 for the right hemisphere; and a set 117×117 matrices containing 6786 unique eta² values for the left. We then used spectral clustering (Meila and Shi, 2001) to partition the insula into clusters of voxels maximizing intra-cluster/minimizing inter-cluster similarity. This produced three sets of clustering solutions for K = 2,…,15, one for each covariance measure. Step 3: Consensus (Site-Level and Multi-Site) Clustering. Where more than one set of clustering solutions is available, it is possible to apply a stability or consensus clustering approach to derive clustering solutions that are stable across instances. For the iFC data, two levels of consensus clustering were possible – one that derived 20 sets of site-level clustering solutions that were stable across individuals within each site, and a second that derived a single set of clustering solutions that were stable across data collection sites. For the structural covariance data, only one level of consensus clustering was possible – the one that captured stable solutions across data collection sites. Because the task coactivation data produced only a single set of clustering solutions at the first level, no consensus clustering was possible for those data. All the scripts used to perform the multisite consensus clustering analysis are available via http://fcon_1000.projects.nitrc.org.

2.2. Insula Cortex Region of Interest

The left and right insula cortex ROIs were defined on the basis of the Harvard-Oxford atlas that accompanies FSL (25% probability; MNI152 space, resampled to 4×4×4mm voxels). The right ROI comprised 134 voxels, while the left ROI comprised 117.

2.3. 1000 Functional Connectomes Data

MRI data for this study were selected from among the 1093 healthy adult datasets included in Biswal et al. (2010) and made publicly available through the 1000 Functional Connectomes Project (FCP; http://fcon_1000.projects.nitrc.org). Each contributing site’s respective ethics committee approved data collection and submission.

We selected a sample of 18 participants (the minimum number of participants available from any one site) from each of the 20 contributing data collection sites for whom resting state and high-resolution structural imaging data with full-brain coverage for participants between 18 and 65 years of age were available. Where more than 18 participants were available for a site, participants were selected at random, otherwise, all available participants were included. After excluding participants whose resting state or structural images contained significant artifacts or motion (>3mm maximum absolute displacement/3 maximum absolute rotation), 1 site comprised 15 participants, 2 sites comprised 17 participants, and the remaining 17 sites comprised 18 participants each, for a total of 355 participants (mean age 29.7±8.4, range 18–65; 173 females). Scan parameters for each of the sites are available at: http://www.nitrc.org/docman/view.php/296/719/fcon_1000_ReleaseTable_20100803.xls

2.4. Intrinsic Functional Connectivity

Data processing was performed using AFNI (Cox, 1996) and FSL (www.fmrib.ox.ac.uk), as previously described (Biswal et al., 2010). Preprocessing comprised: 3-D motion correction, despiking (identification and removal of extreme time series outliers), spatial smoothing (using a Gaussian kernel of FWHM 6mm), mean-based intensity normalization of all volumes by the same factor, temporal band pass filtering (0.009-0.1Hz), and linear and quadratic detrending. Each participant’s preprocessed 4-D volume was then regressed on nine predictors that modeled nuisance signals from white matter (WM), cerebrospinal fluid (CSF), the global signal, and six motion parameters. The resultant 4-D residuals volume was then spatially normalized to MNI152 standard space, with 4mm³ resolution. We used the FSL linear registration tool FLIRT to register each participant’s functional time series to the space of their high-resolution structural image, and the high-resolution structural images to the MNI152 template (Jenkinson et al., 2002; Jenkinson and Smith, 2001). Time series for each insula voxel (134 right hemisphere; 117 left), were then extracted from this standard-space preprocessed image.

For each participant, we computed the Pearson correlation between each insula voxel’s preprocessed resting state time series (extracted in the previous step) and that of every other voxel in the brain. This step was performed in native functional space in order to reduce processing and storage demands of both the iFC computation, and the subsequent comparisons of iFC images using eta². The resultant native-space correlation images were then Fisher-z-transformed.

2.5. eta²

Clustering algorithms are used to partition (classify) data into natural subsets (clusters) so that observations assigned to the same cluster are more similar to one another than they are to observations assigned to another cluster. Here, we used eta² to quantify the similarity between all possible pairs of iFC maps (delineating putative intrinsic connectivity networks; ICNs) associated with voxels in the insula. The eta² statistic was first applied to iFC data for this purpose by Cohen et al. (2008), who suggested that it provides a better measure of similarity between two images than spatial correlation, because it takes into account differences in scaling and offset between two images, while correlation is unaffected by these factors. The eta² statistic, as written by Cohen et al. (2008), is calculated as follows:

$${\mathit{\text{eta}}}^2=1-\frac{{\displaystyle \sum _{i=1}^n}[{(a_i-m_i)}^2+{(b_i-m_i)}^2]}{{\displaystyle \sum _{i=1}^n}[{(a_i-\mathrm{M̅})}^2+{(b_i-\mathrm{M̅})}^2]}$$

where a_i and b_i are the iFC values at voxel i in iFC maps a and b, m_i is the mean value of the two images at that voxel and M̅ is the grand iFC value across all voxels in both iFC maps.

For each participant, we computed eta² for every pairing of the whole-brain ICNs associated with voxels in the insula, separately for each hemisphere. This produced 355 (i.e., one for each participant) 134×134 matrices containing 8911 unique eta² values ranging between 0 and 1 for the right hemisphere; and 355 117×117 matrices containing 6786 unique eta² values for the left. Given concerns about the use of global signal regression (GSR) as a preprocessing step in iFC analyses (Murphy et al., 2009), in supplementary analyses we repeated the iFC analyses omitting the GSR step.

2.6. Structural Covariance

First described by Mechelli et al. (2005), voxel-wise structural covariance quantifies the extent to which grey matter volumes covary among different regions of the brain, across participants. The group-level structural covariance networks (SCNs) revealed using this approach exhibit strong correspondence with those derived using iFC methods (Seeley et al., 2009), and show similar developmental trajectories (Zielinski et al., 2010). This suggests that structural covariance reflects the same long-term use-related trophic influences that shape iFC (Zielinski et al., 2010).

Structural covariance was estimated using the same 355 FCP participants whose data were used in the iFC analyses. The first step was to estimate voxel-wise grey matter volumes using FSL’s VBM pipeline and each participant’s T1 structural image. Each participant’s high-resolution anatomical image was skull-stripped to remove non-brain material, and segmented into grey matter (GM), white matter and cerebrospinal fluid. The resultant GM images were registered to the ICBM152 grey matter template (included with FSL) with 2×2×2mm resolution, using a 12 degrees-of-freedom affine registration (FLIRT). These images were then averaged together to create a study-specific GM template. Each individual’s native GM image was then registered to this study-specific GM template using FNIRT nonlinear registration, and each voxel was subsequently divided by the Jacobian of the nonlinear warp field (Good et al., 2001) in order to compensate (“modulate”) for contraction or enlargement caused by the non-linear transformation. The modulated, normalized GM images were then smoothed with an isotropic Gaussian kernel with sigma 3mm (~7mm FWHM).

Structural covariance is a group-level (across subjects) measure. Consequently, it was only possible to compute structural covariance for each data collection site (rather than participant, as was possible for iFC). For each site (i.e., group of 15–18 participants; see Section 2.3, above), we computed the structural covariance of each insula voxel using previously described approaches (Mechelli et al., 2005; Seeley et al., 2009). Specifically, we extracted the grey matter volume at each insular voxel from every participant’s smoothed, modulated, normalized GM image. Next, separately for each site and each insular voxel, these values were entered as covariates-of-interest in group-level analyses that identified voxels whose grey matter intensity covaried significantly with that of the seed voxel, across subjects within a site. Finally, separately for each site and each hemisphere, we computed the similarity between every pairing of the resultant whole-brain structural covariance images using eta². This produced a total of 20 (the number of data collection sites) 134×134 matrices containing 8911 unique eta² values ranging between 0 and 1 for the right hemisphere; and 20 117×117 matrices containing 6786 unique eta² values for the left.

2.7. Task-based Coactivation

Following the methods described in Toro et al. (Toro et al., 2008) (and available at: http://coactivationmap.sourceforge.net) we generated task-based coactivation maps for each insula voxel, based on the >75,000 peak coordinates from approximately 2,000 articles, comprising over 35,000 participants, that were available in the BrainMap database in October 2010 (Laird et al., 2005; http://brainmap.org).

Briefly, for each experiment in the BrainMap database, an image volume was created with each of the reported stereotaxic coordinates forming the center of a spherical region of interest with volume 1cm³. The statistical dependence of pairs of voxels across experiments (i.e., their coactivation) was then quantified using a maximum likelihood approach. For each voxel in the brain, this produced a 3-D volume quantifying that voxel’s coactivation with every other brain voxel.

Using the coactivationmap software (http://coactivationmap.sourceforge.net), we extracted the 3-D coactivation volume associated with each of the 134 voxels in the right insula and the 117 voxels in the left insula. Then, separately for each hemisphere, we computed the similarity between every pairing of the task-based coactivation map images using eta². This produced a single 134×134 matrix containing 8911 unique eta² values ranging between 0 and 1 for the right hemisphere; and a single 117×117 matrix containing 6786 unique eta² values for the left.

2.8. Spectral Clustering

As described previously (Kelly et al., 2010), we used the spectral clustering toolbox written for Matlab by Verma and Meila (available at http://www.stat.washington.edu/spectral/). Specifically, we used the Meila-Shi (multicut) algorithm (Meila and Shi, 2001), which performs a generalized eigen-decomposition of the normalized Laplacian of a given similarity matrix (here, an eta² matrix), then applies the k-means clustering algorithm to partition the data into K clusters on the basis of the K highest eigenvectors. We applied this spectral clustering algorithm to the eta² matrices produced for each of the three data types to partition the right and left insula ROIs into K clusters, where K ranged from 2 to 15 (we refer to these as scales K).

As described above, analysis of the task-based coactivation data produced only one eta² matrix, and accordingly, only one set of clustering solutions (for K = 2,…,15). In contrast, because iFC was computed at the level of each individual participant, it was possible to generate eta² matrices for each of the 355 participants included. Consequently, a set of clustering solutions (for K = 2,…,15) was derived for the right and left insula for each of these 355 participants. Finally, because structural covariance was computed at the site level (i.e., based on groups of participants), eta² matrices were generated for each of the 20 data collection sites. A set of clustering solutions (for K = 2,…,15) was therefore derived for the right and left insula for each of these 20 sites.

2.9. Consensus Clustering

Where more than one set of clustering solutions is available for a particular data type (i.e., iFC and structural covariance), it is possible to apply a stability or consensus clustering approach. Consensus clustering is a popular approach within the statistics and machine learning literatures, (e.g., Monti et al., 2003; Steinley, 2008; Strehl and Ghosh, 2002), and has been successfully applied to iFC data in several previous studies (Bellec et al., 2010; Kelly et al., 2010; van den Heuvel et al., 2008). The aim of consensus clustering is to improve the robustness of clustering results to sampling variability. It involves quantifying the agreement among multiple clusterings; that is, the stability with which pairs of voxels were assigned to the same cluster, across instances (e.g., iterations, individuals, or groups). A clustering algorithm can then be applied to the resultant consensus matrices in order to derive group-level clustering solutions. Here, we used the consensus clustering approach to identify clustering solutions that were stable across individuals (iFC data) and sites (iFC and structural covariance data), and which thus minimized the effects of interindividual and site-related variability.

Following this strategy for the iFC data, for each K, each data collection site, and each hemisphere, a site-level consensus matrix was derived which quantified the stability with which pairs of voxels were placed in the same cluster, across all subjects within a single site (between 15 and 18 subjects, depending on site).

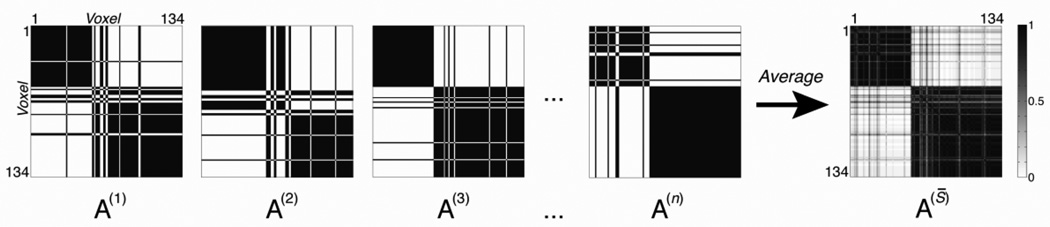
First, for each subject (s), each hemisphere, and each K, we constructed an adjacency matrix (here, for the right insula ROI):

$$A^{(s)}={\left(a_{\mathit{\text{ij}}}^{(s)}\right)}_{134x134}$$

where each element of the matrix, $a_{\mathit{\text{ij}}}^{(s)}=1$ if voxels i and j are assigned to the same cluster k, and 0 otherwise. Figure 2 depicts example adjacency matrices for K = 2.

Figure 2. Consensus clustering schematic for K = 2.

The schematic illustrates the consensus clustering process. For each scale K, each clustering instance contributes an adjacency matrix A^(s), each element $a_{\mathit{\text{ij}}}^{(s)}$ of which contains a value of 1 if voxels i and j are assigned to the same cluster k, and 0 otherwise. In this example, let each instance be a data collection site, so A⁽¹⁾ is contributed by Bangor; A⁽²⁾ is contributed by Berlin, etc. A consensus matrix A^(S̅) is derived by averaging across adjacency matrices. Each element of the consensus matrix thus contains a number between 0 and 1, corresponding to the proportion of times a given pair of voxels appeared in the same cluster, across instances (here, data collection sites). The spectral clustering algorithm can then be applied to identify the most stable pattern of cluster assignments across instances, using the same scale K that was used to generate the consensus matrix (here, K = 2).

Next, for each data collection site, hemisphere, and K, we computed a consensus matrix,

$$A^{(\mathrm{S̅})}=\frac{1}{S}{\displaystyle \sum _{S=1}^S}{A}^{(s)}$$

such that each element of the matrix (134×134 for the right insula or 117×117 for the left) is a number between 0 and 1, corresponding to the proportion of times a given pair of voxels appeared in the same cluster, across participants within that site (i.e., it is the mean of the summed adjacency matrices for that K and that data collection site). In other words, each column of the consensus matrix represents the probabilistic map of the clusters associated with a particular voxel across instances. Note that cluster identity is not important here; what this process quantifies is the stability or consistency of voxel groupings across instances. Perfect consensus would be indicated by a consensus matrix in which all entries were either 0 or 1. This process produced 2 (left and right insula) × 20 (sites) × 14 (scales K) consensus matrices. Figure 2 depicts an example consensus matrix for K = 2 (right hemisphere).

For each consensus matrix (i.e., each K), the spectral clustering algorithm can then be applied to identify the most stable pattern of cluster assignments across subjects, using the same K that was used to generate the consensus matrix. For instance, the Bangor site left insula consensus matrix for K=2 can be clustered to provide 2 group- or site-level left insula clusters. The resultant clusters reflect the stable features of the clustering solutions, across instances (here, subjects) (Bellec et al., 2010). We refer to these clusters as site-level solutions, because they were derived on the basis of the stability of cluster assignments across subjects within each of the 20 data collection sites. This process produced 2 (left and right insula) × 20 (sites) × 14 (scales K) site-level cluster solutions.

Carrying the same logic to the next level, for each hemisphere and each K, we derived a multisite consensus matrix, which quantified the stability with which pairs of voxels were placed in the same cluster, across the 20 data collection sites. This process produced 2 (left and right insula) × 14 (scales K) consensus matrices. The spectral clustering algorithm was then applied to these consensus matrices to provide the final 2 sets of 14 multisite iFC cluster solutions for the right and left insula. For each cluster at a particular K, the corresponding multisite consensus matrix can also be used to compute the mean intra-cluster stability. For each voxel within a particular cluster, we computed the mean stability with which that voxel was placed in the same cluster as all other voxels within that cluster, across sites, by averaging across corresponding values in the multi-site consensus matrix. We then computed an intra-cluster average consensus, by averaging across all the voxels within the cluster.

The same consensus clustering strategy was followed for the structural covariance data, except that, because structural covariance is computed across subjects (i.e., at the group/site level) and produced 20 sets of site-level cluster solutions (for K = 2,…,15) for the right and left insula, only the final (multisite) level of consensus matrix clustering was possible. Specifically, a multisite consensus matrix was derived for each hemisphere and K, which quantified the stability with which pairs of voxels were placed in the same cluster, across sites. This process produced 2 (left and right insula) × 14 (scales K) consensus matrices. The spectral clustering algorithm was applied to these consensus matrices to provide the final 2 sets of 14 multisite structural covariance cluster solutions for the right and left insula.

Because the task coactivation data produced only a single set of clustering solutions at the first level, no consensus clustering was possible for those data.

All the scripts used to perform the multisite consensus clustering analysis are available via http://fcon_1000.projects.nitrc.org.

2.10. Determination of Optimal Clustering Solutions

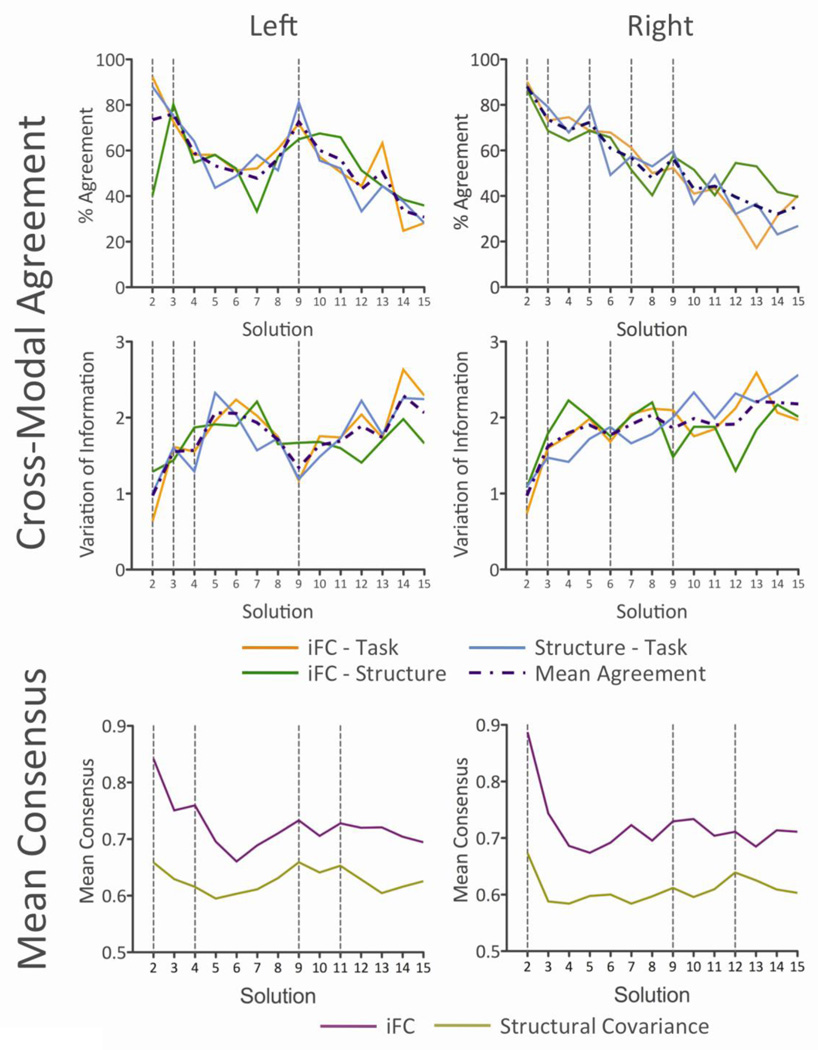
Because K (the number of clusters) is a free parameter, and the true number of clusters within the insula is unknown, we must choose some criterion on which to decide which K(s) provide the best or optimal fit for the data. Here, we used cross-modal correspondence as the criterion on which to select optimal clustering solutions. For each value of K, we compared the cluster solutions generated for each modality using two metrics: Percent Agreement and Variation of Information (VI; Meila, 2007). That is, we quantified the similarity (distance in the case of VI) between cluster solutions, between all possible pairings of modalities. For a given pair of clustering solutions (e.g., the K=2 multisite solutions for iFC and structural covariance), Percent Agreement is computed by dividing the number of voxels that are assigned to the same cluster across the two modalities (identified by computing the cross-tabs), expressed as a percentage of the total number of voxels (117 for the left insula; 134 for the right). It corresponds to the intersection of Solution A and Solution B, divided by the total number of elements (voxels). Percent Agreement thus quantifies the similarity between two clustering solutions, and relatively high values (peaks) indicate “better” or “optimal” solutions. VI is an information theoretic measure that quantifies the distance between two clustering solutions in terms of the information gained and lost in choosing Solution A over Solution B (Meila, 2007). VI thus quantifies the dissimilarity between two clustering solutions; relatively low values (troughs) indicate optimal solutions. As there were three modalities, each associated with a set of solutions, 3 pairings or comparisons between modalities were possible: iFC-Structural Covariance; iFC-Task Coactivation; and Task Coactivation-Structural Covariance. We therefore computed the “Mean Agreement” (mean Percent Agreement or mean VI; purple line in Figure 3) across these 3 comparisons and used that mean value to identify optimal solutions.

Figure 3. Clustering metrics.

We identified optimal clustering solutions on the basis of their cross-modal correspondence. For each value of K, we compared the cluster solutions generated for each modality using Percent Agreement (top two panels) and Variation of Information (VI; middle two panels). We selected the values of K showing the highest mean Percent Agreement or lowest mean VI (purple dashed lines), across the three different pairings of the three modalities. In addition to strong agreement for the trivial K = 2 solutions, these metrics indicated that strong agreement was obtained for K = 2, 3, 4 and 9 (left hemisphere), and 3, 5, 6, 7 and 9 (right hemisphere). The bottom two panels show, for iFC and structural covariance, the mean intra-cluster consensus (stability) values for each K. The locations of peaks in the Mean Consensus (K = 2, 4, 9, and 11, left hemisphere; K = 2, 9, and 12, right hemisphere) plots show good correspondence with the locations of peaks in the Agreement plots, suggesting that the solutions showing the best agreement across modalities also exhibited the strongest stability, across data collection sites.

In the introduction, we stated that clustering on the basis of functional connectivity provides an opportunity to examine functional organization at multiple scales. Consistent with this idea, there are likely to be multiple solutions of potentially equal validity - a single optimal number of clusters may not exist. Accordingly, we identified several local maxima/minima in mean Percent Agreement and VI to highlight solutions at different resolutions or spatial scales.

To illustrate the differential patterns of whole brain functional connectivity contributing to the clustering solutions, we elucidated the patterns of iFC associated with each of the clusters within two of the optimal solutions identified (left K = 4 and right K = 5), across all subjects and all sites. Specifically, for each subject, each hemisphere, and each cluster we computed the partial correlation between the mean cluster time series and all other brain voxels (taking into account the time series of all other clusters within that solution). We then derived the multi-site group-level iFC for each cluster.

2.11. Behavioral Domains

We used the behavioral domain classification of experiments in the BrainMap database to empirically identify the functional domains associated with the coactivation networks for each of the insular clusters obtained. In the taxonomy of BrainMap, experiments can belong to one or more of 6 primary behavioral domains, namely, action, cognition, perception, emotion, interoception, or pharmacology. These primary behavioral domains contain sub-domains, providing a finer taxonomic specification of the experiment.

Initially, we examined the primary behavioral domains associated with each of the coactivation maps associated with each insula cluster. For each of the K clusters for a given K value we determined the list of experiments with a location overlapping the peak locations of that cluster's coactivation map. Each list contained a variable number of experiments: N_i, i=1,…,K. Next, we counted the number of behavioral domain “hits” for each cluster, to produce 6 “observed” behavioral domain hit counts per cluster. To estimate the significance of these hit counts, we used a resampling procedure (1000 iterations) to generate a null distribution. First, we made a list containing all the experiments overlapping any of the coactivation networks for the given K value. Next, we created K random lists of N_i experiments each, i=1,…,K, to match the observed number of experiments per cluster, and counted the number of hits per list for each of the 6 primary behavioral domains. We used the distribution of the number of hits in the random list to estimate the “expected” hit counts for each cluster. The observed frequency of behavioral domain hits was then considered significant if it exceeded a Bonferroni threshold computed on the basis of the number of clusters and domains examined (e.g., for K = 9, the Bonferroni threshold would be 9 (clusters) × 6 (primary behavioral domains) = 0.05/54 = 0.00093). To ensure a comprehensive assessment of the behavioral domains associated with each cluster, we also identified the domains whose frequency exceeded the more liberal threshold of p < 0.05.

For behavioral domains whose frequency exceeded the Bonferroni threshold in the positive direction (i.e., the number of hits was significantly greater than the Bonferroni threshold), we used the same methods to examine the corresponding subdomains to gain additional insight into the functions associated with each cluster. The subdomains for each primary behavioral domain are: Action: Execution, Imagination, Inhibition, Motor, Observation, Preparation, Rest; Cognition: Attention, Language, Memory, Music, Reasoning, Social, Soma, Space, Time; Emotion: Anger, Anxiety, Disgust, Fear, Happiness, Sadness; Interoception: Air Hunger, Baroregulation, Bladder, Hunger, Osmoregulation, Sexuality, Sleep, Thermoregulation, Thirst; Perception: Audition, Gustation, Olfaction, Somesthesis, Vision; Pharmacology: Alcohol, Amphetamines, Caffeine, Capsaicin, Cocaine, Ketamine, Marijuana, Nicotine, Inflammatory, Opioids, Psychiatric, Steroids. Significant subdomains were identified in the same way as significant primary domains – using a Bonferroni threshold computed on the basis of the number of clusters and subdomains examined.

3. Results

3.1. Convergent Clustering Solutions

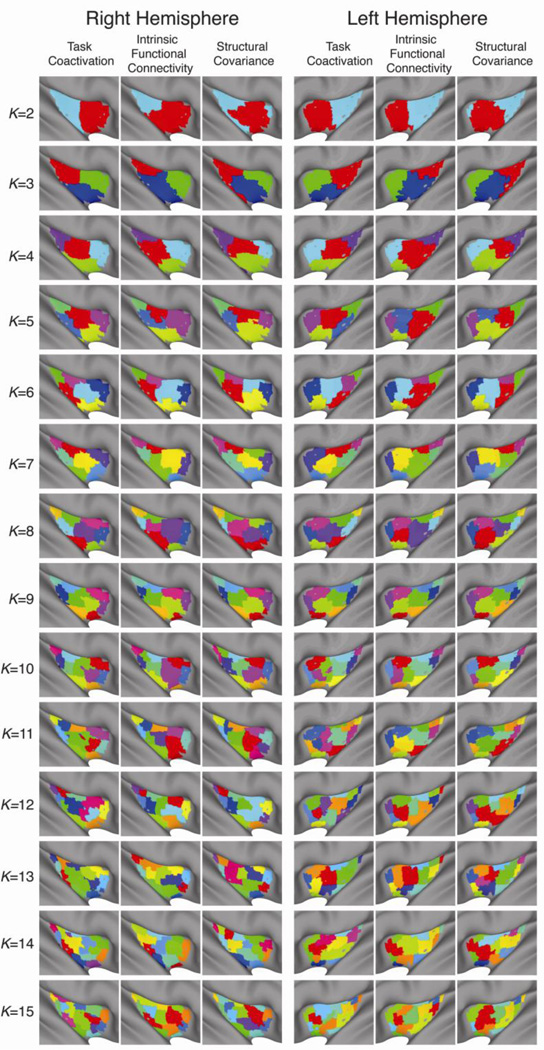
As Figure 4 shows, there was a remarkable degree of agreement in the final clustering solutions obtained for each of the different data types, across all solutions. This suggests that the patterns of whole-brain functional and structural covariance quantified by each of the measures (iFC, structural covariance and task coactivation) are highly similar across multiple spatial scales – from the coarse scale of the K=2 cluster solution, to the finer scale of solutions such as K=9.

Figure 4. Final cluster solutions.

Consensus/multi-site cluster solutions for K = 2,…,15 for the structural covariance, intrinsic functional connectivity (iFC) and task-based coactivation data.

Using two metrics (Percent Agreement and VI, top two panels of Figure 3), we identified the clustering solutions that showed particularly strong pair-wise correspondence (Mean Agreement: indicated by purple broken line in Figure 3) among the three data types. Identifying local maxima (mean Percent Agreement) and minima (mean VI) in the metric values suggests that solutions K = 2, 3, 4 and 9 (left hemisphere), and 2, 3, 5, 6, 7 and 9 (right hemisphere) showed the highest consistency across modalities. Figure 3 also shows, for iFC and structural covariance, the mean intra-cluster consensus (stability) values for each K (bottom panels). The locations of peaks in the Mean Consensus plots show good correspondence with the locations of peaks in the Agreement plots, suggesting that the solutions showing the best agreement across modalities also exhibited the strongest stability, across data collection sites.

To illustrate the differential patterns of whole brain functional connectivity contributing to the clustering solutions, Supplementary Figure S1 shows iFC across 340 participants (one site was excluded because of incomplete coverage of the parietal lobes), for the left (K = 4) and right (K = 5) hemisphere.

Looking at the individual site-level cluster solutions for iFC and structural covariance (for K = 2,…,9; Supplementary Figures S2–S9), it is clear that these solutions were particularly robust, both across sites and across data types. At the individual site level, the consistency of solutions decreased considerably for K > 10, therefore these are not shown. Supplementary Figures S2–S9 and S10 also depict the results of clustering carried out on iFC data analyzed without global signal regression. These findings suggest that global signal regression does not have a significant impact – the similarities and differences among voxels in terms of their whole-brain patterns of functional connectivity are largely the same regardless of global correction. Confirming this qualitative impression, statistical comparisons (paired t-tests) of the Percent Agreement and VI metrics assessing the similarity between the solutions for the three different data types revealed no significant differences, either at the single-site or multi-site levels (Supplementary Figure S11). Finally, Supplementary Figure S12 shows, for each cluster and each K (for K = 2,…,12), the voxels exhibiting the strongest consensus (those falling within the top 50% of a rank ordering of voxel-wise consensus scores within each cluster). To create the figure, for each voxel within each cluster, we computed the mean stability with which that voxel was placed in the same cluster as all other voxels within the cluster, across sites, by averaging across corresponding values within that voxel’s column in the multi-site consensus matrix. Next, within each cluster, voxels were rank ordered according to their mean stability, and those falling within the top 50% (i.e., those exhibiting the strongest stability) were rendered on the surface. Consistent with previous work demonstrating that clustering confidence or stability is stronger at cluster centers and weaker at the edges or boundaries between clusters (Buckner et al., 2011; Nanetti et al., 2009; Yeo et al., 2011), these voxels are predominantly located at the centers of the clusters, while voxels at the edges/boundaries between clusters exhibited weaker consensus (i.e., fell within the bottom 50% and so are not shown).

It is interesting to note that the clustering method employed here is not expressly hierarchical: the spectral clustering is applied independently for each K and the resulting partitions do not have to be nested. The solutions obtained nonetheless exhibit a structure that is near hierarchical. This is not to say that borders between divisions were strictly maintained, but rather that a pseudo-hierarchical organization emerged across several scales. For example, consistent with previous studies (Cauda et al., 2011; Nanetti et al., 2009), the two-cluster solutions separate anterior and posterior divisions of the insula. In the left-hemisphere four-cluster solution, the anterior division separates into a dorsal and ventral part, while the posterior division separates into a middle and posterior part, also consistent with previous observations (Kurth et al., 2010b). Finally, in the nine-cluster solution (both hemispheres), four “anterior” clusters are obtained along with five “posterior” clusters exhibiting an organization consistent with the lower-scale solutions. A similar multiscale organization has been observed in previous studies using both clustering and independent component analysis (ICA)-based approaches, at the level of the entire brain (Bellec et al., 2010; Smith et al., 2009; Yeo et al., 2011), as well as specific regions such as the cerebellum (Buckner et al., 2011). MNI-space masks containing the optimal solutions for each hemisphere are available via http://fcon_1000.projects.nitrc.org.

3.2. Behavioral Domains

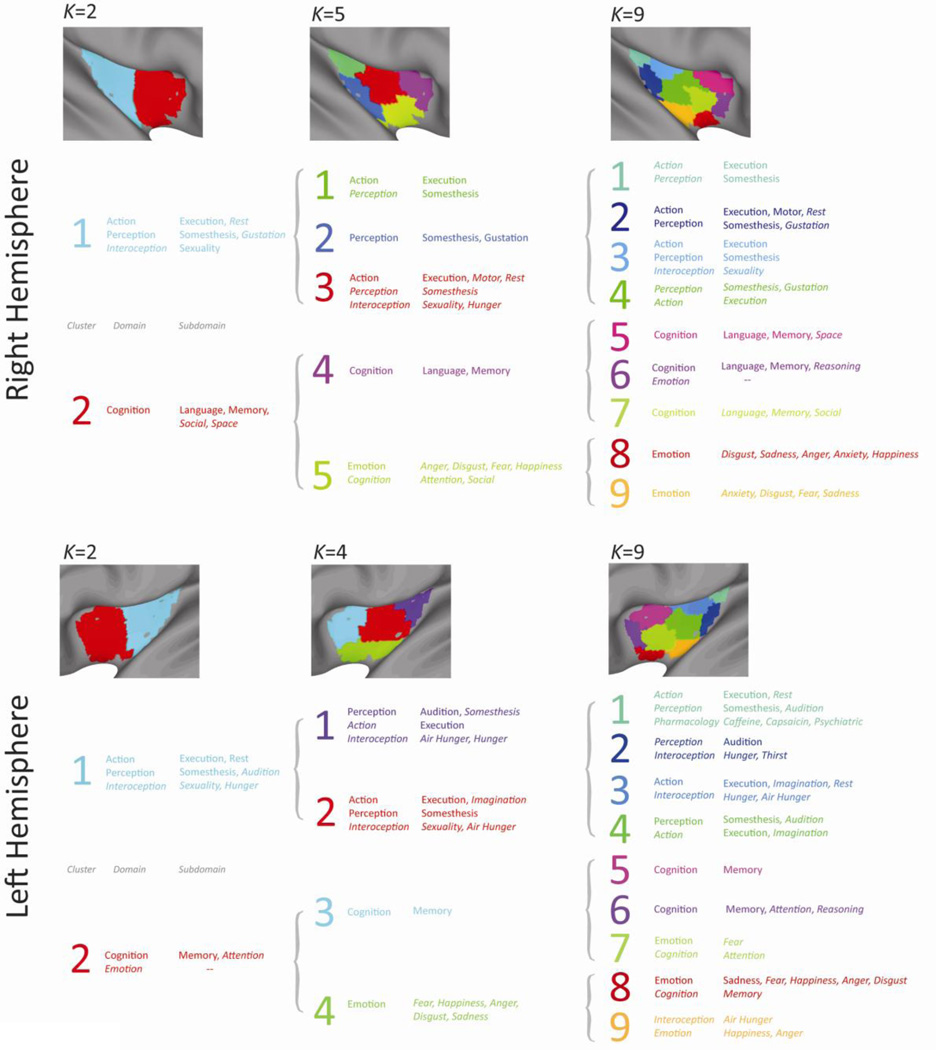
A pseudo-hierarchical organization is also suggested by the behavioral domain analysis (Figure 5). Histograms depicting the frequency of domain hits and null distribution for each domain and K, and the Bonferroni threshold for significance, are shown in Supplemental Figures S13–S18. Across low scales, in both hemispheres, anterior-most clusters were most strongly associated with cognitive and emotional processes, while posterior clusters were most strongly associated with perceptual and motor processes. At higher scales, emotional processes were assigned to ventral anterior clusters, while cognitive processes were assigned to dorsal anterior clusters. Middle insula clusters were associated with sensory perception, somesthesis, and interoception, while dorsal posterior and ventral posterior clusters were associated with action and perception, respectively. These behavioral domain associations are highly consistent with previous studies.

Figure 5. Behavioral domain analysis.

Significant behavioral domains (and subdomains) identified for K = 2, 4 and 9 (left hemisphere), and 2, 5 and 9 (right hemisphere). Domains and subdomains exceeding an uncorrected threshold of p < 0.05 but not the Bonferroni threshold are in italics. Distributions for each domain and cluster are shown in Supplemental Figures S13–S18.

It is important to emphasize that the analysis employed to assign task domains to clusters identified behavioral domains that were over-represented in each cluster, relative to the distribution of behavioral domains across clusters. The analysis thus identified the predominant but by no means the unique behavioral domain associated with a cluster. This aspect of the behavioral domain associations can be seen clearly in Supplementary Figures S13–S18, which show that the behavioral domains exhibited large numbers of hits across multiple clusters. This is particularly evident for a behavioral domain such as Cognition – this domain registered 580 hits even for a cluster whose network was associated with significantly fewer than expected hits for this domain (Cluster 3, Right Insula, K=5; Supplementary Figure S14).

This high degree of overlap among clusters in terms of behavioral domains, particularly for the higher-K solutions, suggests that although differentiable insular clusters (subregions) can be identified on the basis of large-scale patterns of functional and structural covariance, these subregions also support overlapping functions and tasks. This observation is consistent with previous empirical and theoretical work suggesting that the insula exhibits both local functional heterogeneity and emergent or integrative functions that likely rely on processing across multiple subregions (Craig, 2009a, b, 2011; Kurth et al., 2010b). This overlap may also reflect limitations in the taxonomic resolution of the task domains currently mapped in the BrainMap database, or it may suggest that the finer resolution of the higher-K solutions overestimates functional differentiation in the insula.

4. Discussion

A convergent multiscale organization of the insula was revealed by three covariance-based network measures derived from three distinct neuroimaging modalities. Previous work has demonstrated convergence among large-scale networks defined by iFC, task-based coactivation (Smith et al., 2009; Toro et al., 2008), electrophysiological measures of neuronal activity (He et al., 2008; Keller et al., 2011), and brain structure (Mars et al., 2011a; Seeley et al., 2009). Moving beyond correspondence at a macro scale, we demonstrated convergence among modalities at a finer resolution, commensurate with the resolution of intra-areal functional distinctions previously revealed with task-based fMRI studies. Together, our findings support the hypothesis that both structural and functional covariance-based measures provide complementary insights into the brain’s intrinsic network organization at multiple spatial scales.

4.1. Multimodal Convergence

Cohen et al. (Cohen et al., 2008) first demonstrated that boundaries between functionally distinct brain areas could be delineated by detecting the locations at which patterns of whole-brain iFC diverge. Here, we showed that this approach can be applied at a finer spatial scale to derive the putative functional elements of a complex region such as the insula. Further, the same topography was revealed when this approach was applied to two different measures of functional and structural organization: grey matter structural covariance and meta-analytic patterns of task-based coactivation. One could argue that the presence of shared structural information (e.g., registration error) between the iFC and structural covariance measurements could explain similarities among their associated clustering solutions. On the other hand, it is not obvious that such an explanation could also underlie convergence with the solutions computed on the basis of coordinate-based meta-analytic patterns of task coactivation. This suggests that, despite considerable methodological variations, the large-scale covariance patterns detected by these different methods and modalities share a common basis, most likely the neuronal connectivity of the brain.

Our findings are consistent with a recent clustering analysis of the insula using diffusion-based connectivity data (Nanetti et al., 2009), as well as work on other brain areas such as lateral parietal cortex, which have demonstrated convergence between parcellations derived on the basis of diffusion-based measures of connectivity and iFC (Mars et al., 2011a; Mars et al., 2011b). We would expect, therefore, that applying our analysis to DTI connectivity data would reveal a similar insular topography. Although structural and functional connectivity do not exhibit a 1:1 relationship (Hagmann et al., 2008; Honey et al., 2009; Roy et al., 2009; Vincent et al., 2007), the present work further bolsters evidence that similarities and differences between large-scale patterns of connectivity are shared between structural and functional measures. Given that recent work suggests structure-function relationships strengthen from childhood to adulthood (Hagmann et al., 2010), it will be important to examine whether the convergence among these modalities breaks down in children, in elderly populations, or in clinical or psychiatric conditions. Such an examination may reveal novel objective markers of typical and atypical development.

4.2. Partitioning the Insula

The optimal clustering solutions identified for the right and left insula demonstrate an organization that is highly consistent with previous clustering and meta-analytic studies of the region, while offering additional insights into its functional organization at somewhat higher resolution (>4 parcels). Several of these studies used a network-based approach similar to that outlined here to partition the insula on the basis of whole-brain patterns of iFC. In one such study, Deen et al. (2011) detected three insula subdivisions, each associated with divergent patterns of whole-brain iFC. These three subdivisions are highly consistent with our K = 3 solutions, comprising a large mid-posterior cluster, a dorsal-anterior cluster and a ventral anterior cluster. Function differentiation among these clusters was suggested by greater task-related responses to disgusting images in the anterior than posterior clusters. In another study, Cauda et al. (2011) obtained two insula regions (anterior and posterior) exhibiting divergent whole-brain patterns of iFC. Finally, restricting their interest to the anterior insula and neighboring frontal operculum, Nelson et al. (2010b) delineated divergent patterns of whole-brain iFC and divergent task-evoked responses to a memory retrieval task. They identified three functionally distinct regions, the more anterior of which (both dorsal and ventral) exhibited task activity related to top-down and bottom-up aspects of task control, while a posterior region did not. Given their focus on regions extending beyond the insula itself, consistency between the findings of Nelson et al. and our data is somewhat difficult to ascertain, although the two studies appear to agree in the assignment of cognitive functions to dorsal anterior insula.

The degree to which our results are consistent with partitions identified on the basis of other modalities, such as cytoarchitecture, remains to be seen. Recent studies (e.g., Gallay et al., 2012; Kurth et al., 2010a) have refined the classically defined granular (posterior), agranular (ventral anterior) and dysgranular (dorsal anterior and mid) cytoarchitectonic divisions described in the macaque (Mesulam and Mufson, 1982a). For example, on the basis of a highly detailed analysis of posterior insula in ten postmortem human brains, Kurth et al. (2010a) described 3 cytoarchitectonically distinct posterior insula regions. The topography of those regions appears to correspond to that observed for the 3 posterior-most clusters in our 9-cluster solution. It is important to note, however, that while our analysis provides one kind of insight into insular functional organization, based on intrinsic covariance patterns analyzed at a macro scale, other topographies may be revealed with alternative types of information, methodologies and analyses. For example, there are dynamic aspects of functional connectivity that are not captured using the iFC methods adopted in the present study (e.g., Chang and Glover, 2010; Kang et al., 2011). Further, recent work (Mennes et al., In Press) has demonstrated that iFC is not globally identical with task-evoked coactivation. Instead, Mennes et al. showed that the strength of the correspondence between these measures exhibits regional variation across the brain, with subcortical regions such as the striatum exhibiting relatively weak correspondence. This suggests that although some brain areas may exhibit predominant modes of functional interaction that are captured with standard iFC measures, others exhibit context-specific modulations of interaction that may be best identified using task-based approaches. As such, our work does not provide a definitive picture of insular organization, as alternatives are likely to exist. Nonetheless, the multiscale architecture we have described appears to capture an aspect of insular organization that reflects a fundamental property of the brain’s functional architecture more globally.

4.3. Behavioral Architecture of the Insula

Previous studies have also examined insular functional differentiation using meta-analytic approaches. For example, Kurth et al. (2010b) performed an activation-likelihood-estimation (ALE) meta-analysis of 1,768 studies (from the BrainMap database), after grouping the coordinates according to 4 superordinate functional categories. They found that the resultant meta-analytic activations in each functional category exhibited a topographic organization within the insula. Specifically, they observed four distinct insula functional regions: a ventral anterior social-emotional region (emotion, empathy), a dorsal anterior cognitive portion (attention, language, speech, working memory, memory), a central olfacto-gustatory region (olfaction, gustation) in the right hemisphere only, and a mid-posterior sensorimotor region (interoception, pain, somatosensory, motor). In addition, Kurth et al. identified a region in dorsal anterior insula that exhibited overlap among all the functional categories examined, with the exception of somatosensory and motor processing, suggesting that this region supports a basic or integrative functional role. Although based on a much smaller number of studies, and restricted to the anterior and mid-insula, Mutschler et al. (2009) detected a similar anterior-posterior gradient of localization for cognitive (e.g., language) and sensorimotor processes. Our mapping of the BrainMap task domains, whereby sensory, motor and interoceptive domains mapped to mid- and posterior insula regions, cognitive domains to dorsal anterior insula and emotional domains to ventral anterior insula, closely follows these previously described topographies, although with finer localization of task domains for higher scales. As in Kurth et al. (2010b), we did not observe strict functional differentiation among clusters, rather, we observed a high degree of overlap among clusters in terms of their associated behavioral domains, particularly for the higher-K solutions. Further, while not constrained to be hierarchical, we observed a pseudohierarchical modular organization of the insula across multiple cluster solutions, both in terms of parcellation and behavioral domains. For example, in the nine-cluster solution, the gross anterior/posterior distinction of lower scales is observable in terms of the four “anterior” clusters and five “posterior” clusters that were obtained (Fig. 3; Fig. 4). These observations suggest that although distinct regions of the insula can be identified on the basis of differentiated large-scale patterns of functional and structural covariance, these subregions also support overlapping functions and tasks. This interpretation is consistent with a multiscale functional organization, discussed above, and with previous work suggesting that the insula exhibits both local functional heterogeneity and emergent functions that involve the integration of processing occurring across multiple regions (Craig, 2009a, b, 2011; Kurth et al., 2010b).

Although both the parcellation topography and behavioral domain associations were largely symmetrical, some hemispheric asymmetries in insula behavioral associations were observed. Evidence from neuroimaging and neuropsychological studies (e.g., Harrison et al., 2010; Ibanez et al., 2010; Paulus et al., 2003), as well as theoretical work (Craig, 2005), suggests that some aspects of emotional and interoceptive processing in the insula exhibit hemispheric asymmetries, such that the right insula supports processing of sympathetic arousal and responds more strongly to aversive emotion such as disgust and anxiety. In contrast, the left insula is thought to be more strongly activated by parasympathetic nervous function and to support positive emotions and appetitive behavior. Though we did not observe any unequivocal lateralization, these observations are consistent with our data in that: (1) disgust and anxiety were predominantly associated with right hemisphere-based coactivation networks; (2) interoceptive processing related to hunger and thirst, as well pharmacological agents were more associated with left hemisphere-based networks; and (3) somesthesis and sexuality were more strongly associated with right-hemisphere coactivation networks. On the other hand, we did not observe other common asymmetries in insular function, such as that reported for language processing (left hemisphere) (e.g., Chee et al., 2004; Nestor et al., 2003). In fact, in our data, language was predominantly associated with right hemisphere-based networks, rather than left hemisphere networks. While these observations may suggest that some proposed asymmetries in insular function may not be reflected across the neuroimaging literature (also suggested by the work of Kurth et al., 2010b), they may also reflect the particular methods used to detect significant behavioral domains. Finally, our observations are an inevitable reflection of the studies currently entered into the BrainMap database and the taxonomic resolution of the database. Indeed, more comprehensive and detailed text-based meta-analytic methods, such as those implemented in NeuroSynth (Yarkoni et al., 2011), may be required to derive a thorough and representative mapping of insular functional domains.

4.4. Perspectives

Delineating the functional building blocks of the insula has utility beyond our understanding of functional differentiation. One troublesome aspect of the neuroimaging literature, elegantly outlined by Devlin and Poldrack (2007), is imprecision and lack of consistency in the application of neuroanatomical labels. This problem is particularly salient within the insula literature – researchers often ascribe activations to the insula when the activation is actually in the nearby frontal, temporal or parietal opercula, which leads to considerable confusion with regard to insula function. In addition to their potential use in seed-based analyses of iFC, it is our hope that by making available the MNI-space ROIs from our analyses (http://fcon_1000.projects.nitrc.org), researchers can use these ROIs to more accurately describe the locations of the (peaks of) their activation or connectivity in the insula. The incorporation of ROI-based analyses can also reduce computational complexity and requirements for multiple comparisons correction. Finally, as others have pointed out (Deen et al., 2011; Laird et al., 2011) the use of pre-defined ROIs allows researchers to test hypotheses concerning differential localization or timing of stimulus or task-evoked responses without “double-dipping” (Kriegeskorte et al., 2009; Vul et al., 2009).

4.5. Limitations

As with most clustering techniques, the number of clusters (K), is a free parameter that must be selected by the user. Here, we capitalized both on the multi-site nature of the data, as well as the inclusion of 3 different modalities to detect the most stable and consistent solutions between K =2 and K =15. The upper bound of 15 primarily reflects pragmatic constraints - the original resolution of the data, the size of the insular ROIs interrogated, and the fact that we were performing an analysis both across subjects and across data collection sites. Future studies using higher resolution data may reveal more fine-grained distinctions than obtained here.

In contrast to the approach described by Cohen et al. (2008), we adopted a volume-based rather than surface-based approach. While the task-coactivation patterns could potentially be transformed to surface space, such transformation would introduce additional potential error into data that are already several steps removed (by virtue of being coordinate-based) from “true” task coactivation data. Surface-based analysis also cannot take into account subcortical connectivity, an important consideration for analyses of the insula. Finally, surface-based analyses remain less common than volume-based, and are subject to their own limitations. For example, because of the low resolution of functional data, signal from one side of a sulcus could be incorrectly imputed to a geodesically distant region, thus blurring differentiation between functionally distinct regions and networks. Consequently we concluded that a volume-based analysis has wider applicability.

As discussed above, by examining whole-brain patterns of covariance, we have identified what may be the predominant and most stable modes of interaction of these regions, but they may not be the only modes of interaction. It is becoming increasingly clear that patterns of functional connectivity may be more dynamic and malleable than previously appreciated and some regions or networks may exhibit less stability than others. Or, stability may differ between groups as a result of clinical or psychiatric conditions. The examination of temporal stability within an individual across different contexts (e.g., rest, task etc.) may shed light on this issue.

We adopted a consensus clustering approach in order to delineate insular clusters that were robust to individual (and site) variation. Thus, although the influence of interindividual variability in morphometry and functional organization on the parcellations obtained is of considerable interest (e.g., Di Martino et al., 2009b), an examination of interindividual variation is beyond the scope of the present work. The investigation of interindividual and group differences in insular functional organization using homogeneous (i.e., single-site) and higher resolution data is a goal of future work.

Concerns remain over the use of global signal regression as a preprocessing step in iFC analyses (Anderson et al., 2011; Murphy et al., 2009). Our findings were largely robust to the effects of global signal regression (see Supplementary Figures S2–S9, S10, S11). This suggests that, at least for within-subject comparisons of patterns of functional connectivity, global signal regression does not have a significant impact – the similarities and differences among voxels in terms of their whole-brain patterns of functional connectivity are largely the same regardless of global correction. While issues clearly remain concerning patterns of negative iFC, particularly with regard to comparisons between groups or relationships with phenotypic variables, our results suggest that for the purposes of the delineation of functional networks and boundaries, including global signal regression is not detrimental to our understanding of the brain’s functional architecture.

5. Conclusions

Using a network-based approach, we showed that clustering of three covariance-based measures, captured with distinct MRI modalities, revealed a convergent elemental organization of the insula that likely reflects a fundamental brain architecture governing both brain structure and function at multiple spatial scales. By incorporating a behavioral domain analysis, we elucidated the broad functional dissociations associated with the insular topography we observed. Further work will apply this approach to other brain areas and examine how these findings can be utilized for the detection of dysfunctional brain organization and its implication in clinical disorders.