Limiting Values of the ¹⁵N Chemical Shift of the Imidazole Ring of Histidine at High-pH

Abstract

Tautomeric identification by direct observation of ¹⁵N chemical shifts of the imidazole ring of histidine (His) has become a common practice in NMR spectroscopy. However, such applications require knowledge of the “canonical” limiting values of the ¹⁵N chemical shift of the imidazole ring of His in which each form of His, namely the protonated (H⁺) and the tautomeric N^ε2-H and N^δ1-H forms, respectively, is present to the extent of 100%. So far, the adopted canonical limiting values of the ¹⁵N chemical shift have been those available from model compounds. As to whether these canonical values reflect those of the individual pure forms of His is investigated here by carrying out an analysis of the second-order shielding differences, ΔΔ = |Δ^ε − Δ^δ, with Δ^ξ(ξ = ε or δ) being the DFT-computed average shielding differences between the two nitrogens of the imidazole ring of His in each pure tautomeric form. In the high-pH limit the results indicate that the (i) ΔΔ values from the DFT-computed shielding, but not from the commonly-used canonical limiting values, are in closer agreement with those obtained with experimental chemical shift data from model compounds in solution and solid-state NMR; and (ii) commonly-used canonical limiting values of the ¹⁵N chemical shifts lead to an average tautomeric equilibrium constant that differs by a factor of ~2.6 from the one computed by using DFT-based ¹⁵N limiting values, raising concern about the practice of using canonical limiting ¹⁵N values; this can be avoided by reporting tautomeric equilibrium constants computed by using only limiting ¹⁵N values for the N^ε2-H tautomer.

Introduction

Since chemical shifts were first observed by Arnold et al., in 1951 (1), using Nuclear Magnetic Resonance (NMR) spectroscopy, Mandel (2), in a pioneering NMR experiment, in 1965, first detected the imidazole (C2) protons of histidine (His) residues in Ribonuclease A and, soon after that in 1966, Bradbury & Scheraga (3) in a seminal NMR spectroscopic work were able to distinguish between the histidine residues of Ribonuclease A; namely, they resolved the peaks of three out of four histidines of this enzyme. Afterward, use of NMR spectroscopy, X-ray crystallography and theoretical studies, based on quantum-chemistry calculations, continuously evolved in the ability to determine the properties of the histidine residues in solution and in the solid state (4–27). The reason for this persistent interest in His is due to the fact that this residue is unique among all 20 naturally occurring amino acids, among other reasons, because ~50% of all enzymes use His in their active sites (19). This is, mainly, because of the versatility of its imidazole His ring, which includes two neutral, chemically-distinct forms (N^δ1−H and N^ε2−H tautomers) and a charged H⁺ form, with one form favored over the other by the protein environment and pH. In addition, His with a pK^o of 6.6 (28) is the only ionizable residue that titrates around neutral pH, allowing the nonprotonated nitrogen of its imidazole ring to serve as an effective ligand for metal binding (23), or to play a crucial role in the proton-transfer process (26).

As noted by Markley (6), there are mainly three factors that contribute to the observed chemical shifts of the nuclei imidazole ring of His, namely: (a) the “intrinsic” chemical shifts, which can be determined theoretically, at the DFT-level of theory, from model peptides, e.g., by using a model tripeptide with the sequence: Ac-GHG-NMe (29). The conformational-average intrinsic values of the ¹⁵N chemical shifts, for a given His form, are averages over all conformations, i.e., ~35,000, for which the shieldings were computed here at the DFT level of theory, namely for each nitrogen in the imidazole ring of His; (b) he “local environment” of each His residue in the protein, which can be very different for different His residues in the sequence; with the tautomeric coexistence being a function of the “local environment” of each His residue (27); and (c) the “proton binding/release equilibrium” of the imidazole His ring which, at a given fixed pH, is influenced by the presence of nearby positively or negatively charged side chains that will lower or raise the pK´ of a given His; overall, this factor determines the fraction of the protonated His form and, hence, those of the neutral form (27). Here, focus is directed to determining the conformational-average intrinsic values of the ¹⁵N chemical shifts for each of the two tautomeric forms of the imidazole ring of His as representative of the canonical values at high-pH, in other words, a theoretically determined set with which to represent the limiting values of the ¹⁵N chemical shift. Hereafter, the computed conformational-average values of the intrinsic ¹⁵N chemical shift will be referred to us as DFT-computed limiting ¹⁵N values.

The fact, that NMR spectroscopy is a powerful tool with which to investigate the role of histidine residues located in active sites of proteins, is an observation that goes back to pioneering NMR experiments on histidine by Mandel (2), who concluded “…This provides us with a window to observe the active site under various conditions…” Since this prediction was made, several methods are currently used to identify the protonation states of the imidazole ring of His as well as to distinguish between different tautomers (13, 22). Most of these methods rely on the observation of ¹⁵N chemical shifts of the imidazole ring of His, although an alternative to the use of ¹⁵N chemical shifts has recently been presented (27), namely a new method based on the observed ¹³C^γ and ¹³C^δ2 chemical shifts for the imidazole ring of His. Nevertheless, for a quantitative analysis of the tautomeric structure of the imidazole ring of His, use of ¹⁵N chemical-shift data is very desirable for a number of reasons, among others because ¹⁵N chemical shifts of the imidazole His ring are spread over a wide range and, even more important, are very sensitive to the presence or absence of a directly bonded proton (13). However, such applications require an accurate determination of the canonical limiting value of the chemical shift of each nitrogen in the imidazole ring of His, in each of the pure tautomers (10). Such determination, based on model compounds is not an easy task since the difference between the chemical shifts of the nitrogens of the imidazole ring of His may vary significantly among different solvents (12). In fact, for the neutral imidazole ring of N^δ1-methylimidazole at 25 °C, values of 83, 96 and 104 ppm (8) have been observed in water, chloroform and benzene, respectively. In addition, it is not yet clear which solvent represents the histidine environment better in a protein. Together, such evidence raises the question about the accuracy of the canonical limiting values of the ¹⁵N chemical shift obtained from model compounds, e.g., such as those listed by Pelton et al. (13) as commonly used in the literature (24).

Consequently, it is our interest here to explore whether the gas-phase DFT-computed ¹⁵N values, from ~35,000 conformations of each tautomeric form of His (27) at high-pH, could provide a standard with which to compare the canonical limiting values of the ¹⁵N chemical shift obtained from model compounds (from here on referred to us as: canonical ¹⁵N values). The existence of possible differences between DFT-computed and canonical ¹⁵N values together with existing experimental evidence will enable us to determine the magnitude of changes of some properties of His residues, such as the tautomeric distribution at high pH, as a function of the adopted ¹⁵N limiting values of the chemical shift.

Method

Computation of the ¹⁵N shielding of the imidazole ring of His at high-pH

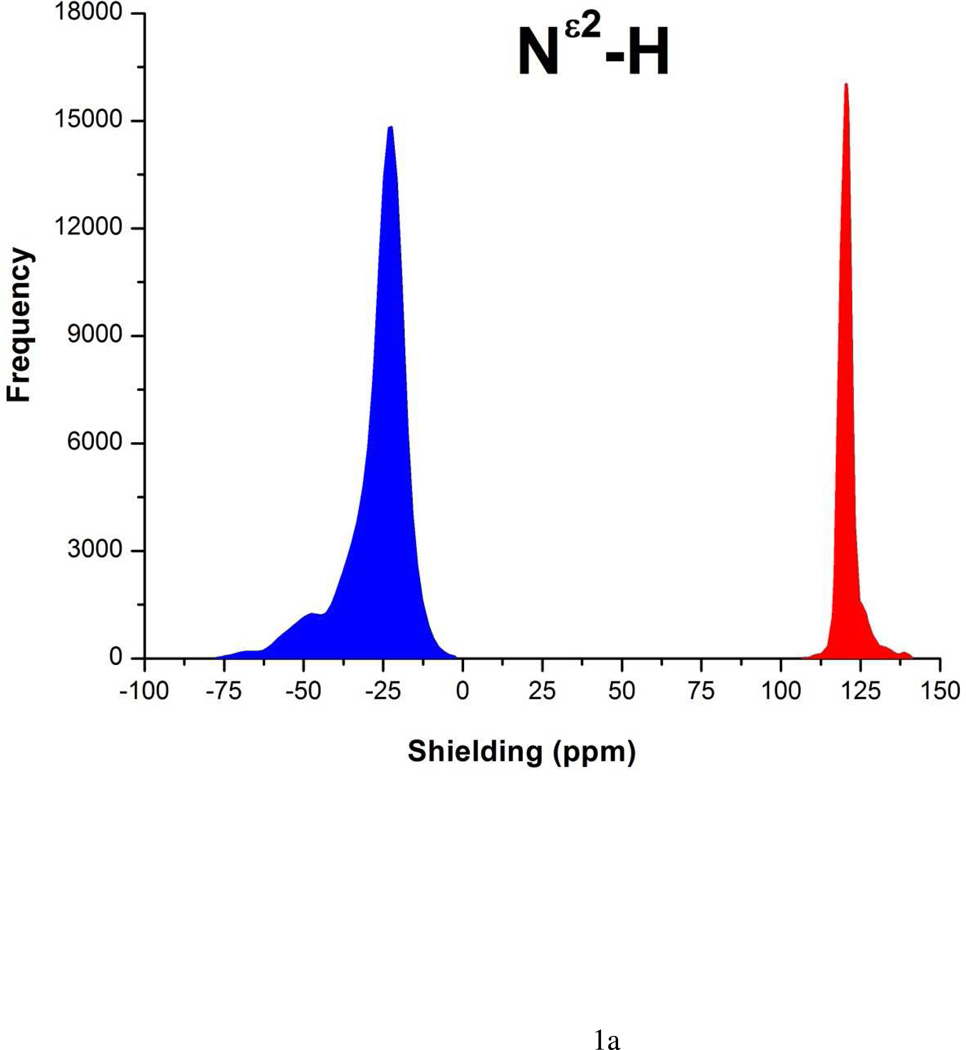
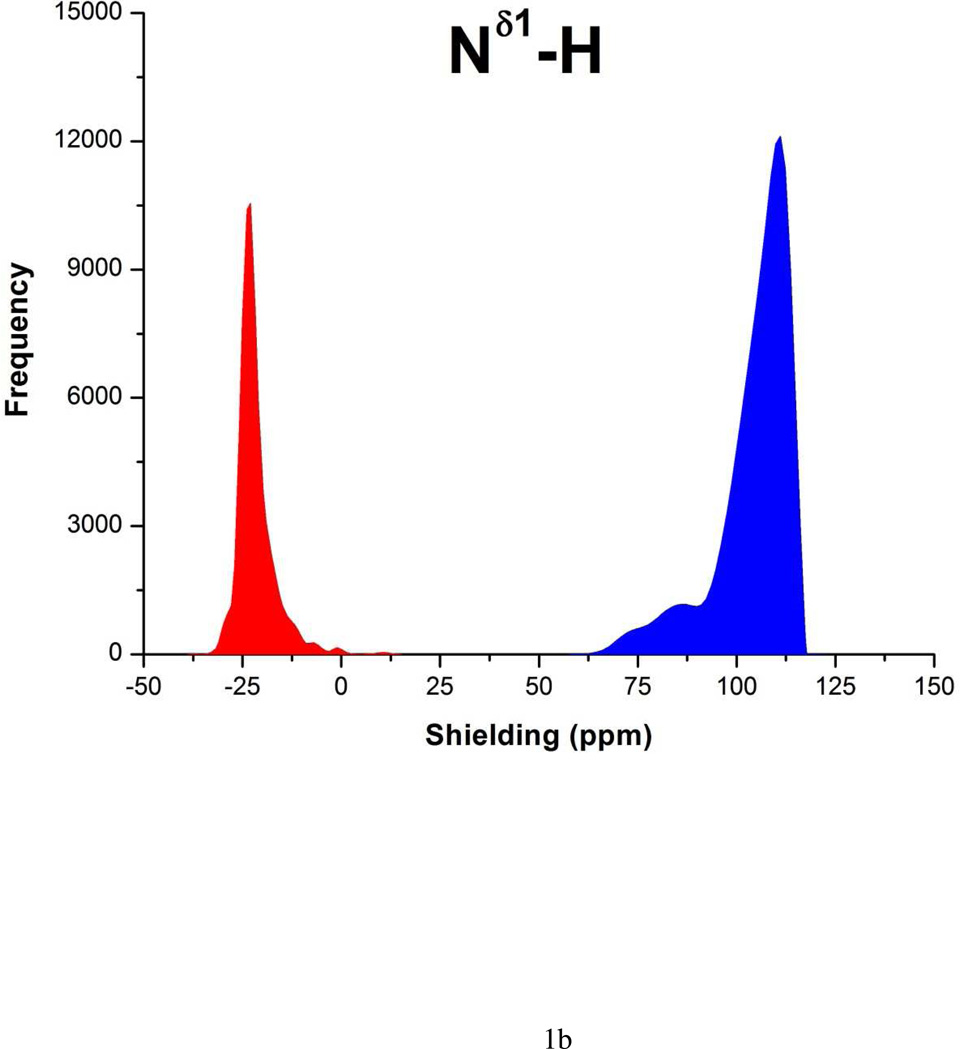
Each form of His is represented as a terminally-blocked model tripeptide with the sequence: Ac-GH^ξG-NMe (27), with H^ξ in the N^δ1-H or the N^ε2-H tautomer form, respectively. The analysis of the charged form, H⁺, was omitted because this form does not exist at high pH. For each tautomer a set of more than ~35,000 conformations, each representing a uniform sampling of the whole Ramachandran map as a function of the ϕ, ψ, ω, χ¹ and χ² torsional angles, was generated. For each of the ~35,000 conformations, the gas-phase, isotropic shielding value of the His residue was calculated with the Gaussian 03 package (30) following the identical procedure that was already used for the computation of the ¹³C^α shielding data-base (27). Finally, the distribution of the computed shielding for each ¹⁵N of the imidazole ring of His was analyzed. For each ¹⁵N nucleus, namely, ¹⁵N^δ1 and¹⁵N^ε2, the histogram of the shielding distribution, among all ~35,000 conformations, is shown in Figure 1a–b, together with the average values and standard deviations.

Figure 1.

(a) The red-filled and blue-filled profiles for the shielding of the ¹⁵N^ε2 and ¹⁵N^δ1 nucleus, respectively, of the imidazole ring of His, in the ¹⁵N^ε2-H tautomer represent the histogram of the ~35,000 DFT-computed shielding distribution from the model tripeptide Ac-GHG-NMe; the corresponding average value and standard deviation of the red-filled and blue-filled profiles are: 121 ± 3 ppm and −27 ± 10 ppm, respectively; and (b) same as (a) with average value and standard deviation of: −22 ± 5 ppm and 105 ± 9 ppm, respectively, for the ¹⁵N^δ1-H tautomer.

Analysis of the computed ¹⁵N shieldings for the tautomeric forms

For each tautomeric form, the average-shielding value, and its standard deviation, for each nitrogen of the imidazole ring of His were computed from the generated ~ 35,000 conformations, and the results are shown in Figures 1a–b. These average values were used to compute the shielding differences between nitrogens of the imidazole ring of His (Δ^ξ values shown in Table 1), which is a common way to analyze ¹⁵N chemical shifts (11). Chemical shift differences are equivalent to shielding differences because of cancelation of the reference value, thereby avoiding any source of error in the reference value (21). Consequently, the nitrogen shielding differences, Δ^ξ = ‖σ_15Nε2| − |σ_15Nδ1‖, with σ denoting the average-shielding and ξ = ε or δ, denoting each of the tautomeric forms of the imidazole ring of His, namely the N^ε2-H and N^δ1-H form, respectively.

Table 1.

Values of the chemical shift difference, Δ^ξ

Δξa	Canonicalb (ppm)	DFT-Computedc (ppm)	Observed (ppm)
Δδ	82	83	79d; 77e; 76f
Δε	82	94	92d; 83e; 83f

^aΔ^ξ = ‖ζ_15Nδ1|−|ζ_15Nε2‖ with ζ denoting the average-shielding (σ) DFT-computed value, shown in the Figure Caption of Figure 1a–b, or alternatively, the observed chemical shift (δ) for each of the imidazole ring nitrogens (13); and ξ = δ or ε denoting each of the tautomeric forms of the imidazole ring of His, namely, the N^δ1-H and N^ε2-H form, respectively.

^bUsing ¹⁵N chemical shift limiting values listed by Pelton et al. (13).

^cFrom average DFT-computed ¹⁵N shielding values (see Figures 1a–b);

^dFrom solid-state NMR, at pH 8.5, from Hu et al. (26);

^eFrom Farr-Jones et al.(12) for histidine at −55 °C at pH 11.2 in Ethanol;

^fFrom Farr-Jones et al.(12) for N^ξ-methylhistidine at 25 °C in H₂O.

Results

Analysis of the differences between nitrogens in the imidazole ring of His: Δ^ξ

From Table 1, we conclude that the following inequality holds: Δ^ε > Δ^δ, if DFT-computed data, or data from model compounds or solid-state NMR, are used. On the other hand, the use of standard (12) canonical ¹⁵N values (see Table 1) gives the following equality: Δ^ε = Δ^δ.

We have also computed the second-order difference as ΔΔ = |Δ^ε − Δ^δ|. In general, use of Δ^ξ values, with ξ = ε or δ, calculated with DFT-computed shieldings agree qualitatively with data from model compounds and solid-state NMR (see Table 1), i.e., all of them predicting ΔΔ = |Δ^ε − Δ^δ| > 0. In particular, DFT-computed and solid-state NMR-data lead to close quantitative agreement, namely ΔΔ = 11 and 13 ppm, respectively. Since observed isotropic ¹⁵N chemical shifts for histidine and imidazole in the solid state do not differ appreciably from those measured in solution (10) the latter result is significant. By contrast, a similar analysis carried out using canonical ¹⁵N values (see Table 1), gives ΔΔ = 0.

Overall, the experimental evidence and DFT-based calculations, but not canonical ¹⁵N values, predict Δ^ε ≠ Δ^δ. The consequences of this finding will be discussed in the next sections.

Determining DFT-computed limiting values of ¹⁵N chemical shifts in the high-pH limit

A question of central importance, that goes beyond the existence of the differences in terms of Δ^ξ or ΔΔ mentioned above, is related to the relevance of such discrepancies; for example, in the prediction of the tautomeric fractions at high-pH. In order to answer this question, we first need to determine a set of DFT-computed limiting values of ¹⁵N chemical shift differences.

The chemical shifts (δ) can be calculated by employing the equation δ = σ_ref – |σ_subst|, where σ denotes the shielding of the reference substance (σ_ref) or the substance of interest (σ_subst), respectively. Use of this definition enables us to find an effective-reference value (σ_ref) with which all DFT-computed average-shielding values can be converted into chemical shifts and, hence, a set of DFT-computed ¹⁵N limiting values of chemical shifts can be determined.

Therefore, in order to compute an effective reference, the following assumption was adopted: the DFT-computed chemical shift for the ¹⁵N^ε2 nucleus (δ_15Nε2), in the N^ε2-H tautomeric form of the imidazole ring of His, is assumed to be the canonical limiting value reported for this nucleus (13), namely δ_15Nε2 = 167.5 ppm (see Table 2). We choose this chemical shift as a starting point because the ¹⁵N^ε2 nucleus shows the lowest standard deviation (3 ppm) among all four DFT-computed ¹⁵N average shielding values (see Figure Caption of Figure 1a–b). Consequently, the effective reference is σ_ref = 288.5 ppm, i.e., computed as σ_ref = (δ_15Nε2 + σ_15Nε2), with σ_15Nε2 = 121 ppm (see Figure Caption of Figure 1a) representing the DFT-computed average-shielding value for the ¹⁵N^ε2 nucleus. Hence, the chemical shift of the ¹⁵N^δ1 nucleus in the N^δ1-H tautomeric form is δ_15Nδ1 = 183.5 ppm; this value was obtained by using the computed average-shielding value (σ_15Nδ1 =105 ppm, see Figure Caption of Figure 1b) together with the above determined effective reference. Up to this point, we have been able to determine the chemical shifts for the protonated ¹⁵N nucleus of the imidazole ring of His in the N^ε2-H and the N^δ1-H tautomeric form, respectively.

Table 2.

Limiting values of ¹⁵N chemical shift at high-pH ^a

Tautomer	Canonical (ppm)		DFT-Computed (ppm)
	15Nε2	15Nδ1	15Nε2	15Nδ1
Nδ1-H	249.5	167.5	266.5	183.5
Nε2-H	167.5	249.5	167.5	261.5

^aThe canonical limiting values are those listed by Pelton et al. (13). See the text for details about the derivation of the DFT-computed limiting values.

The chemical shift for the nonprotonated ¹⁵N nucleus in each tautomeric form can be computed straightforwardly by using the definition of Δ^ξ together with the constraints given in Table 1, i.e., by using the following relations: Δ^δ = |δ_15Nε2 − 183.5| = 83 ppm, and Δ^ε = |δ_15Nδ1 − 167.5| = 94 ppm. As a result, the following chemical-shift values were obtained: δ_15Nε2 = 266.5 ppm and δ_15Nδ1 = 261.5 ppm, i.e., for the nonprotonated nucleus in the N^δ1-H and N^ε2-H tautomeric forms, respectively. Table 2 lists all DFT-computed and the canonical ¹⁵N limiting values, for comparison.

Calculation of the tautomeric fraction, at high-pH, from ¹⁵N chemical shifts

The significance of the use of the DFT-computed rather than the canonical ¹⁵N value is illustrated by calculating the tautomeric fractions for His61 in plastocyanin (24) at high-pH as the average ratio between the tautomeric populations (24), namely as: (P_δ/P_ε) = (δ_ε – δ₀)/(δ₀ – δ_δ) where P_δ and P_ε are the populations of the N^ε2-H and N^δ1-H tautomeric form, respectively; δ_ε and δδ are the corresponding limiting values of the ¹⁵N chemical shift, and δ₀ is the observed ¹⁵N chemical shift at high-pH. It is worth noting that, at high-pH, computation of the ratio (P_δ/P_ε) is equivalent to determining the tautomeric equilibrium constant KT (22), i.e., with K_T = (N^δ1-H tautomer) / (N^ε2-H tautomer), which is 0.25 in aqueous solution (11). Use of the canonical ¹⁵N value led Hass et al (24) to obtain K_T,canonical ~ 0.102, as an average of the 0.096 and 0.108 values obtained for the (P_δ/P_ε) ratio computed from the fits of the ¹⁵N^ε2 and ¹⁵N^δ1 titration curves, respectively. Thus, the computed average K_T,canonical ~ 0.102 would correspond to a fraction of ~0.91 and ~0.09 for the N^ε2-H and N^δ1-H tautomers of His61, respectively. This result was obtained by using chemical shift data, at high pH, from the titration curve of the imidazole ring of His61 (24); namely, by using δ₀ observed values of ~241 and ~175 ppm for the ¹⁵N^δ1 and ¹⁵Nε² chemical shifts values, respectively.

This set of δ₀ observed values (~241 and ~175 ppm) obtained at high-pH can be used to re-compute the average tautomeric equilibrium constant for His61 in plastocyanin by using DFT-computed rather than canonical limiting ¹⁵N values (see Table 2). In this case, we obtain K_T,DFT ~ 0.265, as an average of the 0.086 and 0.443 values obtained for the (P_δ/P_ε) ratio computed by using ¹⁵N limiting values for the N^ε2-H and N^δ1-H tautomeric form, respectively. Hence, the computed average KT,DFT ~0.265 corresponds to a fraction of ~0.79 and ~0.21 for the N^ε2-H and N^δ1-H tautomer, respectively.

Therefore, the commonly-used canonical limiting values of the ¹⁵N chemical shifts lead to an average tautomeric equilibrium constant (~0.102) that differs, by a factor of ~2.6, from the average one computed by using DFT-computed ¹⁵N limiting values (~0.265). The origin of this difference lies in the fact that DFT-computed ¹⁵N limiting values, but not the canonical ones, lead to obtain a very different ratio between the tautomeric populations (P_δ/P_ε) depending on the chosen tautomer. In other words, the DFT-computed, but not the canonical ones, limiting ¹⁵N values are asymmetrical between tautomers (see Table2). As a result, the difference in the equilibrium constants computed by using canonical and DFT-computed limiting ¹⁵N values shows a minimum when only data from the N^ε2-H tautomer are used to estimate the (P_δ/P_ε) ratio. At this minimum, as shown above, K_T,canonical is ~0.096 and K_T,DFT is ~0.086; hence, these fractions lead to a close estimation of the population of the N^ε2-H and N^δ1-H tautomer in solution, namely ~0.92 and 0.08, for the N^ε2-H and N^δ1-H tautomer, respectively.

Overall, considering that (i) the ¹⁵N^ε2 nucleus shows the lowest standard deviation among all DFT-computed ¹⁵N average shielding values (see Figure Caption of Figure 1a–b), (ii) the second-order differences values, ΔΔ, from the DFT-computed shielding, but not from the commonly-used canonical limiting values, are in closer agreement with those obtained with the experimental chemical shift data from model compounds in solution and solid-state NMR; and (iii) the tautomeric predictions computed using canonical and DFT-computed ¹⁵N values for the ¹⁵N^ε2, but not for the ¹⁵N^δ1, nucleus are in close agreement, it is recommended that the equilibrium constant, K_T, computed by using the ¹⁵N limiting values for only the N^ε2-H tautomer be reported. In other words, this option would help to reduce inaccuracies associated with the existing uncertainty in the set of limiting ¹⁵N values (22). As to whether this conclusion depends on the N^δ1-H tautomeric fraction, remains to be proved.

Conclusions

Overall, our results suggest that a considerable difference for the average tautomeric equilibrium constant, K_T, can be obtained if DFT-computed ¹⁵N limiting values rather than canonical values are used. Furthermore, since the DFT-computed, but not the canonical, second-order shielding differences, ΔΔ, are in agreement with those obtained with experimental chemical shift data from model compounds in solution and solid-state NMR, our results also raise concerns about the magnitude of the uncertainty associated with the usual predictions of the tautomeric fractions and, hence, their impact in studies of the mechanism of action of enzymes in which His dynamics may play a central role. To minimize the magnitude of such uncertainty, it is recommended here that the equilibrium constant, and then the tautomeric fractions, computed by using only limiting ¹⁵N canonical or DFT-computed values for the N^ε2-H tautomer be reported.