Population pharmacokinetics of ciclosporin in haematopoietic allogeneic stem cell transplantation with emphasis on limited sampling strategy

Abstract

AIM

To develop a population pharmacokinetic model of ciclosporin (CsA) in haematopoietic allogeneic stem cell transplantation to facilitate a limited sampling strategy to determine systemic exposure (area under the curve [AUC]), in order to optimize CsA therapy in this patient population.

METHODS

The pharmacokinetics of CsA were investigated prospectively in 20 patients following allogeneic haematopoietic stem cell transplantation (HSCT). CsA was given twice daily, as a 3 h i.v. infusion starting at day 1 of the conditioning scheme, and orally later on, when oral intake was well tolerated. Fluconazole was given as antimycotic prophylaxis. Pharmacokinetic parameter estimation was performed using nonlinear mixed effect modelling as implemented in the NONMEM program. A first order absorption model with lag time was compared with Erlang frequency distribution and Weibull distribution models. The influence of demographic variables on the individual empirical Bayesian estimates of clearance and distribution volume was tested. Subsequently two limited sampling strategies (LSS) were evaluated: posterior Bayesian fitting and limited sampling equations.

RESULTS

Twenty patients were included and 435 samples were collected after i.v. and oral administration of CsA. A two compartment model with first order absorption best described the data. Clearance (CL) was 21.9 l h⁻¹ (relative standard deviation [RSD]± 5.2%) with an inter-individual variability of 21%. The central volume of distribution (V_c) was 18.3 l (RSD ± 8.7%) with an inter-individual variability of 29%. Bioavailability (F) was 0.71 (RSD ± 9.9%) with and inter-individual variability of 25% and lag time (t_lag) was 0.44 h (RSD 5.5%). Weight, body surface area, haematocrit, albumin, ALAT and ASAT had no significant influence on pharmacokinetic parameters. The best multiple point combination for posterior Bayesian fitting, in terms of estimating systemic CsA exposure, appeared to be C0 + C2 + C3.

Two selected LSS two time point equations and all selected three and four time point equations predicted de all AUC(0,12 h) within 15% bias and prediction.

CONCLUSIONS

The i.v. and oralcurves were best described with a two compartment model with first-order absorption with lag time. With the Bayesian estimators from this model, the area under the concentration−time curve in HSCT patients taking fluconazole can be estimated with only three blood samples (0, 2, 3 h) with a bias of 1% and precision of 4%.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• The population pharmacokinetics and limited sampling strategies for ciclosporin monitoring have been extensively studied in renal and liver transplant recipients. Little is known about the pharmacokinetics of ciclosporin in patients undergoing haematopoietic allogeneic stem cell transplantation (HSCT).

• It is anticipated that there is a difference in pharmacokinetics in patients after kidney or liver transplantation compared with patients undergoing stem cell transplantation, because of mucositis and interacting drugs (e.g. fluconazole).

• Data on the pharmacokinetics of ciclosporin and the relationship between its systemic exposure, as reflected by the area under the curve (AUC), and the biological effect as graft vs. host-disease (GVHD) prophylaxis and graft vs. tumour (GVT) response are scarce in patients after HSCT.

WHAT THIS STUDY ADDS

• A pharmacokinetic model was developed for orally and intravenously administered ciclosporin, enabling an adequate estimate of the systemic exposure of ciclosporin in patients after HSCT. A limited sampling strategy was tested that may serve as a tool to study the optimum systemic exposure (AUC) of ciclosporin in HSCT to prevent GVHD but establish adequate GVT response and to guide therapeutic drug monitoring.

Introduction

Allogeneic haematopoietic stem cell transplantation (HSCT) has become a well-established treatment modality for the treatment of certain haematological malignancies, solid tumours and acquired or congenital non-malignant disorders [1, 2]. Over the past decade, peripheral blood stem cells have largely replaced bone marrow as the source for HSCT. Pharmacological management of the donor-derived alloreactive immune response plays a central role in reducing the morbidity and mortality of graft vs. host disease (GVHD), which still remains the major cause of toxicity after allogeneic stem cell transplantation.

The most commonly used prophylactic immunosuppressive agent in HSCT is ciclosporin (cyclosporin A, CsA) [3, 4]. The pharmacodynamics and pharmacokinetics of CsA are complex and, as a result, drug exposure is difficult to predict. CsA is extensively metabolized by cytochrome P4503A enzymes in the gut and liver to numerous active and inactive metabolites [5, 6]. P-glycoprotein (P-gp) is the main transporter involved in CsA absorption and disposition [7]. CYP and P-gp activity will contribute to inter-individual variation in pharmacokinetics as well as drug–drug interactions, e.g. with fluconazole. As a result CsA has high intra- and inter-patient pharmacokinetic variability and low, highly variable oral absorption, depending on dose, formulation, disease state and presence of food and bile in the gut [8–11]. CsA is also a potent inhibitor of cytochrome P4503A enzymes, it is highly protein bound and has a narrow therapeutic range. Therefore, therapeutic monitoring of CsA blood concentrations and subsequent adjustment of dosing is mandatory [12]. Despite years of extensive clinical experience with CsA and the development of clinical algorithms for dose adjustments [13], prompt achievement and maintenance of the CsA therapeutic target ranges is still difficult. Most patients require multiple dose adjustments in the early post transplant period. Failure or delay in achieving the blood concentration target can result in adverse reactions such as renal dysfunction, hypertension, hyperglycaemia and central nervous system toxicity, as well as extensive GVHD and poor stem cell engraftment [14–16]. In all, insufficient post transplant immunosuppression is one of the most important determinants of relapse risk through its impact on the potency of an immunologically mediated graft vs. malignancy effect. This is particularly relevant in patients undergoing allogeneic HSCT using a reduced-intensity conditioning regimen, where a graft vs. malignancy effect represents the dominant anti-tumour mechanism [4, 17–22].

Therefore, a model that predicts ciclosporin pharmacokinetics and dose requirements to achieve the desired therapeutic target in an individual HSCT patient would be highly useful. CsA pharmacokinetic studies in HSCT recipients are scarce and most have evaluated only small numbers of subjects [9, 23–28].

It is anticipated that the pharmacokinetics of CsA in patients after kidney or liver transplantation are different compared with HSCT recipients [29]. Co-medication with fluconazole and chemotherapy related mucositis can account for this difference. Therefore, we decided to study the pharmacokinetics of CsA in stem cell recipients after i.v. and oral dosing in order to establish a pharmacokinetic model for Bayesian prediction. Furthermore, we validated a limited sampling method (LSM) for therapeutic drug monitoring which could also be used in future clinical trials.

Methods

Patients

From January 2005 until February 2008, 20 allogeneic HSCT recipients with various haematological malignancies gave their informed consent to participate in the study. Subjects were eligible when aged between 18 and 70 years and were to receive an HLA-matched allogeneic HSCT according to the local HSCT protocol. Non-myeloablative conditioning consisted of fludarabine combined with cyclophosphamide (25 and 500 mg m⁻² i.v. days −5 to −1, respectively) or fludarabine in combination with total body irradiation (TBI) (30 mg m⁻² i.v. days −3 to −1 and TBI 2 Gy day 0 of transplantation). Myeloablative conditioning consisted of the combination of cyclophosphamide with total body irradiation (60 mg kg⁻¹ i.v. days −5 to −4 and 1.67 Gy twice daily days −3 to −1).

Adequate renal and hepatic function was required as defined by serum bilirubin < 50 µmol l⁻¹ and serum creatinine < two times the upper limit of normal or a creatinine clearance > 60 ml min⁻¹ (by Cockcroft & Gault formula [30]). Exclusion criteria included: haemodynamic instability, known hypersensitivity to CsA or one of the components of the (i.v.) formulation (polyethylene glycol, modified maize oil and castor oil)

No transfusion of blood or blood products (albumin inclusive) was allowed on the days of blood sampling. Systemic antimicrobial and antimycotic prophylaxis and therapy was given according to local standard of care (fluconazole 50 mg once daily; ciprofloxacin 500 mg twice daily; valacyclovir 500 mg twice daily; phenethicillin 250 mg four times daily; co-trimoxazole 960 mg twice daily twice weekly). All concurrent medication was recorded.

Study design

The study was conducted in accordance with the Declaration of Helsinki and its amendments, and was approved by the VU University medical center Ethics Committee. Written informed consent was obtained from each patient.

On day 1 of the conditioning scheme, CsA (Sandimmune®, Novartis the Netherlands) in a dosage of 2.5 mg kg⁻¹ was administered by i.v. infusion over 3 h. Blood samples at each time point were drawn into tubes containing ethylene diamine tetra acetate. To identify the most informative sample time points, the ADAPT II software [31] was used with model 2compcl, using the d-optimization analysis provided by the SAMPLE module. Blood samples were taken directly before and at 0.25, 0.5, 1, 1.5, 2.5, 4, 4.5, 6.5, 9, 10 and 12 h after start of the infusion. After start of CsA therapy, dosing was modified to attain trough concentrations between 200–400 µg l⁻¹. To obtain oral absorption profiles a second 12 h curve was sampled after the patient could tolerate oral administration of CsA (Neoral®, Novartis, the Netherlands). Blood samples were taken directly before and at 0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 5, 8 and 12 h after the morning administration. Blood was collected from a peripheral venous cannula or a central venous line of which the first 5 ml were discarded. Blood samples were homogenized, stored at 2–8°C and analyzed within a few days [32].

Drug analysis

CsA concentrations in whole blood were measured by the use of a validated specific fluorescence polarization immunoassay (FPIA) (AxSYM Abbott Diagnostics, Hoofddorp, the Netherlands). The coefficient of variation was less than 10%. The lower limit of quantification (LLOQ) was 80 µg l⁻¹. Results above 800 µg l⁻¹ were diluted with blank whole blood, re-analyzed and the results were corrected for dilution. Accuracy was 96% (400 µg l⁻¹) and precision in the range applied (80–800 µg l⁻¹ CsA) was described by the polynomial function: standard deviation = 1.2009 + 0.1278 ×[CsA]− 0.0005 ×[CsA]²+ 7 × 10⁻⁷×[CsA]³. Compared with other immunoassays the FPIA (AxSYM) has low cross-reactivity towards CsA metabolites: 5.5% (AM1), 13.7% (AM9), 2.1% (AM4n) and 2.5% (AM19) [33].

Pharmacokinetic analysis

All analyses were performed using a nonlinear mixed effects modelling program (NONMEM, version VI, level 2.0, ICON Development Solutions, Ellicott City, MD, USA). The first order conditional estimation method (FOCE) with INTERACTION between inter-individual and residual variability was used throughout. Standard errors for all parameters were calculated using the COVARIANCE option of NONMEM.

The performance of various models was evaluated using both graphical and statistical methods. The minimum value of the objective function (equal to minus twice the log likelihood of the data) was used to determine goodness-of-fit. An increase in the latter is reflected by a decrease in the objective function, and a change >6.6 points was considered a significant improvement (P < 0.01) in goodness-of-fit. Graphical analysis was performed using predicted vs. observed concentrations, individually predicted vs. observed concentrations and predicted concentrations vs. weighted residuals.

Basic pharmacokinetic model

Based on pharmacokinetic studies in renal transplant patients, a two compartment open model was chosen in all cases and the following approaches were tested for describing the absorption process after oral dosing: 1) a zero order input with or without lag time parameter (ADVAN3 TRANS3 subroutine), 2) a first order rate constant with or without lag time (ADVAN4 TRANS3 subroutine), 3) a Weibull distribution, previously proposed for PK transfer modelling and for CsA (ADVAN6 SS6) [34] and 4) an Erlang distribution (ADVAN5 SS5 subroutine) proposed by Rousseau et al. [35]. I.v. administration was modelled as a 3 h infusion in the central compartment.

The entire population was used to estimate population means and coefficients of variation of the pharmacokinetic parameters for CsA. The distribution of individual clearance (CL), absorption rate constant (k_a), oral bioavailability (F), volumes of distribution (V₁ central; V₂ peripheral) and intercompartmental clearance (Q) was assumed to be log-normal, based on the following equation:

in which CLi is the clearance of the i^th subject, CL is the typical value of the clearance of the whole population, and ηi is the intersubject variability of the ith subject (η is assumed to be normally distributed, with a mean of zero and a variance of ω²). A full variance-covariance matrix was estimated for the different distributions of ηi. Residual variability was described by a combined proportional and additional error model.

Covariate model building

In order to establish possible relationships between the pharmacokinetics of CsA and patient characteristics, the following covariates were subsequently tested with respect to their correlation with pharmacokinetic parameters such as CL: weight (WT), body surface area (BSA), co-medication with enzyme inducers (IND) and co-medication with enzyme inhibitors (INH). Covariates were entered individually into the basic population pharmacokinetic model by forward inclusion. Continuous covariates such as patient weight were centred to their median values. For example, the relationship between CL and body weight was described by:

where θ₁ represents CL of a (median) patient with a body weight of 84 kg, and θ₂ is the increase or decrease in CL kg⁻¹ difference in body weight. Dichotomous covariates such as co medication with enzyme inducers (IND) were modelled by:

where θ₁ represents the CL value in absence of inducers (IND = 0) and θ₂ is the change in CL in presence of inducers (IND = 1).

A covariate was included in an intermediate model when its addition to the basic model was both statistically significant (Δ objective function >−6.6, P < 0.01) and relevant. The latter was assumed when the typical value of a parameter changed at least 20% within the observed range of that covariate in the population. Finally, a stepwise backward elimination procedure was performed, in which each of the covariates was deleted sequentially. Again, a covariate was only retained in the model when its influence was statistically significant and relevant (as defined earlier).

The level of significance of those covariates that were included in the model was assessed using a randomization test, in which a large number of data sets was generated based on the null hypothesis (i.e. that the covariate is not related to the pharmacokinetic parameter). Wings for NONMEM (version 405) was used to perform the randomization test [36]. Data sets were generated by random permutation of the empirical distribution of the covariate in the original data set. The final model was applied to these data sets. The distribution of the difference in objective function between models with and without the randomly permutated covariate was obtained and the level of significance calculated. For each significant covariate that remained in the model at least 1000 data sets were generated.

Model validation

Model validation was performed using the bootstrap option of Wings for NONMEM. Bootstrap replicates were generated by randomly sampling 65% from the original data set with replacement. The final model was fitted to over 2000 of these replicate data sets and parameter estimates were obtained. The stability of the model was evaluated by visual inspection of the distribution of the model parameters. Furthermore, the median parameter values and the 2.5–97.5 percentile of the bootstrap replicates were compared with the estimates of the original data set [37].

Posterior Bayesian fitting

The population pharmacokinetic parameters from the final model were individualized for each of the patients after oral dosing, based on their CsA dosing and a single or a combination of measured blood concentrations (0h, 2h, 3h, 5h, 8h, 0 + 2h, 0 + 3h, 0 + 5h, 0 + 8h, 0 + 1 + 2h, 0 + 1 + 3h, 0 + 1.5 + 3h, 0 + 2 + 3h, 0 + 2 + 5h, 0 + 2 + 8h, 0 + 3 + 5h, 0 + 3 + 8h, 0 + 1 + 2 + 3h, 0 + 2 + 3 + 5h, 0 + 2 + 3 + 8h, 0 + 1 + 2 + 3 + 5 + 8 + 12h) according to the maximum a posteriori (MAP) Bayesian fitting method [38], using the the software package MW\Pharm version 3.60 (Mediware, Groningen, the Netherlands). From the individualized pharmacokinetic parameters the area under the CsA blood concentration–time curve (AUC(0,12 h)) was calculated for each combination of measured blood concentrations. Predictive performance of the different combinations of timed concentrations was investigated by calculating the prediction precision and bias according to Sheiner & Beal [39]. Prediction bias was calculated as the mean prediction error (MPE), i.e. the mean of differences between the AUC according to the different methods and trapezoidal AUC. Prediction precision was calculated as the mean absolute prediction error (MAPE), i.e. the mean of the absolute differences between the AUC according to the several different methods and the trapezoidal AUC. Smaller values for MPE and MAPE indicate less bias and greater precision.

Limited sampling strategy equation

Multiple linear regression was performed to estimate abbreviated AUC (dependent variable) and each time point of CsA concentrations (independent variables) that best fitted the CsA AUC(0,12 h). Selected models are those with P < 0.05 for any sampling time, a high correlation coefficient (r² > 0.85) and a maximum of four concentrations. These analyses produced equations of the form AUC = α₁C₁ … +α_nC_n + β, where α_n and β are coefficients and n is the number of samples. Of all resulting equations, those that met the preset selection criteria were considered for further validation.

In the absence of an independent group of patients, the predictive performance of our models was analyzed using the jack-knife method [40]. It is a resampling scheme that uses the equation derived from n− 1 patients to predict the dependent variable of the nth patient. Thus, a slightly different model is used to predict the AUC of each patient. Guidelines suggested by Sheiner & Beal for testing the predictive performance were again followed [39]. All statistical analysis was performed using SPSS software for Windows (version 16.0 SPSS Inc, Chicago, IL, USA). P values less than 0.05 were considered significant.

Results

Data from 20 patients were available and summarized in Table 1.

Table 1.

Demographic data, disease and conditioning regimen

Parameter	Median	Range
n (M/F)	20	13/7
Age (years)	54	37–66
Weight (kg)	84	53–110
BSA (m2)	2.02	1.48–2.43
Serum creatinine (µmol l−1)	91	70–125
Disease
Acute myeloïd leukaemia	7
Non-Hodgkin lymphoma	6
Chronic lymphoblastic leukaemia	2
Other	5
Conditioning regimen
Fludarabine/cyclophosphamide	10
Fludarabine/total body irradiation	6
Cyclophosphamide/total body irradiation	4

A total number of 436 CsA whole blood concentrations were available for pharmacokinetic analysis. Two oral curves could not be obtained because of discontinued consent and discharge of the patient, respectively. Other samples were missing because of transfer (4), discharge (1), clotted peripheral venous cannula (5) and other sampling problems (10). The CsA whole blood 12 h concentration profiles for all patients are shown in Figure 1. After the 2.5 mg kg⁻¹ i.v. dose, the mean AUC(0,12 h) was 8580 ± 2290 µg l⁻¹ h and C_max 1937 ± 497 µg l⁻¹. The mean oral dose (± SD) during the recording of the absorption profile was 2.77 ± 0.81 mg kg⁻¹. The mean non-compartmental parameters of these profiles were: AUC(0,12 h) 7081 ± 1429 µg l⁻¹ h, C_max 1080 ± 284 µg l⁻¹, t_max 2.0 ± 0.6 and C₁₂ 308 ± 121 µg l⁻¹. Correlation between dose normalized AUC(0,12 h, i.v.) and AUC(0,12 h, oral) was weak (r² = 0.298, P < 0.05).

Figure 1.

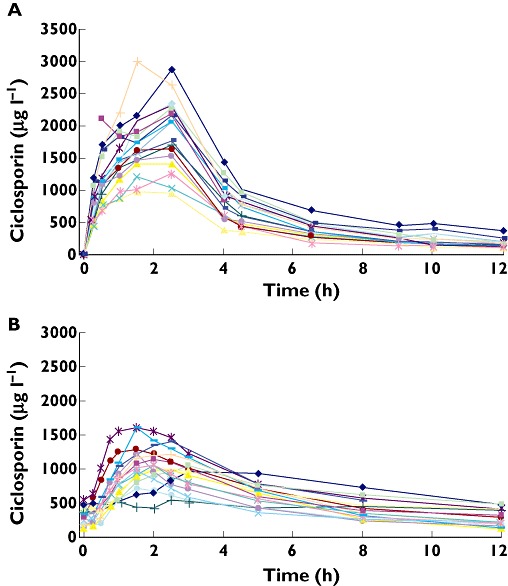
Individual whole blood concentration– time curves of ciclosporin in patients after stem cell transplantation. (A) after i.v. administration of 2.5 mg kg⁻¹ by infusion over 3 h and (B) after oral administration. Each line represents individual patient data

Model building

The results obtained with the different structural models for absorption are represented in Table 2. The likelihood (i.e., the objective function value) suggested that the first order absorption model with lag time was better than a zero-order absorption rate with or without lag time. Pharmacokinetic models using the Weibull and Erlang distributions (with two to five sequential compartments) did not perform better, as shown by both the objective function value and the residuals. Residual variability consisted of a combined additional and proportional error of 65 µg l⁻¹ and 9%, respectively. These values are low, and it is noteworthy that the additional part is close to the LLOQ of the FPIA assay. The mean values of the population parameters estimated with the first order absorption with lag time are reported in Table 3. Good estimation of all the model parameters was obtained: standard error of estimates <15% of mean and <10% for CL, V₁, V₂ and Q.

Table 2.

Comparison of the different absorption models tested

Step	Model tested	Objective function	Residual variability Proportional (%)	Additive (ug l−1)
1	First order absorption	4943	10	46
	First order absorbtion with lag time	4826	9	65
2	Zero order absorption	5135	23	17
	Zero order absorption with lag time	5114	23	22
3	Weibull distribution	4985	21	12
4	Erlang distribution (with two sequential compartments)	4874	5	97
	Erlang distribution (with three sequential compartments)	4999	4	123
	Erlang distribution (with four sequerntial compartments)	5089	3	144
	Erlang distribution (with five sequential compartments)	5114	20	58
	Erlang distribution (with six sequential compartments)	5124	2	113

Table 3.

Final parameters estimates of the pharmacokinetic model of ciclosporin

	Final model		Bootstrap Analysis
	Estimate	RSD (%)	Median	95% CI
CL (l h-1)	21.9	5.2%	21.9	20.3, 23.8
V1 (l)	16.6	8.7%	18	15.9, 20.4
Q (l h-1)	24.2	9.3%	23.6	19.5, 27.8
V2 (l)	59.0	8.8%	58.2	50.7, 68.9
ka (h-1)	0.280	14.6%	0.261	0.206, 0.340
F	0.710	9.9%	0.642	0.562, 0.730
tlag (h)	0.440	5.5%	0.457	0.381, 0.536
Interindividual variability CL (%)	22.2	55	19.9	14.2, 25.3
Interindividual variability V1 (%)	26.9	53	29.1	20.2, 37.7
Interindividual variability Q (%)	28.2	73	26.3	3.0, 38.3
Interindividual variability V2 (%)	30.6	62	29.1	16.4, 48.3
Interindividual variability ka (%)	43.8	66	44.4	28.4, 64.8
Interindividual variability F (%)	25.0	64	25.7	14.1, 35.9
Interindividual variability tlag (%)	18.1	90	27.0	13.3, 48.7
Proportional error (%)	8.8	84%	11.4	7.8, 15.0
Additive error (µg l−1)	65	86%	40	0, 65

CL indicates clearance, V₁ volume of distribution of the central compartment, Q intercompartmental clearance, V₂ volume of distribution of the peripheral compartment, k_a absorbtion constant, F bioavailability, t_lag lag time. 95% CI: 95% confidence interval.

The different covariates were introduced separately into the model. None of the covariates investigated for their influence on CL and V₁ (WT, BSA, INH, IND) proved to be significant.

In Figure 2, the predicted model and individually predicted plasma concentrations are shown. The model based predictions are distributed symmetrically around the line of identity (Figure 2A) clearly showing the power of the model to predict the individual plasma concentrations (Figure 2B).

Figure 2.

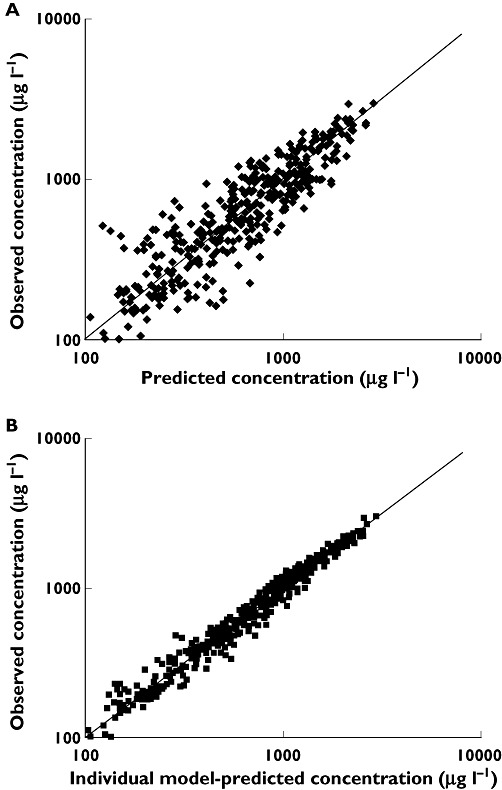
Log-log scatter plots of (A) population model-predicted concentrations (PRED) (µg l⁻¹) vs. observed concentrations (DV) (µg l⁻¹) and (B) individual model-predicted concentrations (IPRED) (µg l⁻¹) vs. DV (µg l⁻¹)

Table 3 lists the results of the bootstrap procedure (n = 2000), presented as median and 2.5–97.5 percentiles. Comparison with the original data set resulted in similar figures, indicating that the model is precise. The only exception was the inter-individual variability in V₂ and Q, which was larger in the bootstrap analysis. Visual analysis of the data showed that all parameters were normally distributed.

Posterior Bayesian fitting

The population parameters obtained with the final model (Table 3) were employed as priors for Bayesian estimation using a limited sampling method. The results for the different combinations of sample times are shown in Table 4. The results of prediction bias (MPE) and prediction precision (MAPE) are presented as a percentage of the target AUC value.

Table 4.

Bias (MPE), precision (MAPE) (%) of different combinations of blood sampling time points used with the population model to estimate the CsA AUC, compared with the AUC calculated according to the trapezoidal method

Time points blood sampling (h)	Bias	(95% CI) (%)	Precision	(95% CI) (%)
0 (with model)	3.5	(−1.9, 8.8)	10.0	(7.0, 13.1)
2	4.4	(−6.5, 15.4)	20.2	(14.2, 26.3)
3	4.9	(−0.8, 10.6)	11.1	(7.7, 14.5)
5	−4.7	(−11.0, 1.7)	11.7	(7.7, 15.7)
8	5.1	(−0.8, 11.0)	10.8	(6.8, 14.8)
0, 2	1.7	(−2.3, 5.6)	6.5	(3.7, 9.2)
0, 3	2.2	(−2.0, 6.3)	7.7	(5.3, 10.0)
0, 5	−2.3	(−7.8, 3.1)	9.2	(5.6, 12.7)
0, 8	−10.6	(−16.5, −4.7)	14.6	(10.8, 18.3)
0, 1, 2	1.3	(−2.6, 5.2)	6.0	(3.2, 8.8)
0, 1, 3	−0.1	(−3.7, 3.6)	5.8	(3.4, 8.3)
0, 1.5, 3	1.6	(−1.2, 4.5)	4.6	(2.6, 6.7)
0, 2, 3	1.0	(−1.4, 3.4)	3.7	(2.1, 5.3)
0, 2, 5	4.1	(1.4, 6.8)	5.7	(3.8, 7.7)
0, 2, 8	1.7	(−0.9, 4.3)	4.4	(2.6, 6.2)
0, 3, 5	7.1	(4.2, 10.0)	8.0	(5.7, 10.3)
0; 3; 8	8.4	(4.7, 12.0)	9.1	(5.9, 12.3)
0, 1, 2, 3	4.6	(2.3, 6.8)	5.9	(4.4, 7.4)
0, 2, 3, 5	4.5	(1.9, 7.1)	5.9	(4.1, 7.8)
0, 2, 3, 8	2.8	(0.4, 5.1)	4.5	(2.8, 6.2)
0, 1, 2, 3, 5, 8, 12	−0.7	(−1.7, 0.3)	1.9	(1.2, 2.5)

The one point approaches including the trough concentrations (C0) have a weak correlation with the trapezoidal AUC(0,12 h). The associated r² values differed from 0.26 (C2) to 0.75 (C3). Two point and three point approaches, such as C0 +C3 (r² = 0.85 [MPE/MAPE 2/8]), C0 +C1 +C3 (r² = 0.88 [0/6]) and C0 +C2 +C8 (r² = 0.94 [2/4]), provided close associations with CsA exposure. Addition of more time points did not significantly improve bias and precision.

The best multiple point combination in terms of estimating systemic CsA exposure appeared to be C0 +C2 +C3 (r² = 0.95 [1/4]), which showed excellent performance with the gold standard AUC(0,12 h). In Figure 3A, the relationship between trough concentrations and the AUC(0,12 h) calculated using the trapezoidal method is plotted. Figure 3B and C illustrate that the AUC is estimated well by the model and that predictive performance improves when three concentration–time points are included. The variation of the actual AUC(0,12 h) was less when estimating the AUC(0,12 h) using any of the models when compared with the estimation of the systemic exposure from the trough concentrations.

Figure 3.

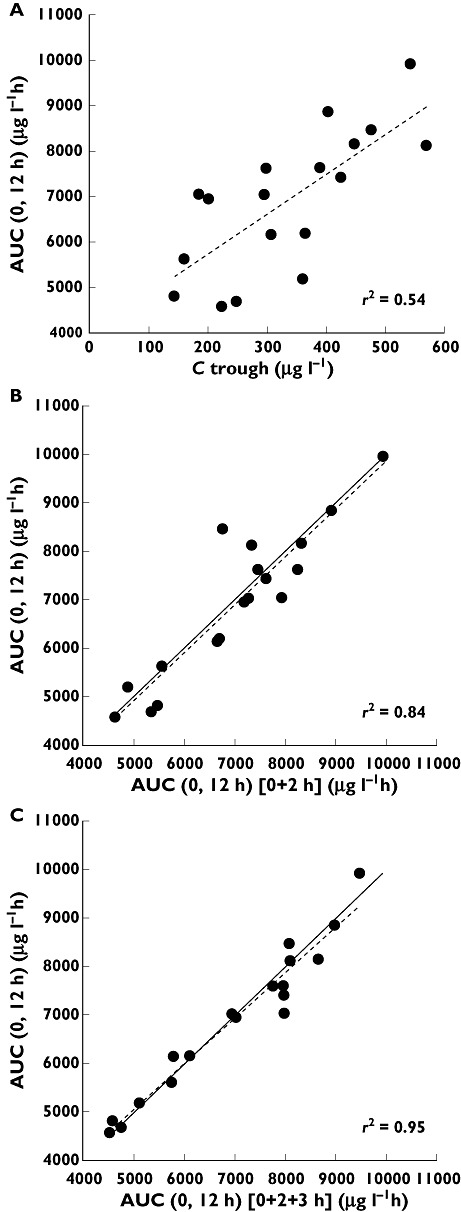
(A) Relationship between C_trough and AUC calculated using the trapezoidal method. Relationship between the Bayesian estimated AUC and blood concentration taken at (B) 0 and 2 h and (C) 0, 2 and 3 and the trapezoidal AUC in 18 subjects. The regression line (dotted line) and line of identity (solid line) are shown

Limited sampling strategy equations

The oral curves of 18 patients were available for analysis. Using linear regression analysis the correlation coefficient (r²) between sampling time points and AUC(0,12 h) was highest (0.77) for the 5 h concentration post dose. The correlation coefficient between trough concentration and AUC(0,12 h) was 0.54 and this was the best single time point correlation up to the third hour post dose. Following subset regression analysis, two, three, and four time point LSS were developed. The correlation coefficient (r²) for the best two (2 + 8 h), three (0 + 3 + 5 h) and four time point (0 + 2 + 3 + 8 h) LSS was 0.98, 0.98 and 0.99, respectively. The predictive performance and percent of profiles within ± 15% precision and bias after jack-knife validation of the LSS equations are shown in Table 5. The two selected LSS two time point equations and all selected three and four time point equations predicted the AUC(0,12 h) within 15% bias and precision.

Table 5.

Predictive performance of the model after jack-knife validation. Bias (MPE), precision (MAPE) (%) and percent of profiles within ± 15% Precision and bias of different combinations of blood sampling time points derived LSS equations, compared with the AUC calculated according to the trapezoidal method

LSS equation for AUC(0,12 h) (µg l−1 h for AUC, µg l−1 for Cx)	Bias	(95% CI) (%)	Precision	(95% CI) (%)	Percent of profiles within ± 15% precision and bias
419 + 6.67 ×C0 + 4.66 ×C3	0.1	(−2.7, 2.9)	3.5	(2.0, 5.0)	100
1197 + 4.32 ×C0 + 6.70 ×C5	0.7	(−6.1, 7.6)	8.2	(4.1, 12.2)	83
284 + 1 ×C1 + 7.97 ×C5	−0.3	(−6.7, 6.0)	8.5	(5.9, 11.2)	94
1106 + 2.60 ×C1 + 8.59 ×C8	0.3	(−6.0, 6.6)	8.2	(5.2, 11.2)	83
−152 + 3.×C2 + 8.86 ×C8	1.2	(−0.8, 3.2)	2.7	(1.6, 3.8)	100
717 + 4.00 ×C3 + 6.06 ×C8	0.4	(−4.4, 5.1)	5.6	(2.7, 8.4)	100
−96 + 5.33 ×C0 + 2.03 ×C2 + 4.91 × C5	−0.3	(−3.8, 3.3)	4.6	(2.8, 6.3)	100
2.62 + 6.03 ×C0 + 4.05 ×C3 + 1.86 ×C5	−0.1	(−2.6, 2.5)	3.0	(1.5, 4.5)	100
426 + 5.02 ×C0 + 4.40 ×C3 + 1.88 ×C8	0.0	(−2.7, 2.6)	3.4	(2.1, 4.7)	100
121 + 5.81 ×C0 + 0.67 ×C2 + 2.85 ×C3 + 2.44 ×C5	−0.3	(−2.8, 2.2)	3.0	(1.4, 4.5)	100
17.6 + 2.45 ×C0 + 1.88 ×C2 + 1.95 ×C3 + 5.59 ×C8	−0.2	(−2.1, 1.7)	1.5	(2.4, 3.3)	100

Discussion

At present, CsA still constitutes the cornerstone of immunosuppressive regimens for the prevention of excessive GVHD in allogeneic stem cell transplant recipients. In addition, recent data have indicated that the incidence of grade II-IV acute GVHD correlates well with the AUC of the CsA blood concentration–time curve [41].

We present the first study in which the pharmacokinetics of CsA were evaluated with mixed effects modelling in allogeneic HSCT recipients after i.v. and oral dosing, resulting in validated models and practical limited sampling strategies. Absorption was best described with a first order model with lag time. Our study does not support the use of the Weibull nor Erlang distribution in describing the absorption of CsA.

Few pharmacokinetic studies on CsA have been performed in HSCT recipients and most have evaluated only very small numbers of patients [9, 24, 42]. Hendriks et al. measured CsA blood concentrations during 24 h to generate a pharmacokinetic profile in 21 haematopoietic AST recipients who were receiving i.v. CsA 1.5 mg kg⁻¹ by 2 h infusion [24]. The dose normalized AUC(0,12 h) found compares well to the AUC(0,12 h) assessed in our study. Schultz et al. studied the pharmacokinetics of oral CsA micro-emulsion (Neoral®) during the first month after bone marrow transplantation, by adding a single 3 mg kg⁻¹ CsA oral dose to the CsA administered by continuous infusion [42]. The concentration−time curve was constructed by subtracting the concentration of i.v. CsA at steady-state (C_ss). The resulting AUC(0,12 h) was 2356 ± 1131 µg l⁻¹ h, which is only 33% of the AUC we report in this study. Dotti et al. measured the pharmacokinetic profile of the oral CsA micro-emulsion (Neoral®) 4 days after changing from continuous infusion to oral administration. The reported mean AUC(0,12 h), C_max and C12 after 2.5 mg kg⁻¹ (three times daily) were respectively 4776 ± 1084 µg l⁻¹ h, 1027 ± 203 µg l⁻¹ and 184 ± 103 µg l⁻¹[9]. The C_max compares well with our data, whereas AUC(0,12 h) and C12 are significantly lower. The routine combination with the CYP3A4 inhibitor fluconazole as antimycotic prophylaxis in our study group can probably explain large difference between our results and those of Schultz et al. [42] and Dotti et al. [9]

The mean clearance found in our study compares well with the study of Serre-Debeauvais et al. in recipients of bone marrow grafts [43]. After i.v. dosing they reported a mean clearance of 23.3 ± 19.19 l h⁻¹. The CsA clearance in our study was also consistent with reported values for renal transplant recipients [44–47]. The absorption rate constant (k_a) we determined, however, was much lower than reported in these studies. Our sampling schedule, including nine samples within the first 3 h of administration (t_max+ 2 SD), made it possible to determine the absorption rate constant and inter-compartmental clearance with high precision.

We developed and validated individualized population models based on C0 +C2 +C3, which accurately reflect the systemic exposure of CsA with excellent precision and bias. Studies on CsA monitoring involving different types of organ transplantation have revealed that trough concentrations are not the best estimators of systemic exposure of this drug [48–50]. although they are still used in most HSCT centres for therapeutic drug monitoring of CsA. This is again demonstrated in our study, as we show that C0 monitoring did not have a good performance in estimating AUC(0,12 h) with or without using LSS equations and limited sampling model (see Figure 3A).

In adult de novo renal and liver transplant patients, C2 monitoring is internationally advocated as the optimal method to monitor CsA (micro-emulsion formulation) [51–54]. Our study does not support this. On the contrary, the C2 time point was inferior to the other single point estimators for AUC(0,12 h). This finding is in line with two other studies in renal and liver transplant patients. Wacke et al. found a weak correlation between C2 and AUC(0,12 h) (r² = 0.333) in renal transplant patients [55] and Langers et al. reported only a slightly better correlation (r² = 0.50) in liver transplant patients. The variation in peak time in our patients is partially responsible for the large variation in C2 concentrations (Figure 1B). Intestinal mucosal damage due to the conditioning therapy could explain the slow absorption in a subset of our patients. As we demonstrated in our results (and has been shown by others [56]), more sampling time points are needed to overcome this variability in calculating an accurate AUC.

At least two samples were needed for an adequate prediction of the AUC(0,12 h) by limited sampling. C0 and C2/C3 (r² = 0.84–0.85 [MPE/MAPE 2/6–8]). Three time points improved the r² further up to 0.95 and MPE/MAPE 1/4 (C0 +C2 +C3). However, adding more data points did not significantly improve the Pearson's coefficient, or bias and precision (Table 4).

Of the various combinations of two time points in the limited sampling equation C2 +C8 showed the strongest predictive value. The difference between three point and four point approaches was minimal as long as a time point ≥ 3 h was included. This interval corresponds to the time required to reach the mean maximum CsA blood concentration plus 2 SD [2.0 + (2 × 0.6 h)]. The highest r² values were found for the combination of C0 +C2 +C3 +C8 (r² = 0.99, [MPE/MAPE – 0.2/2.4]).

Concerning the three point approaches with the population pharmacokinetic model, we support the strong correlation between predicted and measured AUC applying C0 +C2 +C3 as recently published by Langers et al. in liver transplant recipients [56] and Cremers et al. in kidney and simultaneous pancreas-kidney transplant recipients [57]. They reported r² = 0.92 [MPE/MAPE 2/5], r² = 0.96 [−3/11] and r² = 0.93 [−1/6] respectively vs. r² = 0.95 [3/5] in our study. This further supports that therapeutic drug monitoring using three point AUC methods provides a strong prediction of drug exposure in a practical manner.

The correlations with AUC(0,12 h) for both LSS equations and the population model were satisfying with better results for the LSS using three point approaches. The advantage of the use of a pharmacokinetic model over LSS equations is that the model is flexible and no fixed time points are needed in contrast to the rigid equations. By using Bayesian estimation only the exact time of blood sampling is needed to estimate accurate AUC(0,12 h).

The pharmacokinetics of CsA are prone to a high inter-individual variability in various patient populations. The use of limited sampling strategies may improve the dosing efficacy of CsA. Our current population model and Bayesian fitting clearly approximates this goal for our HSCT patients treated with fluconazole. A similar approach performed well in kidney, combined kidney-pancreas as well as liver transplant patients [57, 58]. We anticipate that our model will lead to more stable CsA dosing with less over or under dosing than with simple C0 or C2 monitoring.

Recently, we published a method for analyzing CsA concentration in dry blood spots (DBS) samples [59]. DBS samples are made with capillary blood, obtained from a finger prick with an automatic lancet, eliminating the need for hospital visits for blood sampling. After appropriate validation the DBS sampling may facilitate a new area in fine-tuning CsA dosing in allogeneic stem cell transplantation recipients based on AUC, and makes sampling at 5–8 h post dose more feasible. However, we must emphasize that the model presented in this paper can only be used in the described HSCT population, provided the same immunoassay is used.

In conclusion, we developed a flexible Bayesian individualized limited sampling method for CsA monitoring using three samples without rigid sampling time points. This strategy was accurate, precise and easy to use in daily practice. Future prospective studies with this model are planned, comparing C0 and AUC(0,12 h) and including clinical outcome parameters, such as incidence and severity of GVHD, relapse and laboratory parameters.

Competing Interests

There are no competing interests to declare.