Contributions of Domain-General Cognitive Resources and Different Forms of Arithmetic Development to Pre-Algebraic Knowledge

Abstract

The purpose of this study was to investigate the contributions of domain-general cognitive resources and different forms of arithmetic development to individual differences in pre-algebraic knowledge. Children (n=279; mean age=7.59 yrs) were assessed on 7 domain-general cognitive resources as well as arithmetic calculations and word problems at start of 2^nd grade and on calculations, word problems, and pre-algebraic knowledge at end of 3^rd grade. Multilevel path analysis, controlling for instructional effects associated with the sequence of classrooms in which students were nested across grades 2–3, indicated arithmetic calculations and word problems are foundational to pre-algebraic knowledge. Also, results revealed direct contributions of nonverbal reasoning and oral language to pre-algebraic knowledge, beyond indirect effects that are mediated via arithmetic calculations and word problems. By contrast, attentive behavior, phonological processing, and processing speed contributed to pre-algebraic knowledge only indirectly via arithmetic calculations and word problems.

Little is known about individual differences in the development of competence with algebra. This is unfortunate because, in recent years, consensus has emerged that algebra not only represents a gateway to higher forms of learning in mathematics, science, technology, and engineering, but also is required for successful participation in our workforce (National Mathematics Advisory Panel [NMAP], 2008; RAND Mathematics Study Panel, 2003). Accordingly, passing an algebra course is increasingly required for high-school graduation. Yet, 35% of students fail to complete such a course, and 93% of 17-year-olds cannot solve multistep algebra problems (U.S. Department of Education, 2008). Perhaps due to such difficulty, interest in algebraic cognition among 6- to 12-year-old children has increased in the past decade, with the 2003 RAND report calling for systematic inquiry on this topic. In the present study, we assessed the contributions of domain-general cognitive resources and arithmetic (calculations and word problems) at start of second grade, as well as arithmetic development across grades 2–3, to individual differences in pre-algebraic knowledge at the end of third grade. This is in line with NMAP’s recommendation that, “Longitudinal research is needed to identify early predictors of success or failure with algebra. The identification of these predictors will help to guide the design of interventions that will build the foundational skills needed for success with algebra” (p. 33).

Development of Algebraic Knowledge

Algebra involves symbolizing and operating on numerical relationships and mathematical structures. Algebraic expressions can be treated procedurally, by substituting numerical values to yield numerical results (Kieran, 1990). This suggests that understanding of arithmetic principles involves generalizations that are algebraic in nature, such that algebra warrants a prominent role in early instruction (Blanton & Kaput, 2001; Carraher & Schliemann, 2002; NMAP, 2008). Others (e.g., e.g., Balacheff, 2001; Linchevsky, 2001) suggest an interference effect that makes algebra developmentally inappropriate for young children. Sfard (1991) referred to “a deep ontological gap” (p. 4), whereas Linchevski and Herscovics (1996) used the term cognitive gap (p. 39). Many researchers, however, espouse a third view, closely connected to the first, which supports a connection – if arithmetic instruction is deliberately designed to facilitate the transition (Herscovics & Kieran, 1980).

Underpinning the third perspective is Pillay, Wilss, and Boulton-Lewis’s (1998) model of learning, which incorporated the work of Kieran (1990) to reinterpret the cognitive “cut or gap” in terms of a developmental progression. In this model, the first stage of learning is arithmetic competence: the capacity to operate numerically as well as understanding of operational laws and relational meaning of the equal sign in standard equations (i.e., both sides of the equal sign are the same value). This provides the foundation for a pre-algebraic stage, characterized by understanding of relational meaning of the equal sign to include nonstandard equations, the concept of unknowns in equations, and the concept of a variable. This stage supports development of formal algebraic competence. Pillay et al.’s model is consistent with a connection between arithmetic and algebra, as expressed in the first perspective. It is, however, more central to the third perspective by specifying an intermediary stage that clarifies the nature of that connection, even as the model captures essential foci for measuring the progression from arithmetic to algebra and designing early instruction to support the transition.

For example, research illustrates how conventional instruction (Powell, in press) causes most students to understand the equal sign operationally (Baroody & Ginsberg, 1983; McNeil & Alibali, 2005). Consider the problem 7 + 5 = __ + 3. Common errors are 12 (in which students ignore the operation to the right side of the equal sign) and 15 (in which they add all knowns) (Falkner, Levi, & Carpenter, 1999). Both errors reflect misunderstanding about the equal sign. Such confusion persists into high school (NMAP, 2008) and is associated with difficulty in using algebraic notation to represent word problems (Powell & Fuchs, 2010) and solve linear equations (Alibali et al., 2007; Knuth et al., 2006). This literature illustrates how understanding of the equal sign as a relational symbol represents an important form of pre-algebraic knowledge, which can be encouraged via early instruction.

In the present study, we relied on Pillay et al.’s (1998) model to operationalize third-grade pre-algebraic knowledge in terms of understanding of the equal sign and variables. We extended research on the emergence of pre-algebraic knowledge in two related ways. First, we assessed the extent to which different forms of arithmetic competence are foundational for pre-algebraic knowledge, as reflected in Pillay et al. Second, we assessed the extent to which higher-and lower-order cognitive resources affect pre-algebraic knowledge, beyond effects that are mediated via arithmetic. Kieran (1990) argued that the cognitive demands involved in working with algebraic expressions differ from those involved in operating on numbers, just as Wheeler (1989) noted that algebra involves more symbolic complexity. This suggests direct contributions of higher-level cognitive resources (e.g., nonverbal reasoning), whereas lower-order cognitive processes (e.g., processing speed) may be mediated via arithmetic competence.

Foundational Arithmetic and Cognitive Resources Involved in Pre-Algebraic Knowledge

Present thinking about the role of arithmetic and the cognitive resources involved in algebra is based largely on logical analyses of the principles and content of the two domains. Fluency with calculations may support pre-algebra by reducing demands on working memory to free up attention for the challenges associated with handling nonstandard equations and variables (Geary et al., 2008). Fluency with calculations may also reflect a strong foundation in arithmetic operational laws. At the same time, word-problem skill, a second form of arithmetic, not only incorporates calculations. It also involves two forms of symbolic representations (numerals and language) and reflects understanding of the relationships between known and unknown quantities. In fact, a key source of error in word problems involves transforming problem narratives into algebraic equations (Geary et al., 2008). For example, problem solvers translate, “Mary had 6 more than John,” to M = 6 + J, by recognizing the smaller quantity must increase to equal the larger quantity. Yet, a common error is M + 6 = J. For these reasons, word problems may involve greater symbolic complexity than calculations and rely more on the type of mental flexibility, manipulation of symbolic associations, and maintenance of multiple representations that support pre-algebraic knowledge (e.g., Kieran, 1992; Sfard & Linchevski, 1994). Only a handful of relevant studies exist. Lee, Ng, Bull, Pe, and Ho (2011) and Tolar, Lederberg, and Fletcher (2009) found that arithmetic serves as a platform for algebra. Lee et al., however, used arithmetic word problems as a proxy for pre-algebraic knowledge; Tolar et al. focused on college students; and neither study examined the role of arithmetic word problems in algebra.

Moreover, these and other studies suggest algebraic thinking also relies at least in part on general cognitive resources. Working with 10-year-olds, Lee, Ng, Ng, and Lim (2004) found that the central executive, performance IQ, and literacy predicted concurrent pre-algebraic word-problem skill, although effects were small. Lee et al. (2011) found that pattern recognition and calculations completely mediated the effects of updating (a form of working memory). Tolar et al. (2009) showed that fluency with calculations had stronger effects on algebra than working memory or spatial ability, which nevertheless exerted moderate effects.

Present Study Overview and Hypotheses

In the present study, we measured cognitive resources (oral language, nonverbal reasoning, working memory for numerals, working memory for words and sentences, attentive behavior, phonological processing, processing speed) and two forms of arithmetic skill (fluency with single-digit calculations; skill with arithmetic word problems) at the beginning of second grade. Almost two years later, at the end of third grade, we reassessed calculation fluency (single- and multi-digit numbers) and word problems (more complex problems representing the same problem types assessed at the start of second grade). At the end of third grade, we also assessed pre-algebraic knowledge: understanding of the equal sign (i.e., the ability to solve nonstandard equations with one unknown) and the concept of a variable (i.e., the ability to complete function tables). We applied multilevel path analysis to these data, controlling for variance associated with instruction in the sequence of students’ second- and third-grade classrooms.

Based on Pillay et al.’s (1998) model, we expected early arithmetic competence to be foundational for pre-algebraic knowledge. We specified four hypotheses. First, we anticipated direct paths from second-grade calculation fluency and from second-grade word-problem skill to pre-algebra. To create a stringent test of this hypothesis, we controlled for both forms of third-grade arithmetic competence and for second-grade cognitive resources in the analysis. Second, to consider the effect of arithmetic learning across second and third grade, we hypothesized that the effects of second-grade arithmetic are partially mediated by third-grade arithmetic. Third, because arithmetic word problems involve greater symbolic complexity, we hypothesized that the paths for word problems on pre-algebraic knowledge are stronger than for calculation fluency. Fourth, because third-grade arithmetic incorporates more challenging tasks, we hypothesized that third-grade arithmetic also operates directly on pre-algebra.

In terms of other cognitive resources, we hypothesized that nonverbal reasoning, oral language ability, working memory, and attentive behavior also play key roles in pre-algebraic knowledge. Each of these abilities is important in the early stages of learning new things. Nonverbal reasoning (Fuchs, Geary, et al., 2012), working memory (e.g., Geary & Widaman, 1992; Hitch, 1978; Swanson, 1993), and attentive behavior (e.g., Fuchs et al., 2006; Fuchs, Geary, et al., 2010) predict early calculations and word-problem learning. Language predicts early word-problem learning (e.g., Fuchs, Geary, et al. 2010; Fuchs et al., 2006). Because pre-algebra tasks are novel to third graders, just as early calculation and word-problem tasks are novel for younger students, we hypothesized that the effects of these abilities operate directly on pre-algebra. Second, we also anticipated indirect effects via arithmetic skill across second and third grade, because these domain-general abilities also affect early arithmetic skill and learning. Third, assuming arithmetic is foundational to pre-algebraic knowledge, we hypothesized that the effects of the lower-level cognitive resources frequently associated with arithmetic (phonological processing and processing speed) are mediated via calculation skill.

At a broad level, we were interested in assessing the extent to which concrete skills are foundational to abstract forms of competence, when controlling for a broad range of cognitive resources. We were also interested in which cognitive resources operate directly on symbolic forms of performance and which resources instead exert their effects indirectly via foundational skills. Although we situated these questions in the context of mathematics, findings provide the basis for generating hypotheses in other domains of performance in which individuals progress from concrete to abstract forms of competence.

Method

Participants

Seeking to identify a sample of approximately 300 students, we screened a larger pool of second-grade students on a measure of simple addition problems and a measure of simple word-problems. Using another large normative sample to establish cut-points for low performance, we included all students who scored low on one or both screeners and a random sample of about half the remaining students in each class. We excluded 17 students with standard scores below 80 on both subtests of the Wechsler Abbreviated Intelligence Scale (WASI; Wechsler, 1999). In this way, we identified 309 students in fall of second grade as participants. At spring of third grade, 30 students had moved to schools beyond our reach. Little’s (1988) MCAR test indicated data were missing at random (i.e., there was no identifiable pattern to the missing data) such that cases with incomplete data could be dropped without introducing bias. After dropping cases, 279 students with complete data remained, providing a sample that approximated a representative sample for an urban setting, as reflected in their scores on nationally-normed tests. On the 2-subset WASI (Wechsler, 1999), the mean IQ of these 279 students was 96.23 (SD =12.98). On Wide Range Achievement Test-3 (Wilkinson, 1993), the mean score was 95.05 (SD =12.21) on Arithmetic and 100.80 (SD =15.47) on Reading. On KeyMath-Revised (Connolly, 1998), the mean score was 103.42 (SD =11.00) on Addition, 99.78 (SD = 12.60) on Subtraction, and 106.97 (SD =9.99) on Problem Solving. Of the students, 52.3% were female; 76.0% received subsidized lunch; 54.5% were African American, 33.0% white, 11.1% Hispanic, and 1.4% other; 2.2% had a disability; 5.0% were English language learners. Mean age was 7.59 (SD=0.39).

Cognitive Predictors

Nonverbal reasoning

WASI Matrix Reasoning (Wechsler, 1999) includes pattern completion, classification, analogy, and serial reasoning tasks. Children complete matrices. From each, a section is missing, and the child restores the matrix by selecting from 5 options. For example, an item might show a 2 × 2 grid with the same picture of a box, half of one color and half another color, in three cells and a question mark in the fourth cell. The bottom of the page shows a row of 5 boxes, each with the same colors. The tester instructs the child to say which of the five boxes goes where the question mark is. As reported in the test manual, reliability is .94.

Language

We used two tests of language (r = .88), from which we created a unit-weighted composite variable using a principal components factor analysis. Because the principal components factor analysis yielded only one factor, no rotation was necessary. WASI Vocabulary (Wechsler, 1999) measures expressive vocabulary, verbal knowledge, and foundation of information with 42 items. The first four items present pictures; the student identifies the object in the picture. For the remaining items, the tester says a word for the student to define. Responses are awarded a score of 0, 1, or 2 depending on quality. For example, the tester might say, “What is a tree?,” for which the tester awards 0, 1, or 2 points according to a rubric provided in the test manual; this rubric provides more points for more precise definitions. Testing is discontinued after five consecutive scores of 0. As reported by Zhu (1999), split-half reliability is .86. Woodcock Diagnostic Reading Battery (WDRB) - Listening Comprehension (Woodcock, 1997) measures the ability to understand sentences or passages. With 38 items, students supply the word missing at the end of sentences or passages that progress from simple verbal analogies and associations to discerning implications. For example, the tester might say, “Plants are green, the sky is _____.” (For test security and copyright issues, this is not an actual item.) The test manual provides examples of correct responses to guide the tester’s scoring. Reliability, as reported by the test developer, is .80.

Attentive behavior

SWAN is an 18-item teacher rating scale (Swanson, 2004) that samples items from the Diagnostic and Statistical Manual of Mental Disorders-IV (APA, l994) criteria for Attention-Deficit/Hyperactivity Disorder for inattention (items 1–9) and hyperactivity/impulsivity (items 10–18). Items are rated as 1=Far Below, 2=Below, 3=Slightly Below; 4=Average, 5=Slightly Above, 6=Above, 7=Far Above. We report data for the attentive behavior subscale as the average rating across the nine relevant items. We selected this subscale to index attentive behavior, or the ability to maintain focus of attention. SWAN correlates well with other dimensional assessments of behavior related to attention (www.adhd.net). Coefficient alpha in the present study was .98.

Working memory

We used two dual-task central executive subtests from the Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001). Each has six items at span levels from 1–6 to 1–9. Passing four items at a level moves the child to the next level. At each span level, the number of items to be remembered increases by one. Failing three items terminates the subtest. We used the trials correct score. For Listening Recall, the child determines if each sentence in a series is true; then recalls the last word in each sentence. For example, for a series of sentences (e.g., trees have skin; spoons are sharp; cats meow; ice is cold), the child says true or false. After the last sentence, the child says the final word in each sentence (skin, sharp, meow, cold). (For test security and copyright issues, this is not an actual item.) For Counting Recall, the child counts a set of 4, 5, 6, or 7 dots, each on a separate card. After the least card, the child recalls the number of dots on each of the cards. As per the test developer, test-retest reliability is .91–.93. We opted to include both subtests, rather than creating a composite variable, based on prior work (a) showing that listening recall taps the verbal demands of word problems whereas calculations may derive strength from the specific ability to handle numbers within working memory (Fuchs et al., 2010) and (b) suggesting individual differences in working memory for numbers versus words (Siegel & Ryan, 1989; Dark & Benbow, 1991).

Phonological processing

Sound Matching from the Comprehensive Test of Phonological Processing (CTOPP; Wagner, Torgesen, & Rashotte, 1999) has students match first and last sounds in words. For first sound matching, children are presented with a word and asked which of three words (depicted as pictures) start with the same sound. For last sound matching, children are presented with a word and asked which of three words (depicted as pictures) end with the same sound. After three practice items, the test comprises 20 items. As per the developer, test-retest reliability is .83.

Processing speed

With WJ-III Visual Matching (Woodcock, McGrew, & Mather, 2001), children locate and circle two identical numbers in each row of six numbers. They have 3 min to complete 60 rows. As per the test developer, reliability is .91.

Arithmetic Performance

Second-grade calculations

Math Fact Fluency (Fuchs, Hamlett, & Powell, 2003) incorporates two subtests. Simple Addition comprises 25 addition fact problems with sums from 6 to 12 (two items have an addend of 1; one item has an addend of zero). Students have 1 min to write answers. Percentage of agreement, calculated on 20% of protocols by two independent scorers, was 97.8. Coefficient alpha on this sample was .95.

Second-grade word problems

Following Jordan and Hanich (2000), Word Problems comprises 14 brief word problems involving change, combine, compare, and equalize relationships and requiring single-digit addition or subtraction for solution (i.e., sums of 7, 8, or 9 or subtrahends of 6, 7, 8, or 9; there are no addends or minuends of zero or one; and answers to the subtraction problems range from 2 to 6). The tester reads each item aloud; students have 30 sec to respond and can ask for re-reading(s) as needed. The score is the number of correct answers. A second scorer independently re-scored 20% of protocols, with agreement of 99.8%. Coefficient alpha on this sample was .83.

Third-grade calculations

We combined scores from two calculations tests (r = .72). With Math Fact Fluency (Fuchs, Hamlett, & Powell, 2003), students have 1 min to complete of the 25 single-digit addition problems with sums from 6 to 12, 25 single-digit subtraction problems with minuends from 6 to 12; 25 single-digit addition problems with sums from 5 to 18, and 25 single-digit subtraction problems with minuends from 5 to 18. For each subtest, students have 1 min to write answers. Percentage of agreement, calculated on 20% of protocols by 2 independent scorers, was 98.4. Coefficient alpha on this sample was .95. With the Double-Digit Addition Test and the Double-Digit Subtraction Test (Fuchs et al., 2003), students have 5 min to complete 20 2-digit addition problems with and without regrouping and 5 min to complete 20 2- digit subtraction problems with and without regrouping. Agreement on 100% of protocols by 2 independent scorers was 99.3% and 99.1%; coefficient alpha on this sample was .93.

Third-grade word problems

With the Iowa Test of Basic Skills: Problem Solving and Data Interpretation (Hoover, Hieronymous, Dunbar, & Frisbie, 1993), students respond in multi- choice format to 22 word problems. Six problems require students to find relevant information in graphs or to analyze information without calculations. Of the 16 that require calculations, seven are addition (two with single-digit quantities; one with 3 addends); seven are subtraction (one single-digit quantities; six with 2-digit quantities); four are multiplication; and three are division. (These sum to more than 22 problems because some problems involve multiple steps.) As per the test manual, KR20 is .83–.87 at grades 1–5. On this sample, coefficient alpha was .85.

Pre-Algebraic Knowledge

We operationalized pre-algebraic knowledge as understanding of (a) the equal sign as signaling equivalence of both sides of equations, as reflected in the ability to solve nonstandard equations (i.e., with unknown quantity before the equal sign and/or with operations on both sides of the equal sign), and (b) the concept of a variable, as reflected in the ability to complete function tables. Whereas the second problem type is transparently connected to algebra, our first way of representing pre-algebraic knowledge is rooted in studies (e.g.., Knuth et al., 2006) showing how students commonly misunderstand the equal sign as a one-directional operator (i.e., input on the left results in output on the right of the equal sign) and how such misunderstanding is associated with difficulty in using algebraic notation to represent word problems (e.g., Powell & Fuchs, 2010) and solving linear equations (Alibali et al., 2007; Knuth et al.).

Accordingly, the Test of Pre-Algebraic Knowledge (Fuchs, Seethaler, & Powell, 2009) comprises two types of problems. The first (20 items) involves mathematical equivalence items with letters standing for missing quantities: 18 in nonstandard format (e.g., y + 4 = 9; 1 + 5 = 4 + x; 8 − 4 = 6 − y; 8 − × = 3 + 3); two in standard format (i.e., 1 + 5 = x; 8 − 3 = y). The second problem type (4 items) involves function tables, each of which shows a 2-column table. The first column shows a variable, and the second column shows a function involving that variable; each row shows a value for the variable and the resulting value for the function. In one row, the value of the function is empty; the task is to complete that row (see Appendix for a sample item). The functions are x + 3, y − 6, 2x + 1, and 3y. The tester demonstrates how to complete a problem for each problem type (i.e., to ensure students understand the task demands). For example, for functions, the tester says, “Look at the example at the top of the page. Put your finger on the example, and follow along. In the example, I first see if x equals 5, then x plus 1 equals 6. On the next line, I see if x equals 2, then x plus 1 equals 3. On the next line, I see the blank space, so I’ll come back to that. On the last line, I see if x equals 6, then x plus 1 equals 7. Now, I go back to the line with the blank space. If x equals 8, then x plus 1 equals 9. So, I write a 9 in the blank space.” Testers provide 8 min for students to complete the first problem type; as much time as needed (until all but two students are finished) to complete the other problem type. The correlation between the two problem types was .54. The pattern of results was the same for the two problem types; so we used the total score. Coefficient alpha on this sample was .86.

Procedure

Testers (19 at pretesting; 18 at posttesting) were trained to criterion at each testing occasion and used standard directions for administration.¹ In September of second grade, they administered the calculations and word-problem tests in large groups. In September-October of second grade, they administered the domain-general cognitive measures in three individual sessions. In spring of third grade, they administered the calculations, word problems, and pre- algebraic knowledge measures in small groups. Participants did not receive instruction on solving problems similar to those on the pre-algebraic knowledge measure. All individual sessions were audiotaped; 15% of tapes were selected randomly, stratifying by tester, for accuracy checks by an independent scorer. Agreement exceeded 99%.

Data Analysis and Results

See Table 1 for means, SDs, and zero-order correlations. Distributional estimates of skew and kurtosis were not statistically significant, indicating the assumption of univariate normality was met. Pairwise scatterplots revealed strong linear relations among variables and suggested multivariate normality. No significant outliers (|z-score| > 3.5 SDs from the mean) were identified. We created a variable to indicate the sequence of classrooms in which students were nested across grades 2–3. The intraclass correlation showed this nesting effect explained 12.90% of the variance in pre-algebraic knowledge. We therefore ran a multilevel regression analysis, using the Mplus 6.0 (Muthén & Muthén, 1998–2010) path analysis procedures, in conjunction with the COMPLEX sampling command to control for instructional effects associated with the sequence of classrooms in which students were nested.^{2, 3} The COMPLEX sampling command in Mplus computes standard errors and a chi-square test of model fit taking into account non- independence of observations due to clustering (see Muten & Satorra, 1995). In addition, the Model Indirect command in Mplus (see MacKinnon, 2008) was used to decompose effects to allow estimates of the direct effect of each domain-general cognitive resource and each arithmetic skill on pre-algebraic knowledge; the total indirect effect of each domain-general cognitive resource and each arithmetic skill on pre-algebraic knowledge; and the specific indirect effect of domain-general cognitive resources and arithmetic skills on pre-algebraic knowledge. We began with a saturated path model, with 0 degrees of freedom. In the saturated model, the total amount of variance explained in pre-algebraic knowledge was R² = .58 (S.E. = .04), t = 14.24, p < .001 (no fit statistics are available for saturated models).

Table 1.

Means, Standard Deviations, and Correlations (n=279)

	Raw Score		Standard Score		Correlations
	Mean	(SD)	Mean	(SD)	NV	L	A	WM-S	WM-N	PP	PS	2C	2W	3C	3W
Domain-General
Cognitive Resources
Nonverbal Reasoning (NV)	12.28	(5.71)	48.34	(9.74)
Language (L)	0.17	(0.95)	NA		.23
Attentive Behavior (A)	36.72	(11.87)	NA		.26	.46
Working Memory-Sentences (WM-S)	7.74	(3.55)	NA		.26	.28	.25
Working Memory-Numbers (WM-N)	14.34	(3.39)	NA		.29	.21	.26	.35
Phonological Processing (PP)	15.53	(4.22)	9.47	(1.73)	.32	.27	.40	.31	.13
Processing Speed (PS)	11.39	(2.59)	95.06	(12.93)	.27	.21	.28	.27	.11	.21
Arithmetic Skills
Grade 2 Calculations (2C)	8.60	(4.68)	NA		.19	.22	.32	.21	.12	.27	.34
Grade 2 Word Problems (2W)	7.70	(3.78)	NA		.34	.52	.52	.30	.23	.32	.30	.42
Grade 3 Calculations (3C)	94.15	(30.31)	NA		.35	.31	.52	.21	.26	.39	.34	.59	.47
Grade 3 Word Problems (3W)	13.01	(4.02)	44.27	(15.63)	.41	.59	.56	.38	.29	.43	.31	.43	.62	.54
Pre-Algebraic Knowledge	12.37	(5.11)	NA		.43	.48	.51	.26	.27	.40	.33	.42	.56	.65	.63

Notes: p < .05 for coefficients at or above .118 (2-tail probability). Nonverbal reasoning is WASI-Matrix Reasoning. Language is a composite score across Wechsler Abbreviated Scale of Intelligence (WASI)-Vocabulary subtest and Woodcock Diagnostic Reading Battery-Listening Comprehension. Attentive Behavior is SWAN. Working Memory (WM)-Sentences and WM-Numbers, respectively, are Listening Recall and Counting Recall from the Working Memory Test Battery–Children. Phonological Processing is Comprehensive Test of Phonological Processing-Sound Matching. Processing Speed is Woodcock Johnson III Visual Matching. Grade 2 Calculations is Single-Digit Addition. Grace 2 Word Problems is Story Problems. Grade 3 Calculations is a composite score across Single-Digit Addition Double-Digit Addition and Double-Digit Subtraction Tests. Word Problems is the Iowa Test of Basic Skills- Problem Solving and Data Interpretation. Pre-algebraic knowledge is the Pre-algebraic knowledge Test. Standard scores are mean=100 (SD=15) except Vocabulary and Nonverbal Reasoning (mean=50; SD=10), Phonological Processing (mean=10, SD=3), and Word Problems (normal curve equivalents).

We then trimmed nonsignificant direct paths from the domain-general cognitive resources to pre-algebraic knowledge for the final model. In this trimmed model, from which the direct effects of all cognitive resources except nonverbal reasoning and language were excluded, the total variance explained in pre-algebraic knowledge was R² = .57 (S.E. = .04), t = 14.12, p < .001. Fit statistics were adequate (see Hu & Bentler, 1988): χ2(5, N = 279) = 3.129, p = .68; CFI = .99, TLI = .98; RMSE = .001; SRMR = .006. See Tables 2–4 for statistical values associated with direct and indirect effects. (Indirect effects are effects that are mediated by other variables.) Indirect effects with multiple steps were controlled in the model but they are not reported or interpreted (only 5 of 82 such effects were significant). For this reason, the individual indirect effects in Tables 2–4 do not sum to the total of the indirect effects. See Figure 1 for paths that remained significant in the trimmed model. Direct paths are depicted with solid lines; indirect paths with broken lines. Effects for second- and third-grade arithmetic skills are shown in the large rectangular box in the middle of Figure 1.

Table 2.

Direct and Indirect Effects of Arithmetic on Pre-Algebraic Knowledge (n=279)

Type of Effect	Effect of
	G2 Calculations				G2 Word Problems				G3 Calculations				G3 Word Problems
	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p
Direct	.001	.007	0.11	.913	.147	.053	2.78	.005	.391	.060	6.77	<.000	.176	.060	2.92	.004
Total Indirect	.236	.035	6.77	<.001	.067	.029	2.30	.022	.026	.013	2.01	.045	NA
G2W	.032	.013	2.53	.011	NA				NA				NA
G3C	.160	.030	5.33	<.001	.026	.022	1.18	.239	NA				NA
G3W	.018	.012	1.51	.132	.039	.015	2.60	.009	.026	.013	2.01	.045	NA

b=standardized beta value; G=grade; C=calculations; W=word problems. Grade 2 Calculations is Single-Digit Addition. Grace 2 Word Problems is Story Problems. Grade 3 Calculations is a composite score across Single-Digit Addition Double-Digit Addition and Double-Digit Subtraction Tests. Word Problems is the Iowa Test of Basic Skills- Problem Solving and Data Interpretation. Pre-algebraic knowledge is the Pre-algebraic knowledge Test

Table 4.

Direct and Indirect Effects of Working Memory-Numbers, Phonological Processing, and Processing Speed on Pre-Algebraic Knowledge (n=279)

Type of Effect	Effect of
	Working Memory-Numbers				Phonological Processing				Processing Speed
	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p
Direct
Total Indirect	.052	.029	1.76	.078	.099	.029	3.37	.001	.089	.028	3.22	.001
via G2C	.000	.000	0.05	.961	.001	.007	0.11	.913	.002	.015	0.11	.914
G2W	.001	.007	0.20	.839	.002	.008	0.29	.770	.006	.007	0.83	.408
G3C	.042	.021	1.99	.047	.048	.019	2.58	.010	.026	.019	1.37	.171
G3W	.004	.008	0.50	.615	.016	.011	1.40	.161	.002	.008	0.30	.762

G=grade; C=calculations; W=word problems. Nonverbal reasoning is WASI-Matrix Reasoning. Language is a composite score across Wechsler Abbreviated Scale of Intelligence (WASI)-Vocabulary subtest and Woodcock Diagnostic Reading Battery-Listening Comprehension. Attentive Behavior is SWAN. Working Memory (WM)-Sentences and WM-Numbers, respectively, are Listening Recall and Counting Recall from the Working Memory Test Battery–Children. Phonological Processing is Comprehensive Test of Phonological Processing-Sound Matching. Processing Speed is Woodcock Johnson III Visual Matching. Grade 2 Calculations is Single-Digit Addition. Grade 2 Word Problems is Story Problems. Grade 3 Calculations is a composite score across Single-Digit Addition Double-Digit Addition and Double-Digit Subtraction Tests. Word Problems is the Iowa Test of Basic Skills- Problem Solving and Data Interpretation. Pre-algebraic knowledge is the Pre-Algebraic Knowledge Test.

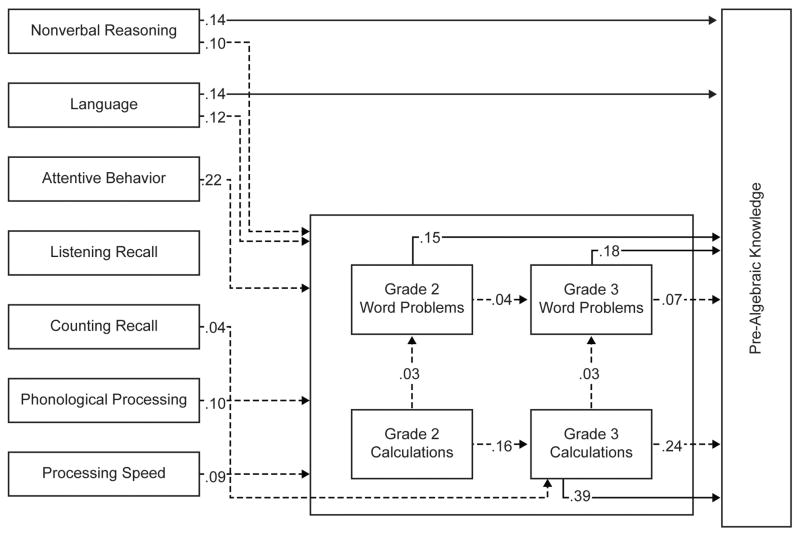
Figure 1.

Trimmed model showing significant direct (solid lines) and indirect (broken lines) effects on pre-algebraic knowledge. Abilities in the first column were measured at beginning of second grade, as was the case for second-grade calculations and word problems. Pre-algebraic knowledge was measured in the spring of third grade, as was the case for third-grade word problems and calculations.

To help readers interpret information presented in this figure and the tables, we explain effects for second-grade word problems (the left-most upper box inside the large rectangle). The direct path from second-grade word problems is the solid line running from word problems to pre-algebra, with a path coefficient of .15. This direct effect is also shown in column 5/row 1 of Table 2. The total indirect effect for second-grade word problems, mediated by third-grade word problems and third-grade calculation fluency, is shown in the broken line running from third-grade word problems to pre-algebra, with a path coefficient of .07. This indirect effect is also shown in column 5/row 2 of Table 2. The remaining rows in column 5 of Table 2 provide information on each of the individual 1-step indirect effects for second-grade word problems. There was one individually significant indirect effect, which occurred via third-grade word problems. This is shown in Figure 1 and Table 2 as .04.

Role of arithmetic competence

See large rectangular box in Figure 1 and Table 2. In the remainder of this paper, numbers in parentheses are path coefficients. We hypothesized direct paths from second-grade calculation fluency and from second-grade word problems to pre- algebra. The direct effect for second-grade word problems was significant; the direct effect for second-grade calculations was not. Respective path coefficients were .15 and .00 (nonsignificant effects are not shown in Figure 1).

To consider the effects of learning in arithmetic skill across grades 2–3, we hypothesized that the direct effects of second-grade arithmetic are partially mediated by third-grade arithmetic. The effects of second-grade calculation skill were in fact entirely mediated; the path coefficient for the total of the direct effects was .24. This total indirect effect was largely explained by improvement in calculation skill across grades 2–3, with the effect of second-grade calculations mediated by third-grade calculations (.16). There was, however, an additional individually significant indirect effect for second-grade calculations, which was mediated via second-grade word problems (.03). For second-grade word problems, the total of the indirect effects on pre- algebra was also significant (.07). Only one individually indirect effect was significant, indicating the partial mediation occurred largely via improvement in word problems across grades 2–3 (.04).

Because third-grade arithmetic incorporates more challenging tasks, we also hypothesized that third-grade calculations and third-grade word problems exert direct effects on pre-algebra. Direct effects were identified for calculations and word problems (.39 and .18). In the case of calculations, there was also an individually significant indirect effect, mediated by third-grade word problems (.03).

Role of domain-general cognitive resources

See Figure 1 and Tables 3 and 4. In terms of domain-general cognitive resources, we hypothesized that nonverbal reasoning, oral language ability, working memory, and attentive behavior exert a direct effect on pre-algebra. We also anticipated that these abilities operate indirectly via arithmetic skill, because these abilities also affect early word problems and calculation skill as well as their development over time. For nonverbal reasoning and language, the direct effect and the total of the indirect effects were significant. Respective direct effect path coefficients were .14 and .14; the total indirect effect path coefficients were .10 and .12. Therefore, the overall effects of these two higher-level abilities were substantial, with some portion of the effect occurring directly on pre-algebra and another portion mediated through arithmetic. In the case of nonverbal reasoning, individually significant indirect effects occurred via third-grade calculations (.04) and third-grade word problems (.02). For oral language, individually significant indirect effects occurred entirely via word problems, at second grade (.04) and at third grade (.05)

Table 3.

Direct and Indirect Effects of Nonverbal Reasoning, Language, Attentive Behavior, and Working-Memory Sentences on Pre-Algebraic Knowledge (n=279)

Type of Effect	Effect of
	Nonverbal Reasoning				Language				Attentive Behavior				Working Memory-Sentences
	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	p	path	S.E.	b/S.E.	P
Direct	.137	.044	3.13	.002	.135	.061	2.21	.027
Total Indirect	.097	.032	3.06	.002	.116	.033	3.48	.001	.218	.041	5.34	<.001	.009	.031	0.29	.771
Via G2C	.000	.002	0.11	.917	.000	.003	0.10	.918	.001	.010	0.11	.914	.000	.003	0.11	.915
G2W	.010	.010	1.94	.051	.044	.018	2.49	.013	.035	.015	2.32	.021	.009	.009	1.04	.299
G3C	.044	.022	1.98	.047	.001	.021	0.05	.962	.096	.024	4.01	<.001	−.030	.020	−1.52	.129
G3W	.023	.012	1.99	.047	.052	.019	2.74	.006	.025	.014	1.82	.067	.018	.010	1.84	.065

G=grade; C=calculations; W=word problems. Nonverbal reasoning is WASI-Matrix Reasoning. Language is a composite score across Wechsler Abbreviated Scale of Intelligence (WASI)-Vocabulary subtest and Woodcock Diagnostic Reading Battery-Listening Comprehension. Attentive Behavior is SWAN. Working Memory (WM)-Sentences and WM-Numbers, respectively, are Listening Recall and Counting Recall from the Working Memory Test Battery–Children. Phonological Processing is Comprehensive Test of Phonological Processing-Sound Matching. Processing Speed is Woodcock Johnson III Visual Matching. Grade 2 Calculations is Single-Digit Addition. Grace 2 Word Problems is Story Problems. Grade 3 Calculations is a composite score across Single-Digit Addition Double-Digit Addition and Double-Digit Subtraction Tests. Word Problems is the Iowa Test of Basic Skills- Problem Solving and Data Interpretation. Pre-algebraic knowledge is the Pre-Algebraic Knowledge Test.

Contrary to hypotheses, no significant direct effect was identified for either form of working memory, and the total of the indirect effect was also not significant. In the case of working memory for numbers, one individual indirect effect was significant: Mediation occurred via third-grade calculations (.04). For attentive behavior, although the direct effect was not significant, the total of the indirect effects was (.22). Much of this indirect effect occurred via third-grade calculations (.10). An additional individually significant indirect effect operated via second-grade word problems (.04).

Finally, assuming arithmetic is foundational to pre-algebra, we hypothesized that the effects of lower-level cognitive resources frequently associated with arithmetic (phonological processing and processing speed) are mediated via arithmetic skill. Accordingly, although the direct effects of these variables were not significant, the total of the indirect effects were (.10 for phonological processing and .09 for processing speed). For phonological processing, the individually indirect effect via third-grade calculations was significant (.05). For processing speed, individually significant indirect effects occurred via multiple steps representing a combination of calculation and word-problem skill and learning.

Discussion

Arithmetic and domain-general cognitive resources made important contributions to individual differences in pre-algebraic knowledge. Together, they accounted for nearly 60% of the variance, similar to results of other individual difference studies focused on predicting calculations or word-problem development (e.g., Fuchs, Geary, et al., 2010).

The Role of Domain-General Cognitive Resources

Based on Pillay et al.’s (1998) learning model, we expected early arithmetic competence to be foundational for pre-algebraic knowledge and hypothesized direct paths from second-grade calculation fluency and from second-grade word problems to pre-algebra. We controlled for both forms of third-grade arithmetic skill and for second-grade cognitive resources to create a stringent test of the hypothesis and found the direct effect was significant for second-grade word problems but not second-grade calculations. Individual differences in second-grade calculation fluency did predict pre-algebra scores, but these effects were entirely mediated. Much of the indirect effect occurred via third-grade calculation fluency, indicating calculation learning predicts pre-algebra. In a similar way, superior learning of word problems predicted stronger pre- algebra performance. Therefore, we conclude that an individual’s capacity to learn early arithmetic forecasts and supports insights into algebra.

We also assumed arithmetic word problems involve greater symbolic complexity than arithmetic calculations. A larger role for nonverbal reasoning and oral language in word problems, compared to calculations, has been documented (e.g., Fuchs et al., 2006, 2008, 2010), perhaps because word problems involve two forms of symbolic representations (numerals and language), understanding of relationships between known and unknown quantities, and transformation of problem narratives into algebraic equations. We therefore hypothesized that the cognitive demands in pre-algebra are closer to word problems. Although the direct path for second-grade word problems was stronger than for second-grade calculations, the pattern was reversed at third grade. And the total indirect effects of second-grade calculations were stronger than the indirect effects of second-grade word problems; yet, a portion of calculation’s indirect effects was mediated by word problems. In these ways, results indicate an important role for both forms of early arithmetic skill or learning in supporting pre-algebra.

These results lend credence to Pillay et al.’s (1998) model, which posits that arithmetic competence provides the foundation for pre-algebra. Finding that arithmetic predicts individual differences in the pre-algebraic stage provides support for the view that arithmetic involves generalizations that are algebraic in nature (Carraher & Schliemann, 2002; NMAP, 2008), rather than creating an interference effect (Balacheff, 2001; Linchevsky, 2001). At the same time, results indicate a third view that suggests the connection between arithmetic and algebra is strengthened when early instruction is designed to facilitate the transition (e.g., Herscovics & Kieran, 1980). Therefore, infusing arithmetic instruction with an emphasis on unknowns, variables, and relational understanding of the equal sign, in line with Pillay et al., may enhance pre-algebraic knowledge and further strengthen the connection between arithmetic and algebra.

The Role of Domain-General Cognitive Resources

In terms of domain-general cognitive resources, we expected nonverbal reasoning, oral language ability, working memory, and attentive behavior, each of which predicts the rate of learning new things, to play key roles in pre-algebraic knowledge. Findings partially support these hypotheses. Direct effects on pre-algebra occurred for nonverbal reasoning and language, indicating the cognitive demands involved in working with algebraic expressions differ from those involved in operating on numbers (Kieran, 1990). As expected, additional effects for both abilities were mediated via arithmetic. A mix of calculation and word-problem skill mediated the effects of nonverbal reasoning, but the individually significant mediation effects for oral language occurred exclusively via word problems. This suggests nonverbal reasoning is a robust index of learning potential, whereas the effects of oral language are more circumscribed, affecting learning more closely contextualized in language. Across nonverbal reasoning and oral language (i.e., constructs frequently included in intelligence tests), findings corroborate the importance of intelligence in school learning (e.g., Deary et al., 2007).

We also expected direct effects for attentive behavior and working memory, given their importance in learning challenging new tasks. These abilities seem important due to the attentional, planning, and sequencing demands of identifying and testing number replacements for variables and in handling operations on both sides of the equal sign. It was surprising, therefore, that neither direct effect uniquely predicted pre-algebra. The total indirect effect for attentive behavior was, however, significant, and was largely mediated by third-grade calculations. So in working on the pre-algebra tasks, attentive behavior appears active during the calculation phase of problem solving, not in deciphering how to set up calculation problems. Future work should explore this hypothesis.

In terms of working memory, the absence of significant total indirect effects was surprising, given that the direct effect also failed to materialize. Lee et al. (2001) found the effects of updating were completely mediated by arithmetic and pattern recognition. Other studies suggest a relation between working memory and algebra (e.g., Ayres, 2006; Case, 1978; Cooper, & Sweller, 2005; Pawley et al., 2005). One specific indirect effect was significant: The effect of working memory was mediated by third-grade calculations. As with attentive behavior, this suggests working memory is active during the calculation phase of problem solving. Given a large literature showing that working memory supports learning, readers should use caution when interpreting the lack of direct effect. Future studies should continue to explore its role in algebra while controlling for other cognitive resources and different forms of arithmetic performance and while contrasting ways of operationalizing working memory (e.g., inhibition and updating; Miyake & Shah, 1999). We predict that individual differences in working memory will emerge as a predictor of individual differences in performance on more complex algebra tasks.

Finally, we hypothesized that phonological processing and processing speed, lower-level cognitive resources frequently associated with arithmetic, operate only indirectly via arithmetic. Accordingly, only the total of the indirect effects, were significant; neither direct effect was. We had expected these indirect effects to accrue via calculations more than word problems. This was true for phonological processing, which may support calculations as students count to pair problem stems with answers. Effects of processing speed, however, were mediated by multiple- step effects involving a mix of calculations and word problems. Perhaps deriving correct answers to calculation problems, in and outside of word problems, depends on efficient processing to hold the pairing of problem stems and answers before they are lost from working memory.

How Arithmetic and Domain-General Abilities Support Pre-Algebraic Knowledge

These results, in combination with prior studies (e.g., Falkner et al., 1999; McNeil, 2007; McNeil & Alibali, 2005; Perry, Church, & Goldin-Meadow, 1988; Rittle-Johnson & Alibali, 1999; Sherman & Bisanz, 2009), provide the basis for generating a scenario by which arithmetic and domain-general abilities work together to support pre-algebraic knowledge. In terms of relatively simple nonstandard equations (e.g., 6 = 2 + x), students may begin by locating the equal sign to derive a meaningful equivalency statement (i.e., 6 is the same 2 + x). This initial step seems critical. Failing to focus on the equal sign suggests an operational understanding of its meaning, leading many students to add the given numbers (6 + 2) to derive an answer of 8. This was a frequent error in the present study, as revealed in previous work (e.g., Falkner et al., 1990). After establishing the equivalency meaning of the equation, students locate the letter and interpret it as a missing quantity, which they must replace with a number to make the equivalency statement true. Understanding a letter can stand for a missing number requires pre- algebraic knowledge, but students may also deduce that an unknown, in the context of a mathematical statement in which the equal sign and operator are provided, stands for some number. Such insight may be supported by skill with word problems, which center on the relationship between known and unknown numerical values. It is also likely that, in the absence of explicit school instruction on the equal sign or unknowns (as suggested by McNeil et al., 2006), these two steps (i.e., interpreting the equal sign and inferring the letter stands for a missing numerical value) represent symbolic challenges that invoke nonverbal reasoning and oral language abilities, which are associated with overall intelligence.

Once students have constructed meaning for the nonstandard equation in these ways, they must determine which number replaces the unknown in a manner that makes the equivalency statement true. Students may do this in a variety of ways. They may engage in a trial and error process perhaps supported by estimation that invokes their nonverbal reasoning ability (e.g., if 2 plus some number is the same as 6, the missing number is between 2 and 6). Instead, they may rely on their number knowledge (i.e., 6 can be decomposed into 2 and 4), which is associated with nonverbal reasoning (Fuchs, Geary, et al., 2012). Alternatively, they may directly retrieve the relevant answer that has been committed to long-term memory via phonological processing and processing speed strengths, as already described. Or they may use procedural counting strategies they deduced over time, supported by nonverbal reasoning (these are rarely taught explicitly in school; Fuchs, Powell, et al., 2010). For example, they might use the relatively sophisticated min strategy (3, 4, 5, 6, to determine there are 4 counts between 2 and 6), thereby figuring the numerical distance between the sum and the known addend. This engages phonological processing to count and processing speed/attentive behavior to ensure problem resolution before decay sets in.

The sequence of steps may be similar but more complicated as nonstandard equations become more complex and the nature of the symbolic as well as lower-level challenges increase. For example, y + 4 = 5 + 2 involves an extra calculation step, and it increases the difficulty of interpreting the relational meaning of the equal sign. In fact, many students in our study failed to grasp the meaning of the equal sign in the context of this equation (even when they succeeded with the more simple 6 = 2 + x). They added all three givens to produce an answer of 11 (also see Falkner et al., 1990; McNeil & Alibali, 2005; Perry et al., 1988). The equation 5 − 2 = y − 1 not only adds another calculation step and creates additional complexity in the relational meaning of the equal sign, but also involves the conceptually and procedurally more difficult subtraction operation. A common error in our study was 3, which students derived by ignoring −1 for which they presumably could attach no meaning. The complexity of subtraction in the context of nonstandard equations is also illustrated by the more simple 3 = y − 4, for which a common error was 1 (in which students subtract the two givens, wherever they occur in the equation).

Nonstandard equations are fundamentally different from the function task, although some conceptual and procedural features apply across tasks. Important commonalities are that students must recognize that a letter stands for an unknown numerical value and understand relationships between knowns and unknowns. They must also rely on arithmetic and related cognitive processes to replace the known with the correct numerical value. Key differences include the following. Students must deduce the implied equal sign: as in the problem shown in the appendix, x + 3 is equal to or “the same as” each value in each row under that column. Students must also know or deduce the concept of a variable, in which the value of x + 3 changes in a predictable way (an increase of 3) as the value of x changes. This transparently involves nonverbal reasoning; it may also rely in part on oral language facility, in which such deductions are mediated by inner language. These pre-algebraic insights may also be supported by skill with word problems, which involve relationships between known and unknown numerical values.

Limitations and Conclusions

Although our predictors captured a substantial portion of the variance in pre-algebraic knowledge, a figure similar to findings in other individual difference studies in mathematics, 43% of the variance remained unexplained. Considering additional higher-order cognitive resources, such as other forms of working memory (e.g., inhibition and updating; Miyake & Shah, 1999), 3-D spatial visualization (Tolar et al., 2009), and analogical or inferential reasoning (e.g., Holyoak & Thagard, 1997), may produce insights into additional mechanisms that support the transition from arithmetic to pre-algebraic knowledge.

In interpreting findings, readers should also consider limitations. First, our measure of pre-algebraic knowledge assessed solving unknowns in nonstandard equations and identifying unknowns in function tables. Other methods for operationalizing pre-algebra may produce different results. Future work should contrast strategies. Second, although we included a large set of domain-general cognitive resources, we measured each construct with a particular measure. Including multiple measures to permit use of latent constructs is preferable, and this should be pursued. Third, we oversampled low income and African American children, which limits external validity. Findings do, however, pertain to vulnerable populations for whom success with algebra may represent a means for reducing racial and economic disparities. Fourth, we noted unknowns in equations with x, instead of boxes or blanks as in previous studies with this age group. Although we explained to participating children that x stands for the unknown, readers should note this variation. Finally, conclusions about causality should be avoided because, although predictive relations were examined, our methods are at root correlational.

These limitations notwithstanding, findings suggest, at a broad level, nonverbal reasoning and oral language ability operate directly on more symbolic forms of performance, even as they contribute to ongoing learning of more concrete skills. Other types of cognitive resources exert their effects on symbolic forms of performance indirectly via the concrete skills. Moreover, concrete skills play a foundational role in abstract forms of competence, even when the effects of a broad range of cognitive resources are controlled in the analysis. In the present study, we identified these relations in the context of mathematics. But findings may also provide the basis for generating hypotheses in other domains of performance in which individuals progress from concrete to abstract forms of competence. In comprehending text, for example, results suggest that direct and indirect effects of foundational components of reading skill (decoding and word- recognition skill), higher-order cognitive resources (nonverbal reasoning and oral language ability), and lower-order cognitive resources (phonological processing, rapid automatized naming ability) (see Perfetti, Landi, & Oakhill, 2005).

In terms of the present study’s specific focus, present findings, derived from an individual differences perspective, supplement experimental studies (e.g., McNeil & Alibali, 2005), quasi-experiments (e.g., Baroody & Ginsberg, 1983; Blanton & Kaput, 2005; Powell & Fuchs, 2010), and case studies (Capraro et al., 2007) to contribute to a small but growing literature on the transition from arithmetic to a pre-algebra stage. Results indicate an important role for domain-general resources, which are difficult to modify. So it is reassuring that calculation and word-problem skill also appear to play important foundational roles in pre- algebra. To circumvent some of the problematic effects created by deficits in domain-general cognitive resources, schools should strengthen mathematics instruction to enhance calculation and word-problem skill. Moreover, as represented in the third view on the connection between arithmetic and algebra, infusing arithmetic instruction with an emphasis on unknowns, variables, and relational understanding of the equal sign, as per the Pillay et al. (l998) model, may ease the transition to pre-algebra, even as it further strengthens the connection between arithmetic and algebra.

Appendix A: Sample Test Item

Test of Early Algebraic Cognition: Example of Function Problem Type

X	X + 3
8	11
1	4
7
3	6