In Vivo Photoacoustic Tomography of Total Blood Flow and Potential Imaging of Cancer Angiogenesis and Hypermetabolism

Abstract

Blood flow is a key parameter in studying cancer angiogenesis and hypermetabolism. Current photoacoustic blood flow estimation methods focus on either the axial or transverse component of the flow vector. However, the Doppler angle (beam-to-flow angle) is needed to calculate the total flow speed, and it cannot always be estimated accurately in practice, especially when the system’s axial and lateral resolutions are different. To overcome this problem, we propose a method to compute the total flow speed and Doppler angle by combining the axial and transverse flow measurements. The method has been verified by flowing bovine blood in a plastic tube at various speeds and Doppler angles. The error was experimentally determined to be less than 0.3 mm/s for total flow speed, and less than 15° for the Doppler angle. In addition, the method was tested in vivo on a mouse ear. We believe that the proposed method has the potential to be used for cancer angiogenesis and hypermetabolism imaging.

Introduction

As a hallmark of cancer, angiogenesis is often activated to support uncontrolled tumor cell growth by increasing blood flow (1). Such increase in blood flow is also crucial for cancer hypermetabolism, because glycolysis of cancer cells is much less efficient than aerobic respiration of normal cells (1). Volumetric blood flow measurement is important to understanding the tumor microenvironment and developing new means to treat cancer. By seamlessly combining optical and ultrasonic waves, photoacoustic microscopy (PAM) has proven powerful for in vivo cancer angiogenesis and hypermetabolism research (2-5). In PAM, a nanosecond pulsed laser beam is focused into the biological tissue to generate wide-band ultrasonic waves, which are detected by a focused ultrasonic transducer placed outside the tissue.

Raster scanning and piecing together the depth-resolved 1D images (A-lines) yield high-resolution tomographic images. The spatial resolutions of PAM are either optically or acoustically determined, depending on the depths targeted (6). Our studies here were performed on optical-resolution PAM. Unlike other high-resolution pure optical or ultrasonic imaging modalities, PAM takes advantage of both rich optical absorption contrast and weak ultrasonic scattering, and thus yields high-contrast, high-resolution images with relatively deep penetration (6). By spectrally unmixing contributions from various endogenous or exogenous chromophores, PAM is capable of anatomical, functional, and molecular imaging (6,7). Hemodynamic parameters pertinent to cancer angiogenesis and hypermetabolism such as vessel density, vessel length, vessel tortuosity, total hemoglobin concentration (C_Hb), oxygen saturation of hemoglobin (sO₂), blood flow rate, and metabolic rate of oxygen (MRO₂), have been measured by PAM. In particular, blood flow measurement using the photoacoustic method has drawn increasing attention because of the excellent signal-to-noise ratio (SNR) provided by hemoglobin. Compared with the structural imaging of cancer angiogenesis, blood flow imaging can provide functionality information about these new vessels. Only those vessels with flowing blood can contribute to tumor hypermetabolism.

So far, photoacoustic flow measurements have focused on either the axial (8-11) or transverse (12-16) component of the flow vector. However, to quantify the total flow vector, the Doppler angle (angle of the flow direction relative to the axis of the received acoustic wave) is needed. The Doppler angle can be estimated by tracing the vessel centerline either manually or automatically in a volumetric image. In practice, however, volumetric information is not always available, as in the case of M-mode imaging. In addition, despite the additional time required for volumetric imaging, accurate estimation of the Doppler angle is challenging if the system’s resolutions are insufficient. Here, using PAM, we propose a simple method for measuring total flow and the Doppler angle by combining the axial and transverse flow measurements. Briefly, the axial flow speed is estimated from the phase shift between consecutive Hilbert transformed pairs of A-lines (17). The sign of the phase shift provides the axial flow direction. The transverse flow speed is quantified from the bandwidth broadening via the Fourier transformation of sequential A-lines (14). The transverse flow direction can be measured by bi-directional scanning (14). We first verified this method by flowing bovine blood in a plastic tube (inner diameter: 200 μm) at different total speeds (0–7.5 mm/s) and Doppler angles (30–330°). Then, in a mouse ear, we measured the total flow speed and Doppler angle in vivo.

Materials and methods

Theory

Inspired by previous work in ultrasound imaging (18) and optical coherence tomography (17), we use the following formula to compute the axial component v_a pixelwise:

$$v_a=\frac{1}{2\pi }\times \frac{c}{T}\times \frac{\Delta \varphi }{f_0},$$ [1]

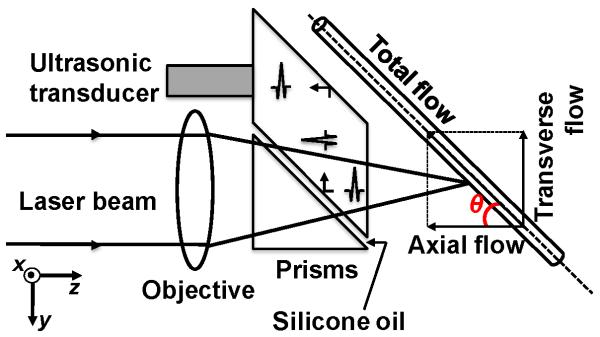
where c is the speed of sound in water (1500 m/s), T is the time interval between the two consecutive A-lines acquired in M-mode, Δφ is the phase shift in each pixel between two consecutive A-lines, and f₀ is the central frequency of an ultrasonic transducer. The phase shift Δφ is quantified via the Hilbert transformation. The sign of Δφ provides the axial flow direction, where positive Δφ means a flow towards the ultrasonic transducer and vice versa. The axial flow velocity v_a is related to the total flow velocity v through v.cos(θ), where θ is the Doppler angle (Fig. 1).

Figure 1.

Schematic of the total flow measurement by photoacoustic microscopy. θ: Doppler angle.

It has also been demonstrated that the transverse flow component v_t, which equals v.sin(φ), can be estimated by (14,19,20)

$$v_t=k\cdot \frac{B_d\cdot c\cdot F}{W\cdot f_0},$$ [2]

where B_d is the bandwidth broadening, and F and W are the focal length and diameter of the ultrasonic transducer, respectively. k is an experimentally determined calibration factor, which is 0.5 for the round-trip pulse-echo Doppler ultrasound system (19). For a PAM system with confocal alignment but different optical and acoustic focal sizes, k mostly accounts for the discrepancy in the two foci. In the case of the optical-resolution PAM (OR-PAM) used in this study (21), shown in Fig. 1, where the optical focusing (~5 μm) is much tighter than the acoustic focusing (~45 μm), B_d mainly comes from the PA amplitude fluctuation caused by particles passing through the optical focal zone. Therefore, k is mostly determined by the beam geometry of the optical focusing and equals 0.02 here. Several other minor factors, such as Brownian motion, particle size and shape, and velocity distribution across the focal zone may contribute to B_d. Since all these bandwidth broadening mechanisms have a linear dependence on the mean transverse velocity (8), their contributions can also be incorporated into k. The transverse flow direction can be measured by bi-directional scanning, as long as the transverse flow is not perpendicular to the scanning line (14). If the transverse flow has a positive projection along the positive scanning direction, we define it as a positive flow, and vice versa.

From the axial and transverse flow components, the Doppler angle θ can be derived as θ=tan⁻¹(v_t /v_a), which ranges from 0° to 360°. Since the inverse tangent covers angles ranging only from −90° to 90°, θ needs to be adjusted according to the flow direction. In Matlab, function tan2 can be used instead of tan to account directly for the flow direction. The total flow speed v is computed by $v=\sqrt{v_a^2+v_t^2}$.

Optical-resolution PAM

The improved OR-PAM (Fig. 1) used throughout this study has proven capable of non-invasively imaging microvasculature using endogenous contrast with high spatial resolution (lateral resolution ~5 μm; axial resolution ~15 μm; penetration depth ~1.2 mm) (21,22). Briefly, a tunable dye laser (CBR-D, Sirah) pumped by a Nd:YLF laser (INNOSAB, Edgewave, 523 nm) produced short pulses with an energy of ~80 nJ that were focused by a microscope objective lens (Olympus 4×, NA=0.1) into the object. Ultrasonic detection was achieved through a spherically focused ultrasonic transducer (V2012-BC, Panametrics-NDT, central frequency: 75 MHz), which was placed confocally with the objective. A newly designed ultrasound/light splitter, composed of a thin layer of silicone oil sandwiched between a right-angle prism and a rhomboid prism, increased the detection sensitivity by 18 dB (22). The motion controller provided the trigger signals for laser firing, data acquisition, and raster scanning. The three-dimensional data was acquired by two-dimensional raster scanning of the sample for lateral resolution in combination with time-resolved acoustic detection for depth resolution. Unless otherwise specified, all the flow measurements were performed at 590 nm, with a pulse repetition frequency (PRF) of 3 kHz. When measurement of the transverse flow direction was needed, the motor was scanned bi-directionally with a speed of ~0.3 mm/s and a step size of 0.1 μm along the central line of the tube. Each A-line contained 200 data points sampled at 200 MHz. Because the step size was 0.1 μm on the fast axis and 2.5 μm on the slow axis, a flow image of 1×0.5 mm² in our in vivo study consisted of 10000×200 pixels. With the laser rep rate of 3 kHz, the data acquisition took ~11 minutes.

Flow phantom

Defibrinated oxygenated bovine blood (B-A8775, Materials Bio, hematocrit: 44%) was used for the flow phantom. The blood flowed in a transparent plastic tube (508-001, Silastic, inner diameter ~200 μm), driven by a syringe pump (BSP-99M, Braintree Scientific) with a 5 mL syringe (Multifit; Becton, Dickinson & Co). Two experiments were performed using this phantom. First, by changing the pumping speed, the mean flow speed was adjusted from 0 to 7.5 mm/s, with a step size of 0.25 mm/s, while the Doppler angle was fixed at 30°. Second, by mounting the tube on a goniometer stage (GN05, Thorlabs), the Doppler angle was adjusted from 30° to 330° with a step size of 30°, while the mean total flow speed was fixed at 1.0 mm/s. If we take the blood density as 1060 kg/m³ and the blood viscosity as 3×10⁻³ kg/(m·s) at room temperature, the Reynolds number was estimated to be far less than 1. Therefore, the flow in the tube was considered to be laminar (23). It is worth mentioning that the 1/e penetration depth of light at 590 nm in oxygenated blood is ~130 μm, which is greater than the radius of the plastic tube.

Animal experiment

The left ear of an adult, 8-week-old nude mouse (Hsd: Athymic Nude-Foxl^NU, Harlan Co.; body weight ~20 g) was imaged in vivo. During data acquisition, the animal was held steady with a dental/hard palate fixture, and kept still by using a breathing anesthesia system (E-Z Anesthesia, Euthanex). An area of 1.0×0.5 mm² at the base of the ear was chosen for total flow measurement. A bi-directional scan was performed over this area to measure the transverse flow direction. Oxygen saturation was then imaged on the same area with 584 nm and 590 nm optical wavelengths. After the experiment, the animal recovered naturally and was returned to its cage. All experimental animal procedures were carried out in conformance with the protocol approved by the Animal Studies Committee at Washington University in St. Louis.

Signal processing

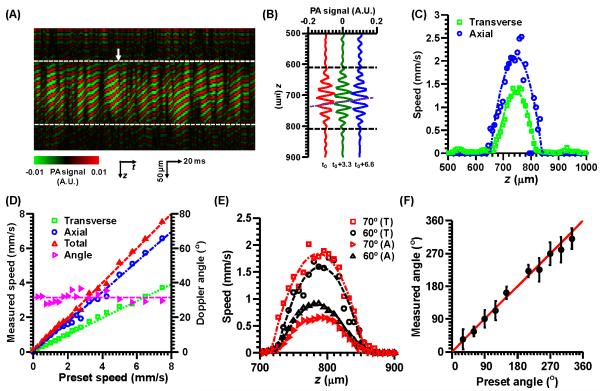
In the phantom studies, 3200 consecutive A-lines were acquired at each position across the tube (M-mode). For axial flow measurement, each A-line was passed through a digital band-pass filter centered at 75 MHz, with a −6 dB bandwidth of 20%. A moving smoothing operation was then performed over each eight sequential A-lines to increase SNR. Fig. 2(A) is a typical M-mode image across the center of the tube, with a Doppler angle of 30° and mean total flow speed of 1.25 mm/s. Fig. 2(B) shows three representative A-lines with a time interval of 3.3 ms. The axial flow speed profile was then calculated from the average phase shift between two consecutive A-lines via Eq. [1] after each A-line was Hilbert transformed. For transverse flow measurement, the original data without filtering was used. The transverse flow was quantified along the lateral direction at each depth, where the bandwidth was computed via the Fourier transformation (13,14).

Figure 2.

Total flow measurement on bovine blood flowing in a plastic tube (diameter: 200 μm). (A) An M-mode image of the tube with a Doppler angle of 30° and mean total flow speed of 1.25 mm/s after passing through a digital filter. The dashed lines indicate the top and bottom boundaries of the tube. (B) Three representative consecutive A-lines with a time interval of 3.3 ms, where t₀ is indicated by the arrow in (A). The horizontal dashed lines indicate the top and bottom boundaries of the tube. The oblique dashed line shows the phase shifts among these A-lines. (C) Transverse and axial speed profiles from (A). (D) Measured transverse, axial, total flow speeds as well as the Doppler angle versus the preset total flow speed. (E) Measured axial and transverse flow speed profiles, with the same total flow speed (mean: 1.0 mm/s) but different Doppler angles (60° and 70°). T, transverse; A, axial. (F) Measured Doppler angle as a function of the preset value. Error bars: standard deviations.

A laminar flow model was used to fit the flow speed profiles along the axial and transverse directions of the tube (24):

$$v(x,z)=v_{\max }(1-\frac{(x-{x_0}^2)+{(z-z_0)}^2}{R^2}).$$ [3]

Here, x and z are the transverse and axial coordinates, respective, (x₀ , z₀) are the tube center coordinates, R is the tube radius, and v_max is the flow speed at the tube center. While (x₀ , z₀) and R can be measured directly from the cross-sectional image of the tube, v_max is the unknown parameter to be fitted for.

The flow processing for the in vivo experiment was the same as that for the phantom study, except that a 1.0×0.5 mm² area instead of only a cross-section was imaged. The absolute C_Hb and sO₂ were computed using the previously published acoustic spectral method (25) and multi-wavelength method (26), respectively.

Results

For the first phantom study, representative axial and transverse flow profiles calculated from Fig. 2(A) are shown in Fig. 2(C). The measured mean axial and transverse speeds were 1.10 ± 0.09 mm/s and 0.65 ± 0.02 mm/s, respectively. The measured mean total flow speed is 1.28 ± 0.09 mm/s, and the measured Doppler angle is 30.6 ± 3.0°, which agrees with the preset value of 30°. Fig. 2(D) shows the measured mean axial, transverse, and total flow speeds as well as the Doppler angle as a function of the preset speeds. The Doppler angle was not calculated at zero flow speed. From the results, the measured speeds agree well with the preset speeds, and the calculated Doppler angles average 31.0 ± 2.7°. The speed measurement errors are less than 0.3 mm/s.

For the second phantom study, Fig. 2(E) shows representative axial and transverse flow profiles with the same mean total flow speed of 1.0 mm/s but two different Doppler angles (60° and 70°). The weighted mean axial and transverse speeds at 60° measure 0.45 ± 0.03 mm/s and 0.80 ± 0.03 mm/s, respectively, yielding a total flow speed of 0.92 ± 0.03 mm/s and a Doppler angle of 60.6 ± 1.9°. The weighted mean axial and transverse speeds at 70° measure 0.33 ± 0.02 mm/s and 0.92 ± 0.10 mm/s, respectively, yielding a total flow speed of 0.98 ± 0.09 mm/s and a Doppler angle of 70.3 ± 2.3°. Furthermore, the measured Doppler angles as a function of preset angles are shown in Fig. 2(F), which shows good agreement, within 15°.

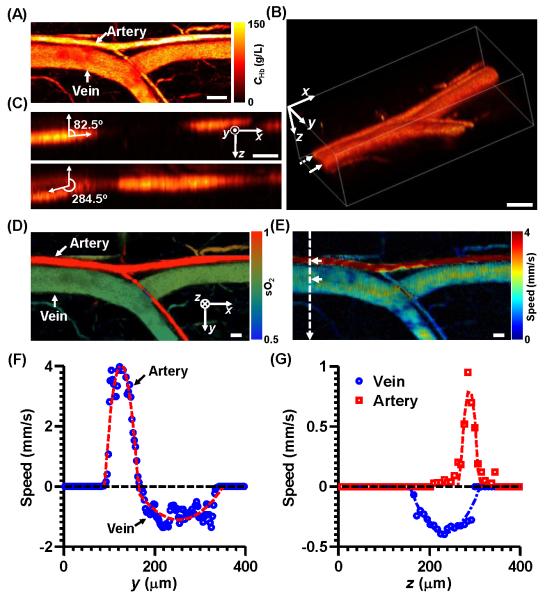
For the in vivo experiment, a typical artery-vein pair at the base of a nude mouse ear was imaged [Fig. 3(A)]. The morphology indicates that the thicker vessel of the pair is the vein, which is confirmed by the sO₂ measurement [Fig. 3(D)]. The volumetric rendering [Fig. 3(B)] shows that the Doppler angles of the artery and vein at the proximal ends were approximately 82.5° and 255.5°, respectively [Figs. 3(C)]. The maximum projection of total flow speed is shown in Fig. 3(E), where the artery has faster flow than the vein. The transverse speeds at the centers of the artery and vein were 3.9 ± 0.25 mm/s and 1.1 ± 0.20 mm/s, respectively, as shown in Fig. 3(F). The transverse flow directions show that the blood in the artery indeed flowed from the proximal end to the distal end, and flowed in the opposite direction in the vein. The axial speeds at the centers of the artery and vein were 0.9 ± 0.25 mm/s and 0.4 ± 0.02 mm/s, respectively, as shown in Fig. 3(G). The axial flow directions show that the blood flowed towards the transducer in the artery, but away from the transducer in the vein. Based on the above information, the total flow speeds at the centers of the artery and vein were 4.0 ± 0.25 mm/s and 1.2 ± 0.19 mm/s, respectively. The Doppler angles at the centers of the artery and vein were 77.0 ± 3.6° and 250.0 ± 3.5°, respectively, which were consistent with the measurements from the volumetric image.

Figure 3.

Multi-parametric PAM of a mouse ear. Scale bar: 100 μm. (A) Maximum amplitude projection of the total hemoglobin concentration image of an artery-vein pair in the mouse ear. C_Hb: total hemoglobin concentration. (B) Volumetric rendering of the same area as in (A). (C) Sagittal cross-section images of the artery (top) and vein (bottom), indicated by the dashed and solid arrows in (B), respectively. (D) sO₂ image of the same area. (E) Total flow speed image of the same area. (F) Transverse speed profiles along the dashed line in (E). Positive transverse flow direction: from left to right. (G) Axial speed profiles along the depth direction at the centers of the artery and vein, indicated by the arrows in (E). Positive axial flow direction: towards the ultrasonic transducer.

Conclusions and discussion

We have demonstrated a method for measuring both total flow velocity and Doppler angle using PAM. By Combining blood flow information with other anatomical and functional parameters such as vessel cross-sections, C_Hb and sO₂, we can quantify the metabolic rate of oxygen (MRO₂) for cancer hypermetabolism studies (27). The advantage of this method is simplicity: No system modification or additional data acquisition is required to use our existing PAM. Both the axial and transverse flow components are measured in M-mode. Collating the A-lines side by side yields a 2D matrix. The axial direction of this matrix (column) is called the fast axis (depth), whereas the lateral direction (row) is called the slow axis (time). The columns are Hilbert transformed to compare the phases for the computation of the axial flow. The rows are Fourier transformed to quantify the bandwidth for the computation of the transverse flow.

In general, both axial and transverse flow directions should be measured to determine the total flow direction. Because blood can only flow along the blood vessels, only one of the two directions is required to be measured as long as the blood vessel can be resolved precisely. However, when there is no axial flow and the transverse flow direction is perpendicular to the bi-directional scanning, four-directional scanning is required.

In theory, the maximum measurable axial and transverse flow speeds are 60.0 mm/s and 21.2 mm/s, respectively, limited by the 3 kHz PRF (10,14,17). The minimum measureable axial and transverse speeds are ~0.1 mm/s, determined by the PRF and SNR (10,14,28). In our studies, since the PRF can be as slow as 1 Hz at the expense of imaging speed, it is the SNR that limits the minimum measureable speeds.

With the imaging depth of 1.2 mm, it is challenging to apply optical-resolution PAM for deep cancer imaging. The current system and method can be used for primarily at least three types of cancers. The first type is skin cancer such as basal cell carcinoma, squamous cell carcinoma and malignant melanoma. Skin cancer generally develops in the epidermis (the outermost layer of skin, usually less than 1.0 mm thick), so a tumor can be well imaged by our method. The second type is gastrointestinal (GI) tract cancer such as esophagus cancer, stomach cancer and intestine cancer. Since most GI tract cancers occur in the epidermal layer of the lumen surface, our method can be applied to imaging these cancers by incorporating it with endoscopic PAM. The third type is the internal organ cancers such as prostate cancer and liver cancer after xenotransplanted to the superficial sites such as skin and ear. Furthermore, the well-developed techniques of dorsal skinfold chamber and skull window can also help utilize our method to image these types of xenotransplanted cancers.