Bayesian analysis of matrix normal graphical models

Abstract

We present Bayesian analyses of matrix-variate normal data with conditional independencies induced by graphical model structuring of the characterizing covariance matrix parameters. This framework of matrix normal graphical models includes prior specifications, posterior computation using Markov chain Monte Carlo methods, evaluation of graphical model uncertainty and model structure search. Extensions to matrix-variate time series embed matrix normal graphs in dynamic models. Examples highlight questions of graphical model uncertainty, search and comparison in matrix data contexts. These models may be applied in a number of areas of multivariate analysis, time series and also spatial modelling.

1. Introduction

We introduce and analyze matrix normal graphical models; that is, matrix normal distributions (Dawid, 1981; Gupta & Nagar, 2000) in which each of the two characterizing covariance matrices reflects conditional independencies consistent with an underlying graphical model (Whittaker, 1990; Lauritzen, 1996). We present fully Bayesian analysis of the matrix normal model as the special case of full graphs, and develop computational methods for marginal likelihood computation on a specified graphical model. This enables graphical model search and comparison for posterior inferences about conditional independence structures. The random sampling framework is extended to matrix-variate time series models that inherit the graphical model structure to represent conditional independencies in matrix time series. We focus on decomposable graphs although the general approach will also apply to nondecomposable models.

Matrix-variate normal distributions have been studied in analysis of two-factor linear models for cross-classified multivariate data (Finn, 1974; Galecki, 1994; Naik & Rao, 2001), in spatio-temporal models (Mardia & Goodall, 1993; Huizenga et al., 2002) and other areas. Some computational and inferential developments, including iterative calculation of maximum likelihood estimates (Dutilleul, 1999; Mitchell et al., 2006) and empirical Bayesian methods for Procrustes analysis with matrix models (Theobald & Wuttke, 2006) have been published. Our work appears to be the first to develop fully Bayesian analysis of the basic matrix normal model alone, though that is only a necessary first step to the broader framework of matrix graphical models.

In time series, graphical modelling of the covariance matrix of multivariate data appears in Carvalho & West (2007a, 2007b). Here we generalize that earlier work to time series of matrix data, providing fully Bayesian inference and graphical model search related to both row and column intra-dependencies in the cross-sectional structure of a matrix-valued time series.

2. Matrix variate normals, graphs and notation

The q × p random matrix Y is matrix normal, Y ∼ N (M, U, V), with mean M (q × p), column and row covariance matrices U = (u_ij) (q × q) and V = (υ_ij) (p × p), respectively, when

$$p(Y)\equiv p(Y|U,V)=k(U,V)\hspace{0.17em}\text{exp}[-\text{tr}\{{(\text{Y}-\text{M})}^{\prime }{\text{U}}^{-1}(\text{Y}-\text{M}){\text{V}}^{-1}/2\}],$$ (1)

where k(U, V) = (2π)^−qp/2|U|^−p/2|V|^−q/2. The rows y_i★ (i = 1, . . ., p), and columns y_★j (j = 1, . . ., q), have margins y_i★ ∼ N (m_i★, u_ii V) and y_★j ∼ N (m_★j, υ_jj U) with precision matrices Λ = V⁻¹ = (λ_ij) and Ω = U⁻¹ = (ω_ij), respectively. The normal conditional distributions have mean vectors and covariance matrices

$$\begin{array}{ll}E(y_{i★}|y_{-i★})=m_{i★}-{\omega }_{ii}^{-1}{\mathrm{\Sigma }}_{s\in (1,\dots ,q\backslash i)}\hspace{0.17em}{\omega }_{is}\hspace{0.17em}(y_{s★}-m_{s★}),\hfill & \text{cov}({\text{y}}_{\text{i}★}|{\text{y}}_{-\text{i}★})={\omega }_{ii}^{-1}V,\hfill \\ E(y_{★j}|y_{-★j})=m_{★j}-{\lambda }_{jj}^{-1}{\mathrm{\Sigma }}_{t\in (1,\dots ,p\backslash j)}\hspace{0.17em}{\lambda }_{tj}\hspace{0.17em}(y_{★t}-m_{★t}),\hfill & \text{cov}({\text{y}}_{★\text{j}}|{\text{y}}_{-★\text{j}})={\lambda }_{jj}^{-1}U,\hfill \end{array}$$

for rows i = 1, . . ., q and columns j = 1, . . ., p. Zeros in Λ and Ω define conditional independencies. If (i, j) ≠ (s, t) then y_ij and y_st may, conditional upon y_−(ij,st) be dependent through either rows or columns; conditional independence is equivalent to: at least one zero among λ_tj and ω_is when s ≠ i, j ≠ t; ω_is = 0 when s ≠ i, j = t; λ_jt = 0 when s = i, j ≠ t. With no loss of generality, in this section we set M = 0.

Undirected graphical models can be applied to each of Λ and Ω to represent strict conditional independencies. A graph G_V on nodes {1, . . ., p} has edges between pairs of column indices (j, t) for which λ_jt ≠ 0; Λ has off-diagonal zeros corresponding to within-row conditional independencies. Similarly, a graph G_U on nodes {1, . . ., q} lacks edges between row indices (i, s) for which ω_is = 0. We focus here on decomposable graphs G_U and G_V. The theory of graphical models can be now overlaid to define conditional factorizations of the matrix normal density over graphs. Over G_V, for example, we have

$$p(Y|U,\hspace{0.17em}V,\hspace{0.17em}{G}_V,\hspace{0.17em}{G}_U)=\prod _{P_V\in {𝒫}_V}p(Y_{★P_V}|U,\hspace{0.17em}{V}_{P_V})/\prod _{S_V\in {𝒮}_V}p(Y_{★S_V}|U,V_{S_V}),$$ (2)

where 𝒫_V is the set of complete prime components, or cliques, of G_V and 𝒮_V is the set of separators. For each subgraph g ∈ {𝒫_V, 𝒮_V}, Y_★g is the q × |g| matrix with variables from the |g| columns of Y defined by the subgraph, and V_g the corresponding submatrix of V. Each term in equation (2) is matrix normal, Y_★g ∼ N (0, U, V_g) with ${\mathrm{\Lambda }}_g=V_g^{-1}$ having no off-diagonal zeros. We can similarly factorize the joint density over G_U.

Now, U and V are not uniquely identified since, for any c > 0, p(Y | U, V) = p(Y | cU, V/c). There are a number of approaches to imposing identification constraints such as tr(V) = p (Theobald & Wuttke, 2006), and possible strategies that use unconstrained parameters; we discuss the latter in § 8. Our use of hyper-Markov priors over each of U and V with underlying graphical models, discussed below, makes it desirable to adopt an explicit constraint and we enforce υ₁₁ = 1 from here on.

3. Matrix graphical modelling

Hyper-inverse Wishart priors are conjugate for covariance matrices in multivariate normal graphical models (Dawid & Lauritzen, 1993). Hyper-inverse Wishart distributions are compatible and consistent across graphs, which is critical when admitting uncertainty about graph structures (Giudici & Green, 1999; Jones et al., 2005). On decomposable graphs, the implied priors on sub-covariance matrices on all components and separators are inverse Wishart. Use of independent hyper-inverse Wishart priors for U, V in the current context is a natural choice, and maintains compatibility and consistency across graphs G_U, G_V. To incorporate the identification constraint υ₁₁ = 1, we use a parameter expansion approach. Parameter expansion involves expanding the parameter space by adding new nuisance parameters, and has been used purely algorithmically to accelerate Markov chain Monte Carlo samplers (Liu et al., 1998; Liu & Wu, 1999), but can also be used to induce new priors (Gelman, 2004, 2006) as is germane here.

We assume the prior p(U, V) = p(U)p(V) where, using the hyper-inverse Wishart notation of Giudici & Green (1999) and Jones et al. (2005), the margins are defined by

$$U\sim {\text{HIW}}_{G_U}\hspace{0.17em}(b,\hspace{0.17em}B),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}V=V^{*}/{\upsilon }_{11}^{*},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{V}^{*}\sim {\text{HIW}}_{G_V}\hspace{0.17em}(d,\hspace{0.17em}D).$$ (3)

The density function for U is, following Dawid & Lauritzen (1993),

$$p(U)=\prod _{P_U\in {𝒫}_U}p(U_{P_U}|b,\hspace{0.17em}{B}_{P_U})/\prod _{S_U\in {𝒮}_U}p(U_{S_U}|b,\hspace{0.17em}{B}_{S_U}),$$

where each component is an inverse Wishart density; p(V^*) has a similar form.

The parameter expansion concept relates to ${\upsilon }_{11}^{*}$ as an added parameter that converts column scales in V to those relative to the scale of the first column. As we move across graphs G_V, the priors p(V | G_V) have the same induced priors over subgraph correlation structures but are no longer in complete agreement for V = V^*/ ${\upsilon }_{11}^{*}$ due to the different parameterizations and interpretations. This is natural and appropriate. Suppose G_V and G′_V are two graphs with a common clique C. Each element in diag(V_C) represents the relative scale of variance of that column to the variance of the first column so that, if G_V and G′_V imply different conditional dependencies between the first column and columns linked to C, then the induced priors over V_C should indeed be different.

The prior p(V) is obtained by transformation from V^*. On any graph G_V, V is determined only by those free elements appearing in the submatrices corresponding to the cliques of the graph, and the nonfree elements of V are deterministic functions of the free elements (Carvalho et al., 2007). Let ν be the number of free elements; then the transformation from V ^* to (V, ${\upsilon }_{11}^{*}$) has Jacobian ${({\upsilon }_{11}^{*})}^{\nu -1}$ leading to

$$p(V,\hspace{0.17em}{\upsilon }_{11}^{*})={\text{HIW}}_{G_V}\hspace{0.17em}({\upsilon }_{11}^{*}\hspace{0.17em}V|d,\hspace{0.17em}D)\hspace{0.17em}{({\upsilon }_{11}^{*})}^{\nu -1}.$$

Coupled with the prior p(U) on G_U, this defines a class of conditionally conjugate priors in the expanded parameter space.

4. Posterior and marginal likelihood computation

4.1. Gibbs sampling on given graphs

Assume an initial random sampling context with q × p data matrices Y_i (i = 1, . . ., n), drawn independently from equation (1), and write Y for the full set of data. It is easy to see that, on specified graphs (G_U, G_V), the posterior p(U, V, ${\upsilon }_{11}^{*}$ |Y) has conditional distributions:

$$\begin{array}{l}(U|V,\hspace{0.17em}{\upsilon }_{11}^{*},\hspace{0.17em}Y)\sim {\text{HIW}}_{G_U}\hspace{0.17em}\left(b+np,B+\sum _{i=1}^n{Y}_i\hspace{0.17em}{V}^{-1}\hspace{0.17em}{Y}_i^{\prime }\right),\\ (V|U,\hspace{0.17em}{\upsilon }_{11}^{*},\hspace{0.17em}Y)\sim {\text{HIW}}_{G_V}\hspace{0.17em}\left(d+nq,\hspace{0.17em}D/{\upsilon }_{11}^{*}+\sum _{i=1}^n{Y}_i^{\prime }\hspace{0.17em}{U}^{-1}\hspace{0.17em}{Y}_i\right)\hspace{0.17em}I({\upsilon }_{11}=1),\\ ({\upsilon }_{11}^{*}|U,\hspace{0.17em}V,\hspace{0.17em}Y)\sim \text{IG}\{a/2-\nu ,\hspace{0.17em}\text{tr}(D{V}^{-1})/2\},\end{array}$$

where a = Σ_PV|P_V|(2|P_V| + d) − Σ_SV|S_V|(2|S_V| + d). These distributions form the basis of Gibbs sampling for the target posterior p(U, V, ${\upsilon }_{11}^{*}$ | Y). This involves iterative resampling from the hyper-inverse Wishart, inverse gamma and new conditional hyper-inverse Wishart distributions. Simulation of the former is based on Carvalho et al. (2007), while sampling the latter can be done as follows. From Lemma 2.18 of Lauritzen (1996), we can always find a perfect ordering of the nodes in G_V so that node 1 is in the first clique, say C, and then initialize the hyper-inverse Wishart sampler of Carvalho et al. (2007) to begin with a simulation of the implied conditional inverse Wishart distribution for the covariance matrix on that first clique. Sampling V_C from an inverse Wishart distribution conditional on the first diagonal element set to unity is straightforward.

4.2. Marginal likelihood

Exploration of uncertainty about graphical model structures involves consideration of the marginal likelihood function over graphs. For any pair (G_U, G_V), this is

$$p(Y)\equiv p(Y|G_U,\hspace{0.17em}{G}_V)=\int p(Y|U,\hspace{0.17em}V)\hspace{0.17em}p(U)\hspace{0.17em}p(V)\text{d}U\hspace{0.17em}\text{d}V.$$

The priors in the integrand depend on the graphs although for clarity we drop that from the notation. In multivariate models, marginal likelihoods can be evaluated in closed form on decomposable graphs (Giudici, 1996; Giudici & Green, 1999; Jones et al., 2005; Carvalho & West, 2007a, 2007b). In our matrix models, the integral cannot be evaluated but we can generate useful approximations via use of the candidate’s formula (Besag, 1989; Chib, 1995). Write Θ = {U, V, ${\upsilon }_{11}^{*}$} for all parameters, and suppose that we can evaluate p(θ| Y) for some sub-set of parameters θ ∈ Θ; the candidate’s formula gives the marginal likelihood via the identity p(Y) = p(Y | θ)/p(θ| Y). Applying this requires that we estimate components of the numerator or denominator. Choosing θ to maximally exploit analytic integration is key, and different choices that integrate over different subsets of parameters will lead to different, parallel approximations of p(Y) that can be compared. We use two approximations based on marginalization over desirably disjoint parameter subsets, namely, (A): p(Y) = p(Y, ${\upsilon }_{11}^{*}$, U)/p( ${\upsilon }_{11}^{*}$, U | Y) at any chosen value of θ = { ${\upsilon }_{11}^{*}$, U}, and (B): p(Y) = p(Y, V)/p(V | Y) at any value of θ = V. We estimate the components of these equations that have no closed form, then insert chosen values U, V, ${\upsilon }_{11}^{*}$, such as approximate posterior means, to provide two estimates of p(Y).

For (A), first rewrite as

$$p(Y)=\frac{p(Y,\hspace{0.17em}{\upsilon }_{11}^{*},\hspace{0.17em}U\hspace{0.17em})\hspace{0.17em}p(V|{\upsilon }_{11}^{*},\hspace{0.17em}U,\hspace{0.17em}Y)}{p({\upsilon }_{11}^{*},\hspace{0.17em}U|Y)\hspace{0.17em}p(V|{\upsilon }_{11}^{*},\hspace{0.17em}U,\hspace{0.17em}Y)}=\frac{p(Y|V,\hspace{0.17em}{\upsilon }_{11}^{*},\hspace{0.17em}U)\hspace{0.17em}p(U)\hspace{0.17em}p(V|{\upsilon }_{11}^{*})\hspace{0.17em}p({\upsilon }_{11}^{*})}{p({\upsilon }_{11}^{*},\hspace{0.17em}U|Y)\hspace{0.17em}p(V|{\upsilon }_{11}^{*},\hspace{0.17em}U,\hspace{0.17em}Y)}.$$

The numerator terms are each easily computed at any {V, ${\upsilon }_{11}^{*}$, U}. The second denominator term p(V | ${\upsilon }_{11}^{*}$, U, Y) has an easily evaluated closed form, as in the Gibbs sampling step. The first denominator term may be approximated by

$$\begin{array}{ll}p({\upsilon }_{11}^{*},\hspace{0.17em}U|Y)\hfill & =\int p({\upsilon }_{11}^{*}|Y,\hspace{0.17em}V)\hspace{0.17em}p(U|Y,\hspace{0.17em}V,\hspace{0.17em}{\upsilon }_{11}^{*})\hspace{0.17em}p(V|Y)\text{d}\hspace{0.17em}V\hfill \\ \hfill & \approx \frac{1}{M}\sum _{j=1}^{M}p({\upsilon }_{11}^{*}|Y,\hspace{0.17em}{V}_j)\hspace{0.17em}p(U|Y,\hspace{0.17em}{V}_j,\hspace{0.17em}{\upsilon }_{11}^{*}),\hfill \end{array}$$

where the sum is over posterior draws V_j; this is easy to compute as it is a sum of the product of inverse gamma and hyper-inverse Wishart densities.

For (B), the numerator can be analytically evaluated as

$$\begin{array}{ll}p(V,\hspace{0.17em}Y)\hfill & =\int p(Y,\hspace{0.17em}U,\hspace{0.17em}V,\hspace{0.17em}{\upsilon }_{11}^{*})\text{d}U\hspace{0.17em}\text{d}{\upsilon }_{11}^{*}\hfill \\ \hfill & =\frac{q_V{(2\pi )}^{-nqp/2}H(b,\hspace{0.17em}B,\hspace{0.17em}{G}_U)H(d,\hspace{0.17em}D,\hspace{0.17em}{G}_V)}{H(b+np,\hspace{0.17em}B+{\sum }_{i=1}^n\hspace{0.17em}{Y}_i\hspace{0.17em}{V}^{-1}\hspace{0.17em}{Y}_i^{\prime },\hspace{0.17em}{G}_U)H\{c,\hspace{0.17em}\text{tr}(D{V}^{-1}),\hspace{0.17em}1\}},\hfill \end{array}$$

where

$$q_V=\prod _{P_V\in {𝒫}_V}{\left|V_{P_V}\right|}^{-(nq+d+2|P_V|)/2}/\prod _{S_V\in {𝒮}_V}|V_{S_V}{|}^{-(nq+d+2|S_V|)/2},$$

the H(·, ·, G_·) terms are normalizing constants of the corresponding hyper-inverse Wishart distributions (Giudici & Green, 1999; Jones et al., 2005) and

$$c=\sum _{P_V\in {𝒫}_V}|P_V|(2|P_V|+d)-\sum _{S_V\in {𝒮}_V}|S_V|(2|S_V|+d)-2\nu .$$

The density function in the denominator is approximated as

$$p(V|Y)=\int p(V|{\upsilon }_{11}^{*},\hspace{0.17em}U,\hspace{0.17em}Y)p({\upsilon }_{11}^{*},\hspace{0.17em}U|Y)\text{d}{\upsilon }_{11}^{*}\hspace{0.17em}\text{d}U\approx \frac{1}{M}\sum _{j=1}^{M}P(V|Y,\hspace{0.17em}{U}_j,\hspace{0.17em}{\upsilon }_{11,j}^{*}),$$

where the sum over posterior draws (U_j, ${\upsilon }_{11,j}^{*}$) can be easily performed, with terms given by conditional hyper-inverse Wishart density evaluations.

4.3. Graphical model uncertainty and search

Now admit uncertainty about graphs (G_U, G_V) using sparsity-encouraging priors in which edge inclusion indicators are independent Bernoulli variates (Dobra et al., 2004; Jones et al., 2005). We now extend Markov chain Monte Carlo simulation for multivariate graphical models (Giudici & Green, 1999; Jones et al., 2005) to learning on (G_U, G_V) in the above matrix model analysis. Our analysis generates multiple graphs with values of approximate posterior probabilities, using the Markov chain simulation for model search. This relies on the computation of the unnormalized posterior over graphs, p(G_U, G_V| Y) ∝ p(Y | G_U, G_V) p(G_U, G_V) involving the marginal likelihood value for any specified model (G_U, G_V) at each search step. For the latter, we average the approximate marginal likelihood values from methods (A) and (B). The work in Jones et al. (2005) includes evaluation of the performance of various stochastic search methods in single multivariate graphical models; for modest dimensions, they recommend simple local-move Metropolis–Hastings steps. Here, given a current pair (G_U, G_V), we can apply local moves in G_U space based on the conditional posterior p(G_U | Y, G_V), and vice-versa. A candidate G′_U is sampled from a proposal distribution q(G′_U; G_U) and accepted with probability

$$\alpha =\text{min}\{1,\hspace{0.17em}p(G_U^{\prime }|Y,\hspace{0.17em}{G}_V)q(G_U;\hspace{0.17em}{G}_U^{\prime })/p(G_U|Y,\hspace{0.17em}{G}_V)q(G_U^{\prime };\hspace{0.17em}{G}_U)\};$$

our examples use the simple random add/delete edge move proposal of Jones et al. (2005). We then couple this with a similar step using p(G_V | Y, G_U) at each iteration. This requires a Markov chain analysis on each graph pair visited in order to evaluate marginal likelihood, so implying a substantial computational burden.

5. Example: a simulated random sample

A sample of size n = 48 was drawn from the (q = 8) × (p = 7) dimensional N (0, U, V) distribution, where, using · to denote zeros to highlight structure, the precision matrices are

$$\begin{array}{l}\mathrm{\Lambda }=\left(\begin{array}{ccccccc}1.85& -0.09& -0.65& .& -0.24& 0.45& .\\ -0.09& 0.21& 0.08& .& .& 0.14& -0.13\\ -0.65& 0.08& 0.58& 0.10& .& -0.30& .\\ .& .& 0.10& 0.48& .& -0.10& .\\ -0.24& .& .& .& 0.70& -0.17& .\\ 0.45& 0.14& -0.30& -0.10& -0.17& 0.61& -0.36\\ .& -0.13& .& .& .& -0.36& 3.72\end{array}\right),\\ \mathrm{\Omega }=\left(\begin{array}{cccccccc}0.99& .& .& -0.33& .& 0.05& .& .\\ .& 3.65& 0.33& .& -0.39& -0.41& .& -0.03\\ .& 0.33& 2.23& .& .& -0.38& .& .\\ -0.33& .& .& 1.65& .& .& .& .\\ .& -0.39& .& .& 2.91& -0.30& .& .\\ 0.05& -0.41& -0.38& .& -0.30& 4.71& -0.13& -0.40\\ .& .& .& .& .& -0.13& 1.07& -0.26\\ .& -0.03& .& .& .& -0.40& -0.26& 1.45\end{array}\right)\end{array}$$

First consider analysis on the true graphs under priors with b = d = 3 and B = 5I₈, D = 5I₇ and simulation sample size 8000 after an initial, discarded burn-in of 2000 iterations. Convergence is rapid and apparently fast-mixing in this as in other simulated examples. The corresponding posterior means of the precision matrices are

$$\begin{array}{l}\widehat{\mathrm{\Lambda }}=\left(\begin{array}{ccccccc}1.86& -0.11& -0.68& .& -0.28& 0.44& .\\ -0.11& 0.28& 0.14& .& .& 0.16& -0.21\\ -0.68& 0.14& 0.68& 0.16& .& -0.33& .\\ .& .& 0.16& 0.59& .& -0.15& .\\ -0.28& .& .& .& 0.75& -0.14& .\\ 0.44& 0.16& -0.33& -0.15& -0.14& 0.71& -0.45\\ .& -0.21& .& .& .& -0.45& 4.14\end{array}\right),\\ \widehat{\mathrm{\Omega }}=\left(\begin{array}{cccccccc}0.90& .& .& -0.27& .& 0.02& .& .\\ .& 3.23& 0.50& .& -0.35& -0.22& .& -0.12\\ .& 0.50& 2.14& .& .& -0.37& .& .\\ -0.27& .& .& 1.46& .& .& .& .\\ .& -0.35& .& .& 2.88& -0.41& .& .\\ 0.02& -0.22& -0.37& .& -0.41& 4.20& -0.29& -0.08\\ .& .& .& .& .& -0.29& 0.91& -0.26\\ .& -0.12& .& .& .& -0.08& -0.26& 1.58\end{array}\right)\end{array}$$

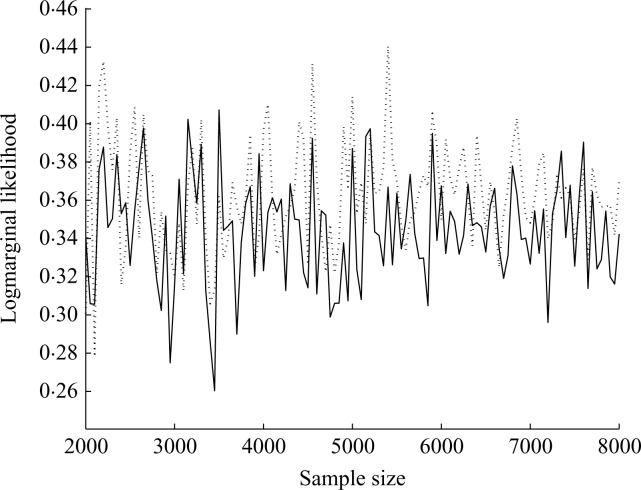
Figure 1 gives an implementation check on the concordance of the two marginal likelihood estimates. These are very close and differ negligibly on the log probability scale even at small Monte Carlo sample sizes.

Fig. 1.

Logmarginal likelihood values in the example of § 5. The two estimates A (full line) and B (dashed line) of § 4.2 were successively re-evaluated and plotted here at differing simulation sample sizes. The vertical scale has been adjusted by addition of 3583 for clarity.

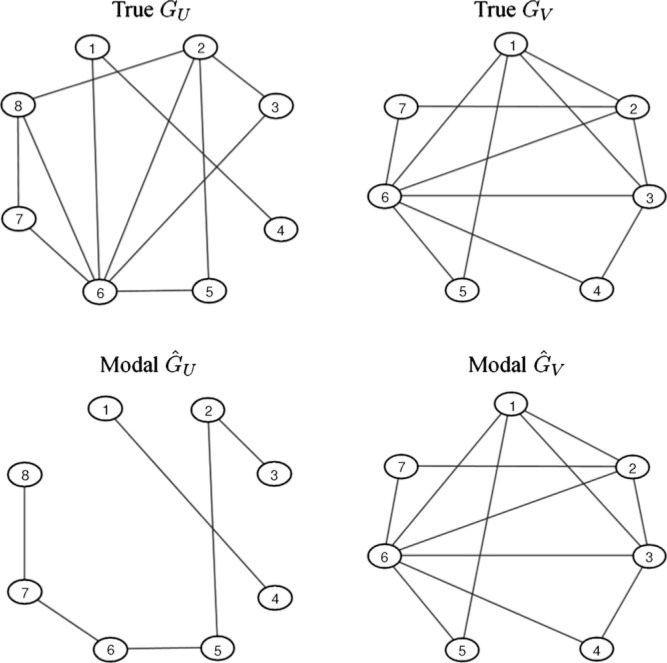
Consider graphical model uncertainty with prior edge inclusion probabilities 2/(q − 1) for G_U and 2/(p − 1) for G_V. Repeat explorations suggest stability of the marginal likelihood estimation using smaller Monte Carlo sample sizes, and we use 2000 draws within each step of the model search. The add/delete Metropolis-within-Gibbs was run for 20 000 iterates starting from empty graphs. Results are essentially replicated starting at the full graphs. The most probable graphs visited, (Ĝ_U, Ĝ_V), are shown in Fig. 2; these are local modes and also have greater posterior probability than the true graphs also displayed, and this model was first visited after 2614 Markov chain steps. The edges in (Ĝ_U, Ĝ_V) generally have higher posterior edge inclusion probability than those not included; the lowest probability included edge has probability 0.52, while the highest probability excluded edge has probability 0.59. Thus, graphs discovered by highest posterior probability and by aggregating high probability edges are not dramatically different. The modal Ĝ_U is sparser than the true G_U, reflecting the difficulties in identifying very weak signals; for example, the modal graph lacks an edge corresponding to the true Ω_1,6 = 0.05, and the posterior probability of that edge is naturally low. One measure of inferred sparsity is the posterior mean of the proportion of edges in each graph; these are about 28%, 59.6% for G_U, G_V, respectively. Additional posterior summaries and exploration of the posterior samples suggest clean convergence of the simulation analysis and the Metropolis–Hastings steps over graphs had good empirical acceptance rates of about 26%, 9% for G_U, G_V, respectively.

Fig. 2.

True graphs in the simulated data example together with graphs of highest posterior probability identified from the analysis.

6. Dynamic matrix-variate graphical models for time series

Using the theory and methods for matrix normal models developed above, we are now able to extend our ideas to matrix time series involving two covariance matrices and associated graphical models. In the notation below, the work of Carvalho & West (2007a, 2007b) is the special case of vector data with q = 1, U fixed, and inference on (V, G_V) only.

A q × p matrix-variate times series Y_t follows the dynamic linear model

$$\begin{array}{l}{Y}_t=(I_q\otimes F_t^{\prime }){\mathrm{\Theta }}_t+{\nu }_t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\nu }_t\sim N(0,\hspace{0.17em}U,\hspace{0.17em}V),\\ {\mathrm{\Theta }}_t=(I_q\otimes G_t){\mathrm{\Theta }}_{t-1}+{\mathrm{\Upsilon }}_t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{\Upsilon }}_t\sim N(0,\hspace{0.17em}U\otimes W_t,\hspace{0.17em}V)\end{array}$$

for t = 1, 2, . . ., where (a) Y_t = (Y_t,ij), the q × p matrix observation at time t; (b) Θ_t = (Θ_t,ij), the qs × p state matrix comprised of q × p state vectors Θ_t,ij each of dimension s × 1; (c) ϒt = (ω_t,ij), the qs × p matrix of state evolution innovations comprised of q × p innovation vectors ω_t,ij each of dimension s × 1; (d) ν_t = (ν_t,ij), the q × p matrix of observational errors; (e) W_t is the s × s innovation covariance matrix at time t; (f) for all t, the s-vector F_t and s × s state evolution matrix G_t are known. Also, ϒt follows a matrix-variate normal distribution with mean 0, left covariance matrix U ⊗ W_t and right covariance matrix V. In terms of scalar elements, we have q × p univariate models with individual s-vector state parameters, namely,

$$\begin{array}{l}{Y}_{t,ij}=F_t^{\prime }\hspace{0.17em}{\mathrm{\Theta }}_{t,ij}+{\nu }_{t,ij},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\nu }_{t,ij}\sim N(0,\hspace{0.17em}{u}_{ii}\hspace{0.17em}{\upsilon }_{jj}),\\ {\mathrm{\Theta }}_{t,ij}=G_t\hspace{0.17em}{\mathrm{\Theta }}_{t-1,ij}+{\omega }_{t,ij},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\omega }_{t,ij}\sim N(0,\hspace{0.17em}{u}_{ii}\hspace{0.17em}{\upsilon }_{jj}\hspace{0.17em}{W}_t),\end{array}$$ (4)

for each i, j and t. Each of the scalar series shares the same F_t and G_t elements, and the reference to the model as one of exchangeable time series reflects these symmetries. In the example below, F_t = F and G_t = G, as in many practical models, but the model class includes dynamic regressions when F_t involves predictor variables. This form of model is a standard specification (Quintana & West, 1987; West & Harrison, 1997) in which the correlation structures induced by U and V affect both the observation and evolution errors; for example, if u_ij is large and positive, vector series Y_t,i★ and Y_{t, j★} will show concordant behaviour in movement of their state vectors and in observational variation about their levels. Specification of the entire sequence of W_t in terms of discount factors (West & Harrison, 1997) is also standard practice, typically using multiple discount factors related to components of the state vector and their expected degrees of random change in time, as illustrated in the example below. The innovations here concern graphical modelling and inference on (U, V). The key theory, conditional on U, V, concerns the conjugate sequential learning and forecasting as data is processed, as follows.

Theorem 1. Define D_t = {D_t−1, Y_t} for t = 1, 2, . . ., with D₀ representing prior information. With initial prior (Θ₀ | U, V, D₀) ∼ N (m₀, U ⊗ C₀, V) we have, for all t:

1. posterior at t – 1: (Θ_t−1 | D_t−1, U, V) ∼ N (m_t−1, U ⊗ C_t−1, V);

2. prior at t: (Θ_t | D_t−1, U, V) ∼ N (a_t, U ⊗ R_t, V) where a_t = (I_n ⊗ G_t)m_t−1 and R_t = G_t C_t−1 G′_t + W_t;

3. one-step forecast at t – 1: (Y_t | D_t−1, U, V) ∼ N (f_t, Uq_t, V) with forecast mean matrix f_t = (I_n ⊗ F′₁ G_t)m_t−1 and scalar q_t = F′_t R_t F_t +1; and

4. posterior at t: (Θ_t | D_t, U, V) ∼ N (m_t, U ⊗ C_t, V) with m_t = a_t + (I_q ⊗ A_t)e_t and C_t = R_t − A_t A′_t q_t where A_t = R_t F_t/q_t and e_t = Y_t − f_t.

Proof. This stems from the theory of multivariate models applied to vec(Y_t) (West & Harrison, 1997). The main novelty here concerns the separability of covariance structures. That is: for all t, the distributions for state matrices have separable covariance structures; for example, (Θ_t |D_t, U, V) is such that cov{vec(Θ_t) | D_t, U, V} = V ⊗ U ⊗ C_t; the sequential updating equations for the set of qs × p state matrices are implemented in parallel based on computations for the univariate component models, each of them involving the same scalar q_t, s–vector A_t and s × s matrices R_t, C_t at time t.

Suppose now that U and V are constrained by graphs G_U and G_V, with priors as in equation (3) and sparsity priors over the graphs. Given data over t = 1, . . ., n, the sequential updating analysis on (G_U, G_V) leads to the full joint density

$$P(Y_1,\dots ,Y_n|U,\hspace{0.17em}V)=\prod _{t=1}^{n}p(Y_t|U,\hspace{0.17em}V,\hspace{0.17em}{D}_{t-1})=\prod _{t=1}^{n}N(e_t|0,\hspace{0.17em}{q}_{t}U,\hspace{0.17em}V),$$

marginalized with respect to all state vectors. The one-step forecast error matrices e_t are conditionally independent matrix normal variates. Apart from the scalars q_t, this is essentially the framework of § 2. Thus, with a small change to insert the q_t, we are able to directly fit and explore dynamic graphical models using the analysis for random samples with embedded sequential updating computations.

7. A macro-economic example

An example concerns exploration of conditional dependence structures in macroeconomic time series related to US labour market employment. The data are Current Employment Statistics for the eight US states, New Jersey, New York, Massachusetts, Georgia, North Carolina, Virginia, Illinois and Ohio. We explore these data across nine industrial sectors: construction; manufacturing; trade, transportation and utilities; information; financial activities; professional and business services; education and health services; leisure and hospitality; and government. In our model framework, we have q = 8, p = 9 and monthly data over several years. Then U characterizes the residual conditional dependencies among states while V does the same for industrial sectors, in the context of an overall model that incorporates time-varying state parameters for underlying trend and annual seasonal structure in the series. Trend and seasonal elements are represented in standard form, the former as random walks and the latter as randomly varying seasonal effects. Specifically, in month t, the monthly employment change in state i and sector j is Y_t,ij, modelled as a first-order polynomial/seasonal effect model (West & Harrison, 1997) with the state vector comprising a local-level parameter and 12 seasonal factors, so that the state dimension is s = 13.

The univariate models of equation (4) have state vectors Θ_t,ij = (μ_t,ij, ϕ_t,ij)′, where μ_t,ij is the local level and ϕ_t,ij = (ϕ_t,ij,k, ϕ_t,ij,k+1, . . ., ϕ_t,ij,11, ϕ_t,ij,0, . . ., ϕ_t,ij,k−1) contains current monthly seasonal factors, subject to 1′ϕ_t,ij = 0 for all i, j and t. Further, F_t = F (13 × 1) and G_t = G (13 × 13) for all t, where F′ = (1, 1, 0, . . ., 0). The state matrix G and the sequence of state evolution covariance matrices W_t (13 × 13) are

$$G=\left(\begin{array}{cc}1& 0\\ 0& P\end{array}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P=\left(\begin{array}{cc}0& I_{11}\\ 1& 0^{\prime }\end{array}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{W}_t=\left(\begin{array}{cc}{W}_{t,\mu }& 0\\ 0& W_{t,\varphi }\end{array}\right),$$

with the latter having entries as follows. The univariate W_t,μ and 12 × 12 matrix W_t,ϕ are defined via discount factors δ_l and δ_s and the corresponding block components of C_t as W_t,μ = C_t−1,,μ (1 − δ_l)/δ_l and W_t,ϕ = PC_t−1,ϕ P′(1 − δ_s)/δ_s for each t. The discount factor δ_l reflects the rate at which the levels μ_t,ij are expected to vary between months, with 100( ${\delta }_l^{-1}$ − 1)% of information on these parameters decaying each month. The factor δ_s plays the same role for seasonal parameters. We use δ_l = 0.9, δ_s = 0.95 to allow more adaptation to level changes than seasonal factors (West & Harrison, 1997); results, in terms of graphical model search and structure, are substantially similar using other values in appropriate ranges. In application, we can estimate discount factors and also extend the model to allow changes in discount factors to model change-points and other events impacting the series, based on monitoring and intervention methods (Pole et al., 1994; West & Harrison, 1997). Such considerations are secondary to our purposes in using this model for illustration of computational model search analysis for (U, V, G_U, G_V), but practically very germane. Model completion uses initial, vague priors with m₀ = 0, the 104 × 9 matrix, and C₀ = 100I₁₃. The constraint that 1′ϕ_t,ij = 0 is imposed by transforming m₀ and C₀ as discussed in West & Harrison (1997).

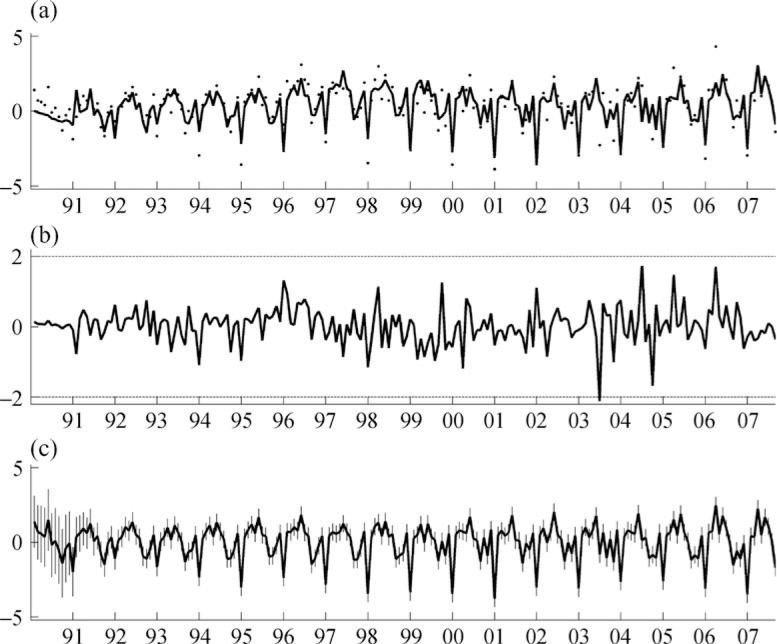
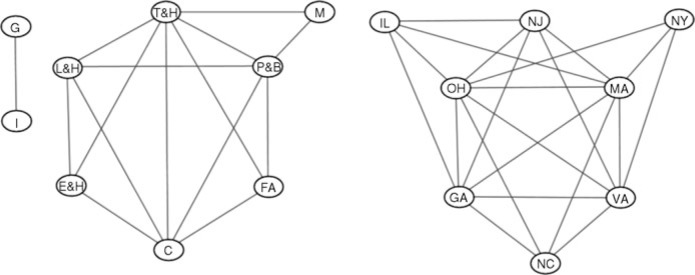
Model fitting estimates the movements in trend and seasonality, sequentially generating matrix series e_t whose row and column covariance patterns relate to (U, V). The North Carolina financial activities data and some aspects of the sequential model fit are graphed in Fig. 3. Priors for (U, V) use B = 5I₈, D = 5I₉ and b = d = 3, reflecting the range of residual variation, sparsity-encouraging priors with prior edge inclusion probabilities 2/(q − 1) for G_U and 2/(p − 1) for G_V. The add/delete Metropolis-within-Gibbs sampler was run for 20 000 steps. Two chains were run: one starting at empty graphs and one at full graphs. The most probable model identified, (Ĝ_U, Ĝ_V), is shown in Fig. 4. This, and the acceptance rates of graphs, were insensitive to the starting points. Beginning with empty graphs, the most probable model visited was found after 401 steps; its log posterior probability is −27 695.40, the sparsity of (Ĝ_U, Ĝ_V) in terms of percentage of edges included is (72.4%, 42.1%) and the acceptance rates are (7.3%, 11.9%). Beginning with full graphs led to a most probable model with log posterior probability −27 695.43 after 2194 steps, sparsity (73.7%, 41.9%) and acceptance rates (7.7%, 12.2%). Posterior edge inclusion probabilities are also consistent between the two runs; see Table 1. Further, the most probable graphs sit in a region of graphs of similar sparsity and posterior probability and the posterior is dense around this mode; see Fig. 5.

Fig. 3.

One of the 72 time series in the econometric example, plotted over 1990–2007. (a): Dots are monthly changes in employment of North Carolina financial activities and the line joins the corresponding one-step ahead forecasts over time. (b): Corresponding standardized one-step ahead forecast errors e_t/ √ q_t. (c): Corresponding on-line estimated seasonal pattern with 95% point-wise credible intervals indicated by vertical bars at each month.

Fig. 4.

Highest posterior probability graphs that illustrate aspects of inferred conditional dependencies among industrial sectors and among states in analysis of the econometric time series data.

Table 1.

Posterior edge inclusion probabilities in graphical model analysis of the matrix econometric time series data

	NJ	NY	MA	GA	NC	VA	IL	OH
NJ	1	0.05	1.00	0.55	0.01	1.00	1.00	1.00
NY		1	1.00	0.19	0.00	1.00	0.00	0.59
MA			1	0.98	0.96	1.00	1.00	1.00
GA				1	0.93	0.89	0.75	1.00
NC					1	1.00	0.06	1.00
VA						1	0.31	1.00
IL							1	1.00
OH								1
	C	M	T&U	I	FA	P&BS	E&H	L&H	G
C	1	0.02	1.00	0.16	0.75	1.00	0.99	1.00	0.06
M		1	1.00	0.28	0.02	0.98	0.01	0.03	0.01
T&U			1	0.02	1.00	1.00	0.93	1.00	0.02
I				1	0.06	0.34	0.02	0.01	0.55
FA					1	1.00	0.00	0.04	0.02
P&BS						1	0.02	1.00	0.00
E&H							1	0.75	0.02
L&H								1	0.01
G									1

US states: NJ, New Jersey; NY, New York; MA, Massachusetts; GA, Georgia; NC, North Carolina; VA, Virginia; IL, Illinois; OH, Ohio. Industrial sectors: C, industrial construction; M, manufacturing; T&U, trade, transportation & utilities; I, information; FA, financial activities; P&BS, professional & business services; E&H, education & health services; L&H, leisure & hospitality; G, government.

Fig. 5.

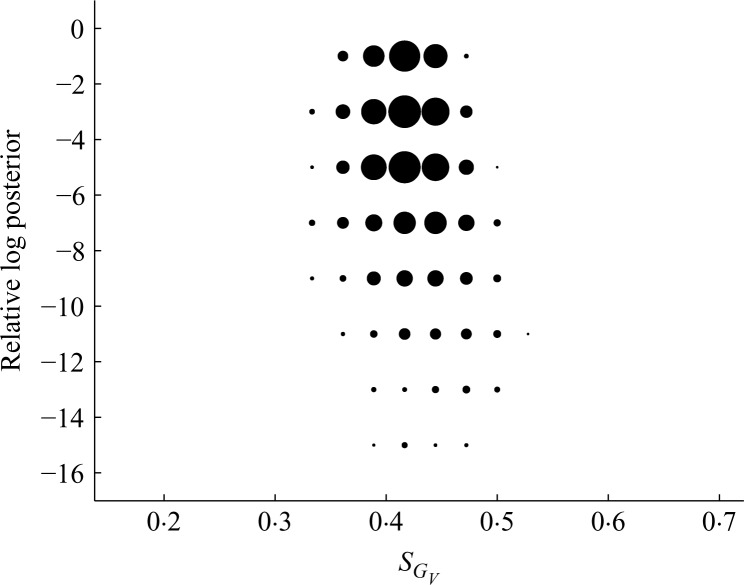
Summary of posterior on sparsity of G_V in the econometric example. Circled areas are proportional to the fraction of posterior sampled graphs at several levels of posterior probability plotted against levels of sparsity S_GV measured as the proportion of edges included.

Graphs with high probability in the region of the mode seem to reflect relevant dependencies in the econometric context. There are strongly evident conditional independencies particularly among subsets of the industrial sectors; see Table 1. Further, the posterior indicates overall sparsity levels through posterior means of about 73% for the proportion of edges included in G_U and about 42% in G_V. Figure 5 further illustrates aspects of the posterior over sparsity for G_V.

8. Further comments

We have introduced Bayesian analysis of matrix-variate graphical models in random sampling and time series contexts. The main innovations include new priors for matrix normal graphical models, use of the parameter expansion approach, inference via Markov chain Monte Carlo for a specific graphical model, evaluation of marginal likelihoods over graphs using coupled candidate’s formula approximations, and the extension of graphical modelling to matrix time series analysis.

On the use of parameter expansion, Roy & Hobert (2007) and Hobert & Marchev (2008) provide theoretical support for the method in Gibbs samplers; in our models, this approach induces tractable and computationally accessible posteriors, leads to good mixing of Markov chain simulations, and is theoretically fundamental to the new model/prior framework in addressing identification issues directly and naturally.

On model identification, an alternative approach might use unconstrained hyper-inverse Wishart priors for each of (U, V) and run the Markov chain Monte Carlo simulation on the unconstrained parameters, similar to a strategy sometimes used in multinomial probit models (McCulloch et al., 2000). It can be argued that this is computationally less demanding than using our explicitly constrained prior and that inferences can be constructed from the simulation output by transforming to constraint-compatible parameters (U υ₁₁, V/υ₁₁). We had considered this, and note that posterior simulation analysis is marginally faster than under the explicitly identified model; in empirical studies, however, we find the computational benefit to be of negligible practical significance. Importantly, this approach relies on a proper prior for the effectively free, unidentified parameter υ₁₁, and is sensitive to that choice. More importantly, the implied prior on (U υ₁₁, V/υ₁₁) is nonstandard and difficult to interpret, and raises questions in prior elicitation and specification; for example, the implied margins for variances are those of ratios of inverse gamma variates and difficult to assess compared to the traditional inverse gamma, and there are now dependencies in priors on left and right covariance matrices. Perhaps most important are the resulting effects on approximate marginal likelihoods; in examples we have studied, the approach yields very different marginal likelihoods and the impact of the marginal prior on the unidentified υ₁₁ plays a key role in that. In contrast, and though very slightly more computationally demanding, the direct and explicitly constrained hyper-inverse Wishart prior is easy to interpret, specify and, with results from Carvalho et al. (2007), implement; synthetic examples have verified the resulting efficacy of the simulation and model search computations.

Our use of candidate’s formula to provide different approximations to marginal likelihoods over graphs can be extended to multiple such approximations. We have explored other constructions, and found no obvious practical differences in the resulting estimates in simulated examples. This is an area open for theoretical investigation and in other model contexts. This also offers a route to extending the analysis here to nondecomposable graphical models.

Our examples are in modest dimensional problems where local move Metropolis–Hastings methods for the graphical model components of the analysis can be expected to be effective, building on experiences in multivariate models (Jones et al., 2005). To scale to higher dimensions, alternative computational strategies such as shotgun stochastic search over graphs (Dobra et al., 2004; Jones et al., 2005; Hans et al., 2007) become relevant. A critical perspective is to define analysis that will rapidly find regions of graphical model space supported by the data. It is far better to work with a small selection of high-probability models than a grossly incorrect model on full graphs, and as dimensions scale the latter quickly becomes infeasible. Shotgun stochastic search and related methods reflect this and offer a path towards faster, parallelizable model search. There is also potential for computationally faster approximations using expectation-maximization style and variational methods (Jordan et al., 1999).

An interesting class of matrix graphical structures arises under autoregressive correlation specifications for the two covariance matrices. This generates a class of Markov random field models that is of potential interest in applications such as texture image modelling. With the matrix data representing a spatial process on a rectangular grid, taking covariance matrices U and V as those of two stationary autoregressive processes provides flexibility in modelling patterns separately in horizontal and vertical directions. We have experimented with examples that suggest potential for this direction in applying the new theory and methods we have presented.