Abstract
There is a serious and growing concern about the increased risk of radiation-induced second cancers and late tissue injuries associated with radiation treatment. To better understand and to more accurately quantify non-target organ doses due to scatter and leakage radiation from medical accelerators, a detailed Monte Carlo model of the medical linear accelerator is needed. This paper describes the development and validation of a detailed accelerator model of the Varian Clinac operating at 6 and 18 MV beam energies. Over 100 accelerator components have been defined and integrated using the Monte Carlo code MCNPX. A series of in-field and out-of-field dose validation studies were performed. In-field dose distributions calculated using the accelerator models were tuned to match measurement data that are considered the de facto ‘gold standard’ for the Varian Clinac accelerator provided by the manufacturer. Field sizes of 4 cm × 4 cm, 10 cm × 10 cm, 20 cm × 20 cm and 40 cm × 40 cm were considered. The local difference between calculated and measured dose on the percent depth dose curve was less than 2% for all locations. The local difference between calculated and measured dose on the dose profile curve was less than 2% in the plateau region and less than 2 mm in the penumbra region for all locations. Out-of-field dose profiles were calculated and compared to measurement data for both beam energies for field sizes of 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm. For all field sizes considered in this study, the average local difference between calculated and measured dose for the 6 and 18 MV beams was 14 and 16%, respectively. In addition, a method for determining neutron contamination in the 18 MV operating model was validated by comparing calculated in-air neutron fluence with reported calculations and measurements. The average difference between calculated and measured neutron fluence was 20%. As one of the most detailed accelerator models for both in-field and out-of-field dose calculations, the model will be combined with anatomically realistic computational patient phantoms into a computational framework to calculate non-target organ doses to patients from various radiation treatment plans.
1. Introduction
The goal of radiation therapy is to deliver an optimal amount of radiation dose to the tumor volume while sparing the dose to surrounding healthy tissues. For most clinical situations, organs far away from the tumor volume are assumed to receive a small amount of radiation dose and are therefore not accounted for as part of the treatment planning. However, it has long been known that such a relatively low level of dose outside the treatment volume can potentially lead to the induction of second cancers in patients after radiation treatment (for a review article on second cancers, see Xu et al (2008)). Recently, there has been a renewed interest in the implication of such second cancers because new treatment delivery techniques tend to increase the scattered and leakage radiation exposure to the patient (Followill et al 1997, Brenner et al 2000, Hall and Wuu 2003, Kry et al 2005a, 2005b, Howell et al 2006, Paganetti et al 2006, Xu et al 2008). Several international committees have recognized the need to address this important issue. The International Commission on Radiological Protection (ICRP 1991) organized a task group on the ‘Evaluation and management of secondary cancer risk in radiation therapy’. The National Council on Radiation Protection and Measurement (NCRP) Scientific Committee 1–17 is finalizing a report on ‘Second cancers and cardiopulmonary effects after radiotherapy’. Also, the American Association of Physicist in Medicine (AAPM) organized a symposium on ‘Secondary cancer risk for emerging radiation treatments’ during the 2006 AAPM annual meeting in Orlando, FL, and subsequently formed a task group 158 on ‘Measurements and calculations of doses outside the treated volume’.
Monte Carlo models of the medical accelerator for scatter and leakage radiation are necessary to assess out-of-field dose up to and beyond 60 cm from the beam isocenter. However, most existing accelerators models do not consider the detailed shielding components that surround the so-called beam-line components in the accelerator head. For the most part, the Monte Carlo methods have been widely used to simulate the primary radiation treatment fields from medical linear accelerators (for a review article, see Verhaegen and Seuntjens (2003)). For most of these studies, particular attention was afforded to modeling in-field (rather than out-of-field) dose distributions in solid phantoms (water or acrylic) in terms of depth–dose and dose profile curves. Only the beam-line components—such as the target, primary collimator, flattening filter, jaws and multi-leaf collimator—were modeled. Treatment planning systems using Monte Carlo have also been developed (Hartmann Siantar 2001 and Rogers et al 2004). For other studies, please refer to the AAPM Task Group Report No 105 (Chetty et al 2007). Although these studies reported excellent agreement between calculated and measured data, the out-of-field dose distribution was typically ignored. A few groups have used Monte Carlo methods to simulate the out-of-field dose distributions from medical linear accelerators. Kry et al (2006, 2007) described a method for modeling and validating both 6 and 18 MV beams of a Varian Clinac accelerator for out-of-field Monte Carlo dosimetry studies. Both beam-line and secondary shielding were modeled. The secondary shielding includes several components consisting of lead, tungsten and iron that surround the beam-line components. Another study by Lehmann et al (2006) compared out-of-field doses from measurement and Monte Carlo simulations at locations less than 15 cm from the central axis. But the authors only modeled the beam-line components ignoring the influence of the secondary shielding on the out-of-field dose. For the most part, both of these studies did not examine techniques to reduce the dose outside the treatment field. Furthermore, these past studies typically did not use computational patient phantoms that contain well-defined organs for either measurement or Monte Carlo calculation. To quantify the organ doses from the out-of-the-field irradiation, one needs to combine the accelerator model with whole-body computational phantoms. The use of Monte Carlo methods with whole-body patient computational phantoms, although very powerful in understanding organ doses to the exposed patient, has not been widely practiced due partially to a number of technical difficulties (Xu et al 2008).
This paper describes a study to develop and validate detailed Monte Carlo computational models of a Varian Clinac medical linear accelerator, containing the necessary shielding surrounding the beam-line components, operating at 6 and 18 MV beam energies (Bednarz 2008). The validation process involved tuning the initial electron beam parameters in order to match calculated in-field dose distributions with de facto ‘gold standard’ measurement data from the manufacturer (Kry 2008). The out-of-field photon dose distributions were compared with published measurements (Kry et al 2006, 2007). Furthermore, this paper also compares neutron contamination from the 18 MV operating mode to measurement data (Kry et al 2007). Finally, this paper discusses how the accelerator models will be used to quantify intermediate-and low-level radiation doses to patients during radiation treatments and to help remedy strategies to reduce such dose. In a subsequent paper, the methods and results to apply the accelerator modeling to non-target organ dose calculations will be presented in detail based on a recent doctoral thesis (Bednarz 2008).
2. Methods and materials
2.1. The Varian Clinac accelerator model
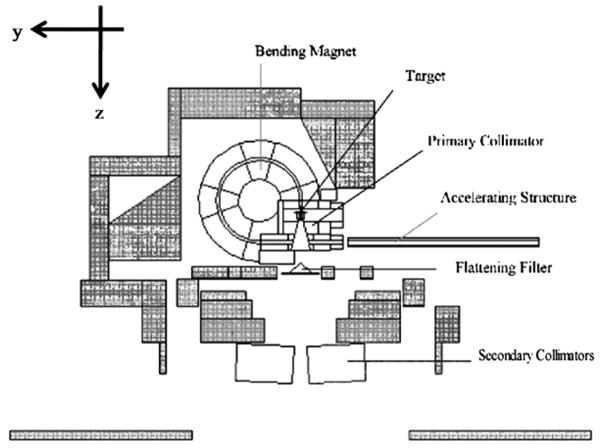
A composite of information from various sources was used to model the geometries and materials of the accelerator components. The beam-line component geometries and materials were based on detailed blueprints provided by the vendor (Varian Medical Systems, Palo Alto, CA). An 80-leaf MLC was also modeled based on the vendor blueprints. Shielding geometries and materials were adopted from information provided by Kase et al (1998). Figure 1 illustrates the in-plane plot of the medical accelerator model. The coordinate system of the accelerator model is defined as follows: the positive-z direction extends from the electron target toward the isocenter (beam-line), the positive-x direction extends from the isocenter toward the right edge of the treatment couch (cross-plane) and the positive-y direction extends from the isocenter toward the direction away from the gantry (in-plane). Figure 1 also labels several beam-line and secondary shielding components shaded in gray.
Figure 1.
Plot of the Varian Clinac accelerator model using the plotting feature in the MCNPX code. All secondary shielding components are shaded in gray. The MLC was modeled although not plotted here.
2.2. In-field validation of the accelerator model
The percent depth dose (PDD) and lateral dose profile data were calculated for a simulated water phantom for both the 6 and 18 MV beams. The water phantom had dimensions of 140 cm × 140 cm × 35 cm, and was placed at a source-to-surface distance (SSD) of 100 cm from the center of the target. The gantry was assumed to be at the 03 for all simulations. The type 1 electron ‘pedep’ mesh tally was used to score the absorbed dose to voxels inside the phantom (Hendricks et al 2004). The voxel dimensions for the simulations varied with position from the beam central axis in order to account for dose gradients in the PDD and lateral dose profile curves. For both the 6 and 18 MV beams, PDDs and lateral dose profiles were generated for 4 cm × 4 cm, 10 cm × 10 cm, 20 cm × 20 cm and 40 cm × 40 cm field sizes. The PDDs were tallied along the central axis. The lateral dose profiles were calculated in the cross-plane direction at depths of dmax, 5, 10 and 20 cm, respectively. All distributions were normalized to the maximum dose depending on the particular field size. The calculated PDDs and lateral dose profiles were then compared to measurement data produced by the machine’s manufacturer as the de facto ‘gold standard’ for this particular accelerator model (Kry 2008).
The in-field validation of the accelerator model followed a fine-tuning procedure to adjust the parameters as described in several previous studies (Sheikh-Bagheri and Rogers 2002, Keall et al 2005, Cho et al 2005). The FWHM of the electron-beam Gaussian energy distribution was kept constant at 3% of the mean for all simulations. Several iterations adjusting both the mean energy and radial intensity distribution of the electron beam were performed until the agreement between the calculated PDD and lateral dose profile curves and measured data were within the pre-defined acceptance criteria: for the PDD curves the average of the percent local difference between the measured and calculated dose in the fall-off region (dmax to 30 cm) had to be less than 2%; for the dose profile curves the average of the percent local difference between the measured and calculated dose in the plateau region had to be less than 2% and the average distance in the penumbra region had to be less than 0.2 cm. It was determined that for the 6 MV beam, the mean energy of the electron beam was consistent with Kry et al (2006) at 6.2 MeV, but the FWHM of the spatial spread was 1.3. For the 18 MV beam, the FWHM of the spatial spread of the electron beam was consistent with Kry et al (2007) at 1 mm, but the mean energy was 18.3 MeV.
2.3. Out-of-field validation of the accelerator model
2.3.1. Photons
Next, using the initial beam parameters determined from the previous in-field benchmark, the photon dose distributions outside the treatment field were simulated for both the 6 and 18 MV beams. The out-of-field in-plane lateral dose profiles were also evaluated using a type 1 electron ‘pedep’ mesh tally (Hendricks et al 2004) in a 140 cm × 140 cm × 35 cm acrylic phantom at 100 cm SSD. The acrylic phantom had a composition of 8% hydrogen, 60% carbon and 32% oxygen. For all simulations, the voxel dimensions were 2 cm in the beam-line direction, 5 cm in the cross-plane direction and 1 cm in the in-plane direction. The large voxel size helped to reduce the statistical uncertainty of the calculated dose in each voxel. It has been previously reported that large voxel sizes are acceptable for out-of-field dose simulations (Kry et al 2006, 2007). The out-of-field absolute dose profiles were determined for field sizes of 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm for both the 6 and 18 MV beams. The MLC in the accelerator was used to define the 4 cm × 4 cm field, where the jaws were set to 4.2 cm × 4.2 cm. The 10 cm × 10 cm and 20 cm × 20 cm fields were defined by the jaws and the MLC was retracted. All profiles were calculated at a 3.75 cm depth in the acrylic phantom. The calculated profiles were compared to measurement data provided by Kry et al (2006, 2007) for the same type of accelerators and field set-up.
The tally result provided by MCNPX is normalized per source history. In order to determine the absolute dose from each field size, the dose per source electron in MCNPX was converted to dose per cGy in the following manner. First, a water tank was modeled at 100 cm SSD, and the number of electrons needed to deliver 1 cGy at dmax in the tank under reference conditions (i.e. 10 cm × 10 cm field with the MLCs retracted) was determined. The resulting value gives a conversion factor between dose per source particle and dose per cGy. Assuming that the accelerator delivers 1 cGy MU−1, the final out-of-field dose is provided in dose per MU. The number of source electrons required to produce 1 cGy at dmax was kept constant for all field sizes. Keeping this value constant for all field sizes could possibly hide discrepancies in the output factor, since the dose at dmax changes with different field sizes. However, as pointed out by Kry et al (2006), the dependence of dose at dmax on field size is rather insignificant when calculating dose outside the treatment field.
2.3.2. Neutrons
Neutron contamination occurs in high-energy radiotherapy beams as a result of photonuclear interactions in the medical accelerator head. Consequently, neutrons will contribute to the out-of-field dose during high-energy treatments, typically from 10 to 18 MV beam energies. To characterize the neutron contamination in the 18 MV Varian Clinac medical accelerator, direct neutron fluences from the accelerator head were calculated in air at various locations along the y-axis (in-plane) in the patient plane. Only the direct neutron fluence was considered in this study since the scattered and thermal neutron fluences depend on the specific treatment room that houses the accelerator. Although the scattered and thermal neutron fluence will contribute to the out-of-field dose, the contribution of these components to the neutron fluence near the patient is rather insignificant compared to the contribution of direct neutrons (Pena et al 2005). The fluences were calculated using a point detector tally (F5:n) (Hendricks et al 2004). The F5 tally is considered a partial deterministic method implemented into MCNPX. At every source and collision site the F5 tally scores the probability that a pseudoparticle will reach the detector without undergoing any further interactions. The use of the F5 tally for calculating neutron fluences from medical accelerators has been previously reported (Facure et al 2007). Three different field sizes were considered: a closed field with both the MLC and jaws fully closed, a 9 cm × 9 cm MLC-defined field with the jaws set to 10 cm × 10 cm and a 20 cm × 20 cm field defined by the jaws with the MLC retracted. The field sizes are consistent with those found in Kry et al (2007) who reported calculated and measured in-air fluences at several out-of-field locations for various field sizes. The calculated neutron fluences were compared to calculated fluences provided by Kry et al (2007) and Howell et al (2005) and measured neutron fluences provided by Kry et al (2007).
Since thermal neutrons were not measured by Kry et al (2007), the cut-off energy for neutron simulations in our study was set to the cadmium cut-off energy of 0.6 eV. In order to reduce computation time, the photon and electron cut-off energies were both set to 5 MeV. The high photon and electron cut-offs are reasonable since only neutrons are tracked and these values are well below the photonuclear threshold energies for all materials in the problem geometry.
3. Results and discussion
The following sections summarize the results of the in-field and out-of-field validation of the 6 and 18 MV Varian Clinac 2100C accelerator model. All simulations were run on a 3 GHz Intel® CPU. For the 6 MV in-field simulations, a total of 3 × 107 initial source electrons were sampled. For the 18 MV in-field simulations, a total of 1 × 107 source electrons were sampled. For the 6 MV out-of-field simulations, a total of 5 × 107 electrons were sampled for the 4 cm × 4 cm and 10 cm × 10 cm fields and 3 × 107 electrons were sampled for the 20 cm × 20 cm field. For the 18 MV beam, a total of 1 × 107 electrons were sampled for the 4 cm × 4 cm and 10 cm × 10 cm fields and 7 × 106 electrons were sampled for the 20 cm × 20 cm field. The 20 cm × 20 cm field required less source electrons since more collisions occurred in the phantom due to the larger field size.
3.1. In-field photon dose comparison between calculations and measurements
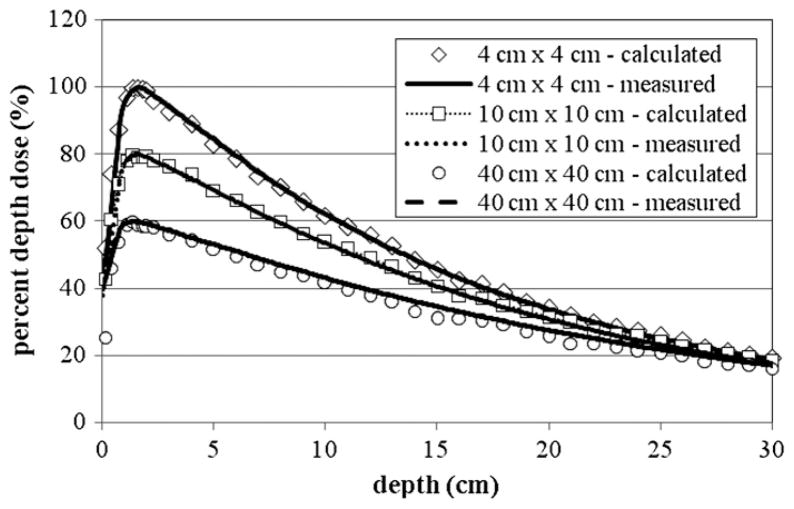
Figure 2 shows the PDD curves for the 6 MV beam for the 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields, where good agreement between the calculated and measured photon dose values can be seen. Using the criteria described earlier, acceptable agreement was also achieved for the 10 cm × 10 cm and 4 cm × 4 cm fields. The calculated dmax for the 10 cm × 10 cm field was 1.4 cm compared to a measured value of 1.5 cm. For all doses below the dmax, the average local difference between the measured and calculated PDD curves was 1.6%. The depth at maximum dose (dmax) for the 4 cm × 4 cm field was calculated to be 1.6 cm, which compares well with the measured value of 1.7 cm. For all doses below dmax, the average local difference between the measured and calculated PDD curves was 1.4%. Good agreement was also achieved for the 40 cm × 40 cm field. The calculated dmax was equal to the measured value at 1.4 cm. For all doses below the dmax, the average local difference between the measured and calculated PDD curves was 1.8%. For each tally the uncertainty was less than 2%.
Figure 2.
The PDD curves from the 6 MV beam for the 4 cm × 4 cm, 10 cm × 10 cm and 40 cm × 40 cm fields. The 10 cm × 10 cm field was scaled by 80% and the 40 cm × 40 cm field was scaled by 60% for clarity. Measurement data were produced by the machine’s manufacturer as the ‘gold standard’ for this particular accelerator model (Kry 2008). For each tally the relative error was less than 2%. The relative error is the standard deviation of the mean dose value divided by the mean.
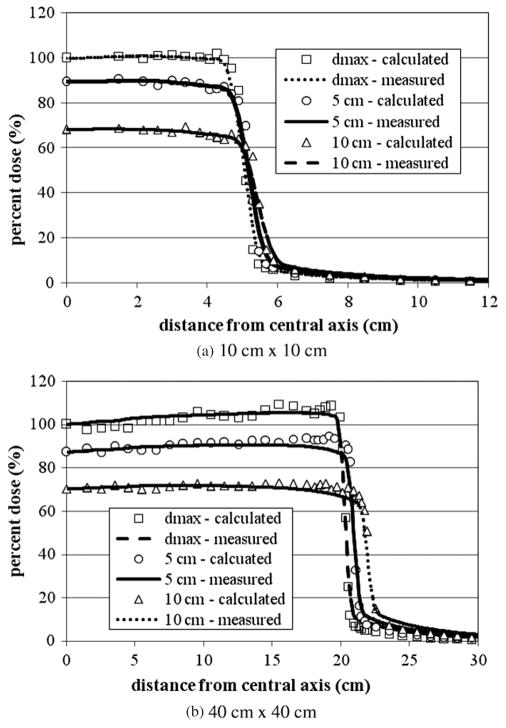
Figures 3(a) and (b) show the 6 MV lateral dose profiles for the 10 cm × 10 cm and 40 cm × 40 cm fields. Despite being calculated, the other fields have been left out to avoid redundancy. For each field size presented in figure 3, three different lateral dose profiles are provided for depths of dmax, 5 and 10 cm. For all fields considered, the average local difference between the calculated and measured dose on the plateau region was within the acceptance criteria of 2%. The average distance between the calculated and measured dose in the penumbra region for all curves was also within the acceptance criteria of 2 mm. For each tally the relative error was less than 2%.
Figure 3.
6 MV lateral dose profiles for (a) 4 cm × 4 cm, (b) 10 cm × 10 cm and (c) 20 cm × 20 cm fields at depths of 5, 10 and 20 cm. All curves are normalized to dose at dmax. For each tally the relative error was less than 2%. Measurement data were produced by the machine’s manufacturer as the de facto ‘gold standard’ for this particular accelerator model (Kry 2008).
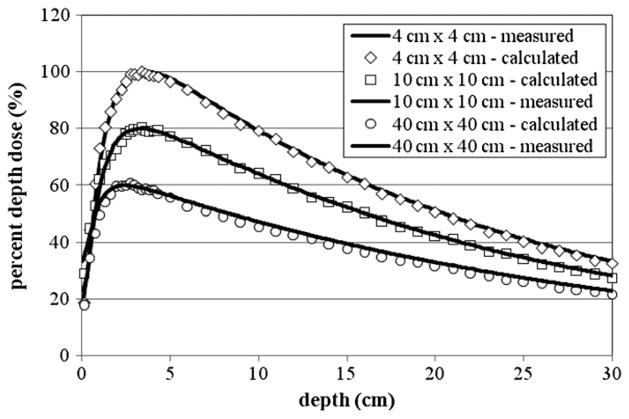
The PDD curves for the 18 MV beam are provided in figure 4 for 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields. The best agreement between the calculated and measured dmax was achieved for the 10 cm × 10 cm field, where the calculated and measured dmax values were both 3.4 cm. For this case, the average local difference between the calculated and measured dose beyond dmax was 1.06%. Good agreement was also achieved for the 4 cm × 4 cm field, where the calculated dmax was 3.4 cm, which compares well with the measured dmax of 3.6 cm. The average local difference between calculated and measured doses beyond dmax was 1.50%. For the 40 cm × 40 cm PDD, the calculated dmax of 2.6 cm was different than the measured dmax of 2.5 cm. The average local difference between calculated and measured doses beyond dmax was 0.72%.
Figure 4.
The PDD curves from the 18 MV beam for 4 cm × 4 cm, 10 cm × 10 cm and 40 cm × 40 cm fields. The 10 cm × 10 cm field was scaled by 80% and the 40 cm × 40 cm field was scaled by 60% for clarity. For each tally the relative error was less than 2%. Measurement data were produced by the machine’s manufacturer as the de facto ‘gold standard’ for this particular accelerator model (Kry 2008).
Figures 5(a) and 6(b), (c) show the lateral dose profiles for the 18 MV beam for 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields. Three different lateral dose profiles at depths of dmax, 5 and 10 cm are provided for each field size. There was good agreement between the calculated and measured lateral dose profiles. Once again, for all curves the average local difference between the measured and calculated dose in the plateau region was within the acecptance criteria of 2%. The average distance between the measured and calculated dose in the penumbra region was also within the 2 mm acceptance criteria.
Figure 5.
The 18 MV lateral dose profiles for (a) 10 cm × 10 cm and (b) 40 cm × 40 cm fields at depths of dmax, 5 and 10 cm. No plot is provided for the 40 cm × 40 cm field at a depth of dmax since no measurement data were available at the time of the study. All curves are normalized to dose at dmax. In order to improve clarity in (a), the calculated and measured data for depths of 5 and 10 cm are reduced by 20 and 40%, respectively. Measurement data were produced by the machine’s manufacturer as the de facto ‘gold standard’ for this particular accelerator model (Kry 2008).
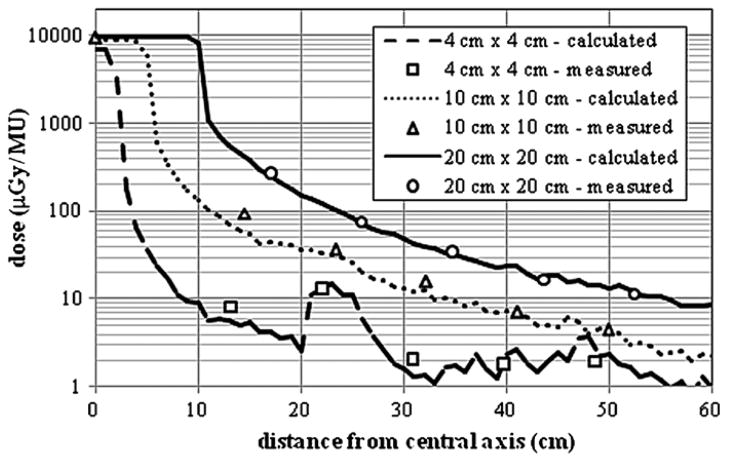
Figure 6.
Comparison of measured and calculated out-of-field dose profile data from the 6 MV beam for field sizes of 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm at a depth of 3.75 cm in an acrylic phantom. The measurement data shown in the figure were taken from Kry et al (2006).
3.2. Out-of-field dose comparison between calculations and measurements
The results of the out-of-field dose validation are presented in the following sections. In section 3.2.1 comparisons of out-of-field photon dose between calculations and measurements for both the 6 and 18 MV beams are provided. Section 3.2.2 provides a comparison between in-air out-of-field neutron fluence calculations and measurements for the 18 MV beam.
3.2.1. Photons
A comparison of measured and calculated out-of-field absolute dose data from the 6 MV beam for field sizes of 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm is provided in figure 6. There is good agreement between calculated and measured out-of-field absolute doses for all field sizes considered. The best agreement was achieved for the 20 cm × 20 cm field, where the average difference between the calculated and measured absolute dose was 6.2% with differences never exceeding 10.7% for distances less than 60 cm from the isocenter. For the 10 cm × 10 cm field, the average local difference was 14.2% with differences never exceeding 34% for distances less than 60 cm from the isocenter. Acceptable agreement was also seen for the 4 cm × 4 cm field where the average local difference between the calculated and measured out-of-field absolute dose was 21% with differences never exceeding 30%. Most of the difference is due to points far away from the isocenter. The ‘spike’ seen in both the measured and calculated out-of-field dose distributions is due to the effects of the abrupt ending of the MLC in this region. The dose just outside the MLC leaves is substantially higher because of the absence of this additional shielding. The spikes are not seen in the larger field sizes because the MLC was extracted for these calculations and measurements. The statistical uncertainties in the calculated doses were less than 10% for distances up to 25 cm from the central axis. The average statistical uncertainty in calculated doses up to 60 cm from the central axis was 19, 14 and 6% for the 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields, respectively. The decrease in statistical uncertainty with increasing field is due to higher photon fluence in the out-of-field region from larger field sizes. The uncertainty in the measurements reported by Kry et al (2006) was 1.9%.
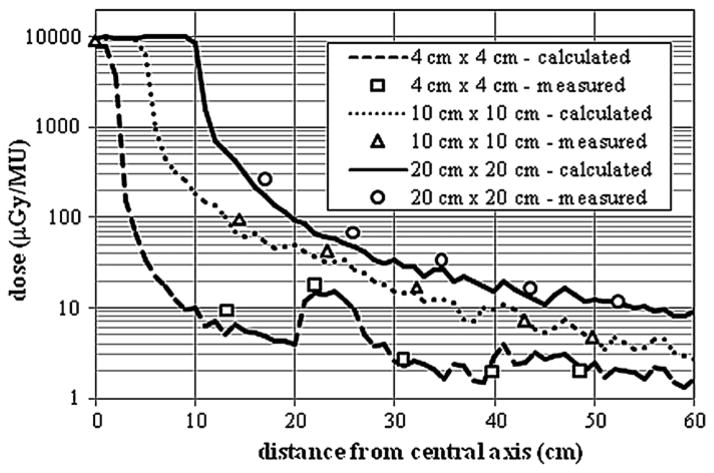
Figure 7 shows a comparison of the measured and calculated out-of-field absolute dose from the 18 MV beam for 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields. Once again, acceptable agreement was achieved between calculated and measured out-of-field absolute doses for all field sizes. The best agreement was achieved for the 10 cm × 10 cm field, where the average local dose difference was 11.5%. Good agreement was also achieved for the 20 cm × 20 cm field. The average local difference between calculated and measured out-of-field absolute doses for distances less than 60 cm from the field edge was 19.4%. Acceptable agreement was achieved for the 4 cm × 4 cm field where the average local difference between the calculated and measured absolute dose was 18.6% for distances less than 60 cm from the field edge. Again, the dose ‘spike’ in the 4 cm × 4 cm profiles was due to the effects of the sudden ending of the MLC in this region. The statistical uncertainties in the calculated doses were less than 10% for distances up to 25 cm from the central axis. The average statistical uncertainty in calculated doses up to 60 cm from the central axis was 19, 10 and 8% for the 4 cm × 4 cm, 10 cm × 10 cm and 20 cm × 20 cm fields, respectively. Again, this decrease in uncertainty is due to higher concentrations of photons in the out-of-field region from larger field sizes. The uncertainty in the measurements reported by Kry et al (2006) was 3.2%. The uncertainty for each tally ranged from less than 1% along the isocenter to 25% at the furthest distance from the isocenter.
Figure 7.
Comparison of measured and calculated out-of-field absolute dose data from the 18 MV beam for field sizes of 4 cm × 4 cm, 10 cm × 10 cm and 25 cm × 25 cm at a depth of 3.75 cm in an acrylic phantom. The measurement data plotted in the figure were taken from Kry et al (2007).
3.2.2. Neutrons
Calculated in-air neutron fluences for a closed field and field sizes of 9 cm × 9 cm and 20 cm × 20 cm are compared with calculated and measured neutron fluences reported by Kry et al (2007) and Howell et al (2005) in table 1. The calculated and measured fluences provided by these authors were from the same accelerator model, using the same field sizes and measurement locations. The fluence data calculated in this study and the calculated data provided by Kry et al (2007) differ by less than 9.5% averaged for all locations which is very good considering the possible differences in the accelerator modeling, including variations in the accelerator head and room geometries and differences in the photonuclear cross-section data used for the simulations. The largest differences were on the central axis for the closed field and the 20 cm × 20 cm field, which were 16 and 17.5%, respectively. The average percent difference between our calculations and those provided by Howell et al (2005) was 13.7%. Calculated fluence data were also compared to measured fluence data provided by Kry et al (2007). The calculated neutron fluence systematically overestimated the measured neutron fluence for almost all locations. While the worst agreement between calculation and measurement was 39% for the 9 cm × 9 cm field at a distance of 30 cm from the central axis, on average the percent difference for all locations was 20%. Considering the large errors in the measurement data, which were estimated to be 10% (Kry et al 2007), this agreement is also satisfactory.
Table 1.
In-air neutron fluences from the 18 MV accelerator model calculated at different distances from the central axis for different field sizes. The positive distances correspond to positions extending from the isocenter to the front end of the accelerator and the negative distances correspond to positions extending from the isocenter toward the accelerator gantry. The isocenter is located at 0 cm. Calculated neutron fluences from this study are compared to calculated and measured neutron fluences reported by Kry et al (2007) and Howell et al (2005). All neutron fluences calculated in this study had relative errors below 2%. Kry et al (2007) reported relative errors below 1 and 10% for their calculated and measure neutron fluences, respectively
| Field size (cm2) | Distance (cm) | Calculated (103 n cm−2 MU−1)
|
Measured (103 n cm−2 MU−1)
|
||||
|---|---|---|---|---|---|---|---|
| This study | Reported by Kry et al (2007) | Reported by Howell et al (2005) | Percent differencea | Reported by Kry et al (2007) | Percent differenceb | ||
| 0 × 0 | +60 | 82.3 | 98 | – | −16.0 | 78 | 5.60 |
| +30 | 98.5 | 103 | – | −4.40 | 75 | 31.3 | |
| +21 | 85.8 | – | 116 | −26.0 | – | – | |
| 0 | 85.9 | 103 | – | −16.0 | 89 | −3.50 | |
| −30 | 91.0 | 93 | – | −2.20 | 83 | 9.60 | |
| 5 × 5 | 21 | 97.7 | – | 115 | −15.0 | – | – |
| 9 × 9 | +60 | 88.8 | 95 | – | −6.50 | 109 | −18.5 |
| +30 | 111.2 | 104 | – | 6.90 | 80 | 39.0 | |
| −30 | 99.8 | 93 | – | 7.40 | 74 | 34.9 | |
| 10 × 10 | +21 | 106 | – | 106 | 0.0 | – | – |
| 20 × 20 | 0 | 204.5 | 174 | – | 17.5 | 160 | 27.8 |
| −50 | 92.7 | 86 | – | 7.80 | 102 | −9.10 | |
Percent difference is given as the difference between the fluences calculated in this study and the fluence calculated by Kry et al (2007) or Howell et al (2005) divided by the fluence calculated by Kry et al (2007) or Howell et al (2005) times 100.
Percent difference is given as the difference between the fluence calculated in this study and the fluence measured by Kry et al (2007) divided by the fluence measured by Kry et al (2007) times 100.
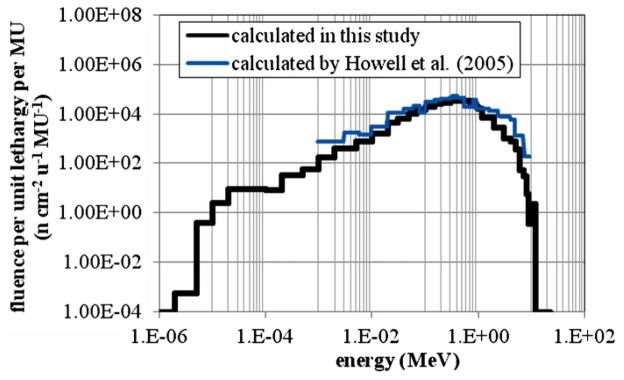
The neutron fluence (per unit lethargy per unit MU) as a function of energy is shown in figure 8 at a distance of 21 cm from the central axis in the in-plane direction. The calculated neutron fluence from this study is compared to the calculated neutron fluence spectrum provided by Howell et al (2005) for the same irradiation conditions. The average energy of the calculated neutron spectrum was 0.55 MeV, which agrees within statistical uncertainties with the average energy of 0.51 MeV calculated by Howell et al (2005).
Figure 8.
Neutron fluence spectrum from direct neutrons at a distance of +21 cm from the central axis in the in-plane direction. The fluence is normalized per unit lethargy, u, and MU.
3.3. Comparison of calculation versus measurement
The following section addresses the differences between calculated and measured dosimetry data presented in this paper. The agreement between calculated and measured in-field dose distributions was within the acceptance criteria discussed in section 2.2. For the most part, this agreement can be attributed to the rigorous tuning procedure that was used to determine the optimal initial electron beam parameters for both accelerator models. The matching criteria established between calculation and measurement were similar to criteria that have been previously reported (Keall et al 2005, Cho et al 2005). In addition, the modification to the default indexing method in MCNPX by invoking the ITS indexing method improved the accuracy of the transport of primary and secondary electrons. Kim et al (2006) used MCNPX to calculate in-field dose distributions from 6 and 10 MV beams. The group reported an agreement within 2% of measurement at depths beyond dmax for the PDD curve. For the lateral dose profile curves, the calculated dose on the plateau region agreed with measurement within 2%, while in the penumbra region agreement was within 1 mm. The agreements presented in this paper are markedly similar to those presented by Kim et al (2006).
The agreement between calculated and measured out-of-field photon dose distributions was not as accurate as the in-field dose agreement. However, the larger differences in the out-of-field region were expected (Kry et al 2006, 2007), since these regions are subjected to lower radiation doses, and larger uncertainties in the calculated data were unavoidable. Again, for very large distances from the central axis, the calculated out-of-field dose reported in this paper for the 6 and 18 MV beams had relative errors exceeding 20%. Large relative errors in calculated out-of-field dose data were also reported by Kry et al (2006, 2007), which reached values of 20%. Despite these differences the agreement reported in this paper compares well with the agreement of calculated and measured dose provided in Kry et al (2006, 2007). The average local differences between calculation and measurement for all field sizes were 14 and 16% for the 6 and 18 MV beam, which are similar to the differences reported by Kry et al (2006, 2007) of 16 and 17%, respectively. Similarly, the calculated neutron fluences in this study agree within statistical uncertainties with the measured fluences reported by Kry et al (2007).
The advantages of using Monte Carlo methods over detailed measurements for quantifying dose outside the treatment volume during radiation treatments has recently been discussed (Xu et al 2008, Bednarz and Xu 2008). To experimentally measure organ doses from radiation treatments requires placing several dosimeters in corresponding cavity locations inside an anthropomorphic physical phantom. Such measurements are laborious, time consuming and can lead to an overestimate or underestimate of the true organ dose value since optimal dosimetry locations are often uncertain. Alternatively, the detailed structures of the patient and accelerator can be accurately described in Monte Carlo codes. Currently, several anatomically detailed computational phantoms have been adopted into Monte Carlo codes for organ dose calcualtions (Xu et al 2008). The validated accelerator models presented in this paper can be combined with whole-body computational phantoms to calculate organ doses from selected treatment plans. In a subsquent paper, a computational framework that integrates the accelerator models validated in this paper with anatomically realistic patient phantoms will be presented using data from a doctoral research project (Bednarz 2008). Various treatment plans will be used to calculate organ equivalent doses for several phantoms including adult male, adult female and pediatric patients. Risks for radiation-induced second cancers associated with these exposures will be calculated and analyzed to demonstrate the usefulness of these tools in the management of second cancer exposure in radiotherapeutically treated patients.
4. Conclusions
This paper described the development and validation of a detailed Monte Carlo model of the Varian Clinac accelerator operating at 6 and 18 MV beam energies for both in-field and out-of-field radiation componenets. This work was motivated by the need to develop accurate computational tools to assess organ-averaged equivalent doses in various organs of the patients during radiation therapy treatments. Such relatively low levels of exposures have been linked to radiation-induced second cancers in patients that develop sometime later in their lifetimes. The quantifications of such exposures are expected to improve an understanding of radiation-induced second cancer risk from radiation therapy treatments and to aid in the development of strategies to reduce these exposures.
Acknowledgments
This project was funded in part by a National Cancer Institute grant (R01CA116743). The authors would like to thank Dr Stephen Kry for prodiving measurement data used in this work.
References
- Bednarz B, Xu XG. A feasibility study to calculate unshielded fetal doses to pregnant patients in 6-MV photon treatments using Monte Carlo methods and anatomically realistic phantoms. Med Phys. 2008;35:3054–61. doi: 10.1118/1.2938519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednarz B. PhD Dissertation. Rensselaer Polytechnic Institute; New York: 2008. Detailed Varian Clinac accelerator modeling for calculating intermediate- and low-level non-target organ doses from radiation treatments. [Google Scholar]
- Brenner DJ, Curtis RE, Hall EJ, Ron E. Second malignancies in prostate carcinoma patients after radiotherapy compared with surgery. Cancer. 2000;88:398–406. doi: 10.1002/(sici)1097-0142(20000115)88:2<398::aid-cncr22>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- Chetty I, et al. Report of the AAPM Task Group No. 105: issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys. 2007;34:4818–53. doi: 10.1118/1.2795842. [DOI] [PubMed] [Google Scholar]
- Cho SH, et al. Reference photon dosimetry data and reference phase space data for the 6-MV photon beam from Varian Clinac 2100 series linear accelerators. Med Phys. 2005;32:137–48. doi: 10.1118/1.1829172. [DOI] [PubMed] [Google Scholar]
- Facure A, Da Silva AX, Falcao RC. Monte Carlo simulation of scattered and thermal photoneutron fluences inside a radiotherapy room. Radiat Prot Dosim. 2007;123:56–61. doi: 10.1093/rpd/ncl080. [DOI] [PubMed] [Google Scholar]
- Followill D, Geis P, Boyer A. Estimates of whole-body dose equivalent produced by beam intensity modulated conformal therapy. Int J Radiat Oncol Biol Phys. 1997;38:667–72. doi: 10.1016/s0360-3016(97)00012-6. [DOI] [PubMed] [Google Scholar]
- Hartmann Siantar CL. Description and dosimetric verification of the PEREGRINE Monte Carlo dose calculation system for photon beams incident on a water phantom. Med Phys. 2001;28:1322–37. doi: 10.1118/1.1381551. [DOI] [PubMed] [Google Scholar]
- Hall E, Wuu CS. Radiation induced second cancers: the impact of 3D-CRT and IMRT. Int J Radiat Oncol Biol Phys. 2003;56:83–89. doi: 10.1016/s0360-3016(03)00073-7. [DOI] [PubMed] [Google Scholar]
- Hendricks, et al. MCNPX version 2.5.0 LA-UR-04-0569. Los Alamos, NM: 2004. [Google Scholar]
- Howell R, Ferenci M, Hertel N, Fullerton G. Investigation of secondary neutron dose for 18 MV dynamic MLC IMRT delivery. Med Phys. 2005;32:786–93. doi: 10.1118/1.1861162. [DOI] [PubMed] [Google Scholar]
- Howell RM, Hertel NE, Wang Z, Hutchinson J, Fullerton GD. Calculation of effective dose from measurement of secondary neutron spectra and scattered photon dose from dynamic MLC IMRT for 6-MV, 15-MV, and 18-MV beam energies. Med Phys. 2006;33:360–8. doi: 10.1118/1.2140119. [DOI] [PubMed] [Google Scholar]
- ICRP. 1990 Recommendations of the ICRP Publication. Vol. 60. Oxford: Pergamon; 1991. [Google Scholar]
- ICRU. Report. Vol. 49. Bethesda, MD: ICRU; 1993. Stopping Powers and Ranges for Protons and Alpha Particles. [PubMed] [Google Scholar]
- Jeraj R, Keall P, Ostwald P. Comparison between MCNP, EGS4, and experiment for clinical electron beams. Phys Med Biol. 1999;44:705–17. doi: 10.1088/0031-9155/44/3/013. [DOI] [PubMed] [Google Scholar]
- Kawrakow I, Fippel M, Friedrich K. 3D electron dose calculation using a voxel based Monte Carlo algorithm (VMC) Med Phys. 1996;23:445–57. doi: 10.1118/1.597673. [DOI] [PubMed] [Google Scholar]
- Kase KR, Mao XS, Nelson WR, Liu JC, Kleck JH, Elsalim M. Neutron fluence and energy spectra around the Varian clinac 2100C/2300C medical accelerator. Health Phys. 1998;74:38–47. doi: 10.1097/00004032-199801000-00005. [DOI] [PubMed] [Google Scholar]
- Keall P, et al. Determining the incident electron fluence for Monte Carlo-based photon treatment planning using standard measured data set. Med Phys. 2005;30:574–82. doi: 10.1118/1.1561623. [DOI] [PubMed] [Google Scholar]
- Kim HK, et al. Monte Carlo simulations of the photon beam characteristics from medical linear accelerators. Radiat Prot Dosim. 2006;119:510–3. doi: 10.1093/rpd/nci636. [DOI] [PubMed] [Google Scholar]
- Kry SF. Personnel communication. 2008.
- Kry SF, Salehpour M, Followill DS, Stovall M, Kuban DA, White RA, Rosen II. Out-of-field photon and neutron dose equivalents from step-and-shoot intensity-modulated radiation therapy. Int J Radiat Oncol Biol Phys. 2005a;62:1204–16. doi: 10.1016/j.ijrobp.2004.12.091. [DOI] [PubMed] [Google Scholar]
- Kry SF, Salehpour M, Followill DS, Stovall M, Kuban DA, White RA, Rosen I. The calculated risk of fatal secondary malignancies from intensity-modulated radiation therapy. Int J Radiat Oncol Biol Phys. 2005b;621:195–203. doi: 10.1016/j.ijrobp.2005.03.053. [DOI] [PubMed] [Google Scholar]
- Kry SF, Titt U, Ponisch F, Followill DS, Vassiliev ON, White RA, Mohan R, Salehpour M. A Monte Carlo model for calculating out-of-field dose from a Varian 6-MV beam. Med Phys. 2006;33:4405–13. doi: 10.1118/1.2360013. [DOI] [PubMed] [Google Scholar]
- Kry SF, Titt U, Followill DS, Ponisch F, Vassiliev ON, White RA, Stovall M, Salehpour M. A Monte Carlo model for out-of-field dose calculation from high-energy photon therapy. Med Phys. 2007;34:3489–99. doi: 10.1118/1.2756940. [DOI] [PubMed] [Google Scholar]
- Lehmann J, et al. Dosimetry for quantitative analysis of the effects of low-dose ionizing radiation in radiation therapy patients. Radiat Res. 2006;165:240–7. doi: 10.1667/rr3480.1. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Bortfeld T, Delaney TF. Neutron dose in proton radiation therapy: in regard to Eric J. Hall. Int J Radiat Oncol Biol Phys. 2006;66:1595. doi: 10.1016/j.ijrobp.2006.08.005. [DOI] [PubMed] [Google Scholar]
- Pena J, et al. Monte Carlo study of Siemens Primus photoneutron production. Phys Med Biol. 2006;50:5921–33. doi: 10.1088/0031-9155/50/24/011. [DOI] [PubMed] [Google Scholar]
- Rogers DWO, Walters B, Kawrakow I. NRC Report PIRS 509(a) revH. 2004. BEAMnrc Users Manual. [Google Scholar]
- Sheikh-Bagheri D, Rogers DWO. Monte Carlo calculation of nine megavoltage photon beam spectra using the BEAM code. Med Phys. 2002;29:391–402. doi: 10.1118/1.1445413. [DOI] [PubMed] [Google Scholar]
- Stovall M, et al. Fetal dose from radiotherapy with photon beams: report of AAPM Radiation Therapy Committee Task Group No. 36. Med Phys. 1995;22:63–82. doi: 10.1118/1.597525. [DOI] [PubMed] [Google Scholar]
- Titt U, et al. A flattening filter free photon treatment concept evaluation with Monte Carlo. Med Phys. 2006;33:1595–602. doi: 10.1118/1.2198327. [DOI] [PubMed] [Google Scholar]
- Verhaegen F, Seuntjens J. Monte Carlo modeling of external radiotherapy photon beams. Phys Med Biol. 2003;48:R107–64. doi: 10.1088/0031-9155/48/21/r01. [DOI] [PubMed] [Google Scholar]
- Xu XG, Bednarz B, Paganetti H. A review of dosimetry studies on external-beam radiation treatment with respect to second cancer induction. Phys Med Biol. 2008;53:R193–241. doi: 10.1088/0031-9155/53/13/R01. [DOI] [PMC free article] [PubMed] [Google Scholar]