Linking white matter integrity loss to associated cortical regions using structural connectivity information in Alzheimer’s disease and Fronto-temporal dementia: the Loss in Connectivity (LoCo) score

Abstract

It is well known that gray matter changes occur in neurodegenerative diseases like Alzheimer’s (AD) and fronto-temporal dementia (FTD), and several studies have investigated their respective patterns of atrophy progression. Recent work, however, has revealed that diffusion MRI that is able to detect white matter integrity changes may be an earlier or more sensitive biomarker in both diseases. However, studies that examine white matter changes only are limited in that they do not provide the functional specificity of GM region-based analysis. In this study, we develop a new metric called the Loss in Connectivity (LoCo) score that gives the amount of structural network disruption incurred by a gray matter region for a particular pattern of white matter integrity loss. Leveraging the relative strengths of WM and GM markers, this metric links areas of WM integrity loss to their connected GM regions as a first step in understanding their functional implications. The LoCo score is calculated for three groups: 18 AD, 18 FTD, and 19 age-matched normal controls. We show significant correlations of the LoCo with the respective atrophy patterns in AD (R = 0.51, p = 2.2 × 10⁻⁹) and FTD (R = 0.49, p = 2.5 × 10⁻⁸) for a standard 116 region gray matter atlas. In addition, we demonstrate that the LoCo outperforms a measure of gray matter atrophy when classifying individuals into AD, FTD, and normal groups.

1. Introduction

Alzheimer’s disease (AD) has been classically characterized as neuronal death that primarily affects the cerebral gray matter (GM) (Brun and Englund 1986; Jack et al. 1997; Thompson et al. 2003; Frisoni et al. 2009). Neuropathological evidence points to a neuronal/synaptic polioencephalopathy (Braak et al. 2000) with accumulation of beta amyloid and/or tau protein in the GM resulting in neuron loss and gross atrophy. Recently, sophisticated algorithms have enabled accurate measurement of baseline and longitudinal atrophy patterns from structural MRI data (Apostolova et al. 2007; Thompson et al. 2003) via a well-established pipeline involving segmentation, atlas-based parcellation (Wu et al. 2007), and volumetric/thickness analysis (e.g. FreeSurfer (Fischl et al. 2002), FSL (Smith et al. 2004) and SPM (Klauschen et al. 2009)). Areas specifically associated with atrophy under AD pathology include the hippocampus, amygdala, medial temporal lobe, posterior cingulate and parietal regions. Functional MRI (fMRI) studies have detected patterns of connectivity losses, especially in the posterior cingulate cortex and medial prefrontal cortex, even in amnesiac mild cognitive impairment (a-MCI) before GM atrophy is detectable (Gili et al. 2011). In Chételat et al. (2008), it was shown that hypometabolism largely exceeds GM atrophy in most regions of the cortex in AD patients. In frontotemporal dementia (FTD), significant brain atrophy in the frontal and temporal lobes (Avants et al. 2010; Krueger et al. 2011), disruptions in functional activation patterns (Zhou et al. 2010), and changes in metabolism (Jeong et al. 2005) have been shown in GM. It has also been shown that different dementias target different dissociated networks in the brain - the posterior temporal heteromodal network in AD (Buckner et al. 2005; Acosta-Cabronero et al. 2010), and the orbitofrontal network in FTD (Seeley et al. 2009). The latter study conclusively showed dissociated targeting and selective vulnerability of certain corticocortical networks in various neurodegenerative diseases.

Although dementias may have been seen as primarily GM-mediated diseases, it is now well known that the progression involves white matter (WM) fiber pathways (Villain et al. 2008; Englund et al. 1988; Kuczynski et al. 2010). Studies of measures of WM integrity such as fractional anisotropy (FA) measured from diffusion MRI data have shown significant findings that are sensitive to early changes, sometimes earlier than gross cortical atrophy is measurable (Douaud et al. 2011; Smith et al. 2010; Gold et al. 2010; Bendlin et al. 2010; Zhang et al. 2009; Avants et al. 2010). Disease is known to progress along extant fiber pathways via secondary Wallerian degeneration, disconnection, loss of myelinated axons, loss of signaling, axonal reaction and post-synaptic dendrite retraction (Seeley et al. 2009). There is some evidence that misfolded proteins in AD may propagate along WM pathways and across synapses (Frost and Diamond 2010; Liu et al. 2012). The idea that distal cortical regions can be affected by atrophy via the WM architecture is sometimes called the “disconnection” or “diaschisis” hypothesis (Pearson et al. 1985; Villain et al. 2008). Many new studies have confirmed these observations in both AD and FTD. Loss of WM integrity resulting from GM atrophy finds support in numerous studies showing strong correlations between the two in selected isolated GM and WM structures, for instance the relationship between the hippocampal formation and the cingulum bundle that projects to the posterior cingulate cortex (Villain et al. 2008; Yasmin et al. 2008; Xie et al. 2005; Acosta-Cabronero et al. 2010, Zhang et al. 2007). Stricker et al. (2009) reported higher radial diffusivity in late-myelinating WM tracts, including the inferior longitudinal fasciculum (ILF), splenium, fornix/stria terminalus and cingulum pathways, and indicated a clear connection with atrophy in terminating GM structures in the mesial temporal lobe. WM integrity changes have been shown to occur in FTD patients (Larsson et al. 2004; Yoshiura et al. 2006; Borroni et al. 2007; Forman et al. 2002; Neumann et al. 2007; Matsuo et al. 2009, Hornberger et al. 2011) mainly in the frontal and temporal lobes, and are consistent with the distributions of GM atrophy. One study in particular (Whitwell et al. 2010) showed increases in mean diffusivity of the GM regions that were atrophic in FTD, as well as the tracts that interconnect them. There is even evidence of, in addition to Wallerian degeneration, primary WM integrity losses in FTD due to mechanisms like tau, TDP, gliosis etc., that are not related to the topography of GM disease (Agosta et al. 2011). A few studies have compared the two diseases, each showing a more prominent frontal and temporal WM integrity loss in FTD than AD (Zhang et al. 2009; Avants et al. 2010).

It is therefore clear that both GM and WM play a role in the disease process in dementia; however, there has been a relative lack of investigation of the interactions of the two tissue types together. Acosta-Cabronero et al. (2010) performed tract-based spatial statistics (TBSS) on DTI data of AD patients and found support for the evolving view that WM involvement appears as part of the posterior temporal heteromodal network. While their GM atrophy maps created using VBM appear to be consistent with diffusivity changes in the projecting fibers, especially the posterior cingulum WM, they did not perform any correlation analysis to quantitatively establish this observation because there is no overlap between their WM diffusivity and GM atrophy maps. Specifically, no study has taken into account the actual WM fiber topology and its relationship to atrophied GM regions on a whole-brain regionally unbiased basis. While many recent studies have reported correlations between isolated and somewhat arbitrarily chosen regions in WM and GM (Villain et al. 2008; Yasmin et al. 2008; Xie et al. 2005; Zhang et al. 2007) and have the advantage of being able to address specific hypotheses, this ad hoc approach is not sufficient. Since the mapping between the fiber tracts and cortical regions is not one-toone, but many-to-many, looking at an ad hoc tract-cortical ROI pair cannot provide a complete picture. One interesting study did utilize a method incorporating global tractography (Bozzali et al. 2011) called Anatomical Connectivity Mapping (ACM) that compares the number of fiber tracts (streamlines) per voxel in AD, a-MCI to age-matched normal controls. Contrary to the negative results they found with FA comparison, Bozzali et al. found areas of both decreased (in the supramarginal gyrus) and increased (in the putamen) ACM in patients with AD. ACM of the supramarginal gyrus was also strongly associated with measures of short-term memory in healthy subjects. While this study shows the promise of using streamlines to measure anatomical changes due to AD, it utilizes tractography in a patient population with even noisier diffusion images than normal subjects which can be a problem for already delicate tracography algorithms. In addition, there is no way to quantify the GM regions affected by decreased ACM in the way it was presented except by nearest cortical proximity of the affected voxels.

Consider the study by Villain et al. (2008) that found correlations between structures in the medial temporal lobe and the cingulate cortex and WM structures connecting them. In a follow up paper, they showed association between baseline atrophy and hypometabolism in the selected GM regions and longitudinal atrophy changes in selected WM regions (Villain et al. 2010). Even though the authors report that hippocampal atrophy and hypometabolism are locally associated with FA reduction in the uncinate fasciculus and the cingulum bundle, the global GM-WM connection in AD is not revealed. For example, neuroanatomical studies suggest the cingulum bundle connects not only to parahippocampal gyrus, enterorhinal cortex and the hippocampus proper, but also sends long distance projections between anterior and posterior cingulates, connecting all parts of the limbic system. Similarly, the uncinate fasciculus connects temporal structures with orbitofrontal structures, apart from hippocampus and amygdala. Without considering all terminating GM regions and all connecting fibers between them, it is difficult to reveal the associations of GM and WM alterations in dementia.

What is needed, therefore, is an approach which can combine the attractive features of WM measures (i.e. sensitivity) with those of GM measures (i.e. regional and functional specificity). Some progress on spatially unbiased whole brain GM and WM analysis has been made recently. Avants et al. (2010) used sparse canonical correlation analysis to identify areas of correlated WM integrity changes and GM atrophy in both neurodegenerative diseases, and found that the affected areas are what would be inferred if considering structural connectivity information. However, this study does not incorporate fiber tract (in this article, we use the word tract interchangeably with streamline), information nor explicitly consider whole brain connectivity information. The question remains to what extent the reported correlations are due to spatial proximity or the fiber connectivity architecture. Buckner et al. (2005) report spatially dispersed, intersecting but distinct maps of amyloid deposition, metabolism (FDG-PET) and atrophy in AD patients, and default functional (FDG-PET) activity in young adults. A remarkable homology was found by Seeley et al. (2009) between the pattern of atrophy in AD and the default mode functional network. All of this evidence points to the need for a distributed whole brain approach requiring a meaningful integration of the relative strengths of WM and GM markers.

1.1 Paper Contribution

In this work, we propose a computational methodology that integrates diffusion MRI, tractography and structural MRI of a cohort of young healthy controls, FTD and AD patients as well as age-matched normal controls (NC). This fully quantitative and spatially unbiased approach overcomes numerous deficiencies in current methods, which are either restricted to ad hoc structures, do not utilize the sensitivity of WM measures or functional specificity of GM measures, and do not integrate the topology of structural WM fiber connections in the healthy brain. Our approach exploits the enhanced sensitivity of WM-specific measurements to obtain a spatially distributed GM-specific measure that is expected to be much more sensitive and specific than gross measurements of cortical atrophy. Specifically, we propose a new metric, the Loss in Connectivity (LoCo) that measures GM regions’ connectivity disruption via WM integrity losses in their connecting fibers, without having to perform tractography in abnormal cohorts. The two hypotheses tested in this paper are:

1. LoCo is associated with GM atrophy in AD and FTD.

2. Due to differences in sensitivity between WM and GM imaging (diffusion MR versus structural MR), the LoCo can detect brain changes that are more specific to AD and FTD than classical measures like GM atrophy.

We must point out that the first hypothesis does not state that LoCo scores correspond exactly to GM atrophy, because changes that are detectable with diffusion MRI in WM may not yet be present in MR images used to detect GM atrophy. This could either be because of the lower sensitivity of the MR imaging or that GM changes associated with primary WM integrity loss have not yet occurred. We test and validate the first hypothesis by measuring a moderate, yet significant, statistical correlation between whole brain WM and GM measurements in both AD and FTD. We test and validate the second hypothesis by showing that the LoCo scores are a better and more sensitive measure of dementia related changes than GM atrophy. In comparison to analyzing WM integrity losses only, LoCo scores have the advantage of linking the WM integrity losses to their connected GM regions as a first step in understanding their functional implications.

2. Materials and Methods

2.1 “Atlas” Data

This study’s normal young subject data (from here on referred to as “atlas” data) were collected jointly by Weill Cornell Medical College and the Brain Trauma Foundation. Fourteen healthy subjects (9 male, 5 female, 23.1 ± 4.7 years) were used to create the normative connectivity information in the form of tractograms. The conditions for exclusion were pregnancy, a history of neurological or psychiatric diagnosis, seizure, or drug or alcohol abuse. T1-weighted structural and diffusion weighted MR images were collected on a 3 Tesla GE Signa EXCITE scanner (GE Healthcare, Waukesha, WI, USA). The High Angular Resolution Diffusion Images (HARDI) data were acquired with 55 isotropically distributed diffusion-encoding directions at b = 1000 s/mm² and one at b = 0 s/mm², acquired from 72 1.8-mm thick interleaved slices (no slice gap) and 128 × 128 matrix size, zero-filled during reconstruction to 256 × 256, with a field of view (FOV) of 230 mm². The structural scan was an axial 3D inversion recovery fast spoiled gradient recalled echo (FSPGR) sequence (TE = 1.5 ms, TR = 6.3 ms, TI = 400 ms, flip angle of 15°) with a 256 × 256 matrix over a 230 mm² FOV and 156 1.0-mm contiguous partitions.

2.2 AD, FTD, and CN data

This study’s AD, FTD and cognitively normal age-matched cohort (CN) data are the same as those described in the previous study (Zhang et al. 2009). The groups include 18 FTD patients (mean age and standard deviation: 62.1 ± 10.7 years) with a Mini-Mental State Examination (MMSE) (Folstein et al. 1975) score of on average 24.1 ± 4.7, 18 patients with Alzheimer’s disease (age: 62.8 ± 7.1 years; MMSE: 21.7 ± 5.8) and 19 age-matched cognitively normal (CN) subjects (age: 61.5 ± 10.6 years; MMSE: 29.5 ± 0.5). The patients with FTD and Alzheimer’s disease were recruited from the Memory and Aging Center of the University of California, San Francisco. Conditions for exclusion were a history of brain trauma, brain tumor, stroke, epilepsy, alcoholism, psychiatric illness and other systemic diseases that affect brain function. All subjects’ MR scans were used to rule out major neuropathologies such as tumors, strokes, severe WM disease or in ammation but not for diagnosis. Written informed consent was given by all subjects or their guardians before participating in the study, which was approved by the Committees of Human Research at the University of California at San Francisco.

Information obtained during an extensive clinical history and physical examination was used in diagnosis. The consensus criteria established by (Neary et al. 1998) was used for the diagnosis of behavior variant type of FTD. Two FTD patients had concurrent motor neuron-related symptoms. The National Institute of Neurological and Communicative Disorders and Stroke-Alzheimer’s Disease and Related Disorders Association (NINCDS/ADRDA) (McKhann et al. 1984) criteria were used for the diagnosis of probable Alzheimer’s disease. MMSE scores and the Clinical Dementia Rating (CDR) scale (Morris 1993) were used to measure global cognitive function. These tests were used to characterize the cognitive de cits of the patients and not for clinical diagnosis. White matter signal hyperintensities (WMSH) on MRI were identified by an experienced radiologist and classi ed as mild (score 1), moderate (score 2) or severe (score >3), according to the Schelten’s rating scale (Scheltens et al. 1993).

All scans for the CN, AD and FTD were performed on a 4 Tesla (Bruker/Siemens) MRI system with a single housing birdcage transmit and eight-channel receive coil. T1-weighted images were obtained using a 3D volumetric magnetization prepared rapid gradient echo (MPRAGE) sequence with TR/TE/TI = 2300/3/950 ms, 7-degree flip angle, 1.0 × 1.0 × 1.0 mm³ resolution, and 157 continuous sagittal slices. T2-weighted images were acquired with a variable flip (VFL) angle turbo spin-echo sequence with TR/TE = 4000/30 ms, and had the same resolution matrix and field of view of MPRAGE. In addition, FLAIR (fluid attenuated inversion recovery) images with timing TR/TE/TI = 5000/355/1900 ms were acquired. T2-weighted and FLAIR images were used for registration and evaluation of visual WMSH. The diffusion scans were based on a dual spin-echo echo-planar imaging (EPI) sequence supplemented with parallel imaging acceleration (GRAPPA) (Griswold et al., 2002) with a factor 2 to reduce susceptibility distortions. The TR/TE was 6000/77 ms, eld of view 256 × 224 mm², and the matrix size was 128 × 112 mm², yielding 2 mm × 2 mm in-plane resolution with 40 continuous 3 mm slices. One reference image (b = 0) and six diffusion-weighted images (b = 800 s/mm²) were acquired. To increase the signal-to-noise ratio, four DTI scans were performed and averaged after motion correction.

2.3 Image Analysis of “Atlas” data

To obtain normative tractograms, the “atlas” images were processed by first parcellating the GM into 116 different regions on the subjects’ T1 scans and then performing tractography. Briefly, the surface voxels of the parcellated cortical and subcortical structures were used to seed the tracts. Proposed and validated in Iturria-Medina et al. (2005), the tractography algorithm implemented here incorporates tissue classification probability and ODF information in a Bayesian manner. A tract terminated when the algorithm reached the boundary of an image volume, the edge of a gray matter region, a voxel not in the gray or white matter masks, or when the angle between subsequent steps exceeded π/3. This analysis was done using Statistical Parametric Mapping (SPM), (Friston et al. 2006) a software package within Matlab R2009a (Natick, MA, The Mathworks Inc.), and the Individual Based Atlas (IBASPM) toolbox (Alemán-Gómez, et al. 2005) within SPM. Further details of the image processing and tractography method are given in (Kuceyeski et al. 2011).

2.4 LoCo calculation using AD, FTD and CN data

As described in detail in (Zhang et al. 2009), maps of FA, longitudinal diffusivity (LD) and radial diffusivity (RD) were computed using Volume-one and dTV software (Masutani et al. 2003). LD is the magnitude of the largest eigenvalue of the tensor and RD is the average of the other two eigenvalues. DTI b0 images were spatially normalized to an EPI template in MNI space with SPM’s normalize function that computes and implements a 12-parameter non-linear transformation. This transformation was then applied to the FA, RD and LD maps and group-wise comparisons of AD vs. CN and FTD vs. CN were performed, resulting in two sets of three t-maps. It must be emphasized that only the age-matched normal controls (NC), and not the “atlas” data, were used to calculate the group-wise (t-map) differences in WM integrity measures for the AD and FTD groups. The t-maps and the mean FA volume (calculated using only NC) in standardized space are used in the following procedure (summarized in Figure 1):

Figure 1.

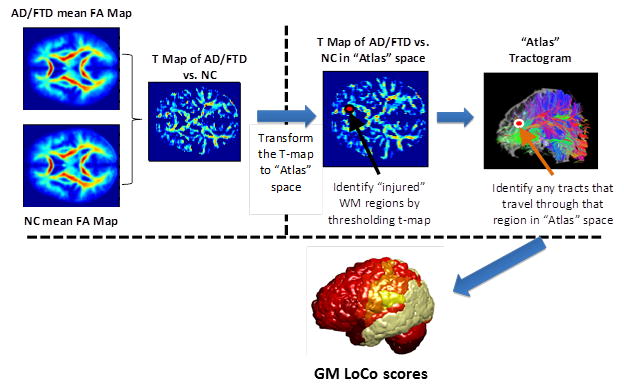
The process to calculate the Loss in Connectivity (LoCo), i.e. the percent of WM tracts out of the total connecting to a GM region in a normal control that pass through voxels identified in a WM “injury” map.

1. The mean FA volume in standardized space is coregistered to an “atlas” individual’s FA map using SPM’s 12-parameter non-affine registration, and that same transformation is applied to the other two sets of three t-maps (FA, RD, and LD).

2. The t-maps are now intersected with that individual “atlas” WM mask (generated in SPM) to ensure the comparisons are only taken for voxels in that tissue class. The t-maps are thresholded utilizing a significance level of p = 0.05 (adjustment for multiple comparisons is performed using voxel-wise False Discovery Rate (FDR) method (Genovese et al. 2002)) to find areas of significant WM integrity loss. The union of the three binary masks is taken, resulting in a WM “injury” mask in the space of the “atlas” individual.

3. In the “atlas” tractogram, the tracts passing through WM “injury” mask were recorded, along with their connecting GM regions.

4. The Loss in Connectivity (LoCo) (Kuceyeski and Raj 2011) was calculated for each GM region. The LoCo is defined for each GM region and gives the percent of tracts going through “injured” regions out of total that are connected to that GM region; note that scores closer to 1 indicate greater connectivity disruption.

Steps 1–4 are repeated for each of the 14 “atlas” subjects, and the mean vector of LoCo scores is found by taking the standard average over these values. To clarify, the WM injury mask includes voxels with at least one of the diffusion summary statistics (FA, RD and LD) significantly different from the age-matched normal controls. This union operation results in an all-inclusive “worst case” scenario of WM injury that will, if anything, overestimate the amount of connectivity disruption. Since we use a stringent requirement for identifying significant differences per voxel, the method should be identifying areas with true underlying physiological changes.

To find the WM injury masks, we compared the AD/FTD data against age-matched normal controls (NC), all of which are acquired at the same DTI acquisition and field strength. The “atlas” and NC data do come from scanners with different field strengths (3T vs. 4T), but the only time this could be an issue is in Step 1 during the coregistration of the two groups’ FA maps. We visually inspected these results which was quite good, so conclude that any differences due to field strength were minor enough to be overcome by SPM’s coregistration routine.

Note that the process described above is not specific to the individual; it gives LoCo scores for AD and FTD group differences. To get a LoCo score for an individual, this exact process was repeated for each NC, AD, and FTD subject by replacing the group-wise t-map with the individual’s z-scores of WM integrity statistics (using the NC mean and standard deviation maps for normalization).

GM atrophy can mimic WM integrity losses, particularly in regions at the WM/GM interface. To prevent confounds of GM atrophy, we created an aged WM mask by including only those voxels that had an FA of greater than 0.1 in the mean age-matched normal controls’ FA map. After we coregistered the aged brains to the “atlas” data, we then only considered those voxels that were also in the WM mask of that “atlas” image. If anything, this process is conservative because taking only those voxels in the “atlas” WM mask will exclude WM voxels at the WM-GM boundary that should otherwise be included in the aged group.

In addition to the LoCo calculation, more standard metrics of GM and WM involvement were used. The T1 images from the AD/FTD/CN group were normalized to MNI space and the cortices parcellated into 116 regions using the same process as the “atlas” data (IBASPM). GM volume and was then measured by counting the number of voxels assigned to each region and dividing by the sum of all those voxels to normalize for head size. Whole-brain WM integrity metrics were calculated from diffusion images by taking the average z-score of WM integrity FA, LD and RD over each of 106 superficial and deep WM regions in JHU-MNI-ss atlas, or “Eve” atlas (Oishi et al. 2009).

2.5 Classification Methodology

One very basic characteristic that a metric of disease should have is that it differentiates between various disease states and the normal populations. Participants are classified via linear discriminant analysis (Krzanowski 1988) into AD, FTD and NC groups by the jack-knife or leave-one-out process, wherein each subject is classified using the remaining data (Raj et al. 2010). To test the quality of classification, we calculate the classification rate (percent of correctly classified individuals).

Since there are 116 values for the LoCo and each GM region metric (one for every ROI), it is desirable to perform dimensionality reduction on the data for better classification. We chose to use the standard singular value decomposition (SVD), a process that is very similar to Principal Component Analysis. The SVD is used to project the data into a smaller number of dimensions that maximizes the data’s variance. We performed several unsupervised reductions and chose the optimal number of dimensions for each metric to be the one that gave the maximum classification rate.

3. Results

3.1 Group-wise Analysis

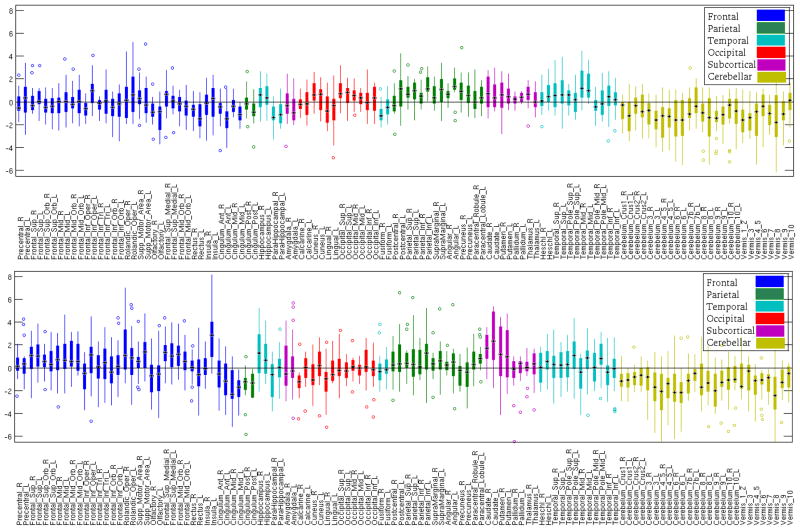
First, we evaluated the reproducibility of the LoCo for each of 116 GM regions across the 14 “atlas” individuals for the AD and FTD WM injury maps. Figure B.1 in Appendix B shows the boxplots for the LoCo scores. Generally, there are not many outliers (plotted with a circle) and the standard deviations increase with larger means. The variability of the LoCo is different in the two diseases for different lobes (AD – higher variation in occipital, parietal and temporal, FTD – higher variation in frontal, subcortical). In a more quantitative analysis, Spearman’s correlation coefficient of the LoCo was calculated between each pair of the 14 “atlas” subjects to check for agreement. All correlations for the LoCo derived from the AD injury map were significant at a level of 0.005 (Bonferroni corrected for multiple comparisons) and the coefficients had a mean of 0.75 and a standard deviation of 0.13. In the case of the FTD, all correlations but one (significant at a level of 0.05) were significant at a level of 0.005 (Bonferroni corrected for multiple comparisons), and the coefficients had a mean of 0.85 and a standard deviation of 0.16. Due to the high correlation of the LoCo metrics across “atlas” individuals, we conclude that the amount of individual variability present in the normal tractograms does not greatly influence the results.

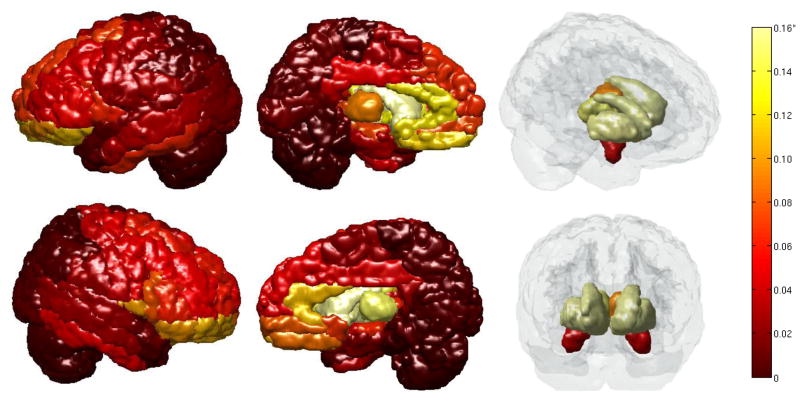
Figure 2 displays the cortical regions with the color of the region indicating its LoCo (dark - low, light – high). We inspected this map for agreement with GM regions known to be involved in the degenerative process of AD. The GM regions most classically associated with AD, the hippocampi, were in the top 15% most affected. The bilateral posterior cingulate structures, thalami, and many temporal (inferior and middle) structures were also in the top 20%, see Appendix A for an ordered list. Many structures normally associated with the default mode network were affected, i.e. the cuneus, precuneus, and other parietal regions. In addition to the agreement of involved regions with known pathology, cortical structures that are uninvolved in AD had low LoCo. The motor cortex was relatively spared and the cerebellum was not at all affected, in accordance with clinical observations of the progression of the disease. There was some disagreement with known pathology, however; in particular the right angular gyrus had low AD LoCo scores, even though it is known that this region is normally atrophied in AD and is in the top 20% of the atrophied regions in this cohort. The occipital regions had high LoCo scores for AD and are not generally affected in the disease. However, the bilateral superior occipital and right middle occipital were in the top 20% most atrophied regions in this group of AD subjects.

Figure 2.

The GM regions and their LoCo scores for AD patients. *Colorbar: indicates changes from 0 (dark red) to 0.02 (light yellow), note that the few regions with a LoCo higher than 0.02 are grouped into the lightest yellow. The GM regions generally associated with AD (hippocampus, temporal and parietal lobes, cingulate structures) display high LoCo. (Left to Right): lateral views left & right, medial views, left & right.

The LoCo in the FTD cohort also agrees generally with what is known about the pattern of the disease, see Figure 3. The areas with the highest 20% LoCo scores were those subcortical and medial frontal cortices such as the bilateral globus pallidus, caudate, putamen, inferior, medial and superior orbito-frontal gyri, anterior cingulates and thalami. Many of those regions with high LoCo have been implicated in FTD by both glucose and GM atrophy studies. In particular, (Jeong et al. 2005) noted significant hypometabolism via FTG-PET in prefrontal areas, cingulate gyri, anterior temporal and left inferior parietal regions and trends for hypometabolism in the bilateral insula and uncus, left putamen and globus pallidus, and medial thalamic structures. The temporal lobes and some parts of the frontal lobes that are usually associated with FTD, especially in the dorso-lateral pre-frontal cortex (DLPFC), do not have high LoCo scores. However, it must be noted that in this cohort of 18 FTD patients the temporal and DLPFC regions do not show high levels of atrophy (see Appendix B). Only the left middle and superior temporal poles were in the top 20% most atrophied regions, and the inferior frontal triangularis and operculum (the regions in the atlas that best overlap with DLPFC) are not very atrophied. Therefore, while in disagreement with classically associated GM regions in FTD, the LoCo results reflect the atrophy pattern in this sample. It must be noted that the cohort of 18 FTD patients were the clinical subtypes of behavioral variant FTD (bvFTD), which features orbitobasal, medial, and dorsolateral frontal involvements. It is reasonable to see minimal temporal lobe changes because patients with semantic dementia (SD), also known as temporal FTD, were not included in this group. Finally, it is interesting to note that the LoCo scores in the FTD population are around 10 times greater than that of the AD population. This agrees with previous studies (Zhang et al. 2009; Zhang et al. 2011; Krueger et al. 2011; Avants et al. 2010) that demonstrate larger volumes of tissue with significant WM integrity loss in FTD when compared to AD.

Figure 3.

The GM regions and their LoCo scores for FTD patients. *Colorbar: indicates changes from 0 (dark red) to 0.16 (light yellow), note that the few regions with a LoCo higher than 0.16 are grouped into the lightest yellow. The GM regions with high LoCo agree with known FTD pathology: the fronto-orbital, anterior cingulate structures, and some temporal.

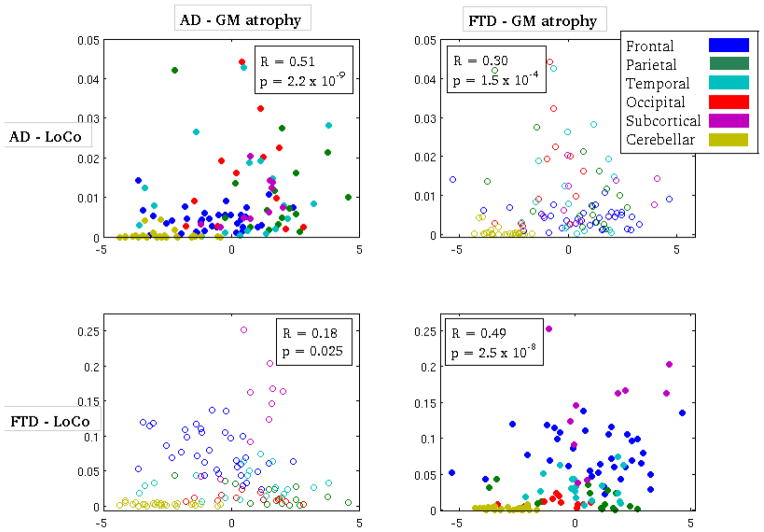
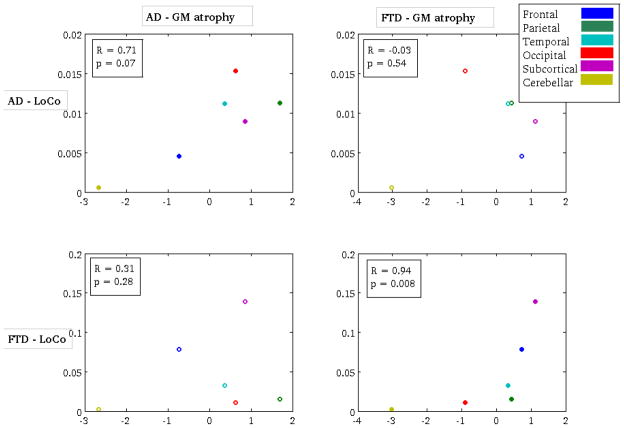
In a more quantitative validation study, Spearman’s correlation coefficient was calculated between the LoCo and t-scores measuring GM atrophy in the 116 different GM regions. The non-parametric rank correlation was used because the LoCo scores are not Gaussian, and have many values near zero. There was a highly significant correlation (after Bonferroni correction) for both the AD group (R = 0.51, p = 2.2 × 10⁻⁹) and FTD group (R = 0.49, p = 2.5 × 10⁻⁸), as shown in Figure 4. The cross-disease correlations (of AD’s LoCo and FTD’s GM atrophy and vice versa) were either non-significant or had lower R values. There was a significant correlation of AD LoCo and FTD atrophy; however, this is not surprising as the AD and FTD atrophy are actually correlated themselves (Pearson’s r = 0.63, p = 2.14 × 10⁻¹⁴). There exists inherent noise in both the LoCo and GM atrophy measurements that can be smoothed out by averaging the values of the 116-regions over the lobe to which they belong. In Figure B.3, we show the scatter plots and corresponding Spearman’s correlation for the two groups’ metrics (AD: R = 0.71, p = 0.07; FTD: R = 0.94, p = 0.008). We see a much more visually convincing correlation in the upper left and bottom right plots, even if the correlation is not statistically significant for AD. This is most likely a result of the small number of points in the analysis. The reproducibility of the correlation results per lobe also provides evidence that the LoCo scores are not biased by the choice of this particular 116-region GM atlas.

Figure 4.

A scatter plot of the Loss in Connectivity (LoCo) score versus GM atrophy in the 116 GM regions for the following pairs of metrics - top left: AD atrophy vs. AD LoCo, top right: FTD atrophy vs. AD LoCo, bottom left: AD atrophy vs. FTD LoCo, and bottom right FTD atrophy vs. FTD LoCo. Spearman’s correlation coefficient and the corresponding p-values appear in the boxes in the figures.

3.2 Individual LoCo Analysis

The results of the classification into NC, AD, and FTD using LoCo, MMSE, GM atrophy, three WM metrics (z-scores of average FA, RD and LD over the 106 region WM atlas), and a “Combined” measure are shown in Figure 5. The Combined measure, a concatenation of the highest performing WM integrity statistic (RD) and GM atrophy, was created to test if the incorporation of measures of the two tissue types would be any better than each measure alone. In Figure 5, the colors in each row are that patient’s classification using the various metrics (columns). We see that the classification results are not consistent across the various metrics, which is unsurprising. Each metric capture a different physiological quantity, and thus the results will inherently differ in the quality of classification. The first column corresponds to the true diagnosis of that patient (dark – CN, medium – AD, light – FTD). We see that the LoCo, WM integrity measures of RD and LD, and Combined score have very similar overall classification rates that are 8–13% higher than the GM atrophy and 25–30% higher than the MMSE classification rates (see Table 1). The LoCo and RD metrics also had the highest values of sensitivity and specificity for the three groups, as indicated in Table 1 with gray shading. These results demonstrate the superiority of the diffusion-derived metrics in discerning between disease states. It must also be noted that while the LoCo, RD and LD metrics had similar classification rates, the LoCo did so with a half to a quarter of the number of dimensions (# eigenvectors), speaking to the robustness of the metric. It is also interesting to note that the Combined score does not perform any better than the WM integrity statistics alone, indicating that the errors in GM atrophy measurements are so large that they do not add anything informative to the WM integrity statistics for classification.

Figure 5.

The classification results for each metric (LoCo, MMSE, GM atrophy, three WM imaging metrics, and the GM-WM Combined measure). The colors in each row and column are that patient’s (row) classification using the various metrics (columns). The first column corresponds to the true diagnosis of that patient (dark – CN, medium – AD, light – FTD).

Table 1.

The classification results for the LoCo, MMSE, GM atrophy, 3 WM metrics and Combined (GM atrophy and RD) score. The first column is the number of eigenvectors were used in the dimensionality reduction (or N/A for the scalar metric), and were chosen to give the maximal classification rate for that modality. The cells shaded in gray indicate the highest values in each column across the different metrics.

Metric	# Eigen-vectors	Specificity (NC)	Sensitivity (NC)	Specificity (AD)	Sensitivity (AD)	Specificity (FTD)	Sensitivity (FTD)	Class. Rate (%)
LoCo	4	1.000	0.8056	0.8333	0.8919	0.7778	0.9189	87.27
MMSE	N/A	1.000	0.3611	0.3889	0.6757	0.3333	0.7027	58.18
GM atrophy	15	0.8947	0.6944	0.7222	0.7837	0.6667	0.8108	76.36
Av. z-score FA	3	0.6842	0.8056	0.7778	0.7568	0.8333	0.7297	76.36
Av. z-score RD	15	1.0000	0.8333	0.9444	0.8649	0.7222	0.9730	89.09
Av. z-score LD	7	0.9474	0.8056	0.8333	0.8649	0.7778	0.8919	85.45
Combined	15	0.9474	0.7778	0.8889	0.8108	0.6667	0.9189	83.64

4. Discussion and Conclusions

We proposed a new automatic, whole brain, spatially unbiased computational methodology that integrates diffusion and structural MRI and tractography. Maps of WM integrity loss in disease are combined with whole brain tractography in healthy individuals to obtain associated connectivity disruptions of GM, called the LoCo score. We showed that LoCo is a sensitive biomarker of dementias and it is correlated to observed GM atrophy from morphometric MRI analysis in this cohort. The LoCo combined the higher sensitivity of WM biomarkers like FA, RD and LD with the spatial and functional specificity of GM-based biomarkers like cortical volume and thickness. These results represent one of the first attempts to link WM integrity loss in dementia patients to their connected GM regions using tractograms constructed in young healthy controls. The LoCo gives a measure of the amount of WM connectivity disruption for each GM region within the whole-brain network, as a first step in understanding the functional implications of WM injury.

The results are promising in that GM regions identified by LoCo generally agree with clinical knowledge of the pathology of both AD (hippocampi, temporal, and posterior cingulate structures) and FTD (orbito-frontal, anterior cingulate, and subcortical structures). There was some disagreement, however; in particular the right angular gyrus had low LoCo scores for AD, even though this region is known to be atrophied in AD and was shown to be atrophied in this cohort. In addition, occipital regions that are not generally affected in AD had high LoCo scores. In FTD, low LoCo scores were found in the temporal lobes and DLPFC which agreed with the atrophy patterns found in this cohort but not with general knowledge of the pathology of FTD. This could be due to the fact that only the clinical subtypes of bvFTD were included in this study, which have minimal temporal involvement when compared to other sub-types such as SD. The diagnosis of FTD was done using the widely-accepted Neary criteria (Neary et al. 1998) that without histopathological evidence has an error rate of up to 30% (Forman et al. 2006), which could add noise to the atrophy measurements. It could also be possible that the patients had not progressed into the later stages of their disease so the atrophy is not as detectable with the relatively low sensitivity of the structural MR. It is to be expected that these sources of error, natural population variability and measurement limitations prevent a perfect match between LoCo and GM atrophy. Even with these few disagreements, the LoCo of GM regions is correlated with actual observed atrophy in AD and FTD patients in this cohort, and it is the among the best disease classifiers in the various metrics of GM atrophy, WM integrity loss, and MMSE scores.

The classification rates found here for the WM based metrics are comparable to other attempts using multivariate imaging measures. It was shown in de Leon et al. 2005 that two CSF biomarkers combined with hippocampal atrophy measurements resulted in about a 90% diagnostic accuracy of MCI versus normal elderly at both baseline and follow-up evaluations. In a series of more recent whole-brain based studies, the SPARE-AD (Spatial Pattern of Abnormalities for Recognition of Early AD) measure differentiated between converters and non-converters from MCI to AD (Misra et al. 2009) and elderly normal to MCI (Davatzikos et al. 2009), and a differentiated between AD and FTD patients at a rate of 84% (Davatzikos et al. 2008). In another imaging based study, Boccardi et al. 2003 showed 93% specificity and 90% specificity in classifying FTD from AD by using a measure of hemispheric asymmetry in brain atrophy.

The LoCo scores did not outperform the other WM integrity statistics in differentiating between diseases. However, it must be noted that comparison with WM measures like FA is likely to be facile, because both our LoCo and FA are essentially derived from the same information (but LoCo adds cortical region specificity to this information). It would be indeed be surprising if the LoCo measure was able to greatly outperform WM measures in classifier tasks. In actuality, the right comparison of our classification results is with purely GM measures like atrophy, which the LoCo outperformed. In any case, it must be emphasized our goal in this study was not the classification itself. Our goal here was to demonstrate how to use normal tractograms to predict GM connectivity changes due to WM losses. Knowing which GM areas are likely to be compromised because of a specific WM lesion can inform the patient’s type of cognitive or physical disabilities that only looking at the location of a WM lesion on a parcellated atlas does not provide. In AD in particular, where it has been shown that misfolded proteins can propagate across a synapse, knowing the topology of the brain network at a fiber-wise level can help in prediction the progression of disease.

To determine the WM injury mask, we imposed a somewhat strict requirement, i.e. that the diffusion summary statistics be significantly different from normal after FDR correction for multiple comparisons. Because the t-scores were very high, we can assume that the underlying physiology has been severely compromised and therefore connectivity disruption has occurred. It is our hypothesis that there is an association between WM damage and changes in the connecting GM region; however we do not assume that the anatomic endpoint of GM involvement has occurred yet or is necessarily measurable by morphometric tools. Our correlation results suggest that there is indeed an association between WM damage and GM atrophy in our data, but we are not in a position to speculate on the possible mechanisms thereof.

4.1 Limitations and Future Work

Normalizing images to a common space is a difficult issue, especially when dealing with individual WM streamlines that are quite small where relatively large errors may be introduced. Future studies will be done on accurately normalizing tractograms into a common space (MNI) and minimizing error in the process, so that the calculation of the LoCo scores is much easier and the variability of the individual tractograms maintained. This amalgamation of normal tracts will be made publicly available. It will enable the user to provide a mask of WM injury that has been coregistered to MNI space, and the output will be LoCo measures as well as a list of changes that particular pattern of WM injury would illicit in the overall brain network, i.e. efficiency, characteristic path length, degree, etc. This tool would allow investigation of alterations in brain connectivity in various disease states without having to perform tractography in patients with abnormal WM integrity, a well-known and difficult problem. Potential applications of this tool include stroke, tumor, trauma, Multiple Sclerosis and other demyelinating diseases.

It may be that the choice of GM atlas caused bias in the results, a concern that was somewhat assuaged by analyzing the correlation results of atrophy and LoCo scores by lobe and seeing even stronger correlations. We plan to incorporate into the tool many different GM atlases so that the sensitivity of the results to this choice can be analyzed.

There are many ways to determine if the WM tract is in fact injured, and the approach here could be modified to account for not just a binary injured/not injured status. Instead, one could require that a certain minimum length of the tract be in an “injured” region before it is in fact considered compromised. We could also create a WM mask that is continuous and not binary, where each voxel captures the amount of deviation from normal that particular voxel’s diffusion summary statistics are.

We showed that individual variability among the “atlas” individuals does not have a large influence on the results by demonstrating a high correlation of the AD/FTD LoCos calculated from different “atlas” data. We believe that any variations that are present could be further mitigated by increasing the sample size of the “atlas” group, which we also plan to do in the future.

Our moderate sample size compared to the number of statistical comparisons we perform raises the issue of sampling error and overfitting. The question of overfitting to the given data is not an insignificant one, and it is imposible to know the extent of this confounding factor as there is no way to infer the underlying population distribution. Therefore, confidence in the generalization of the results should be cautioned. We do have some encouraging signs, however, that these subjects are indeed representative of the population as a whole, evidenced by the observation that the LoCo scores agreed for the most part with the general pathology of the two disease populations. In addition, the leave-one-out cross validation helped to minimize the effect of overfitting in the three-way classification. In an attempt to further minimize its effects, we will perform the same analysis on a larger set of AD and FTD subjects in the future, i.e. with ADNI 2 data that will contain diffusion imaging (Weiner et al. 2012).

Tractography is an imperfect tool at the present, especially in dealing with partial volume effects and crossing and kissing fibers. Probabilistic tractography, in particular, has the drawback of assigning higher probabilities to shorter fibers and WM that is adjacent to GM regions may have a larger number of tracts. Alternatively, many U-fibers may be invisible to diffusion MRI due to limited spatial and angular resolution. These two issues may partially cancel each other, but currently no quantification exists of their joint effects. The advancement of tractography and imaging techniques should remove many, if not all, of these concerns. It must be noted that this paper is not proposing an alternative method for tractography, but merely its use for important clinical and exploratory analyses.

While a state-of-the-art coregistration tool was used, there still could be problems with coregistering the WM integrity templates to the “atlas” space, especially due to the age differences in the two groups. Coregistering individual brains that have anatomical abnormalities to a common space is a well-known and difficult problem. It is particularly difficult when working with atrophied or resected brains, and this specific issue is not investigated in the proposed work. There are tools available to minimize coregistration errors, including the new DARTEL registration tool in SPM. For example, it was shown in Pereira et al. (2010) that DARTEL combined with preprocessing steps of skull-stripping and bias correction resulted in good registration of atrophied brains in AD, Semantic Dementia, and FTD. This method will be used in future studies requiring coregistration.

While the current analysis does not answer the question of a causal or temporal relationship between GM and WM damage, it represents one step in a future longitudinal study using this methodology that may be able to discern the details of such a relationship. Knowing the progression of degeneration in the brain cortico-cortical network may lead to more accurate early detection as well as an increased precision in tracking of the disease. It may provide useful information to physicians for better prognosis, treatment and assessment of Alzheimer’s disease and Fronto-temporal dementia.

Appendix A: LoCos for AD and FTD

GM Regions (AD)	LoCo (AD)	GM Region (FTD)	LoCo (FTD)
Occipital_Inf_L	0.0443	Pallidum_R	0.2518
Temporal_Inf_L	0.0427	Caudate_L	0.2028
Cingulum_Post_L	0.0421	Putamen_L	0.1668
Occipital_Mid_L	0.0323	Caudate_R	0.1630
Temporal_Mid_L	0.0281	Putamen_R	0.1624
Precuneus_L	0.0274	Thalamus_R	0.1456
Fusiform_L	0.0264	Insula_R	0.1374
Occipital_Sup_L	0.0224	Insula_L	0.1349
Angular_L	0.0213	Pallidum_L	0.1238
Thalamus_L	0.0204	Cingulum_Ant_L	0.1198
Cuneus_L	0.0201	Olfactory_L	0.1184
Calcarine_L	0.0193	Frontal_Sup_Orb_L	0.1164
Hippocampus_L	0.0193	Rectus_L	0.1145
Temporal_Inf_R	0.0189	Frontal_Inf_Orb_L	0.1108
SupraMarginal_L	0.0163	Cingulum_Ant_R	0.1084
Occipital_Inf_R	0.0162	Frontal_Mid_Orb_R	0.1052
Hippocampus_R	0.0148	Frontal_Sup_Orb_R	0.1051
Caudate_L	0.0143	Rolandic_Oper_R	0.0992
Cingulum_Mid_L	0.0142	Frontal_Inf_Orb_R	0.0986
Putamen_L	0.0138	Frontal_Mid_Orb_L	0.0966
Cingulum_Post_R	0.0136	Thalamus_L	0.0916
Fusiform_R	0.0124	Rectus_R	0.0857
Thalamus_R	0.0124	Frontal_Mid_Orb_R	0.0801
Postcentral_L	0.0117	Frontal_Inf_Oper_R	0.0775
Rolandic_Oper_L	0.0107	Hippocampus_L	0.0748
Parietal_Inf_L	0.0100	Frontal_Mid_Orb_L	0.0717
Occipital_Mid_R	0.0098	Frontal_Sup_L	0.0694
Lingual_L	0.0091	Olfactory_R	0.0686
Insula_L	0.0091	Frontal_Sup_Medial_L	0.0651
Temporal_Mid_R	0.0083	Frontal_Inf_Oper_L	0.0637
Temporal_Sup_L	0.0079	Hippocampus_R	0.0631
ParaHippocampal_L	0.0079	Temporal_Inf_L	0.0631
Cingulum_Ant_R	0.0076	Frontal_Inf_Tri_R	0.0619
Precentral_L	0.0075	Rolandic_Oper_L	0.0604
Caudate_R	0.0075	Frontal_Sup_R	0.0600
Frontal_Inf_Oper_L	0.0074	Frontal_Inf_Tri_L	0.0550
Parietal_Sup_L	0.0072	Cingulum_Mid_L	0.0528
Paracentral_Robule_L	0.0068	Frontal_Mid_R	0.0521
Cingulum_Ant_L	0.0068	Temporal_Inf_R	0.0507
Pallidum_L	0.0062	Frontal_Sup_Medial_R	0.0491
Cingulum_Mid_R	0.0061	Precentral_R	0.0466
Precuneus_R	0.0058	Frontal_Mid_L	0.0437
Frontal_Mid_L	0.0056	Fusiform_L	0.0436
Frontal_Mid_Orb_L	0.0055	Cingulum_Mid_R	0.0435
Frontal_Mid_Orb_R	0.0055	Cingulum_Post_L	0.0432
Precentral_R	0.0054	Heschl_R	0.0431
Olfactory_L	0.0052	Amygdala_L	0.0425
Frontal_Sup_L	0.0050	Amygdala_R	0.0384
Angular_R	0.0048	Postcentral_R	0.0359
Postcentral_R	0.0048	Temporal_Mid_L	0.0335
Pallidum_R	0.0048	ParaHippocampal_L	0.0327
Frontal_Inf_Orb_R	0.0047	Precentral_L	0.0326
Heschl_L	0.0047	Cingulum_Post_R	0.0310
Putamen_R	0.0045	Fusiform_R	0.0296
Frontal_Mid_Orb_R	0.0045	Supp_Motor_Area_L	0.0291
Frontal_Sup_R	0.0044	SupraMarginal_L	0.0281
Cerebelum_Crus1_L	0.0044	Temporal_Sup_R	0.0269
Frontal_Sup_Orb_R	0.0043	Temporal_Mid_R	0.0260
Olfactory_R	0.0042	SupraMarginal_R	0.0241
Cerebelum_6_L	0.0041	Postcentral_L	0.0240
Frontal_Inf_Orb_L	0.0039	Heschl_L	0.0237
Rectus_R	0.0035	Occipital_Inf_L	0.0233
Frontal_Inf_Tri_L	0.0034	Supp_Motor_Area_R	0.0231
Amygdala_L	0.0032	Occipital_Mid_L	0.0193
Parietal_Inf_R	0.0031	ParaHippocampal_R	0.0183
ParaHippocampal_R	0.0030	Temporal_Sup_L	0.0171
Supp_Motor_Area_R	0.0030	Calcarine_L	0.0154
Lingual_R	0.0028	Temporal_Pole_Sup_R	0.0138
Calcarine_R	0.0027	Angular_L	0.0123
Insula_R	0.0027	Temporal_Pole_Mid_L	0.0118
Supp_Motor_Area_L	0.0026	Lingual_L	0.0117
Frontal_Sup_Medial_R	0.0025	Precuneus_L	0.0116
Amygdala_R	0.0025	Occipital_Inf_R	0.0111
Occipital_Sup_R	0.0024	Occipital_Sup_L	0.0107
Paracentral_Robule_R	0.0024	Temporal_Pole_Sup_L	0.0096
Frontal_Mid_R	0.0024	Precuneus_R	0.0089
Temporal_Sup_R	0.0021	Cuneus_L	0.0088
Cuneus_R	0.0020	Parietal_Inf_R	0.0086
SupraMarginal_R	0.0018	Calcarine_R	0.0082
Cerebelum_Crus1_R	0.0017	Occipital_Mid_R	0.0082
Frontal_Inf_Tri_R	0.0016	Vermis_1_R	0.0080
Heschl_R	0.0015	Cuneus_R	0.0069
Rolandic_Oper_R	0.0014	Temporal_Pole_Mid_R	0.0068
Parietal_Sup_R	0.0013	Lingual_R	0.0058
Frontal_Sup_Orb_L	0.0013	Cerebelum_3_L	0.0054
Cerebelum_6_R	0.0011	Parietal_Inf_L	0.0053
Frontal_Sup_Medial_L	0.0011	Cerebelum_4_5_L	0.0049
Frontal_Mid_Orb_L	0.0010	Cerebelum_3_R	0.0048
Temporal_Pole_Mid_L	0.0010	Cerebelum_6_R	0.0041
Temporal_Pole_Sup_R	0.0009	Angular_R	0.0036
Frontal_Inf_Oper_R	0.0007	Paracentral_Robule_R	0.0035
Cerebelum_4_5_L	0.0004	Cerebelum_10_R	0.0035
Temporal_Pole_Sup_L	0.0004	Cerebelum_7b_R	0.0033
Rectus_L	0.0004	Cerebelum_Crus1_L	0.0031
Cerebelum_7b_R	0.0004	Cerebelum_6_L	0.0029
Vermis_4_5	0.0004	Cerebelum_9_R	0.0028
Cerebelum_8_R	0.0003	Cerebelum_8_R	0.0028
Cerebelum_4_5_R	0.0003	Occipital_Sup_R	0.0026
Temporal_Pole_Mid_R	0.0002	Vermis_4_5	0.0025
Cerebelum_Crus2_R	0.0001	Cerebelum_Crus1_R	0.0022
Cerebelum_8_L	0.0001	Vermis_6	0.0020
Cerebelum_3_L	0.0001	Vermis_10	0.0020
Cerebelum_Crus2_L	0.0001	Cerebelum_Crus2_R	0.0020
Cerebelum_10_L	0.0000	Paracentral_Robule_L	0.0019
Cerebelum_7b_L	0.0000	Cerebelum_4_5_R	0.0017
Cerebelum_9_R	0.0000	Parietal_Sup_L	0.0016
Cerebelum_3_R	0.0000	Vermis_8	0.0010
Cerebelum_9_L	0.0000	Vermis_3	0.0009
Cerebelum_10_R	0.0000	Cerebelum_Crus2_L	0.0009
Vermis_1_L	0.0000	Cerebelum_8_L	0.0007
Vermis_3	0.0000	Parietal_Sup_R	0.0006
Vermis_6	0.0000	Vermis_9	0.0006
Vermis_7	0.0000	Cerebelum_10_L	0.0003
Vermis_8	0.0000	Cerebelum_7b_L	0.0002
Vermis_9	0.0000	Cerebelum_9_L	0.0002
Vermis_10	0.0000	Vermis_7	0.0000

Appendix B

Figure B.1.

Figure B.1 shows the boxplots of the various labeled regions’ LoCo scores for the groupwise AD (top) and FTD (bottom) injury maps across the 14 “atlas” tractograms. Each boxplot shows the mean (black bar), 25^th and 75^th percentiles (bottom and top edge of colored box), range (colored lines extending from box), and any outliers (colored circles). Each lobe is plotted in a different color. It must be noted that the scale of the AD and FTD results are quite different, with the maximal value in the AD figure at 0.14 and the maximal value in the FTD plot at 0.6.

Figure B.2.

Figure B.2 shows the boxplots of the various labeled regions’ GM atrophy scores (z-scores of volume, normalized by the CN group) for the AD (top) and FTD (bottom). Positive values correspond to atrophy. Each boxplot shows the mean (black bar), 25^th and 75^th percentiles (bottom and top edge of colored box), range (colored lines extending from box), and any outliers (colored circles). Each lobe is plotted in a different color.

Figure B.3.

Figure B.3 shows a scatter plot of the Loss in Connectivity (LoCo) score (averaged over each lobe) versus the GM regions’ atrophy (averaged over each lobe) for the following pairs of metrics - top left: AD atrophy vs. AD LoCo, top right: FTD atrophy vs. AD LoCo, bottom left: AD atrophy vs. FTD LoCo, and bottom right FTD atrophy vs. FTD LoCo. Spearman’s correlation coefficient and the corresponding p-values appear in the boxes in the figures.