That hydrogen bonds play a central role in forming Watson–Crick (W–C) A⋅T and G⋅C base pairs is a fundamental paradigm dating from the discovery of the structure of DNA in 1953. In addition to interstrand H bonding, intrastrand base-stacking and interstrand cross-stacking interactions are important in maintaining the bases in a stacked structure along the length of the DNA backbone. In general, H bonds between W–C base pairs are viewed as “informational,” whereas the base-stacking interactions are regarded as “noninformational,” merely stabilizing the double helix. Consequently, it is a common perception that the H bonds pairing A with T and G with C are primarily responsible for the ability of DNA polymerases to synthesize DNA with high fidelity.
Difluorotoluene, a nonpolar isosteric analog of thymine (T), contains fluorine atoms in place of oxygens on the pyrimidine ring and thus cannot form H bonds with A (1). Nevertheless, A⋅F base pairs are formed almost as well as A⋅T pairs by Escherichia coli proofreading-defective DNA polymerase I (KF exo−), as Moran et al. (2) report in this issue of the Proceedings [the chemical structures of F and T and space-filling models of each are shown in Moran et al. (2), figure 1]. The observation that KF exo− fails to discriminate strongly against A⋅F pairs applies when F is present either as a template base on DNA (3) or as a dFTP substrate (2). The apparently inescapable conclusion is that H bonds are not absolutely required for polymerase to form W–C base pairs selectively.
These results provide an impetus to reconsider what role H bonds actually play in stabilizing DNA and enhancing DNA polymerase fidelity. Mismatched base pairs in a duplex DNA oligomer do cause marked reductions in DNA melting temperatures (4). The loss of H bonds upon replacement of T with F has this type of destabilizing effect (2). However, the notion that H bonds alone keep the two strands of a DNA double helix together, which is found in many textbooks, seems inadequate. When one considers that duplex alternating copolymers poly d(A,T) or poly d(G,C) have melting temperatures in aqueous solution that differ substantially from their respective homopolymer counterparts poly dA⋅poly dT or poly dG⋅poly dC, it becomes clear that base-stacking interactions have an important, perhaps dominant, sequence-dependent effect on duplex stability.
Furthermore, the free-energy differences (ΔΔG0) between matched and mismatched base pairs deduced from melting data are in a range of about 0.2–4.0 kcal/mol (4–6), depending on the identity of the mispair, the surrounding sequence context, and its location near the center or at the DNA terminus. These ΔΔG0 values, as measured in solution, are insufficient to account for the high nucleotide insertion fidelities of virtually all polymerases, including those that seem to be especially “error prone” such as eukaryotic Pol β (7) or HIV-1 reverse transcriptase (8–10). For example, ΔΔG0 ≈3.7 kcal/mol measured for the natural base pairs A⋅T versus A⋅C (6) should result in an A⋅C misinsertion frequency of about 2 × 10−3. However, dAMP⋅C and dCMP⋅A misinsertion frequencies are typically about one to two orders of magnitude lower than that (11).
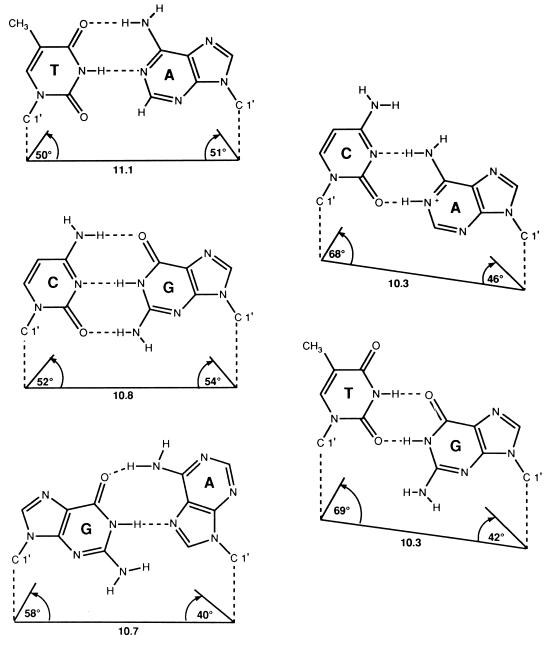
The recognition that base-pairing free-energy differences are too small to completely account for polymerase insertion selectivities prompted H. Echols and me to propose a “geometric selection” mechanism as a key component of insertion specificity (12, 13). The idea is that geometrical and electrostatic properties of the polymerase active site are likely to have a profound influence on nucleotide-insertion specificities. This influence would strongly favor insertion of bases having an optimal geometry, such that the C1′ distances and bond angles most closely approximate those of the Watson–Crick base pairs. For example, G⋅T, G⋅A, and C⋅A mispairs have markedly different bond angles than A⋅T and G⋅C pairs (Fig. 1) (14).
Figure 1.
Geometric properties of Watson–Crick and mismatched base pairs. This figure is based on x-ray crystallography of duplex B-DNA oligonucleotides. The striking geometric identity of the Watson–Crick A⋅T and G⋅C base pairs is not matched by the A⋅C protonated wobble and G⋅T wobble base mispairs or by the G(anti)⋅A(syn) base mispair. [Reproduced with permission from ref. 14 (copyright 1987, Springer, Heidelberg).]
The observation by Moran et al. (2) that insertion of the base analog F opposite A is reduced by only 40-fold compared with its isosteric parent compound T opposite A suggests that the geometrical alignment of the substrate and template bases is a major determinant of polymerase fidelity. This result can be compared with earlier studies using the base analog 2-aminopurine (2AP), which forms 2AP⋅T base pairs with two H bonds in a proper W–C geometry and is reduced by 7-fold compared with A⋅T (15, 16). Thus, the absence of H bonds in the incorporation of F opposite A decreases selectivity only about 6-fold relative to incorporation of 2AP opposite T. Considering that mispairs assuming non-W–C geometries such as G⋅T (wobble), A⋅C (protonated wobble), G⋅A (anti–syn) (Fig. 1) are misinserted with frequencies on the order of 10−3–10−6 (11), geometric constraints imposed at the polymerase active site may improve selectivities by perhaps three orders of magnitude or more.
There are at least three possible check points for proper geometric alignment during base insertion by polymerases: initial dNTP binding (16, 17), postbinding selection for the correct geometry (12, 18) by an induced-fit mechanism (19–21), and the chemical step of phosphodiester formation. Previous data suggest there are significant differences in the extent to which different polymerases use each of the check points. We have suggested that the remarkable base-insertion fidelity of DNA polymerases derives from the sequential application of each check point to provide exquisite sensitivity to Watson–Crick geometry at the transition state for phosphodiester formation (13).
Taking the geometrical constraints imposed by the polymerase active site into consideration in conjunction with the active site electrostatic environment, it may be possible to relate the polymerase-insertion selectivity to solution free-energy differences between matched and mismatched base pairs. Measurements of ΔG0 = ΔH0 − TΔS0 indicate relatively small differences between right and wrong base pairs at 37°C; ΔΔG0 is in a range of 0.2–4 kcal/mol, as mentioned above. The differences are small because ΔS0 correlates with ΔH0 (5, 22), a phenomenon called enthalpy–entropy compensation, which is observed in aqueous solution (23). That is, it takes more energy to melt highly stable, rigidly constrained base pairs than it does to melt less stable, weakly constrained base pairs. However, rigid base pairs having fewer degrees of freedom in the double helix will gain more degrees of freedom upon melting, whereas the opposite is true for less stable base pairs. As long as entropy and enthalpy changes are proportional, ΔΔH0 is reduced by TΔΔS0, resulting in a small ΔΔG0 (5).
How might polymerases increase free-energy differences to achieve high discrimination? Perhaps the geometric constraints imposed on the substrate and template bases in the polymerase active cleft can suppress ΔΔS enough to bring ΔΔG much closer in magnitude to ΔΔH. Typical values of ΔΔH0 measured in aqueous solution are, by themselves, almost large enough to accommodate polymerase-insertion fidelities (5). Then, to the extent that dNTP and template bases confront each other in a lower dielectric medium that acts to partially exclude water, ΔΔH values may be even larger than in water (24). Thus, a polymerase active site that snugly accommodates correct base pairs by geometric selection and also reduces water in the vicinity of the base pair may amplify base pair free-energy differences by reducing entropy differences and increasing enthalpy differences by amounts sufficient to account for nucleotide-insertion fidelity.
In addition to discrimination during nucleotide insertion, fidelity in DNA replication is often enhanced by an associated exonuclease activity. Proofreading exonucleases increase fidelity by approximately 40- to 200-fold (25), displaying significantly less selectivity than polymerases. It is generally believed that exonuclease relies on the “melting capacity” of the 3′ terminus to distinguish between correct and incorrect insertions (26, 27). It is reasoned that polymerization and proofreading are competing reactions at a primer-3′ terminus, requiring an annealed or melted terminus, respectively (16, 17). Discrimination arises because the 3′ terminus is more likely to be annealed following correct insertions, favoring polymerization, but much more likely to be melted out following incorrect insertions, favoring excision (16, 28). It is tempting to ask if a geometric selection mechanism might be occurring in the exonuclease active site, enhancing the excision of non-Watson–Crick base pairs beyond what would be expected based solely on the relative stabilities of base pairs in solution.
Qualitatively, differences in base pair stabilities appear to be sufficient. Evidence comes from presteady state kinetics measurements on the excision of 2AP paired opposite T, C, A, and G using bacteriophage T4 DNA polymerase (29). The rate of excision of 2AP from a primer-3′ terminus is inversely correlated with the melting temperature of 2AP⋅N base pairs imbedded in an oligomer DNA duplex. For example, when present in the same sequence context, a “stable” 2AP⋅T Watson–Crick base pair is hydrolyzed much more slowly than an unstable 2AP⋅C wobble mispair. However, a terminal 2AP⋅T in a A-T rich environment is hydrolyzed more rapidly than 2AP⋅C in a G-C rich environment. Thus, exonuclease specificity appears to be more strongly tied to DNA stability than to terminal base pair geometry.
Nevertheless, it would be of great interest to use proofreading-proficient polymerases to measure the excision of difluorotoluene. Based on thermal denaturation measurements, Moran et al. (2) demonstrate that F pairs poorly with all of the natural bases. Significantly, the magnitude of the free energy difference between F⋅A and T⋅A base pairs is 3.6 kcal/mol, similar to that found for C⋅A versus T⋅A base pairs (6). If proofreading activities are governed primarily by primer stability and not geometric selection, then one would expect F to be excised much more rapidly than T opposite A, and, furthermore, the rate of excision of F might be the same whatever natural bases with which it paired.
The surface has barely been scratched in terms of understanding the interactions between polymerases and DNA that determine replication fidelity. The magnitude and location of mutations depend on a complex interplay between polymerases, proofreading exonucleases, processivity factors and the properties of the DNA primer-template sequences. Although models have been proposed to include polymerase steady-state kinetic parameters along with base stacking and sequence context to explain fidelity (11), precise molecular mechanisms governing mutagenic hot and cold spots remain obscure. Different polymerases copying the same primer-template DNA can exhibit markedly different mutation frequencies and spectra. The ability to separate the effects of H bonding from base stacking holds the promise of new progress in these directions. The future use of the difluorotoluene T analog along with an anticipated group of other non-H bonding base analogs should enable a precise determination of the effects of nearest-neighbor base stacking on misinsertion frequencies and proofreading efficiencies, and shed light on how different polymerase and exonuclease active sites sense the presence of nearby primer and template bases.
I acknowledge the fundamental contribution of Hatch Echols in recognizing the importance of geometric selection in the determination of polymerase fidelity, and I thank D. Kuchnir Fygenson, John Petruska, Ken Breslauer, and Sharon Wald Krauss for their insightful, intellectual contributions and generous advice. This work was supported by the National Institutes of Health (GM21422) and by the Hedco Molecular Biology Laboratory at the University of Southern California.
References
- 1.Schweitzer B A, Kool E T. J Org Chem. 1994;59:7238–7242. doi: 10.1021/jo00103a013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Moran S, Ren R X-F, Kool E T. Proc Natl Acad Sci USA. 1997;94:10506–10511. doi: 10.1073/pnas.94.20.10506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moran S, Ren R X-F, Rumney S, Kool E T. J Am Chem Soc. 1997;119:2056–2057. doi: 10.1021/ja963718g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aboul-ela F, Koh D, Tinoco I J, Martin F H. Nucleic Acids Res. 1985;13:4811–4825. doi: 10.1093/nar/13.13.4811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Petruska J, Goodman M F, Boosalis M S, Sowers L C, Cheong C, Tinoco I., Jr Proc Natl Acad Sci USA. 1988;85:6252–6256. doi: 10.1073/pnas.85.17.6252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Law S M, Eritja R, Goodman M F, Breslauer K J. Biochemistry. 1996;35:12329–12337. doi: 10.1021/bi9614545. [DOI] [PubMed] [Google Scholar]
- 7.Kunkel T A. J Biol Chem. 1985;260:5787–5796. [PubMed] [Google Scholar]
- 8.Preston B D, Poiesz B J, Loeb L A. Science. 1988;242:1168–1171. doi: 10.1126/science.2460924. [DOI] [PubMed] [Google Scholar]
- 9.Roberts J D, Bebenek K, Kunkel T A. Science. 1988;242:1171–1173. doi: 10.1126/science.2460925. [DOI] [PubMed] [Google Scholar]
- 10.Yu H, Goodman M F. J Biol Chem. 1992;267:10888–10896. [PubMed] [Google Scholar]
- 11.Mendelman L V, Boosalis M S, Petruska J, Goodman M F. J Biol Chem. 1989;264:14415–14423. [PubMed] [Google Scholar]
- 12.Sloane D L, Goodman M F, Echols H. Nucleic Acids Res. 1988;16:6465–6475. doi: 10.1093/nar/16.14.6465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Echols H, Goodman M F. Annu Rev Biochem. 1991;60:477–511. doi: 10.1146/annurev.bi.60.070191.002401. [DOI] [PubMed] [Google Scholar]
- 14.Kennard O. In: Nucleic Acids and Molecular Biology. Eckstein F, Lilley D M J, editors. Heidelberg: Springer; 1987. pp. 25–52. [Google Scholar]
- 15.Bessman M J, Muzyczka N, Goodman M F, Schnaar R L. J Mol Biol. 1974;88:409–421. doi: 10.1016/0022-2836(74)90491-4. [DOI] [PubMed] [Google Scholar]
- 16.Clayton L K, Goodman M F, Branscomb E W, Galas D J. J Biol Chem. 1979;254:1902–1912. [PubMed] [Google Scholar]
- 17.Galas D J, Branscomb E W. J Mol Biol. 1978;88:653–687. doi: 10.1016/0022-2836(78)90176-6. [DOI] [PubMed] [Google Scholar]
- 18.Echols H. Biochimie. 1982;64:571–575. doi: 10.1016/s0300-9084(82)80089-8. [DOI] [PubMed] [Google Scholar]
- 19.Kuchta R D, Mizrahi V, Benkovic P A, Johnson K A, Benkovic S J. Biochemistry. 1987;26:8410–8417. doi: 10.1021/bi00399a057. [DOI] [PubMed] [Google Scholar]
- 20.Kuchta R D, Benkovic P, Benkovic S J. Biochemistry. 1988;27:6716–6725. doi: 10.1021/bi00418a012. [DOI] [PubMed] [Google Scholar]
- 21.Wong I, Patel S S, Johnson K A. Biochemistry. 1991;30:526–537. doi: 10.1021/bi00216a030. [DOI] [PubMed] [Google Scholar]
- 22.Petruska J, Goodman M F. J Biol Chem. 1995;270:746–750. doi: 10.1074/jbc.270.2.746. [DOI] [PubMed] [Google Scholar]
- 23.Lumry R, Rajender S. Biopolymers. 1970;9:1125–1227. doi: 10.1002/bip.1970.360091002. [DOI] [PubMed] [Google Scholar]
- 24.Petruska J, Sowers L C, Goodman M F. Proc Natl Acad Sci USA. 1986;83:1559–1562. doi: 10.1073/pnas.83.6.1559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schaaper R M. J Biol Chem. 1993;268:23762–23765. [PubMed] [Google Scholar]
- 26.Brutlag D, Kornberg A. J Biol Chem. 1972;247:241–248. [PubMed] [Google Scholar]
- 27.Muzyczka N, Poland R L, Bessman M J. J Biol Chem. 1972;247:7116–7122. [PubMed] [Google Scholar]
- 28.Bessman M J, Reha-Krantz L J. J Mol Biol. 1977;116:115–123. doi: 10.1016/0022-2836(77)90122-x. [DOI] [PubMed] [Google Scholar]
- 29.Bloom L B, Otto M R, Eritja R, Reha-Krantz L J, Goodman M F, Beechem J M. Biochemistry. 1994;33:7576–7586. doi: 10.1021/bi00190a010. [DOI] [PubMed] [Google Scholar]