Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 May 1.
Published in final edited form as: Microfluid Nanofluidics. 2011 Dec 18;12(6):887–895. doi: 10.1007/s10404-011-0908-0

A compact microfluidic gradient generator using passive pumping

Yandong Gao 1, Jiashu Sun 1, Wan-Hsin Lin 2, Donna Webb 2,3, Deyu Li 1,*
PMCID: PMC3377175  NIHMSID: NIHMS374342  PMID: 22737106

Abstract

Creating and maintaining a precise molecular gradient which is stable in space and time are essential to studies of chemotaxis. This paper describes a simple, compact, and user-friendly microfluidic device using a passive pumping method to drive the liquid flow to generate a stable concentration gradient. A fluidic circuit is designed to offset the effects of the pressure imbalance between the two inlets. After loading approximately the same amount of culture media containing different concentrations of a certain chemotactic agent into the two inlet reservoirs, a linear concentration gradient will be automatically and quickly established at the downstream. Our device takes advantage of passive pumping and is compact enough to fit into a Petri dish, which is an attractive feature to biologists. Furthermore, this microfluidic gradient generator offers a platform for a facile way of long-term imaging and analysis using high resolution microscopy.

Keywords: Concentration gradient, Passive pumping, Chemotaxis, Microfluidic device

1. Introduction

Cell migration plays an important role in many biological and pathological processes including embryogenesis, the immune response, wound healing, tissue repair, and tumor metastasis (Lauffenburger and Horwitz 1996). Chemotaxis is a phenomenon in which a cell migrates directionally in response to a certain concentration gradient. During chemotaxis, a cell senses a relatively shallow gradient of a chemotactic agent and responds with highly oriented polarity and motility (Weiner 2002). Thus, an understanding of the molecular basis of chemotaxis could lead to new therapeutic opportunities for many pathological processes underlying cell migration.

Not surprisingly, there have been considerable interests in developing assays to generate chemotactic gradients. Traditional methods to create gradients of chemotactic agents include the pipette-based assay (Gerisch and Keller 1981), the under-agarose assay (Kohidai 1995), the Boyden/transwell assay (Boyden 1962), and the Dunn assay (Zicha et al. 1997; Zicha et al. 1991). In recent years, various microfluidic chemotactic platforms have been developed which were typically miniaturized variations of these traditional assays. For example, with the Dunn chamber, the linear chemotactic gradient was originally created in a glass bridge between two concentric wells, and the microfluidic version included a source/sink construct to generate the chemotactic gradient in a microfabricated device (Shamloo et al. 2008; Cheng et al. 2007; Abhyankar et al. 2006; Diao et al. 2006). To slow down the decay of the gradient, microcapillaries (Shamloo et al. 2008), hydrogels (Cheng et al. 2007), and membranes (Abhyankar et al. 2006; Diao et al. 2006) were used to serve as high fluidic resistances to minimize convective transport and maintain a diffusion-dominating environment.

However, in real device operation, various factors can prevent the formation of precise molecular gradients that are stable in space and time for biological studies. In the Dunn chamber, for example, the agents will deplete in the source and accumulate in the sink, which will lead to a drift of the concentration gradient over time. To prevent this drift, two continuous fluid streams with prescribed chemotactic agent concentrations have been used to replace the two still liquid reservoirs in the microfluidic platforms (Irimia et al. 2007; Saadi et al. 2007). Another very successful assay of microfluidic concentration gradient generators was a pyramidal microfluidic device presented first by Whitesides and co-workers (Jeon et al. 2000; Dertinger et al. 2001; Jeon et al. 2002; Dertinger et al. 2002). In this scheme, two laminar streams carrying different concentrations of chemotactic agents created a concentration gradient perpendicular to the flow direction after they were repeatedly split, mixed, and recombined in the microfluidic network extending in a pyramidal way. However, both of the above-mentioned schemes require external syringe pumps to maintain equal flow rates/pressures of the two loading streams, which is essential to the generation and maintenance of the stable concentration gradient. This requirement limits the widespread use of these devices for long-term cell culture. Even though active pumping methods such as syringe pumps or electroosmotic pumps can provide more accurate and adjustable volumetric flow rates, the utilization of these pumps requires external equipment which is generally large in size and complex to operate. Moreover, considering the series of activities in cell culture and biological investigations such as cell seeding, culture maintenance, treatment, and observation, the external instruments and their connections complicate the device's experimental usages and increase the chance of introducing contamination.

In view of this, it is desirable to develop a simple microfluidic platform that can generate a stable concentration gradient without the need of complex external instruments. The passive pumping method (Berthier and Beebe 2007; Lynn and Dandy 2009; Walker and Beebe 2002) provides an easy approach to drive fluid flow through microchannels. However, it is difficult to apply this pumping method directly to create a concentration gradient because of the inability of control of the flow rates and balance of the pressures between two streams from individual passive pumps. Considering the various factors that can affect the pressure and the flow rate in passive pumping, tiny operational variations may lead to significant drifts in the final generated concentration gradient.

In this paper, a fluid circuit has been designed to balance the pressures between two streams from two separate passive pumps. By feeding the pyramidal microfluidic circuit with these two streams, a linear concentration gradient is created and maintained at the downstream. The microfluidic platform sheds the external syringe pumps and the associated connections. Its compact nature, therefore, allows the platform to be placed into a 75-mm-diameter Petri dish, compatible with the everyday practice of experimental cell biologists. The final platform is also extremely easy for biologists to operate and to be mounted on conventional microscopes for long-term, high-resolution live-cell imaging.

2. Design Principle of the Pressure Balance Circuit

Compared to reported microfluidic gradient generators (Jeon et al. 2000; Dertinger et al. 2001), we changed the pumping component from the external syringe pumps to the semi-autonomous pumps. This passive pumping method (Berthier and Beebe 2007; Lynn and Dandy 2009; Walker and Beebe 2002) eliminated any connections and ensured that the whole device was compact enough to be placed into a Petri dish. However, the passive semi-autonomous pumps also face challenges. The main issue confronting the passive pumping method is to maintain pressure equilibrium between the two feeding streams of different chemotactic agent concentrations to form a linear concentration gradient. Pressure imbalance between the two streams will disturb the side-by-side streams. As a result, they cannot be split and recombined equally in the pyramidal microfluidic circuit as expected.

In passive pumping, the laminar flow inside the microfluidic channels and chambers is maintained by the pressure difference between the loading and waste wells (reservoirs) due to the elevation and capillary effects. It is extremely difficult to achieve a precise pressure balance between the two inlets because of the inevitable slight variations in the amount of media loaded into each well, the physical properties of the media (e.g., capillary properties, viscosities, etc.), and the inner surface properties of each reservoir. In practice, for example, the only control is to load equal amounts of media measured by the pipette; however, slight differences always exist because of the inevitable operational variations. The combination of these effects could disrupt the stable and reproducible concentration gradient. To overcome the issue of the imbalanced pressure and flow rate between the two feeding streams, we designed and implemented a fluidic circuit including a balance zone and an equilibrium zone at the upstream as shown in Fig. 1(a), through which two streams with equivalent pressure were generated automatically.

Figure 1.

Figure 1

Open in a new tab

Design of the microfluidic concentration gradient generator. (a) A schematic of the microfluidic circuit. Once the two streams, A and B, with different concentrations of a chemotactic agent, travel through the balance zone and equilibrium zone, their flow rates and pressures become the same, which is critical for generation of a stable and linear concentration gradient in the culture and observation zone. (b) An enlarged view of the balance zone and equilibrium zone. (c) An equivalent electrical circuit model. (d) A picture of the assembled device. Water and Ink were added to the left and right reservoirs and allowed to flow through the device.

The balance zone includes two serpentine channels with high flow resistance functioning as counter-pressure-difference channels (Fig. 1(b)). Each channel is connected with a liquid reservoir for holding media. After the two fluidic steams travel down these two serpentine channels, they meet at a contact zone which is designed to equilibrate their pressures. It is worth noting that the equilibrium zone has been used by Irimia et al. (2007); however, in their scheme, there is no balance zone with high flow resistance serpentine channels before the two stream meet at the contact zone. Once passing this contact zone, the pressures of the two streams become the same. Note that mixing can occur when the media flow through the contact zone and a small portion of the media from the higher pressure stream are pushed to the stream of a lower pressure. To reduce the effects from mixing, each stream will flow through another serpentine channel in which the media will mix to achieve a new uniform concentration. Then, they continuously travel down into the pyramidal microfluidic network and form a concentration gradient in the cell culture and observation zone.

To demonstrate the design principle, an equivalent electric circuit model of the microfluidic network is shown in Fig. 1(c). A simple analogy led to the following equation,

iA−iB=PA−PBRb, (1)

where PA and PB represent the pressure at each inlet; Rb represents the flow resistance of the counter-pressure-difference channel; and iA and iB denote the flow rate of each stream. Our aim is to minimize the difference between these two flow rates. According to Eqn. (1), this goal can be achieved through either reducing the pressure difference (PA - PB) or increasing the flow resistance Rb. As mentioned above, a pressure difference cannot be completely avoided in reality. Therefore, we increased the flow resistance of the counter-pressure-difference channel, Rb, as a mean of diminishing the effect of the pressure imbalance, which is the reason for adding two long serpentine channels before the contact zone (Fig. 1(b)).

3. Results and Discussion

3.1 Device fabrication and dimensions

The microfluidic devices were fabricated using standard soft-lithography techniques (Dertinger et al. 2001) by replica molding polydimethylsiloxane (PDMS) (Ellsworth Adhesives, Germantown, WI). PDMS was chosen as the construction material because of its attractive features such as biocompatibility, thermal and chemical stability, and optical transparency for imaging. The mold was created using a photosensitive material (SU-8 2025) patterned through a transparent mask and positioned over a silicon wafer (McDonald and Whitesides 2002). A pre-polymer solution of PDMS was then mixed with a curing agent at a 10:1 ratio and poured over the mold. After degassing, the PDMS layer was allowed to solidify over their molds at 70°C for 2 h. The solidified layer of PDMS was then peeled from its mold, and a sharp metal puncher was used to generate holes for the media wells. After the surfaces were treated with oxygen plasma, the PDMS was bonded to a glass coverslip (No. 1, VWR Vista Vision, Suwanee, GA). The thin glass coverslip was used as the base to facilitate observations by high resolution microscopy. The microfluidic system was finished by attaching three cloning cylinders (Fisher Scientific, Pittsburg, PA) to the punched holes as reservoirs. An image of the assembled devices is shown in Fig. 1(d).

Two types of devices have been fabricated. The channel heights of both devices are 60 μm. In device I, the compensation channel and each branch in the splitting and mixing zone have a width of 100 μm and a length of 7 mm. The contact zone is 500 μm wide and 750 μm long. An 18 mm long and 100 μm wide serpentine channel works as the counter-pressure-difference channel, whose flow resistance is 2.57 times that of the flow resistance of the compensation channel. In device II, the counter-pressure-difference channel is replaced by a 19 mm long and 50 μm wide serpentine channel. As a result, its flow resistance increases to 9.82 times that of the compensation channel.

3.2 Numerical simulations of the device performance

To validate our designs, two-dimensional numerical modeling was performed to illustrate the working mechanisms of the concentration gradient generator. In the simulation, the diffusion coefficient of the chemotactic agent was chosen as 7 × 10-10 m2/s (for comparison, the diffusion coefficients of glucose and glycine are 6.7 × 10-10 and 10.1 × 10-10 m2/s, respectively (Longsworth 1953)). The density of the media was taken as 103 kg/m3 and its viscosity as 10-3 Pa·s.

At the inlet A, the chemokine concentration c was set to be 1, while it was set as 0 at the inlet B. The pressure at the inlet and outlet was set as 1 Pa and 0 Pa, respectively. With these parameters, the maximum flow rate in the microchannels was about 40 μm/s. To generate the desired concentration gradient in the cell culture and observation zone, the two streams entering the spliting and mixing zone should have the same flow rate and pressure as shown in Fig. 2(a). Otherwise, the streams would not be split at the downstreams equally and create an acceptable concentration gradient.

Figure 2.

Figure 2

Open in a new tab

Simulation results of the concentration distribution at the top of the microfluidic network. (a, b) without the balance zone, the microfluidic platform will fail to generate satisfatory gradients if there is a small pressure difference (5%) between the two inlets. (c, d) with a balance zone, a good concentration difference can be maintained even if there is a pressure difference as large as 25%. (c) In device I, the flow resistance of counter-pressure-difference channels is 2.57 times that of the compensation channel. (d) In device II, the flow resistance of counter-pressure-difference channels is 9.82 times that of the compensation channel.

In practice, however, the above mentioned ideal case usually cannot be achieved. There always exists a pressure difference between these two inlets because of variations in the liquid heights in the two inlet wells, liquid surface shapes, and/or other factors in the experiment. Imbalanced pressure would eventually generate an undesired concentration profile at the cell culture and observation zone. As shown in Fig. 2(b), if the pressure at inlet B is higher than that at inlet A by 5%, the concentration of the left stream in the compensation channel will decrease dramatically to 0.35, instead of 0.95 as in Fig. 2(a). This is exactly the reason why we need a pressure balance zone with long serpentine channels to reduce the pressure difference between the two streams.

According to Eqn. (1), the flow rate difference between the two streams would decrease as the flow resistance of the counter-pressure-difference channels increases. To demonstrate this effect, two more cases with the presence of counter-pressure-difference channels were simulated. If we denote the flow resistance of each compensation channel as R, then the flow resistance of the counter-pressure-difference channel is 2.57R for device I as in Fig. 2(c) and 9.82R for device II as in Fig. 2(d). With the counter-pressure-difference channels, even when the pressure at inlet B is higher than that at inlet A by 25%, the concentration of the left stream in the compensation channel only decreases to 0.72 for device I, and 0.83 for device II, which is dramatically better than that without the counter-pressure-difference channels. These results demonstrate that the counter-pressure-difference channel can effectively offset the effects of the pressure difference between the two streams and diminish the effect of inlet pressure variations during device operation.

The concentration distributions at the outlet of the cell culture and observation chamber for the two devices are plotted in Fig. 3 for various pressure differences. Even when the pressure difference is as high as 50%, it is still possible to obtain a reasonable concentration gradient with the well-designed pressure balance circuit.

Figure 3.

Figure 3

Open in a new tab

Simulation results of the concentration distributions at the outlet of (a) device I, and (b) device II.

3.3 Experimental validation of concentration gradients

Verification of the reagent concentration distribution was performed using digital imaging of a fluorescent marker (FITC, Thermo Fisher, Pierce, IL). The images for the concentration distribution were taken using a fluorescent inverted microscope with a CCD camera.

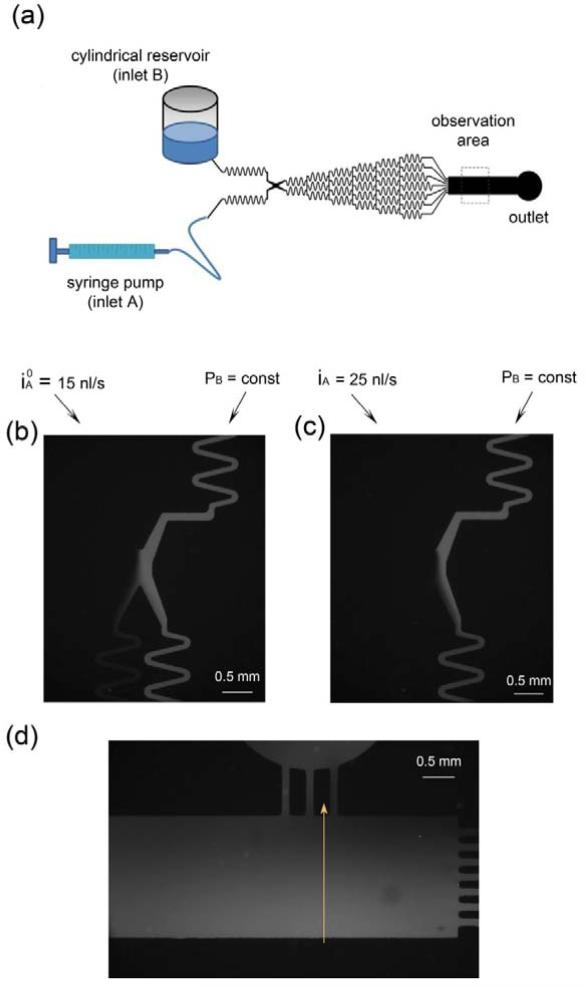
As shown in Fig. 4(a), inlet A was connected to a syringe pump to inject deionized (DI) water and inlet B was connected to a cylindrical reservoir that held FITC diluted into DI water. For a short time period during the experiment, the pressure of inlet B and the outlet can be regarded as constant, and the pressure difference between the two inlets can be evaluated from the equivalent electrical circuit as,

PA−PB=[(Rb+2Rm+Rc)iA−PB]RbRb+Rm+0.5Rc, (2)

where Rb, Rc, Rm are the flow resistance of the counter-pressure-difference channel, the compensation channel and the splitting and mixing zone, respectively. They were calculated by (White 2006)

R=L4ba33μ[1−192aπ5bΣi=1,3,5…∞tanh(iπb∕2a)i5]. (3)

Here b and a are half of the channel height and the channel width, respectively. L is the length of the channel. The flow rate iA was read from the syringe pump. The pressure of inlet B represented by PB in the equivalent circuit was determined from the fluorescence micrographs around the contact zone. By adjusting the flow rate iA, the two streams met in the middle as shown in Fig. 4(b). We assumed that the two flow rates from inlet A and B were approximately equal in this case. The flow rate was recorded as iA0. Then the value of PB was obtained by

PB=(Rb+2Rm+Rc)iA0. (4)

Once PB was determined, the pressure difference was calculated by Eqn. (2). Fig. 4(c) shows the fluorescent intensity profile as the flow rate iA was increased to 25 nl/s (corresponding to a pressure difference of 27.09% based on the calculation as described above).

Figure 4.

Figure 4

Open in a new tab

Experimental validation of the concentration gradient generator. (a) A schematic of the experimental set-up to verify the concentration gradient. (b, c) Fluorescent micrographs around the equilibrium zone. Image (b) was used to determine the equilibrium flow rate and pressure. (d) A fluorescent micrograph in the cell culture and observation zone. The line is the place along which the fluorescent intensities are extracted to plot the intensity profiles in Fig. 5.

The concentration profiles along the line in the cell culture and observation chamber are plotted in Fig. 5 for both types of devices. The results confirmed the effectiveness of the pressure balance circuit in the microfluidic device. With the pressure balance circuit, the microfluidic concentration generator can sustain a large pressure imbalance between the two inlets. The larger the flow resistance of the balance zone, the better the performance of the microfluidic gradient generator.

Figure 5.

Figure 5

Open in a new tab

Fluorescent intensity profiles in the cell culture and observation zone. (a) device I (Rb = 15,978 Pa·s/μl) (b) device II (Rb = 61,009 Pa·s/μl). Both cases have Rc = 6,213.9 Pa·s/μl and Rm = 7,298.2 Pa·s/μl.

3.4 Comparison with devices without the pressure balance circuit

To further demonstrate the effectiveness of the pressure balance circuits, we have compared the fluorescent intensity profiles from devices with and without the balance zone. We fabricated a total of 8 type I devices (as shown in Fig. 1(d)) and another 8 devices without the balance zone where the two streams from the passive pumps went to the equilibrium zone directly (as shown in Fig. 2(a, b)). During tests, 400 μl of DI water alone or with FITC were loaded into each reservoir, respectively. After 30 minutes, fluorescent images were recorded at the cell culture chambers. The tests were repeated twice for each device and 16 results for each type of concentration gradient generators were obtained as shown in Fig. 6. It can be clearly seen that without the pressure balance circuit the intensity profiles (stars in Fig. 6) are difficult to reproduce, because of the inevitable slight variations in the loading process and device parameters. However, the intensity profiles from the type I microfluidic devices (shown with solid circles) form approximately linear gradients, which are bounded in a region. These results show that the pressure balance circuit could effectively improve the performance of the microfluidic gradient generator.

Figure 6.

Figure 6

Open in a new tab

Comparison of fluorescent intensity profiles of microfluidic devices with and without the balance zone.

3.5 Concentration gradients in a long term

We also conducted an experiment to monitor the concentration profile as a function of time. 400 μl of ovalbumin (at a concentration of 0.1 mg/ml) and 400 μl of 10× PBS were loaded into the upstream reservoirs in a type II device. The initial incomplete meniscus in the waste reservoirs generated a fast flow to build up the concentration gradient quickly. After 30 min, 100 μl of 10× PBS was added in the waste reservoir to form a complete meniscus to slow down the flow rate. This operation also avoided the abrupt flow rate change caused by the transition from incomplete to complete meniscus. After the loading reservoirs were covered by two slabs of PDMS to reduce the effect of evaporation, the microfluidic platform was mounted onto the microscope stage. Fluorescent images were taken every half an hour, and the results are plotted in Fig. 7(a). We also extracted the data ranging from 0.3 mm to 1.8 mm and found the gradient of each line (intensity per mm) that fitted the data in a least squares sense. The gradients at each time point were plotted in Fig. 7(b). The gradient profiles are relatively consistent for up to 12 h. To further improve the performance, the flow resistance of the counter-pressure-difference channel can be further increased.

Figure 7.

Figure 7

Open in a new tab

Long time behaviors of the concentration gradients. (a) Concentration profiles for 12 hours. (b) Concentration gradient versus time.

4. Summary

Microfluidic devices would have a significant impact on current experimental methods if they were widely accepted and used in biological laboratories. We recognized that the passive pumping method, because of its simplicity, could lead to microfluidic devices that are user friendly and compatible with traditional biological cell culture practice. Without the need of external complex connections and expensive equipment, the devices are simple to operate and compact to fit into a Petri dish, which are attractive to end users - biologists. On the other hand, the semi-autonomous flow from the passive pump is difficult to control precisely. Some elaborated flow patterns such as two parallel streams with equal pressure and flow rate are difficult to acquire. Therefore, we designed a fluidic circuit that can generate two streams with equivalent pressure from the two passive pumps. Numerical simulations and experimental tests based on fluorescent imaging technique confirmed the functions of the fluidic circuit. By feeding the pyramidal microfluidic circuit with these two streams, a linear concentration gradient was created and maintained at the downstream. A thin coverslip as the base and transparent PDMS as the construct material would facilitate optical imaging at high resolution. In addition, the pressure balance circuit may be applied to a variety of lab-on-a-chip applications that requires two streams with balanced pressure and flow rate.

Acknowledgements

We thank Devi Majumdar and Rebecca Michaud for helpful discussion. This work was supported by National Institutes of Health (NIH) grant GM092914 to D.J.W and by National Science Fundation (NSF) grant CBET0643583 to D.L.

References

  1. Abhyankar VV, Lokuta MA, Huttenlocher A, Beebe DJ. Characterization of a membrane-based gradient generator for use in cell-signaling studies. Lab on a Chip. 2006;6(3):389–393. doi: 10.1039/b514133h. doi:10.1039/b514133h. [DOI] [PubMed] [Google Scholar]
  2. Berthier E, Beebe DJ. Flow rate analysis of a surface tension driven passive micropump. Lab on a Chip. 2007;7(11):1475–1478. doi: 10.1039/b707637a. doi:10.1039/B707637a. [DOI] [PubMed] [Google Scholar]
  3. Boyden S. The chemotactic effect of mixtures of antibody and antigen on polymorphonuclear leucocytes. J Exp Med. 1962;115:453–466. doi: 10.1084/jem.115.3.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cheng SY, Heilman S, Wasserman M, Archer S, Shuler ML, Wu M. A hydrogel-based microfluidic device for the studies of directed cell migration. Lab on a Chip. 2007;7(6):763–769. doi: 10.1039/b618463d. doi:10.1039/b618463d. [DOI] [PubMed] [Google Scholar]
  5. Dertinger SKW, Chiu DT, Jeon NL, Whitesides GM. Generation of gradients having complex shapes using microfluidic networks. Anal Chem. 2001;73(6):1240–1246. doi:10.1021/ac001132d. [Google Scholar]
  6. Dertinger SKW, Jiang XY, Li ZY, Murthy VN, Whitesides GM. Gradients of substrate-bound laminin orient axonal specification of neurons. P Natl Acad Sci USA. 2002;99(20):12542–12547. doi: 10.1073/pnas.192457199. doi:10.1073/pnas.192457199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Diao J, Young L, Kim S, Fogarty EA, Heilman SM, Zhou P, Shuler ML, Wu M, DeLisa MP. A three-channel microfluidic device for generating static linear gradients and its application to the quantitative analysis of bacterial chemotaxis. Lab on a Chip. 2006;6(3):381–388. doi: 10.1039/b511958h. doi:10.1039/b511958h. [DOI] [PubMed] [Google Scholar]
  8. Gerisch G, Keller HU. Chemotactic reorientation of granulocytes stimulated with micropipettes containing fMet-Leu-Phe. J Cell Sci. 1981;52:1–10. doi: 10.1242/jcs.52.1.1. [DOI] [PubMed] [Google Scholar]
  9. Irimia D, Charras G, Agrawal N, Mitchison T, Toner M. Polar stimulation and constrained cell migration in microfluidic channels. Lab on a Chip. 2007;7(12):1783–1790. doi: 10.1039/b710524j. doi:10.1039/B710524j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Jeon NL, Baskaran H, Dertinger SKW, Whitesides GM, Van de Water L, Toner M. Neutrophil chemotaxis in linear and complex gradients of interleukin-8 formed in a microfabricated device. Nat Biotechnol. 2002;20(8):826–830. doi: 10.1038/nbt712. doi:10.1038/Nbt712. [DOI] [PubMed] [Google Scholar]
  11. Jeon NL, Dertinger SKW, Chiu DT, Choi IS, Stroock AD, Whitesides GM. Generation of solution and surface gradients using microfluidic systems. Langmuir. 2000;16(22):8311–8316. doi:10.1021/la000600b. [Google Scholar]
  12. Kohidai L. Method for Determination of Chemoattraction in Tetrahymena-Pyriformis. Curr Microbiol. 1995;30(4):251–253. doi: 10.1007/BF00293642. [DOI] [PubMed] [Google Scholar]
  13. Lauffenburger DA, Horwitz AF. Cell migration: A physically integrated molecular process. Cell. 1996;84(3):359–369. doi: 10.1016/s0092-8674(00)81280-5. doi:10.1016/S0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
  14. Longsworth LG. Diffusion Measurements, at 25°, of Aqueous Solutions of Amino Acids, Peptides and Sugars. J Am Chem Soc. 1953;75(22):5. doi:10.1021/ja01118a065. [Google Scholar]
  15. Lynn NS, Dandy DS. Passive microfluidic pumping using coupled capillary/evaporation effects. Lab on a Chip. 2009;9(23):3422–3429. doi: 10.1039/b912213c. doi:10.1039/B912213c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. McDonald JC, Whitesides GM. Poly(dimethylsiloxane) as a material for fabricating microfluidic devices. Accounts Chem Res. 2002;35(7):491–499. doi: 10.1021/ar010110q. doi:10.1021/Ar010110q. [DOI] [PubMed] [Google Scholar]
  17. Saadi W, Rhee SW, Lin F, Vahidi B, Chung BG, Jeon NL. Generation of stable concentration gradients in 2D and 3D environments using a microfluidic ladder chamber. Biomed Microdevices. 2007;9(5):627–635. doi: 10.1007/s10544-007-9051-9. doi:10.1007/s10544-007-9051-9. [DOI] [PubMed] [Google Scholar]
  18. Shamloo A, Ma N, Poo MM, Sohn LL, Heilshorn SC. Endothelial cell polarization and chemotaxis in a microfluidic device. Lab on a Chip. 2008;8(8):1292–1299. doi: 10.1039/b719788h. doi:10.1039/b719788h. [DOI] [PubMed] [Google Scholar]
  19. Walker GM, Beebe DJ. A passive pumping method for microfluidic devices. Lab on a Chip. 2002;2(3):131–134. doi: 10.1039/b204381e. doi:10.1039/B204381E. [DOI] [PubMed] [Google Scholar]
  20. Weiner OD. Regulation of cell polarity during eukaryotic chemotaxis: the chemotactic compass. Curr Opin Cell Biol. 2002;14(2):196–202. doi: 10.1016/s0955-0674(02)00310-1. doi:10.1016/S0955-0674(02)00310-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. White FM. McGraw-Hill series in mechanical engineering. 3rd edn. McGraw-Hill Higher Education; New York, NY: 2006. Viscous fluid flow. [Google Scholar]
  22. Zicha D, Dunn G, Jones G. Analyzing chemotaxis using the Dunn direct-viewing chamber. Methods in Molecular Biology. 1997;75:449–457. doi: 10.1385/0-89603-441-0:449. doi:10.1385/0-89603-441-0:449. [DOI] [PubMed] [Google Scholar]
  23. Zicha D, Dunn GA, Brown AF. A new direct-viewing chemotaxis chamber. Journal of Cell Science. 1991;99(Pt 4):769–775. doi: 10.1242/jcs.99.4.769. [DOI] [PubMed] [Google Scholar]

RESOURCES