The spectra and periodograms of anti-correlated discrete fractional Gaussian noise

Abstract

Discrete fractional Gaussian noise (dFGN) has been proposed as a model for interpreting a wide variety of physiological data. The form of actual spectra of dFGN for frequencies near zero varies as f^1–2H, where 0 < H < 1 is the Hurst coefficient; however, this form for the spectra need not be a good approximation at other frequencies. When H approaches zero, dFGN spectra exhibit the 1 – 2H power-law behavior only over a range of low frequencies that is vanishingly small. When dealing with a time series of finite length drawn from a dFGN process with unknown H, practitioners must deal with estimated spectra in lieu of actual spectra. The most basic spectral estimator is the periodogram. The expected value of the periodogram for dFGN with small H also exhibits non-power-law behavior. At the lowest Fourier frequencies associated with a time series of N values sampled from a dFGN process, the expected value of the periodogram for H approaching zero varies as f⁰ rather than f^1–2H. For finite N and small H, the expected value of the periodogram can in fact exhibit a local power-law behavior with a spectral exponent of 1 – 2H at only two distinct frequencies.

1. Introduction

Recently, there has been considerable interest in the use of stochastic fractal models to help interpret physiological data [1]. Two models that have been investigated extensively in this context are fractional Brownian motion (FBM) and fractional Gaussian noise (FGN) [2]. These two models are related to one another, but the connection between them and how they are used in practical applications brings up some subtle issues that have not been fully appreciated amongst practitioners and that are the focus of the present manuscript.

Our starting point is FBM, which we denote here as B_H(t), 0 ≤ t ≤ ∞. FBM is a continuous parameter stochastic process that depends upon a parameter H, the Hurst coefficient, where 0 < H < 1. The qualifier ‘continuous parameter’ refers to the fact that the independent variable, t, ranges over all non-negative real values. In practical applications, we must deal with sampled data, which leads us to consider B_H(t) at just the integers t =0, 1, 2,… . This sampling leads to a discrete parameter version of FBM, which we refer to as dFBM. For clarity, we henceforth refer to the continuous parameter version of FBM as cFBM.

Flandrin [3] shows that, even though cFBM is a non-stationary process, it has a well-de6ned power spectrum S(f) that obeys a power law exactly over all frequencies; i.e., S(f) is proportional to f^−1–2H for −∞ < f < ∞. Flandrin also considers a form of a derivative of cFBM, namely, a process defined as lim_δ→0 ((B_H(t + δ)–B_H(t))/δ). He shows that this derivative process also has a spectrum that obeys a power law exactly over all frequencies and is given by S(f) ~ f^1–2H. The concept of FGN as formulated by Mandelbrot and Van Ness is related to this derivative process in that, rather than letting δ decrease to zero, we fix it at unity. This leads us to what we will refer to as continuous FGN (cFGN) and discrete FGN (dFGN). cFGN is defined as X(t)= B_H(t + 1) – B_H(t), where 0 ≤ t ≤ ∞, resulting in a spectrum given by the product of the squared gain function for a first difference filter and the spectrum of cFBM, i.e., S(f) ~ 4 sin² (πf)f^−1–2H, which approaches a power law only as f → 0. dFGN is obtained by restricting t to the non-negative integers. Note that, in addition to being the sampled version of cFGN, the process dFGN can be regarded as the first difference of dFBM. We also note that, due to the sampling, the spectra for dFBM and dFGN are even periodic functions with a period of unity, so the frequencies of interest satisfy −1/2 ≤ f ≤ 1/2, and their respective spectra also approach power laws only as f → 0.

Both dFGN and dFBM have found application in many areas of science and have been applied to discretely sampled time series of many natural processes. The fact that cFBM and its derivative have spectra that exactly obey a power law over −∞ < f < ∞ has sometimes mistakenly been taken to hold both for the spectra of dFBM over −1/2 ≤ f ≤ 1/2 and for estimates of these spectra given by the periodogram. Sometimes the power-law expression is cited directly, and it is implied or assumed that the expected estimated spectra as computed by the periodogram for dFGN are a power law everywhere [4-6]. The idea that the spectra of cFGN are a power law everywhere has been transferred to power-law behavior of dFGN spectral estimates, and the caveat that the actual spectra for dFGN are only a power law in the limit as f → 0 appears to be unheeded. Churilla et al. [4] posit separate power-law behavior for the low frequencies and the high frequencies of the periodogram and derive separate Hurst coefficients for both by fitting each band of frequencies with a different power law based on the power-law formulation. The spectral synthesis method of Peitgen and Saupe [7] and that modified by Bassingthwaighte and Raymond [8] generated dFGN by an inverse Fourier transform of the power-law spectral coefficients after phase randomization and multiplying the amplitudes by random Gaussian numbers. The expected value of periodograms from this kind of process will be a power law, and does not have the same spectrum as a dFGN. Pilgram and Kaplan [5] useda spectral synthesis method whose basis is the power-law spectrum, but studied only spectra for H ≥ 0.5 and therefore did not observe the incorrect spectral representation at the low frequencies though their method does also represent the highest frequencies incorrectly.

If we plot S(f)= f^1–2H versus f on a log–log scale, we see a line with a slope of 1 – 2H. To determine frequencies over which S(f) for dFGN varies as f^1–2H, we define a local spectral exponent

$$e(f,\delta )=\frac{\log \left(S\right(f+\delta \left)\right)-\log \left(S\right(f-\delta \left)\right)}{\log (f+\delta )-\log (f-\delta )},$$ (1)

where 0 < δ < f. As δ → 0, f → 0, e(f,δ) → 1 – 2H. We also define a local Hurst coefficient

$$H(f,\delta )=(1-e(f,\delta \left)\right)∕2.$$ (2)

By plotting H (f,δ) as a function of f with δ set to a small number, it is possible to see at what frequencies this function is approximately equal to the Hurst coefficient, showing the region where S(f) varies as f^1–2H to a good approximation. It is not widely appreciated how very low the frequency must become when H is also small for the spectra to exhibit power-law behavior.

Marked departure from nominal 1 – 2H behavior of dFGN spectra occurs under several conditions. At high frequencies near f =0.5 (the Nyquist frequency for the data set sampled from cFGN), the dFGN spectra flatten out and the local spectral exponent is zero. When H is near zero, a significant portion of the frequency band beginning at f = 0.5 and extending through mid-range frequencies also deviates from nominal 1 – 2H power-law behavior. The only spectrum of dFGN that obeys the nominal power law everywhere is for H = 0.5, i.e., the ‘white’ noise spectrum with zero exponent everywhere. For H > 0.5, the spectra of correlated or persistent dFGN exhibit a significant discrepancy from nominal power-law behavior only near the highest frequencies. The flatness of these spectra near f=0.5 is less remarkable than the overall impression of power-law behavior [9, p. 54]. For H < 0.5, the spectra of anti-correlated or anti-persistent dFGN have more extensive regions of non-power-law behavior than what is observed for positively correlated dFGN spectra. More attention has been paid to positively correlated than to anti-correlated series, and consequently the impression of power-law behavior for all spectra of dFGN has been inadvertently reinforced.

The next three sections of this paper are devoted to (1) calculating the local Hurst coefficients, H(f, δ) from Eq. (2) for the spectra of dFGN; (2) comparing the local H(f, δ) from spectra and periodograms and showing the effects of series length, N; and (3) evaluating the utility of the local spectral exponents, e(f, δ), obtained at the lowest available frequencies of the periodograms. The results emphasize that the 1 – 2H power-law behavior of the spectra applies only to a very small range of frequencies when the Hurst coefficient is small; the expected value of the periodogram exhibits power-law behavior only over a small frequency band, if at all; the expected values of the periodograms at the lowest available frequencies for anti-correlated dFGN do not converge to the actual spectra as N increases; and for very small H, the local spectral exponent of the smallest available frequencies from the periodogram of dFGN is zero.

2. Calculating the local Hurst coefficients, H( f, δ), for the spectra of dFGN

The spectral density function (SDF) for dFGN is given by Sinai [10] and Beran [9] as

$$S\left(f\right)=4{\sigma }^2{C}_H{\sin }^2\left(\pi f\right)\sum _{j=-\infty }^{\infty }\frac{1}{{\mid f+j\mid }^{2H+1}},\mid f\mid \le 1∕2,$$ (3)

where σ² is the variance of the process, 0 < H < 1 is the Hurst coefficient, and

$$C_H=\Gamma (2H+1)\sin \left(\pi H\right)∕{\left(2\pi \right)}^{2H+1}.$$ (4)

Eq. (3) is not useful in calculating the SDF when H < 0.5 because of the slow convergence of the infinite summation. The SDF can be approximated and computational efficiency gained by using an Euler–Maclaurin summation [11, p. 280]:

$$S\left(f\right)\approx \tilde{S}\left(f\right)=4{\sigma }^2{C}_H{\sin }^2\left(\pi f\right)[\left(\sum _{j=-M}^M\frac{1}{{\mid f+j\mid }^{2H+1}}\right)+\sum _{j=-1,1}(\frac{1}{2H{(lf+M+1)}^{2H}}-\frac{(2H+1)(2H+2)(2H+3)}{720{(lf+M+1)}^{2H+4}}+\frac{2H+1}{12{(lf+M+1)}^{2H+2}}+\frac{1}{2{(lf+M+1)}^{2H+1}}\left)\right].$$ (5)

Only 2M + 3 terms need to be evaluated (note that the second summation is over 1 and −1, not 0), and choosing M = 100 gives |S(f) – S̃)f|/S(f) < 10⁻⁶.

Fig. 1 shows the local Hurst coefficient, H(f, δ), calculated from the SDFs for 12 Hurst coefficients, H = 0.99, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.01 and 0.001, with δ = 0.005f. In Table 1, we have calculated the frequency below which |H(f, δ) – H| ≤ 0.1H, i.e., the frequency below which the local Hurst coefficients are within 10% of the nominal H. For positively correlated FGNs, 0.5 < H < 1, as f is decreased from 0.5, H(f, δ) rises sharply above the true H and then soon decreases to within 10% of the nominal Hurst coefficient when f is about 0.2 and to within about 1% when f < 0.03. The local Hurst coefficient for a white noise spectra, (H =0.5) is everywhere 0.5.

Fig. 1.

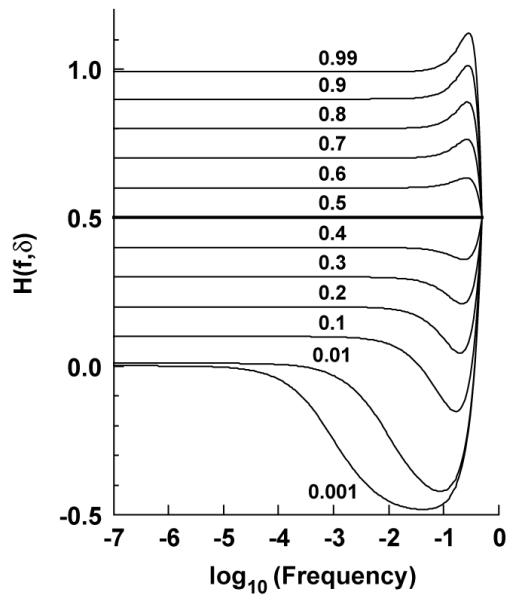
Estimate of the local Hurst coefficient, H(f, δ), versus frequency for dFGN of varied true H. The power-law region where the similarity scaling in the power spectrum exists, or where H(f, δ) is approximately equal to a constant, is relatively short for Hurst coefficients below 0.1.

Table 1.

The power-law frequency limits

H	f such that |H(f, δ) – H| < 0.1H
0.99	f ≤ 2:1 × 10−1
0.9	f ≤ 2:1 × 10−1
0.8	f ≤ 2:3 × 10−1
0.7	f ≤ 4:4 × 10−1
0.6	f ≤ 4:7 × 10−1
0.5	f ≤ 5:0 × 10−1
0.4	f ≤ 2:2 × 10−1
0.3	f ≤ 6:5 × 10−2
0.2	f ≤ 2:3 × 10−2
0.1	f ≤ 4:5 × 10−3
0.01	f ≤ 2:4 × 10−5
0.001	f ≤ 2:0 × 10−7

For the anti-correlated dFGNs, 0 < H < 0.5, H(f, δ) drops steeply as f decreases from 0.5, undershooting the true or nominal value of the Hurst coefficient (Fig. 1, lower section). The local Hurst coefficient then slowly converges to the nominal H at low frequencies. The convergence is markedly slower than for positively correlated dFGN. For anti-correlated dFGN, the highest frequency at which H(f, δ) is within 10% of H decreases as H decreases. For a Hurst coefficient of 0.001, only at frequencies lower than 2.0 × 10⁻⁷ is H(f, δ) within 10% of H. The lowest non-zero Fourier frequency in a periodogram that is computed for a time series of length N is given by 1/N. If we could accurately determine the spectrum by computing the periodogram, we would need a series at least as long as 5 million points when H = 0.001 in order to achieve a power law at f = 1/N (as will be shown in the next section; in fact, estimation of the spectrum via the periodogram is problematic). Summarizing, Fig. 1 indicates that neither positively correlatednor anti-correlated dFGNs have spectra following 1– 2H power-law scaling over the complete range of frequencies. Only a white noise dFGN has a power spectral exponent of 1 – 2H, namely zero.

3. Comparing the local H(f, δ) from dFGN spectra and periodograms with H = 0.001 to 0.1

Given a time series X₀,X₁,…,X_N–1 of length N, a basic estimate of the SDF is the periodogram:

$${\widehat{S}}^{\left(p\right)}\left(f\right)=\frac{1}{N}{\mid \sum _{t=0}^{N-1}{X}_t{\mathrm{e}}^{-i2\pi ft}\mid }^2.$$ (6)

The expected value of the periodogram is given by the convolution of Fejér’s kernel,

$$F\left(f\right)=\frac{1}{N}{\left[\frac{\sin \left(N\pi f\right)}{\sin \left(\pi f\right)}\right]}^2$$ (7)

with the SDF:

$$E\left[{\widehat{S}}^{\left(p\right)}\right(f\left)\right]={\int }_{-1∕2}^{1∕2}F(f-f^{\prime })S\left(f^{\prime }\right)\mathrm{d}{f}^{\prime },$$ (8)

where S(f) is given by Eq. (3). The contribution to this expectation at a particular frequency from distant frequencies is called spectral leakage and occurs because of an interplay between the shape of Fejér’s kernel and the distribution of power in the spectra. The leakage of power into the lowest frequencies is especially severe as the Hurst coefficient approaches zero. For a long time series, it is tricky to calculate the expected value of the periodogram via numerical evaluation of the integral in Eq. (8).

Fortunately, the following method avoids the convolution integral of Eq. (8) and is computationally more efficient. Let X_j, j = 0,…,N – 1, denote a portion of a dFGN process with zero mean. The autocovariance sequence is given by Mandelbrot [12, p. 353]:

$$E\left[X_j{X}_k\right]=({\sigma }^2∕2)({\mid j-k-1\mid }^{2H}-2{\mid j-k\mid }^{2H}+{\mid j-k+1\mid }^{2H}),$$ (9)

where σ² = var(X_j) and H is the Hurst coefficient. The expected value of the periodogram, E[Ŝ^(p)], is given by Percival and Walden [13, Eq. 198] as

$$E\left[{\widehat{S}}^{\left(p\right)}\right(f\left)\right]=\frac{{\sigma }^2}{2N}\sum _{j=-(N-1)}^{N-1}\left({\mid j-1\mid }^{2H}-2{\mid j\mid }^{2H}+{\mid j+1\mid }^{2H}\right)\times \cos \left(2\pi fj\right)(N-\mid j\mid ).$$ (10)

The estimated spectra from the periodogram is an asymptotically unbiased estimator of S(f) [13, p. 199]. Thus, for any particular frequency,

$$\underset{N\to \infty }{\lim }E\left[{\widehat{S}}^{\left(p\right)}\right(f\left)\right]=S\left(f\right).$$ (11)

Once f is fixed, the expected value of the periodogram will equal the actual spectral density at that frequency as the length of the series increases without bound. However, in general,

$$\underset{N\to \infty }{\lim }E\left[{\widehat{S}}^{\left(p\right)}\right(1∕N\left)\right]\ne S(1∕N).$$ (12)

For anti-correlated dFGN with small H, the periodogram at the lowest non-zero Fourier frequency does not give the actual spectra or power-law behavior for dFGN.

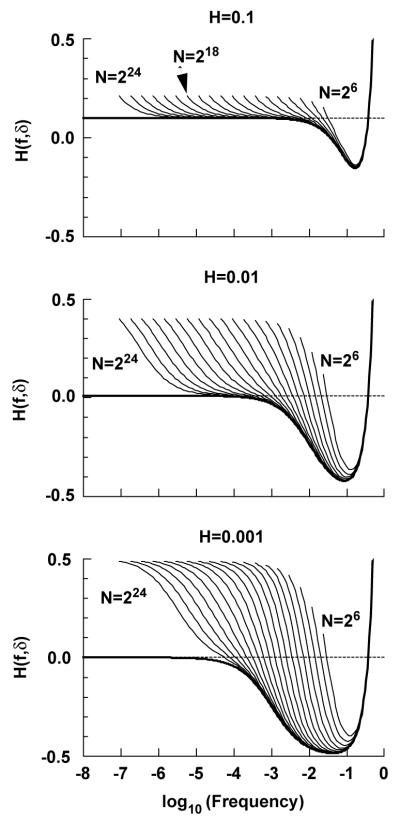
In Fig. 2, for H = 0.1, 0.01, and 0.001, the expected values of the periodogram for series of lengths 2^k, (k = 6, 7,…,24) (series length N = 64, 128,…, 16, 777, 216) (thin lines) have been usedto calculate H(f, δ) with δ = 1/(2N) for 1/N ≤ f ≤ 1/2. The values from the actual spectra are plotted with darker lines for comparison. The corresponding H is indicated by the horizontal dashed lines.

Fig. 2.

Comparison of H(f, δ) from actual spectra (thick lines), power law (dashedlines), and periodograms (thin lines).

For H = 0.1, top panel of Fig. 2, for the local Hurst coefficient of the periodogram, H(f, δ), to be within 10% of H for the range 10⁻⁴ < f < 10⁻³ requires a series of length N ≥ 2¹⁸. Fitting the log of the expected values of the periodogram versus log frequency to a straight line at the lowest frequencies would give a Hurst coefficient close to 0.2 for N ≥ 2⁹. For short series, N ≥ 2¹², the local Hurst coefficient has no significantly long range of frequencies over which it is close to the nominal H = 0.1, even though it passes through the correct value.

For H = 0.01, middle panel of Fig. 2, a series of N ≥ 2²⁴ (16, 777, 216) points is required to get a substantial range of frequencies over which H(f, δ) is close to H. Computing e(f, δ) at the lowest frequencies gives a local Hurst coefficient close to 0.4 for N ≥ 2¹⁰.

For H = 0.001, bottom panel of Fig. 2, a series of N =2²⁴ points is not long enough to identify the nominal H. Roughly speaking, a series of approximately one billion points or longer is required to get even a small range of frequencies where there is power-law scaling giving H(f, δ) ≈ H. At the lowest frequencies the local slope, e(f, δ), would give a local Hurst coefficient close to 0.5 for N ≥ 2¹⁰.

Fig. 3 displays the information on the upper panel of Fig. 2 in another way: it shows the frequency ranges where the local Hurst coefficient of both the spectra and the periodogram are within 10% of the nominal Hurst coefficient when H =0.1. For series of length N < 2¹², no such significant range exists. Series of length 2¹² < N < 2¹⁸ barely contain a significant frequency bandwithin 10% of the nominal H. Series of length greater than one million points are necessary to have a significant frequency band within 10% of the nominal H. The periodogram estimates associated with both the highest and lowest frequencies are always outside this region.

Fig. 3.

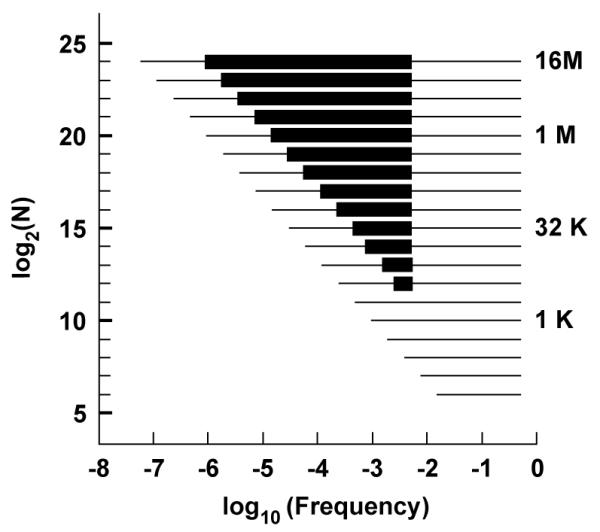
For series with H = 0.1 (top, Fig. 2), the range of series lengths andsegments of the frequency range where the local slope, e(f, δ) gives acceptable estimates of H. The thin lines represent the span of the non-zero Fourier frequencies j/N, j = 1,…,N/2, N = 2^k, k = 6, 7…,24. The dark bars are the regions where |H(f, δ) – H| ≤ 0.1H for both the spectra and expected value of the periodogram when H = 0.1.

In conclusion, for a given Hurst coefficient for anti-correlated dFGN and a long enough series, a portion of the expected value of the periodogram will vary approximately as f^1–2H, but the interval of frequencies over which this occurs does not include the lowest available Fourier frequencies. If the series is not long enough, there is no substantive region where the periodogram can be expected to vary as f^1–2H.

4. The local spectral exponents, e(f, δ), for periodograms of varied H at the lowest available frequencies

In Fig. 4, for 10⁻⁴ < H < 1, the local spectral exponent, e(f, δ) is shown as the thick line for a set of series, all of length N = 2¹⁵, where f = (1+1/2)/N and δ = (1/2)/N. This choice of f and δ means that e(f, δ) depends on the expected value of the periodogram at its two lowest non-zero Fourier frequencies, namely 1/N and 2/N. The local spectral exponent goes to zero as H goes to zero. On a log–log plot of the periodogram versus frequency, the lowest frequency end behaves as f⁰ instead of f^1–2H as H approaches zero. The departure from the nominal power law, |H(f, δ) – H | ≤ 0.1H occurs when H ≤ 0.27.

Fig. 4.

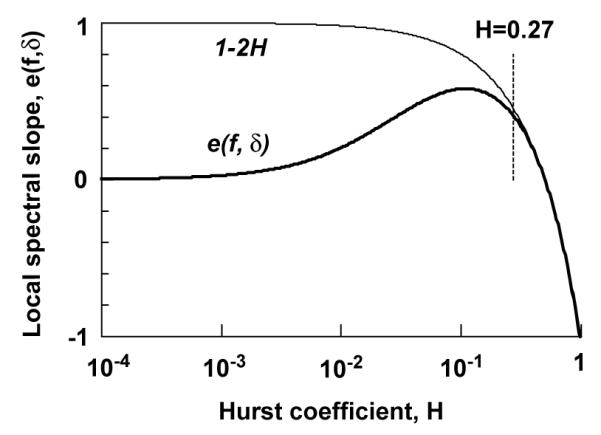
The local spectral exponent, e(f, δ) (thick line), for series with 10⁻⁴ < H < 1 of length N = 2¹⁵, taken from the lowest frequencies of the periodogram where f = (1 + 1/2)/N and δ = (1/2)/N. The thin line is 1 – 2H. The vertical dashed line is at H = 0.27, values above which |H(f, δ) – H| ≤ 0.1H.

5. Summary and conclusions

Although the SDF for dFGN approaches a power law when the frequency approaches zero, it is not everywhere a power law, except when the Hurst coefficient equals 0.5. For anti-correlated dFGN, the frequency where the SDF becomes a power law to a decent approximation depends on the Hurst coefficient. As H → 0, the frequency at which the power-law region becomes discernible approaches zero as well. There is an obvious implication for methods generating dFGN. Attempting to generate dFGN by the Fourier transform of a spectra that is a power law everywhere [7,8,5] gives series that always deviate from dFGN except when H =0.5.

The expected value of the periodogram for an anti-correlated dFGN can diLer more markedly from the corresponding true spectrum than does that for a positively correlated dFGN. When H approaches zero, the local spectral exponent for the expected value of the periodogram tends to diLer significantly from the power law nominally associated with H even for quite large sample sizes N. Unlike the actual spectra, the estimates from the lowest frequencies of the periodogram available from a series of length N (i.e., f = 1/N,2/N,…) never converge to the nominal power law because of spectral leakage from other frequencies. At high frequencies, the expectedvalue of the periodogram is approximately equal to the true spectrum, but, over these frequencies, the local Hurst coefficient, H(f, δ), is not close to H. These facts have two implications. First, practitioners must be very cautious about attempting to deduce H from the periodogram, particularly for anti-correlated time series. Blind application of regression analysis to the log periodogram can lead to estimates of H that are not good quantifiers of the observed phenomena, even in the case where dFGN is an appropriate model. Second, attempts to make use of the log periodogram for estimating H have been motivated largely by the fact that the exact maximum likelihood estimator of H is computationally infeasible for large sample sizes [9]. Although the expected value of the periodogram can diLer significantly from the true spectrum, these values do exhibit a dependence on H. Rather than trying to fit portions of the periodogram to the true spectrum via least squares, it might be better to fit the periodogram to its expected value for various hypothesized values of H. This suggestion would lead to a nonlinear procedure for deducing H, which might form the basis for an attractive alternative to the computationally infeasible maximum likelihood estimator. Exploration of this scheme is a topic for future research.