Abstract
One of the limiting factors in large-scale cryopreservation is the formation of fractures. The prevalence of cracking in cryopreserved bulky tissues is frequently associated with temperature gradients, which lead to non-uniform thermal contraction of the tissue. With new cryoprotectants available, it may be possible to reduce temperature gradients to much lower levels, in which case other contributions to mechanical stress development and cracking will become more significant. One potential contributor to such stress is the difference in thermal expansion between tissue and the cryoprotectant. The current study addresses the role of thermal expansion mismatch by drawing upon recently obtained experimental data and engineering models for the development of thermal stresses. This question is addressed for the case of cryopreservation via vitrification (glass formation), for which crystal formation is avoided, and tissues and solutions gradually transition from fluid-like to solid-like response, as the viscosity increases with decreasing temperature.
Keywords: Cracking, Cryopreservation, Vitrification, Solid Mechanics, Modeling
INTRODUCTION
It has been demonstrated that constraints on thermal contraction during cooling, which induce mechanical stresses, are one major cause of cracking in cryopreserved tissues (3,7,9,14). Cracking can readily occur when the tissue and its surrounding cryoprotectant are preserved in a rigid container, for example when cryopreserving blood vessel segments in a vial. The thermal expansion coefficient of the vial is much lower than that of the cryoprotective agent (CPA), and the CPA adheres to the vial wall (13,16). If the constraints of a rigid wall, adherence of the CPA to the wall, and differential thermal expansion between the wall and the CPA are removed (for example, when tissue is cryopreserved in a plastic bag (2)), and cracking still occurs, then cracking is more likely associated with temperature gradients within the CPA-tissue system, which cause thermal expansion gradients.
It has been demonstrated recently that function recovery of blood vessels segments is feasible even at relatively slow cooling rates, even if the conditions for vitrification are not fully met and some limited crystallization develop (1). Another possibility to reduce the required cooling rates is with the application of so-called synthetic ice blockers (SIB), which strongly interact with the water molecules in the CPA solution (20) (this technology is currently at the developmental stage and has drawn significant attention in recent years in the cryobiology community). Either way, reducing the required cooling rates for vitrification leads to smaller temperature gradients and, as a result, decreases the likelihood of cracking. If temperature gradients are neglected, and the CPA and bag have comparable thermal expansion coefficients, then differences in thermal expansion coefficient between the tissue and the CPA remain the only potential mechanism to produce mechanical stress. The development of stresses under these circumstances has been studied for the case of partial vitrification, in which a blood vessel segment crystallizes while the CPA vitrifies (17).
The current paper takes the analysis one step further by considering the ideal case of a fully vitrified tissue-CPA system, and evaluating whether stresses due to thermal expansion coefficient differences alone—between the vitrified specimen and its vitrified surrounding medium—could result in cracking. That is, we take an engineering approach and pose the following hypothetical question: if temperature gradients can be minimized, can a specimen be brought safely to a convenient storage temperature near the liquid nitrogen boiling point after thermal equilibration in the vicinity of its glass transition temperature? Note that initial cooling down to a few degrees above the glass transition temperature without the devastating effect of cracking has been demonstrated; however, further cooling in the glassy state remains a challenge. The current report addresses this question by drawing upon recently developed data for thermal expansion and viscosity at relevant temperatures (5,8,10,12), as well as methods of analyzing thermal stresses in vitrifying materials (14,16–19). Consistent with our previous reports, the current study uses the cryopreserved blood vessel as a tissue model for investigation.
CRACKING STRESS DUE TO THERMAL EXPANSION MISMATCH
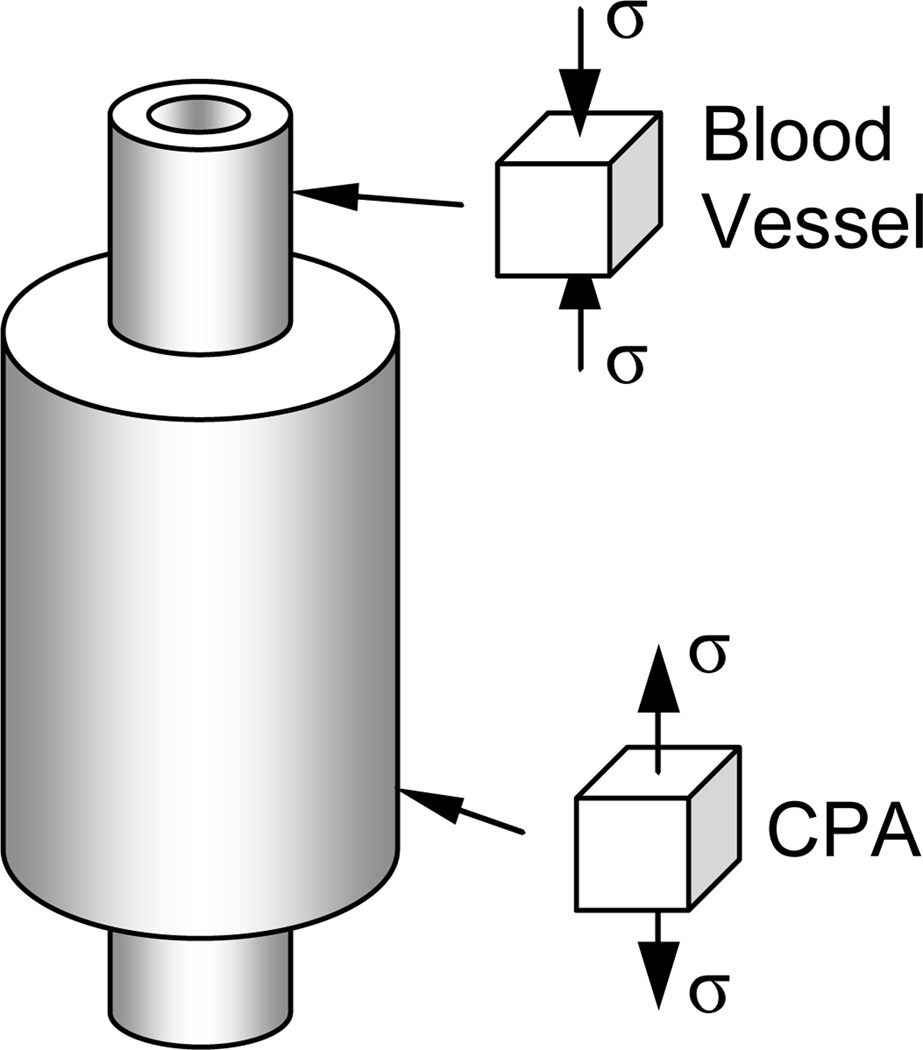
The potential for cracking in a vitrifying blood vessel that is submerged in a vitrifying CPA domain is analyzed here, where the entire blood vessel-CPA domain is presumed to be cooled subject to a condition of spatially uniform temperature. In particular, the stress is predicted for the simple geometry of a very long cylindrical blood vessel permeated with CPA and surrounded by a cylindrical domain of CPA, as illustrated in Fig. 1 (not drawn to scale). This composite cylinder analysis is similar to that presented earlier for the case of a partially vitrified blood vessel (17), where the same calculation process is repeated here. (In favor of keeping this report short and concise, and since the calculation process itself has not been changed, the presentation of the mathematical formulation from (17) is not repeated here).
Figure 1.
Schematic illustration of the blood vessel-CPA system analyzed to predict stress below glass transition; note that the inner cylinder (blood vessel) extends beyond the outer cylinder (CPA) for illustration purposes only, while, in fact, the mathematical model assumes both to be infinite cylinders.
In short, stresses are assumed to be zero down to the temperature at which the vessel and CPA first act solid-like (this transition of behavior occurs around the so-called “set-temperature”, which is defined below). Below this temperature, both the CPA and blood vessel are assumed to experience thermal strains consistent with their respective thermal expansion coefficients and to behave linear elastically with the same elastic modulus value, as recently measured for a vitrified blood vessel (6). There is no constraining effect of a vial or bag. Then, the axial stress is tensile in the CPA (which contracts more) and compressive in the blood vessel, together satisfying zero net axial force. All stresses are proportional to the thermal expansion difference between the CPA and the vessel. It is shown in (17) that stress is not an explicit function of the blood vessel radius or wall thickness, but only a function of one dimensionless number, namely the cross-sectional area ratio of CPA to blood vessel. Further note that the modeling assumes the blood vessel to be homogeneous and isotropic, with possible cellular-level mechanical effects are neglected, which is deemed adequate for the current purpose of analyzing large-scale cracking. Predictions of the composite cylinder model displayed in Fig. 1 were found to compare reasonably well with those of a full 3D curled blood segment, vitrified in a vial of CPA (17).
RELEVANT DATA ON BLOOD VESSEL SEGMENTS AND CPAs
The current study refers to experimental data on the CPA cocktails DP6 and VS55: DP6 is a cocktail of 3M DMSO and 3M propylene glycol in Euro Collins solution; VS55 is a cocktail of 3.1M DMSO, 2.2M propylene glycol, and 3.1M formamide, in Euro Collins solution.
Due to the dramatic increase in viscosity with decreasing temperature, thermal expansion measurements have been obtained using different experimental techniques at the upper (4,11) and lower (4) parts of the cryogenic temperature range. Measurements of thermal expansion for three CPAs studied previously are relevant to the predictions presented here. At the upper part of the cryogenic temperature range, where the specimen (pure CPA or tissue permeated with CPA) relaxes rapidly due to viscous flow (above ~−90°C in those prior studies for the CPA cocktail VS55 and 7.05M DMSO as a reference CPA solution), measurements were obtained for the CPA and the blood vessel specimens separately; for more discussion see (13,16). At the lower part of the cryogenic temperature range, where the material behaves as solid over any practical time scale, thermal expansion data is available only for the tissue permeated with CPA (down to about −170°C). To predict stress development due to thermal expansion differences at low temperatures, thermal expansion of the pure CPA at that lower temperature range must be estimated, as proposed here for the first time.
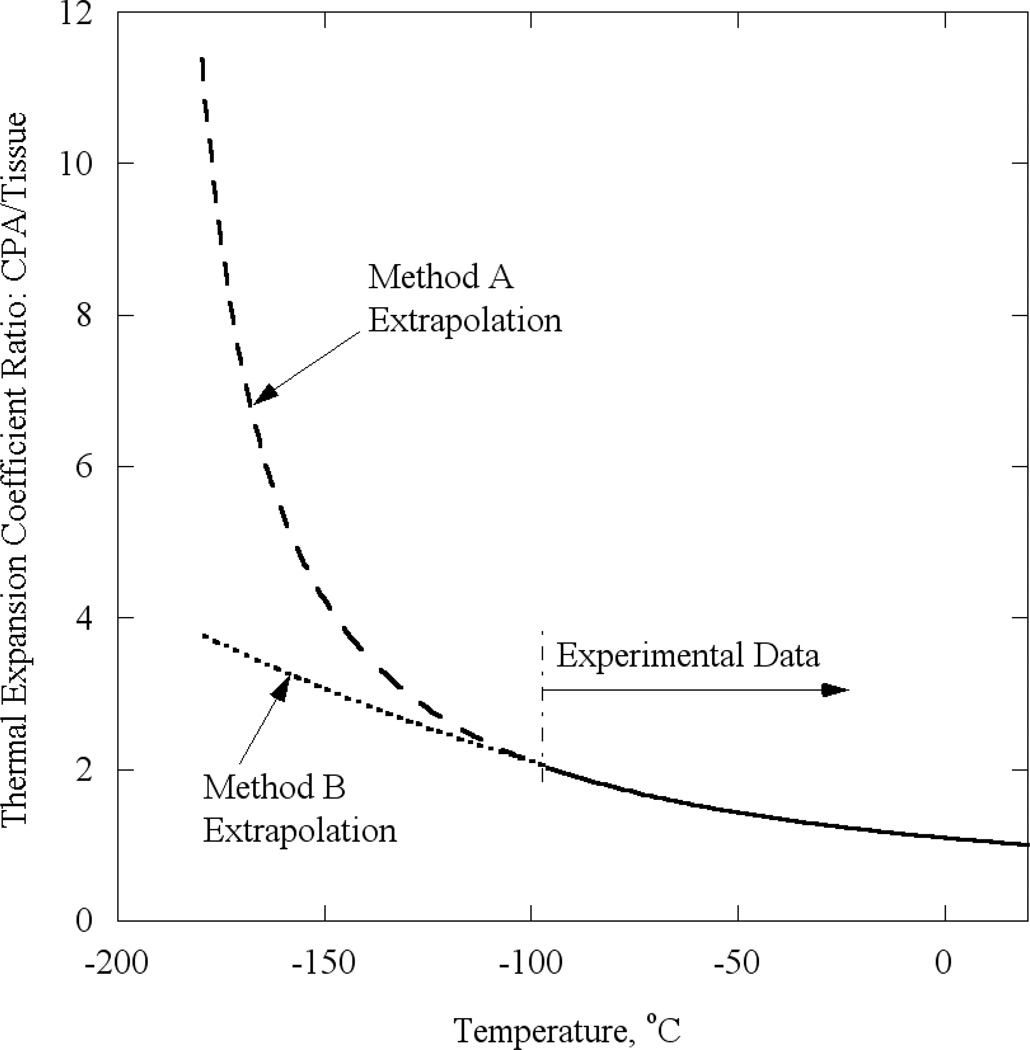
Two alternative methods are used in the current study to estimate the thermal expansion of the CPA at lower temperatures: (A) by direct extrapolation from experimental data available at higher temperatures, and (B) by extrapolation of the ratio of CPA thermal expansion to tissue thermal expansion available at higher temperatures, in combination with the newly available thermal expansion data for the tissue at lower temperatures. Method A is self-explanatory, and method B is applied as follows. The ratio of thermal expansion of CPA to tissue at higher temperature is calculated first, and best fitted with a second order polynomial. Next, this fitted ratio is extrapolated to lower temperatures. Finally, the extrapolated ratio is multiplied by the known thermal expansion of the tissue at lower temperatures, to yield the thermal expansion of the CPA. The thermal expansion ratio at higher temperatures (based on experimental data) and at lower temperatures, using each of the extrapolation methods, is presented in Fig. 2 for 7.05M DMSO. The authors of this report believe that method B of extrapolation is more appropriate, as it presumes consistent behavior over the entire cryogenic temperature range, and especially during glass transition. Nevertheless, the results are obtained for both scenarios to gauge how variations away from the presumed behavior of method B might affect the results.
Figure 2.
Ratio of thermal expansion coefficient of 7.05 DMSO to blood vessel permeated with 7.05 DMSO based on experimental data at the upper part of the cryogenic temperature range, and on two proposed methods of extrapolation for the lower part of the cryogenic temperature range: (A) direct extrapolation of the CPA thermal expansion divided by the measured thermal expansion of the tissue sample; and (B) extrapolation of the CPA-to-tissue thermal-expansion ratio from the upper part of the cryogenic temperature range (solid line).
Since the CPA has low viscosity at higher cryogenic temperatures, negligible stresses are expected to develop during the cooling process until it approaches glass transition. The variation of viscosity with temperature dictates the temperature at which the CPA starts acting like a solid, which is critical to the concentric cylinder analysis of stresses. Viscosity of CPAs just above the glass transition temperature has also been measured recently (8), by measuring the force to pull a rod out from a cylindrical container of vitrified CPA at constant velocity. The viscosity was found to increase exponentially with decreasing temperature as the glass transition temperature was approached.
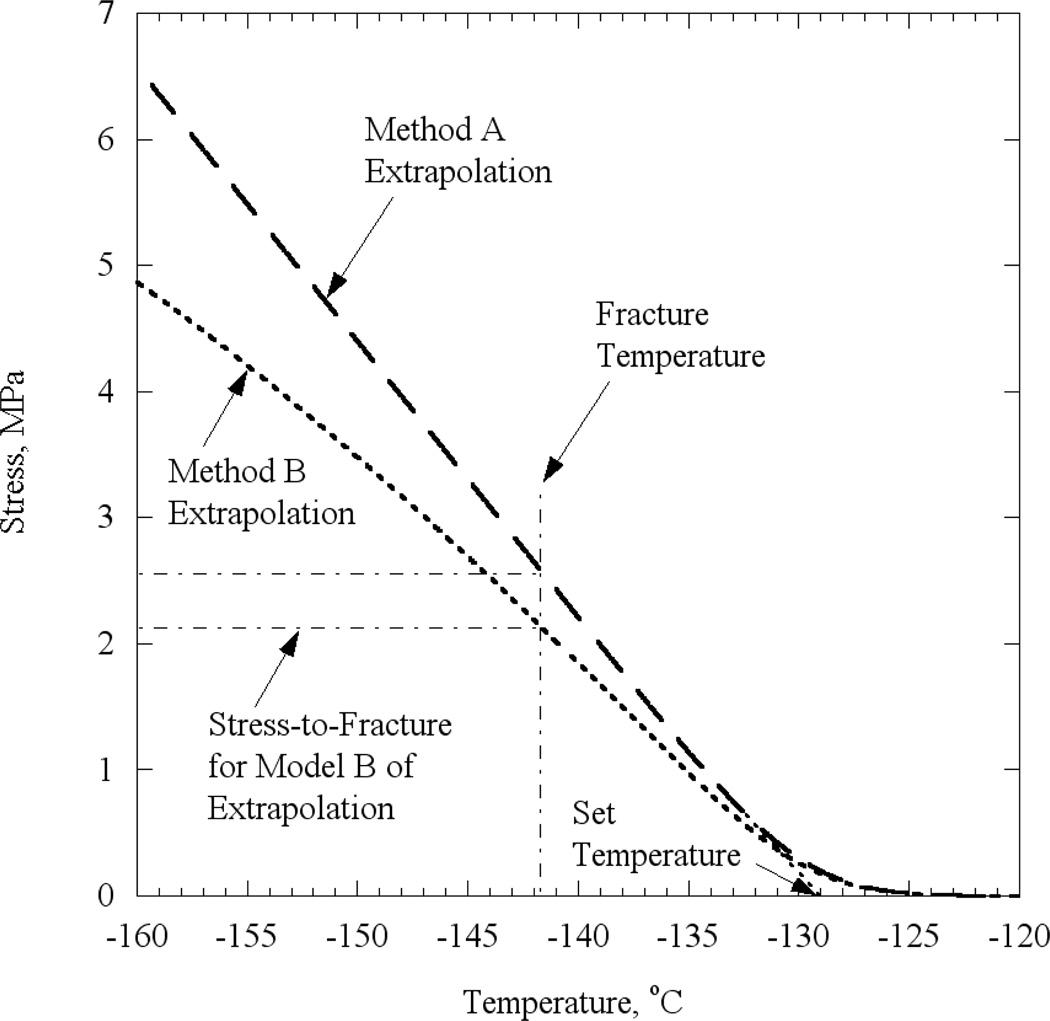
Previous work has also established a basis for predicting the temperature at which the CPA acts like a solid and then the stress at which the solid CPA cracks. A thin droplet of CPA was cooled in a controlled manner on a thermo-mechanically characterized substrate (14). Eventually, the thin droplet cracked because the much stiffer substrate constrained the film’s thermal contraction. The droplet was modeled mathematically as a thin film and its stress (appropriately assumed to be uniform except at the edges) was predicted as a function of decreasing temperature; this modeling required data on thermal expansion and viscosity. Figure 3 refines previous predictions of the droplet stress as a function of temperature by incorporating the recently measured CPA viscosity, and the two methods of extrapolating CPA thermal expansion to lower temperatures, as described above. As expected, there are insignificant stresses in the droplet at high temperatures, when viscous flow can readily occur. As the viscosity rises with cooling, a critical temperature was reached (i.e., the set-temperature) at which significant stresses started to develop. For lower temperatures, the CPA is predicted to behave as an elastic solid, with the stress increasing with decreasing temperature. Deviations from linearity of the stress-temperature relationship as the specimen cooled far below the set temperature are due to the variation of the thermal expansion with temperature (a temperature-independent thermal expansion coefficient would result in a linear relationship, starting from a few degrees Celsius below the set temperature).
Figure 3.
Predicted tensile stress in a thin film of 7.05 DMSO, when cooled isothermally, based on two extrapolation models. Cracking stress, shown as dotted line, inferred from observed cracking temperature (13) for a particular experiment.
When predictions of stress development are combined with the temperature at which the droplet on the substrate is observed to crack (−141.7°C in the experiment related to Fig. 3), the stress-to-fracture of the CPA was inferred. The observed cracking temperatures are displayed in Table 1, along with the currently inferred cracking strain. The predicted stresses are proportional the Young’s modulus and, for the purpose of further calculations, one may assume Young’s modulus to be 1 GPa. Note that the stress predictions are sensitive to how the thermal-expansion behavior of the CPA is extrapolated to lower temperatures (Method A vs. Method B).
Table 1.
Observed fracture temperatures and inferred strain-to-fracture values, based on the two models for extrapolating thermal expansion of CPA to lower temperatures (see also Fig. 2).
| DMSO | VS55 | DP6 | |
|---|---|---|---|
| Observed Fracture Temperature (13), °C | −141.7 | −134.7 | −133.3 |
| Inferred strain-to–fracture subject to Method A | 0.00258 | 0.00186 | 0.00138 |
| Inferred strain-to–fracture subject to Method B | 0.00214 | 0.00135 | 0.00131 |
RESULTS AND DISCUSSION
As has been discussed earlier (17), since the stress in the surrounding CPA is tensile, the stress is greatest in the axial direction, and the CPA is brittle at very low temperatures, cracks are expected to initiate within the CPA and run perpendicular to the vessel axis. Once initiated, crack propagation will be either arrested at the compressed blood vessel wall, or continue propagating through it, if the wall is thin enough and the energy of cracking is high enough. Even if the compressed blood vessel wall will serve as a barrier, and arrest cracking propagation, at least the outer-most layer of the blood vessel—the endothelium—is likely to be damaged. Thus, cracking in the CPA is taken to signal the onset of damage in the blood vessel. Refining our predictions of the temperature at which the CPA is likely to begin cracking is, essentially, the main motivation for the current analysis.
Table 2 lists computed results for the temperature at which the onset of CPA cracking is predicted during vitrification, based on the concentric cylinder stress model (Fig. 1) and the critical strain to fracture listed in Table 1. These predictions depend on the cross-sectional area ratio of the blood vessel specimen to its surrounding CPA, RA. (While this functional behavior could have been presented as a function of the respective radii ratio, the area ratio is more practical, as it can also be applicable approximately to non-circular CPA volumes). No cracking is predicted if the critical strain has not been reached when the final storage temperature reaches the liquid nitrogen boiling point (i.e., −196°C).
Table 2.
Predicted cracking temperatures (°C) for several values of cross-sectional area ratio of blood vessel to surrounding CPA, RA. Note that the strain is not an explicit function of the blood vessel radius or wall thickness, but a function of only one dimensionless number, that is RA.
| RA | DMSO | VS55 | DP6 | |||
|---|---|---|---|---|---|---|
| Method A | Method B | Method A | Method B | Method A | Method B | |
| 3 | −149.9 | −152.2 | −145.9 | −156.5 | −160.4 | −170.9 |
| 1.25 | −156.3 | −161.4 | −153.4 | No Crack | −175.3 | No Crack |
| 0.78 | −162.9 | −173.2 | −160.9 | No Crack | −190.9 | No Crack |
| 0.44 | −175.4 | No Crack | −175.0 | No Crack | No Crack | No Crack |
It can be seen from Table 2 that the likelihood of cracking increases with RA, that is with decreasing amount of CPA surrounding the blood vessel. This observation can be explained by the fact that the compressive force developing in the blood vessel is balanced by a tensile force in the surrounding CPA. This force is being distributed over a larger cross-sectional area with increasing volume of CPA (the stress is the force divided by the cross-sectional area). Note again that the current predictions assume a uniform temperature distribution across the blood vessel and the CPA, which can only be achieved either in smaller cryopreserved volumes or subject to lower cooling rates.
Cracking is predicted to occur at relatively higher temperatures when calculations are based on Method A of extrapolating the thermal expansion behavior (Fig. 2). If Method A truly captures the thermal expansion behavior, it would be inadvisable to bring samples to very low cryogenic storage temperatures under any practical cryopreservation conditions. For Method B of extrapolation, no cracking is predicted in many, but not all, cases. We consider Method B to offer the more plausible extrapolation: Method A directly extrapolates CPA from temperatures above glass transition to temperatures below it, and thereby ignores the existence of this notable transition. Note that a significant change in thermal expansion is observed around glass transition; in fact, an alternative means of evaluating the glass transition temperature is by measuring the temperature at which this change reaches its maximum (15). By contrast, Method B accounts for this transition in thermal strain by using blood vessel data that extend across the relevant temperature range. Thus, we conclude that cracking due to differences in thermal expansion is not likely to occur in many cases, if an appropriate CPA volume is selected, and if the system is cooled in a manner which creates minimal temperature gradients. Regardless of whether Model A or Model B better predicts CPA behavior at lower temperatures, increasing the amount of surrounding CPA reduces the tensile strain in the CPA and, thus, enables lower storage temperatures. The drawback in this case may be that more CPA may increase temperature gradients in the domain—an effect which was ignored in the current analysis.
This analysis signals that cracking in the CPA, and hence the tissue, is unlikely to occur when cooling to temperatures very much below the glass transition temperature, provided there are minimal temperature gradients. There is some uncertainty regarding this conclusion which can only be resolved if and when the thermal expansion behavior of pure CPA at lower cryogenic temperatures is measured directly. However, such measurements would appear to require the development of new experimental techniques.
Acknowledgements
This study has been supported in part by National Institute of Health (NIH), grant number R01HL069944.
References
- 1.Baicu S, Taylor MJ, Chen Z, Rabin Y. Cryobiology. 2008;57(1):1–8. doi: 10.1016/j.cryobiol.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brockbank KGM, Walsh RJ, Song YC. Proceedings of the International Society for Applied Cardiovascular Biology. Savannah, GA: 2004. [Google Scholar]
- 3.Fahy GM, Saur J, Williams RJ. Cryobiology. 1990;27:492–510. doi: 10.1016/0011-2240(90)90038-6. [DOI] [PubMed] [Google Scholar]
- 4.Jimenez Rios JL, Rabin Y. Cryobiology. 2006;52(2):269–283. doi: 10.1016/j.cryobiol.2005.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jimenez Rios JL, Rabin Y. Cryobiology. 2006;52(2):284–294. doi: 10.1016/j.cryobiol.2005.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jimenez Rios JL, Steif PS, Rabin Y. Annals of Biomed Eng. 2007;35(12):2077–2086. doi: 10.1007/s10439-007-9372-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kroener C, Luyet BJ. Biodynamica. 1966;10(201):47–52. [PubMed] [Google Scholar]
- 8.Noday DA, Steif PS, Rabin Y. Journal of Experimental Mechanics. 2008 doi: 10.1007/s11340-008-9191-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pegg DE, Wusteman MC, Boylan S. Cryobiology. 1997;34(2):183–192. doi: 10.1006/cryo.1996.1997. [DOI] [PubMed] [Google Scholar]
- 10.Plitz J, Rabin Y, Walsh J. Cell Preservation Technology. 2004;2(3):215–226. [Google Scholar]
- 11.Rabin Y, Bell E. Cryobiology. 2003;46(3):254–263. doi: 10.1016/s0011-2240(03)00042-7. [DOI] [PubMed] [Google Scholar]
- 12.Rabin Y, Plitz J. Annals of Biomedical Engineering. 2005;33(9):1213–1228. doi: 10.1007/s10439-005-5364-0. [DOI] [PubMed] [Google Scholar]
- 13.Rabin Y, Taylor MJ, Walsh JR, Baicu S, Steif PS. Cell Preservation Technology. 2005;3(3):169–183. doi: 10.1089/cpt.2005.3.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rabin Y, Steif PS, Hess KC, Jimenez-Rios JL, Palastro MC. Cryobiology. 2006;53:75–95. doi: 10.1016/j.cryobiol.2006.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Scholtze H. Glass. New York, Berlin, Heidlberg: Springer-Verlag; 1991. [Google Scholar]
- 16.Steif PS, Palastro M, Wen CR, Baicu S, Taylor MJ, Rabin Y. Cell Preservation Technology. 2005;3(3):184–200. doi: 10.1089/cpt.2005.3.184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Steif PS, Palastro MC, Rabin Y. Medical Engineering & Physics. 2006;29(6):661–670. doi: 10.1016/j.medengphy.2006.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Steif PS, Palastro MC, Rabin Y. Cell Preservation Technology. 2007;5(2):104–115. doi: 10.1089/cpt.2007.9994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Steif PS, Palastro MC, Rabin Y. ASME Biomechanical Engineering. 2008;130(2):021006. doi: 10.1115/1.2898716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Taylor MJ, Song YC, Brockbank KGM. Chap. 22. In: Fuller BJ, Lane N, Benson E, editors. Life in the Frozen State. London: Taylor & Francis Books; 2004. pp. 603–642. [Google Scholar]