Modeling Oxygen and Carbon Dioxide Transport and Exchange Using a Closed Loop Circulatory System

Abstract

The binding and buffering of O₂ and CO₂ in the blood influence their exchange in lung and tissues and their transport through the circulation. To investigate the binding and buffering effects, a model of blood-tissue gas exchange is used. The model accounts for hemoglobin saturation, the simultaneous binding of o₂ CO₂. H⁺, 2,3-DPG to hemoglobin, and temperature effects [1,2]. Invertible Hill-type saturation equations facilitate rapid calculation of respiratory gas redistribution among the plasma, red blood cell and issue that occur along the concentration gradients in the lung and in the capillary-tissue exchange regions. These equations are well-suited to analysis of transients in tissue metabolism and partial pressures of inhaled gas. The modeling illustrates that because red blood cell velocities in the flowing blood are higher than plasma velocities after a transient there can be prolonged differences between RBC and plasma oxygen partial pressures. The blood-tissue gas exchange model has been incorporated into a higher level model of the circulatory system plus pulmonary mechanics and gas exchange using the RBC and plasma equations to account for pH and CO₂ buffering in the blood.

39.1 Introduction

The exchange of O₂ and CO₂ between the tissue and vasculature depends on adequate delivery and removal of these gases. Oxygen delivery begins with inhalation of ambient air into the airspaces of the lung, transport to the blood from the alveoli, transport through the arterial system, and then exchange between the blood and the peripheral tissue. In a closed circulatory system, venous blood returns to the lungs where CO₂ is expired. Quantifying O₂ and CO₂ transport requires accounting for their solubility in plasma, RBCs and tissue as well as their binding and release from the hemoglobin (Hb) in the RBCs and, in addition, for O₂ only, its binding to myoglobin in tissue. Hemoglobin dissociation curves were developed that described the fraction of O₂ and CO₂ bound to Hb in the steady state as a function of P_O2, P_CO2. pH, 2,3-DPG and temperature [1], These expressions were used to describe the steady state transport of O₂ and CO₂ as well as H⁺ and HCO₃⁻ in a blood-tissue exchange model with convective transport and axial diffusion in the capillary along with exchange and metabolism in the surrounding tissue region [2].

The model presented in this study accounts for ventilatory exchange between outside air and lung alveoli, exchange with alveolar capillary blood, convective transport in arteries, the exchange in tissue capillaries and arterioles, and return of venous blood to the lungs. The model describes transport of O₂ and CO₂ to tissue as influenced by respiration rate, composition of inspired gas, H⁺ and CO₂ production and O₂ consumption in tissue and buffering in the blood.

A feature of biophysical interest but modest physiological importance is the persistence of disequilibria between plasma and RBC P_O2 due to the higher velocities of RBC than plasma. This difference in velocity exists in all regions of the vasculature but is at a maximum in the microcirculation. Bloch [3] observed the existence of a layer of plasma close to the vessel wall, which he called the peripheral plasma layer. The average ratio of total layer thickness to vessel inside diameter was 1:4 in the 5–10 µm capillariies in Bloch’s study, which agrees with more recent observations of the endothelial surface layer seen by Vink and Duling [4]. Because this layer is close to the capillary wall the velocity of the plasma in that region is slower than the centerline axial velocity of the RBCs. To quantify the relative velocity ratio of RBC to plasma we have looked at indicator dilution studies that document the mean transit time of RBC-tagged versus plasma-tagged indicators by Goresky [5]. Goresky showed that the mean transit time of RBCs was on the order of 2/3 of that of the plasma through the entire hepatic vasculature.

39.2 Description of the Model

39.2.1 Lung-Blood Exchange Region

The lung module is composed of three serial compartments [6]: a low compliance compartment representing the oral/nasal cavity and the cartilaginous airways, a moderately compliant compartment characterizing the collapsible bronchial airways and a high compliance compartment resembling the alveolar space. In the model, the lung can be ventilated by positive pressure or by periodic chest expansion reducing intrapleural pressure, both resulting in bidirectional airflow and inflation and deflation of the lung. Convective flow between compartments is modeled as pressure-driven flow through a resistance. Equations for convective and diffusive transport of oxygen and carbon dioxide between adjacent lung compartments are similar to those used in previous models [6]. Each lung compartment is assumed to be well-mixed. The alveolar compartment exchanges respiratory gases with the plasma region of a blood-tissue exchange unit [2], which contains a region of red cells surrounded by a plasma region. The inhaled partial pressure of each species is a model input.

39.2.2 Blood-Tissue Exchange Region

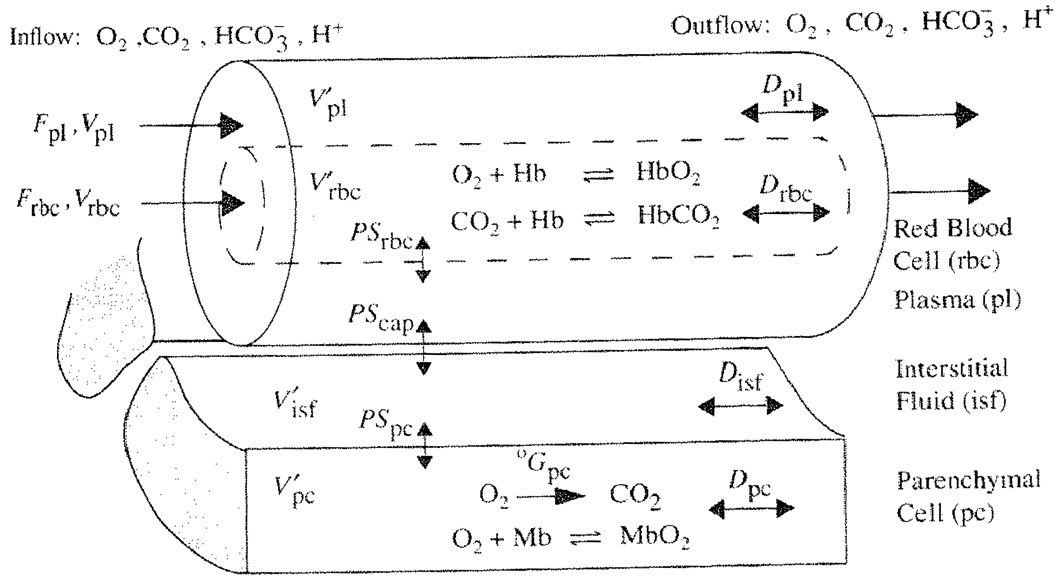
Figure 39.1 shows a previously described one-dimensional blood-tissue exchange model [2]. The lumen of a permeable vessel is divided into a flowing core of RBCs surrounded by a plasma sleeve. Hemoglobin binding is represented in the RBC region by the invertible hemoglobin dissociation expressions [1]. The exchange vessel endothelial barrier is treated as purely passive and is surrounded by an interstitial fluid layer giving access to parenchymal cells. In the parenchymal cells, where myoglobin buffers O₂, oxygen is consumed and CO₂ is produced in accord with the respiratory quotient: RQ = moles CO₂ per mole O₂ and a specified metabolic rate. Each region is axially-distributed, exhibiting concentration gradients from entrance to exit but well-mixed radially, and is represented by a 1-dimensional partial differential equation. Interregional conductances, defined by the permeability surface area product (PS_x), can be adjusted to accommodate slow diffusional processes. Axial diffusion or dispersion (D_x) smoothes the axial concentration gradients.

Fig. 39.1.

Blood-tissue exchange unit showing red blood cell, plasma, interstitial fluid, and parenchymal cell regions, convection of RBC and plasma, solute transport between regions, the PSs, axial diffusion, binding, and buffering within regions. Bicarbonate buffering occurs in all regions. Each region is axially-distributed and radially well-mixed.

The ratio of RBC to plasma velocity in the blood tissue exchange region was calculated using experimental morphometric data on intramyocardial arterioles and venules from Kassab et al [7], and the reduction in hematocrit as a function of vessel diameter documented by Lipowsky [8], In our model we have represented the blood tissue exchange region as the arterioles and capillaries smaller than 100 µm in diameter because studies by Duling and Berne [9] show significant oxygen loss in the precapillary arterioles. For porcine coronary branching trees of Kassab, flow through the blood tissue exchange region has a relative velocity ratio, V_RBC/V_pl of 1.2 to 1.9. Therefore an intermediate value of v_RBC/V_pl, was taken as 1.5 in lung and tissue exchange regions.

39.2.3 Arterial and Venous Convective Regions

Lung capillary blood is carried through nonexchanging convective conduits (left atrium, left ventricle, aorta, arteries) to the tissue. RBC-plasma solute exchange continues. Red cell-plasma concentration differences persist when their velocities differ. Metabolism is zero, but buffering reactions continue. Values of the ratio of RBC to plasma velocity in the arteries and veins were taken to be 1.1 and 1.05 respectively, though the choice of these numbers is dependent on the range of diameters represented.

39.2.4 Numerical Methods and Simulation Procedures

Numerical methods are those described previously [10] using a Lagrangian sliding fluid element algorithm. Other partial differential equation solvers (Mac-Cormack, TOMS 731) are also available under the JSim simulation system. Parameter values in this model were those used previously [2] with a few exceptions. The flow rate is allowed to range from 5 L/min at rest to 25 L/min during exercise. Also the permeability surface area product for the RBCs (PS_RBC) has been recalculated according to experimental evidence [11] to reflect the combination of a small hindrance to permeation of its membrane and the times required for binding and unbinding. The hemoglobin equations incorrectly assume instantaneous equilibration instead of taking several milliseconds. The lung model described here is similar in structure to the model by Lutchen et al. [6].

39.3 Results and Discussion

Two cases are examined in this study. The first concerns respiratory gas transport during normal and elevated ventilation, perfusion, and metabolism. For normal levels, the parameters are respiratory rate of 12 breaths/min, tidal volume of ~500 ml driven by 10 mmHg of inspiratory positive pressure at the mouth for 2 seconds and inspired air with P_O2 = 150 and P_CO2 = 0 mmHg. Blood flow was set to ~5 L/min and metabolic rate was adjusted so pulmonary end-capillary blood partial pressures of O₂ and CO₂ were ~100 and ~40 mmHg while venous values were 70 and 45 mmHg. The end tidal P_O2 was 105 and P_CO2 was 34 mmHg. The second case focuses on the equilibration of O₂ between plasma and RBCs upon entering the arterial region and the effect of the relative velocity difference between plasma and RBCs on equilibration. To investigate the equilibration, the plasma partial pressure of oxygen is increased from 25 to 100 mmHg and the transient effects are observed. To investigate the effect of the relative velocity difference, a pulsed increase in plasma P_O2 is applied at the upstream end and the difference between the plasma and RBC P_O2 is quantified along the length of the arterial region.

39.3.1 Respiratory Gas Transport

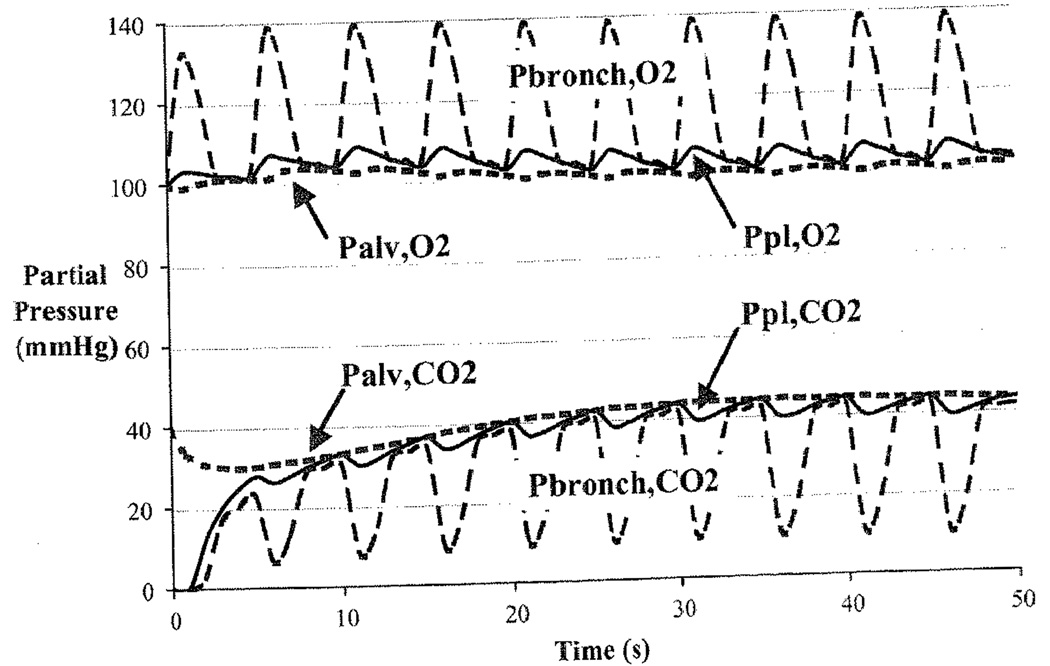
Figure 39.2 shows that the breathing cycle causes a cyclical variation in the partial pressures of O₂ and CO₂ in bronchiolar and alveolar air and in capillary plasma. Dispersion along the airways dampens the magnitude of the fluctuations. The partial pressure of CO₂ in plasma is almost unaffected by the ventilatory cycle because it is buffered by the large bicarbonate pool in the blood.

Fig. 39.2.

Displays the partial pressures of O₂ and CO₂ in the plasma region of the blood (pl), the alveoli (alv), and the collapsible airways (bronch).

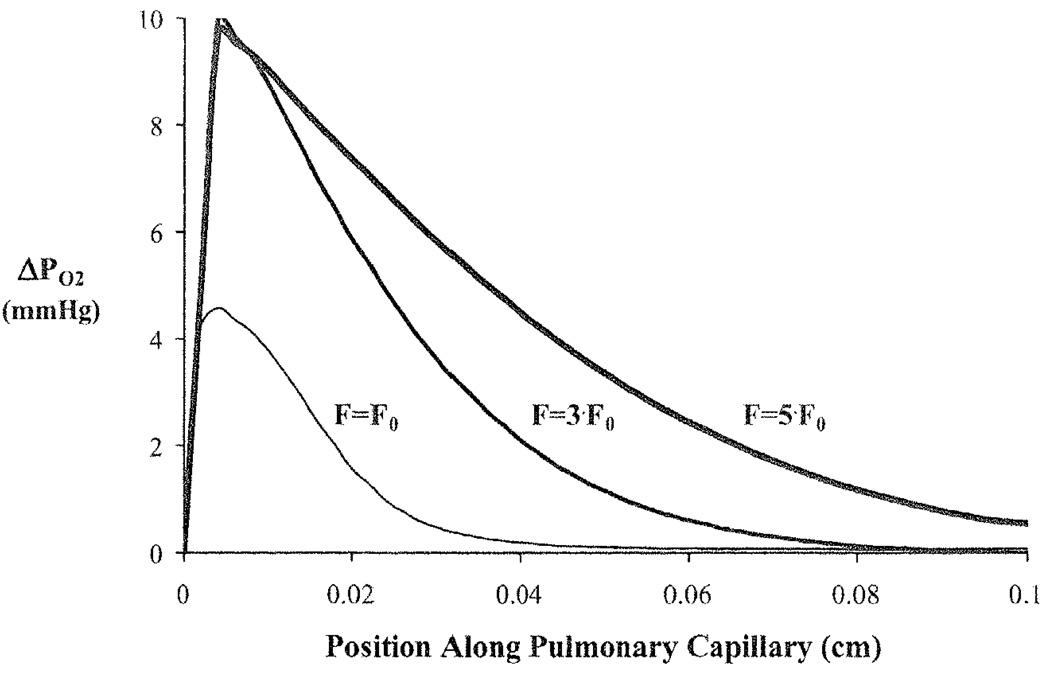
To load the red blood cell (RBC) with oxygen, oxygen moves from the well-mixed alveolar space through the plasma and into the RBC as the red blood cell moves along the length of the capillary. The relative speeds of these processes cause an axial and radial oxygen gradient to be established in the pulmonary capillary. Under normal conditions (given above), a large gradient between the plasma and RBC appears as the blood enters the capillary and disappears after the plasma and RBC have traveled ~40% of the capillary length (Fig. 39.3). However, if the normal ventilation (F_{alv, 0}) and perfusion (F₀) rate are both increased 3-fold (to offset a corresponding increase in tissue O₂ metabolism), the initial gradient between plasma and RBC increases and the two regions only equilibrate after traversing ~80% of the capillary length. A 5-fold increase in ventilation and perfusion causes the two blood components to never equilibrate while in the pulmonary capillary.

Fig. 39.3.

Oxygen partial pressure gradients between the plasma and red blood cell (ΔP_O2) at end-exhalation for a normal ventilation rate (F_alv,0) and blood flow (F₀) and when ventilation, blood flow, and metabolism are increased by 3-times and 5-times the normal rates.

ΔP_O2 = P_O2 (plasma) – P_O2 (RBC).

39.3.2 Disequilibrium Between pO₂ in Plasma and RBCs in Arteries

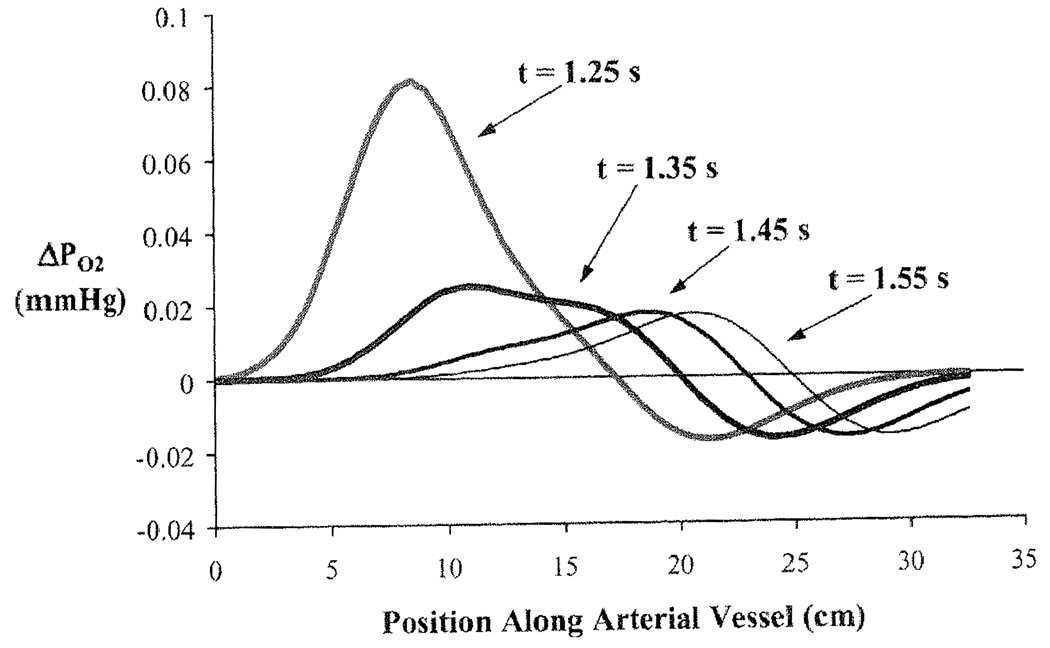
When RBC and plasma velocities are equal then equilibration across the RBC membrane occurs rapidly with a time constant governed by PS_RBC/V_pl. In contrast, when V_RBC/V_pl > 1 there is a continuing disequilibrium. To show this, the arterial module is isolated from the rest of the closed loop model and beginning with equilibrated P_O2 at 25mmHg the plasma P_O2 is increased to 100 mmHg while leaving the RBC P_O2 unchanged. The relative velocity is given a value of 1.5 to illustrate the relative disequilibrium. In this simulation the concentration front has traveled about 7 cm. before the RBC and plasma concentrations equilibrate. Beyond this, the RBCs near the wavefront of heightened plasma P_O2, having taken up O₂, advance in the central stream ahead of the plasma front and release O₂ into the plasma where the P_O2 is still 25 mmHg. This process of RBCs taking up O₂ behind the plasma front and then releasing it to raise the plasma P_O2 continues. In Fig. 39.4 are shown plots of the ΔP_O2 across the RBC membrane as a function of position along the aorta at 4 times, a tenth of a second apart after the step increase in plasma P_O2 at x = 0 and t = 0. Initially the ΔP_O2 is ~75 mmHg, but is quickly dissipated as plasma O₂ enters the huge sink of the RBC Hb. Then as the RBCs that have taken up oxygen from the plasma advance ahead of the depleted plasma layer, they have a slightly higher P_O2 than that in the plasma that had entered the tube before the pulsed increase and therefore lose oxygen to the plasma. The peak in ΔP_O2 travels at V_RBC = 25 cm/s. This peak ΔP_O2 is very small because the carrying capacity for O₂ in plasma is so small compared to that of RBC. The ΔP_O2 is larger when RBCs are fully loaded as they travel through a region where oxygen is consumed in tissue; it is high when PS_cap is high compared to PS_RBC and low in the reverse situation. It is relevant to the interpretation of plasma P_O2 as measured by oxygen-dependent phosphorescent probes [12].

Fig. 39.4.

Difference in partial pressure of O₂ between RBC and plasma along vessel length for a Gaussian shaped pulsed increase in plasma P_O2 at the vessel entry. The four curves represent the pulse at four different times.

39.4 Conclusions

We have linked together a series of blood-tissue gas exchange models with a model of gas transport in the lung to describe respiratory gas exchange between the lung and tissue via circulating blood. We illustrated that changes in metabolism causing increases in CO₂ production and O₂ consumption can be compensated by simultaneous increases in ventilation and perfusion. O₂ gradients between the plasma and red blood cell can persist along the length of the pulmonary capillary and in the arterial system because RBCs have higher velocities than plasma. The model is ideally suited for investigating questions concerning the integrative effects of pulmonary ventilation, chemical binding kinetics, vascular transport, and tissue metabolism on whole body respiratory gas exchange.