Do design variations in the artificial disc influence cervical spine biomechanics? A finite element investigation

Abstract

Various ball and socket-type designs of cervical artificial discs are in use or under investigation. Many artificial disc designs claim to restore the normal kinematics of the cervical spine. What differentiates one type of design from another design is currently not well understood. In this study, authors examined various clinically relevant parameters using a finite element model of C3–C7 cervical spine to study the effects of variations of ball and socket disc designs. Four variations of ball and socket-type artificial disc were placed at the C5–C6 level in an experimentally validated finite element model. Biomechanical effects of the shape (oval vs. spherical ball) and location (inferior vs. superior ball) were studied in detail. Range of motion, facet loading, implant stresses and capsule ligament strains were computed to investigate the influence of disc designs on resulting biomechanics. Motions at the implant level tended to increase following disc replacement. No major kinematic differences were observed among the disc designs tested. However, implant stresses were substantially higher in the spherical designs when compared to the oval designs. For both spherical and oval designs, the facet loads were lower for the designs with an inferior ball component. The capsule ligament strains were lower for the oval design with an inferior ball component. Overall, the oval design with an inferior ball component, produced motion, facet loads, implant stresses and capsule ligament strains closest to the intact spine, which may be key to long-term implant survival.

Introduction

Ball and socket (B&S) shape designs are common for total disc replacement (TDR) in the spine [6, 7, 21]. Many of the B&S type designs are under investigation for their potential to preserve normal physiologic motion and circumventing accelerated disc degeneration at adjacent levels. The articulation between the ball and socket components of the artificial disc plays an important role in determining the success and survival of the implant. This articulation may utilize a hemispherical ball component rolling over a matched socket component (e.g. Prodisc-C, Synthes Spine Solutions, West Chester, PA). Other variations of the spherical design, such as oval-shaped designs are also feasible. Yet, another design may utilize a hemispherical or oval-shaped ball component articulating with the curved surface of the socket component, where both the bearing surfaces may not exactly match (e.g. Prestige, Medtronic Sofamor Danek, Memphis, TN). The biomechanical response of cervical spine after implantation with variations of B&S design could be expected to vary. However, to the author’s knowledge, there are no previous studies delineating the biomechanical effects following implantation with variations of B&S type cervical disc replacement.

DiAngelo et al. [7, 21] studied the cervical spine biomechanics following the implantation of a ball and socket-type disc arthroplasty (Prodisc-C, Synthes Spine Solutions, West Chester, PA) using human cadaver spines. DiAngelo et al. [6] conducted a similar study using a variation of ball and socket design (Prestige ST Cervical Disc System, Medtronic Sofamor Danek, Memphis, TN). The design allowed for some translational motion between the implant’s components along with the typical rotational motion. These authors compared the biomechanical response of the intact, fused and artificial disc implanted cervical spine.

A recent finite element modeling-based study conducted by Rousseau et al. [22] utilized a C5–C6 motion segment to study the biomechanical differences following implantation of artificial discs. A ball-and-socket artificial disc was placed in a validated three-dimensional nonlinear finite element model of the cervical spine (posterior geometric center, large radius). The model was loaded in flexion, extension, lateral bending and axial torsion (40 N compression + 1.6 Nm of moment). They also investigated two variant designs: anterior center and small radius. The intervertebral range of motion, the mean center of rotation and the contact forces in the facet joints and in the bearing surface of the prosthesis were investigated. The authors demonstrated that the range of motion was similar with all the prosthesis. The facet loads were found to be below the normal values for posterior center and large disc design. These authors did not quantify the adjacent level effects as they used a functional spine unit model to study three types of typical ball and socket designs (having matching spherical ball and socket components). Also, switching the inferior and superior components of the implant might have significant effects on the biomechanics as well. Such variations were not investigated by these authors.

The purpose of this study was to investigate the biomechanical effects of shape (oval vs. spherical ball) and location (inferior vs. superior ball) of various cervical artificial disc replacements. The parameters measured were range of motion, hybrid moments, facet loading, implant stresses and facet capsule ligament strains.

Materials and methods

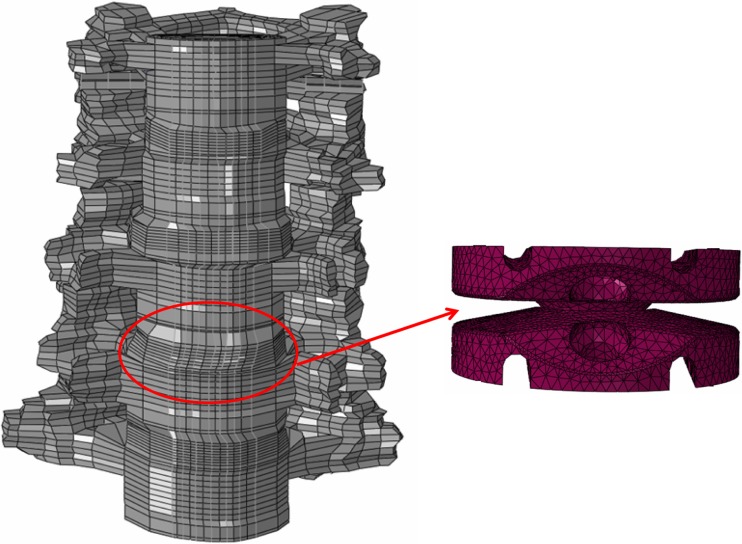
An experimentally validated, three-dimensional, ligamentous, finite element model of the C3–C7 cervical spine segments was used for this study, Fig. 1. This previously developed and validated model has been used to address various clinically relevant issues relating to lower cervical spine in prior studies [5, 9, 12, 23].

Fig. 1.

FE models of the C3–C7 cervical spine and a typical artificial disc implanted at C5–C6

C3–C7 cervical spine model formulation

The intact finite element model contained 24,732 nodes and 21,895 elements. The vertebral body consisted of a thin cortical shell surrounding a softer cancellous core, both of which were interposed between inferior and superior endplates. The cortical region of the vertebral body was modeled as a 0.5 mm (average) thick shell surrounding a softer cancellous core. The posterior region of the model was assigned attributes which lay between those of the cortical and cancellous regions. Three-dimensional, isoparametric solid elements were used to define the osseous geometry, Table 1.

Table 1.

Material properties and model characteristics of the C3–C7 cervical spine model

Element group name	Number of elements	Element type	Young’s modulus (MPa)	Poisson’s ratio	Cross sectional area (mm2)
Cortical bone	1,440	C3D8	10,000	0.3	–
Cancellous bone	6,480	C3D8	450	0.25	–
Posterior bone	4,364	C3D8	3,500	0.25	–
Annulus ground substance	3,744	C3D8	4.2	0.25	–
Annulus fibers	–	Rebar	450	0.45	–
Facet joints	–	Surface	Softened—3,500	–	–
Ligaments	1,326	T3D2	NA	NA	–
Anterior longitudinal ligament (ALL)	672	T3D2	15 (<12%); 30 (>12%)	0.3	33
Posterior longitudinal ligament (PLL)	480	T3D2	10 (<12%); 20 (>12%)	0.3	33
Ligamentum flavum (LF)	20	T3D2	7 (<12%); 30 (>12%)	0.3	50.1
Interspinous ligament (ISL)	16	T3D2	5 (<25%); 10 (>25%)	0.3	13
Capsular ligament (CAP)	138	T3D2	15 (20–40%); 30 (>40%)	0.3	46.6

The facet joints were modeled using surface definitions, where initial surface gaps between each facet region were assumed to be 0.5 mm based upon CT imaging and dissection procedures. A “softened contact” parameter was assigned to the interface which allowed for an exponentially increasing modulus as the gap distance between the inferior and superior facets decreased, simulating the presence of cartilage in the facet region. The facets were oriented at 45° approximately from the horizontal plane, with some variation in the sagittal plane alignment, according to CT geometry. The facets were also of varying curvatures from right to left sides, indicating the possibility of varying contact during right or left loading modalities from the right to left facets.

The annulus fibrosis was modeled as a composite configuration wherein a series of fibers simulating the lamellae of the disc were embedded in a ground substance surrounding a more gelatinous nucleus region. Each layer of ground substance contained two alternating layers of fibers arranged at ±65° from the transverse plane with an overall fiber content of 20% of the annular volume assumed [4, 20]. The fibers were modeled utilizing the “rebar” parameter available in the ABAQUS program. Additionally, a “no compression” option was enforced, thereby allowing the fiber elements to only be active in tension, to adequately model the role of the fibers within the intervertebral disc. The ground substance of the annulus was modeled using three-dimensional, 8-nodal “brick” elements (C3D8). The nucleus pulposus was modeled as an incompressible fluid using a fluid definition available in ABAQUS.

Luschka’s joints were modeled as well. These were simulated around the area of the uncinate processes by creating a space between the annulus horizontal layers around the uncinate processes and placing gap elements in the resulting fissures. The elements adjacent to the fissures were reinforced with fibers which were aligned approximately parallel to the fissure to adequately model Luschka’s joints.

The ligaments of the lower cervical spine included the anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL), interspinous ligament (ISL), ligamentum flavum (LF) and the capsular ligaments (CAP). The ligaments were modeled using three-dimensional truss elements (T3D2). These elastic elements were allowed to behave nonlinearly via a “hypoelastic” option. This option also allowed a “neutral zone” to be incorporated in which the ligament provided little stability under minimally applied external loads.

Disc arthroplasty model formulation

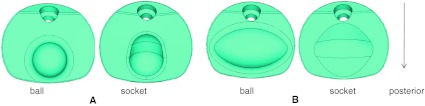
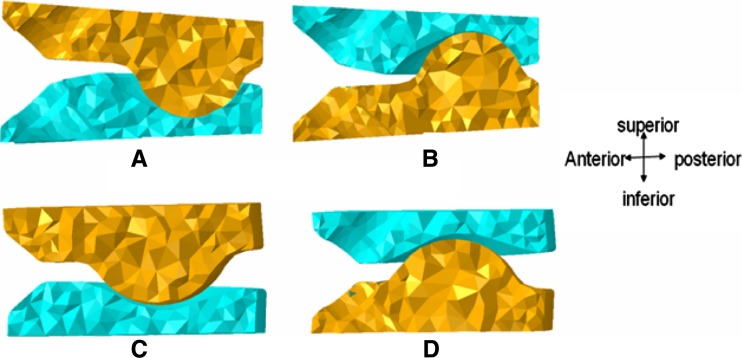
Two basic B&S disc design types were modeled and placed at C5–C6 level in ABAQUS 6.7 program (Dassault Systèmes, Providence, RI, USA). For each design, one component possessed a hemisphere-shaped ball or an oval-shaped ball while the other component possessed a corresponding socket-type profile for a smooth articulation. The profiles of the superior and inferior components were not exactly matching. Hence, they did not snugly fit into each other, Fig. 2. The shape of the ball components gave rise to two different types of implants (spherical or oval shape). Moreover, two additional types of designs were formulated by exchanging the superior and inferior components (inferior or superior ball component). Therefore, these combinations produced four different variations of disc designs, Fig. 3

1. Design with superior component having a spherical-shaped ball design (SPH-S)

2. Design with inferior component having a spherical-shaped ball design (SPH-I)

3. Design with superior component having a oval-shaped ball design (OVL-S)

4. Design with inferior component having a oval-shaped ball design (OVL-I)

Fig. 2.

a Spherical disc design components; b oval disc design components

Fig. 3.

Cross sectional view of the different designs, a SPH-S; b SPH-I; c OVL-S; d OVL-I. In the spherical designs (SPH-I and SPH-S), small radius ball component articulated with socket component. On the other hand, in the oval designs (OVL-I and OVL-S), large radius ball component articulated with a nonconforming socket component

The implant components were assigned the material properties of titanium (Young’s modulus 115GPa and Poisson’s ratio 0.34).

TDR surgery simulations

The intact C3–C7 model was modified to accommodate the disc implants at C5–C6 level. The anterior longitudinal ligament was removed first. Then an anterior window was created by removal of anterior part of annulus fibrosus. Next, the nucleus was removed completely to create space for the disc implant. The posterior part of annulus and posterior longitudinal ligament were also resected to simulate a typical decompression. Lateral structures, such as the lateral parts of annulus and uncinate processes were left intact. Implant mesh was created using tetrahedral elements.

Interactions, loading and boundary conditions

Both the superior and inferior components of the implants were attached to the respective endplates of the vertebral bodies to simulate solid incorporation. In ABAQUS 6.7, this was achieved by using the “tie” command which made sure that there was no relative motion between the two surfaces. A “hard contact” command with a friction coefficient of 0.1 was defined between the two metallic components of the implant to simulate a realistic articulation between the superior and inferior components (Coulomb’s law with slip). Finally, the bottom of the C7 vertebra was fixed in all degrees of freedom.

A follower load of 75 N was applied using a set of springs (with nonlinear load vs. displacement behavior) on the models to simulate the muscle forces and the weight of the head. These load values were close to values (73.6 N) reported in literature [18, 19]. The advantage of application of a follower load through springs was that it made sure that there was “no rotation” of the spine after follower load application. This was achieved by using two springs attached on each of the four motion segments. The springs were attached at the left and right sides of each vertebral body. These springs passed through the flexion–extension center of rotation (in sagittal plane) of the motion segments. This produced a “no rotation” scenario after follower load application. Once activated, these springs applied a constant preload of 75 N throughout the simulation. Along with the follower load, a moment of 1.5 Nm was also applied at the top of C3 vertebra to simulate extension (ext), flexion (flex), lateral bending (lb) and axial rotation (ar) motions in the intact spine. In contrast, for the disc implanted models, hybrid-type loading was applied [13]. Under hybrid loading, increasing moments were applied until the overall motion (C3–C7) of the disc implanted model was equal to that in the intact model motion [13]. This ensured that total overall motions across C3–C7 were equal for all models; however, the individual motion segments could have different motions (e.g. C5–C6 motion could be different for each model). The hybrid moment required to achieve the intact motion was recorded in all the cases. Range of motion, hybrid moments, facet loading, implant stresses and facet capsule ligament strains were compared among various designs.

Results

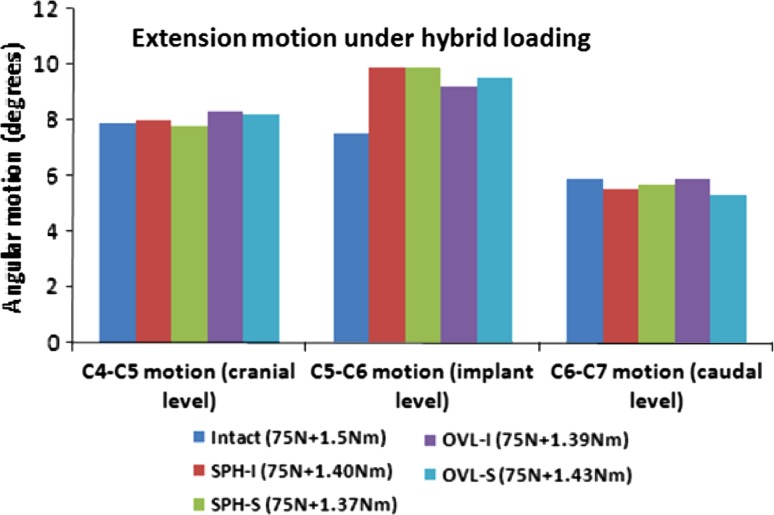
Figure 4 depicts the extension motion and hybrid moments of the cervical spine at the implanted level C5–C6 and the adjacent levels C4–C5 and C6–C7. The variations in the hybrid moments after TDR were <10% of the intact value in all the cases. Compared to intact, the index level extension motion increased with all the four designs. The maximum increases were with SPH-I and SPH-S designs (~32%) and the minimum were with OVL-I design (~23%). The adjacent level motions at the C4–C5 and C6–C7 levels were not significantly affected by TDR.

Fig. 4.

Extension motion at the implant level and adjacent levels under hybrid loading. The moments required to achieve the same overall motion as in the intact model are also shown. Two spherical-shaped designs with inferior and superior ball (SPH-I and SPH-S) components were modeled. Similarly, two oval-shaped designs with inferior and superior ball (OVL-I and OVL-S) components were modeled

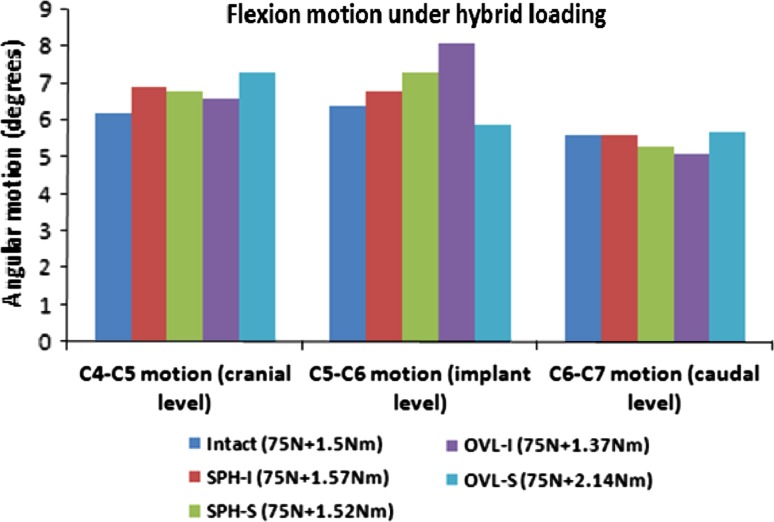
Figure 5 depicts the flexion motion of the cervical spine at the implanted level C5–C6 and the adjacent levels C4–C5 and C6–C7. The required hybrid moments were close to the intact moment of 1.5 Nm (~10% difference). However, OVL-S design required much higher hybrid moment (~40% more). Moreover, the OVL-I design provided the least stiffness to the spine. Compared to intact, the index level motions increased with SPH-I and SPH-S designs (<15%). The index level motion also increased with OVL-I design (~25%) while it decreased with OVL-S design (~7%). The adjacent level motions were similar to the intact motions for the SPH-I, SPH-S and OVL-I designs (<10% change). However, C4–C5 motion was ~17% more than intact with OVL-S design due to lower motion at the implanted level.

Fig. 5.

Flexion motion at the implant level and adjacent levels under hybrid loading. The moments required to achieve the same overall motion as in the intact model are also shown

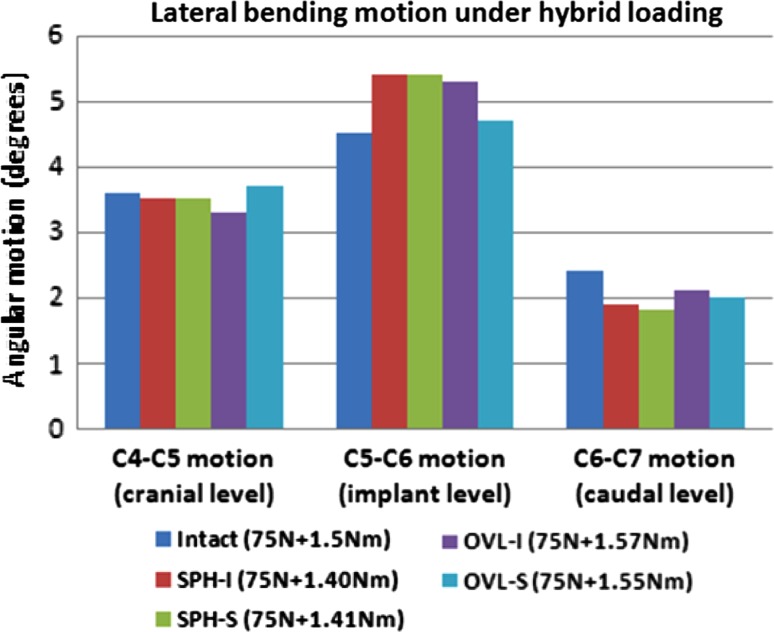
Figure 6 depicts the lateral bending motion of the cervical spine at the implanted level C5–C6 and the adjacent levels C4–C5 and C6–C7. Compared to the intact, the variation in the hybrid moments was <10% in all the cases. The index level motion increased with SPH-I and SPH-S designs (~20%) as compared to intact. With the OVL-I and OVL-S designs, the increase in motion was 19% and 5%, respectively. The adjacent level motions were largely lower than the intact motions with one exception (OVL-S design at C4-C5 level).

Fig. 6.

Lateral bending motion at the implant level and adjacent levels under hybrid loading. The moments required to achieve the same overall motion as in the intact model are also shown

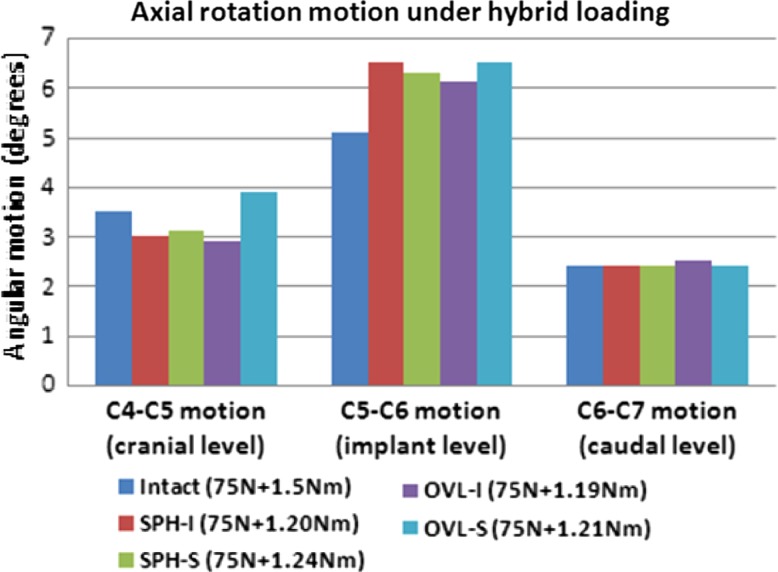
Figure 7 depicts the axial rotation motion of the cervical spine at the implanted level C5–C6 and the adjacent levels C4–C5 and C6–C7. The hybrid moments are also depicted in the figure. The stiffness of the disc implanted models was much less than the intact. The hybrid moments required to achieve intact motion (under 75 N compression + 1.5 Nm moment) for SPH-I, SPH-S, OVL-I and OVL-S designs were lower than the intact value (~20% lower). The index level motions increased from 20 to 25% approximately in all the designs as compared to intact. The adjacent level motions did not show any significant increase compared to the intact values.

Fig. 7.

Axial rotation motion at the implant level and adjacent levels under hybrid loading. The moments required to achieve the same overall motion as in the intact model are also shown

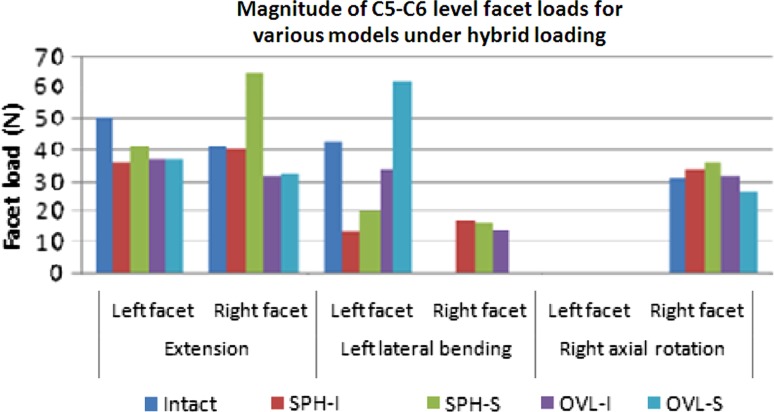
Figure 8 depicts the facet loads under hybrid loading conditions at the implanted level C5–C6. The facet loads were highest during extension motion in all the cases. Total C5–C6 extension facet loads for intact, SPH-I, SPH-S, OVL-I and OVL-S designs were 91 N, 76 N, 106 N, 69 N and 70 N, respectively. The facet loads were zero during flexion motion in all the cases. During lateral bending, the total facet loads for intact, SPH-I, SPH-S, OVL-I and OVL-S designs were 43 N, 30 N, 36 N, 48 N and 62 N, respectively. In axial rotation, the corresponding facet loads were 31 N, 34 N, 36 N, 32 N and 26 N, respectively.

Fig. 8.

Magnitudes of FE predicted facet loads (N) in various models. Facet loads were zero in all the models in flexion. Two spherical-shaped designs with inferior and superior ball (SPH-I and SPH-S) components were modeled. Similarly, two oval-shaped designs with inferior and superior ball (OVL-I and OVL-S) components were modeled

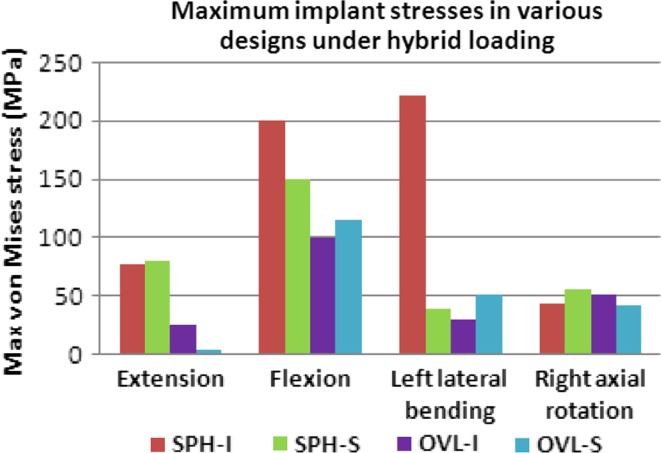
Under hybrid loading, the maximum implant stresses (Von Mises) varied among various models, Fig. 9. SPH-I design led to highest implant stresses, especially during flexion and lateral bending motions (maximum of 221 MPa). Maximum implant stresses with SPH-S were lower (maximum of 150 MPa). Similarly, the implant stress values were lower for the oval designs in most cases (maximum of 100 MPa for OVL-I and 115 MPa for OVL-S designs).

Fig. 9.

Maximum Von Mises stresses (MPa) in the implants under hybrid loading. Two spherical-shaped designs with inferior and superior ball (SPH-I and SPH-S) components were modeled. Similarly, two oval-shaped designs with inferior and superior ball (OVL-I and OVL-S) components were modeled

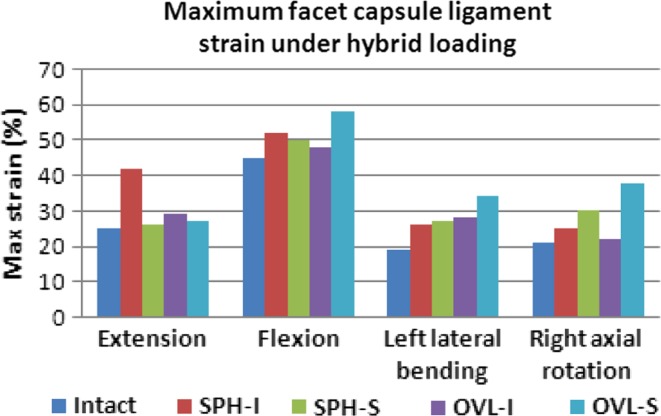
The maximum facet capsule ligament strains are reported in Fig. 10. During extension motion, the maximum capsule strains were similar to intact in all the models (~25%) except with the SPH-I design, where maximum strain was 42%. During flexion motion, maximum strains were close to the intact (~45%) except with the OVL-S design, where maximum strain increased to 58%. During lateral bending and axial rotation motions, the maximum capsule strains were lower than those during flexion motion. The maximum strain did not increase beyond 40% during lateral bending and axial rotation motions.

Fig. 10.

Maximum capsular ligament strain (%) under hybrid loading in various models. Two spherical-shaped designs with inferior and superior ball (SPH-I and SPH-S) components were modeled. Similarly, two oval-shaped designs with inferior and superior ball (OVL-I and OVL-S) components were modeled

Discussion

Variations of ball and socket-type designs for the cervical artificial discs are already in use. However, there is limited published data comparing the biomechanics of cervical spine implanted with various types of disc designs. Many of the previous in vitro studies concerning TDR were conducted as part of the FDA approval process, focusing primarily on comparisons between specific types of TDR with the fusion system. The present FE studies provide useful data for quantification of the kinetic and stress differences (large or small) among various disc designs.

Motion data

Several previous biomechanical studies have confirmed that cervical arthroplasty devices preserve motion much better than fusion [3, 6, 7, 21]. These authors examined specific types of disc implant [6, 7, 11, 14, 15, 21]; with the exception of Rousseau et al. [22], who investigated three types of matching ball and socket designs.

In the present study, we used hybrid loading protocol to simulate in vivo loading conditions. We found that the implanted level extension motions were higher than the intact motion while hybrid moments were lower than the intact moment during extension motion. This indicates that the TDR implanted spine becomes less stiff compared to the intact spine during extension. The spherical design allowed for more extension motion than the oval design (32% vs. 23% increase as compared to intact). Moreover, switching the inferior and superior components had smaller effect (<5% change) on the oval design, and it had no significant effect on the spherical design. The spherical designs (both SPH-I and SPH-S) are assembled in such a way that during extension motion, the components act as matching ball and socket parts which facilitate “pure” rotation motion, Fig. 3. The rotational motion is the same whether the design is SPH-I or SPH-S. This explains why switching of components does not have any substantial effect on extension motion for the spherical designs. The adjacent level motions were not much affected either.

The implanted level flexion motions also increased following TDR, except with the OVL-S design. Designs with room for anterior–posterior translation motion allowed for higher flexion motion. For instance, among the SPH-I and SPH-S designs, SPH-S design allowed for greater motion than the SPH-I design (~10%) owing to the availability of translational motion along with the rotation motion, Fig. 3. For the oval designs, the flexion motions demonstrated much larger effects of switching of the components.

During lateral bending, switching of components did not affect the implanted level motions for the spherical designs (similar to extension). In contrast, switching of components affected the motion for the oval designs (~13% change). Unlike the spherical design, the oval design utilizes a larger radius ball component articulating on a nonconforming socket component. Such characteristics of the oval design lead to larger changes in the motion when the superior and inferior components are switched.

During axial rotation, the stiffness of the disc implanted models was the lowest (~20% lower hybrid moment). The shapes of the ball components (spherical or oval) appeared to have very small effect on the implant level motions. Switching components (inferior or superior ball) had small effect in both the spherical and oval designs (~5% change in motion).

No increases in motion were found at C3–C4 level. This indicates that none of the discs will have any adverse effect on the health of the C3–C4 disc.

The motion data is in line with the results of the study conducted by Rousseau et al. [22] who demonstrated that implanted level motion increased after disc arthroplasty. However, no major inter implant difference in motion were found.

Facet load data

Following TDR, the C5–C6 level facet loads were less than the intact facet load values in most cases. During extension motion, the total facet loads increased only with SPH-S design (~17%). During flexion, the facets were moving away from each other. Due to the absence of contact between the superior and inferior facets, the facets did not demonstrate any loading in flexion. During lateral bending motion, the facet loads at the implanted level were similar to or lower than the intact values in SPH-I, SPH-S and OVL-I designs. With these three designs, the implant level facet loads were distributed on both the facets during lateral bending. Such distribution was unlike the distribution in the intact model, where only left facets were loaded during left bending. This suggests that TDR may also alter the distribution of loads on the left and right facet joints. Nevertheless, the facet load values were lower than the intact with the above three designs. With the OVL-S design, the facet loads increased in lateral bending (~44%). The facet loads during axial rotation were similar to intact for all the disc designs. Overall, the disc designs with inferior ball components led to lower facet loading (SPH-I and OVL-I). The facet loads in left and right bending and in left and right rotation were similar in magnitude and distribution. Moreover, none of the disc designs increased the facet loads at the adjacent levels. Therefore, adjacent level facet degeneration may not be a major concern following disc replacement.

Chang et al. [3] found that following TDR, the facet loads increased at the index level in all the bending modes. However, maximum increase in the facet loads was during extension motion. Metzger et al. [17] also conducted in vitro studies to investigate the changes in the facet load profile with the variation in the device positioning in the disc space. The authors found that facet forces were sensitive to the device placement location and thereby indicated that improper positioning could potentially lead to higher facet loads following TDR. In contrast, a similar study conducted by Steiber et al. [24] using ovine spines demonstrated no significant increase in the facet loading following TDR. Our data suggests that under hybrid loading conditions TDR maintains total facet loads similar to the intact facet loads—with lower facet loads for the SPH-I and OVL-I designs. The clinical implications of the disc arthroplasty induced increase in the facet loads indicate a need for more in vivo studies. Long-term clinical follow ups of the disc implant recipients may provide insight into the issue.

Maximum capsule ligament strain

The higher capsule ligament strain may also cause facet-related pain due to the presence of pain receptors in them. Under hybrid loading conditions, the capsules were stretched maximum during flexion motion. In general, OVL-S design led to higher capsule strains while the OVL-I design led to capsule strains similar to intact. SPH-I and SPH-S designs led to strains similar to intact—except for the SPH-I design in extension—which demonstrated a sharp increase in the capsule strains.

The facet capsule injuries are studied in hyperextension (such as whiplash) and they are known to cause facet-related pain [16, 25, 26]. Such studies have demonstrated that the capsule ligaments rupture at mean strain values greater than 100%. The strain values predicted in this study are much lower than those. We believe that during normal activities following TDR, the facet capsule will not be stretched as much as that during whiplash.

Implant stresses

The stresses in the implant under physiological loading conditions govern the long-term wear pattern of the disc implants. The repetitive higher stresses in the implant may cause localized wear of the implant leading to alteration in the articulation between the superior and inferior components. The altered articulation, if significant, may alter the biomechanics of the involved segment as well.

The maximum implant stresses varied with all the four designs. Significantly higher stresses in the spherical designs may lead to higher wear rate of these implants. Oval designs (OVL-I and OVL-S), owing to their nonconforming ball and socket components led to much lower stresses. These designs may be more robust in long term.

The maximum von Mises stresses in the disc implants were lower than the yield (~350–400 MPa) and fatigue strengths (~250 MPa at 10 million cycles) of titanium in all the models for all the four designs. It suggests that implant failure may not be a possibility in cervical TDR. Few previous studies have investigated the wear of disc implants in cervical spine, they demonstrated that artificial disc wear did not occur to harmful levels [1, 2].

Assumptions and limitations of the study

Although extra care was taken during implant placement and analysis, the FE models have many limitations, just like the cadaver studies and like studies published by others, that should be kept in mind while interpreting the results of the present study. The FE model results are strong functions of the inputs, such as material properties, loading conditions and implant locations, etc. The cervical biomechanics are expected to be affected by alteration in the location of the implant in the disc space. For example, by shifting the implant in the anterior, posterior or in the lateral directions, or by changing the orientation of the implant in the disc space, the resulting biomechanics might get influenced as predicted by the studies in both lumbar and cervical spine [8, 10]. This opens a new area of exploration which has not been studied in cervical spine thoroughly. Anterior longitudinal ligament was removed in all the disc replacement models; however, no scar tissue formation was simulated. Formation of scar tissue might further reduce the inter-implant differences as shown by our previous study concerning lumbar disc arthroplasty [8].

Application of preload may also affect the final results significantly. We applied the preload using set of springs that maintained the “no rotation” of the motion segments in the intact spine. However, following TDR, the application of muscle forces may not be similar to the intact spine. It is possible that various muscles would respond in a different manner after TDR surgery when compared to a normal spine. For the current study, we used the same preload locations and magnitude in all the cases in order to be consistent. Such issues give a different dimension to the biomechanics of cervical spine following TDR surgery, just like the lumbar procedures. Additionally, application of preload during lateral bending and axial rotation motions might have affected the results as well. This is because the “no rotation” was maintained in the sagittal plane while lateral bending and axial rotation motions occur out of this plane.

The articulation between the two components of the disc implant was modeled as hard contact with a friction coefficient of 0.1 which may vary in vivo. However, this is a comparative study and the variations caused by frictional factors or material properties are expected to induce the similar effects in all the disc designs. In our sensitivity analyses, where we varied the coefficient of friction between 0.05 and 0.15, we did not find any drastic differences in the motion behavior and the stress pattern due to variation in friction.

A single set of material properties was studied. Similarly, effects of artificial disc only at C5–C6 level were investigated. Variation in above parameters may have influence on the results; however, we believe that the tendencies will be similar to the presented results.

Conclusions

The present study highlighted that cervical TDR do “maintain” the implanted level motion and also the normal motion at adjacent levels. Under hybrid loading, there were no major differences in the motion of the cervical spine implanted with four different designs of artificial disc. The facet loads were close to intact for the SPH-I and OVL-I designs. The implant stresses were lower for OVL-I and OVL-S designs. Nevertheless, the implant stresses were lower than the yield and fatigue strengths of material in all the cases. Capsule ligament strains were closer to intact with the OVL-I design. Although the motions were similar for all the four designs; the facet loading, implant stress and ligament strain data suggest that OVL-I design may be more successful in long term. The favorable biomechanics of OVL-I design may be attributed to its shape, larger radius and the assembly configuration. Moreover, as more clinical data is collected on Prestige and Prodisc-C (designs similar to studied here), a correlation could be established between the present biomechanical results and the clinical outcomes.