Abstract
Alteration of the native mitral valve (MV) shape has been hypothesized to have a profound effect on the local tissue stress distribution, and is potentially linked to limitations in repair durability. The present study was undertaken to elucidate the relation between MV annular shape and central mitral valve anterior leaflet (MVAL) strain history, using flat annuloplasty in an ovine model. In addition, we report for the first time the presence of residual in-vivo leaflet strains. In-vivo leaflet deformations were measured using sonocrystal transducers sutured to the MVAL (n=10), with the 3D positions acquired over the full cardiac cycle. In six animals a flat ring was sutured to the annulus and the transducer positions recorded, while in the remaining four the MV was excised from the exsanguinated heart and the stress-free transducer positions obtained. In the central region of the MVAL the peak stretch values, referenced to the minimum left ventricular pressure (LVP), were 1.10 ± 0.01 and 1.31 ± 0.03 (mean ± standard error) in the circumferential and radial directions, respectively. Following flat ring annuloplasty, the central MVAL contracted 28% circumferentially and elongated 16% radially at minimum LVP, and the circumferential direction was under a negative strain state during the entire cardiac cycle. After valve excision from the exsanguinated heart, the MVAL contracted significantly (18% and 30% in the circumferential and radial directions, respectively), indicating the presence of substantial in-vivo residual strains. While the physiological function of the residual strains (and their associated stresses) are at present unknown, accounting for their presence is clearly necessary for accurate computational simulations of MV function. Moreover, we demonstrated that changes in annular geometry dramatically alter valvular functional strains in-vivo. As levels of homeostatic strains are related to tissue remodeling and homeostasis, our results suggest that surgically-introduced alterations in MV shape could lead to the long term MV mechanobiological and microstructural alterations that could ultimately affect MV repair durability.
KEY TERMS: Flat ring annuloplasty, Repair surgery, Stress-free state
INTRODUCTION
Mitral valve (MV) repair procedures are commonly used to treat valvular dysfunctions such as regurgitation or stenosis (1,46). Whenever possible, repair procedures are preferred to valve replacements as they maintain better ventricular mechanics and lead to fewer postsurgical complications such as endocarditis, thromboembolism, and anticoagulant-related hemorrhage (5,22,23,69). A comparative study (49) conducted on 100 patients over 7 years, has shown that MV repair was associated with fewer overall valve-related deaths, procedure-related morbidity and mortality, and reoperation when compared with valve replacement with either mechanical or bioprosthetic devices.
Despite the benefits of repair recent data have indicated the durability of such procedures to be significantly less than previously thought. For example, 10%–16% of patients undergoing mitral valve repair for myxomatous disease required reoperation for severe regurgitation within 10 years (5,12,13,21,22). Repair failure rates for patients with ischemic mitral regurgitation are even more sobering with a 30% recurrence rate of significant MR at 6 months after surgery and a 3 to 5 year rate approaching 60%. For both diseases, repair failures are associated with disruption of both leaflet and annular suture lines (21). Such failure mechanisms suggest the repair-induced changes in the mechanical loading of the valvular tissue as an etiological factor.
Ring annuloplasty is a technical main-stay of all MV repair procedures, the purpose of which is to restore normal annular size and shape, and consequently to facilitate more natural leaflet motion and coaptation (7). The pre-operative MV annulus is generally larger than normal functioning annulus and in-vitro studies have shown that the shape of annuloplasty ring affect the leaflet deformations (29,47). In particular, a saddle shape annuloplasty ring reduces the systolic strain both in the MV anterior and MV posterior leaflets (29,47). In addition, in-vivo studies have shown that annuloplasty ring shape influences both leaflet geometry and function (3,4,42,43,54). Such dramatic anatomical changes may lead to changes in the valvular functioning strains and stresses.
In biomechanics, the presence of normal tissue stresses has long been considered closely related to tissue homeostasis (10,11,19). Moreover, it has been shown that pathophysiological alteration in mechanical loading can lead to stress changes and subsequent tissue adaptation (20,41). In the MV, numerous pathological factors such as tachycardiainduced cardiomyopathy (63), mitral regurgitation (37,51), and abnormal ventricular wall motion (37,51) as well as surgically- introduced anatomical changes (62) have been shown to change the microstructural components. Collectively, our knowledge of disease and repair-induced alternations in MV geometry suggests that they lead to altered tissue stresses, which ultimately affects the durability of the repaired valve. For example, altering valvular mechanical loading could lead to concomitant changes in collagen biosynthesis, the main load-bearing structural component of the MV extracellular matrix (ECM) (45). As shown by Stephens et al. (62) changing the MV tissue mechanical loading simply by making a surgical hole into the mitral valve leaflet altered MV ECM collagen content. In addition, recent studies have suggested that decreasing the amount of mechanical strain would lead to an increased rate of collagen degradation (6,70). In short, changes in the tissue deformations from those normally experienced in-vivo, induced by surgical repair procedures, may lead to cellular responses and tissue remodeling that would ultimately dictate the extent of long-term durability.
For quantifying mechanical in-vivo strains, an unloaded referential strain is required. While not definitely proven, the minimum left ventricular pressure (LVP) has been generally considered as the preferred referential configuration (15). Recent studies (52) have shown that other stages of cardiac cycle used as the referential configuration, notably end-diastole or leaflet separation stages, would also produce strains values similar to those obtained from minimum LVP referential configuration. However, while residual strains are known to exist within the aortic valve layers (61,66,67), it is not known whether residual strain exists in valvular tissues in their in-vivo state. As noted by Fung et al. (18), accounting for residual strains is critical for both constitutive model development and subsequent computational simulations; both highly dependent on precise knowledge of the referential configuration (68). Moreover, critical linkages to the underlying valve interstitial cell mechanobiological responses (55) require a detailed knowledge of the relation between tissue and cellular deformation, which is only possible when the in-vivo strain state is known. Finally, the MV strains have been quantified via in-vitro (27,47,58) and in-vivo (28,32,35,52) measurements. In fact, we recently showed how MV posterior leaflet strain and annulus geometry are related in vitro (47). However, the effects of annular geometry alteration on the anterior leaflet strain have not yet been studied in in vivo. Thus, in the present study we quantified the in vivo strain histories of ovine mitral valve anterior leaflet (MVAL) before and after alteration of the annular geometry, accomplished via the use of a flat ring annuloplasty. In addition, for the first time we determined the actual stress-free referential configuration of the MVAL by performing measurements of leaflet deformation in the exsanguinated heart and completely dissected (stress-free) states.
METHODS
Transducer implantation and data collection
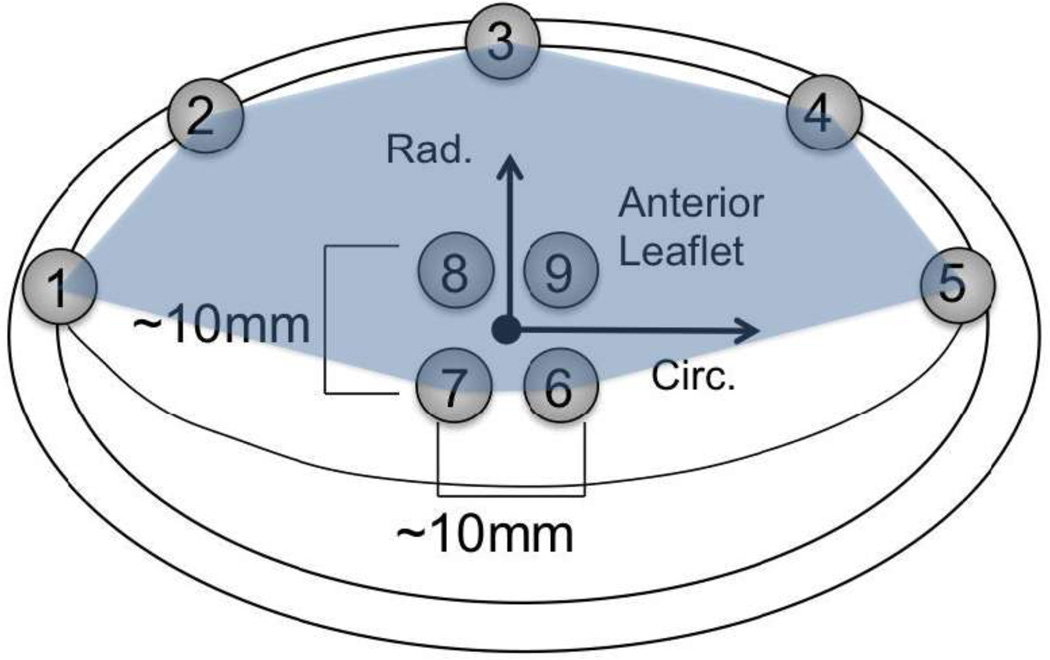
The 3D positional data collection methodology has been previously presented (15,56,57). Briefly, 10 adult (30–40 kg) Dorsett sheep that have been raised for laboratory work by commercial vendors were used. The animal experiments were conducted in compliance with guidelines for humane care (NIH Publication No. 85- 23, revised 1985). To prepare for transducer implantation, the animals were induced with sodium thiopental (10–15 mg/kg IV), intubated, anesthetized, and ventilated with iso-fluorane (1.5–2%) and oxygen. The surface ECG and arterial blood pressure were continuously monitored. A sterile left lateral thoracotomy was then performed and a total of nine 2-mm hemispherical piezoelectric transducers (Sonometrics, London, Ontario) were sutured on the MVAL. Five of the nine transducers were sutured around the annulus (marked as 1–5 in Fig. 1) and the other four on the midsection of the anterior leaflet (marked as 6–9 in Fig. 1). The transducer wires were brought out through the atriotomy incision. The sonocrystal transducer wires were then connected to a Sonometrics Series 5001 Digital Sonomicrometer (Sonometrics Corp., London, Ontario). Sonomicrometry array localization (SAL) was used to determine the three-dimensional coordinates of each transducer every 5 ms throughout the entire cardiac cycle with spatial resolutions of ~0.025 mm for each crystal (24). Sonomicrometry positional data were then taken following neosynephrine infusion titrated to achieve systolic blood pressures of 150 mmHg.
Figure 1.
Arrangement of sonocrystal on the ovine anterior leaflet. Following the ring annuloplasty, crystals 1–5 were removed. The arrows show the circumferential (Circ.) and radial (Rad.) directions used in strain calculation at the midsection of the anterior leaflet. The midsection region surrounded by crystals 6–9 was used in bi-linear finite elements surface fitting and the region surrounded by crystals 1–7 and silhouetted was used in bi-quadratic finite element surface fitting.
To explore the effects of changes in annular geometry on dynamic leaflet strain in-vivo, after data collection was completed for the normal valve (n=6), the annulus crystals were removed and a flat physio ring was sutured on the annulus. Three-dimensional sonomicrometry positional data of the anterior leaflet crystals (marked as 6–9 in Fig. 1) were obtained for fifteen cardiac cycles for each data set. In both normal and post annuloplasty valve the cycle-to-cycle variations were extremely small, so in each case we chose the last cycle as the representative. To obtain stress-free referential configuration of the MV, in four normal valves after data collection (without removing the crystals) the animals were euthanized by an intracoronary infusion of potassium chloride (1mEq/kg). Cardiac arrest was confirmed on ECG. The heart was then dissected, sonomicrometry positional data obtained as above, the MV dissected from the heart, and the stress-free three-dimensional sonomicrometry positional data collected. After resection, the anterior leaflet was gently positioned as flat as possible without imposing any external stress and suspended free-floating in the 0.9% normal saline solution. All stress-free positional data was measured in this state.
Strain Calculation in the normal and post-ring-annuloplasty rings
The method by which the in-vivo strain at the MVAL midsection (area defined by crystals 6–9 in Fig. 1) was calculated from the three-dimensional sonocrystal displacement as described previously (48,58). Briefly, the minimum LVP configuration was chosen as the referential frame of strain calculation. Three-dimensional positions of the four crystals on the midsection of the anterior leaflet (crystals 6–9, Fig. 1) were fitted to a computational domain using a single bi-linear surface finite element. Note that we did not use the sonocrystals as nodes but rather fitted each component of the displacement field to a single element. In particular, 3D postion data were rotated and translated to keep the undeformed position approximately parallel to the XY plane. Therefore, the new X -axis was inside a plane that bisected the two lines made from markers 7 to 9 and from markers 6 to 8 (approximately parallel to the line made by markers 7 and 6), and the new Y-axis was tangent to the surface and inside the other plane that bisected the two lines made from markers 7 to 9 and from markers 6 to 8 (approximately parallel to the markers 9 and 6). In the X and Y directions, the nodal positions of the bilinear element were obtained from the maximum and minimum values of the sonocrystal positional data:
| (1) |
,
| (2) |
, where X̂ and Ŷ were the nodal postions of the bilinear element and ξ, η∈{−1,1}. We then found the Ẑ nodal position of the bilinear finite element by minimizing εfit, the error between the values of sonocrystal data and fitted plane:
| (3) |
, with m being the total number of sonocrystals (m = 4), Zi being the Z-coordinate of i-th -crystal obtained from sonomicrometry positional data, Ẑj being the Z-coordinate of the j-th finite element node (fitting parameter), ξ-η being the computational domain, and ϕj(ξi, ηi) being the j-th bilinear basis function calculated for the i-th sonocrystal. An in-plane curvilinear coordinate system was then defined using the fitted surface. In particular, e1 was tangent to the surface and parallel to the x-axis, e2 was tangent to the surface and parallel to the y-axis, and . Note that e1 and e2 are necessarily not orthogonal. In the deformed configuration, the positional data was related to the undeformed values by minimizing the fitting error εfit:
| (4) |
,
| (5) |
,
| (6) |
.
For the deformed configuration, an in-plane non-orthogonal convective coordinate system was defined. In this coordinate system, of the new curvilinear coordinate system was tangent to the deformed surface and parallel to the X-axis, was tangent to the surface and parallel to the Y-axis, and . Similarly, are not necessarily orthogonal. Since we are utilizing a convective coordinate system, all the information about strain is contained in the change of the metric tensor as the frame of reference is distorted from the original to the deformed configurations. Thus, we can define the strain tensor γαβ from the metric tensor in the current (gαβ (t)) and referential (Gαβ) configurations using
| (7) |
.
The resulting principle values and principle directions of the strain tensor were obtained from solving the eigenvalue problem for the Euler–Almansi strain tensor e(t) expressed in the mixed notation:
| (8) |
.
The eigenvalues e(n1) and e(n2) and their corresponding eigen vectors n1 and n2 were calculated, from which the principal stretch values λ(ni) were obtained using e(ni):
| (9) |
.
The physical components of the Euler–Almansi strain tensor êαβ (t) were obtained from
| (10) |
, where g(αα) ’s are the diagonal components of the metric tensor (i.e. g11 and g22 in the 2-D case). As shown in Fig. 1, at the center of the leaflet midsection, the circumferential direction was defined parallel to e1 (i.e. ec = e1) and the radial direction was defined by . Using er and ec, we calculated the radial and circumferential strains:
| (11) |
,
| (12) |
.
To quantify local areal changes D(t) at the center of the leaflet mid-section, we used
| (13) |
.
We also calculated the shear angle, Δθ(t), defined as the difference between θ0, angle between in-plane unit vectors e1, e2 in the reference configuration, and θ(t) the angle between their deformed the counterparts:
| (14) |
, where
| (15) |
,
| (16) |
.
Local vs. regional strain fields
One question we had was how representative the mid-section strains were in comparison to the region silhouetted in Fig. 1 (most of the MVAL excluding the coaptation region). Using all available crystals (leaflet and annulus) we obtained an approximation of the dynamic strain over this larger region in the normal MVAL. The equations for strain calculations were identical to those of the four-crystal case. The position of all nine crystals was used to construct a single biquadratic finite element. Unlike the bi-linear case, however, the bi-quadratic nodal positions were not the same as the crystal positions. The bi-quadratic nodal positions were obtained using finite element interpolation methods described in our previous works extensively (48,60). The fitted surface was smoothened by adding Sobolev norm penalty terms, as described previously (26). Briefly, the fitting error εfit was defined by:
| (17) |
, with m being the total number of sonocrystals (m = 9), zi being the z-coordinate of i-th -crystal obtained from sonomicrometry positional data, ẑj being the z-coordinate of the j-th finite element node (fitting parameter), ξ-η being the computational domain, ψj(ξi, ηi) being the j-th biquadratic basis function calculated for the i -th sonocrystal, and S[z(ξ, η)] being the Sobolev norm integrand defined by
| (18) |
.
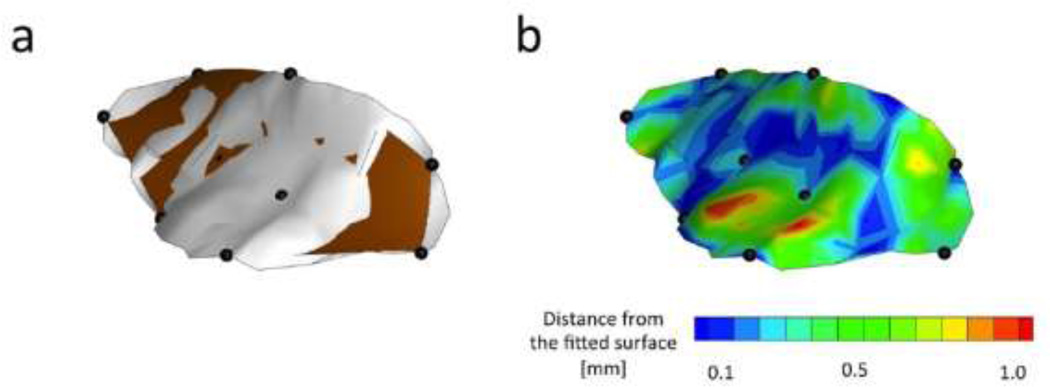
To calibrate the penalty terms A and B, we minimized the error between fitted surface using nine-crystal-method and experimentally measured high spatial density description of a typical MVAL using ultrasound imagining. In particular, we obtained 3D anatomically accurate ultrasound positional data of the atrial surface of a typical ovine MVAL (shown in Fig. 2a in a light color). The image was obtained when the leaflets achieved coaptation. We subsequently selected nine points (Shown in Fig. 2a by dark solid spheres) from the ultrasound data to create a fitted surface using the method explained above (shown in Fig. 2a in a dark color). The positions of these nine representative ultrasound data points were chosen in such way to approximately match the position of nine sonocrystals used in a typical in-vivo experimental measurements. To find the best fitted surface, we explored a range of 10−1–10−5 for A and B. For each value of A and B, we calculated εUS, the shortest distance between the fitted surface and anatomically accurate ultrasound positional data. Using εUS, we calculated the mean square root of error MSREUS:
| (19) |
, where p was the total number of the points available from the anatomically accurate ultrasound positional data. The values of A and B that minimized MSREUS were chosen as the appropriate calibrated penalty term values for the in-vivo data analysis. The ultrasound images for this part were obtained using real-time three-dimensional echocardiographic (rt-3DE) data sets via a Phillips iE33 platform in conjunction with either an x4 external probe or an X7-2t TEE probe. Gated images were acquired over four cardiac cycles at a sampling rate of 25 Hz. Rt-3DE data sets and were exported to a dedicated EchoView (Tomtec Imaging Systems) software workstation. All image manipulation was performed in the EchoView environment.
Figure 2.
(a) A single biquadratic finite element surface fitted to the nine crystals (darker surface) in comparison to the surface obtained from ultrasound data (lighter surface). (b) Fitting error defined as the shortest distance between the ultrasound surface and the fitted surface at each point on the surface.
RESULTS
Surface fitting and regional strain in normal functioning MV
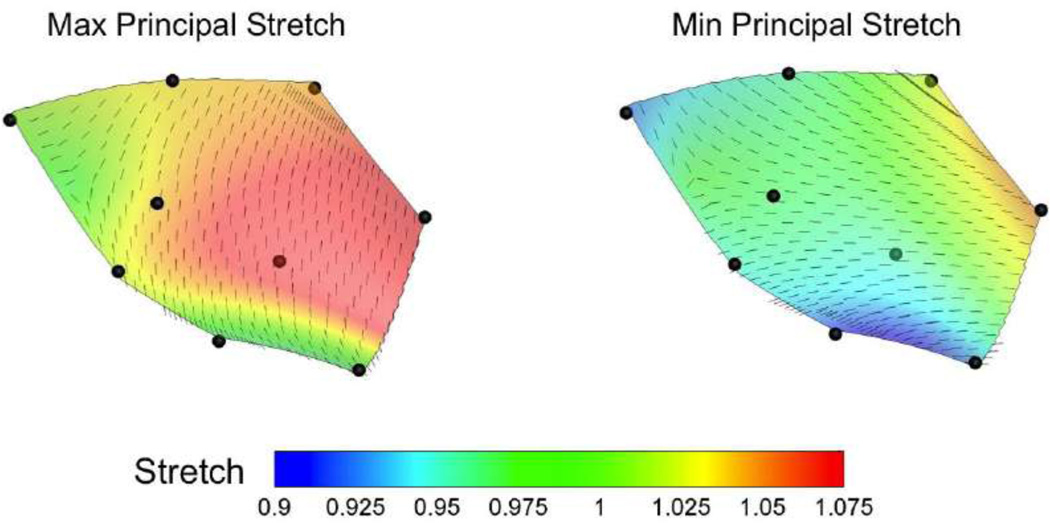
The fitting error was minimized when the values of penalty terms A and B were in the order of ~10−3 (Fig 2b). The atrial surface of the MV is known to be smoother than the ventricular side (14) but the atomically accurate surface obtained from 3D ultrasound positional data still contained few regions with sharp curvatures. Both natural anatomy of the MV atrial surface and the low density of data points obtained from ultrasound imaging could have contributed to this slight lack of smoothness. Although the smoothened surface obtained from nine-crystal-fitting method did not capture the sharp curvature of these regions, the overall fitting error was acceptable (MSREUS < 0.57 mm and εUS < 1.2 mm). The strain calculated via the extended anterior leaflet (using all nine crystals) demonstrated a small variability over the midsection of the anterior leaflet. In particular, both maximum and minimum principal stretches varied only about 10% within the midsection region of the anterior leaflet at maximum LVP in this typical example (Fig. 3). The relative areal change also altered only by 7% within the midsection region bounded by markers 6–9.
Figure 3.
A typical example showing that both the values and directions of maximum and minimum principal strains over the anterior leaf were fairly homogeneous (variation in the order of ~0.1). The principal strains were calculated using the nine crystal biquadratic element fit.
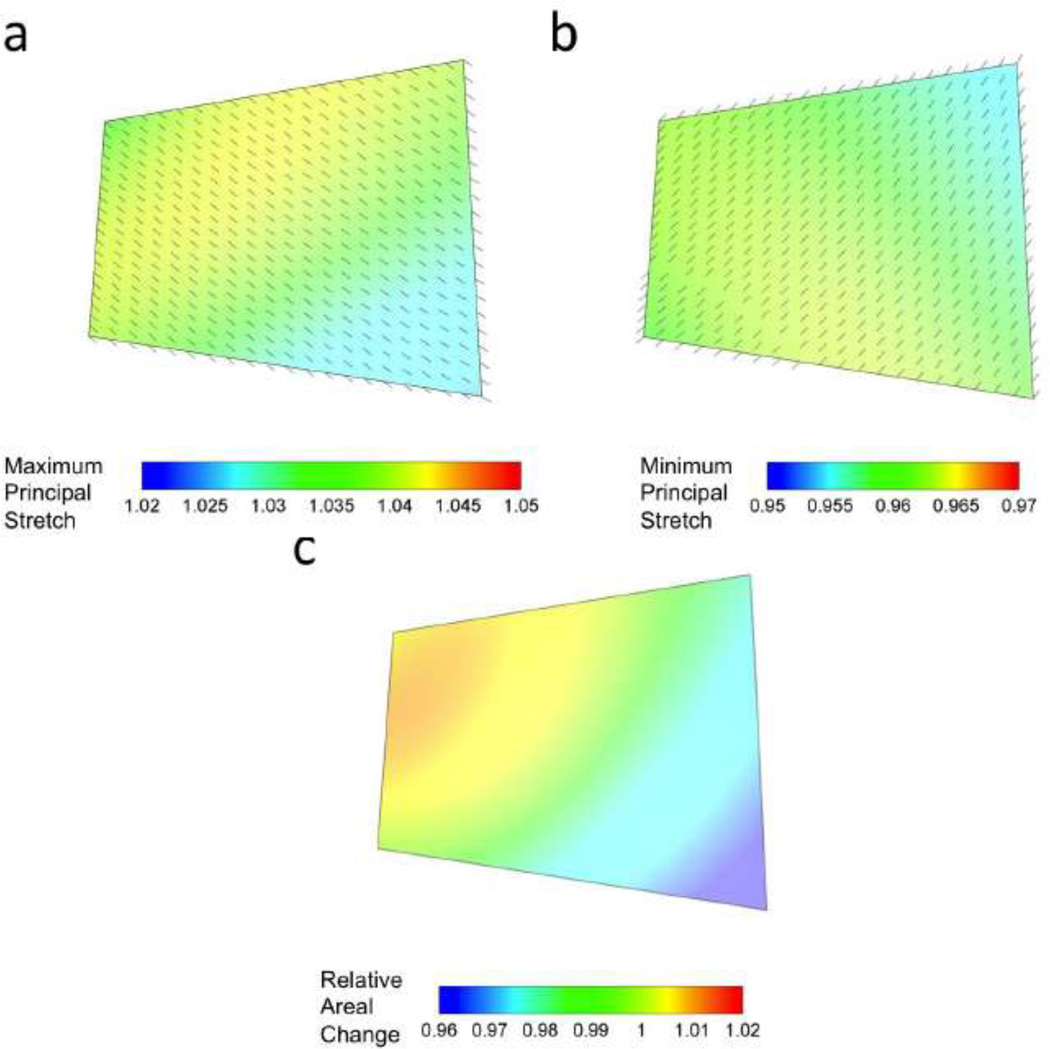
Although not identical to the extended leaflet region, the maximum and minimum stretches within the midsection region were uniform for the four midsection crystals used to calculate the strain at maximum LVP (Figs. 4a,b). The maximum and minimum principal stretches were within the ranges of ~1.02–1.04 and ~0.95–0.96, respectively. The directions of the maximum and minimum principal values were also uniform within this region of the MVAL leaflet. Areal changes demonstrated a small variation when four crystals were used for strain calculation. The areal changes were within the range of ~0.96–1.01 at maximum LVP in this typical example (Fig. 4c). Collectively, it was observed that in both methods (i.e. either using the extended leaflet or only midsection crystals), the kinematical measurements were rather uniform in the midsection region of the valve. Therefore, from hereon we only report the stretch values at the geometric center of midsection region (marked with a solid circle as the origin of the coordinate system shown in Fig. 1). In addition, at the geometric center of midsection region the maximum value of the shear angle (calculated using 4 bisectional crystals) over the entire cardiac cycle was 10.7 ± 1.83 degrees (mean ± standard error, n = 6).
Figure 4.
A typical example showing that both the values and directions of (a) maximum and (b) minimum principal strains over the anterior leaf midsection were fairly homogeneous (variation in the order of ~0.01). The principal strains were calculated using the four crystal bilinear element fit. (c) The variability in the areal changes calculated from four crystal data was also minimal.
Effects of alteration in annular geometry
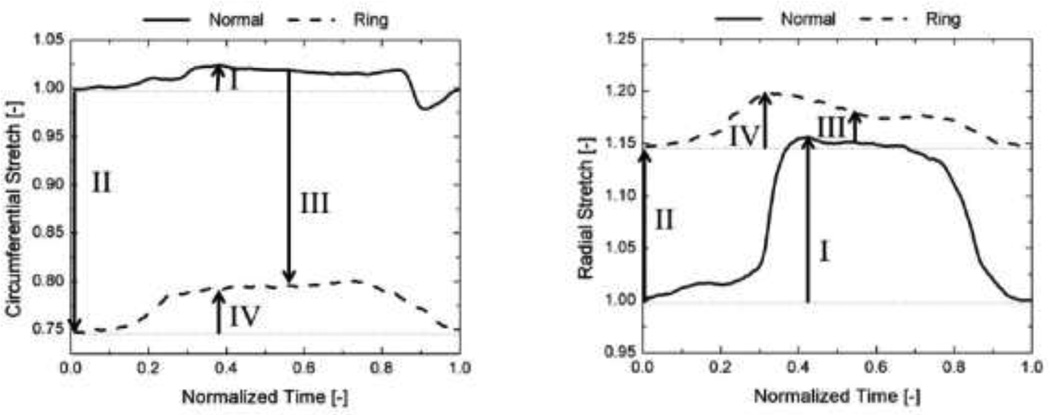
The circumferential and radial stretches changed dramatically following complete geometrical/physical restriction of the annulus (Fig. 5). In the normal valve both, circumferential and radial (Fig. 5) stretches increased as LVP reached its maximum value (“I” in Fig. 5). Restricting the annulus by suturing an annuloplasty ring on the valve caused dramatic changes in the values of stretches. The minimum LVP stretch dropped to 0.74 and increased to 1.15 in the circumferential and radial directions, respectively (“II” in Fig. 5). The dramatic changes in the minimum LVP stretches indicated that following annular restriction the leaflet was contracted in the circumferential direction and stretched in the radial direction.
Figure 5.
A typical example showing the dynamic changes in the circumferential and radial stretches in the normal and annulus-restricted valves. The changes highlighted by roman numbers are further specified with null hypotheses for the collective data in Table 1.
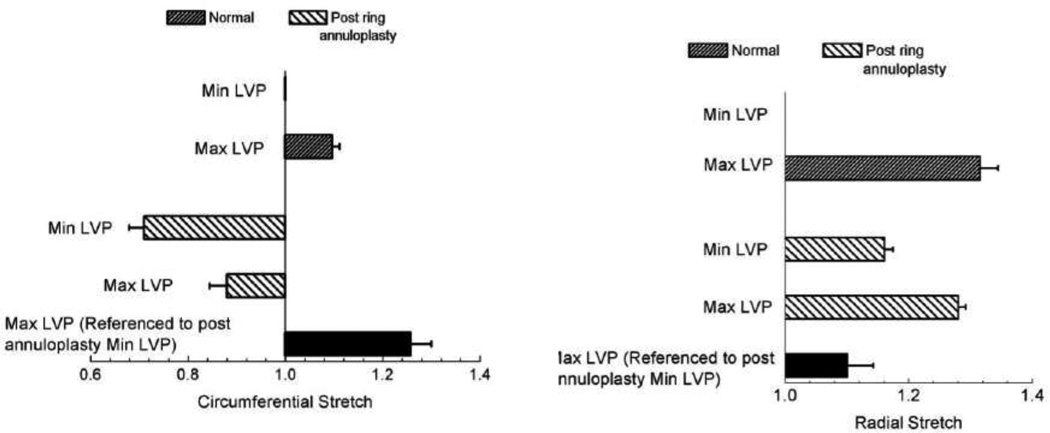
The p-values of the student t-test performed for the stretch values of the normal and post-ring annuloplasty valves are presented in Table 1. In the normal valves, the anterior leaflet stretch at the maximum LVP was significantly larger than 1.0 (the minimum LVP referential value). The maximum LVP stretch was larger in the radial direction (1.31 ± 0.03 (mean ± standard error)) than the circumferential direction (1.10 ± 0.01). Restricting the annulus by suturing flat annuloplasty rings to the valves caused a significant change in the stretch at the minimum LVP. As shown in Fig. 6, the circumferential stretch dropped to 0.72 ± 0.03 whereas the radial stretch increased to 1.16 ± 0.01.
Table 1.
Statistical analysis of in-vivo stretch data in the normal and post ring annuloplasty cases. The null hypotheses correspond to differences highlighted by roman numbers in a typical experiment shown in Fig. 5. p values were obtained from double-sided paired student t-test (n = 6).
| p value | |||
|---|---|---|---|
| Null hypothesis | Radial direction |
Circumferential direction |
|
| I. | In the normal valves, the stretch at max LVP is the same as the stretch at minimum LVP | < 0.05 | < 0.05 |
| II. | Restricting the annulus does not change the minimum LVP stretch. | <0.05 | <0.05 |
| III. | Restricting the annulus does not change the maximum LVP stretch. | 0.67 | <0.05 |
| IV. | The stretch at max LVP is the same as the stretch at minimum LVP when the annulus is geometrically restricted | <0.05 | 0.06 |
Figure 6.
Stretches in the circumferential and radial directions in the normal and annulus-restricted valves at the minimum and maximum functioning left ventricular pressures (LVP). Error bars are standard errors (n = 6).
Following annulus restriction, the stretch at maximum LVP was still less than 1.0 (0.89 ± 0.04) in the circumferential direction. Therefore, the valve was under negative strain in the circumferential direction during the entire cardiac cycle. Had the stretches at the restricted-annulus maximum LVP been calculated in reference to the restricted-annulus minimum LVP configuration of the four crystals, the predicted values of the stretch would have been incorrect. In particular, a smaller value of elongation would have been predicted in the radial direction (shown with a solid bar in Fig. 6). In the circumferential direction, we would have incorrectly concluded that the tissue had been under extension (shown with a solid bar in Fig. 6). Following annulus restriction, the maximum shear angle slightly dropped to 8.4 ± 2.4 degrees. The annulus-restriction-induced changes in the shear angle were not statistically significant (p value = 0.5).
Changes in referential configuration
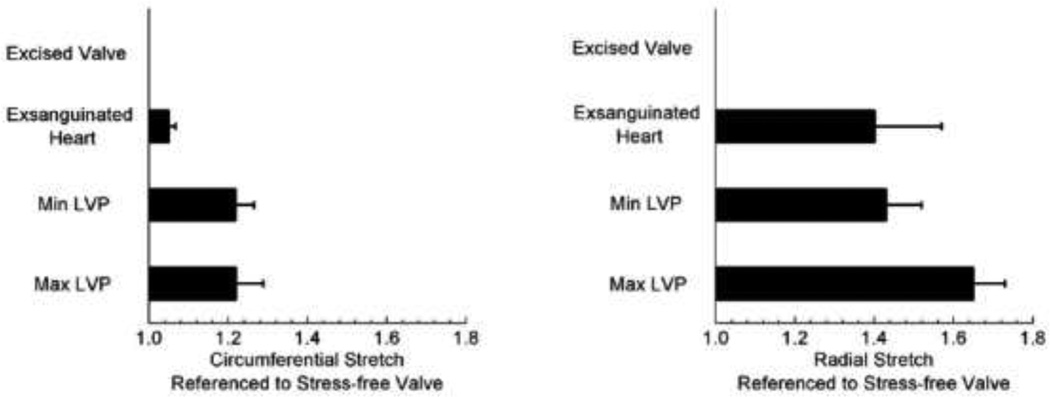
In both circumferential and radial directions, the stretch values were larger when referenced to stress-free state (Fig. 7). In comparison to stress-free state, a normal functioning valve at the minimum LVP is stretched 21% and 41% in the circumferential and radial directions, respectively. Using the stress-free state as the reference, the calculated stretches at the maximum LVP were 1.22 ± 0.07 and 1.65 ± 0.08 in the circumferential and radial directions, respectively. These values were significantly different from those referenced to the minimum LVP discussed above (1.10 ± 0.01 in the circumferential direction and 1.31 ± 0.03 in the radial direction). Therefore, the choice of referential frame has a profound effect on the calculated in-vivo strains. This effect reported for the first time in this study, demonstrates that the normal functional valve is under residual strain/stress.
Figure 7.
Stretches in the circumferential and radial directions in the normal valve referenced to stress-free (excised valve) crystal configurations. Error bars are standard errors (n = 4).
DISCUSSION
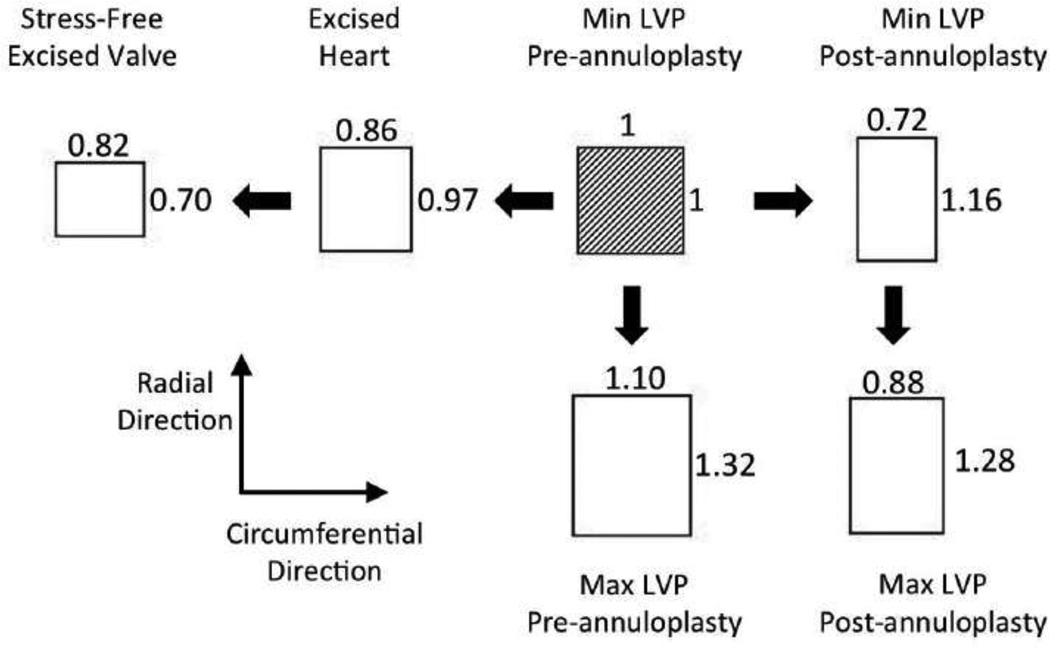
Overall, geometrical changes in the MV annulus could alter MV functional stresses and thus are an etiological factor in modulating long-term durability. In the present study, we demonstrated that a single unit tissue element at the center of the anterior leaflet midsection at minimum LVP underwent dramatic changes during a normal cardiac cycle, after geometrical/physical restriction of the annulus, upon exsanguination, and further upon valve excision (Fig. 8). The magnitude of the residual strains observed in mitral valve is comparable to those observed in the porcine aortic valves following layer separation (61). In particular, following layer separation, the fibrosa underwent 28.2% and 4.8% extension in the circumferential and radial directions, respectively. The ventricularis, contracted 10.9% and 8.2% in circumferential and radial directions, respectively. Although in the current study we did not separate the different layers of MVAL, following MV resection, we observed 10.7% and 29.0% contraction in the circumferential and radial directions, respectively.
Figure 8.
Schematic of a single unit square element at the anterior leaflet midsection at minimum LVP undergoing average values of stretches shown in Fig. 6 and 7.
An important finding of this study was the dramatic changes in the leaflet in vivo strains observed following annular flattening. It has been shown that mitral annuli are saddle shaped (24,30,31,39), and thus suturing a flat ring on the annulus of a normal valve would alter its normal physiological shape. For example, in-vivo measurements have shown that both septal-lateral and commissure-to-commissure dimensions change following annular restriction via flat ring annuloplasty (4). Echocardiographical studies have also shown that both in human (42,43) and ovine (54) subjects, the geometry of the annulus changes following ring annuloplasty. Therefore, ring annuloplasty was chosen in this study as an example of surgically induced geometric/physical restriction in the MV annulus. Yet, neither of these studies has addressed the in-vivo effects. A recent study (3) conducted on ovine valves following annuloplasty with numerous types of rings has shown that the range functional strain changes post annuloplasty. However, since minimum LVP of the normal valve was used for strain calculation of the normal valve and minimum LVP of the post-annuloplasty valve was used for its strain calculation, the direct comparison of the two cases was rendered impossible. Using our in-vivo sonomicrometry positional data we demonstrated that the MVAL leaflet underwent completely different functional strains following annular restriction. In our strain calculations, we used the same referential configuration for strain calculation in both normal and post-annuloplasty ring and consequently we were able to observe the direct effect of annular restriction on the functioning valvular strains.
Previously, using in-vitro models (29,47), we demonstrated that both in the anterior and posterior leaflets, the systolic strains in the midsection region were larger when a flat annulus apparatus was used in comparison to a saddle-shaped annulus. Although there exist a qualitative similarity between the in-vitro and in-vivo measurement, the exact strain values are not similar. Using two different subject species (ovine versus porcine) could have contributed to the lack of quantitative similarities. Another important reason for the lack of similarity is the different choices of referential frames in the in-vivo and in-vitro studies. In the current in-vivo study, we chose the minimum LVP of the normal valve as the referential configuration for the both normal and annulus restricted valves. In the in vitro study, however, the minimum LVP of each case was used as its own strain referential frame. Therefore, the differences between the peak strains were reported relative to multiple referential frames. Finally, in the in-vitro study, the valve was excised first and then mounted on the experimental apparatus. Therefore the leaflet configuration could have changed due to excision and mounting manipulation. Consequently, the in-vitro minimum LVP referential configuration was not necessarily similar to either in-vivo minimum LVP or ex-vivo stress-free referential configurations. Therefore, the qualitative comparison between the in-vivo and in-vitro studies is rendered impossible. In our previous studies (56), we showed that in the midsection of normal ovine MV anterior leaflets, at maximum LVP of 150 mmHg, the in-vivo circumferential and radial strains were ~2.5% and ~22%, respectively. In our current work, we showed that the circumferential and radial stretches were 1.10 ± 0.01 and 1.31 ± 0.03, respectively. Therefore the strains were ~8% and ~21% in the circumferential and radial directions, respectively.
Importance of strain calculation referential frame and the existence of residual stresses
In this study, for the first time, we showed that mitral valve tissues are under residual strains in vivo. As a result, even at minimum LVP, when the functioning valvular stretch is minimized, a normal valve is under residual functioning stresses. One may postulate that, similar to the aortic valve (61), the highly oriented elastin networks in the MV atrialis and ventricularis layers may contribute to residual function stresses and modulate the valve deformation under low pressures. The functioning state of stress is closely related to tissue homeostasis and maintaining of the extracellular integrity (6,70). Accounting for the residual stresses are important as they produce a more efficient load-bearing structure in the presence of functioning stress gradients in the biological tissues (9,11). Further, different levels of homeostatic residual stresses have been considered closely related to tissues growth and remodeling (53,64,65).
Quantification of the strains in reference to stress-free state is also critical to calculate functional in-vivo stresses either via experimental methods or from computational models (16,17,50). In particular, the mechanical properties of the MV are generally obtained from conventional mechanical testing protocols such biaxial (25,40,44) and uniaxial (2,50) tests, in which the stress-free state is generally used for the strain calculation. It is important to be consistent in utilizing the same stress-free reference frame for both mechanical tests and in-vivo stress calculation; otherwise the stress prediction would be incorrect. In the porcine mitral valves, it has been shown that the annular length of an intact valve is shorter than that of an excised valve suggesting a circumferential elongation following resection (36). In the anterior leaflet midsection, however, we observed circumferential and radial contraction following resection. The difference between the annular and belly regions is noteworthy specially in generating finite element models of the MV.
Study limitations
Due to anatomical space limitations, we were able to suture only four sonocrystals on the midsection of the MVAL. Although we stated that the principal values and directions of the stretches were relatively uniform in the midsection region, one should note that using only four position markers limited us to a bi-linear strain variation within the element region (38). We have shown previously (56) using nine position markers located at the same area produced reasonably homogenous strain results over most of the area. Rausch et al. (52) have also confirmed this observation using larger number of position makers. Note too that the use of a 2×2 array greatly simplifies the experimental procedures.
One may also suspect that the MVAL may fold following ring annuloplasty and the bilinear element utilized in this study may falsely calculate a negative strain as the curvature increases. To address this issue, we performed a follow-up study wherein a single crystal was added at the geometric center of the four nodes on the midsection region (i.e. at the origin of the coordinate system in Fig. 1). We calculated the distance from this additional crystal to a plane passing through crystals 6–9. In the normal valve, at minimum LVP pressure, the distance was ~0.95 mm. After performing ring-annuloplasty, at minimum LVP pressure, the distance decreased to ~0.50 mm. Following annuloplasty, had the curvature increased without any planar strain, we would have observed a substantial increase in the distance of the additional crystal from the plane that passes through crystals 6–9. Based on the results of this pilot study, we concluded that the changes in the curvature due to the application of ring annuloplasty were small over the region delimited by the sonocrystals 6–9, and that we are reporting true tissue strains.
Following annular restriction, the strains change over the entire leaflet and not just the midsection. In a normal MV, for example, the annulus dilates and twists over the full cardiac cycle (15). The annulus is, however, completely restricted from dilation or torsion as it is directly connected to the flat ring. The focus of this study was the MVAL midsection region and we did not measure the strain changes at the proximity of the MV annulus following the annulus restriction. In interpreting our results, one should also note that that while our specific results were obtained using an ovine model, general trends are likely to be similar in humans.
Long-term implications on MV function
Increasing or decreasing the tissue strain due to annulus restriction changes the underlying extracellular matrix architecture under valvular functional loading. As discussed in the introduction section, altered (and potentially deleterious) loading may induce structural changes that could affect long-term valve durability. Currently, the most important objective sought in using annuloplasty rings is regaining the valvular normal hemodynamical functions (7). Although an annuloplasty ring chosen by an experienced surgeons with the right size, may well regain the normal coaptation and, at least in the short time, treat mitral valve regurgitation (7), it may dramatically deviate the leaflet from its normal physiological loading. Such changes may affect the tissue homeostasis and lead to remodeling of the ECM (45) that could limit the longterm durability. An ongoing effort has been dedicated to the design of repair procedures that, in addition to regaining the valvular normal hemodynamical functions, could also mimic the physiological shape of the annulus (8). Preliminary estimations have shown that the non-planar shape of the annulus could be advantageous in reducing the valvular stress as well (59). Further investigation is necessary to explore in more details how profound the effect of annular restriction is on the in-vivo stresses and how the stress changes would lead to leaflet remodeling and/or degeneration.
Summary
In this study we demonstrated for the first time that in-vivo functional strains of the MVAL are profoundly following changes in annular geometry induced by a flat annuloplasty ring, including substantial compression in the circumferential direction. We also demonstrated that the MVAL functions under physiological residual strains/stresses. Such dramatic alteration of the in-vivo functional strains may lead to significant changes in the functional stresses, which in-turn affect the constituent MV interstitial cellular population and collagen/elastin fiber stresses. We suggest that MV stress alteration, induced by geometrically restricting the annulus, may lead to cellular and/or microstructural responses that would affect the long-term valvular durability.
Acknowledgements
This research project was supported in part by grants from the National Heart, Lung and Blood Institute of the National Institute of Health, grant numbers F32HL110651, HL63954, and HL73021. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung and Blood Institute of the National Institute of Health. R. Gorman and J. Gorman are supported by individual Established Investigator Awards from the American Heart Association, Dallas, TX. The help from Christopher Caruthers is much appreciated.
References
- 1.Adams DH, Rosenhek R, Falk V. Degenerative mitral valve regurgitation: best practice revolution. Eur Heart J. 2010;31(16):1958–1966. doi: 10.1093/eurheartj/ehq222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Barber JE, Kasper FK, Ratliff NB, Cosgrove DM, Griffin BP, Vesely I. Mechanical properties of myxomatous mitral valves. The Journal of thoracic and cardiovascular surgery. 2001;122(5):955–962. doi: 10.1067/mtc.2001.117621. [DOI] [PubMed] [Google Scholar]
- 3.Bothe W, Kuhl E, Kvitting JP, Rausch MK, Goktepe S, Swanson JC, Farahmandnia S, Ingels NB, Jr, Miller DC. Rigid, complete annuloplasty rings increase anterior mitral leaflet strains in the normal beating ovine heart. Circulation. 2011;124(11 Suppl):S81–S96. doi: 10.1161/CIRCULATIONAHA.110.011163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bothe W, Kvitting JP, Swanson JC, Hartnett S, Ingels NB, Jr, Miller DC. Effects of different annuloplasty rings on anterior mitral leaflet dimensions. J Thorac Cardiovasc Surg. 2010;139(5):1114–1122. doi: 10.1016/j.jtcvs.2009.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Braunberger E, Deloche A, Berrebi A, Abdallah F, Celestin JA, Meimoun P, Chatellier G, Chauvaud S, Fabiani JN, Carpentier A. Very long-term results (more than 20 years) of valve repair with carpentier's techniques in nonrheumatic mitral valve insufficiency. Circulation. 2001;104(12) Suppl 1:I8–I11. [PubMed] [Google Scholar]
- 6.Camp RJ, Liles M, Beale J, Saeidi N, Flynn BP, Moore E, Murthy SK, Ruberti JW. Molecular mechanochemistry: low force switch slows enzymatic cleavage of human type I collagen monomer. Journal of the American Chemical Society. 2011;133(11):4073–4078. doi: 10.1021/ja110098b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Carpentier A. Cardiac valve surgery--the "French correction". J Thorac Cardiovasc Surg. 1983;86(3):323–337. [PubMed] [Google Scholar]
- 8.Carpentier AF, Lessana A, Relland JY, Belli E, Mihaileanu S, Berrebi AJ, Palsky E, Loulmet DF. The "physio-ring": an advanced concept in mitral valve annuloplasty. Ann Thorac Surg. 1995;60(5):1177–1185. doi: 10.1016/0003-4975(95)00753-8. discussion 1185-6. [DOI] [PubMed] [Google Scholar]
- 9.Chuong CJ, Fung YC. On Residual Stress in Arteries. Journal of Biomechanical Engineering. 1986;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- 10.Chuong CJ, Fung YC. On residual stresses in arteries. Journal of Biomechanical Engineering. 1986 May;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- 11.Chuong CJ, Fung YC. Residual Stress in Arteries. In: Schmid-Schonbein G, Woo SLY, Zweifach B, editors. Frontiers in Biomechanics. New York: Springer-Verlag; 1986. pp. 117–129. [Google Scholar]
- 12.Cohn LH, Couper GS, Aranki SF, Rizzo RJ, Kinchla NM, Collins JJ., Jr Long-term results of mitral valve reconstruction for regurgitation of the myxomatous mitral valve. J Thorac Cardiovasc Surg. 1994;107(1):143–150. discussion 150-1. [PubMed] [Google Scholar]
- 13.David TE, Armstrong S, Sun Z, Daniel L. Late results of mitral valve repair for mitral regurgitation due to degenerative disease. Ann Thorac Surg. 1993;56(1):7–12. doi: 10.1016/0003-4975(93)90396-y. discussion 13-4. [DOI] [PubMed] [Google Scholar]
- 14.Duplessis LA, Marchand P. The Anatomy of the Mitral Valve and Its Associated Structures. Thorax. 1964;19:221–227. doi: 10.1136/thx.19.3.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eckert CE, Zubiate B, Vergnat M, Gorman JH, 3rd, Gorman RC, Sacks MS. In vivo dynamic deformation of the mitral valve annulus. Ann Biomed Eng. 2009;37(9):1757–1771. doi: 10.1007/s10439-009-9749-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Einstein DR, Del Pin F, Jiao X, Kuprat AP, Carson JP, Kunzelman KS, Cochran RP, Guccione JM, Ratcliffe MB. Fluid-Structure Interactions of the Mitral Valve and Left Heart: Comprehensive Strategies, Past, Present and Future. International journal for numerical methods in engineering. 2010;26(3–4):348–380. doi: 10.1002/cnm.1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Einstein DR, Reinhall P, Nicosia M, Cochran RP, Kunzelman K. Dynamic finite element implementation of nonlinear, anisotropic hyperelastic biological membranes. Comput Methods Biomech Biomed Engin. 2003;6(1):33–44. doi: 10.1080/1025584021000048983. [DOI] [PubMed] [Google Scholar]
- 18.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York: Springer Verlag; 1993. [Google Scholar]
- 19.Fung YC. What are the residual stresses doing in our blood vessels? Ann Biomed Eng. 1991;19(3):237–249. doi: 10.1007/BF02584301. [DOI] [PubMed] [Google Scholar]
- 20.Fung YC, Liu SQ. Changes of zero-stress state of rat pulmonary arteries in hypoxic hypertension. J Appl Physiol. 1991;70(6):2455–2470. doi: 10.1152/jappl.1991.70.6.2455. [DOI] [PubMed] [Google Scholar]
- 21.Gillinov AM, Blackstone EH, White J, Howard M, Ahkrass R, Marullo A, Cosgrove DM. Durability of combined aortic and mitral valve repair. Ann Thorac Surg. 2001;72(1):20–27. doi: 10.1016/s0003-4975(01)02677-7. [DOI] [PubMed] [Google Scholar]
- 22.Gillinov AM, Cosgrove DM, Blackstone EH, Diaz R, Arnold JH, Lytle BW, Smedira NG, Sabik JF, McCarthy PM, Loop FD. Durability of mitral valve repair for degenerative disease. J Thorac Cardiovasc Surg. 1998;116(5):734–743. doi: 10.1016/S0022-5223(98)00450-4. [DOI] [PubMed] [Google Scholar]
- 23.Goldsmith IR, Lip GY, Patel RL. A prospective study of changes in the quality of life of patients following mitral valve repair and replacement. Eur J Cardiothorac Surg. 2001;20(5):949–955. doi: 10.1016/s1010-7940(01)00952-6. [DOI] [PubMed] [Google Scholar]
- 24.Gorman JH, 3rd, Gupta KB, Streicher JT, Gorman RC, Jackson BM, Ratcliffe MB, Bogen DK, Edmunds LH., Jr Dynamic three-dimensional imaging of the mitral valve and left ventricle by rapid sonomicrometry array localization. J Thorac Cardiovasc Surg. 1996;112(3):712–726. doi: 10.1016/S0022-5223(96)70056-9. [DOI] [PubMed] [Google Scholar]
- 25.Grashow JS, Yoganathan AP, Sacks MS. Biaixal stress-stretch behavior of the mitral valve anterior leaflet at physiologic strain rates. Ann Biomed Eng. 2006;34(2):315–325. doi: 10.1007/s10439-005-9027-y. [DOI] [PubMed] [Google Scholar]
- 26.Hashima AR, Young AA, McCulloch AD, Waldman LK. Nonhomogeneous Analysis of Epicardial Strain Distributions During Acute Myocardial Ischemia in the Dog. Journal of Biomechanics. 1993;26:19–35. doi: 10.1016/0021-9290(93)90610-q. [DOI] [PubMed] [Google Scholar]
- 27.He Z, Ritchie J, Grashow JS, Sacks MS, Yoganathan AP. In vitro dynamic strain behavior of the mitral valve posterior leaflet. J Biomech Eng. 2005;127(3):504–511. doi: 10.1115/1.1894385. [DOI] [PubMed] [Google Scholar]
- 28.Itoh A, Krishnamurthy G, Swanson JC, Ennis DB, Bothe W, Kuhl E, Karlsson M, Davis LR, Miller DC, Ingels NB., Jr Active stiffening of mitral valve leaflets in the beating heart. Am J Physiol Heart Circ Physiol. 2009;296(6):H1766–H1773. doi: 10.1152/ajpheart.00120.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jimenez JH, Liou SW, Padala M, He Z, Sacks M, Gorman RC, Gorman JH, 3rd, Yoganathan AP. A saddle-shaped annulus reduces systolic strain on the central region of the mitral valve anterior leaflet. J Thorac Cardiovasc Surg. 2007;134(6):1562–1568. doi: 10.1016/j.jtcvs.2007.08.037. [DOI] [PubMed] [Google Scholar]
- 30.Kaplan SR, Bashein G, Sheehan FH, Legget ME, Munt B, Li XN, Sivarajan M, Bolson EL, Zeppa M, Arch MZ, Martin RW. Three-dimensional echocardiographic assessment of annular shape changes in the normal and regurgitant mitral valve. Am Heart J. 2000;139(3):378–387. doi: 10.1016/s0002-8703(00)90077-2. [DOI] [PubMed] [Google Scholar]
- 31.Komeda M, Glasson JR, Bolger AF, Daughters GT, 2nd, MacIsaac A, Oesterle SN, Ingels NB, Jr, Miller DC. Geometric determinants of ischemic mitral regurgitation. Circulation. 1997;96(9 Suppl):II-128–II-133. [PubMed] [Google Scholar]
- 32.Krishnamurthy G, Ennis DB, Itoh A, Bothe W, Swanson JC, Karlsson M, Kuhl E, Miller DC, Ingels NB., Jr Material properties of the ovine mitral valve anterior leaflet in vivo from inverse finite element analysis. Am J Physiol Heart Circ Physiol. 2008;295(3):H1141–H1149. doi: 10.1152/ajpheart.00284.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Krishnamurthy G, Itoh A, Bothe W, Swanson JC, Kuhl E, Karlsson M, Craig Miller D, Ingels NB., Jr Stress-strain behavior of mitral valve leaflets in the beating ovine heart. J Biomech. 2009;42(12):1909–1916. doi: 10.1016/j.jbiomech.2009.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Krishnamurthy G, Itoh A, Swanson JC, Bothe W, Karlsson M, Kuhl E, Craig Miller D, Ingels NB., Jr Regional stiffening of the mitral valve anterior leaflet in the beating ovine heart. J Biomech. 2009;42(16):2697–2701. doi: 10.1016/j.jbiomech.2009.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Krishnamurthy G, Itoh A, Swanson JC, Miller DC, Ingels NB., Jr Transient stiffening of mitral valve leaflets in the beating heart. Am J Physiol Heart Circ Physiol. 2010;298(6):H2221–H2225. doi: 10.1152/ajpheart.00215.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kunzelman KS, Cochran RP, Verrier ED, Eberhart RC. Anatomic basis for mitral valve modelling. The Journal of heart valve disease. 1994;3(5):491–496. [PubMed] [Google Scholar]
- 37.Kunzelman KS, Quick DW, Cochran RP. Altered collagen concentration in mitral valve leaflets: biochemical and finite element analysis. Ann Thorac Surg. 1998;66(6 Suppl):S198–S205. doi: 10.1016/s0003-4975(98)01106-0. [DOI] [PubMed] [Google Scholar]
- 38.Kvitting JP, Bothe W, Goktepe S, Rausch MK, Swanson JC, Kuhl E, Ingels NB, Jr, Miller DC. Anterior Mitral Leaflet Curvature During the Cardiac Cycle in the Normal Ovine Heart. Circulation. 2010 doi: 10.1161/CIRCULATIONAHA.110.961243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Levine RA, Handschumacher MD, Sanfilippo AJ, Hagege AA, Harrigan P, Marshall JE, Weyman AE. Three-dimensional echocardiographic reconstruction of the mitral valve, with implications for the diagnosis of mitral valve prolapse. Circulation. 1989;80(3):589–598. doi: 10.1161/01.cir.80.3.589. [DOI] [PubMed] [Google Scholar]
- 40.Liao J, Yang L, Grashow J, Sacks MS. The relation between collagen fibril kinematics and mechanical properties in the mitral valve anterior leaflet. J Biomech Eng. 2007;129(1):78–87. doi: 10.1115/1.2401186. [DOI] [PubMed] [Google Scholar]
- 41.Liu SQ, Fung YC. Relationship between hypertension, hypertrophy, and opening angle of zero-stress state of arteries following aortic constriction. J Biomech Eng. 1989;111(4):325–335. doi: 10.1115/1.3168386. [DOI] [PubMed] [Google Scholar]
- 42.Mahmood F, Gorman JH, 3rd, Subramaniam B, Gorman RC, Panzica PJ, Hagberg RC, Lerner AB, Hess PE, Maslow A, Khabbaz KR. Changes in mitral valve annular geometry after repair: saddle-shaped versus flat annuloplasty rings. Ann Thorac Surg. 2010;90(4):1212–1220. doi: 10.1016/j.athoracsur.2010.03.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mahmood F, Subramaniam B, Gorman JH, 3rd, Levine RM, Gorman RC, Maslow A, Panzica PJ, Hagberg RM, Karthik S, Khabbaz KR. Three-dimensional echocardiographic assessment of changes in mitral valve geometry after valve repair. Ann Thorac Surg. 2009;88(6):1838–1844. doi: 10.1016/j.athoracsur.2009.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.May-Newman K, Yin FC. Biaxial mechanical behavior of excised porcine mitral valve leaflets. Am J Physiol. 1995;269(4 Pt 2):H1319–H1327. doi: 10.1152/ajpheart.1995.269.4.H1319. [DOI] [PubMed] [Google Scholar]
- 45.Merryman WD, Youn I, Lukoff HD, Krueger PM, Guilak F, Hopkins RA, Sacks MS. Correlation between heart valve interstitial cell stiffness and transvalvular pressure: implications for collagen biosynthesis. Am J Physiol Heart Circ Physiol. 2006;290(1):H224–H231. doi: 10.1152/ajpheart.00521.2005. [DOI] [PubMed] [Google Scholar]
- 46.Nowicki ER, Weintraub RW, Birkmeyer NJ, Sanders JH, Dacey LJ, Lahey SJ, Leavitt B, Clough RA, Quinn RD, O'Connor G T. Mitral valve repair and replacement in northern New England. Am Heart J. 2003;145(6):1058–1062. doi: 10.1016/S0002-8703(02)94721-6. [DOI] [PubMed] [Google Scholar]
- 47.Padala M, Hutchison RA, Croft LR, Jimenez JH, Gorman RC, Gorman JH, 3rd, Sacks MS, Yoganathan AP. Saddle shape of the mitral annulus reduces systolic strains on the P2 segment of the posterior mitral leaflet. Ann Thorac Surg. 2009;88(5):1499–1504. doi: 10.1016/j.athoracsur.2009.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Padala M, Sacks MS, Liou SW, Balachandran K, He Z, Yoganathan AP. Mechanics of the mitral valve strut chordae insertion region. J Biomech Eng. 2010;132(8) doi: 10.1115/1.4001682. 081004. [DOI] [PubMed] [Google Scholar]
- 49.Perier P, Deloche A, Chauvaud S, Fabiani JN, Rossant P, Bessou JP, Relland J, Bourezak H, Gomez F, Blondeau P, et al. Comparative evaluation of mitral valve repair and replacement with Starr, Bjork, and porcine valve prostheses. Circulation. 1984;70(3 Pt 2):I187–I192. [PubMed] [Google Scholar]
- 50.Prot V, Skallerud B, Sommer G, Holzapfel GA. On modelling and analysis of healthy and pathological human mitral valves: two case studies. Journal of the mechanical behavior of biomedical materials. 2010;3(2):167–177. doi: 10.1016/j.jmbbm.2009.05.004. [DOI] [PubMed] [Google Scholar]
- 51.Quick DW, Kunzelman KS, Kneebone JM, Cochran RP. Collagen synthesis is upregulated in mitral valves subjected to altered stress. Asaio J. 1997;43(3):181–186. [PubMed] [Google Scholar]
- 52.Rausch MK, Bothe W, Kvitting JP, Goktepe S, Miller DC, Kuhl E. In vivo dynamic strains of the ovine anterior mitral valve leaflet. Journal of Biomechanics. 2011;44(6):1149–1157. doi: 10.1016/j.jbiomech.2011.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Rodriguez EK, Hoger A, McCulloch AD. Stress-dependent finite growth in soft elastic tissues. J Biomech. 1994;27(4):455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- 54.Ryan LP, Jackson BM, Hamamoto H, Eperjesi TJ, Plappert TJ, St John-Sutton M, Gorman RC, Gorman JH., 3rd The influence of annuloplasty ring geometry on mitral leaflet curvature. Ann Thorac Surg. 2008;86(3):749–760. doi: 10.1016/j.athoracsur.2008.03.079. discussion 749-60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sacks MS, David Merryman W, Schmidt DE. On the biomechanics of heart valve function. J Biomech. 2009;42(12):1804–1824. doi: 10.1016/j.jbiomech.2009.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sacks MS, Enomoto Y, Graybill JR, Merryman WD, Zeeshan A, Yoganathan AP, Levy RJ, Gorman RC, Gorman JH., 3rd In-vivo dynamic deformation of the mitral valve anterior leaflet. Ann Thorac Surg. 2006;82(4):1369–1377. doi: 10.1016/j.athoracsur.2006.03.117. [DOI] [PubMed] [Google Scholar]
- 57.Sacks MS, Hamamoto H, Connolly JM, Gorman RC, Gorman JH, 3rd, Levy RJ. In vivo biomechanical assessment of triglycidylamine crosslinked pericardium. Biomaterials. 2007;28(35):5390–5398. doi: 10.1016/j.biomaterials.2007.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sacks MS, He Z, Baijens L, Wanant S, Shah P, Sugimoto H, Yoganathan AP. Surface strains in the anterior leaflet of the functioning mitral valve. Annals of Biomedical Engineering. 2002;30(10):1281–1290. doi: 10.1114/1.1529194. [DOI] [PubMed] [Google Scholar]
- 59.Salgo IS, Gorman JH, 3rd, Gorman RC, Jackson BM, Bowen FW, Plappert T, St John Sutton MG, Edmunds LH., Jr Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106(6):711–717. doi: 10.1161/01.cir.0000025426.39426.83. [DOI] [PubMed] [Google Scholar]
- 60.Smith DB, Sacks MS, Vorp DA, Thornton M. Surface geometric analysis of anatomic structures using biquintic finite element interpolation. Ann Biomed Eng. 2000;28(6):598–611. doi: 10.1114/1.1306342. [DOI] [PubMed] [Google Scholar]
- 61.Stella JA, Sacks MS. On the biaxial mechanical properties of the layers of the aortic valve leaflet. J Biomech Eng. 2007;129(5):757–766. doi: 10.1115/1.2768111. [DOI] [PubMed] [Google Scholar]
- 62.Stephens EH, Nguyen TC, Itoh A, Ingels NB, Jr, Miller DC, Grande-Allen KJ. The effects of mitral regurgitation alone are sufficient for leaflet remodeling. Circulation. 2008;118(14 Suppl):S243–S249. doi: 10.1161/CIRCULATIONAHA.107.757526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Stephens EH, Timek TA, Daughters GT, Kuo JJ, Patton AM, Baggett LS, Ingels NB, Miller DC, Grande-Allen KJ. Significant changes in mitral valve leaflet matrix composition and turnover with tachycardia-induced cardiomyopathy. Circulation. 2009;120(11 Suppl):S112–S119. doi: 10.1161/CIRCULATIONAHA.108.844159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Taber LA. Biomechanics of cardiovascular development. Annu Rev Biomed Eng. 2001;3:1–25. doi: 10.1146/annurev.bioeng.3.1.1. [DOI] [PubMed] [Google Scholar]
- 65.Taber LA, Humphrey JD. Stress-modulated growth, residual stress, and vascular heterogeneity. J Biomech Eng. 2001;123(6):528–535. doi: 10.1115/1.1412451. [DOI] [PubMed] [Google Scholar]
- 66.Vesely I, Lozon A, Talman E. Is zero-pressure fixation of bioprosthetic valves truly stress free? J Thorac Cardiovasc Surg. 1993;106(2):288–298. [PubMed] [Google Scholar]
- 67.Vesely I, Noseworthy R. Micromechanics of the fibrosa and the ventricularis in aortic valve leaflets. Journal of Biomechanics. 1992;25(1):101–113. doi: 10.1016/0021-9290(92)90249-z. [DOI] [PubMed] [Google Scholar]
- 68.Wognum S, Schmidt DE, Sacks MS. On the mechanical role of de novo synthesized elastin in the urinary bladder wall. J Biomech Eng. 2009;131(10) doi: 10.1115/1.4000182. 101018. [DOI] [PubMed] [Google Scholar]
- 69.Yacoub M, Halim M, Radley-Smith R, McKay R, Nijveld A, Towers M. Surgical treatment of mitral regurgitation caused by floppy valves: repair versus replacement. Circulation. 1981;64(2 Pt 2):II210–II216. [PubMed] [Google Scholar]
- 70.Zareian R, Church KP, Saeidi N, Flynn BP, Beale JW, Ruberti JW. Probing collagen/enzyme mechanochemistry in native tissue with dynamic, enzyme-induced creep. Langmuir : the ACS journal of surfaces and colloids. 2010;26(12):9917–9926. doi: 10.1021/la100384e. [DOI] [PMC free article] [PubMed] [Google Scholar]