Characterizing the elastic properties of tissues

Abstract

The quality of life of ageing populations is increasingly determined by age-related changes to the mechanical properties of numerous biological tissues. Degradation and mechanical failure of these tissues has a profound effect on human morbidity and mortality. Soft tissues have complex and intricate structures and, similar to engineering materials, their mechanical properties are controlled by their microstructure. Thus age-relate changes in mechanical behavior are determined by changes in the properties and relative quantities of microstructural tissue components. This review focuses on the cardiovascular system; it discusses the techniques used both in vivo and ex vivo to determine the age-related changes in the mechanical properties of arteries.

In ageing populations, both life expectancy and quality of life are increasingly influenced by adverse changes in the mechanical properties of soft tissues. Within dynamic tissues such as blood vessels, the heart and lungs, the properties of tensile strength and passive elastic recoil are conferred primarily by collagen fibrils and elastic fibers respectively. In contrast to intracellular proteins which are continuously replaced¹, extracellular matrix (ECM) proteins are remarkably long lived^2,3. Elastic fibers in the cardiopulmonary system, may be required to undergo > 10⁹ loading cycles during the average human lifetime⁴. The mechanical failure of these macromolecular assemblies and hence tissues, has a profound effect on human mortality and morbidity. This behavior has obvious parallels with the phenomena of fracture, fatigue and damage accumulation in engineering materials under static and dynamic loading.

In engineering materials mechanical properties are controlled by the microstructure. At the same structural scale in biological materials, the composition and architecture varies: (i) between tissue types, (ii) within individual tissues and crucially (iii) with chronological age and the development of disease. Specifically, in large blood vessels gross arterial stiffness, measured in vivo, increases (arteriosclerosis) both with age and with increased cardiovascular risk factors, including raised blood pressure, diabetes mellitus, and end-stage renal failure^5-9. As a consequence arteriosclerosis, as opposed to or often in conjunction with ‘atherosclerosis’ (referring to the lipid-core, pre-thrombotic, generally inflammatory process including underlying coronary or cerebral vessel occlusions), is thought to be closely linked to hypertension and hence to the development of heart and renal failure, stroke and aortic aneurysms^10-13. Collectively these cardiovascular disorders have a profound effect on human well-being and are the main non-communicable cause of death worldwide (World Health Statistics 2009, World Health Organisation).

Age-related changes in the mechanical properties of other tissues such as the lungs^14-16, may also be associated with increased mortality, however not all such changes are life threatening. The intervertebral disc for example, is a composite structure composed of an inner gelatinous core surrounded by aligned fibrillar sheets arranged in a plywood-like system¹⁷. Its degeneration is closely linked with the development of debilitating lower back pain^17,18, which in turn is the most commonly reported musculoskeletal disorder in adults¹⁹. Despite the immense clinical and economic burdens that result from these disorders, the molecular mechanisms underpinning tissue stiffening and degeneration remain poorly understood. This is because it is difficult to directly correlate age-related changes in structural and molecular tissue components to local changes in mechanical properties^20,21. We believe this is caused by the disparity between the length scale probed using traditional mechanical testing methods (10⁻³ – 10⁻¹ m) and that at which key biological tissue components are organized (10⁻⁶ – 10⁻⁴ m). However, new techniques such as nanoindentation, AFM and ultra high frequency acoustic imaging, dramatically reduce the length scale at which mechanical information can be resolved, leading to exciting new areas of research into how the specific components of microstructures of biological tissues influence their mechanical behavior.

Here, we survey the techniques used to characterize the mechanical properties of tissues and using examples taken from the cardiovascular system, examine how they can be employed to assess the influence of ageing on mechanical behavior.

Tissue structure and ageing

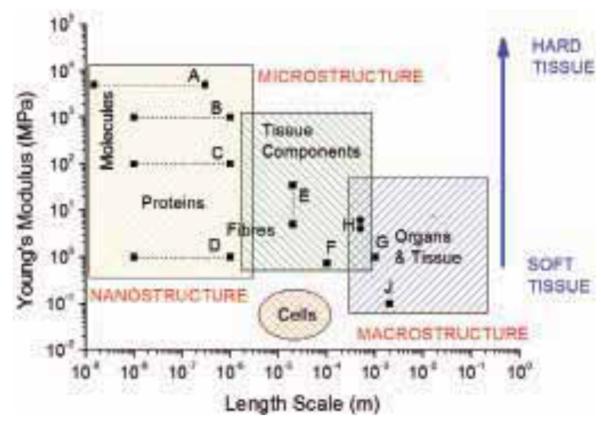
The Young’s modulus, E, of a typical soft tissue is very low compared to engineering materials (E ≈ 1 MPa). In humans and mammals mechanical behavior is controlled by a small number of ECM proteins (mainly, but not limited to, fibrillar proteins such as type I collagen, fibrillin and elastin). With the exception of elastin, these proteins, in their fibrillar form, are thought to be much stiffer than the tissue. There is a general trend for the elastic stiffness of tissue components to decrease as the structural scale of the unit increases. As illustrated in Fig. 1, it is clear that the Young’s modulus of protein fibers is much greater than that of tissue component assemblies, which in turn are significantly stiffer than the elastic properties of bulk tissue samples. The size and elastic property regimes for cells are also shown in Fig. 1 for comparison. To obtain a complete understanding of how age-related changes in tissue microstructure influence tissue mechanical properties, it is necessary to use techniques to measure these properties across the appropriate length scales for tissue and its components, illustrated in Fig. 2. For example, osteoarthritis, a degenerative joint disease that is prevalent amongst the elderly, occurs as a result of degeneration of articular cartilage. Stolz et al.³⁰ have demonstrated that in diseased tissue, the decline in cartilage structure begins at the molecular level and progresses to the higher levels of architecture, resulting in both structural and functional damage. However, the direct link between tissue degradation and mechanical property change for other types of tissues has not been made at each hierarchical level. It is likely that there are similar length scale related changes in other ageing tissues, however the nature and progression of these alterations remains to be determined.

Fig. 1.

Length scale and elastic properties of soft tissues and their structural components. Superimposed are measurements of the elastic moduli of aorta and ECM components at macroscopic, microscopic, and molecular length scales. A: single collagen fibrils²², B: fibrillar collagen²³, C: fibrilin microfibrils²⁴, D: elastin²³, E: ferret aorta components²⁵, F: porcine aorta components²⁶, G: human radial artery²⁷, H: rat aorta²⁸, J: human aorta²⁹.

Fig. 2.

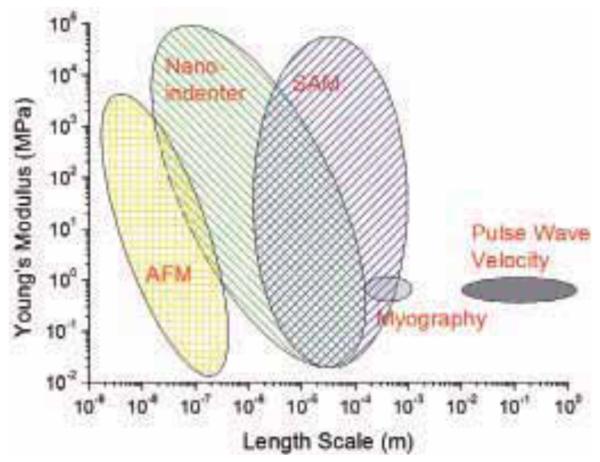
Schematic diagram illustrating the elastic modulus range and length scale of the typical spatial resolution attainable from a number of mechanical testing methods that have been successfully used with soft tissue samples.

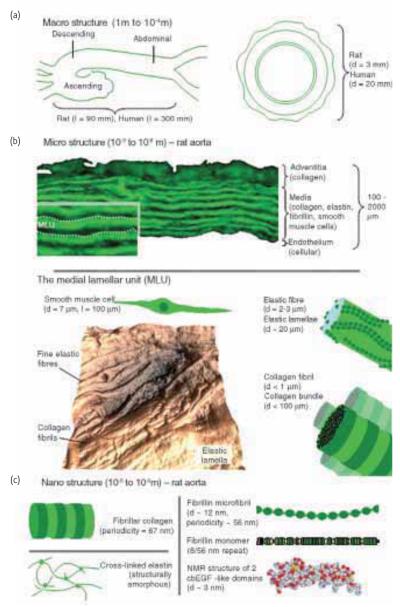
The aorta (Fig. 3) is a good example of the multi-layered organization of soft tissues. This major blood vessel is a composite structure comprised of three main components: collagen fibrils, elastic fibers and vascular smooth muscle cells. In the elastic fiber system, fibrillin microfibrils both direct elastin deposition and subsequently surround the highly compliant elastin matrix where they may act as a stiffer reinforcing phase for this composite fibrous structure²⁴. Collectively, these components are arranged into three concentric layers; intima, media and adventitia. The innermost layer, the intima, is composed of a thin layer of endothelial cells, with the outermost adventitial layer surrounded by loose connective tissue with thick collagen bundles. In terms of mechanical properties the central medial layer plays a crucial role³². In this region, the arterial wall components are organized into repeating medial lamellar units (MLU)³³. Each MLU is composed of elastic fiber lamellae between which are sandwiched collagen fibrils and smooth muscle cells as well as finer, inter-connecting elastin fibers (Fig. 4). The MLUs within the medial layer, store elastic energy under physiological loads to drive recoil back to the resting state, thus allowing these vessels to not only to accommodate high blood pressures but continue to drive ‘smoothed’ blood flow during cardiac relaxation (diastole).

Fig. 3.

Length-scale dependent architecture within the mammalian aorta. (a) At macroscopic length scales the aorta is organized longitudinally into three distinct sections, whilst transversely the vessel is divided into three distinct layers. (b) At the microstructural length scale the discrete architecture of the adventitial, medial and intimal layers is evident in an autofluorescent microscopy image of cryo-sectioned rat aorta. The medial layer, which dominates the structure of the aorta, is composed of alternating medial lamellar units (MLU: demarcated by dotted lines on inset). The MLU is shown in greater detail in Fig. 4. The complex and highly anisotropic organization of this region is evident in an AFM height image of a sheep aorta cryo-section collected using the method outlined by Graham et al.³¹. (c) Nanostructure of major ECM components. With the exception of elastin (which is amorphous), the major ECM assemblies including collagen fibrils and fibrillin microfibrils are organized into characteristic repeating structures. Fibrillin microfibrils are composed of folded monomers each of which is comprised primarily of calcium binding epidermal growth factor-like repeats. In common with many ECM proteins, the structure and hence function of fibrillin is dependent on post-translational modification with oligosaccharide side chains. In all Figs. d refers to diameter and l refers to length.

Fig. 4.

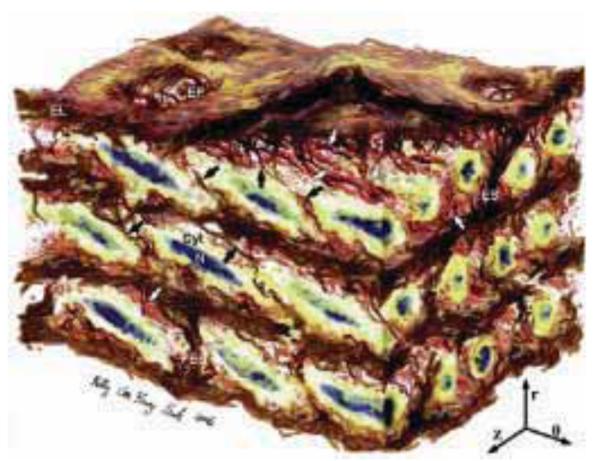
Artistic rendering of a medial lamellar unit (MLU) as presented by O’Connell et al.³³. The aortic media has a complex, interconnected structure. Elastin features include elastic lamellae (EL), a dense network of interlamellar elastin fibers (shown with black arrows), elastin struts (ES), and reinforced elastin pores (EP). Smooth Muscle Cells (SMC) are shown with their elliptical nuclei (N) oriented circumferentially with radial tilt, and cytoplasm (Cyt). Collagen is present as large and small fiber bundles (white arrows) adjacent to lamellar surfaces, arranged in layers of parallel bundles oriented predominantly circumferentially. Image dimensions (θ × Z × r) are 80 μm × 60 μm × 45 μm, with the lumen surface at the top (r indicates radial direction, z axial, and θ circumferential). Reproduced from³³ with permission from Elsevier.

Large elastic arteries such as the aorta progressively stiffen throughout life, yet the underlying mechanisms that lead to this change at each length scale of the tissue architecture remain poorly understood. It has been reported that the elastic lamellae undergo fatigue and become fragmented and disrupted with time,^32,34-36 although changes within the composition of the MLUs may also play a role³³. However, there is no consensus in the literature as to whether the concentration of collagen and elastin increases or remains unchanged in the ageing aorta^37,38. These conflicting observations are possibly related to the wide range of methodologies and tissue sources utilized by different groups⁴. For example, Cattell and co-workers³⁷ state the importance of differentiating between changes in the absolute amount of a tissue component versus changes in its concentration. Both ECM organisation⁴ and relative composition have to be considered to fully understand mechanical property changes in ageing vascular tissues. Further, fundamental differences in the ageing process in distinct species may explain some of the apparent contradictions in the literature³⁹.

Finally, the organization of the ECM⁴ is likely to play a key role in mediating the mechanical properties of tissues. In order therefore to relate structure to function in ageing tissues it is necessary to combine non-destructive ultrastructural imaging³¹ with the high spatial resolution mechanical testing methods that are discussed later. The importance of structure to biological function extends to the nanometer length scale, where molecular changes including aberrant glycation of collagen and elastin^40,41, have been proposed as drivers for age-related macroscopic stiffening.

Characterizing the mechanical properties of tissue

In cardiovascular medicine, two techniques are commonly used to measure the elastic properties of blood vessels: pulse wave velocity (PWV), which is used to estimate large artery stiffness in vivo, and pressure or wire myography, which uses sections of small blood vessels obtained through biopsy and is therefore an ex vivo method.

From a clinical perspective it is desirable to make diagnostic measurements on the patient in vivo, hence PWV is widely used despite its limitations. However, ex vivo methods allow more detailed investigation of both the physiological and mechanical behaviors of tissue. Clearly any technique that requires large biopsy samples is impractical because it leads to significant discomfort to the patient; hence ex vivo methods are limited to very small samples. These techniques are invaluable tools for clinicians as they provide a single parameter indicative of cardiovascular health e.g. a measure of arterial stiffness with PWV. PWV is supported by myography which provides ex vivo measurements that better characterize the pathology of disease and ageing. These methods are therefore advantageous for clinical researchers despite grossly simplifying the actual mechanics. They do not provide detailed mechanical properties or allow the individual constitutive properties of the tissue components to be precisely determined, and thereby the constitutive laws that govern the overall biomechanical response of the tissue are not directly revealed. There are a number of papers which deal with this important topic. For example, Holzapfel et al.⁴² characterized the anisotropic and non-linear mechanical behavior of arteries using numerical calculation and an elegant constitutive approach. Such work has been particularly important in the study of aortic aneurysms⁴³ but a detailed account is beyond the scope of this review.

In vivo measurements: pulse wave velocity

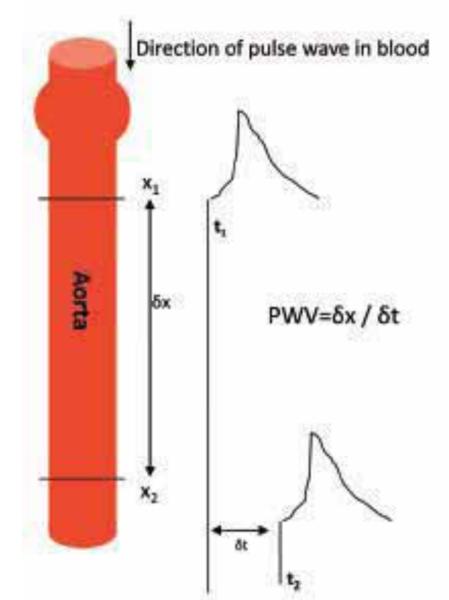
Although a number of techniques can be used to measure arterial stiffness non-invasively in humans⁴⁴, the most widespread index of arterial stiffness is aortic PWV, the speed at which the elastic distortion of the blood vessel wall propagates in response to the pressure pulse from the beating heart (Fig. 5). PWV is recognized by clinicians as a powerful predictor of cardiovascular events⁴⁵ and later mortality, independent of blood pressure and other risk factors. It is generally determined by recording the time (δt) taken for the wave to travel between two separate points (δx), thus PWV = δx/δt (Fig. 5).

Fig. 5.

Schematic demonstrating basis of PWV. As the pulse wave travels down the aorta, the time delay (t) of the two wave points (x₁ and x₂) is recorded. PWV = δx/δt.

PWV is related to vascular wall stiffness through the Moens-Korteweg equation, which in its simplest form is

$$\mathrm{PWV}=\sqrt{\frac{E_{a}h}{2\rho r}}$$ 1

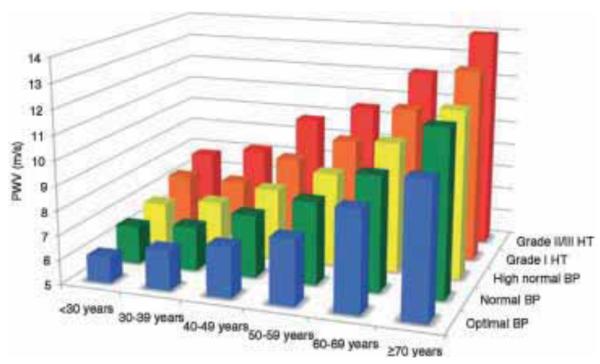
where E_a and h are respectively the mean Young’s modulus and thickness of the arterial wall. The lumen radius is given by r and ρ is the blood density. Modified versions of this equation account for thick-walled tubes as well as blood velocity⁴⁶. PWV measurements in humans are highly reproducible^47,48. PWV rises progressively with age in both diabetic and non-diabetic individuals and is negatively correlated with glucose tolerance⁸. PWV increases in the aorta^49,50 between the ages of 10 and 50 from 6.5 ms⁻¹ to 11 ms⁻¹ and more rapidly after age 45⁵¹. A carotid-femoral pulse wave velocity > 12 ms⁻¹ is considered an indicator of elevated cardiovascular risk⁵². Reference values for PWV as a function of age and blood pressure are shown in Fig. 6. Other techniques that measure arterial stiffness are not readily suitable for standard clinical use. However, PWV-based measurements are not only non-invasive but also simple and sufficiently repeatable to be considered as a routine diagnostic procedure⁴⁵.

Fig. 6.

Reference values for pulse wave velocity (PWV) published by Mattace-Raso et al.⁵³. Mean values for PWV according to age, blood pressure (BP) categories and hypertension (HT). Reproduced from⁵³ with permission from Oxford University Press.

From a materials science perspective, PWV appears to be a very crude method for the measurement of arterial wall elastic properties because of the large number of assumptions inherent in the Moens-Korteweg equation. This is especially the case as the distance δx is maximized in order to allow easier measurement of the time interval. Clinicians prefer this approach for PWV measurement, because using a large value of δx samples a large length or artery and returns a better “clinical average”. Increased PWV is recognized by the European Society of Hypertension as being a factor that influences prognosis as an early index of large artery stiffening⁵².

Tensile testing of aorta samples

Measurements in vivo of increasing arterial stiffness with age are supported by ex vivo mechanical tests using bulk sections of aorta. Vande Geest et al.⁵⁴ found a significant change in the biaxial biomechanical response of aged human abdominal aortic tissue (> 60 years) with loss of the high extensibility seen in youth (< 30 years). Using the same biaxial test setup, Haskett et al.⁵⁵ investigated the relationship between the anisotropic mechanical behavior and the microstructure of the human aorta, finding that the aorta becomes more mechanically and structurally anisotropic after 60 years, with changes occurring preferentially in the abdominal aorta, which is more prone to diseases such as aortic aneurysms. This is in agreement with other studies which have demonstrated that the mechanical properties of the aorta vary along its length with the thoracic aorta being stiffer than the abdominal aorta. The region of the abdominal aorta close to the diaphragm is stiffest^56,57 and a common site of aneurysms. Uniaxial tensile testing of aorta samples also found an increase in stiffness that correlates with changes to the ECM, for example due to diabetes²⁸ as well as in vitro glycation⁵⁸.

Mechanical testing of small arteries

PWV provides a clinical indication of large artery mechanical properties that may change with age or disease. However, even without large artery disease, restriction of blood flow at the microvascular level⁴⁸ is associated with considerable increases in morbidity and mortality. There is debate as to whether the disease process begins in small or large vessels or occurs increasingly in both⁴⁸. Small resistance arterioles with internal diameter < 1 mm can be excised from biopsy samples for diagnosis. Resistance vessels control their lumen diameter by pressure-dependent contraction or relaxation and contribute to precapillary resistance. Their role is to ensure that each capillary is provided with blood of the correct amount and pressure⁵⁹. Mechanical property measurements on small resistance arteries are becoming increasingly important, with growing evidence that structural alterations at the microvascular level may be linked to overall prognosis in hypertension and related diseases^60,61.

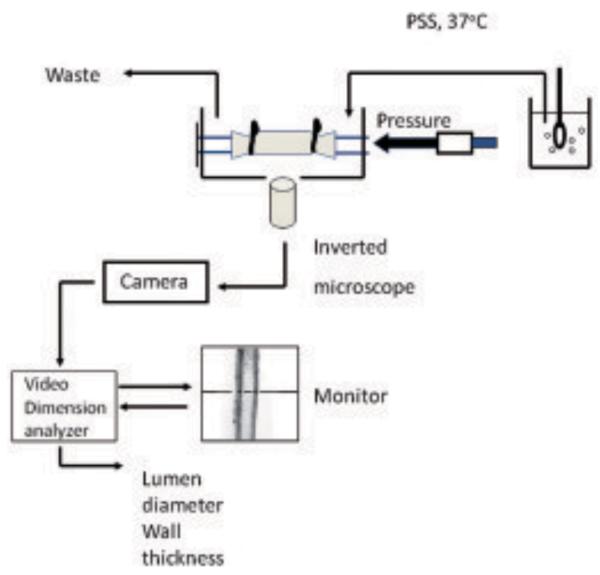
Techniques collectively termed myography have been applied to small resistance arteries over several decades and allow the contractility of these small blood vessels to be measured after agonist stimulation. An early method, wire myography, was developed by Bevan and Osher⁶² where rings of 200 μm diameter vessels were threaded on two fine wires, with wires on each end being clamped to ensure an isometric response. The wires are used to apply tensile loads to the small artery walls during testing. Myographic methods have become increasingly sophisticated since then⁵⁹, including pressure myography where the intralumen pressure is controlled by cannulating the vessel, and thereby allowing pressure/lumen relationships to be determined (Fig. 7). Incremental distensibility is determined as the percentage change of the arterial internal diameter for each mmHg (133 Pa) change in intraluminal pressure⁶³. The circumferential wall stress in the vessel is determined as shown in eq. 2.

$$\sigma =\frac{\left(P2r_i\right)}{2h}$$ 2

where P is the intraluminal pressure, r_i is the observed internal radius, for a given intravascular pressure both measured in calcium-free medium, and h is the wall thickness. The use of a calcium-free medium ensures that the radius and wall thickness of the arteries are determined in their relaxed state and therefore the passive characteristics of the vessels can be measured at a variety of intravascular pressures⁶⁴.

Fig. 7.

The pressure myograph system. Small arteries are mounted between two cannulae in a pressure myograph chamber. Translumenal pressure is set via a pressure servo unit. Arteries are continuously superfused with gassed physiological salt solution (PSS). For determination of passive arterial characteristics this will normally be calcium free. Arteries are viewed via a x10 objective on an inverted microscope. A video tracer system and dimension analyzer allows the continuous measurement of luminal diameter and left and right wall thickness.

Although pressure myography is carried out under more physiological conditions, less-sophisticated wire myography procedures can be advantageous in isometric conditions⁵⁹. Pressure myography has been used on resistance arteries taken from rats, to show an increase in stiffness with age coupled with an increase in the proportion of collagen to elastin^63,65. As with in vivo measures of large artery stiffness (such as PWV), myography only provide stiffness values for the entire vessel and not detailed structure-mechanical property data.

Point probe measurements of mechanical properties

New techniques capable of mapping mechanical properties with micrometre scale resolution can be used to identify the mechanical properties of discrete tissue components and thus probe how the effects of disease-related tissue remodeling influence tissue behavior and function. Nanoindentation, originally developed to characterize engineering materials^66,67, is one such technique and has been used successfully with stiff, calcified tissues^68-70. The technical difficulties in using this method with more compliant materials are challenging⁷¹. Calcified hard tissues can be polished to give a flat surface, which makes the use of nanoindentation relatively straightforward. The surface of soft biological tissue specimens cannot be prepared this way and the resulting high level of surface roughness, coupled with the inherent high compliance of soft tissues, leads to problems with surface detection and data interpretation when testing with a triangular Berkovich indenter. To accommodate this, flat punch and relatively large radius spherical indenters have been used⁷².

To measure the elastic properties of gelatine and agarose gels, Ebenstein and Pruitt⁷² found the most reproducible results using 100 μm radius conospherical indenters. However, as the contact radius of the indenter tip increases, the achievable spatial resolution of the measurement decreases. Large radius tips will tend to measure the average mechanical properties of tissues rather than the micromechanical properties of individual tissue components such as elastic fibers, which have a diameter of 2 – 3 μm (Fig. 3)⁷³. This was acknowledged by Ebenstein and Pruitt⁷⁴ in a recent review. However, nanoindentation testing instruments, protocols and analysis methods continue to be improved, hence the technique may become as powerful a tool for characterizing the micromechanical properties of soft tissues as it is already for hard tissues.

Atomic force microscopy (AFM) was originally developed as a topographic imaging technique. However, it was clear from the outset that the contrast in AFM images is related to the tip/substrate interaction and thus the elastic properties of both tip and substrate. A number of AFM imaging modes have been developed which exploit this mechanical contrast⁷⁵. Extracting quantified (and reproducible) mechanical data from the tip/substrate interaction is, however, more challenging. Using an AFM to measure elastic properties follows an identical procedure to that used with nanoindentation; the force displacement curve is analyzed to deduce the contact stiffness. The elastic properties can then be determined, if the shape of the indenter is known and a displacement/contact area function available⁷⁶. Despite these similarities, the mechanical design of an AFM is fundamentally different from that of a nanoindenter and AFM loading trains are substantially more compliant than those in a nanoindenter. For this reason, AFMs are better suited to measuring the properties of extremely compliant objects and there has been much work probing the mechanical behavior of cells and interpreting the biological significance of changes in their mechanical properties⁷⁷. Cross et al. used AFM to show that metastasizing cancer cells were about five times more compliant than normal cells⁷⁸. Lieber studied the properties of cardiomyocytes and reported an increase in cell stiffness with age⁷⁹. Recent work on the stiffness of cardiomyocytes and the stiffness of tissue in a macaque animal model⁸⁰ suggests that an increase in cell stiffness with age may also contribute to age-related aortic stiffening. Although AFM approaches have great potential, AFM-based indentation of cells is complex and the mechanical analysis used is often grossly simplified, e.g. with the application of Hertzian contact theory to the irregular topography and heterogeneity of cells. There are also limitations inherent in the technique which must be overcome, such as accurately determining the cantilever spring constant, as highlighted in a recent review⁸¹.

Nanoindentation and AFM-based nanoindentation provide new methods for probing the mechanical properties of ageing tissues. The techniques are able to work with unfixed tissue²⁵: an important consideration as the use of fixing agents (chemical cross-linkers used to stabilize tissue samples are commonly used in the preparation of histological specimens) will severely impact upon the mechanical properties. An important issue that still needs to be resolved is the analysis of thin histological sections mounted on glass slides. Such samples have advantages because they can be used for transmission optical microscopy to characterize tissue components; however, the presence of a stiff substrate can result in significantly higher reported elastic modulus values^25,76. Although the influence of such a substrate can be partially compensated by improved mechanical modeling, it can be difficult to measure the thickness of the thin tissue sample being tested, because this may vary significantly across a histological slice as a consequence of specimen preparation methods.

Acoustic analysis of mechanical properties

Scanning acoustic microscopy (SAM) has attracted interest as a method for mapping the mechanical properties of both isolated cells and whole tissues⁸². SAM can provide both histological and elastic properties for soft tissue sections⁸³ and even has potential to be used for intraoperative pathological examination because it does not require any special staining⁸². In the SAM, a pulse of high frequency acoustic waves (100 MHz – 1 GHz) is transmitted from an acoustic lens, through a coupling fluid (either water or a buffered saline solution) to the sample. The reflected signal is the result of interference between the reflected acoustic signal and any retransmission from surface acoustic waves. This generates contrast that varies periodically with defocus, from which the elastic constants can be calculated in elastically stiff materials⁸⁴. The spatial resolution is a function of the wavelength of the acoustic radiation; with a 1 GHz acoustic signal resolution, the spatial resolution is approximately 1 μm. Although this method has been used to characterize the elastic properties of hard biological tissue, e.g. dentin and bone^85,86, it is not suitable for use with soft tissue because of the attenuation of surface acoustic waves.

Jørgensen and Kundu have developed a frequency scanning method using SAM for thin tissue specimens mounted on glass slides; this exploits the interference that is generated from signals reflected at the fluid/sample and sample/substrate interfaces^87,88. The phase relation can be controlled by varying the frequency (and hence wavelength) of the acoustic radiation, and the resulting periodic function, V(f), can be used to determine the acoustic wave speed in the sample, if the sample thickness is known. Because we are recording an interference pattern, the technique is sensitive to small changes in mechanical properties. However, analysis is not straightforward: V(f) is a non-linear function of specimen thickness, the acoustic attenuation through the sample as well as the relative reflection and transmission intensities at each interface. Kundu et al.⁸⁹ addressed this problem by comparing the measured V(f) signal with a computed V(f) and then adjusted the variables of specimen thickness, attenuation and impedance, to optimize the fit between theoretical and experimental curves. Using this approach, relative measurements of tissue elasticity can be made on a microscopic scale without the need for any fixation or special sample preparations.

Recent developments and prospects for the future

Recently, progress has been made in the successful application of nanoindentation and AFM-based indentation methods to soft, biological tissues. New analytical approaches have been in part driven by the interest in characterizing hydrogel materials. Analysis methods developed by Oyen and co-workers determine the time-dependent properties accounting for both the viscoelastic and poroelastic properties of materials⁹⁰. Currently in such work where the time-dependency of soft materials has been characterized, nanoindentation has tended to be conducted with large radius tips. Galli et al.⁹⁰ used a 400 μm tip but spherical indenters > 3 mm have been used to determine time-dependent behavior of kidney tissue and costal cartilage⁹¹. Such methods should, in principle, be applicable to nanoindentation setups with small tip geometries and therefore provide higher spatial resolution measurements.

Lin and Horkay⁹² have reviewed the theories and analytical methods used to characterize the local elastic properties of polymer gels and biological materials. Although progress has been made in this area, they conclude that no hyperelastic model exists that is capable of serving as a universal constitutive law for soft elastic materials.

New experimental methods continue to be developed with AFM. Gavara and Chadwick⁹³ have recently developed a frequency-modulated atomic force microscope (FM-AFM) that was used to assess the graded mechanical properties of guinea pig tectorial membrane. This non-contact method based on a hydrodynamic theory of thin gaps has a spatial resolution of less than 2 μm. This method appears to be relatively easy to implement on conventional AFM instruments and may prove to be particularly useful for characterizing vascular tissues.

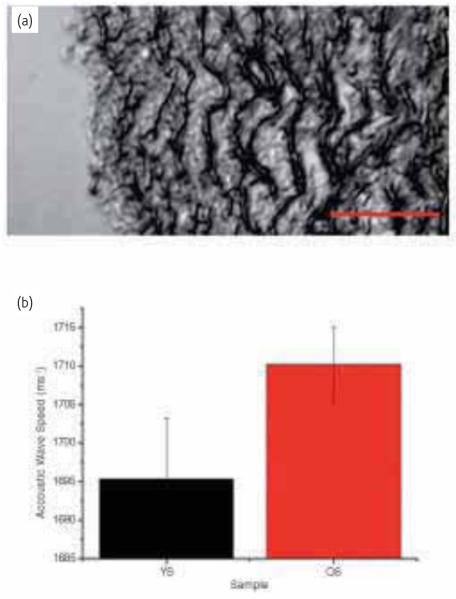
We have been developing methods to determine the microstructural mechanical properties of histological specimens of vascular tissue^25,94 and relate local mechanical property measurements with histological changes in the tissue. Using SAM at 1 GHz, we have mapped the elastic properties of aortic tissue sections for an ovine model of ageing⁹⁵. The increase in stiffness (Fig. 8) correlates with increasing collagen content as determined from the same tissue sections.

Fig. 8.

(a) Scanning acoustic microscopy (SAM) image of a young sheep (18 months) aorta taken at 1 GHz. The intimal surface is at the left hand side of the image. Dark lamellar structures are the elastic fibers. (b) Preliminary data showing acoustic wave speed for young vs old sheep. Old sheep are characterized as being > 8 years. A series of line scans were made offline on each image for wave speed analysis. Each line encompassed around 8 MLUs. The scale bar represents 50 μm.

As stated earlier, a key challenge when characterizing the biomechanical properties of soft tissues is to correlate information from conventional histological approaches with mechanical testing methods. Although SAM allows different histological layers to be visualized without the need for staining, the acoustic images can be difficult to interpret, particularly at higher frequencies (and therefore higher spatial resolutions). An exciting development appears to be the application of non-linear microscopy to soft tissue mechanics; such methods allow three-dimensional, non-invasive imaging of biological structures in response to mechanical strain⁹⁶. This approach has recently been applied to study the structure and mechanical properties of lymphatic vessels⁹⁶ (the lymphatic system is an important but poorly studied component of the circulatory system). The advantages of this technique arise from the fact that it can be applied to fresh, intact and unstained tissues thereby avoiding artifacts that may be introduced by conventional histology.

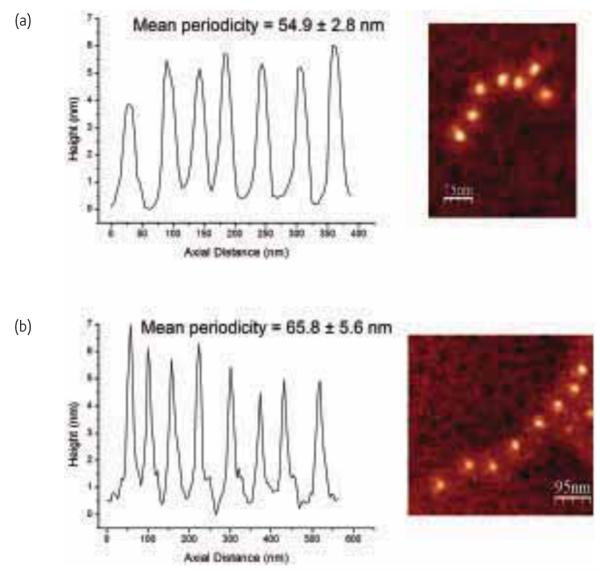
As well as the mechanical properties degrading at the microstructural scale, there is evidence that the molecular components of arteries are also compromised with pathology⁹⁷. Using a technique called molecular combing²⁴ individual fibrillin microfibrils, which have a beads-on-a-string appearance with a typical untensioned periodicity of 56 nm, can be stretched and extended. In turn, the degree of extension gives an indication of the mechanical strength of the microfibrils. Even in the absence of extrinsic factors such as UV radiation, which are known to induce profound ECM remodeling, Sherratt et al.²¹ have demonstrated that microfibrils extracted from photoprotected skin are weakened with age. We have recently shown that the morphology of these microfibrils is altered in a rodent model of type 1 diabetes⁹⁷ and are exploring the mechanical properties of these molecular components with molecular combing (Fig. 9). To better understand age-related pathologies of soft tissues, further work is needed to relate the mechanical properties of tissues such as the aorta at the molecular and microscopic length scales with the macroscopic alterations widely reported.

Fig. 9.

Periodicity profiles shown for fibrillin microfibrils extracted from the aorta of a Wistar rat. (a) Untensioned periodicity. (b) Periodicity following molecular combing where the microfibril has been extended as indicated by the increased bead-bead separation.

This paper summarizes the various methodologies, both in vivo and ex vivo, that are used to determine the mechanical properties of soft tissues, with a particular focus on the vasculature. Further, some recent developments using materials science approaches are highlighted and this review demonstrates that a multi-faceted approach is required to better understand age-related pathologies. With inter-disciplinary approaches utilizing clinical, biomedical and materials expertise our understanding of age-related changes at the micro- and molecular level will continue to be advanced.

Instrument citation.

Bruker Multimode AFM with a Nanoscope IIIa controller, Cambridgeshire, UK.

Leica DM5000B microscope coupled to a fluorescence camera (DFC 350FX), Wetzlar, Germany.

PVA TePla SAM2000 Scanning acoustic microscope with a 1 GHz lens, Aalen, Germany