Likelihood-based selection and sharp parameter estimation

Summary

In high-dimensional data analysis, feature selection becomes one means for dimension reduction, which proceeds with parameter estimation. Concerning accuracy of selection and estimation, we study nonconvex constrained and regularized likelihoods in the presence of nuisance parameters. Theoretically, we show that constrained L₀-likelihood and its computational surrogate are optimal in that they achieve feature selection consistency and sharp parameter estimation, under one necessary condition required for any method to be selection consistent and to achieve sharp parameter estimation. It permits up to exponentially many candidate features. Computationally, we develop difference convex methods to implement the computational surrogate through prime and dual subproblems. These results establish a central role of L₀-constrained and regularized likelihoods in feature selection and parameter estimation involving selection. As applications of the general method and theory, we perform feature selection in linear regression and logistic regression, and estimate a precision matrix in Gaussian graphical models. In these situations, we gain a new theoretical insight and obtain favorable numerical results. Finally, we discuss an application to predict the metastasis status of breast cancer patients with their gene expression profiles.

1 Introduction

Feature selection is essential to battle the inherited “curse of dimensionality” in high-dimensional analysis. It removes non-informative features to derive simpler models for interpretability, prediction and inference. In cancer studies, for instance, a patient’s gene expression is linked to her metastasis status of breast cancer, for identifying cancer genes. In a situation as such, our ability of identifying cancer genes is as critical as a model’s predictive accuracy, where selection accuracy becomes extremely important to reproducible findings and generalizable conclusions. Towards accuracy of selection and parameter estimation, we address several core issues in high-dimensional likelihood-based selection.

Consider a selection problem with nuisance parameters, based on a random sample Y = (Y₁, ···, Y_n) with each Y_i following probability density g(θ⁰, y), where θ⁰ = (β⁰, η⁰) is a true parameter vector, ${\mathit{\beta }}^0\equiv ({\beta }_1^0,\cdots ,{\beta }_p^0)=({\mathit{\beta }}_{A_0}^0,{\mathbf{0}}_{A_0^c})$ and ${\mathit{\eta }}^0\equiv ({\eta }_1^0,\cdots ,{\eta }_q^2)$ are the parameters of interest and nuisance parameters respectively, $A_0=\{j:{\beta }_j^0\ne 0\}$ is a set of nonzero coefficients of β⁰ with size |A₀| = p₀, and ${\mathbf{0}}_{A_0^c}$ is a vector of 0’s with ^c denoting the set complement. Here we estimate (β⁰, A₀), where p may greatly exceed n, and q = 0 is permitted.

For estimation and selection, a likelihood is regularized with regard to β, particularly when p > n. This leads to an information criterion:

$$-L(\mathit{\theta })+\lambda \sum _{j=1}^{p}I({\beta }_j\ne 0),$$ (1)

where $L(\mathit{\theta })={\sum }_{i=1}^{n}logg(\mathit{\theta },Y_i)$ is the log-likelihood based on Y, λ > 0 is a regularization parameter, and ${\sum }_{j=1}^{p}I({\beta }_j\ne 0)$ is the L₀-function penalizing an increase in a model’s size. In (1), when θ = β without nuisance parameters, λ = 1 is Akaike’s information criterion, $\lambda =\frac{logn}{2}$ is Bayesian information criterion [21], among others. In fact, essentially all selection rules can be cast into the framework of (1).

Regularization (1) has been of considerable interest for its interpretability and computational merits. Yet its constrained counterpart (2) has not received much attention, which is

$$-L(\mathit{\theta }),\text{subject}\text{to}\sum _{j=1}^{p}I({\beta }_j\ne 0)\le K,$$ (2)

where K ≥ 0 is a tuning parameter corresponding to λ in (1). Minimizing (1) or (2) in θ gives a global minimizer leading to an estimate β̂ = (β̂_Â, 0_Â^c)^T, with  the estimated A₀, where η is un-regularized and possibly profiled out. Note that (1) and (2) may not be equivalent in their global minimizers, which is unlike a convex problem.

This article systematically investigates constrained and regularized likelihoods involving nuisance parameters, for estimating zero components of β⁰ as well as nonzero ones of θ⁰. This includes, but is not limited to, estimating nonzero entries of a precision matrix in graphical models.

There is a huge body on parameter estimation through L₁-regularization in linear regression; see, for instance, [16] for a comprehensive review. For feature selection, consistency of the Lasso [26] has been extensively studied under the irrepresentable assumption; c.f., [15] [34]. Other methods such as the SCAD [6] have been studied. Yet L₀-constrained or regularized likelihood remain largely unexplored. Despite progress, many open issues remain. First, what is the maximum number of candidate features allowed for a likelihood method to reconstruct informative features? Results, such as [13], seem to suggest that the capacity of handling exponentially many features may be attributed primarily to the exponential tail of a Gaussian distribution, which we show is not necessary. Second, can parameter estimation be enhanced through removal of zero components of β? Third, can a selection method continue to perform well for parameters of interest in the presence of a large number of nuisance parameters, as in covariance selection for off-diagonal entries of a precision matrix?

This article intends to address the foregoing three issues. First, we establish finite-sample mis-selection error bounds for constrained L₀-likelihood as well as its computational surrogate, given (n, p₀, p), where the surrogate–a likelihood based on a truncated L₁-function (TLP) approximating the L₀-function, permits efficient computation; see Section 2.1 for a definition. On this basis, we establish feature selection consistency for them as n, p → ∞, under one key condition that is necessary for any method to be selection consistent:

$$C_{min}({\mathit{\theta }}^0)\ge d_0\frac{logp}{n},$$ (3)

where $C_{min}({\mathit{\theta }}^0)\equiv {inf}_{\{{\mathit{\theta }}_A=(({\mathit{\beta }}_A,{\mathbf{0}}_{A^c}),\mathit{\eta }):A\ne A_0,\mid A\mid \le p_0\}}\frac{h^2({\mathit{\theta }}_A,{\mathit{\theta }}^0)}{max(\mid A_0\backslash A\mid ,1)}$, d₀ > 0 is a constant, |·| and \ denote the size of a set and that of set difference, respectively, $h(\mathit{\theta },{\mathit{\theta }}^0)=\frac{1}{2}{\left(\int {(g^{1/2}(\mathit{\theta },y)-g^{1/2}({\mathit{\theta }}^0,y))}^{2}d\mu (y)\right)}^{1/2}$ is the Hellinger-distance for with respect to a dominating measure μ, and g(θ, y) is a probability density for Y₁. As one consequence, exponentially many candidate features $p=exp\left(n\frac{C_{min}({\mathit{\theta }}^0)}{d_0}\right)$ are permitted for selection consistency with a broad class of constrained likelihoods. This challenges the well established result that the maximum number of candidate features permitted for selection consistency depends highly on a likelihood’s tail behavior, c.f., [4]. In fact, selection consistency continues to hold even if the error distribution does not have an exponential tail; see Proportion 1 for linear regression. Second, sharper parameter estimation results from accurate selection by L₀-likelihood and its surrogate as compared to that without such selection. For feature selection in linear regression and logistic regression, the optimal Hellinger risk of the oracle estimator, the maximum likelihood estimate (MLE) based on A₀ as if the true A₀ were known a priori, is recovered by these methods, which is of order of $\sqrt{\frac{p_0}{n}}$ and is uniform over a certain L₀-band of θ⁰ excluding the origin. This is in contrast to the minimax rate $\sqrt{\frac{ulog(p/u)}{n}}$ with u ≥ p₀ for estimation without feature selection in linear regression [17]. In other words, accurate selection by L₀-likelihood and its surrogate over the L₀-band improves accuracy of estimation after non-informative features are removed, without introducing additional bias to estimation. Moreover, in estimating a precision matrix in Gaussian graphical models, the foregoing conclusions extend but with a different rate at $\sqrt{\frac{p_{0}logp}{n}}$, where a log p factor is due to estimation of 2p nuisance parameters as compared to logistic regression. Third, two difference of convex (DC) methods are employed for computation of (1) and (2), which relax nonconvex minimization through a sequence of convex problems.

Two disparate applications are considered, namely, feature selection in generalized linear models (GLMs), as well as estimation of a precision matrix in Gaussian graphical models. In GLMs, feature selection in nonlinear regression appears more challenging than linear regression for a high-dimensional problem. In statistical modeling of a precision matrix in Gaussian graphical models, two major approaches have emerged to exploit matrix sparsity by likelihood selection and neighborhood selection. Papers based on these two approaches include [15] [12] [28] [2] [8] [19] [20] [18], among others. As suggested by [19], existing methods may not perform well when the dimension of a matrix exceeds the sample size n, although they give estimates better than the sample covariance matrix. In addition, theoretical aspects for a likelihood approach remain to be under studied. In these situations, the proposed method compares favorably against its competitors in simulations, and novel theoretical results provide an insight into a selection process.

This article is organized as follows. Section 2 develops the proposed method for L₀-regularized and constrained likelihoods. Section 3 presents main theoretical results for selection consistency and parameter estimation involving selection, followed by a necessary condition for selection consistency. Section 4 applies the general method and theory to feature selection in GLMs. Section 5 is devoted to estimation of a precision matrix in Gaussian graphical models. Section 6 presents an application to predict the metastasis status of breast cancer patients with their gene expression profiles. Section 7 contains technical proofs.

2 Method and computation

2.1 Method

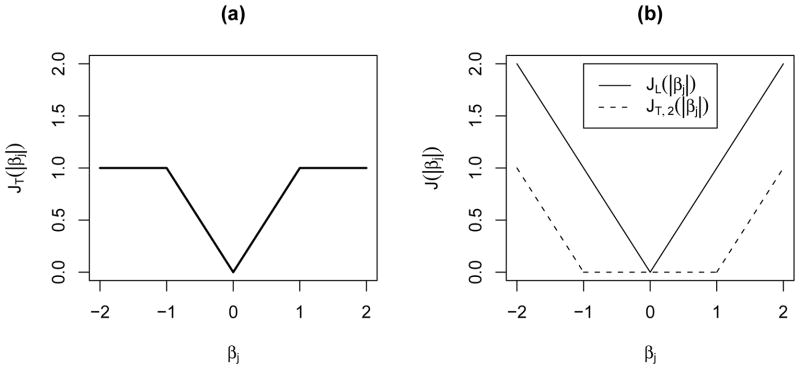
In a high-dimensional situation, it is computationally infeasible to minimize a discontinuous cost function involving the L₀-function in (1) and (2). As a surrogate, we seek a good approximation of the L₀-function by the TLP, defined as $J(\mid z\mid )=\lambda min\left(\frac{\mid z\mid }{\tau },1\right)$, with τ > 0 a tuning parameter controlling the degree of approximation; see Figure 1 for a display. This τ decides which individual coefficients to be shrunk towards zero. The advantages of J(|z|) are fourfold, although J(z) has been considered in other contexts [9]:

Figure 1.

Truncated L₁ function J_t (|β_j|) with τ = 1 in (a), and its DC decomposition into a dfference of two convex functions J_L and J_T,2 in (b).

1. (Surrogate) It performs the model selection task of the L₀-function, while providing a computationally efficient means. Note that the approximation error of the TLP function to the L₀-function becomes zero when τ is tuned such that $\tau <min\{\mid {\beta }_k^0\mid :k\in A_0\}$, seeking the sparsest solution by minimizing the number of non-zero coefficients.

2. (Adaptive model selection through adaptive shrinkage) It performs adaptive model selection [23] through a computationally efficient means when λ is tuned. Moreover, it corrects the Lasso bias through adaptive shrinkage combining shrinkage with thresholding.

3. (Piecewise linearity) It is piecewise linear, gaining computational advantages.

4. (Low resolutions) It discriminates small from large coefficients through thresholding. Consequently, it is capable of handling many low-resolution coefficients, through tuning τ.

To treat nonconvex minimization, we replace the L₀-function by its surrogate J(·) to construct an approximation of (2) and that of (1):

$$-L(\mathit{\theta }),\text{subject}\text{to}\sum _{j=1}^{p}J(\mid {\beta }_j\mid )\le K,$$ (4)

$$S(\mathit{\theta })=-L(\mathit{\theta })+\lambda \sum _{j=1}^{p}J(\mid {\beta }_j\mid ),$$ (5)

where (5) is a dual problem of (4). To solve (5) and (4), we develop difference convex methods for the primal and dual problems, for efficient computation.

2.2 Unconstrained dual and constrained primal problems

Our DC method for the dual problem (5) begins with a DC decomposition of S(θ): S(θ) = S₁(θ) − S₂(β), where $S_1(\mathit{\theta })=-L(\mathit{\theta })+\lambda {\sum }_{j=1}^p{J}_1(\mid {\beta }_j\mid ),S_2(\mathit{\beta })=\lambda {\sum }_{j=1}^p{J}_2(\mid {\beta }_j\mid ),J_1(\mid {\beta }_j\mid )=\frac{\mid {\beta }_j\mid }{\tau }$, and $J_2(\mid {\beta }_j\mid )=\frac{\mid {\beta }_j\mid }{\tau }-max\left(\frac{\mid {\beta }_j\mid }{\tau }-1,0\right)$. Without loss of generality, assume that −L is convex in θ; otherwise, a DC decomposition of −L is required and can be treated similarly. Given this DC decomposition, a sequence of upper approximations of S(θ) is constructed iteratively, say, at iteration m, with ∇S₂ a subgradient of S₂ in |β|: S^(m)(θ) = S₁(θ) − (S₂(β̂^{(m − 1)})+(|β| − |β̂^(m-1)|)^T∇S₂ (|β̂^(m-1)|)), by successively replacing S₂(β) by its minorization, where |·| for a vector takes the absolute value in each component. After ignoring $S_2({\widehat{\mathit{\beta }}}^{(m-1)})-\frac{\lambda }{\tau }{\sum }_{j=1}^p\mid {\widehat{\beta }}_j^{(m-1)}\mid I(\mid {\widehat{\beta }}_j^{(m-1)}\mid >\tau )$ that is independent of θ, the problem reduces to

$$S^{(m)}(\mathit{\theta })=-L(\mathit{\theta })+\frac{\lambda }{\tau }\sum _{j=1}^p\mid {\beta }_j\mid I(\mid {\widehat{\beta }}_j^{(m-1)}\mid \le \tau ).$$ (6)

Minimizing (6) in θ yields its minimizer θ̂^(m). The process continues in m until termination occurs. Our unconstrained DC method is summarized as follows.

Algorithm 1

• Step 1.

  (Initialization) Supply a good initial estimate θ̂⁽⁰⁾, such as the minimizer of S₁(θ).

• Step 2.

  (Iteration) At iteration m, compute θ̂^(m) by solving (6).

• Step 3.

  (Termination) Terminate when S(θ̂^(m−1)) − S(θ̂^(m)) ≤ ε, and no components of β̂^(m) is at ±τ. Otherwise, add ε to that components whose absolute value is τ, and go to Step 2, where ε is the square root of the machine precision. Then the estimate θ̂ = θ̂^(m*), where m^* is the smallest index at the termination criterion.

In Algorithm 1, (6) reduces to a general weighted Lasso problem: $-L(\mathit{\theta })+{\sum }_{j=1}^p{\lambda }_j\mid {\beta }_j\mid$, with ${\lambda }_j=\frac{\lambda }{\tau }I(\mid {\widehat{\beta }}_j^{(m-1)}\mid \le \tau )$. Therefore any efficient software is applicable.

For (4), we decompose the nonconvex constraint into a difference of two convex functions to construct a sequence of approximating convex constraints. This amounts to solving the mth subproblem in a parallel fashion as in (6):

$$\underset{\mathit{\beta }}{min}-L(\mathit{\theta }),\text{subject}\text{to}\frac{1}{\tau }\sum _{j=1}^p\mid {\beta }_j\mid I(\mid {\widehat{\beta }}_j^{(m-1)}\mid \le \tau )\le K-\sum _{j=1}^{p}I(\mid {\widehat{\beta }}_j^{(m-1)}\mid >\tau ).$$ (7)

This leads to a constrained DC algorithm—Algorithm 2 for solving (4) by replacing (5) in Algorithm 1 by (4).

Algorithms 1 and 2 are a generalization of those in [24] for a general likelihood, where all the computational properties there extend to the present situation, including equivalence of the DC solutions of the two algorithms and their convergence. Next we shall work with (5) due to its computational advantage. For instance, a coordinate decent method that works well with (5) breaks down for (4), c.f., [24].

3 Theory

This section presents a general theory for accuracy of reconstruction of the oracle estimator θ̂^ml = (β̂^ml, η̂^ml) with ${\widehat{\mathit{\beta }}}^{ml}=({\widehat{\mathit{\beta }}}_{A_0}^{ml},{\mathbf{0}}_{A_0})$ given A₀, which is the MLE provided that the knowledge about A₀ were known a priori. As direct consequences, feature selection consistency is studied as as well as optimal parameter estimation defined by the oracle estimator. In addition, a necessary condition for feature selection will be established as well. A parallel theory for regularized likelihood is similar and thus is omitted.

3.1 Constrained L₀-likelihood

In (2), assume that a global minimizer exists, denoted by θ̂^L₀ = (β̂^L₀, η̂^L₀) with ${\widehat{\mathit{\beta }}}^{L_0}=({\widehat{\mathit{\beta }}}_{{\widehat{A}}^{L_0}}^{L_0},{\mathbf{0}}_{{({\widehat{A}}^{L_0})}^c})$. Write β as (β_A, 0|_A^c|), with β_A being (β₁, …, β|_A|)^T for any subset A ⊂ {1, ···, p} of nonzero coefficients.

Before proceeding, we define a complexity measure for the size of a space . The bracketing Hellinger metric entropy of , denoted by the function H(·, ), is defined by logarithm of the cardinality of the u-bracketing (of ) of the smallest size. That is, for a bracket covering $S(\epsilon ,m)=\{f_1^l,f_1^u,\cdots ,f_m^l,f_m^u\}\subset {\mathcal{L}}_2$ satisfying ${max}_{1\le j\le m}{\left|\right|f_j^u-f_j^l\left|\right|}_2\le \epsilon$ and for any f ∈ , there exists a j such that $f_j^l\le f\le f_j^u$, a.e. P, then H(u, ) is log(min{m : S(u, m)}), where ||f||₂ = ∫ f²(z)dμ. For more discussions about metric entropy of this type, see [14].

Assumption A (Size of parameter space)

For some constant c₀ > 0 and any $\frac{\epsilon }{2^4}<t<\epsilon \le 1$, H(t, 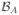) ≤ c₀(log p)²|A| log(2ε/t), with |A| ≤ p₀, where 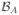= 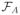∩ {h(θ, θ⁰) ≤ 2ε} is a local parameter space, and 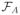= {g^1/2(θ, y) : θ = (β, η), β = (β_A, 0)} be a collection of square-root densities.

Theorem 1 (Error bound and oracle properties)

Under Assumption A, if K = p₀, then, there exists a constant c₂ > 0, say $c_2=\frac{2}{27}\frac{1}{963}$, such that for (n, p₀, p),

$$P({\widehat{\mathit{\theta }}}^{L_0}\ne {\widehat{\mathit{\theta }}}^{ml})\le exp(-c_2{nC}_{min}({\mathit{\theta }}^0)+2log(p+1)+3)).$$ (8)

Moreover, under (3) with $d_0>max(\frac{2}{c_2},{(2c_0)}^{1/2}{c}_4^{-1}log(2^{1/2}/c_3))$, θ̂^L₀ reconstructs the oracle estimator θ̂^ml with probability tending to one as n, p → ∞. Three oracle properties hold as n, p → ∞:

1. (Selection consistency) Estimator Â^L₀ is selection consistent, that is, P(Â^L₀ ≠ A₀) → 0.

2. (Optimal parameter estimation) For θ⁰, ${Eh}^2({\widehat{\mathit{\theta }}}^{L_0},{\mathit{\theta }}^0)=(1+o(1)){Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)=O({\epsilon }_{n,p}^2)$ and $h^2({\widehat{\mathit{\theta }}}^{L_0},{\mathit{\theta }}^0)=O_p({\epsilon }_{n,p_0,p}^2)$, provided that Eh²(θ̂^ml, θ⁰) does not tend to zero too fast in that $\frac{c_2}{2}{nC}_{min}({\mathit{\theta }}^0)+log{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)\to \infty$, where ε_n,p0p is any solution for ε:

   $${\int }_{2^{-8}{\epsilon }^2}^{2^{1/2}\epsilon }{H}^{1/2}(t/c_3,{\mathcal{B}}_{A_0})dt\le c_4{n}^{1/2}{\epsilon }^2.$$ (9)

3. (Uniformity over a L₀-band) The reconstruction holds uniformly over B₀(u, l), namely, sup_{θ⁰∈B0(u,l)} P(θ̂^L₀ ≠ θ̂^ml) → 0, where B₀(u,l) is a L₀-band, defined as $\{(\mathit{\beta },{\eta }_0):p_0={\sum }_{j=1}^{p}I({\beta }_j\ne 0)\le u,C_{min}(\mathit{\theta })\ge l\}$ with 0 < u ≤ min(n, p), $l=d_0{\sigma }^2\frac{logp}{n}$, and u < min(n, p). This implies feature selection consistency sup_{θ⁰∈B0(u,l)} P(Â^L₀ ≠ A₀) → 0, and optimal parameter estimation $\frac{{sup}_{\mathit{\theta }}{0}_{\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\theta }}}^{L_0},{\mathit{\theta }}^0)}{{sup}_{\mathit{\theta }}{0}_{\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)}\to 1$, with ${sup}_{{\mathit{\theta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)=O({\epsilon }_{n,u,p}^2)$, provided that Eh²(θ̂^ml, θ⁰) does not tend to zero too fast in that $\frac{c_2}{2}{nC}_{min}({\mathit{\theta }}^0)+log{sup}_{{\mathit{\theta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)\to \infty$.

The L₀-method consistently reconstructs the oracle estimator when the degree of separation exceeds the minimal level, precisely under (3). As a result, selection consistency is established for the L₀-method. This, combined with that in Theorem 3, suggests that the L₀-method is optimal in feature selection against any method, matching up with the lower bound requirement under the degree of separation with respect to (p, p₀, n) except a constant factor d₀ > 0 in Theorem 3. Moreover, the optimality extends further to parameter estimation, where sharper parameter estimation is obtained from accurate L₀ selection, achieving the optimal Hellinger risk of the oracle estimator asymptotically. By comparison, such a result is not expected for L₁-regularization. As suggested in [17], selection consistency of Lasso does not give sharper parameter estimation, where the rate of convergence of a L₁-method in the L₂ risk remains to be $\sqrt{\frac{p_{0}log(p/p_0)}{n}}$ in linear regression. This is because a L₁-method is nonadaptive and overpenalizes large coefficients as a result of shrinking small coefficients towards zero. Similarly, in feature selection in logistic regression, the L₀-method is expected to give rise to better estimation precision than a L₁-method, although a parallel result for a L₁-method has not been available. Finally, the uniform result in (C) is over a L₀-band B₀(u, l), which is not expected over a L₀-ball B₀(u, 0) in view of the result of Theorem 3.

3.2 Constrained truncated L₁-likelihood

For constrained truncated L₁-likelihood, one additional regularity condition–Assumption B is assumed, which is generally met with a smooth likelihood; see Section 4 for an example. It requires the Hellinger-distance to be smooth so that the TLP approximation to the L₀-function becomes adequate through tuning τ.

Assumption B

For some constants d₁−d₃ > 0,

$$h^2(\mathit{\theta },{\mathit{\theta }}^0)\ge d_1{h}^2({\mathit{\theta }}_{{\tau }^{+}},{\mathit{\theta }}^0)-d_{3}p{\tau }^{d_2},A^{{\tau }^{+}}\equiv \{j:\mid {\beta }_j\mid \ge \tau \},$$ (10)

where θ_τ⁺ = (β₁I(|β₁| ≥ τ), ···, β_pI(|β_p| ≥ τ), η₁, ···, η_q).

Theorem 2 (Error bound and oracle properties)

Under Assumption A with 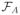replaced by {g^1/2(θ, y) : θ = (β, η) : β = (β_A, β_A^c), ||β_A^c||_ℓ∞ ≤ τ}, say 0 ≤ τ ≤ c′ε for some constant c′, and Assumption B, if K = p₀ and τ ≤ max(c′, (d₁C_min(θ⁰)/2pd₃)^1/d₂>), then there exists a constant c₂ > 0, such that for any (n, p₀, p),

$$P({\widehat{\mathit{\theta }}}^T\ne {\widehat{\mathit{\theta }}}^{ml})\le exp\left(-c_2{nC}_{min}({\mathit{\theta }}^0)+2log(p+1)+3\right).$$ (11)

Moreover, under (3) with sufficiently large constant d₀ > 0, θ̂^T has the three oracle properties (A)–(C) of θ̂^L₀, provided that $\frac{c_2{d}_1}{4}{nC}_{min}({\mathit{\theta }}^0)+log{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)\to \infty$. For (C), $\tau \le {(\frac{d_{1}l}{2{pd}_3})}^{1/d_2}$ is required as well as $\frac{c_2{d}_1}{4}{nC}_{min}({\mathit{\theta }}^0)+log{sup}_{{\mathit{\theta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)\to \infty$.

Remark

Constants in Theorem 1 can be made precise. For instance, $c_2=\frac{4}{27}\frac{1}{1926}$ and $d_0>max(\frac{4}{c_2{d}_1},{(2c_0)}^{1/2}{c}_4^{-1}log(2^{1/2}/c_3))$.

Theorem 2 says that the oracle properties of the L₀-function are attained by its computational surrogate when τ is sufficiently small.

3.3 Necessary condition for selection consistency

This section establishes the necessary condition (3) by estimating the minimal value d₀ in (3), required for feature selection consistency.

Let K(θ₁, θ₂) = E log g(θ₁, Y)/g(θ₂, Y) be the Kullback-Leibler loss for θ₁ versus θ₂, where E is taken with regard to g(θ₁, Y). Let ${\gamma }_{min}({\mathit{\theta }}^0)\equiv min\{\mid {\beta }_k^0\mid :k\in A_0\}>0$.

Assumption C

For a constant r > 0, $K({\mathit{\theta }}_j,{\mathit{\theta }}_k)\le r{\gamma }_{min}^2(\mathit{\beta })$. Here {θ_j = (β_j, η⁰), j = 1, ···, p} is a set of parameters, where ${\mathit{\beta }}_j={\sum }_{k=1}^{p_0}{\gamma }_{\mathit{min}}{\mathit{e}}_k-{\gamma }_{\mathit{min}}{e}_j$; j = 1, ···, p₀}, and ${\mathit{\beta }}_j={\sum }_{k=1}^{p_0}{\gamma }_{\mathit{min}}{\mathit{e}}_k+{\gamma }_{\mathit{min}}{\mathit{e}}_j$; j = p₀ + 1, ···, p, and ${\mathit{e}}_j={(\underset{j-1}{\underbrace{0,\dots ,0}},1,\underset{p-j-1}{\underbrace{0,\dots ,0}})}^T$. Assume that $s\equiv {inf}_{{\mathit{\theta }}^0}\frac{C_{min}({\mathit{\theta }}^0)}{{\gamma }_{min}^2({\mathit{\theta }}^0)}>0$.

Theorem 3 (Necessary condition for feature selection consistency)

Under Assumption C, for any constant c_* ∈ (0, 1), any (n, p₀, p) with p₀ ≤ p/2, and any η⁰, we have

$$\underset{\widehat{A}}{inf}\underset{\{{\mathit{\beta }}^0:C_{min}({\mathit{\theta }}^0)=R^{\ast }\}}{sup}P\left(\widehat{A}\ne A_0\right)\ge c_{\ast },$$ (12)

with $R^{\ast }=\frac{s(1-c_{\ast })logp}{4rn}$. Moreover,

$$\underset{\widehat{A}}{inf}\underset{{\mathit{\theta }}^0\in B_0(u,l)}{sup}P\left(\widehat{A}\ne A_0\right)\ge c_{\ast },asn,p\to \infty ,$$ (13)

where u ≤ min(p/2, n), $l=d_0\frac{logp}{n}$, and $d_0=\frac{(1-c^{\ast })s}{4r}$.

Theorem 3 says that feature selection inconsistency occurs when $d_0<\frac{s}{4r}$ in (3). There the minimal value $d_0=\frac{s}{4r}$ yields a requirement for feature selection consistency in (3).

4 Generalized linear models

For GLMs, observations Y_i = (Z_i, X_i) are paired, response Z_i is assumed to follow an exponential family with density function g(z_i; θ_i, φ) = exp{[z_iθ_i − b(θ_i)]/a(φ) + c(z_i, φ)}, where θ_i is the natural parameter that is related to the mean μ_i = E(z_i) = b′(θ_i), and φ is a dispersion parameter. With a link function g, a regression model becomes η_i = g(μ_i) = β^Tx_i. The penalized likelihood for estimating regression coefficient vectors β is $-L(\mathit{\beta })+{\sum }_{j=1}^{p}J(\mid {\beta }_j\mid ;\lambda ,\tau )$, where $L(\mathit{\beta })={\sum }_{i=1}^n[z_i{\mu }_i-b({\mu }_i)]/a(\phi )+c(z_i,\phi )$ is the log-likelihood, and $J(\mid {\beta }_j\mid ;\lambda ,\tau )=\frac{\lambda }{\tau }min(\mid {\beta }_j\mid ,\tau )$ is the TLP penalty.

For parameter estimation and feature selection, we apply Algorithm 1, where (6) becomes a series of weighted lasso for GLMs, for which some existing routines are applicable, for simplicity. In implementation, we use the function wtlassoglm() in R package SIS.

Next we examine effectiveness of the proposed method through simulated examples in feature selection. In linear regression and logistic regression, the Lasso, SCAD [6], SCAD-OS, TLP and TLP-OS are compared in terms of predictive accuracy and identification of the true model, where SCAD-OS and TLP-OS are SCAD and TLP with only one iteration step in the DC iterative process, and SCAD-OS is proposed in [33]. The latter four methods use the Lasso as an initial estimate.

4.1 Simulations

For simulations predictors X_i’s are iid from N (0, V), where V is a p × p matrix whose ijth element is 0.5^|i−j|. In linear regression, Z_i = β^TX_i + ε_i, ε_i ~ N (0, σ²); i = 1, ···, n, and random error ε_i is independent of X_i; in logistic regression, a binary response is generated from logit Pr(Z_i = 1) = β^TX_i. In both cases, β = (β₁, ···, β_p)^T with β₁ = 1, β₂ = 0.5 and β₅ = 0.75; β_j = 0 for j ≠ 1, 2, 5. This set-up was similar to that considered in [33]; here we examine various situations with respect to p, n. Each simulation is based on 1000 independent replications.

For any given tuning parameter λ, all other methods use the Lasso estimate as an initial estimate. For each method, we choose its tuning parameter values by maximizing the log-likelihood based on a common tuning dataset with an equal sample size of the training data and independent of the training data. This is achieved through a grid search over 21 λ values returned by glmnet() for all the methods, and additionally over a grid of 10 τ values that are the 9th-, 19th-, 29th-, ···, 99th-percentiles of the final Lasso estimate for the TLP.

The model error (ME) is used to evaluate predictive performance of β̂, defined as ME(β̂) = (β̂ − β⁰)^TV (β̂ − β⁰), which is the prediction error minus σ² in linear regression, corresponding to the test error over an independent test sample of size T = ∞. In our context, the median ME’s are reported over 1000 simulation replications, due to possible skewness of the distribution of ME. In addition, the mean parameter estimates of the nonzero elements of β will be reported, together with the mean true positive (TP) and mean false positive (FP) numbers: $\#TP={\sum }_{j=1}^{p}I({\beta }_j\ne 0,{\widehat{\beta }}_j\ne 0)$ and $\#FP={\sum }_{j=1}^{p}I({\beta }_j=0,{\widehat{\beta }}_j\ne 0)$.

For linear regression, simulation results are reported for the cases of p = 12, 500, 1000, n = 50, 100, and σ² = 1 in Table 1. As suggested by Table 1, the TLP performs best: it gives the smallest estimation and prediction error as measured by the ME, the smallest mean false positive number (FP) while maintaining a comparable mean number of true positives (TP) around 3. Most critically, as p increases, the TLP’s performance remains much more stable than its competitors. On a relative basis, the TLP outperforms its competitors more in more difficult situations.

Table 1.

Median ME’s, means (SD in parentheses) nonzero coefficients (β₁, β₂, β₅), and true positive (TP) and false positive (FP) numbers of nonzero estimates, for linear regression, based on 1000 simulation replications.

n	p	Method	ME	β1 = 1	β2 = .5	β5 = .75	#TP	#FP
50	12	Lasso	.129	.91(.17)	.41(.18)	.60(.16)	2.98(0.14)	3.82(2.39)
		SCAD-OS	.109	1.02(.19)	.40(.22)	.68(.18)	2.92(0.27)	2.50(1.97)
		SCAD	.118	1.04(.20)	.39(.24)	.71(.18)	2.88(0.32)	2.30(1.90)
		TLP-OS	.088	1.01(.18)	.41(.20)	.68(.17)	2.94(0.25)	1.65(2.04)
		TLP	.090	1.01(.19)	.41(.21)	.69(.17)	2.92(0.27)	1.57(1.98)
50	500	Lasso	.431	.76(.19)	.29(.18)	.41(.17)	2.90(0.30)	14.7(10.48)
		SCAD-OS	.327	1.01(.24)	.25(.25)	.52(.24)	2.70(0.47)	14.81(8.69)
		SCAD	.301	1.09(.26)	.21(.27)	.59(.26)	2.53(0.53)	12.25(7.63)
		TLP-OS	.150	1.02(.21)	.39(.26)	.67(.22)	2.75(0.45)	4.27(6.86)
		TLP	.143	1.02(.21)	.39(.26)	.68(.22)	2.75(0.45)	4.10(6.89)
50	1000	Lasso	.501	.72(.19)	.28(.18)	.37(.18)	2.88(0.33)	17.20(11.49)
		SCAD-OS	.370	.99(.25)	.26(.25)	.51(.26)	2.67(0.49)	18.76(9.60)
		SCAD	.327	1.08(.26)	.20(.28)	.57(.29)	2.49(0.54)	15.19(8.41)
		TLP-OS	.182	1.01(.20)	.40(.27)	.66(.25)	2.72(0.47)	5.43(8.69)
		TLP	.175	1.02(.20)	.40(.27)	.66(.25)	2.72(0.47)	5.06(8.30)
100	12	Lasso	.063	.94(.12)	.44(.13)	.65(.11)	3.00(0.00)	3.94(2.42)
		SCAD-OS	.042	1.01(.12)	.45(.14)	.72(.11)	2.99(0.08)	2.17(2.04)
		SCAD	.042	1.02(.13)	.45(.15)	.74(.11)	2.99(0.09)	2.06(2.01)
		TLP-OS	.037	1.01(.12)	.45(.13)	.71(.11)	3.00(0.06)	1.51(1.99)
		TLP	.036	1.01(.12)	.45(.13)	.72(.11)	3.00(0.07)	1.46(1.95)
100	500	Lasso	.186	.84(.12)	.36(.12)	.52(.11)	3.00(0.04)	15.61(11.04)
		SCAD-OS	.118	1.06(.14)	.32(.18)	.66(.14)	2.94(0.24)	14.92(10.45)
		SCAD	.121	1.10(.15)	.30(.21)	.71(.12)	2.89(0.31)	14.20(10.00)
		TLP-OS	.036	1.01(.12)	.47(.14)	.72(.11)	2.99(0.12)	3.64(6.57)
		TLP	.035	1.01(.12)	.46(.14)	.72(.11)	2.99(0.12)	3.49(6.69)
100	1000	Lasso	.211	.83(.13)	.34(.13)	.51(.12)	3.00(0.06)	18.10(12.50)
		SCAD-OS	.142	1.06(.15)	.30(.19)	.66(.15)	2.91(0.29)	19.70(13.35)
		SCAD	.147	1.10(.15)	.27(.22)	.72(.14)	2.83(0.38)	18.80(12.74)
		TLP-OS	.037	1.01(.13)	.46(.15)	.74(.12)	2.97(0.18)	3.93(7.04)
		TLP	.037	1.01(.13)	.46(.15)	.74(.12)	2.97(0.18)	3.80(6.94)

For logistic regression, simulation results are summarized for the cases of p = 12, 200, 500 and n = 100, 200 in Table 2. As expected, the TLP continues to outperform other methods with the smallest median ME’s. It gives less biased estimates than the Lasso estimates. The TLP’s superior performance remains strong over other methods, as p increases.

Table 2.

Median ME’s, means (SD in parentheses) nonzero coefficients (β₁, β₂, β₅), and true positive (TP) and false positive (FP) numbers of nonzero estimates, for logistic regression, based on 1000 simulation replications.

n	p	Method	ME	β1 = 1	β2 = .5	β5 = .75	#TP	#FP
100	12	Lasso	.388	.80(.27)	.35(.25)	.49(.27)	2.8(0.4)	3.8(2.2)
		SCAD-OS	.416	1.03(.37)	.39(.36)	.61(.40)	2.5(0.7)	1.6(1.9)
		SCAD	.472	1.10(.41)	.38(.39)	.67(.44)	2.4(0.7)	1.1(1.9)
		TLP-OS	.350	.98(.35)	.36(.32)	.59(.35)	2.7(0.5)	1.8(2.0)
		TLP	.355	.98(.35)	.35(.32)	.58(.35)	2.6(0.6)	1.8(2.0)
100	200	Lasso	.947	.57(.25)	.20(.19)	.26(.21)	2.6(0.6)	11.7(7.1)
		SCAD-OS	.733	.96(.45)	.23(.36)	.40(.41)	2.0(0.7)	3.1(2.9)
		SCAD	.827	1.08(.53)	.23(.42)	.46(.53)	1.7(0.6)	1.1(1.4)
		TLP-OS	.649	.99(.42)	.31(.36)	.49(.46)	2.2(0.7)	3.8(5.2)
		TLP	.664	.99(.43)	.30(.37)	.48(.47)	2.2(0.7)	3.6(5.2)
100	500	Lasso	1.166	.48(.24)	.18(.19)	.19(.19)	2.4(0.7)	13.6(9.1)
		SCAD-OS	.867	.84(.48)	.23(.35)	.29(.37)	1.8(0.7)	3.9(3.6)
		SCAD	.847	1.00(.57)	.25(.46)	.34(.50)	1.6(0.6)	1.3(1.5)
		TLP-OS	.791	.93(.45)	.30(.39)	.38(.45)	2.0(0.7)	4.4(6.5)
		TLP	.811	.94(.46)	.29(.40)	.38(.45)	2.0(0.7)	4.1(6.4)
200	12	Lasso	.203	.87(.20)	.39(.20)	.57(.20)	3.0(0.2)	4.3(2.4)
		SCAD-OS	.173	1.06(.25)	.44(.28)	.72(.26)	2.8(0.4)	1.6(2.2)
		SCAD	.202	1.08(.25)	.45(.30)	.77(.25)	2.8(0.5)	1.2(2.1)
		TLP-OS	.155	1.00(.24)	.40(.24)	.67(.24)	2.9(0.3)	1.8(2.1)
		TLP	.157	1.00(.24)	.40(.24)	.67(.24)	2.9(0.3)	1.8(2.1)
200	200	Lasso	.540	.68(.18)	.27(.17)	.38(.17)	2.9(0.3)	14.1(8.9)
		SCAD-OS	.271	1.07(.26)	.34(.32)	.64(.32)	2.6(0.6)	3.2(3.3)
		SCAD	.262	1.12(.29)	.30(.37)	.68(.36)	2.3(0.6)	0.8(1.4)
		TLP-OS	.204	1.04(.25)	.40(.29)	.68(.27)	2.7(0.5)	3.3(5.5)
		TLP	.204	1.04(.26)	.39(.30)	.68(.28)	2.7(0.5)	3.2(5.8)
200	500	Lasso	.651	.64(.17)	.24(.16)	.33(.15)	2.9(0.3)	18.0(10.5)
		SCAD-OS	.289	1.07(.27)	.31(.32)	.57(.31)	2.5(0.5)	4.1(4.0)
		SCAD	.262	1.13(.28)	.29(.37)	.66(.36)	2.3(0.6)	1.4(1.7)
		TLP-OS	.231	1.04(.27)	.39(.30)	.65(.29)	2.7(0.5)	4.1(6.8)
		TLP	.231	1.04(.27)	.38(.30)	.65(.30)	2.7(0.5)	3.8(6.8)

4.2 Theory for feature selection

This section establishes some theoretical results to gain an insight into performance of the proposed method in feature selection. Let Y = (Z, X), and $g(\mathit{\beta },Z)=\frac{1}{2\sqrt{\pi }\sigma }exp(-\frac{1}{2{\sigma }^2}{(Z-{\mathit{\beta }}^T\mathit{X})}^2)$ and g(β, Z) = p^Z(1 − p)^1−Z in linear and logistic regression. Assume that ${\mathit{\beta }}^T\mathit{x}={\mathit{\beta }}_A^T{\mathit{x}}_A$ belongs to a compact parameter space for any model size |A| ≤ p₀. In this case, selection does not involve nuisance parameters, where θ = β. Under (14), we establish feature selection consistency as well as optimal parameter estimation for the TLP:

$$\begin{array}{l}{C}_{min}({\mathit{\beta }}^0)=\underset{A:\mid A\mid \le p_0,A\ne A_0}{min}\frac{1}{max(\mid A_0\backslash A\mid ,1)}{\left({\mathit{\beta }}_{A_0\backslash A}^0\right)}^T\left({\mathrm{\sum }}_{A_0\backslash A}-{\mathrm{\sum }}_{A_0\backslash A,A}{\mathrm{\sum }}_A^{-1}{\mathrm{\sum }}_{A,A_0\backslash A}\right){\mathit{\beta }}_{A_0\backslash A}^0\\ \ge d_0\frac{logp}{n},\end{array}$$ (14)

where d₀ > 0 is a constant independent of (n, p, p₀), and Σ_B is a sub-matrix given a subset B of predictors, of covariance matrix Σ with the jkth element Cov(X_j, X_k), independent of β⁰. A simpler but stronger condition can be used for verification of (14):

$${\gamma }_{min}^2\underset{A:\mid A\mid \le p_0,A\ne A_0}{min}{c}_{min}\left({\mathrm{\sum }}_{A_0\backslash A}-{\mathrm{\sum }}_{A_0\backslash A,A}{\mathrm{\sum }}_A^{-1}{\mathrm{\sum }}_{A,A_0\backslash A}\right)\ge d_0\frac{logp}{n},$$ (15)

where ${\gamma }_{min}={\gamma }_{min}({\mathit{\beta }}^0)\equiv min\{\mid {\beta }_k^0\mid :{\beta }_k^0\ne 0\}$ is the resolution level of the true regression coefficients, ${min}_{A:\mid A\mid \le p_0,A\ne A_0}{c}_{min}\left({\mathrm{\sum }}_{A_0\backslash A}-{\mathrm{\sum }}_{A_0\backslash A,A}{\mathrm{\sum }}_A^{-1}{\mathrm{\sum }}_{A,A_0\backslash A}\right)\ge {min}_{B\supset A_0:\mid B\mid \le 2p_0}{c}_{min}({\mathrm{\sum }}_B)$, and c_min denotes the smallest eigenvalue. Note that (14) is necessary for any method to be selection consistent except constant d₀ if ${min}_{A:\mid A\mid \le p_0,A\ne A_0}{c}_{min}\left({\mathrm{\sum }}_{A_0\backslash A}-{\mathrm{\sum }}_{A_0\backslash A,A}{\mathrm{\sum }}_A^{-1}{\mathrm{\sum }}_{A,A_0\backslash A}\right)>0$.

Proposition 1

Under (14), the constrained MLE β̂^T of (4) consistently reconstructs the oracle estimate β̂^ml. As n, p → ∞, feature selection consistency is established for the TLP as well as optimal parameter estimation ${Eh}^2({\widehat{\mathit{\beta }}}^T,{\mathit{\beta }}^0)={Eh}^2({\widehat{\mathit{\beta }}}^{ml},{\mathit{\beta }}^0)=O(\frac{p_0}{n})$ under the Hellinger distance h(·, ·). Moreover, the results hold uniformly over a L₀-band $B_0(u,l)=\{{\mathit{\beta }}_0:{\sum }_{j=1}^{p}I({\beta }_j^0\ne 0)\le u,{\gamma }_{min}^2({\mathit{\beta }}^0){min}_{B\supset A_0:\mid B\mid \le 2p_0}{c}_{min}({\mathrm{\sum }}_B)\ge l\}$, with 0 < u ≤ min(n, p), $l=d_0{\sigma }^2\frac{logp}{n}$, that is, as n, p → ∞,

$$\underset{{\mathit{\beta }}^0\in B_0(u,l)}{sup}P\left({\widehat{\mathit{\beta }}}^T\ne {\widehat{\mathit{\beta }}}^{ml}\right)\to 0,\frac{{sup}_{{\mathit{\beta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\beta }}}^T,{\mathit{\beta }}^0)}{{sup}_{{\mathit{\beta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\beta }}}^{ml},{\mathit{\beta }}^0)}\to 1,$$

with ${sup}_{{\mathit{\beta }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathit{\beta }}}^{ml},{\mathit{\beta }}^0)=d^{\ast }\frac{u}{n}$ for some d^*.

Various conditions have been proposed for studying feature selection consistency in linear regression. In particular, a condition on γ_min is usually imposed, in addition to assumptions on the design matrix X such as the sparse Riesz condition in [32]. To compare (14) with existing assumptions for consistent selection, note that these assumptions imply a fixed design version of (14) by necessity of consistent feature selection. For instance, as showed in [32], the sparse Riesz condition with dimension restriction and ${\gamma }_{min}^2\ge c^{\prime }\frac{log(p-u)}{n}$, required for the minimum concavity penalty to be consistent, imply (15) with p replaced by p − u thus (14) when p/u bounded away from 1, where u ≥ p₀. Moreover, the number of over-selected variables is proved to be bounded but may not tend to zero for thresholding Lasso in Theorem 1.1 of [35], under a restrictive eigenvalue condition [1] and a requirement on γ_min. Finally, in linear regression, only finite variance σ² is required for the proposed method, which is in contrast to a commonly used assumption on sub-Gaussian distribution of ε_i.

In conclusion, the computational surrogate–the TLP method indeed shares desirable oracle properties of the L₀-method, which is optimal against any selection method, for feature selection and parameter estimation.

5 Estimation of a precision matrix

Given n random samples from a p-dimensional normal distribution Y₁, ···, Y_n ~ N (μ, Σ), we estimate the inverse covariance matrix Ω = Σ⁻¹ that is p × p positive definite, denoted by Ω ≻ 0. For estimation of (μ, Ω), the log-likelihood is proportional to

$$\frac{n}{2}log\mathit{det}(\mathbf{\Omega })-\frac{1}{2}\sum _{i=1}^n{({\mathit{Y}}_i-\mathit{\mu })}^T\mathbf{\Omega }({\mathit{Y}}_i-\mathit{\mu }).$$ (16)

The profile log-likelihood for Ω, after μ is maximized out, is proportional to $\frac{n}{2}log\mathit{det}(\mathbf{\Omega })-\frac{1}{2}tr(\mathit{S}\mathbf{\Omega })$, where $\overline{\mathit{Y}}=n^{-1}{\sum }_{i=1}^n{\mathit{Y}}_i$ and $\mathit{S}=n^{-1}{\sum }_{i=1}^n({\mathit{Y}}_i-\overline{\mathit{Y}}){({\mathit{Y}}_i-\overline{\mathit{Y}})}^T$ are the corresponding sample mean and covariance matrix, det and tr denote the determinant and trace. In (16), the number of unknown parameters p² in Ω can greatly exceed the sample size n in the presence of 2p nuisance parameters (μ, {Ω_jj : j = 1, ···, p}), where Ω_jk denotes the jkth elements of Ω. To avoid non-identifiability in estimation, we regularize off-diagonal elements of Ω in (16) through a nonnegative penalty function J(·) for the $\frac{p(p-1)}{2}$ parameters of interest:

$$S(\mathbf{\Omega })=log\mathit{det}(\mathbf{\Omega })-\frac{1}{2}tr(\mathit{S}\mathbf{\Omega })-\sum _{j,k=1,j\ne k}^{p}J(\{{\mathrm{\Omega }}_{jk},j\ne k\}).$$ (17)

In estimation, the TLP function $J(\{{\mathrm{\Omega }}_{jk},j\ne k\})=\frac{\lambda }{\tau }min(\mid {\mathrm{\Omega }}_{jk}\mid ,\tau )$ is employed for both parameter estimation and covariance selection in (17). Towards this end, we apply Algorithm 1 to solve (6) sequentially, which reduces to a series of weighted graphical lasso problems, and is solved by taking advantage of existing software. In implementation, we use R package glasso [8] for (6).

5.1 Simulations

Simulations are performed, where a tridiagonal precision matrix is used as in [7]. In particular, Σ is AR(1)-structured with its ij-element being σ_ij = exp(−a|s_i − s_j|), and s₁ < s₂ < ···< s_p are randomly chosen: s_i − s_i−1 ~ Unif(0.5, 1), for some a > 0; i = 2, ···, p. The following situations are considered: (n, p) = (120, 30) or (n, p) = (120, 200), and a = 0.9 or a = 0.6, based on 100 replications.

Five competing methods are compared, including Lasso, adaptive Lasso (ALasso), SCAD-OS and SCAD, and TLP-OS and TLP. ALasso uses weight $\lambda /\mid {\widehat{\beta }}_j^{(0)}{\mid }^{\gamma }$, where β̂⁽⁰⁾ is an initial estimate and γ = 1/2 as in [7].

To measure performance of estimator Ω̂, we use the entropy loss and quadratic loss: loss₁(Ω, Ω̂) = tr(Ω⁻¹Ω̂) − log |Ω⁻¹Ω̂| − p, and loss₂(Ω, Ω̂) = tr(Ω⁻¹Ω̂ − I)², as well as the true positive (TP) and false positive (FP) numbers: #TP = Σ_i,j I(Ω_ij ≠ 0, Ω̂_ij ≠ 0); #FP = Σ_i,j I(ω_ij = 0, Ω̂_ij ≠ 0).

For small p = 30, TLP and TLP-OS are always among the winners. It is also confirmed that the one-step approximation to SCAD or TLP gives similar performance to that of the fully iterated SCAD or TLP, respectively. For large p, to save computing time, as advocated in [7], we only run SCAD-OS and TLP-OS. In such a situation, an improvement of TLP-OS over other methods is more substantial for large p = 200 than for small = 30. Overall, the proposed method delivers higher performance in low-dimensional and high-dimensional situations, respectively.

5.2 Theory for precision matrix

To perform theoretical analysis, we specify a parameter space Θ in which Ω ❻ 0 with 0 < max_1≤j≤p |Ω_jj| ≤ M₂, c_min(Ω) ≥ M₁ > 0, for some constants M₁, M₂ > 0, independent of (n, p, p₀). Let A = {(j, k) : j ≠ k, Ω_jk ≠ 0} be the set of nonzero off diagonal elements of Ω, where |A| = p₀ is an even number by symmetry of Ω, and Ω depends on A. Results in Theorem 1 imply that the constrained MLE yields covariance selection consistency under one assumption:

$$C_{min}({\mathbf{\Omega }}^0)\ge d_0\frac{logp}{n},$$ (18)

which is necessary for covariance selection consistency indeed for any method, up to constant d₀ when c_min(H) > 0, where d₀ > 0 is a constant independent of (n, p, p₀), and $H=\left(\frac{{\partial }^2(-logdet(\mathbf{\Omega }))}{{\partial }^2\mathbf{\Omega }}\right){\mid }_{\mathrm{\Omega }={\mathrm{\Omega }}_0}$ is the p² ×p² Hessian matrix of −log det(Ω), whose (Ω_jk, Ω_j′k′) element is tr(Σ⁰Δ_jkΣ⁰Δ_j′k′), c.f., [3], Δ_jK is a p × p with the jk-element being 1 and 0 otherwise. Sufficiently, (18) can be verified using

$$C_{min}({\mathbf{\Omega }}^0)\ge {\gamma }_{\mathit{min}}^2{c}_{min}(H),$$ (19)

with ${\gamma }_{min}({\mathbf{\Omega }}^0)\equiv {\gamma }_{min}=min\{\mid {\mathrm{\Omega }}_{jk}^0\mid :{\mathrm{\Omega }}_{jk}^0\ne 0,j\ne k\}$.

Proposition 2

Under (18), the constrained MLE Ω̂^T of (4) consistently reconstructs the oracle estimator Ω̂^ml. As n, p → ∞, covariance selection consistency is established for the TLP as well as optimal parameter estimation ${Eh}^2({\widehat{\mathbf{\Omega }}}^T,{\mathbf{\Omega }}^0)=(1+o(1)){Eh}^2({\widehat{\mathbf{\Omega }}}^{ml},{\mathbf{\Omega }}^0)=O(\frac{p_{0}logp}{n})$, where $h^2(\mathbf{\Omega },{\mathbf{\Omega }}^0)=1-\sqrt{\frac{{(\mathit{det}(\mathbf{\Omega })\mathit{det}({\mathbf{\Omega }}^0))}^{1/2}}{\mathit{det}(\frac{\mathbf{\Omega }+{\mathbf{\Omega }}^0}{2})}}$ is the squared Hellinger distance for Ω versus Ω⁰. Moreover, the above results hold uniformly over a L₀-band $B_0(u,l)=\{{\mathbf{\Omega }}^0:{\sum }_{j,k=1,j\ne k}^{p}I({\mathrm{\Omega }}_{jk}^0\ne 0)\le u,{\gamma }_{\mathit{min}}^2({\mathbf{\Omega }}^0)c_{min}(H)\le l\}$, with 0 < u ≤ min(n, p) and $l=d_0{\sigma }^2\frac{logp}{n}$, that is, as n, p → ∞,

$$\underset{{\mathbf{\Omega }}^0\in B_0(u,l)}{sup}P\left({\widehat{\mathbf{\Omega }}}^T\ne {\widehat{\mathbf{\Omega }}}^{ml}\right)\to 0,\frac{{sup}_{{\mathbf{\Omega }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathrm{\Omega }}}^T,{\mathbf{\Omega }}^0)}{{sup}_{{\mathbf{\Omega }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathrm{\Omega }}}^{ml},{\mathbf{\Omega }}^0)}\to 1,$$

with ${sup}_{{\mathbf{\Omega }}^0\in B_0(u,l)}{Eh}^2({\widehat{\mathbf{\Omega }}}^{ml},{\mathbf{\Omega }}^0)=d^{\ast }\frac{\mathit{u}logp}{n}$ for some d^* > 0.

In short, the TLP method is optimal against any method in covariance selection, permitting p up to exponentially large in the sample size, or $p^2\le p_{0}exp\left(n\frac{{\gamma }_{min}^2{c}_{min}(H)}{d_0}\right)$. Moreover, as a result of accurate selection of this method, parameter estimation can be sharply enhanced at an order of $\sqrt{\frac{p_{0}logp}{n}}$, as measured by the Hellinger distance, after zero off-diagonal elements are removed. Note that the log p factor is due to estimation of 2p nuisance parameters as compared to the rate of $\sqrt{\frac{p_0}{n}}$ in logistic regression. In view of the result in Lemma 1, this result seems to be consistent with the minimax rate $\sqrt{\frac{logp}{n}}$ under the L_∞ matrix norm [20].

6 Metastasis status of breast cancer patients

We apply the penalized logistic regression methods to analyze a microarray gene expression dataset of [29], where our objectives are (1) to develop a model predicting the metastasis status, and (2) to identify cancer genes, for breast cancer patients. Among the 286 patients, metastasis was detected in 106 patients during follow-ups within 5 years after surgery. Their expression profiles were obtained from primary breast tumors with Affymetrix HG-133a GeneChips.

In [29], a 76-gene signature was developed based on a training set of 115 patients, which yielded a misclassification error rate of 64/171=37.4% when applied to the remaining samples. [30] compared the performance of a variety of classifiers using a subset of 245 genes drawn from 33 cancer-related pathways: based on a 10-fold cross-validation (CV). Their non-parametric pathway-based regression method yielded the smallest error rate at 29%, while random forest, bagging and Support Vector Machine (SVM) had error rates of 33%, 35% and 42%.

In our analysis, we first performed a preliminary screening of the genes using a marginal t-test to select the top p genes with most significant p-values, based on the training data for each fold of a 10-fold-CV. Then the training data were split into two parts to fit penalized logistic models and to select tuning parameters, respectively. The results were summarized in Table 3, including the total misclassification errors and average model sizes (i.e. non-zero estimates) based on 10-fold CV. A final model is obtained by fitting the best model selected from a 10-fold CV to the entire data set.

With regard to prediction, no large difference is seen among various methods, with the error rates ranging from 102/286=35.7% (of TLP and TLP-OS with p = 200) to 118/286=41.3% (of ALasso with p = 200). The TLP performed similar to the TLP-OS, both were among the winners. In addition, the Lasso gave the least sparse models while the SCAD gave the most sparse models.

With regard to identifying cancer genes, the Lasso, TLP-OS and TLP yield the same model, identifying the largest number of cancer genes, whereas the SCAD and SCAD-OS give the most sparse models with only at most 2 cancer genes, and ALasso only yields 10 cancer genes. Here cancer genes are defined according to the Cancer Gene Database [10].

In summary, the TLP and TLP-OS identify a good proportion of cancer genes and lead to a model giving a reasonably good predictive accuracy of the metastasis status. In this sense, they perform well with regard to the foregoing two objectives.

Table 3.

Averaged (with SD in parentheses) entropy loss (loss₁), quadratic loss (loss₂), true positive (TP) and false positive (FP) numbers of nonzero parameters based on 100 simulations, for estimating a precision matrix in Gaussian graphical models in Section 4.

Set-up	Method	loss1	loss2	#TP	#FP
p = 30, a = 0.9	Lasso	1.55(.15)	2.96(.42)	88.0(.0)	314.0(41.6)
	ALasso	1.02(.15)	1.99(.37)	88.0(.0)	95.5(30.2)
	SCAD-OS	0.93(.16)	1.99(.44)	88.0(.0)	126.0(39.4)
	SCAD	0.74(.16)	1.60(.42)	87.9(.5)	85.5(18.0)
	TLP-OS	0.66(.18)	1.47(.47)	87.9(.5)	28.1(21.4)
	TLP	0.63(.18)	1.39(.48)	87.8(.7)	22.4(17.0)
p = 30, a = 0.6	Lasso	1.69(.16)	3.28(.46)	88.0(.0)	342.5(35.5)
	ALasso	1.01(.15)	1.97(.37)	88.0(.0)	103.9(17.4)
	SCAD-OS	0.75(.14)	1.61(.36)	88.0(.0)	83.8(29.0)
	SCAD	0.56(.12)	1.20(.30)	88.0(.2)	26.1(15.0)
	TLP-OS	0.57(.14)	1.26(.37)	88.0(.0)	14.7(13.0)
	TLP	0.54(.14)	1.18(.36)	88.0(.0)	7.3(10.6)
p = 200, a = 0.9	Lasso	20.16(.50)	34.50(1.85)	597.9(.4)	4847.8(614.7)
	ALasso	10.62(.53)	19.64(1.20)	597.3(1.2)	936.8(37.9)
	SCAD-OS	11.46(.60)	24.03(1.67)	597.7(.8)	2453.6(251.2)
	TLP-OS	6.16(.77)	13.99(2.10)	593.6(3.0)	284.8(158.0)
p = 200, a = 0.6	Lasso	24.86(.54)	46.18(3.72)	598.0(.0)	6161.7(863.0)
	ALasso	11.06(.48)	21.53(1.18)	598.0(.0)	1526.1(118.6)
	SCAD-OS	9.43(.49)	20.871.77)	598.0(.0)	2754.8(523.6)
	TLP-OS	4.45(.48)	9.89(1.29)	597.7(.7)	185.5(76.3)

Table 4.

Analysis results with various numbers (p) of predictors for the breast cancer data. The numbers of total classification errors (#Err), including false positives (#FP), and mean numbers of nonzero estimates (#Nonzero) from 10-fold CV, and the total numbers of nonzero estimates and cancer genes in the final models are shown.

p	Method	10-fold CV			Final model
		#Err	#FP	#Nonzero	#Nonzero	#Cancer genes
200	Lasso	107	17	40.1	62	13
	ALasso	118	27	18.8	39	9
	SCAD-OS	107	4	9.5	15	2
	SCAD	107	1	4.7	2	0
	TLP-OS	102	8	33.5	62	13
	TLP	102	8	33.2	62	13
400	Lasso	107	19	46.9	95	26
	ALasso	112	19	14.4	32	10
	SCAD-OS	108	8	11.1	15	2
	SCAD	106	0	4.1	2	0
	TLP-OS	106	15	40.1	95	26
	TLP	106	14	38.2	95	26

7 Appendix

Proof of Theorem 1

The proof uses a large deviation probability inequality of [27] to treat one-sided log-likelihood ratios with constraints. This enables us to obtain sharp results without a moment condition on both tails of the log-likelihood ratios.

When K = p₀, |Â^L₀| ≤ p₀. If Â^L₀ = A₀, then β̂^L₀ = β̂^ml. Let a class of candidate subsets be {A : A ≠ A₀, |A| ≤ p₀} for feature selection. Note that A ⊂ {1, ···, p} can be partitioned into (A \ A₀) ∪ (A₀ ∩ A). Let B_kj = {θ = (β_A, 0, η) : A ≠ A₀, |A₀ ∩ A| = k, |A \ A₀| = j, (p₀ − k)C_min(θ⁰) ≤ h²(θ, θ⁰)} ⊂ 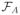; k = 0, ···, p₀ − 1, j = 1, ···, p₀ − k. Note that B_kj consists of $\left(\begin{array}{c}{p}_0\\ k\end{array}\right)\left(\begin{array}{c}p-p_0\\ j\end{array}\right)$ different elements A’s of sizes |A₀ ∩ A| = k and |A \ A₀| = j. By definition, $\{\mathit{\theta }=({\mathit{\beta }}_A,\mathbf{0},\mathit{\eta }):A\ne A_0:C_{min}({\mathit{\theta }}^0)\le h^2(\mathit{\theta },{\mathit{\theta }}^0),\mid A\mid \le p_0\}\subset {\cup }_{k=0}^{p_0-1}{\cup }_{j=1}^{p_0}{B}_{kj}$. Hence

$$\begin{array}{l}P({\widehat{\mathit{\theta }}}^{L_0}\ne {\widehat{\mathit{\theta }}}^{ml})\le P^{\ast }\left(\underset{\mathit{\theta }=(\mathit{\beta },\mathit{\eta }):\mathit{\beta }=({\mathit{\beta }}_A,\mathbf{0}),A\ne A_0,\mid A\mid \le p_0}{sup}(L(\mathit{\theta })-L({\widehat{\mathit{\theta }}}^{ml}))>0\right)\\ \le P^{\ast }\left(\underset{\mathit{\theta }=(\mathit{\beta },\mathit{\eta }):\mathit{\beta }=({\mathit{\beta }}_A,\mathbf{0}),A\ne A_0,\mid A\mid \le p_0}{sup}(L(\mathit{\theta })-L({\mathit{\theta }}^0))>0\right)\\ \le \sum _{A\subset \{1,\cdots ,p\}:A\ne A_0,\mid A\mid \le p_0}{P}^{\ast }\left(\underset{\mathit{\theta }=(\mathit{\beta },\mathit{\eta }):\mathit{\beta }=({\mathit{\beta }}_A,\mathbf{0})}{sup}(L(\mathit{\theta })-L({\mathit{\theta }}^0))\ge 0\right)\equiv I\end{array}$$

where P^* is the outer measure and L(θ̂^ml) ≥ L(θ ⁰) by definition.

For I, we apply Theorem 1 of [27] to bound each term. Towards this end, we verify the entropy condition (3.1) there for the local entropy over 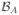. Note that under Assumption A $\epsilon ={\epsilon }_{n,p_0,p}={(2c_0)}^{1/2}{c}_4^{-1}log(2^{1/2}/c_3)logp{(\frac{p_0}{n})}^{1/2}$ satisfies there with respect to ε > 0, that is,

$$\underset{\{0\le \mid A\mid \le p_0\}}{sup}{\int }_{2^{-8}{\epsilon }^2}^{2^{1/2}\epsilon }{H}^{1/2}(t/c_3,{\mathcal{B}}_A)dt\le p_0^{1/2}{2}^{1/2}\epsilon log(2/2^{1/2}{c}_3)\le c_4{n}^{1/2}{\epsilon }^2.$$ (20)

for some constant c₃ > 0 and c₄, say c₃ = 10 and $c_4=\frac{{(2/3)}^{5/2}}{512}$. Moreover, by Theorem 2.6 of [25], $\left(\begin{array}{c}b\\ a\end{array}\right)\le \frac{b^{b+1/2}}{\sqrt{2\pi }{a}^{a+1/2}{(b-a)}^{b-a+1/2}}\le exp((a+1/2)log(b/a)+a)$ for any integers a < b. By (3), $C_{min}({\mathit{\theta }}^0)\ge {\epsilon }_{n,p_0,p}^2$ implies (20), provided that $d_0>{(2c_0)}^{1/2}{c}_4^{-1}log(2^{1/2}/c_3)$. Using the facts about binomial coefficients: ${\sum }_{j=0}^{p_0-k}\left(\begin{array}{c}p-p_0\\ j\end{array}\right)\le {(p-p_0+1)}^{p_0-k}$ and $\left(\begin{array}{c}{p}_0\\ i\end{array}\right)\le p_0^i$, we obtain, by

Theorem 1 of [27], that for a constant c₂ > 0, say $c_2=\frac{4}{27}\frac{1}{1926}$, I is upper bounded by

$$\begin{array}{l}\sum _{k=0}^{p_0-1}\sum _{j=0}^{p_0-k}{P}^{\ast }(\underset{\mathit{\theta }\in B_{kj}}{sup}(L(\mathit{\theta })-L({\mathit{\theta }}^0))\ge 0)\le 4\sum _{k=0}^{p_0-1}\left(\begin{array}{c}{p}_0\\ k\end{array}\right)exp(-c_{2}n(p_0-k)C_{min}({\mathit{\theta }}^0))\sum _{j=0}^{p_0-k}\left(\begin{array}{c}p-p_0\\ j\end{array}\right)\\ \le 4\sum _{i=1}^{p_0}exp\left(-i(c_2{nC}_{min}({\mathit{\theta }}^0)-log(p-p_0+1)-log{p}_0)\right)\\ \le R\left(exp(-(c_2{nC}_{min}({\mathit{\theta }}^0)-log(p-p_0+1)-log{p}_0))\right),\end{array}$$

where R(x) = x/(1 − x) is the exponentiated logistic function. Note, moreover, that I ≤ 1 and $log(p-p_0+1)+log{p}_0\le 2log(p+1)/2\le 2log\frac{p+1}{2}$. Then

$$I\le 5exp(-c_2{nC}_{min}({\mathit{\theta }}^0)+2log\frac{p+1}{2})\le exp(-c_2{nC}_{min}({\mathit{\theta }}^0)+2log(p+1)+3).$$

Finally, (A) follows from P(Â^L₀ ≠ A₀) ≤ P (θ̂^L₀ ≠ θ̂^ml), (8) and (3) with $d_0>\frac{2}{c_2}$, as n, p → ∞. For (B), let G = {θ̂^L₀ ≠ θ̂^ml} and P(G) ≤ 8 exp(−c₂nC_min/4) by (8) and (3). For the risk property, Eh²(θ̂^L₀, θ⁰) ≤ Eh²(θ̂^ml, θ̂⁰) + Eh²(θ̂^L₀, θ⁰)I(G) is upper bounded by

$${Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0)+4exp(-c_2{nC}_{min}/2)=(1+o(1)){Eh}^2({\widehat{\mathit{\theta }}}^{ml},{\mathit{\theta }}^0),$$

using the fact that h(θ̂^L₀, θ⁰) ≤ 1. Then (B) is established. Similarly (C) follows. This completes the proof.

Proof of Theorem 2

The proof is basically the same as that in Theorem 1 with a modification that A is replaced by A^τ+. Now B_kj = {θ_τ⁺ : A^τ+ ≠ A₀, |A₀ ∩ A^τ+| = k, |A^τ+ \A₀| = j, (d₁(p₀ − k)C_min(θ⁰) − d₃pτ^d₂) ≤ h²(θ_τ⁺, θ⁰)}; j = 1, ···, p₀. Then $\{\mathit{\theta }=({\mathit{\beta }}_A,\mathbf{0},\mathit{\eta }):A\ne A_0:{\sum }_{j=1}^{p}J(\mid {\beta }_j\mid )\le p_0,C_{min}({\mathit{\theta }}^0)\le h^2(\mathit{\theta },{\mathit{\theta }}^0)\}\subset {\cup }_{k=0}^{p_0-1}{\cup }_{j=1}^{p_0-k}{B}_{kj}$.

When K = p₀, ${\sum }_{j=1}^{p}J(\mid {\beta }_j\mid )\le p_0$, implying that |Â⁺| ≤ p₀. If |Â⁺| = p₀, then ${\sum }_{j=1}^p\mid {\beta }_j\mid I(\mid {\beta }_j\mid \le \tau )=0$, implying that θ̂^T = θ̂^ml. Then we focus our attention to the case of A⁺ ≠ A₀. Note that, with θ = (β, η) and β = (β_A, 0),

$$\begin{array}{l}{P}^{\ast }\left(\underset{\mathit{\theta }:A\ne A_0,{\sum }_{j=1}^{p}J(\mid {\beta }_j\mid )\le p_0}{sup}(L(\mathit{\theta })-L({\mathit{\theta }}^0))\ge 0\right)\le \sum _{j=1}^{p_0}{P}^{\ast }\left(\underset{\mathit{\theta }\in B_j}{sup}(L(\mathit{\theta }))-L({\mathit{\theta }}^0))\ge 0\right)\\ \le 4\sum _{k=0}^{p_0-1}\sum _{j=0}^{p_0-k}\left(\begin{array}{c}p-p_0\\ j\end{array}\right)\left(\begin{array}{c}{p}_0\\ k\end{array}\right)exp(-c_{2}n(d_1{C}_{min}({\mathit{\theta }}^0)-d_{3}p{\tau }^{d_2}))\\ \le 5exp(-(c_2{d}_1/2){nC}_{min}({\mathit{\theta }}^0)+2log\frac{p+1}{2})\le exp(-c_2{nC}_{min}({\mathit{\theta }}^0)+2log(p+1)+3),\end{array}$$

provided that τ ≤ (d₁C_min(θ ⁰)/2pd₃)^1/d₂. The rest of the proof proceeds as in the proof of Theorem 1. This completes the proof.

Proof of Theorem 3

The main idea of the proof is the same as that for Theorem 1 of [24], which constructs an approximated least favorable situation for feature selection and uses Fano’s Lemma. According to Fano’s Lemma [11], for any mapping T = T(Y₁, ···, Y_n) taking values in S = {1, ···, ∣S∣}, $\mid S{\mid }^{-1}{\sum }_{j=1}^{\mid S\mid }{P}_j(T(Y_1,\cdots ,Y_n)=j)\le {\sum }_{1\le j,k\le \mid S\mid }\frac{nK(q_j,q_k)+log2}{{\mid S\mid }^{2}log(\mid S\mid -1)}$, where K(q_j, q_k) = ∫ q_j log(q_j/q_k) is the Kullback-Leibler information for densities q_j versus q_k corresponding P_j and P_k.

To construct an approximated least favorable set of parameters S for A₀ versus $A_0^c$, define β to be ( ${\gamma }_{min}{\mathbf{1}}_{\mid A_0\mid },{\mathbf{0}}_{\mid A_0^c\mid }$). Let $S={\{{\mathit{\theta }}_j=({\mathit{\beta }}_j,{\mathit{\eta }}^0)\}}_{j=0}^p$ be a collection of parameters with components equal to γ_min or 0 satisfying that for any 1 ≤ j, j′ = p, ${\left|\right|{\mathit{\beta }}_{j^{\prime }}-{\mathit{\beta }}_j\left|\right|}^2\le 4{\gamma }_{\mathit{min}}^2$, as defined in Assumption C. Then for any θ_j, θ_k ∈ S, $K({\mathit{\theta }}_j,{\mathit{\theta }}_k)\le r{\gamma }_{min}^2\le n\frac{r}{s}{C}_{min}({\mathit{\theta }}^0)$ by Assumption C.

By Fano’s lemma, ${\mid S\mid }^{-1}{\sum }_{j\in S}{P}_j(T=j)\le \frac{n(r/s)C_{min}({\mathit{\theta }}^0)+log2}{logp}$, implying that

$$\underset{\{\mathit{\theta }:C_{min}({\mathit{\theta }}^0)=R^{\ast }\}}{sup}P(\widehat{A}\ne A_0)\ge 1-\frac{{\mathit{nrC}}_{min}({\mathit{\theta }}^0)+slog2}{\mathit{s}logp},$$

bounded below by c_* with $R^{\ast }=\frac{s(1-c_{\ast })logp}{4rn}$. This yields (12). For (13), it follows that R^* ≥ l with $l=d_1\frac{logp}{n}$ and $d_1=\frac{(1-c^{\ast })s}{4r}$, for any θ⁰ ∈ B₀(u, l). This completes the proof.

Proof of Proposition 1

We now verify Assumptions A–C. Note that

$$h^2(\mathit{\beta },{\mathit{\beta }}^0)=2E\left(1-exp(-\frac{1}{8}{({\mathit{\beta }}^T\mathit{X}-{({\mathit{\beta }}^0)}^T\mathit{X})}^2)\right)$$

for linear regression, and h²(β, β⁰) is

$$\frac{1}{2}\left(E{({\mu }^{1/2}({({\mathit{\beta }}^0)}^T\mathit{X})-{\mu }^{1/2}({\mathit{\beta }}^T\mathit{X}))}^2+{(1-\mu ({({\mathit{\beta }}^0)}^T\mathit{X}))}^{1/2}-{(1-\mu ({\mathit{\beta }}^T\mathit{X}))}^{1/2}\right),$$

for logistic regression, where μ(s) = (1 + exp(s))⁻¹.

Assumption A follows from [14]. Note that $A=A^{{\tau }^{+}}\cup A_2^{{\tau }^{-}}$ and $\left|\frac{\partial h^2(\mathit{\beta },{\mathit{\beta }}^0)}{\partial {\beta }_j}\right|\le \frac{1}{2}E(\mid X_j\mid )$, for 1 ≤ j ≤ p and β ∈ 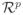. Thus

$$\mid h^2(\mathit{\beta },{\mathit{\beta }}^0)-h^2({\mathit{\beta }}_{{\tau }^{+}},{\mathit{\beta }}^0)\mid =\tau {\left|\sum _{j\in A^{{\tau }^{-}}}\frac{\partial h^2(\mathit{\beta },{\mathit{\beta }}^0)}{\partial {\beta }_j}\right|}_{\mathit{\beta }={\mathit{\beta }}^{★}}|\le 2\tau \sum _{j\in A^{{\tau }^{+}}}E(\mid X_j\mid )\le 2\tau p\underset{j}{max}{\mathrm{\sum }}_{jj}.$$

Then Assumption B is fulfilled with d₁ = d₂ = 1 and d₃ = 2 max_j Σ_jj.

To simplify (3), we derive an inequality through some straightforward calculations: with β̃ = ((β_A, 0) − (0, β_A0))

$$\begin{array}{l}{C}_{min}({\mathit{\beta }}^0)\ge c_1^{\ast }\underset{{\mathit{\beta }}_A:A\ne A_0,\mid A\mid \le p_0}{min}{\mid A_0\backslash A\mid }^{-1}E{({\mathit{\beta }}_A{\mathit{X}}_A-{\mathit{\beta }}_{A_0}{\mathit{X}}_{A_0})}^2\\ \ge c_1^{\ast }\underset{{\mathit{\beta }}_A:A\ne A_0,\mid A\mid \le p_0}{min}{\mid A_0\backslash A\mid }^{-1}{\stackrel{\sim }{\mathit{\beta }}}^T{\mathrm{\sum }}_{A\cup A_0}\stackrel{\sim }{\mathit{\beta }}\ge {\gamma }_{min}^2\underset{B:\mid B\mid \le 2p_0,A_0\subset B}{min}{c}_{min}({\mathrm{\sum }}_B).\end{array}$$

for some constant $c_1^{\ast }>0$, because the derivative of $1-exp(-\frac{1}{8}{x}^2)$ and (1 + exp(x))^−1/2 are bounded away from zero under the compactness assumption. This leads to (14). By Theorem 2, the TLP has the properties (A)–(C) there, through tuning.

Finally, $K({\mathit{\beta }}_j,{\mathit{\beta }}_k)\le cE{({\mathit{\beta }}_{A_j}{\mathit{X}}_{A_j}-{\mathit{\beta }}_{A_k}{\mathit{X}}_{A_k})}^2\le r{\gamma }_{min}^2$ by the compactness assumption, where r = c max_(Aj,Ak) E(β_Aj X_Aj − β_Ak X_Ak)². By Theorem 3, (14) except a constant d₀ > 0 is necessary for any method to be feature selection consistent. This completes the proof.

Proof of Proposition 2

To obtain the desired results, Theorems 1–3 are applied. First a lower bound of C_min(θ⁰) is derived to simplify (3). Given the squared Hellinger distance $h^2(\mathit{\theta },{\mathit{\theta }}^0)=1-\sqrt{\frac{{(\mathit{det}(\mathbf{\Omega })\mathit{det}({\mathbf{\Omega }}^0))}^{1/2}}{\mathit{det}(\frac{\mathbf{\Omega }+{\mathbf{\Omega }}^0}{2})}}{e}^{-\frac{1}{4}{(\mathit{\mu }-{\mathit{\mu }}^0)}^T(\mathbf{\Omega }+{\mathbf{\Omega }}^0)(\mathit{\mu }-{\mathit{\mu }}^0)}$, by strong convexity of −log det(Ω), c.f., [3], for any θ ∈ Θ and a constant c^* > 0 depending on M₁,

$$\begin{array}{l}-2log(1-h^2(\mathit{\theta },{\mathit{\theta }}^0))\ge -\frac{1}{2}(logdet(\mathbf{\Omega })+logdet({\mathbf{\Omega }}^0))+logdet\left(\frac{\mathbf{\Omega }+{\mathbf{\Omega }}^0}{2}\right)\\ \ge \frac{1}{8}tr({({\mathbf{\Omega }}^{\ast })}^{-1}(\mathbf{\Omega }-{\mathbf{\Omega }}^0){({\mathbf{\Omega }}^{\ast })}^{-1}(\mathbf{\Omega }-{\mathbf{\Omega }}^0))\ge c^{\ast }\mid A^0\backslash A\mid c_{min}(H){\gamma }_{min}^2,\end{array}$$

where A⁰ and A are as defined in Section 4.2, and Ω^* is an intermediate value between Ω and Ω⁰; see A.4.3 of [3] of such an expansion. Moreover, C_min(θ⁰) ≥ inf_{ΩAA≠A0,|A|≤p0} log (1 − h²(Ω, Ω⁰)), yielding (18).

For Assumption A, note that |Ω_jk| ≤ (Ω_jjΩ_kk) ≤ M₂; j ≠ k, because Ω ≻ 0 and det(Ω) is bounded away from zero. To calculate the bracketing Hellinger metric entropy, we apply Proposition 1 of [22]. Let Ω_A be a submatrix, consisting of p₀ nonzero off-diagonal elements of Ω. Note that g(θ, y) of Y₁ is proportional to h₀(θ_A, y) Π_j∈A^c h_j(θ_j, y₁), where $h_0({\mathit{\theta }}_A,\mathit{y})={(\mathit{det}({\mathbf{\Omega }}_A))}^{n/2}exp(-\frac{1}{2}{({\mathit{y}}_A-{\mathit{\mu }}_A)}^T{\mathbf{\Omega }}_A({\mathit{y}}_A-{\mathit{\mu }}_A)),h_j({\theta }_j,\mathit{y})=\mathit{det}({\mathrm{\Omega }}_{jj})exp(-\frac{1}{2}{(y_j-{\mu }_j)}^2{\mathrm{\Omega }}_{jj})$, and y_A and θ_A are the sub-vectors of y and θ corresponding to Ω_A. Then for some constants k_j > 0; j = 1, 2 and any Ω̄, Ω ∈ Θ,

$$\begin{array}{l}\mid g^{1/2}(\overline{\theta },\mathit{y})-g^{1/2}(\mathit{\theta },\mathit{y})\mid \le k\mid g(\overline{\theta },\mathit{y})-g(\mathit{\theta },\mathit{y})\mid \\ \le k_1{k}_2^{p-p_0}\left(\mid h_0({\overline{\theta }}_A,\mathit{y})-h_0({\mathit{\theta }}_A,\mathit{y})\mid +\sum _{j\in A^c}\mid h_j({\overline{\theta }}_j,\mathit{y})-h_j({\theta }_j,\mathit{y})\mid \right).\end{array}$$

This implies that H(t, 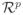) = c₀(|A| log(2εp/t)+log((p −|A|)p/t))) by [14] for some constant c₀, which in turn yields Assumption A. For Assumption B, note that, for j ≠ k = 1, ···, p, for any θ ∈ Θ,

$$\mid \frac{\partial h^2(\mathit{\theta },{\mathit{\theta }}^0)}{\partial {\mathrm{\Omega }}_{jk}}\mid =\frac{1}{4}\mid (1-h^2(\mathit{\theta },{\mathit{\theta }}^0))tr((2{(\frac{\mathbf{\Omega }+{\mathbf{\Omega }}^0}{2})}^{-1}-{\mathbf{\Omega }}^{-1}){\mathbf{\Delta }}_{jk})\mid ,$$

which is upper bounded by $\mid \frac{1}{c_{min}(\mathbf{\Omega })+c_{min}\left({\mathbf{\Omega }}^0\right)}+\frac{1}{4c_{min}(\mathbf{\Omega })}\mid \le \frac{2}{M_1}$; j ≠ k = 1, ···, p. With $A=A^{{\tau }^{+}}\cup A_2^{{\tau }^{-}},\mid h^2(\mathit{\theta },{\mathit{\theta }}^0)-h^2({\mathit{\theta }}_{{\tau }^{+}},{\mathit{\theta }}^0)\mid =\tau {\left|{\sum }_{j\in A^{{\tau }^{-}}}\frac{\partial h^2(\mathit{\theta },{\mathit{\theta }}^0)}{\partial {\mathrm{\Omega }}_{jk}}\right|}_{\mathbf{\Omega }={\mathbf{\Omega }}^{★}}|$. This implies Assumption B with d₁ = d₂ = 1 and $d_3=\frac{2}{M_1}$. For Assumption C, note that the Kullback-Leibler for θ⁰ versus θ is $\frac{1}{2n}(log\frac{\mathit{det}({\mathbf{\Omega }}^0)}{\mathit{det}(\mathbf{\Omega })}+tr(\mathbf{\Omega }{\mathbf{\sum }}^0)+{(\mathit{\mu }-{\mathit{\mu }}^0)}^T\mathbf{\Omega }(\mathit{\mu }-{\mathit{\mu }}^0)-n)$, which is upper bounded by h²(θ, θ⁰), because the likelihood ratios are uniformly bounded. An application of Taylor’s expansion as in verification of Assumption A yields that $-2log(1-h^2(\mathit{\theta },{\mathit{\theta }}^0))\le r{\gamma }_{min}^2$, where r = c^*c_max(H), leading to Assumption C.

The results in (18) follow from Theorems 1–3 with ${\epsilon }_{n,p_0,p}=max({(p_{0}logp)}^{1/2},{(log(p-p_0)p_0)}^{1/2})n^{-1/2}=\sqrt{\frac{p_{0}logp}{n}}$ by solving (9). This completes the proof.