PEG-albumin supraplasma expansion is due to increased vessel wall shear stress induced by blood viscosity shear thinning

Abstract

We studied the extreme hemodilution to a hematocrit of 11% induced by three plasma expanders: polyethylene glycol (PEG)-conjugated albumin (PEG-Alb), 6% 70-kDa dextran, and 6% 500-kDa dextran. The experimental component of our study relied on microelectrodes and cardiac output to measure both the rheological properties of plasma-expander blood mixtures and nitric oxide (NO) bioavailability in vessel walls. The modeling component consisted of an analysis of the distribution of wall shear stress (WSS) in the microvessels. Our experiments demonstrated that plasma expansion with PEG-Alb caused a state of supraperfusion with cardiac output 40% above baseline, significantly increased NO vessel wall bioavailability, and lowered peripheral vascular resistance. We attributed this behavior to the shear thinning nature of blood and PEG-Alb mixtures. To substantiate this hypothesis, we developed a mathematical model of non-Newtonian blood flow in a vessel. Our model used the Quemada rheological constitutive relationship to express blood viscosity in terms of both hematocrit and shear rate. The model revealed that the net effect of the hemodilution induced by relatively low-viscosity shear thinning PEG-Alb plasma expanders is to reduce overall blood viscosity and to increase the WSS, thus intensifying endothelial NO production. These changes act synergistically, significantly increasing cardiac output and perfusion due to lowered overall peripheral vascular resistance.

hemodilution with conventional plasma expanders (including colloids) beyond a hematocrit (Hct) reduction of ∼60% decreases functional capillary density and blood flow. This problem can be avoided by using high-viscosity plasma expanders, such as high-molecular-weight dextrans and alginates, which elevate plasma viscosity to ∼2.0–2.8 cP (43). This effect is due to increased vessel wall shear stress (WSS) and nitric oxide (NO) bioavailability (11, 41). Plasma expansion with polyethylene glycol (PEG)-conjugated albumin (PEG-Alb) shows the same effects as high-viscosity plasma expanders. This is despite the fact that (in hamsters) the plasma viscosity of ∼1.3 cP, measured after hemodilution with 4% PEG-Alb by weight (∼1% concentration in plasma), is only marginally larger than the viscosity of normal plasma (1.2 cP) (13).

The low plasma viscosity attained with PEG-Alb hemodilution indicates a low WSS. It also suggests that PEG-Alb may operate via a mechanism other than WSS-based biochemical mechanotransduction, which causes flow-dependent vasodilatation in high-viscosity plasma expansion (30, 37). The latter mechanism would be possible if plasma containing PEG-Alb behaved like a Newtonian fluid whose rheology is independent of shear rate. However, both PEG-Alb and PEG-Alb blood mixtures exhibit high viscosity at low shear rates and vice versa, a property that is known as shear thinning. Transfer of shear stress from the red blood cell (RBC) blood column core to the periphery of the flowing blood can increase WSS. A blood velocity profile that is blunted relative the parabolic (Poiseuille) profile typical of Newtonian fluids is a manifestation of such an effect.

To explore the influence of shear thinning on WSS during hemodilution with PEG-Alb, we developed a mathematical model that relies on the rheological properties of blood diluted with 4% PEG-Alb determined in vitro. Our analysis led to a relationship between WSS and both Hct and the rheological properties of blood/plasma expander mixtures. The latter were measured in blood samples obtained after hemodilution with PEG-Alb, 70-kDa dextran, and 500 kDa dextran of low and high viscosity, respectively. The rationale for this study was to explore the mechanisms of circulatory regulation in anemia and hemodilution. These mechanisms are not apparent in Hct reductions usually encountered under physiological and/or clinical conditions (10–13, 43). This study demonstrates the physiologically beneficial state of supraperfusion caused by this new form of plasma expansion. It also advances the hypothesis that this condition is a physiological consequence of augmented NO bioavailability. Therefore, we related our findings to perivascular measurements and calculations of the vessel wall NO concentration and cardiac output.

EXPERIMENTAL PROCEDURES

Materials.

Alb was conjugated with PEG according to the extension arm facilitated protocol (EAF PEGylation) previously described in Ref. 25. Briefly, lyophilized preparations of Alb (Sigma-Aldrich, St. Louis, MO) were subjected to cold (4°C) EAF PEGylation overnight at a protein concentration of 0.5 mM in the presence of 5 mM 2-IT (for thiolation of the protein) using 10 mM maleimidophenyl PEG (5 kDa, custom synthesized). Under these experimental conditions, on average, six to seven copies of PEG 5-kDa chains are conjugated to the protein. The hexaPEGylated Alb thus generated was purified through tangential flow filtration and concentrated to a 4 g·% solution with respect to Alb (2 g·% solution with respect to PEG, or a 6 g·% solution with respect to EAF PEG-Alb calculated based on the molecular mass of EAF PEG-Alb to be 95–100 kDa) and stored at −80°C. Dextran solutions were obtained from Pharmacia (Uppsala, Sweden).

Measurement of hemodiluted blood viscosity.

The rheological behavior of blood hemodiluted with plasma expanders was studied experimentally to characterize changes of fluid viscosity with shear rate. The plasma expanders used were 1) 4% PEG-Alb solution, 2) 6% 70-kDa dextran solution (a low-viscosity plasma expander), and 3) 6% 500-kDa dextran solution (a high-viscosity plasma expander). These fluids were mixed with hamster blood to reproduce the plasma composition after hemodilution to 11% Hct in previous experiments (41). In these experiments, plasma was obtained from hamster blood collected in heparinized tubes and centrifuged.

A special protocol was followed to compare the results with in vivo data on extreme hemodilution that included NO measurements (41). Progressive stepwise hemodilution to a final systemic Hct of 25% of baseline was implemented with three exchange steps. Level 1 consisted of exchanging 40% of the blood volume with 6% 70-kDa dextran. This was followed with level 2 exchange, which reduced Hct to 60% of normal. Level 3 exchange was with the test solutions, causing extreme hemodilution with Hct reduced by 75% of normal. The third blood exchange was performed with 70-kDa dextran, 500-kDa dextran, or PEG-Alb. This procedure was carried in vitro and in separate experiments in vivo using an infusion pump to deliver the fluids. The protocol was approved by the Institutional Animal Care and Use Committee of the University of California-San Diego.

To measure the rheological properties of the suspension, we used a computerized cone-plate rheometer, AR-G2 (TA Instruments, New Castle, DE), with a 4-cm diameter and 2° angle cone cells. The rheometer was calibrated with the viscosity standards for fluids of low viscosity at 37°C. Measurements were carried out under standardized temperature conditions (37°C) and shear rates between 0.18 and 450 s⁻¹ in two steps: 1) the ascending shear rate and 2) the descending shear rate.

Plasma viscosities were measured after centrifugation of the suspension only using clean supernatant solution. Measurements were made with a cone-plate LVDV-II (Brookfield Engineering Labs, Middleboro, MA) using a CP-40 spindle. Measurements were carried out at 37°C and shear rates between 50 and 450 s⁻¹ in two steps: 1) the ascending shear rate and 2) the descending shear rate.

RESULTS

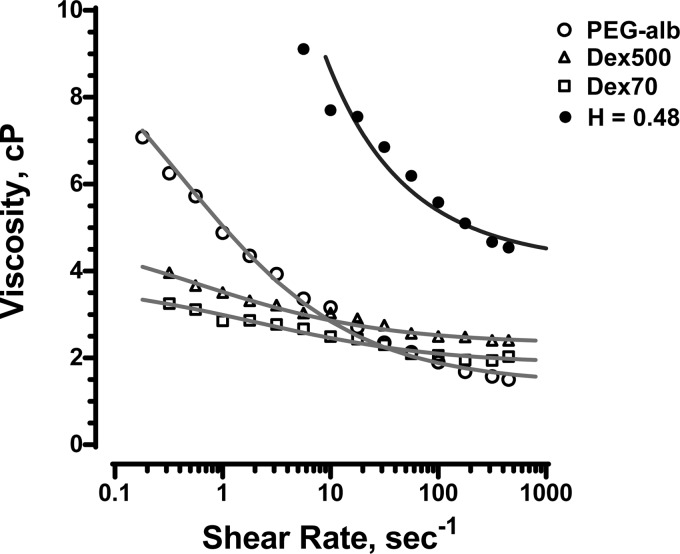
Figure 1 shows the results for blood diluted with the three plasma expanders under consideration. At shear rates below 20 s⁻¹, the blood diluted with PEG-Alb exhibited more pronounced shear thinning behavior than the blood diluted with either 70- or 500-kDa dextran. PEG-Alb-diluted blood had greater viscosities than blood diluted with dextran-based plasma expanders up to a shear rate of 10 s⁻¹. At high shear rates, the viscosity of the PEG-Alb-diluted blood was significantly lower. The Quemada rheological model (see Eqs. 3 and 4 below) was fitted to these data, leading to the viscosity-shear rate curves shown in Fig. 1. The corresponding fitting parameters are shown in Table 1.

Fig. 1.

Dependence of viscosity on shear rate for polyethylene glycol (PEG)-conjugated albumin (PEG-Alb), 70-kDa dextran (Dex70; a low-viscosity plasma expander) and 500-kDa dextran (Dex500; a high-viscosity plasma expander) solutions mixed with blood at 11% hematocrit (Hct). The fitted curves represent the Quemada rheological model. Also shown are curves for blood at 48% Hct (H = 0.48) without any plasma expanders present.

Table 1.

Fitting parameters in the Quemada rheological model for 11% Hct blood diluted with 70-kDa dextran, 500-kDa dextran, and PEG-Alb plasma expanders to 11% Hct as well as data for 48% Hct blood without any plasma expanders present

Fluid	Plasma Viscosity, cP	k0	k∞	γc, s−1
Whole blood (48% Hct)	1.2	4.3	2.05	2.8
Blood diluted with 70-kDa dextran	1.4	7.1	2.4	6
Blood diluted with 500-kDa dextran	2.2	6.2	0.5	1.9
Blood diluted with PEG-Alb	1.3	11.9	0.3	7.3

Hct, hematocrit; PEG-Alb, polyethylene glycol-conjugated albumin.

Mathematical model of blood flow in arterioles.

The mathematical model presented below allows one to compute flow velocity profiles, WSS, and core Hct in arterioles for a given value of systemic Hct. Our model qualitatively captured the blunted blood velocity profiles observed in experiments (14, 24, 34, 44), predicted the impact of various plasma expanders on WSS, and verified the hypothesis that the introduction of either 500-kDa dextran or PEG-albumin increases WSS.

Empirical power laws, which are often used to describe velocity profiles in arterioles (5, 19, 22, 24), do not account for changes in the rheological properties of blood caused by Hct variations. To accommodate this phenomenon, we modeled blood as an inhomogeneous (33, 35) fluid that exhibits both a nonuniform radial distribution of Hct in the vessel lumen (24, 34, 44) and a cell-free layer near the blood vessel wall (21). Non-Newtonian rheology of blood was described with the Quemada constitutive law (26, 33, 35), a three-parameter expression that captures the variation of blood viscosity with shear rate and Hct. Blood plasma was modeled as a Newtonian fluid. We considered pseudosteady flow regimes, which are typical for arteriole flows characterized by low Womersley's numbers (3).

Consider blood flow in an arteriole of fixed radius R. The flow is driven by an externally imposed pressure gradient (J), with no-slip boundary and no-flow conditions imposed at the vessel walls. Blood was modeled as a fluid consisting of an inner region densely packed by RBCs and an outer plasma layer with fewer RBCs (14, 24, 34, 44). The nominal plasma layer thickness (δ; normalized with the arteriole radius R) varies linearly with systemic Hct (H_d) (37, 43),

$$\delta =m{\text{H}}_{\text{d}}+c$$ (1)

where m = −7.55/R and c = 6.91/R for H_d up to 0.65. We assumed that the localized Hct (H) decreases smoothly from its maximum value [H = core Hct (H_c)] at the arteriole's center to H = 0 at the arteriole's wall according to the following sigmoidal curve:

$$\begin{array}{cc}\text{H}(\xi )={\text{H}}_{\text{c}}\text{tanh}(\frac{1-\xi }{a\delta }\pi ),& 0\le \xi <1\end{array}$$ (2)

where ξ is the radial distance from the centerline (normalized with R) and a is a fitting parameter. Based on the data reported in Ref. 43, we set a = 4.

The Quemada rheological model (33, 35) postulates that the effective blood viscosity (η) varies with H and the shear rate (γ) as follows:

$$\begin{array}{cc}\eta ={\eta }_{\text{p}}{(1-k\text{H}/2)}^{-2},& k=\frac{k_0+{\text{k}}_{\infty }\sqrt{\gamma /{\gamma }_{\text{c}}}}{1+\sqrt{\gamma /{\gamma }_{\text{c}}}}\end{array}$$ (3)

where η_p is plasma viscosity and the fitting parameters k₀, k_∞, and γ_c vary with H according to the experimental observations reported in Refs. 15, 26, and 31. For small shear rates (γ→0)_, Eq. 3 reduces to η = η_p(1 − k₀H/2)⁻². At low Hct (H→0), this equation yields the Einstein model for a dilute suspension of rigid spheres, η = η_p(1 + k₀H), with k₀ = 2.5. Recalling that shear stress (τ) = ηγ, Eq. 3 can be rewritten as follows (33):

$$\frac{\tau }{\gamma }={(\sqrt{{\eta }_{\infty }}+\frac{\sqrt{{\tau }_0}}{\sqrt{\lambda }+\sqrt{\gamma }})}^2$$ (4)

where

$$\begin{array}{c}{\tau }_0={\eta }_{\text{p}}\frac{{\gamma }_{\text{c}}\text{H}(k_0-k_{\infty })}{2{(1-k_{\infty }\text{H}/2)}^4},\end{array}\begin{array}{c}{\eta }_{\infty }={\eta }_{\text{p}}{(1-k_{\infty }\text{H}/2)}^{-2},\end{array}\begin{array}{c}\lambda ={\gamma }_{\text{c}}(\frac{2-k_0\text{H}}{2-k_{\infty }\text{H}})\end{array}$$ (5)

The radial distribution of the shear stress τ(ξ) in the non-Newtonian fluid, whose viscosity η(ξ) varies with the normalized radius ξ in accordance with Eq. 3, satisfies the following steady-state axisymmetric Cauchy equation of motion:

$$\begin{array}{cc}0=-J+\frac{1}{R\xi }\frac{\partial (\xi \tau )}{\partial \xi },& 0\le \xi \le 1\end{array}$$ (6)

The resulting blood velocity profiles [v(ξ)] must be symmetric with respect to the arteriole's center (ξ = 0), i.e., dv/dξ = 0 at ξ = 0. Recalling the definition of τ, this yields a boundary condition for Eq. 6, τ(0) = 0. A solution of this boundary value problem gives the following distribution of shear stress across the arteriole:

$$\tau =\frac{JR\xi }{2}$$ (7)

Combining Eqs. 4 and 7 yields the following shear rate distribution across the arteriole (33):

$$\begin{array}{cc}\gamma =\frac{\text{J}R}{4{\eta }_{\infty }}\left[\xi -\alpha (1+\text{q})\sqrt{\xi }+{\alpha }^2+(\sqrt{\xi }-\alpha )\sqrt{\xi -2\alpha \text{q}\sqrt{\xi }+{\alpha }^2}\right],& 0\le \xi \le 1\end{array}$$ (8)

where

$$\begin{array}{cc}\alpha =\frac{\sqrt{{\tau }_0}+\sqrt{{\eta }_{\infty }\lambda }}{\sqrt{{\tau }_{\text{w}}}},& \text{q}=\frac{\sqrt{{\tau }_0}-\sqrt{{\eta }_{\infty }\lambda }}{\sqrt{{\tau }_0}+\sqrt{{\eta }_{\infty }\lambda }}\end{array}$$ (9)

and τ_w = JR/2 is the shear stress at the arteriole wall ξ = 1.

To compute the blood velocity distribution v(ξ), we recalled the definition of τ in Eq. 7 and enforced the no-slip boundary condition at the arteriole wall (ξ = 1), as follows:

$$\begin{array}{cc}\frac{\text{d}v}{\text{d}\xi }=\frac{JR\xi }{2\eta [\text{H}(\xi )]},& v(\xi =1)=0\end{array}$$ (10)

The interdependence between the parameters entering the relationship η[H(ξ)] given by Eqs. 1–3 introduces an additional constraint. Specifically, mass conservation of RBCs inside the arteriole imposes the following relationship between H and H_d (23):

$${\displaystyle \underset{0}{\overset{1}{\int }}\text{H}(\xi )v(\xi )\xi \text{d}\xi ={\text{H}}_{\text{d}}{\displaystyle \underset{0}{\overset{1}{\int }}v(\xi )\xi \text{d}\xi }}$$ (11)

For a given value of H_d, we used the following iterative procedure (38) to compute the blood velocity distribution v(ξ) from the boundary value problem (Eq. 10) subjected to the integral constraint (Eq. 11):

• 1. Guess a value of H_c (e.g., by adopting a linear relationship between H_c and H_d).

• 2. Use Eqs. 1 and 2 to compute H(ξ).

• 3. Use Eq. 3 to compute η[H(ξ)].

• 4. Solve the boundary value problem (Eq. 10) to compute the blood velocity distribution v(ξ).

• 5. Use Eq. 11 to verify if the resulting velocity profile v(ξ) yields H_d consistent with the given value of systemic Hct (with prescribed tolerance ε). If yes, the simulation is completed. If not, set H_c = H_c + Δ (where Δ is a prescribed constant) and go back to step 2.

In the simulations reported below, we set ε = 10⁻⁴ and Δ = 10⁻⁴.

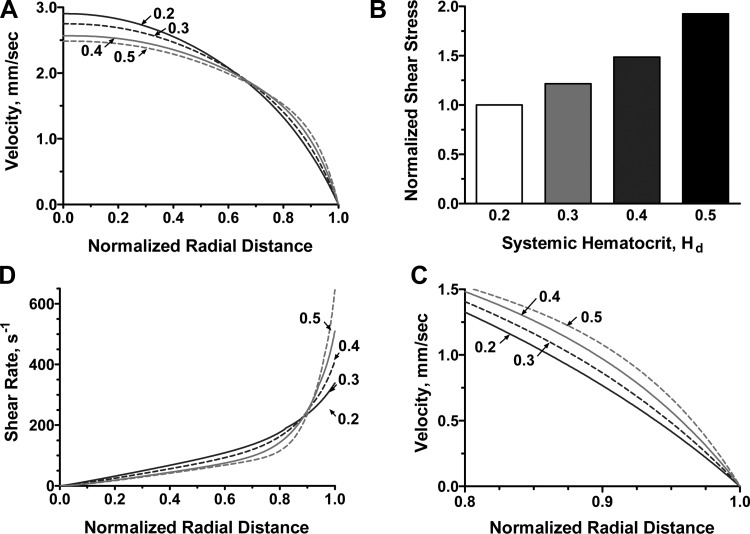
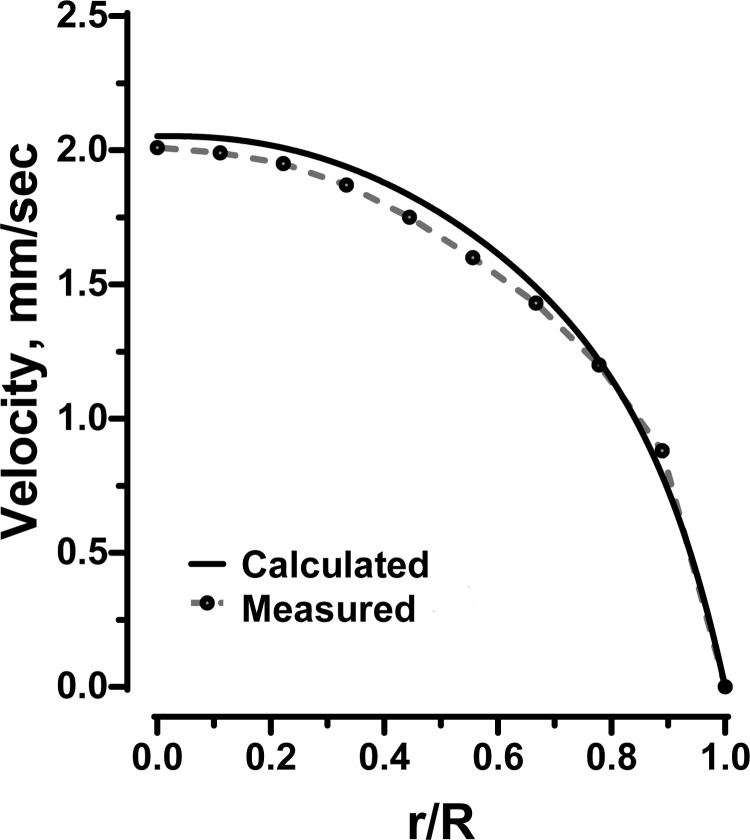
The resulting velocity profiles v_z(ξ) for different systemic Hcts are shown in Fig. 2A. These profiles were qualitatively similar to the observed velocity profiles (6, 22, 24) in that they were continuous across the arteriole. This is in contrast with models that treat blood as a two-phase liquid, e.g., Ref. 36, yielding discontinuities in the velocity profile at the interface between the RBC-rich core and the plasma layer. As H_d increased, the non-Newtonian nature of blood flow became more pronounced, with the velocity profiles becoming blunter. Figure 3 shows a comparison of the velocity profile v(ξ) predicted with our model and the experimentally observed velocity profile for R = 27.1 μm, H_d = 33.5%, and J = 3,736 dyn/cm³.

Fig. 2.

A: velocity profiles for several values of systemic Hct (H_d). B: corresponding variations in wall shear stress (WSS). C: velocity profiles near the vessel wall. D: variations of shear rate near the vessel wall.

Fig. 3.

Predicted (solid line) and experimentally determined (24) (dotted line) velocity profiles for human blood at H_d = 33.5% in a 54.2-μm-diameter glass tube at a pressure gradient of 3,736 dyn/cm³. r/R is normalized radial distance from center line.

Higher Hct values imply higher WSS, as larger pressure gradients are required to drive the flow; hence, WSS increased very quickly with H_d (Fig. 2B). Figure 2, C and D, shows the spatial variability of flow velocity and shear rate near the arteriole walls for different values of H_d. As H_d increased, both velocity and shear rate profiles became steeper near the arteriole wall and blunter near the arteriole centerline. This phenomenon was a manifestation of the non-Newtonian behavior of blood that increases with H_d.

It is worthwhile emphasizing that the model presented above is valid for both steady (constant J) and quasisteady (pulsating J) flows in small arterioles, for which the Womersley number is small (the arterioles considered in this study have R = 20 μm, resulting in Womersley numbers on the order of 10⁻²). This is because this flow regime allows one to neglect the inertial term in the Navier-Stokes equations even if J = J(t), where t is time (3).

Flow in the presence of plasma expanders.

We used our mathematical model of blood flow to assess the effectiveness of plasma expanders (PEG-Alb, 70-kDa dextran, and 500-kDa dextran) by analyzing their impacts on WSS. Experimental data were used to parameterize the flow model as follows. First, we used the data shown in Fig. 1 to parameterize the Quemada model for the mixtures of blood and plasma expanders. Second, we used the measurements (13) of arteriole radius and centerline velocity at baseline and upon hemodilution with each plasma expander to prescribe the baseline arteriole radius in our model. The data on centerline velocity were used to establish a constraint in our model, as follows.

Our flow model requires pressure gradients (Eq. 8) to calculate shear rates and velocity profiles. However, experimental data on pressure gradients were not available. Hence, we calculated pressure gradients in arterioles associated with each plasma expander using the following iterative procedure:

• 1. For given blood rheology and vessel radius (from experimental data), we assumed a value of the pressure gradient and calculated velocity profiles and centerline velocity.

• 2. We compared calculated values of centerline velocity with the experimental value. If the calculated and experimental values did not match, we corrected our estimate of the pressure gradient. If calculated centerline velocity exceeded the experimental value, the pressure gradient was reduced, and vice versa, in case the calculated centerline velocity was less than the experimental value.

• 3. Steps 1 and 2 were repeated until the calculated centerline velocity converged with the experimental value.

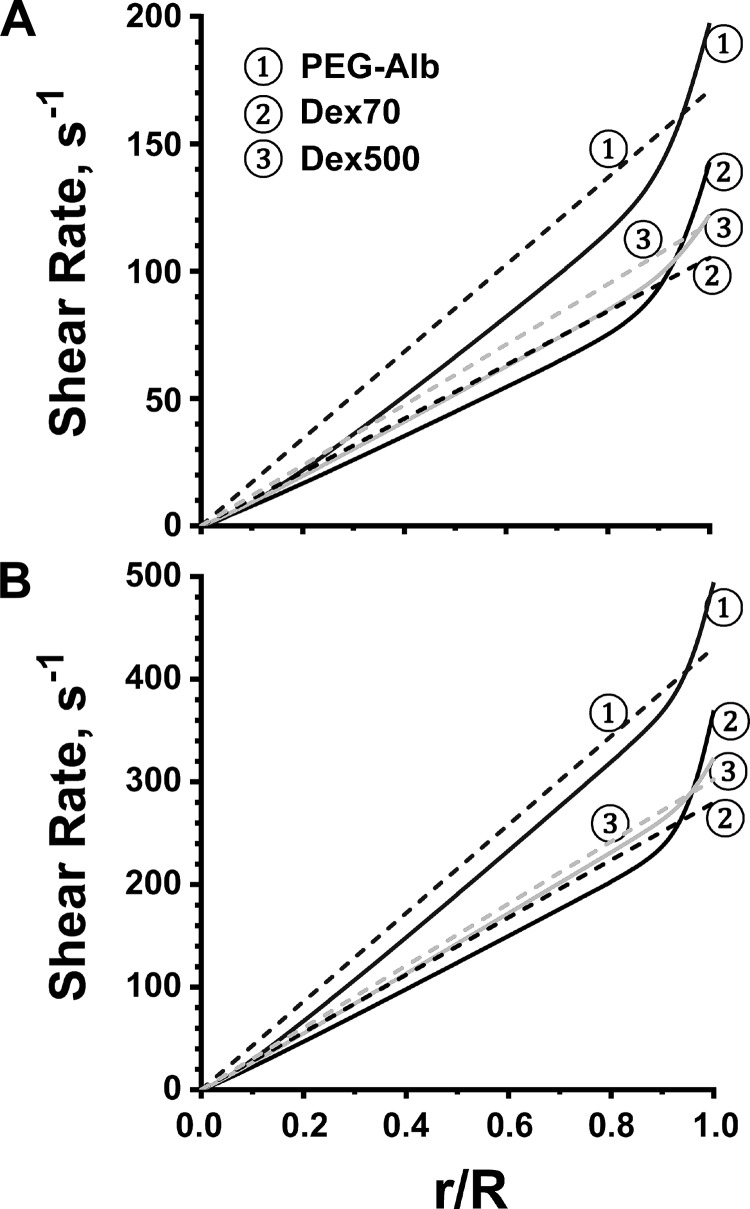
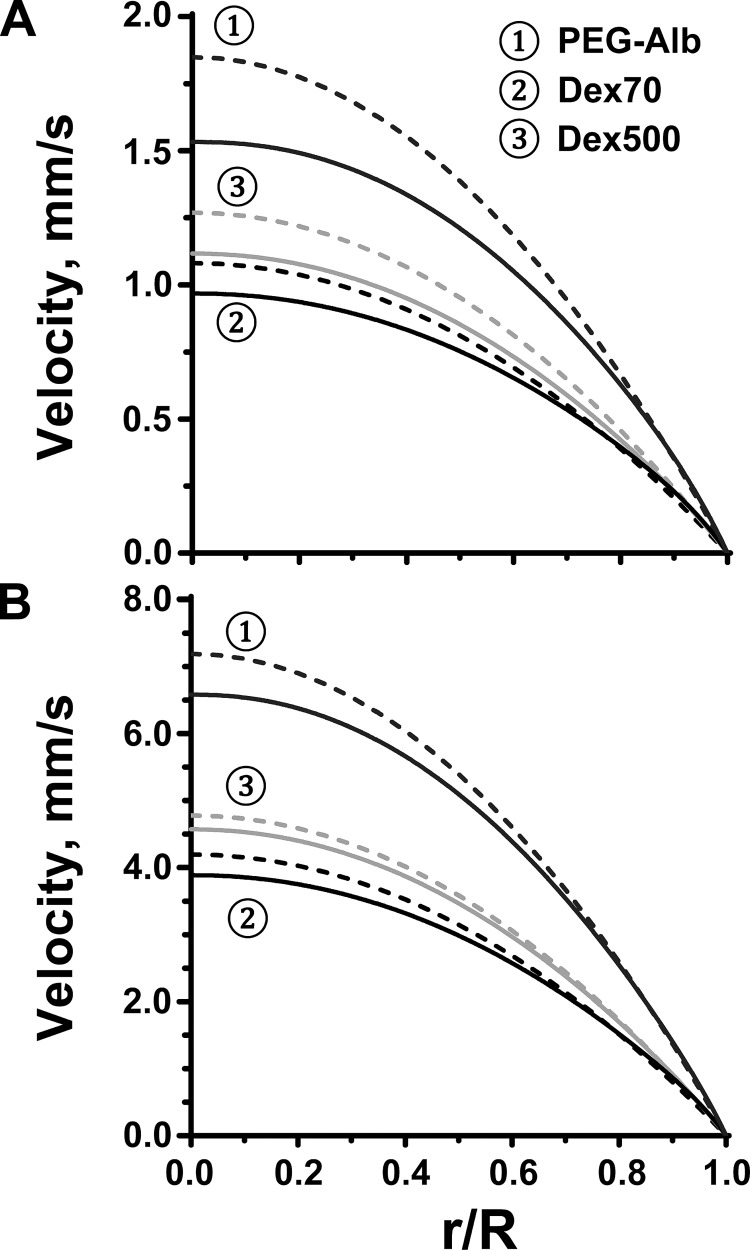
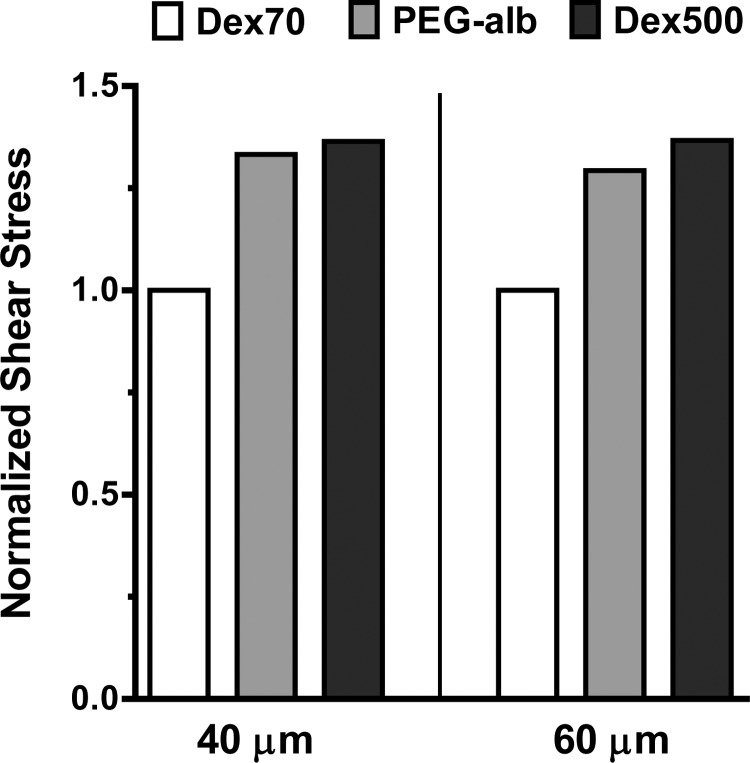
For the calculated pressure gradients, the shear rate and velocity profiles are shown in Figs. 4 and 5, respectively. Finally, we used both the calculated value of the pressure gradient and the experimentally determined variation of the vessel radius to predict WSS associated with each plasma expander (Fig. 6). All the calculations were carried out for arterioles with two baseline diameters: 40 and 60 μm.

Fig. 4.

Shear rate profiles (solid lines) for the flow of blood diluted with the three plasma expanders in arterioles whose baseline diameter was 40 μm (A) and 60 μm (B). The dashed lines represent shear rate profiles predicted with Poiseuille's law at the same pressure gradients.

Fig. 5.

Velocity profiles (solid lines) for the flow of blood diluted with the three plasma expanders in arterioles whose baseline diameter was 40 μm (A) and 60 μm (B). The dashed lines represent velocity profiles predicted with Poiseuille's law at the same pressure gradients.

Fig. 6.

WSS for Dex70, Dex500, and PEG-Alb plasma expanders (normalized with WSS for Dex70) in arterioles whose baseline diameter was 40 μm (A) and 60 μm (B). The corresponding WSS values (in dyn/cm²) were 1.99 for Dex70, 2.73 for Dex500, and 2.67 for PEG-Alb (A) and 5.18 for Dex70, 6.95 for Dex500, and 6.68 for PEG-Alb (B).

To elucidate the importance of shear thinning, Figs. 4 and 5 also show the shear rates and velocities computed by treating blood as a Newtonian fluid, i.e., by relying on Poiseuille's law. Our non-Newtonian model predicted a sharp increase in shear rate near the arteriole wall (Fig. 4), which implied that the reliance on Poiseuille's law would significantly underestimate WSS. This effect, and the underlying blunting of the velocity profiles (Fig. 5), was more significant in a baseline 40-μm-diameter arteriole than in a baseline 60-μm-diameter arteriole, as shear rates are lower in smaller vessels, leading to more pronounced shear thinning behavior. Both PEG-Alb and 500-kDa dextran led to appreciable increases in WSS relative to 70-kDa dextran.

Viscosity values measured at high shear rates (at which viscosity becomes independent of shear rate and rheological behavior becomes Newtonian) were assumed for calculation of the Poiseuille flows, with the same pressure gradients and vessel radii as the corresponding non-Newtonian flows.

The model results were under the assumption of steady flow, with the oscillatory component of the flow neglected. Hence, the resulting calculations for WSS were equivalent to a time-averaged value, with the average of the oscillatory component of flow equal to zero.

Measurements of perivascular NO.

We used the experimental technique described in Ref. 41 to measure the concentration of NO in the vessel wall. The experimental procedure relied on carbon electrodes coated with Nafion to measure the current produced by the application of a +0.8-V potential relative to a silver-silver chloride reference electrode. It was used to measure NO concentrations in arterioles and venules of the hamster window chamber model; detailed descriptions of the three-step procedure used to study perivascular NO levels for high and low viscosity in extreme hemodilution can be found in Refs. 7, 10, and 34. The present study followed the same procedure except that the finial hemodilution step was performed using 4% PEG-Alb.

In brief, the method consisted of removing the coverglass of the window chamber after the third exchange and superfusing the tissue with physiological Krebs salt solution (33–34°C). Perivascular measurements were made by penetrating the perivascular tissue with the micropipette so that the tip was close to the microvessel without visibly touching and deforming the wall (7). The electrode current was measured with a potentiostat and electrometer (Keithley model 619C, Cleveland, OH).

Results of perivascular NO measurements.

Six animals were entered into this study for the measurement of NO, and all animals tolerated the hemodilution protocol without visible signs of discomfort. Two animals were used as controls to insure that the system calibration and animal preparation were the same as previous control measurements (42). However, PEG-Alb perivascular NO levels have not been previously published.

Physiological conditions and the rheological properties of blood after level 3 exchange are shown in Table 2. For comparison, data on low-viscosity hemodilution using 70-kDa dextran and high-viscosity hemodilution using 500-kDa dextran from a previous study by Tsai et al. (41) were also included. NO measurements in all experiments were performed during a period of 1–2 h after hemodilution.

Table 2.

Hemodilution with low-viscosity 70-kDa dextran, high-viscosity 500-kDa dextran, and PEG-Alb

	Control*	70-kDa Dextran*	500-kDa Dextran†	PEG-Alb*
Hct, %	49.3 ± 1.8	11.1 ± 0.9	11.0 ± 0.6	11.2 ± 0.7
Mean arterial pressure, mmHg	103 ± 6	64 ± 8	87 ± 6	79 ± 7
Heart rate, beats/min	414 ± 35	418 ± 41	453 ± 38	460 ± 31
Cardiac output, ml/min	17.8 ± 1.6	14.2 ± 1.9	19.6 ± 3.5	24.2 ± 1.6
Base-excess, mmol/l	3.2 ± 1.5	−4.6 ± 2.6	0.8 ± 1.6	1.3 ± 1.4
Plasma viscosity, cP‡	1.2 ± 0.1	1.4 ± 0.2	2.2 ± 0.2	1.3 ± 0.1
Blood viscosity, cP‡	4.1 ± 0.4	2.1 ± 0.2	2.8 ± 0.2	1.8 ± 0.1
Peripheral resistance§	1.00	0.78	0.76	0.57
Arterial blood pH	7.35 ± 0.03	7.32 ± 0.09	7.35 ± 0.06	7.36 ± 0.04

^*Data from Ref. 13.

^†Data from Ref. 10.

^‡Viscosity measured in a Brookfield cone-and-plate viscometer at 200 s⁻¹.

^§Ratio of mean arterial blood pressure and cardiac output normalized relative to baseline.

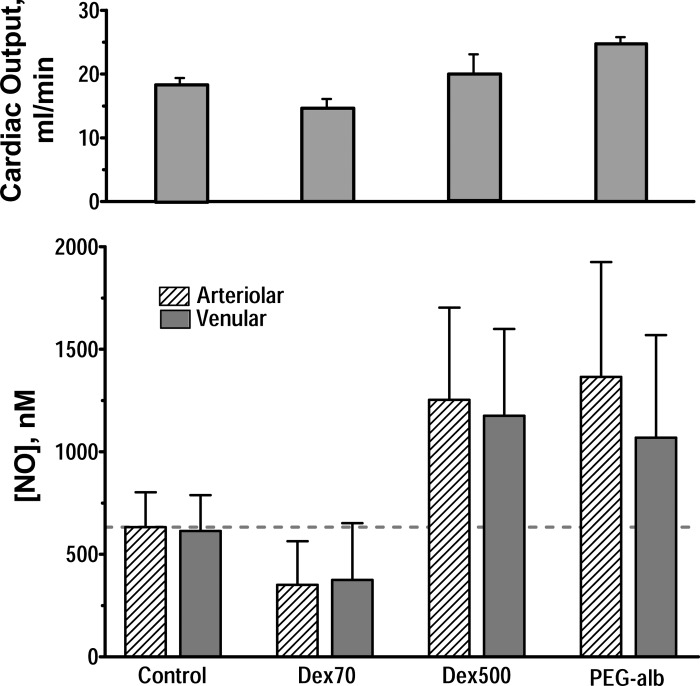
Figure 7 shows the principal finding from these measurements: increased perfusion found in extreme hemodilution using PEG-Alb was associated with increased arteriolar and venular perivascular NO. These NO concentrations were significantly greater than in control and when extreme hemodilution was performed using 70-kDa dextran. NO concentrations were the same as those found using 500-kDa dextran.

Fig. 7.

Bottom: perivascular microelectrode nitric oxide (NO) measurements during hemodilution at 11% Hct using a three-step protocol that started with hemodilution with 6% Dex70, resulting in a final concentration of 1% by weight of either Dex70, Dex500, or PEG-Alb at the time of measurement. Top: comparison with cardiac output measured at the same time point by thermodilution (9). All measurements were statistically different from control (P < 0.05).

Effect of NO synthase inhibition.

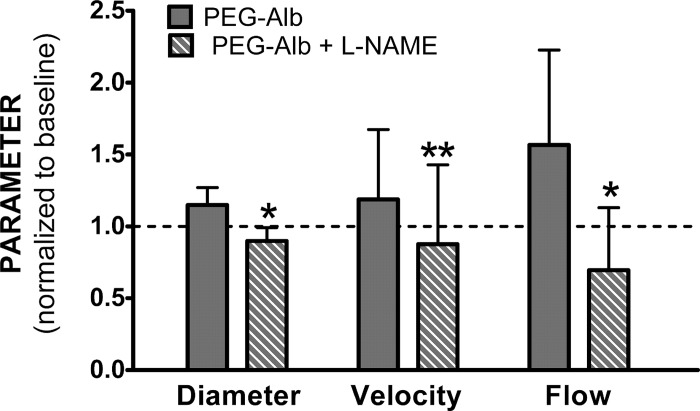
To further support the hypothesis that enhanced NO production is the primary cause for the observed increase of perfusion, we performed hemodilution with PEG-Alb followed by treatment with the NO synthase inhibitor N-nitro-l-arginine methyl ester (l-NAME). This allowed us to determine the extent of the dependence of supraperfusion on enhanced NO production. In these experiments, it was not possible to apply l-NAME after extreme hemodilution to 11% since the combination of a significant decrease in the intrinsic oxygen-carrying capacity due to hemodilution and perfusion due to l-NAME administration caused all animals to succumb. Therefore, we hemodiluted the animals to 35% Hct with 70-kDa dextran and then carried out a second hemodilution to 18% Hct with PEG-Alb. This group was subsequently treated with l-NAME. The results (Fig. 8) showed that l-NAME treatment eliminated vasodilatation and the increased perfusion response due to hemodilution with PEG-Alb. This supports the hypothesis that in the time frame of these experiments (1–2 h), the observed vasodilation and supraperfusion are due to increased WSS and NO production.

Fig. 8.

Vessel diameter, centerline velocity, and blood flow rate in arterioles of the hamster widow model. Animals were first hemodiluted with 6% Dex70 to 35% Hct and then subsequently to 18% Hct using 4% PEG-Alb (n = 5, 25 arterioles, 40–60 μm diameter) and finally treated with N-nitro-l-arginine methyl ester (l-NAME). Data were normalized relative to baseline. Significance of differences between untreated and l-NAME-treated PEG-Alb hemodilution: *P < 0.001 and **P < 0.05.

DISCUSSION

This study shows that the supraperfusion condition established during extreme hemodilution with PEG-Alb was directly associated with increased WSS and related to an increased NO vessel wall concentration. The increase in WSS was shown by mathematical modeling to be a consequence of the shear thinning properties that PEG-Alb confers to 70-kDa dextran-diluted blood. The significance of these findings is that extreme hemodilution with PEG-Alb results in a >40% reduction of peripheral vascular resistance and a corresponding increase in blood flow and perfusion, a condition that we term “supraperfusion” (Table 2 and Fig. 7).

The increase in WSS increases NO production by the endothelium, as evidenced by its direct measurement in the vessel wall with microelectrodes. In principle, increased WSS requires increased plasma viscosity and/or flow of the fluid component directly in contact with the endothelium. This is the case of high-viscosity plasma expanders, such as 500-kDa dextran, whose rheology is nearly Newtonian at the low value of Hct down to which hemodilution is performed. In contrast, blood diluted with PEG-Alb is strongly shear thinning, even at 11% Hct. This effect redistributes shear rate energy expenditure from the bulk of the flow to the periphery and also increases the apparent viscosity of the fluid, accounting for the increase in WSS.

The increase of NO production with shear stress is consistent with previous experimental studies (28, 29) of the endothelial response to WSS conducted in flow chambers. While these experiments did not exactly reproduce in vivo conditions due to the absence of pulsatility, they showed that NO production increases with increasing WSS in steady (and slowly varying) flow regimes. Flow in arterioles is pulsatile (20) in synchrony with the heart and has a random variability in the region of the cell-free plasma layer due to the continuous realignment of the RBCs that limit the cell-free plasma layer on the blood side (1, 18) and the spatial variability of the endothelial surface layer (32).

The increase of WSS in microvessels associated with PEG-Alb is a property of laminar flow at low shear rates; in the heart, where most fluid volumes have significant velocity gradients (and high shear rates), the viscosity of blood mixed with PEG-Alb is low. Conversely, if blood is diluted with a high-viscosity plasma expander, the fluid in the heart has the corresponding higher viscosity. This leads to a different mechanical expenditure by the heart in pumping blood diluted with these different plasma expanders.

Table 2 and Fig. 7 show that these effects are important, with perivascular NO concentrations being higher with dilution with PEG-Alb and 500-kDa dextran than with 70-kDa dextran or under baseline conditions. Simply lowering blood viscosity by hemodilution with a conventional colloidal plasma expander, such as 70-kDa dextran, significantly lowers blood viscosity and blood pressure but not peripheral vascular resistance. This occurs because microcirculatory WSS is not sufficient to sustain NO production and maintain normal vasodilation. Increasing plasma viscosity with a Newtonian fluid pressurizes the circulation and improves flow and WSS, lowering peripheral vascular resistance; however, the effect on peripheral vascular resistance is partially negated by the increased blood viscosity throughout the circulation. PEG-Alb increases viscosity in the blood vessel core and lowers blood viscosity in the high-shear rate regions of the circulation, synergistically increasing perfusion. In accounting for this synergistic mechanism by which PEG-Alb increases perfusion, we ruled out hypoxic vasodilation by RBCs as a contributing factor since the hemodilution achieved in these experiments corresponds to Po₂ levels in the range of 23.5–48.0 mmHg (vs. 45.0–58.8 mmHg for normal baseline) (43), which is above the range of Po₂ levels where the phenomenon of RBC-facilitated vasodilation is expected to occur (16).

Our model of blood flow in an arteriole treated blood as a non-Newtonian fluid with the Quemada constitutive model. The model yields velocity profiles and radial variations of shear rate that are in qualitative agreement with experimental data reported in Refs. 24, 39, and 40. Since our model is suitable for a wide range of Hcts, it can be used to analyze data from blood flow experiments in vivo and in vitro (5, 24, 39, 40, 44).

The shear thinning effect is expected to be due to PEG-Alb inducing an increase in the interaction between RBCs, although by a mechanism different to the one causing aggregation by 500-kDa dextran. Aggregation due to 500-kDa dextran causes large RBC aggregates at higher Hcts but not in extreme hemodilution. Aggregation due to the presence of PEG proteins was not evident in our experiments, even at higher Hcts. The increase in WSS evidenced by our modeling study of the effect of shear thinning is primarily due to the increase in shear rate in the proximity of the vessel wall due to a combination of factors, including the increased flow, the blunting of the velocity profile, and the small increase in plasma viscosity (from 1.2 to 1.3 cP). The potential beneficial effect of increased blood aggregability has been reviewed and discussed in Refs. 2 and 4.

This study showed that treating blood as a non-Newtonian shear thinning fluid predicts significantly higher shear rates (and hence shear stresses) at the vessel walls relative to shear rate estimates obtained from Poiseuille's law. Hence, previous studies of plasma expanders (10, 12, 13) probably underestimated the relative increase of WSS with the introduction of 500-kDa dextran and PEG-Alb plasma expanders.

Alternative mechanisms for supraperfusion.

A host of other mechanisms may play a role in enhancing perfusion.

Extreme hemodilution and changes in blood viscosity significantly change the distribution of pressure in the circulation, interacting with the mechanical properties of blood vessels and the Bayliss effect. In previous studies, we modeled the effects of a 10% increase in blood viscosity from baseline and found that it induced a significant decrease in peripheral vascular resistance (8), explaining the in vivo findings of Martini et al. (27), who carried the same procedure in unanesthetized hamsters and mice. This effect could be present with 500-kDa dextran extreme hemodilution relative to 70-kDa dextran extreme hemodilution since blood viscosity increases from 2.1 to 2.8 cP. However, for extreme hemodilution with PEG-Alb, blood viscosity was reduced to 1.8 cP, which should cause even further constriction from that present with 70-kDa dextran. Nonetheless, this is a hypothesis that should be investigated considering the significant redistribution of intravascular pressure associated with extreme hemodilution.

Increased NO bioavailability is a factor in hemodilution, because it increases the width of the cell-free layer. Our analytically study (38) showed that in hemodilution, the effect due to WSS dominates the effect of NO scavenging by RBC hemoglobin. Both blood viscosity and RBC aggregability influence the width of the cell-free layer. Since RBC aggregability causes shear thinning, it is likely that PEG-Alb increases NO bioavailability relative to colloids, which induce low or no aggregability.

Acidosis due to massive dilution with sodium chloride causes dilatation and could be a factor; however, this was not observed in our experiments, as shown in Table 2.

To verify that the increased perfusion associated with PEG-Alb was due to increased NO production, we carried out hemodilution with PEG-Alb followed by treatment with l-NAME. The introduction of l-NAME (which served to inhibit NO production) effectively eliminated improvements in perfusion achieved with the use of PEG-Alb as a plasma expander. This helps to justify our claim that the introduction of PEG-Alb induces higher WSS in the microcirculation, thereby stimulating NO production and increasing perfusion.

In summary, 70-kDa dextran, 500-kDa dextran, and PEG-Alb mixed with blood in conditions of extreme hemodilution exhibit the behavior of non-Newtonian shear thinning fluids. Previous hemodilution experiments using the plasma expanders studied (10, 12, 13) indicated that 500-kDa dextran and PEG-Alb increased blood flow and diameter to a significantly greater extent than 70-kDa dextran. It was hypothesized that both 500-kDa dextran and PEG-Alb used as plasma expanders improved cardiac performance by elevating WSS, thereby increasing NO bioavailability and inducing vasodilation. We tested this hypothesis by developing a mathematical model to calculate WSS in arterioles under hemodilution with each plasma expander. The results (Fig. 6) showed that both 500-kDa dextran and PEG-Alb significantly increased WSS. This led to significant increases in perivascular NO concentration relative to 70-kDa dextran hemodilution and baseline conditions.

The significance of these findings is that they explain why PEG-Alb hemodilution produces a state of supraperfusion. This occurs because blood is diluted, lowering blood viscosity in high shear rate zones of the circulation, like the heart and major vessels, whereas apparent viscosity and WSS increase in the microcirculation, promoting the production of NO by the endothelium and vasodilatation. An extreme case of this effect is the conversion of the fluid in the blood vessel core into a solid piston (maximum viscosity at zero shear rate), with a thin peripheral lubricating layer between the piston and cylinder. This synergy of such mechanisms, including a possible contribution from the Bayliss mechanism not explored in the present study, should also be operational in the heart muscle, allowing the heart to maintain blood pressure and to increase cardiac output, leading to the beneficial effect found in using the PEG-Alb plasma expander.

The clinical significance of our findings is expressed by a recent meta-analysis (17) of the hemodynamic factors that determine the survival of high-risk surgical patients. This study found that “for most high-risk patients, the main cause of death is more often related to tissue perfusion dysfunction than to a cardiac problem” and concluded that in “high-risk surgical patients with no evident organ dysfunction before surgery, maintaining tissue perfusion preoperatively according to a specific protocol reduces postoperative mortality and morbidity.”

GRANTS

This work was supported in part by National Heart, Lung, and Blood Institute Grants R24-HL-064395 and R01-HL-062354 (to M. Intaglietta) and R01-HL52684 (to P. Cabrales) and by United States Army Medical Research Acquisition Activity Award W81XWH1120012 (to A. G. Tsai).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: K.S., P.C., F.M., S.A.A., D.M.T., and M.I. conception and design of research; K.S., P.C., and D.M.T. analyzed data; K.S., F.M., S.A.A., and M.I. interpreted results of experiments; K.S. and A.G.T. prepared figures; K.S. drafted manuscript; K.S., P.C., and D.M.T. edited and revised manuscript; A.G.T. and P.C. performed experiments; D.M.T. and M.I. approved final version of manuscript.