Calculation of Host-Guest Binding Affinities Using a Quantum-Mechanical Energy Model

Abstract

The prediction of protein-ligand binding affinities is of central interest in computer-aided drug discovery, but it is still difficult to achieve a high degree of accuracy. Recent studies suggesting that available force fields may be a key source of error motivate the present study, which reports the first mining minima (M2) binding affinity calculations based on a quantum mechanical energy model, rather than an empirical force field. We apply a semi-empirical quantum-mechanical energy function, PM6-DH+, coupled with the COSMO solvation model, to 29 host-guest systems with a wide range of measured binding affinities. After correction for a systematic error, which appears to derive from the treatment of polar solvation, the computed absolute binding affinities agree well with experimental measurements, with a mean error 1.6 kcal/mol and a correlation coefficient of 0.91. These calculations also delineate the contributions of various energy components, including solute energy, configurational entropy, and solvation free energy, to the binding free energies of these host-guest complexes. Comparison with our previous calculations, which used empirical force fields, point to significant differences in both the energetic and entropic components of the binding free energy. The present study demonstrates successful combination of a quantum mechanical Hamiltonian with the M2 affinity method.

INTRODUCTION

The ability to predict noncovalent binding affinities to within experimental uncertainty is a central goal of computational chemistry and would have broad application in drug discovery and molecular design.^1,2 Efforts to improve methods of computing noncovalent binding affinities have often centered on modeling the association of proteins with drug-like small molecules, because of the direct biomedical significance of such systems. However, the size and flexibility of proteins make it hard to treat them with detailed, physics-based models.³ In particular, it is often difficult to be sure that results obtained from protein simulations are stable with respect to further conformational sampling.⁴ As a consequence, comparisons with experiment are not necessarily informative regarding the accuracy of the energy model one is employing. In contrast, supramolecular host-guest systems can be quite tractable computationally, due to their small size – often only a few hundred atoms -- and limited conformational flexibility. It is thus much easier to achieve adequate conformational sampling of these systems and hence to obtain well-converged binding affinities.^5,6 Consequently, comparisons of computed and measured host-guest binding affinities can be highly informative regarding the accuracy of the energy model and other aspects of the calculations.⁷ Furthermore, today’s host-guest systems span a wide range of binding affinities in aqueous solution, in some cases rivaling even the tightest-binding protein-ligand systems.^8–11 For these reasons, experimental host-guest binding affinities have emerged as highly informative validation data for computational methods,^5,10 occupying a position between solvation free energies, which are easier to compute but uninformative regarding solute-solute interactions; and protein-ligand systems, which are important but harder to simulate.

The potential energy model is a key determinant of accuracy in physics-based calculations of binding affinity. Empirical force fields, such as CHARMm,¹² OPLS,¹³ GAFF,¹⁴ and MMFF¹⁵ must have an appropriate functional form and parameters, while the level of theory plays a key role in quantum-mechanical (QM) models; e.g., Hartree-Fock (HF), density functional theory (DFT), Møller-Plesset perturbation theory, and coupled cluster theory.¹⁶ Even though ab initio QM methods have the potential to be more accurate than classical force fields and have the additional merit of broad applicability, they tend to be too computationally demanding for use in free energy calculations. Recently, there have been encouraging reports of the application of high-level QM energy models for computing protein-ligand binding enthalpies and free energies, based on short molecular dynamics simulations.^17–21 However, these studies have either neglected the changes in configurational entropy on binding or else approximated them by using classical force fields, and these simplifications appear to negatively affect the correlation between computation and experiment.²⁰ It is perhaps not unexpected that the use of different potential energy models for computing different components of the free energy should lead to errors. It is therefore of great interest to know whether accurate binding free energies can be computed if the energetic and entropic components of the free energy are computed consistently with a QM energy model.

In order to provide accurate noncovalent binding affinities, a QM model must account well for nonbonded interactions, including exchange-repulsion, electrostatic, and dispersion forces. However, accurate ab initio calculations of dispersion interactions require relatively high-level methods such as MP2 and CCSD(T),^22,23 which are computationally demanding and scale poorly with system size. Computationally less demanding ab initio and semi-empirical quantum mechanical methods such as HF, DFT, and PM6 perform poorly at calculating dispersion interactions on their own, due to partial or complete neglect of electron correlation energies,^24,25 but show great improvement in accuracy when corrected with supplemental empirical terms.^26–28 In particular, the PM6 semi-empirical Hamiltonian²⁹ has been supplemented with by the addition of dispersion and hydrogen-bonding terms, based on high-level CCSD(T)/CBS QM calculations, to yield the PM6-DH2 and PM6-DH+ Hamiltonians.^30,31 These semi-empirical QM models are orders of magnitude faster than the ab initio methods and scale reasonably well for medium-sized systems with few hundred atoms, such as the host-guest systems studied here. Nevertheless, it still would be difficult to compute binding free energies through molecular dynamics or Monte-Carlo methods using these QM energy models, since the required conformational sampling would be very time-consuming.

The mining minima (M2) method provides a useful alternative framework for incorporating accurate but time-consuming energy models, such as the QM methods, into binding free energy calculations. The M2 method works by identifying energy wells in the conformational energy landscapes of the free molecules and their bound complex, and using a harmonic or closely related method to estimate the free energy of each energy well. These local free energies are then combined to yield the free energies of the free and bound states, and hence the binding free energy.^6,32 M2 calculations with empirical force fields have been used in both retrospective and prospective studies, including the design of novel ultra high-affinity guests for cucurbit[7]uril (CB7).^9,10 Despite these successes, the binding affinities predicted with M2 in SAMPL3, a recent host-guest blind prediction challenge, were found to deviate significantly from the experimental measurements,^7,33 and a retrospective analysis of these calculations suggested that the errors likely originated from the force field.³³ We therefore wished to incorporate a more accurate Hamiltonian into the method. Fortunately, the M2 method requires only a relative modest number of conformational samples, unlike many other free energy methods, and can also use sampling methods that drive over energy barriers without sacrificing numerical accuracy. It is therefore well suited for use with QM energy models, with their relatively costly energy calculations.

Herein, we report the calculation of binding affinities for 29 CB7-guest systems, using the M2 approach combined with the PM6-DH+ semi-empirical QM Hamiltonian and the COSMO solvation model. Low-energy conformations of the hosts, guests, and complexes are determined through conformational search using an empirical force field, and the free energies are then computed using the QM energy model. The calculated binding affinities correlate well with the experiments, and we further report an empirically tuned model based on a simple linear scaling scheme to correct for systematic errors in the calculations. Using these results, we discuss the role of the different free-energy components, solute energy, configurational entropy, and solvation free energy, in determining binding affinity of these host-guest systems. We also compare these QM results to available results obtained with classical potential energy model and discuss the key differences between these models. The present results suggest that binding affinities of small host-guest complexes can be effectively computed using the M2 method with QM energy models and point to directions for further improvement of this approach.

THEORY AND METHOD

Mining Minima

The present method closely follows prior applications of the second-generation Mining Minima (M2) method.⁶ The chief difference is that here we use a QM energy model instead of a classical molecular mechanics potential energy model. In addition, to save computer time, we obtain the thermodynamics of each energy well with the rigid rotor-harmonic oscillator model,³⁴ rather than using mode scanning.³⁵ Finally, we use the quantized form of the molecular partition function, rather than the classical approximation. The underlying theory of these approaches has recently been reviewed,³⁶ and the M2 method is detailed elsewhere,^6,37 so only a brief summary is provided here.

The binding free energy of a host-guest complex is determined from the standard chemical potentials of complex, host, and guest molecules respectively, as

$$\mathrm{\Delta }{G}^o={\mu }_{\mathit{complex}}^o-{\mu }_{\mathit{host}}^o-{\mu }_{\mathit{guest}}^o$$ (1)

Based on the predominant states approximation,³² the standard chemical potential of a molecule is written as a sum over M multiple local energy minima (or conformations) j

$${\mu }^o\approx -RTln\sum _j^M{e}^{-\beta {\mu }_j^o}$$ (2)

$${\mu }_j^o=U_j+W_j-T·{S_j}^o$$ (3)

where β = (RT)⁻¹, R is the gas constant, T is the absolute temperature, and ${\mu }_j^o$, U_j, W_j, and S_j^o, are the standard chemical potential, solute energy, solvation free energy, and entropy of energy well j, respectively. The solute energy is computed as the heat of formation at 25°C in condensed phase; i.e., the heat of formation in gas phase minus PV=RT. Note that the semi-empirical QM energy model used here is parameterized to reproduce the experimental heat of formation at 25°C in gas phase, so the solute energy implicitly includes the zero-point, vibrational, rotational, and translational energies. The solvent is modeled here using an implicit solvation model, and the solvation free energy implicitly includes both the energetic and entropic changes of the solvent. In the rigid-rotor harmonic oscillator (RRHO) approximation,³⁶ the configurational entropy (S_j^o) of the local energy well is decomposed into translational, rotational, and vibrational contributions:

$${S_j}^o=R\{ln\left[{\left(\frac{2\pi m}{\beta h^2}\right)}^{\frac{3}{2}}\frac{e^{\frac{5}{2}}}{C^o}\right]+ln\left[8{\pi }^2{\left(\frac{2\pi e}{\beta h^2}\right)}^{\frac{3}{2}}\sqrt{I_1{I}_2{I}_3}\right]+\sum _i\left[\frac{\beta h{\omega }_i}{2\pi }{\left(e^{\beta h\frac{{\omega }_i}{2\pi }}-1\right)}^{-1}-ln\left(1-e^{-\beta h\frac{{\omega }_i}{2\pi }}\right)\right]\}$$ (4)

Here the first, second, and third terms on the right hand side correspond to the translational, rotational, and vibrational entropies, respectively; m is the molecular mass; h is Planck’s constant, C^o is the standard state concentration (1 M in solution phase); I₁, I₂, and I₃, are the principal rotational moments of inertia associated with energy minimum j; and ω_i is the angular frequency of the i^th vibrational mode for energy minimum j.

It can also be instructive to decompose binding free energies into energetic and entropic components. Ensemble-averaged energies thus are computed as

$$\langle E\rangle =\sum _j{P}_j{E}_j;P_j=\left(\frac{e^{-\beta {\mu }_j^o}}{e^{-\beta {\mu }^o}}\right)$$ (5)

where E is the solute energy, the solvation free energy, or the sum of these two quantities. The weighting factor P_j is the probability of finding the molecule in the j^th local energy well, which in turn is given by the Boltzmann weight of the j^th conformation. The total configurational entropy of a molecule or complex is given by,

$$S^o=\sum _j{P}_j{S_j}^o-R\sum _j{P}_{j}ln(P_j)$$ (6)

where the first and second terms on the right hand side will be referred to as the RRHO entropy and conformational entropy, respectively. Note that, for the association of molecules at room temperature, the quantized RRHO approximation is expected to yield results similar to those from the classical RRHO.³⁶

Computational details and energy model

The starting structure of CB7 was obtained from the Cambridge Structural Database³⁸ (figures 1A & 1B), and the starting structures of the various guest molecules were obtained from the PubChem database (http://pubchem.ncbi.nlm.nih.gov/), if available, or else prepared using the Discovery Studio Visualizer software (v3.0.0.10321, Accelrys, Inc.). Protonation states of the guest molecules were assigned based on the experimental pH and the expected pKa value of the various ionizable groups, without allowing for a possible shift in pKa of these ionizable groups upon binding to the host. Initial structures of the host-guest complexes were generated using the Autodock Vina software,³⁹ by flexibly docking the guest molecules in the binding site of CB7. In cases where the docking software failed to generate an inclusion complex, we manually placed the guest molecule within the binding cavity of the host.

Figure 1.

(A & B) Side and top views of cucurbit[7]uril (CB7). (C) Chemical structures of CB7 guests, shown in their expected protonation states at experimental pH. CB7-guest binding free energies (in kcal/mol) are given in parentheses next to the ligand numbers.

Many low-energy conformations of the host, guest, and complex molecules were generated using the Schrodinger software suite (Schrodinger, LLC.), as now detailed. Potential energy model parameters for the different molecules were assigned from the OPLS-2005 all-atom force field. The initial structures of the host, guest, and the docked complexes were refined using the truncated-Newton conjugate gradient minimization algorithm until the energy gradient fell below 0.001 kcal/mol.Å, or for a maximum of 10,000 steps. Starting with the resulting force field optimized structure, we then performed 1,000 steps of low-mode conformational search using Schrodinger Macromodel software.^40,41 Conformations within 10 kcal/mol of the lowest energy conformation were retained. To avoid double-counting of conformations, we eliminated duplicates by filtering the low-energy conformations based on the root-mean-square deviation (RMSD), with a tolerance value of 0.1 Å. The filtering algorithm also accounted for the symmetry of the molecule. While the host has a single most stable conformation shown in Figure 1, the number of conformations of the guests and the complexes were generally on the order of 10 – 100, and ranged between 5 and 300, depending on the flexibility of the guest.

The low-energy conformations generated using the classical OPLS energy model were then refined with the PM6-DH+ semi-empirical QM energy model and MOPAC 2009 software using the eigenvector following method until the normalized gradient fell below 0.01 kcal/mol.Å.⁴² Solvent (water) effects were accounted for using the COSMO solvation model,⁴³ with the solvent dielectric constant set to 78.4. All other COSMO parameters were set to their default values in MOPAC. The QM optimized structures were further filtered to remove any duplicates. The solute energy and RRHO entropy, and thereby the free energy, at 300 K were computed for each conformation using MOPAC’s thermochemistry module. The polar solvation free energy, which is the electrostatic interaction between the solute and the solvent (treated as a continuum dielectric medium), was computed with the COSMO solvation model.⁴³ This was supplemented with an additional non-polar solvation energy term, in order to account for cavity formation and van der Waals interactions between solute and the solvent, calculated as γ times the molecular surface area, where γ, the surface tension coefficient, was set to 0.006 kcal/mol.Ų for water.⁴⁴ The molecular surface area was calculated with MOPAC, using the algorithm described in the original COSMO solvation model.⁴³

Solvation free energies of small molecules

Solvation free energies were computed using the PM6-DH+ Hamiltonian and the COSMO solvation model, within the MOPAC software. A set of 367 neutral small molecules compose of only H, C, N, and O was compiled from the 504 molecule dataset reported by Mobley et al.⁴⁵ The initial geometries of these molecules were obtained from the same work (see supplementary information of Mobley et al.⁴⁵), and subjected to further refinement using the PM6-DH+ Hamiltonian in the gas phase. Subsequently, the polar solvation free energy was computed as the difference in energy in solvent and gas phases for a single conformation. The solvent parameters including dielectric constant and solvent probe radius were set to the default parameters for water, as described in the previous section. The molecular surface area, which is used to compute the non-polar solvation free energy, was computed using the algorithm described in the original COSMO solvation model,⁴³ as implemented in MOPAC software.

RESULTS

We computed the binding free energies of 29 CB7-guest complexes using the Mining Minima (M2) method and the PM6-DH+/COSMO semi-empirical QM energy model. CB7 and its respective ligands (numbered 1–29) are shown in Figure 1, along with the experimental binding affinities gathered from the literature.^7,8,10,46 The conformational search using an empirical force field took about 1 – 10 hours depending on the flexibility of the guest molecule, and the subsequent QM free energy calculations took several minutes to a few hours for each conformation. In the following subsections, we compare the computed binding affinities to the experimental affinities and report an empirically tuned model; analyze the roles of solute energy, solvation free energy, and configurational entropy; and compare these quantum results with our previous calculations obtained with the CHARMm/Vcharge classical force field.

Computed vs. experimental affinities

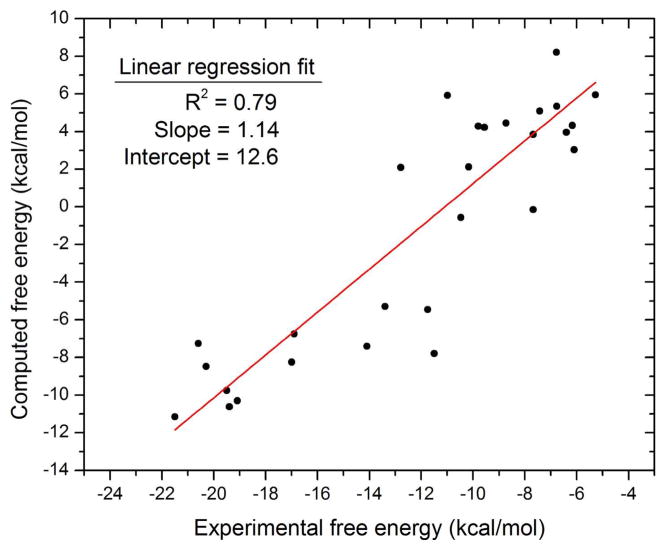
The computed affinities correlate strongly with the experimental affinities (R²=0.79), as illustrated in Figure 2. Although the root-mean-square error (RMSE) of the computed binding free energies is high, at 11.4 kcal/mol, it is evident from Figure 2, as well as the linear regression slope of near unity (1.14), that much of the error corresponds to a constant offset from the experimental affinity. The RMSE of the calculations from the line of linear regression shown in Figure 2 is significantly smaller, 3.1 kcal/mol, though still larger than the commonly posed goal of 1 kcal/mol chemical accuracy.

Figure 2.

Computed versus experimental binding free energies. The red line is the linear fit of the data points.

As a step toward further improving the accuracy of the calculations, we checked for systematic errors in the respective various free energy components by computing their correlation coefficients with respect to the errors in binding free energy. The computed mean changes in solute energy, Δ〈U〉, and the polar solvation free energy, Δ〈W_p〉, correlate somewhat with the error (R² = 0.25 and 0.32 respectively). These two quantities also correlate strongly with each other (R² = 0.98), implying significant compensation of interaction energy by polar solvation free energy change. This is likely a consequence of electrostatic interaction energy compensating for the polar solvation free energy penalty upon binding.^9,10 Nevertheless, because the standard deviation of these quantities from a perfect linear relationship is still high, 7.1 kcal/mol, a simple scaling of the change in solute energy to compute the total energy change would not give accurate binding affinities. The binding entropy, −T.ΔS^o, and the non-polar solvation free energy change, Δ〈W_np〉, correlate even less with the errors, with correlation coefficients of 0.00 and 0.09, respectively. Taken together, these results suggest that some of the error in the computed binding affinities might derive from inaccuracies in the PM6-DH+ energy model and/or the COSMO solvation model.

In light of the above observations, we hypothesized that the computed binding free energies might be improved by empirically correcting the changes in polar solvation free energy or solute energy or both. Since changes in solute energy and polar solvation free energy are strongly correlated to each other, it seemed unnecessary to scale both. Moreover, the PM6-DH+ Hamiltonian used to compute the solute potential energy has been optimized against high-level CCSD(T)/CBS QM calculations and was shown to reproduce these high-level QM interaction energies within 1 kcal/mol.^30,31 Therefore, we regard it as relatively reliable and instead chose to adjust the polar solvation term, using a simple, two-parameter linear scaling. We also allowed for a constant free energy offset, so that the corrected binding free energies are computed as

$$\begin{array}{l}\mathrm{\Delta }{G}^o=\mathrm{\Delta }\langle U\rangle -T\mathrm{\Delta }{S}_{\mathit{config}}^o+\langle W_{\mathit{fit}}\rangle +\delta \\ \langle W_{\mathit{fit}}\rangle \equiv \alpha \langle W_{\mathit{cosmo}}\rangle +\gamma \mathrm{\Delta }\langle \mathit{SASA}\rangle \end{array}$$ (7)

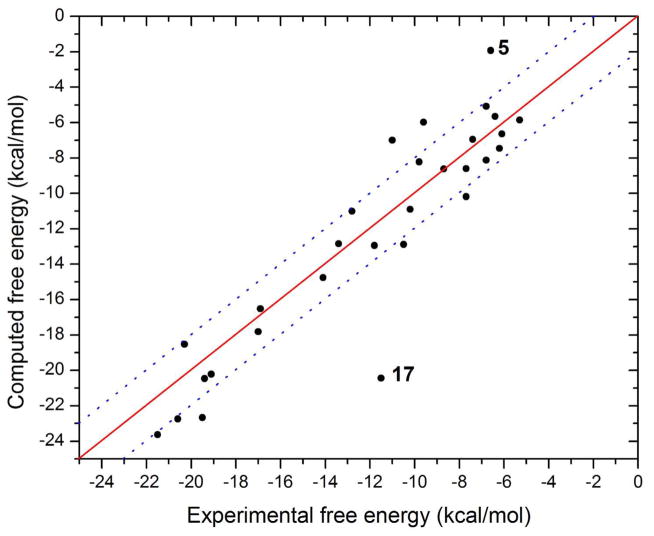
Note that all the energy terms here are ensemble-averaged values. The empirical parameters α, γ, and δ were determined through multiple linear-regression fitting of the experimental binding affinities to the individual free energy components according to equation 7. Guest 17 was identified as a major outlier during the regression analysis (see below), and therefore was excluded from the fitting. The fitted values of α, γ, and δ are 0.9628, 0.0086, and −5.83 kcal/mol, respectively. As shown in Figure 3, the corrected binding free energies correlate well with experiment (R²= 0.91, or 0.84 including the outlier). The mean unsigned error (MUE) and RMSE of the corrected binding affinities are 1.8 and 2.5 kcal/mol respectively, when the outlier is included, and 1.6 and 1.9 kcal/mol respectively, when the outlier is excluded.

Figure 3.

Corrected binding free energies versus the experimental free energies. Guest 17 is highlighted as a major outlier. The dotted lines represent ± 2 kcal/mol deviations from the fit.

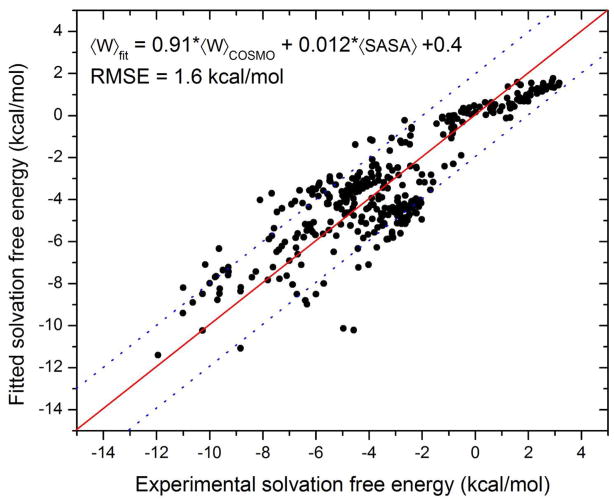
The fact that the fitting points to a ~4% reduction in the polar solvent term (α = 0.9628) led us to ask whether the PM6-DH+/COSMO solvation model systematically overestimates the polar solvation free energy. We addressed this by computing the solvation free energies of 367 neutral small molecules (obtained from Mobley et al.⁴⁵) composed of only H, C, N, and O. Multiple linear regression fitting of the computed COSMO polar solvation free energy and the solvent-accessible surface area (SASA) to the experimental solvation free energies is shown in Figure 4. The linear scaling coefficients for the COSMO polar solvation free energy and the SASA are 0.91 and 0.012, respectively, suggesting an overestimation of polar solvation free energy by the COSMO model. The RMSE of the computed solvation free energies is 1.6 kcal/mol, which is in the same range as the errors in computed binding affinities after the empirical fitting. These additional results are qualitatively consistent with the idea that our initial solvation model overestimated the changes in solvation free energy upon binding.

Figure 4.

Multiple linear regression fitting of COSMO polar solvation free energy and solvent-accessible surface area (SASA) to experimental solvation free energies for 367 neutral small molecules. The dotted lines represent ± 2 kcal/mol deviation from the fit.

The surface-area coefficient of 0.0086 kcal/mol.Ų from the empirical fitting of computed binding affinities is only slightly larger than the initially assigned value of 0.006 kcal/mol.Ų (see Methods), which has been used in prior solvation free energy models.⁴⁴ The larger value which emerges from this fitting exercise makes sense in retrospect, because the value of 0.006 is normally used with the SASA computed as Richards molecular surface area,⁴⁷ whereas the COSMO model employed here uses the van der Waals surface area,⁴³ which is always less than the SASA.

Analysis of outliers

Although the fitted binding free energies of most of the guest molecules fall within 2 kcal/mol of their experimental values, a few show larger deviations. The greatest errors, −8.9 and 4.7, respectively, are observed for guests 17 and 5. Interestingly, these are both adamantine derivatives, and differ only in that the amine groups in guest 17 are replaced by trimethylamines in compound 5. Nonetheless, the calculations yield errors of opposite sign for these two compounds. They are also computed to bind quite differently. In the most stable structures computed for the CB7-guest17 complex, the guest snugly fits inside the binding site of CB7 without straining the host molecule significantly, while the guest’s two primary amines are positioned close to the carbonyl portals of CB7, thus making highly favorable electrostatic interactions, as seen in models of other high-affinity adamantane guests.^9,10 The computed affinity of this guest, −20.4 kcal/mol, was significantly higher than experiment, −11.5 kcal/mol, and is in the same range as that of the other adamantyl amine guests. It is not clear why calculation and experiment disagree so much for this particular guest. In contrast, guest 5 initially failed to dock inside the binding site of the host. Indeed, despite our efforts to force this guest to find a stable pose within the binding site, it repeatedly moved out of the binding site during energy minimization or conformational search using an empirical force field. However, energy minimization of a manually prepared CB7-guest5 complex using the QM energy model showed the opposite result, as the guest stayed within the binding cavity of the host. The computed binding affinity of ligand 5 reported here is based on the single resulting conformation of the complex. The trimethylamine groups of guest 5 lie close the CB7 carbonyl groups in the refined structure, and these additional methyl groups on guest 5 might have resulted in unfavorable van der Waals repulsion leading to a lowered affinity.

Energy, configurational entropy, and solvation free energy

The present calculations provide a breakdown of the binding free energy into contributions from the solute energy (Δ〈U〉), the entropy associated with the flexibility of the host and guest molecules (configurational entropy, −T.ΔS^o, and the polar and non-polar contributions to the solvation free energy change (Δ〈W_p〉 and Δ〈W_np〉, respectively), as listed in Table 1. In all cases, we observe favorable changes in the potential energy plus solvation free energy, Δ〈U + W〉, and in the non-polar solvation free energy, along with unfavorable changes in the polar solvation free energy and the configurational entropy. Note that the solvation free energy, Δ〈W〉, implicitly includes the entropy change of the solvent upon binding. (The solvent entropy change is expected to be positive, as solvent is released from interacting with the solutes.) As a consequence, Δ〈U + W〉 is not purely energetic in nature.

Table 1.

Summary of computed binding free energy components, including potential energy (S.E.), solvation free energy, and entropy (configurational, RRHO, and conformational) using the empirically tuned QM model. Note that the reported polar and non-polar solvation free energies are fitted, as described in the main text, and a constant offset of −5.83 kcal/mol was applied to the computed binding affinities.

Guest	ΔGexp	$\mathrm{\Delta }{G}_{\text{calc}}^{\text{o}}$	Δ〈U + W〉	−T.ΔSo	S.E.	Solvation		Entropy
					Δ〈U〉	Δ〈Wp〉	Δ〈Wnp	$-T.\mathrm{\Delta }{S}_{\mathit{RRHO}}^o$	−T.ΔSconf
1	−5.3	−5.8	−9.5	9.5	−139.8	133.0	−2.7	10.4	−0.9
2	−6.1	−6.6	−16.3	15.5	−100.0	85.5	−1.8	15.9	−0.4
3	−6.2	−7.4	−10.6	9.0	−139.8	131.9	−2.8	9.1	−0.1
4	−6.4	−5.6	−18.2	18.4	−95.3	79.4	−2.3	17.8	0.6
5	−6.6	−1.9	−11.0	14.9	−149.1	141.1	−3.0	14.9	0.0
6	−6.8	−8.1	−11.2	8.9	−189.8	180.7	−2.1	9.0	−0.1
7	−6.8	−5.1	−9.7	10.5	−184.1	176.5	−2.1	11.7	−1.2
8	−7.4	−6.9	−12.2	11.1	−144.0	135.0	−3.2	11.8	−0.7
9	−7.7	−10.2	−13.9	9.6	−104.0	92.2	−2.1	9.2	0.4
10	−7.7	−8.6	−11.1	8.3	−164.1	155.0	−2.0	8.8	−0.5
11	−8.7	−8.6	−11.2	8.4	−179.2	170.2	−2.2	9.1	−0.7
12	−9.6	−6.0	−6.1	5.9	−99.4	95.5	−2.2	7.6	−1.7
13	−9.8	−8.2	−9.1	6.7	−158.0	151.6	−2.7	7.1	0.4
14	−10.2	−10.9	−14.0	8.9	−184.2	171.9	−1.7	9.2	−0.3
15	−10.5	−12.9	−22.2	15.2	−163.0	143.7	−3.0	15.5	−0.3
16	−11.0	−7.0	−12.8	11.7	−174.6	164.1	−2.4	10.8	0.9
17	−11.5	−20.4	−28.4	13.8	−188.4	161.8	−1.8	14.6	−0.8
18	−11.8	−12.9	−15.4	8.3	−36.6	23.7	−2.4	8.7	−0.4
19	−12.8	−11.0	−16.2	11.1	−182.4	168.6	−2.4	11.6	−0.5
20	−13.4	−12.8	−16.6	9.6	−39.4	25.2	−2.4	9.2	0.4
21	−14.1	−14.8	−15.0	6.1	−34.0	21.3	−2.3	6.7	−0.6
22	−16.9	−16.5	−21.7	11.0	−100.9	81.7	−2.5	11.1	−0.1
23	−17.0	−17.8	−20.4	8.5	−95.9	77.8	−2.4	9.3	−0.8
24	−19.1	−20.2	−22.5	8.2	−107.4	87.2	−2.3	8.5	−0.3
25	−19.4	−20.5	−22.0	7.4	−105.1	85.4	−2.3	7.4	0.0
26	−19.5	−22.6	−28.4	11.6	−188.3	162.5	−2.6	11.8	−0.2
27	−20.3	−18.5	−20.6	7.9	−107.6	89.5	−2.4	8.5	−0.6
28	−20.6	−22.7	−32.9	16.0	−252.2	222.7	−3.3	15.8	0.2
29	−21.5	−23.6	−29.9	12.1	−178.2	150.9	−2.6	12.3	−0.2

The mean change in binding energy—the solute energy plus the solvation free energy—contributes significantly to the binding affinities of the guests studied here, ranging from −6.1 to −32.9 kcal/mol. Even though the mean changes in solute energy and solvation free energy individually range from few tens of kcal/mol to a couple of hundred kcal/mol, compensation between these two quantities results in overall energy changes that are small and favorable changes. The changes in solvation free energy may be further decomposed into polar and non-polar contributions, where the polar solvation energy arises from the electrostatic interactions between solute and solvent, as computed with the COSMO continuum solvation model. This polar solvation term forms the major portion of the total solvation free energy change, and the observed compensation between solute potential energy and solvation free energy is therefore essentially electrostatic in nature.^9,10 On the other hand, the non-polar solvation energy contributes a maximum of −3.2 kcal/mol to the binding free energy. Furthermore, the change in non-polar solvation free energy is nearly constant among the different ligands with a mean of −2.4 kcal/mol and a standard deviation of 0.2 kcal/mol. As a consequence, this term plays little role in determining the relative binding affinities.

The computed losses in configurational entropy, which reflect reduced mobility of the host and guest upon binding, yield free energy costs ranging from 5.9 to 18.4 kcal/mol. These quantities are of the same order of magnitude as the net binding free energies, much as previously seen in M2 calculations based on empirical force fields.^6,9,10 The current calculations also provide a detailed breakdown of the configurational entropy change—note that this excludes the solvent entropy change—into the RRHO entropy, which is the mean of the sum of the translational, rotational, and vibrational entropies; and the conformational entropy, which results from the occupancy of multiple local energy minima. As shown in Table 1, the change in configurational entropy arises predominantly from the loss in RRHO entropy. In fact, the change in conformational entropy tends to favor binding by a small amount, rather than opposing binding. This implies, not unreasonably, that the complexes tend to have more roughly equistable energy wells than the corresponding free host and guest species. Thus, the large configurational entropy penalties observed here do not arise from changes in the number of accessible conformations of the host, guest, and complex molecules, but from a narrowing of the accessible energy wells. This conclusion matches that obtained from previous M2 calculations reported for host-guest and protein-ligand systems using classical force fields.^10,48

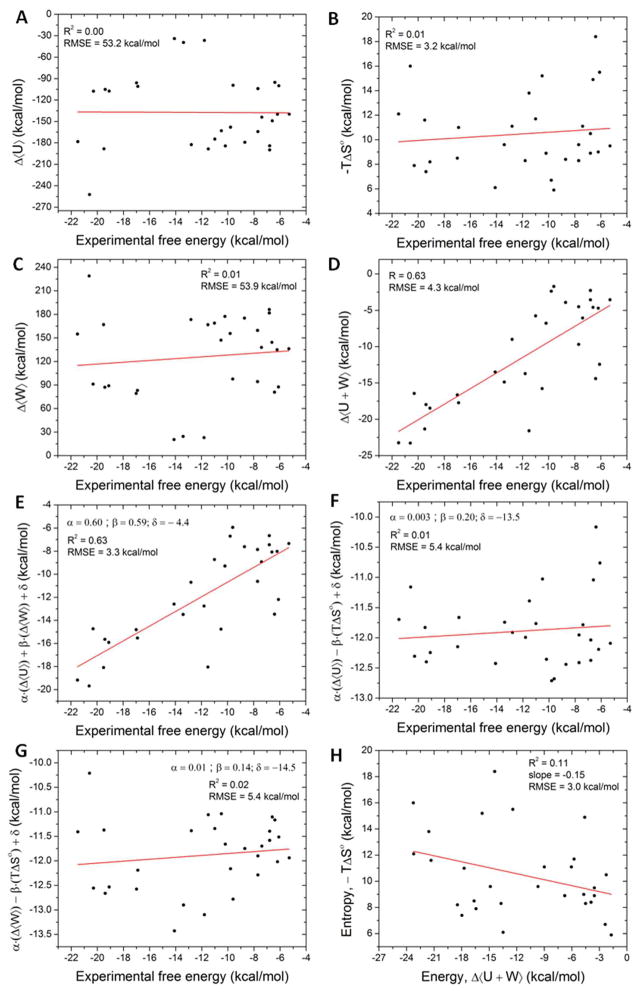
It is of interest to inquire whether these quantum mechanics-based affinity calculations display energy-entropy compensation. As shown in Figure 5H, there is no clear pattern of energy-entropy compensation within the present data (R²=0.11). This is consistent with prior M2 calculations, which indicate clear entropy-energy compensation for a number of host molecules,^5,6 but not for the CB7 host studied here,^9,10 as detailed in Figure 6D. The lack of correlation between energy and entropy means that an ad hoc scaling of energies to account for the loss in configurational entropy will not significantly improve the accuracy of the computed affinities.

Figure 5.

Scatter plots of various free energy components and the experimental binding free energies. Linear regression fits are shown as solid red lines and the corresponding statistics are given in the figure legends.

Figure 6.

Comparison of various free energy components computed using the classical force field and the QM energy models. Linear regression of the data is shown as solid red line with the fit parameters shown in the legend.

Typical docking and scoring functions do not include all of the energy and entropy components that are accounted for in the present calculations. We therefore asked how well a scoring function could perform if it used only one of these energy components. Mean, unfitted changes in solute energy, solvation free energy, and configurational entropy are found to correlate poorly with the measured binding free energies (Figure 5A–C); the correlation coefficients are 0.00, 0.01, and 0.01, respectively. Thus, no one of these components is a good indicator of binding affinity. We then considered pairs of M2 free energy components and found that the mean change in the sum of solute energy and solvation free energy, 〈U + W〉, correlates fairly well with the experimental binding free energies (Figure 5D; R² = 0.63), though not as well as the unfitted M2 calculations, with their correlation coefficient of 0.79 (above; and see Figure 2). In order to put all the comparisons of pairs of M2 free energy components against experiment on an equal footing with the fitted M2 results, we also computed the best linear fittings of pairs of M2 free energy components with experiment, using multiple linear regression fitting. The linear scaling coefficients and the constant offset were optimized to minimize the RMSE of the model. Thus, a linear regression model of solute energy and solvation free energy showed a decent correlation of R² = 0.63 to the experimental binding affinity with an RMS error of 3.3 kcal/mol (Figure 5E), although this is still lower than the correlation coefficient for the fitted full M2 result, 0.84 (above; and see Figure 3). However, the linear regression models of configurational entropy combined with solute energy or solvation free energy correlate only weakly with the experimental binding free energy (R² = 0.01 and 0.02, respectively; Figures 5F and 5G). We conclude that, although the sum of the solute energy and solvation free energy is the major determinant of binding free energy, accounting for the loss in configurational entropy further improves the correlation, as previously observed.^5,9,10

Classical force field vs. quantum mechanical calculations

We now examine the relationship between the present QM M2 calculations and prior force field-based M2 calculations available for a subset of the systems studied here (Table 2). Binding free energies computed with the classical force field correlated well (R² = 0.83) with experiment with an RMS error of 4.8 kcal/mol. The unfitted QM model showed a slightly better correlation (R² = 0.88) but a larger RMSE of 10.2 kcal/mol. For a fair comparison to the tuned QM model (equation 7), we applied a similar linear scaling correction to the prior classical force field calculations (fitted values of α, γ, and δ are 1.005, 0.0055, and 3.37 kcal/mol, respectively) and obtained a correlation coefficient of 0.87 and RMSE of 2.7 kcal/mol. These results are only slightly worse than the correlation coefficient and RMSE for the present tuned QM energy model, i.e., 0.95 and 1.6 kcal/mol, respectively, as reported above. Using the unfitted results, we compared the different free energy components obtained from classical and QM M2 calculations. The changes upon binding of the solute energy, polar solvation free energy, and non-polar solvation free energy, calculated with the classical and QM energy models, are strongly correlated with each other (R²= 0.99, 0.99, and 0.92, respectively), as illustrated in Figure 6. Despite these high correlations, however, the RMS deviations in solute energy, 4.5 kcal/mol, and the polar solvation free energy, 10.7 kcal/mol, are large. The change in the classical force field potential energy systematically overestimates the change in the QM potential energy model, while the Poisson-Boltzmann solvation model systematically underestimates the COSMO solvation model’s change in polar free energy. The RMS deviation in the non-polar solvation energy is negligible, 0.2 kcal/mol; this is not surprising, because both approaches estimate it with a simple surface area model. Interestingly, the classical and QM changes in configuration entropy on binding correlate only weakly (R²= 0.43, RMSE= 5.0 kcal/mol). Since the number of distinct conformations for these host-guest complexes is typically low and the loss in conformational entropy is significantly smaller than the loss in RRHO entropy (see Table 1), the deviations in computed configurational entropies between the classical force field and QM calculations originate primarily from the differences in RRHO entropy. The lack of strong correlation and the high RMSE point to configurational entropy as a key contributor to the deviation between the classical force field and the QM calculations for this set of host-guest systems. Finally, no significant compensation between energy and entropy was observed in the classical force field calculations either, consistent with the current QM calculations.

Table 2.

Summary of computed binding free energy components, including solute energy, solvation free energy, and entropy using the QM energy model and a classical force field (CHARMm). Note that the reported polar and non-polar solvation energies are fitted. Constant offsets of −5.83 and 3.37 kcal/mol are included in the QM and classical free energies, respectively.

		PM6-DH+/COSMO					CHARMm/VCharge/PBSA
#	ΔGexp	$\mathrm{\Delta }{G}_{\text{calc}}^{\text{o}}$	Δ〈U〉	−T.Δ〈So〉	Δ〈Wp〉	Δ〈Wnp〉	$\mathrm{\Delta }{G}_{\text{calc}}^{\text{o}}$	Δ〈U〉	−T.Δ〈So〉	Δ〈Wp〉	Δ〈Wnp〉
3	−6.2	−7.4	−139.8	9.0	131.9	−2.8	−6.6	−143.8	14.2	122.4	−3.1
8	−7.4	−6.9	−144.0	11.1	135.0	−3.2	−7.0	−147.3	16.8	123.1	−3.3
20	−13.4	−12.8	−39.4	9.6	25.2	−2.4	−8.3	−41.3	17.2	14.6	−2.6
21	−14.1	−14.7	−34.0	6.1	21.3	−2.3	−14.6	−37.5	12.6	9.1	−2.4
24	−19.1	−20.2	−107.4	8.2	87.2	−2.3	−20.1	−110.1	12.5	76.4	−2.5
25	−19.4	−20.4	−105.1	7.4	85.4	−2.3	−21.8	−111.2	11.8	76.5	−2.5
26	−19.5	−22.7	−188.3	11.6	162.5	−2.6	−18.7	−191.6	14.5	157.5	−2.7
27	−20.3	−18.5	−107.6	7.9	89.4	−2.4	−21.5	−111.2	13.3	75.4	−2.6
28	−20.6	−22.7	−252.2	16.0	222.7	−3.3	−17.7	−261.4	15.7	227.5	−3.2
29	−21.5	−23.6	−178.2	12.1	150.9	−2.6	−25.3	−181.0	15.7	139.2	−2.8

DISCUSSION

We have used the mining minima (M2) approach with a semi-empirical quantum mechanical Hamiltonian and the COSMO solvation model to compute the affinities of 29 cucurbit[7]uril guest complexes, with measured binding free energies ranging from −5.3 kcal/mol to −21.5 kcal/mol. The calculated free energies correlate strongly with experiment over this broad range of affinities, and a simple linear correction of the polar solvation free energy afforded significant improvement in accuracy. The correlation with experiment is somewhat better than that found in our previous classical calculations for a subset of these systems. Although the QM calculations are 1 – 2 orders of magnitude slower than the previous classical M2 calculations, the time-consuming part of these calculations are quite parallelizable, as the QM free energies of the various conformations can be computed independently across multiple CPUs.

Not surprisingly, the sum of the potential energy and the solvation free energy contributes strongly to the correlation between calculation and experiment. It is thus encouraging that recent advances in localized molecular orbital methods, such as in MOZYME,⁴⁹ DivCon,⁵⁰ LocalSCF,⁵¹ and X-Pol⁵⁶ are making increasingly high quality energy calculations feasible for larger systems, such as protein-ligand complexes. We also observed that accounting for losses in configurational entropy is necessary to achieve optimal correlation with experiment. Unfortunately, it is still quite time-consuming to obtain the entropy of larger systems with QM methods, due to the computational cost of obtaining the second derivative matrix and hence the vibrational spectrum. It is also interesting to note that the computed configurational entropy changes result primarily from the changes in the RRHO entropy, which comprises the translational, rotational and vibrational terms. Thus, the conformational entropy, which accounts for any change in the number of occupied energy wells, contributes minimally. This observation is consistent with the previous M2 calculations reported for protein-ligand binding and other host-guest systems.^10,48

The linear fit discussed above suggests that the mean changes in polar solvation free energy from COSMO solvation model are systematically overestimated by about 4%, which is within the expected accuracy of this solvation model. However, a modest percent error can lead to significant absolute errors for large molecules that undergo substantial changes in solvation on binding. Given that CB7 is much more complicated than the small molecules used in the parameterization of COSMO and other solvation models, and that many of the guest molecules studied here have net charges ranging from +1 to +4, and hence very large solvation free energies, it is very encouraging to see that a simple linear correction of COSMO solvation free energy dramatically improved the accuracy of the calculated affinities. Using higher levels of QM theory, such as DFT, that are known to give better electron density distributions, and more refined solvation models, such as COSMO-RS^52,53 and SMD⁵⁴ might further improve M2 affinity calculations with QM Hamiltonians.

Interestingly, the computed affinities show a constant offset from the experimental affinities; even after the empirical correction for the solvation free energy, there is a significant offset of 5.83 kcal/mol (i.e., δ = −5.83) in the binding free energy. Because this offset is constant across all of the measurements, we conjecture that it reflects an underestimate of the chemical potential of the host molecule free in solution, as this appears in all of the binding free energies. However, the origin of the presumed overstabilization of the host molecule in solution is unclear. Perhaps it results from treating the water within the host’s binding cavity as a continuous medium of uniform dielectric constant, according to the COSMO model. Indeed, preliminary analysis of water structure and thermodynamics within this binding cavity suggests that the water molecules in CB7 cavity are unstable relative to bulk water⁵⁵ (and unpublished data). If so, then treating the water in the cavity as a bulk dielectric might lead to a significant overestimate of the host’s solvation free energy and hence the underestimates of binding affinities observed here. Although prior M2 calculations using the Poisson-Boltzmann solvation model, which also treats all solvent as a dielectric continuum, did not lead to a systematic underestimate of binding free energies,^9,10 they also used an empirical force field which in principle is less accurate than the QM method used here and thus may have masked an error in the solvation free energy. Thus, no definite conclusion can be drawn at this time regarding the origin of the offset observed here.

In summary, the current study demonstrates the use of the M2 method for computing binding affinities of host-guest systems with a quantum mechanical energy model, a step towards improving the accuracy of binding affinity calculations. Due to its highly parallelizable nature, the M2 method is expected to scale well with the number of conformations and hence with the flexibility of molecules. Moreover, the M2 method can in principle be used with any QM energy model, as well as with other solvation models. Thus, with increasing computational power, it is rapidly becoming practical to use higher level QM methods, such as DFT and MP2, for computing host-guest binding affinities. This study also further demonstrates the utility of host-guest systems as informative test beds for validating energy models, and in particular hints at the need to develop further enhanced treatments of solvation for use with QM energy models.