Abstract
This article discusses options to allow comparative analysis of inequalities in the distribution of health workers (HWs) across and within countries using a single summary measure of the distribution. Income inequality generally is measured across individuals, but inequalities in the dispersion of HWs must use geographical areas or population groupings as units of analysis. The article first shows how this change of observational unit creates a resolution problem for various inequality indices and then tests how sensitive a simple ratio measure of the distribution of HWs is to changes in resolution. This ratio of inequality is illustrated first with the global distribution of HWs and then with its distributions within Indonesia. The resolution problem is not solved through this new approach, and indicators of inequalities of access to HWs or health services more generally appear not to be comparable across countries. Investigating geographical inequalities over time in one setting is possible but only if the units of analysis remain the same over time.
Introduction
Inequality in the distribution of health workers (HWs) has been an increasing policy concern (Gravelle and Sutton 1998). Most frequently, attention focuses on the distribution of HWs within countries (Gravelle and Sutton 1998; Gupta et al. 2003), but recently attention has also been directed to inequalities across countries (e.g., Chen et al. 2004). One argument emphasizes that, for example, the main limitations that developing countries face in improving population health is the exodus of their HWs to more developed countries, a trend that reinforces the already unequal global distribution of HWs (Hagopian et al. 2004).
A single summary measure of inequality is useful to have when comparing the inequality of HWs’ distributions. Many measures are available to describe income inequality (Anand et al. 2001), but the study of the distribution of HWs is less advanced. The Gini coefficient has been used most frequently (e.g., Brown 1994; Gravelle and Sutton 1998; Gupta et al. 2003), although Gravelle and Sutton (1998) also use the Atkinson index to summarize the distribution of general practitioners in England and Wales.
The reasons for the choice of these indicators are not always discussed, but all of the standard inequality indicators are susceptible to the both scale and resolution problems—an inequality estimate changes with a change in the extent of geographical coverage (scale) and with the average size of size of the areal unit (resolution). This change makes comparing estimates of inequality in the distribution of HWs across countries meaningless except in the special case where the geographical coverage and the average sizes of the geographical areas being considered are the same. The resolution problem applies to changes in inequality over time in one country: if population size increases or administrative boundaries are changed, the estimates of inequality are not comparable.
For this reason, we explore whether an indicator that is not sensitive to the resolution problem is possible to select.
Materials and Methods
In selecting inequality indicators, Anand et al. (2001) argue that the following four key issues should be considered:
The population grouping across which inequality is to be assessed. The value of most inequality measures changes if larger or smaller groupings of a population are chosen; inequalities are more accentuated when described across smaller geographical divisions (Anand et al. 2001). This issue is known as the modifiable areal unit problem (MAUP) and is caused by the failure to incorporate areal or spatial effects into an analysis (Openshaw 1984; Holt et al. 1996). The two major components of the MAUP are the resolution effect and the zoning effect: changing the number of areal units or modifying the partitioning of space within a map, while keeping the same number of areal units, can influence the interpretation of a geographical phenomenon. In the context of HWs, the value of a given inequality measure can change for the same population, depending on whether it is measured by comparing people grouped at, say, the state or province level, or at some more local level of government.
The reference group or norm against which differences are measured. Inequality may be measured against a benchmark (i.e., an “optimal” number of HWs per inhabitant within a country or a mean [e.g., the standard deviation of logarithms of numbers, the Theil coefficient], or by comparing every pair of units [e.g., the Gini coefficient]). A judgment must be made about whether policy should be concerned with interindividual differences or differences compared to some standard or norm.
The choice between absolute versus relative measures. A family of measures quantifies relative inequality: for example, they may be unaffected by doubling the number of HWs per inhabitant in each geographical area. However, they do change if the absolute number of HWs per capita increases by the same amount in each area. A second family of indicators measures absolute inequality. Increasing the number of HWs per capita in each area by the same number so that the absolute differences among areas are preserved would have no effect on them, while doubling the number in each area would. This comparison can be illustrated with two areas in which the average number of HWs per capita is nine (area 1) and three (area 2) in year 1, and four (area 1) and one (area 2) in year 2. The absolute difference between the two areas decreases from six (9–3) to three (4–1) while the relative difference increases from three (9/3) to four (4/1). Using different indicators can result in different interpretations of inequality.
The weights to be attached to various points in a distribution. Different measures give more weight to changes in the upper tail (e.g., the Theil coefficient), in the lower tail (e.g., the mean of logarithms), or to the middle of a distribution (Gini). The Atkinson index incorporates an “aversion to inequality” parameter, which captures a society’s preference for changes in distribution along its length (Anand et al. 2001). Gakidou, Murray, and Frenk (2003) introduce a similar concept (called “alpha”) that could be used to differentiate changes at different points in a distribution. One argument asserts that improvements in HWs’ availability in the worst areas should be weighted more than improvements in areas with more workers per capita.
Table 1 classifies the most common inequality indicators according to the four categories. For formal definitions, see Anand et al. (2001) and Mackenbach and Kunst (1997).
Table 1.
Characteristics of Major Summary Measures of Inequality for Continuous Variables
| Inequality Index | Reference Group | Absolute vs. Relative Measure | Weights Attached |
|---|---|---|---|
| Gini Coefficient | Interindividual | Relative | Middle of the distribution |
| Standard Deviation of the Logs | Mean | Relative | Lower tail of the distribution |
| Theil Index | Mean | Relative | Upper tail of the distribution |
| Atkinson Index | Interindividual | Relative | Depends on the value of the parameter of aversion to inequality |
| Decile Ratio | Intergroup | Relative | Both tails of the distribution |
| Index of Dissimilarity | Intergroup | Relative/Absolute | Both tails of the distribution |
| Variance | Mean | Absolute | Both tails of the distribution |
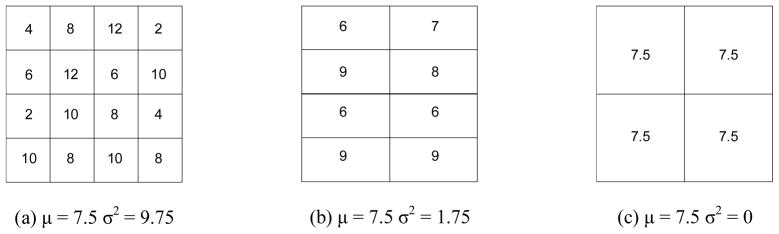
Although all of these considerations are important, we limit attention here to the resolution issue (MAUP). Income inequality generally is measured across individuals, and hence the resolution problem does not apply. This is not the case for inequalities in the dispersion of HWs, where geographical areas or population groupings must be used. Fig. 1 illustrates the resolution problem, showing the number of HWs per capita. We illustrate the problem with the variance, but the values of all of the summary indicators in Table 1 can be shown to suffer from the same problem if they are used to summarize the distribution of HWs.
Figure 1.
Effects of areal aggregation on the mean and variance of the distribution of HWs’ rates.
In Fig. 1(a), the areal distribution is shown in an area with 16 cells—here called municipalities—with an equal population in each. The mean value is μ = 7.5, and the variance is σ2 = 9.75. In Fig. 1(b), these data are aggregated into larger units (districts) by merging neighboring cells. The value in each cell is the average number of HWs per population derived by aggregating the data in Fig. 1(a). This averaging leads to the same mean value, as well as to a smaller variance for the aggregated rates. Repeating this operation results in no variance at all (Fig. 1[c]).
Although this illustration is somewhat extreme, the general rule is that the variance decreases through the aggregation of units. More generally, aggregating geographical units can show decreasing levels of inequality for all of the indicators listed in Table 1.
Therefore, we explore if a simple ratio measure of inequality solves this problem. We consider two ways of estimating the proportion of the health workforce available to the top 10% of the population, compared to the bottom 10%, and test the extent to which the ratio is also sensitive to the level of aggregation.
Ratios to express inequality
Simple ratios
A ratio of HWs for two groups has intuitive appeal because it allows a comparison of groups that do not coincide with administrative or geographical areas. There are two ways to calculate the ratio for HWs and both require a preliminary stratification of a population according to the availability of HWs per inhabitant. In the first, the HWs per capita for the population at the 10th and the 90th percentile are calculated. For example, if the number of HWs per 1,000 habitants separating percentile 10 from the 11th percentile is two, and the number of HWs per 1,000 habitants separating the 89th from the 90th percentile is 15, the ratio equals 7.5. The main advantage of using this version of the ratio is that it is relatively robust to the existence of outliers (extremes at the top or at the bottom of a distribution); the main limitation is that it uses only two points from an entire distribution.
The second way of calculating the ratio is based on the Lorenz curve (using the so-called Kuznets ratios). The share of total HWs available for different population groupings is ordered from lowest to highest, as in Table 2. If we assume that the two HWs per 1,000 habitants is equally spread over the population in state A, the bottom 10% of the population has access to 3.95% (7.9/2) of HWs. Similarly, the top 10% has access to 19.6% (39.2/2) of HWs. This “decile ratio” equals 4.96.
Table 2.
Worktable for HWs’ Decile Ratio Calculations
| Province | Population | Share of Total Population | HWs per 1,000 Inhabitants | Share of the Total HWs |
|---|---|---|---|---|
| A | 2,000 | 20% | 2 | 7.9 % |
| B | 3,000 | 30% | 3 | 17.6 % |
| C | 1,000 | 10% | 4 | 7.9 % |
| D | 2,000 | 20% | 7 | 27.4 % |
| E | 2,000 | 20% | 10 | 39.2 % |
| Total | 10,000 | 100% | 5.1 | 100 % |
The impact of the resolution problem on the decile ratio is illustrated in the results section. For the sake of comparison, we include the Gini coefficient, the indicator that has most commonly been used in measuring inequality in the distribution of HWs.
More complex ratios: The variance versus unit size slope indicator
As the aggregation (i.e., size of a geographical unit) increases, the variance of the aggregated values (i.e., HWs’ rate) is expected to decrease, recalling the example described in Fig. 1. The rate of decrease of this variance depends on parameters such as the size of the aggregation units or the degree of spatial continuity of the original rates (Isaaks and Srivastava 1990). Consider, for example, a very homogeneous process corresponding to the situation where high and low rates are intertwined across a study area. The aggregation leads to a rapid decrease of the variance because the aggregation of these low and high values creates medium values across the study area. In the Fig. 1 example, the variance decreases from 9.75 to 1.75, and finally to zero. Conversely, a very heterogeneous process corresponds to the situation where large clusters of high and low rates are observed. Aggregation leads to a very slow decrease of the variance because the aggregation of these clusters of low and high values still creates patches of low and high values across the study area.
Based on these observations, the slope of the linear regression of variance versus the logarithm of the size of aggregation units might be used as an empirical measure of the spatial homogeneity of an aggregation process. A dimensionless homogeneity criterion is obtained by dividing the slope computed from observed rates by the slope of a homogeneous process created by random shuffling of the observed rates. The closer this criterion is to one, the more homogeneous is the distribution of the variable under study. Smaller values of this criterion indicate an unequal repartitioning of HWs, with the existence of zones of high and low values. This criterion has the advantage of accounting for the spatial distribution of rates, as compared to a nonspatial statistic such as the variance measure used in Fig. 1.
The homogeneity criterion may be illustrated with the spatial distribution of all workers in Indonesia. The first step is to overlay a fine grid over the country. A grid spacing of 2.5 km was used for Indonesia. For each geographical unit (i.e., provinces/regencies for Indonesia), the HWs’ rates and population size are assigned to each grid node falling within that unit. The same rate is assigned to each node while the population is divided equally among these nodes, corresponding to the implicit assumption that the population is uniformly distributed within a unit. The next step is to define a grid of square aggregation cells, and within each cell compute the total population (i.e., simply sum the population assigned to each node within a cell) and population-weighted mean of rates. These two operations are repeated for cells of increasing size. By default, the minimum cell size is set to the median area of geographical units (assuming that each unit is a square), while the maximum cell size is such that, at this level of aggregation, a minimum of 25 observations are available for computation of the variance. This upper limit ensures that enough cell values are available to compute a meaningful variance. Furthermore, the choice of the position of the grid over the country—i.e., the origin of the grid (e.g., coordinates of the lower left corner)—is important. Shifting the grid even by 1 km changes the results of an aggregation because it affects the relative proportion of each administrative unit that is included in each cell. If we translate the grid by, say, 1 km, the relative proportion of the regency belonging to a particular cell might drop from 75% to 60%, leading to a change in the number of HWs allocated to that cell. Consequently, the aggregated values would change and so would the variance. The choice of the origin of a grid is arbitrary. Therefore, we randomly choose five different origins and average the results, reducing the sensitivity of the results to the position of a grid. Every time, we repeat the allocation of HWs to each cell and then compute the variance of the aggregated number of HWs.
Finally, the population-weighted variance of cell values is plotted against the logarithm of the length of corresponding aggregation cells, and the slope of a linear regression model is computed. Since the blocks are square, the length can be interpreted as the square root of the area. This scaling linearizes the relationship between size and variance, similar to the use of logarithms to linearize relationships that are nonlinear in natural units.
The slope value expected under a completely homogeneous process is estimated using the same procedure, except that the rates and corresponding population sizes first are randomly shuffled among all units. To reduce sampling fluctuations, the randomization is performed five times (which corresponds to the default number used in the statistical program used for calculations), and the results (i.e., population-weighted variance) are averaged. The slope computed from observed rates is divided by the slope obtained for the homogeneous process, leading to the proposed criterion.
The data
We illustrate the various summary measures of inequality in two ways. The first explores the variability of HWs across countries globally. The second explores inequality in one country, Indonesia. Country-specific analysis was also undertaken for Vietnam and Brazil (Speybroeck et al., 2006), which shows the same results (these can be obtained from the authors on request).
World
Data about the number of HWs in 192 countries belonging to the World Health Organization (WHO) were updated and revised for the 2006 World Health Report. In our analysis, they also were grouped into six geographical regions. This is the most complete database available, but information for all countries is complete only for doctors, nurses, and midwives, so those are the data used here.
Indonesia
Data about HWs were obtained from the Ministry of Health (MOH) Inventory for 2001, which includes records for public and private hospitals and public health centers. Independent private practitioners are not included in this dataset. Human resources data were not available for approximately 8% of all hospitals (accounting for 3% of beds) and for 12% of all health centers. The Indonesian MOH coding system was used to classify health workers. Population data were obtained from the 2000 census. Health worker numbers were extracted from the 2001 MOH Inventory for 30 provinces and 327 regencies, each of which is an independently administered sub-national unit. Provinces constitute the first, whereas regencies constitute the second, sub-national level units.
Results
Simple ratios
The two versions of the decile ratios are shown in Table 3. The first row summarizes the global distribution of HWs using two geographical groupings: the six WHO regions and countries. We then report the ratios using geographical groupings for Indonesia.
Table 3.
Two Inequality Indicators for the Distribution of HWs across the World and within Indonesia
The values of the decile ratios also depend on the average size of the geographical unit chosen. The smaller the average size of a unit, the greater is the apparent inequality in distribution. Population groups must be used to estimate the decile ratio, and the larger a population group, the less accurate is the estimate of availability at the 10th and 90th percentiles. Consequently, comparisons are not possible for the estimated decile ratio across countries because the size of administrative units typically differs.
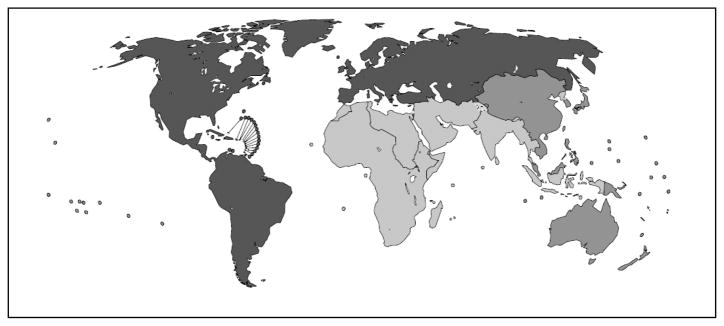
Fig. 2 portrays the distribution of HWs across the world at the regional (a) and national (b) level (WHO 2006). The greatest burden of disease is in the African region of (AFR); it has access to proportionally fewer HWs and proportionally less of the global health expenditure. The regional grouping of countries shows far less inequality than results based upon national boundaries.
Figure 2.
Global distribution of the stock of HWs (per 1,000 inhabitants) at the regional (a) and national (b) level (WHO 2006).
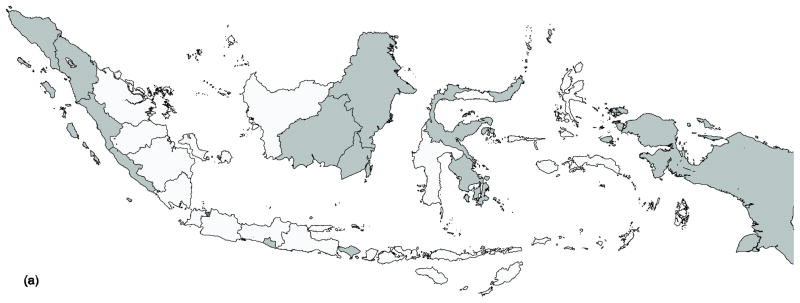
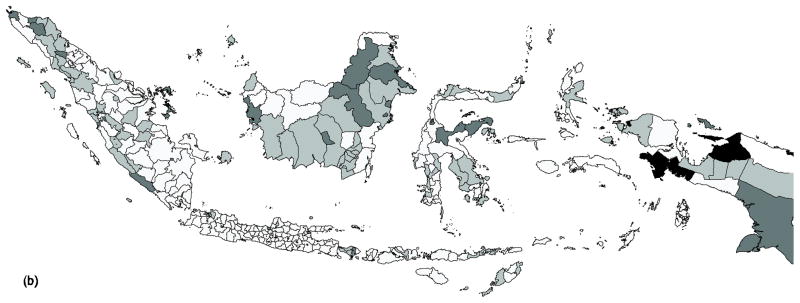
Similar patterns can be observed for countries, which are illustrated only for Indonesia here (the legend is the same as for Fig. 2). Fig. 3(a) shows that, in Indonesia, for provinces the access ranges between 0.58 and 2.70 HWs per 1,000 habitants, on average. However, inequalities across regencies are stronger, and 25% of all residents have access to less than 0.57 HWs per 1,000 habitants (Fig 3[b]).
Figure 3.
Distribution by provinces (a) and regencies (b) of the stock of HWs in Indonesia (per 1,000 inhabitants). Source: Indonesian MOH Inventory 2001.
More complex ratios: The variance versus unit size slope indicator
A heterogeneous process was created by moving around (i.e., allocating to different geographical units) the observed HWs’ rates and corresponding population sizes such that they form a monotonic east–west (EW) gradient for Indonesia. Then the same rates were shuffled randomly to create a homogeneous process. The results obtained after the spatial ordering or spatial randomization of rates are displayed using short and long dashed lines, respectively, in the two graphs in Fig. 4.
Figure 4.
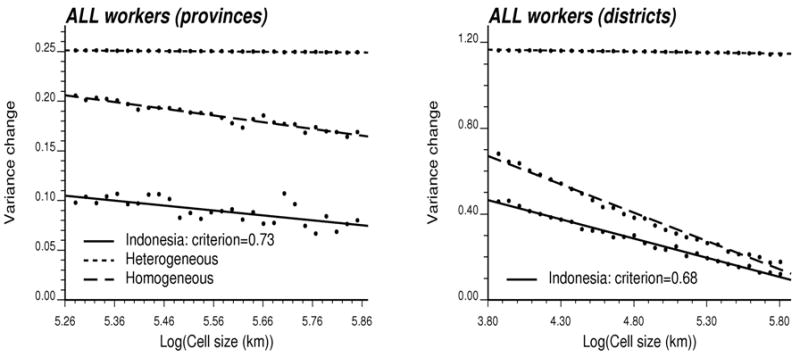
Plot of the population-weighted variance of HWs’ rates versus the logarithm of the length of corresponding aggregation cells for three processes: the reference homogenous and heterogeneous distributions, and the observed spatial repartition of HWs. The criterion measures the degree of homogeneity of the observed distribution. Two types of geographical units are investigated. Source: Indonesian MOH Inventory 2001.
As expected, for Indonesia the homogeneous process displays the largest decrease in variance as the size of the aggregation units increases. Conversely, the variance changes little for the heterogeneous process. The actual distribution of HWs represents an intermediate situation. The regression line provides a reasonable fit for all graphs. Spatial inequalities are larger for Indonesia than for Vietnam: the criterion is 0.68 versus 0.76 for smaller geographical units. However, conclusions regarding the spatial inequalities change with the geography used for the aggregation procedure. When using smaller geographical units in other countries, we showed that the spatial inequalities are smaller (results not shown). At the coarser scale, differences between countries become negligible because the range of cell sizes explored is different: the minimum cell size has been set to the median length of geographical unit.
Discussion
In addition to inequalities in levels of health, several additional dimensions of equity should be monitored as part of health system performance assessments, including the distribution of resources and services. A number of recent attempts have been made to summarize inequalities in the distribution of HWs across countries using a single number, but all the commonly used summary measures, including the variance, Gini coefficient, and Atkinson index, suffer from the resolution or areal aggregation problem. Their values vary with the size of the unit of analysis, which limits the usefulness of the existing studies.
We therefore tested whether a simpler indicator that does not describe the entire distribution, the decile ratio, is also subject to the resolution problem. Intuitively, it is independent of geographical area. However, both forms of the decile ratio are also sensitive to resolution, and hence they cannot be used to compare inequalities across countries either. They can be used to assess inequality over time in the same country, but only if no change in the size of administrative units occurs. Population growth, migration, and changes in administrative boundaries mean that this situation is unlikely for very long periods of time.
We then tested a homogeneity statistic to assess how fast the variance of the rates decreases as the size of the aggregation units increases and compared this value with the one obtained if the HWs are distributed homogeneously across a study area. The more homogeneous the distribution of HWs, the faster the decline in variance with the level of aggregation. Unfortunately, even this statistic is influenced by the size of geographical units: differences between countries [based upon a comparison with other countries (see Speybroeck et al. 2006)] tend to disappear as the rates are initially aggregated within administrative units of large size.
Three additional problems arise when virtually any summary statistic of the overall distribution is applied to spatial data (Barber 1988), often described as the boundary problem, the problem of modifiable units, and the problem of pattern. Combining this complication with the resolution problem results in none of these measures of inequality or dispersion being interpretable independent of a study area, in part because these indices generally overlook most spatial patterns that can be observed on a map. Because information about the number of HWs is usually provided by an administrative area within a country and because these units vary considerably in population size, comparisons of inequality in access to HWs across countries do not produce useful information.
The question, then, is whether any single summary indicator of inequality in the distribution of HWs exists that is not sensitive to the resolution problem. Our analysis suggests that this complication can be avoided only with indicators that take the individual or household as the unit of analysis. If the term scale refers to the spatial extent of the country instead of to the spatial resolution, having individual-level data will not even help because in some cases there may be a tendency for the within-country variance to increase with the size of the country. This condition rules out using HWs’ density as the quantity of interest, because the density for a small group of people has no practical meaning. For example, a number of regencies in Indonesia may not have doctors, nurses, or midwives, but this does not mean they have no access to HWs’ services. Cross-border flows assure service availability.
An alternative approach would be to use mapping techniques (e.g., Bayesian smoothers, binomial or indicator kriging, kernel density estimation) to create continuous surfaces of health outcomes from either individual-level data or rates recorded over geographical units; for example, see Goovaerts (2009).
The appropriate consideration might be whether the individual could use the services of HWs in a reasonable time if needed. This type of measurement might be a promising avenue for future research but would require considerably more work to implement. Determining the time limit for obtaining services would be necessary, which is complicated by many factors determining whether people can use services, including the distance from health facilities, the nature of the terrain, and the costs of transport and of care.
Recent mapping tools (Ebener et al. 2009) might make this type of analysis less onerous by helping to identify the proportion of a population that could reach a health facility within a specified amount of time. For now, the major constraint with such an approach remains the availability of quality disaggregated georeferenced data. Other research addresses inequality measures but not in the context of HWs’ inequalities. For instance, Gaile (1977) proposes use of a measure of relative entropic equality to assess geographical distribution (of income) for planning purposes. This indicator is combined with a measure of aggregate efficiency to include both dimensions in a single coefficient. Measures of “pure” geographical distribution, such as the one proposed in Zhao, Stough, and Li (2003), are not useful in the context at hand because in the case of health workforce distributions the measures must be useful in a policy context.
Countries collect information on the number and location of HWs to help address important policy issues related to access, and these numbers do not have to be summarized in a single measure of inequality to be useful in a policy debate. However, we suggest here that the current studies comparing inequality of access to HWs across countries using existing summary measures of inequality are not meaningful because the indicator values are dependent on the size of the geographical units used as the basis of analysis. Much more work remains to be done to develop indicators of inequality in access, which should be at the individual level.
Acknowledgments
We thank the editor and three anonymous reviewers for their valuable comments and suggestions, and the editor for his very constructive advice and support during the finalizing of this paper. The research by the fourth author, Pierre Goovaerts, was funded by grant R44-CA132347-02 from the National Cancer Institute. The views stated in this publication are those of the author and do not necessarily represent the official views of the NCI. We also thank the National Institute of Health Research and development (Ministry of Health, Indonesia) for allowing us to use data it collected.
References
- Anand S, Diderichsen F, Evans T, Shkolnikov VM, Wirth M. Measuring Disparities in Health: Methods and Indicators. In: Evans T, Whitehead M, Diderichsen F, Bhuiya A, Wirth M, editors. Challenging Inequalities in Health: From Ethics to Action. Oxford: Oxford University Press; 2001. pp. 49–67. [Google Scholar]
- Barber G. Elementary Statistics for Geographers. New York: Guilford Press; 1988. [Google Scholar]
- Brown MC. Using Gini-Style Indices to Evaluate the Spatial Patterns of Health Practitioners: Theoretical Considerations and an Application Based on Alberta Data. Social Science and Medicine. 1994;38:1243–56. doi: 10.1016/0277-9536(94)90189-9. [DOI] [PubMed] [Google Scholar]
- Chen L, Evans T, Anand S, Boufford JI, Brown H, Chowdhury M, Cueto M, Dare L, Dussault G, Elzinga G, Fee E, Habte D, Hanvoravongchai P, Jacobs M, Kurowski C, Michael S, Pablos-Mendez A, Sewankambo N, Solimano G, Stilwell B, De Waal A, Wibulpolprasert S. Human Resources for Health: Overcoming the Crisis. Lancet. 2004;364:1984–90. doi: 10.1016/S0140-6736(04)17482-5. [DOI] [PubMed] [Google Scholar]
- Ebener S, Naphini P, Fleming P, Kafakalawa W, Kondowe OD, Makwiza I, Manda K, Mzembe J, Moyo C. Analysing Geographic Coverage of ART Clinics Using GIS: Example of Collaboration between Several Institutions in Malawi. GIS Development. 2009;13:34–36. [Google Scholar]
- Gaile G. Efficuity: A Comparison of a Measure of Efficiency with and Entropic Measure of the Equality of Discrete Spatial Distributions. Economic Geography. 1977;38(3):265–82. [Google Scholar]
- Gakidou E, Murray CJL, Frenk J. A Framework for Measuring Health Inequality. In: Murray CJL, Evans DB, editors. Health Systems Performance Assessment. Geneva: WHO; 2003. pp. 471–84. [Google Scholar]
- Goovaerts P. Combining Area-based and Individual-Level Data in the Geostatistical Mapping of Late-Stage Cancer Incidence. Spatial and Spatio-Temporal Epidemiology. 2009;1:61–71. doi: 10.1016/j.sste.2009.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravelle H, Sutton M. Trends in Geographical Inequalities in Provision of General Practitioners in England and Wales. Lancet. 1998;352:1910. doi: 10.1016/S0140-6736(05)60402-3. [DOI] [PubMed] [Google Scholar]
- Gupta N, Zurn P, Diallo K, Dal Poz MR. Uses of Population Census Data for Monitoring Geographical Imbalance in the Health Workforce: Snapshots from Three Developing Countries. International Journal for Equity in Health. 2003;2:11–23. doi: 10.1186/1475-9276-2-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagopian A, Thompson MJ, Fordyce M, Johnson KE, Hart LG. The Migration of Physicians from Sub-Saharan Africa to the United States of America: Measures of the African Brain Drain. Human Resources for Health. 2004;2:17–27. doi: 10.1186/1478-4491-2-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt D, Steel DG, Tranmer M, Wrigley N. Aggregation and Ecological Effects in Geographical based Data. Journal of Geographical Analysis. 1996;28:244–62. [Google Scholar]
- Indonesia Ministry of Health Inventory. National Socioeconomic Survey. Jakarta: National Statistical Office; 2001. [Google Scholar]
- Isaaks EH, Srivastava RM. An Introduction to Applied Geostatistics. New York: Oxford University Press; 1990. [Google Scholar]
- Mackenbach JP, Kunst AE. Measuring the Magnitude of SocioEconomic Inequalities in Health: An Overview of Available Measures Illustrated with Two Examples from Europe. Social Science and Medicine. 1997;44:757–71. doi: 10.1016/s0277-9536(96)00073-1. [DOI] [PubMed] [Google Scholar]
- Openshaw S. Ecological Fallacies and the Analysis of Areal Census Data. Environment and Planning A. 1984;16:17–31. doi: 10.1068/a160017. [DOI] [PubMed] [Google Scholar]
- Speybroeck N, Ebener S, Sousa A, Paraje G, Evans D, Prasad A. Discussion Paper. Geneva: World Health Organization; 2006. The World Health Report 2006. [Google Scholar]
- World Health Organization (WHO) [accessed on 18 April 2011];2006 Available at http://apps.who.int/globalatlas.
- Zhao ZQ, Stough RR, Li N. Note on the Measurement of Spatial Imbalance. Geographical Analysis. 2003;35:170–76. [Google Scholar]