Activity of the same motor cortex neurons during repeated experience with perturbed movement dynamics

Abstract

Neurons in the primary motor cortex (M1) have been shown to have persistent, memory-like activity following adaptation to altered movement dynamics. However, the techniques used to study these memory traces limited recordings to only single sessions lasting no more than a few hours. Here, chronically implanted microelectrode arrays were used to study the long-term neuronal responses to repeated experience with perturbing, velocity-dependent force fields. Force-field–related neuronal activity within each session was similar to that found previously. That is, the directional tuning curves of the M1 neurons shifted in a manner appropriate to compensate for the forces. Next, the across-session behavior was examined. Long-term learning was evident in the performance improvements across multiple force-field sessions. Correlated with this change, the neuronal population had smaller within-session spike rate changes as experience with the force field increased. The smaller within-session changes were a result of persistent across-session shifts in directional tuning. The results extend the observation of memory traces of newly learned dynamics and provide further evidence for the role of M1 in early motor memory formation.

performance of a motor skill often improves gradually, reaching a plateau only after several weeks of daily training (Karni et al. 1995; Nudo et al. 1996; Padoa-Schioppa et al. 2004). The neural processes underlying this improvement are distributed and act over multiple timescales (Shadmehr and Holcomb 1997; Ungerleider et al. 2002). Studies using noninvasive stimulation have found that early motor memories are dependent on primary motor cortex (M1) (Hadipour-Niktarash et al. 2007; Muellbacher et al. 2002; Richardson et al. 2006; Tecchio et al. 2010).

Correspondingly, we and others have found correlates of early motor memories in M1 single-unit activity (Arce et al. 2010b; Gandolfo et al. 2000; Li et al. 2001). These studies used the force-field learning paradigm (Shadmehr and Mussa-Ivaldi 1994), in which monkeys adapted their reaching movements to applied velocity-dependent forces. Force-field–related activity changes in a subset of M1 cells (“memory” cells) persisted during postlearning trials, indicating a memory trace of the newly learned dynamics. In these studies, different cells were isolated each recording session using conventional metal microelectrodes. The electrodes were lowered transdurally at the beginning of each session and then removed at the end of each session. Thus the methods restricted our view of the memory trace to only a few hundred postlearning trials performed over less than an hour.

Our primary goal in the present work was to extend this timeframe, by recording with chronically implanted electrodes and presenting the same force field over blocks of five consecutive daily sessions. We analyzed how behavior and neuronal population activity changed from the first to fifth sessions. Furthermore, a number of recent methodologic papers have demonstrated the stability attainable with chronically implanted electrodes (Dickey et al. 2009; Liu et al. 2006; Tolias et al. 2007). Thus, after identifying those units that were stable across sessions, we also assessed how the activity of individual neurons evolved with repeated training.

We found that long-term, force-field learning was correlated, at a population level, with a decrease in field-related changes in spike rate. One explanation for the decrease is that field-appropriate activity was maintained, precluding the need for changes on subsequent force-field exposure. We found evidence that a subset of neurons did indeed maintain field-appropriate activity over multiple sessions, through a persistent shift in their directional tuning curves.

METHODS

Behavioral paradigm.

Two male rhesus macaques (Macaca mulatta), N and M, were trained for 6 to 9 months to perform a visually cued reaching task. The task, as described previously (Richardson et al. 2008), involved making reaching movements with the right arm while holding on to a handle at the end of a two-link robotic manipulandum. Potentiometers on the manipulandum recorded hand position, which was shown as a cursor on a monitor. To start each trial, the monkeys positioned the manipulandum such that the cursor stayed inside a center target also displayed on the monitor. After the 1-s center hold period, a peripheral target appeared on the monitor in one of eight pseudorandomly chosen locations spaced uniformly 45° apart in a 10-cm-radius circle around the center (22.5°, 67.5°, 112.5°, etc.) The target presentation was pseudorandom in the sense that the first target was randomly chosen from the eight targets. If the first trial was successful, the second target was randomly chosen from the remaining seven targets; otherwise, the second target was randomly chosen from all eight targets. If the second trial was successful, the third target was randomly chosen from the remaining six targets; otherwise, the second target was randomly chosen from seven targets. This process continued until all eight targets had been reached successfully, after which a new target presentation block began. The appearance of the peripheral target (i.e., the visual cue) began the instructed-delay period during which the cursor had to remain inside the center target. The duration of the instructed delay was a uniform random variable ranging from 500 to 1,500 ms. Disappearance of the center target marked the end of the instructed-delay period. The monkeys then made a 10-cm reaching movement to position the cursor inside the peripheral target. Each successful trial concluded with a 1-s target hold period followed by a juice reward.

During training, the monkeys were not exposed to any perturbing forces beyond the manipulandum's passive dynamics. During the neural recording sessions, the movement dynamics were periodically altered by forces applied by the manipulandum that were proportional (6 Ns/m) and perpendicular (either clockwise or counterclockwise) to the hand velocity vector. In these learning sessions, the monkeys performed 160 successful trials without applied forces (baseline trials), followed by 160 successful trials with applied forces (force-field trials), and finally another 160 successful trials without applied forces (washout trials). The forces were applied on all movements during force-field trials, including movements from the center to the targets and the targets back to the center. The same type of force field (clockwise or counterclockwise) was used in blocks of five consecutive daily sessions to study long-term adaptation to the novel forces. Between each of these learning-session blocks were several control sessions, in which the monkeys performed 480 successful trials without any applied forces.

Chronic electrophysiology.

One objective of this study was to look at the activity of the same neurons during the monkeys' repeated, daily experience with altered movement dynamics. To achieve stable neuronal recording given the motions that occur between the brain and skull, we used a commercial “floating” microelectrode array (FMA; MicroProbes for Life Science, Gaithersburg, MD), which moved with the brain rather than being anchored to the skull (Musallam et al. 2007; Salcman and Bak 1973). With the monkey under general anesthesia and using aseptic procedures, a 16-electrode FMA was implanted in the left primary motor cortex (M1) at the convexity of the precentral gyrus. The FMAs had an interelectrode distance of 400 μm, impedance of about 1 MΩ at 1 kHz, and electrode length of 1.5 mm (monkey N) or 2.0–2.5 mm (monkey M). Microstimulation through the electrodes (50-ms, 330-Hz trains; 0.2-ms/phase, cathodal-lead biphasic pulses) evoked activity in proximal right arm muscles at intensities of 15 to 80 μA.

In recording sessions, neural signals from the FMA were passed through a unity-gain headstage (HS 16, Neuralynx, Bozeman, MT), filtered from 0.1 to 9,000 Hz, amplified for a resolution of 0.15 μV, and digitized at 30.3 kS/s (Cheetah 16; Neuralynx). The neural and behavioral data were saved to disk for offline analysis. All procedures adhered to National Institutes of Health guidelines on the use of animals and were approved by the MIT Committee for Animal Care.

Single-unit isolation.

Action potentials were detected offline by amplitude thresholding. First, the neural signal was bandpass filtered between 300 and 6,000 Hz. Second, the threshold was set at 3.5 times the SD of the filtered signal. A median-based SD estimate was used to approximate the background noise despite possibly high spike amplitudes or rates (Quiroga et al. 2004). Third, the spike waveforms were extracted (−0.4 to 0.8 ms, 37 samples), upsampled by a factor of 5 using cubic spline interpolation, and aligned on their peak.

After spike detection, spike waveforms were sorted into single units by feature-based clustering. Five features were used: waveform energy, peak-to-trough amplitude, and the first three energy-normalized principal components. An unsupervised clustering algorithm fit a mixture of Gaussians in feature space (KlustaKwik 1.6; K. D. Harris et al., Rutgers University). The resulting clusters of spikes were then inspected to determine if they had a refractory period (i.e., no interspike intervals <1 ms) and were present throughout the recording session. Often spike clusters needed to be merged to meet the latter criterion because the algorithm generally overclustered the data. Typically, a subtle and gradual shift in the shape of the spike waveform could result in two clusters for a single unit with N spike times, where spike times 1 to t were in cluster A and spike times t + 1 to N were in cluster B. Given the low probability of losing and gaining a unit with similar spike rates and waveforms at exactly the same time t, clusters A and B were merged to form one unit that was present throughout the entire session. Clusters meeting these criteria were labeled as single units and passed on to the stability analysis.

Single-unit stability.

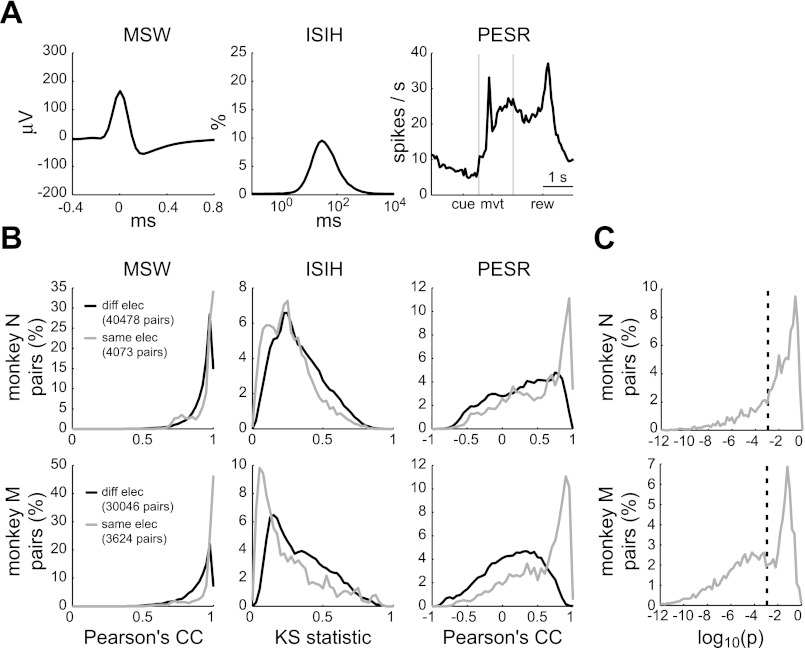
Single units were isolated for each recording session independently. To identify units that were present across multiple sessions, we first computed three attributes of each unit (Fig. 1A): the mean spike waveform (MSW), the interspike interval histogram (ISIH), and the perievent spike rate (PESR). For the ISIH, we used 100 bins uniformly spaced on a logarithmic scale from 0.1 ms to 10 s. The PESR was the spike rate profile computed in 50-ms bins across three perievent windows (−1.0 to 0.5 s relative to the visual cue, −0.4 to 0.6 s relative to movement onset, and −1.0 to 1.0 s relative to the reward) concatenated together and averaged over the 160 baseline trials. The PESR summarized the recruitment of each unit in the baseline reaching task.

Fig. 1.

Single-unit stability analysis. A: three attributes of an example unit: mean spike waveform (MSW), interspike interval histogram (ISIH), and baseline perievent spike rate (PESR). Events used for the PESR were the visual presentation of the peripheral target (cue), the movement onset (mvt), and the reward delivery (rew). The two vertical lines indicate the boundaries of the three perievent windows that comprised the PESR. B: the distributions of similarity statistics (Pearson's correlation coefficient for the MSW and PESR attributes; Kolmogorov–Smirnov statistic for the ISIH attribute) for all pairs of units recorded on different electrodes (black) and on the same electrode (gray). C: the probability that pairs of units recorded on the same electrode were the same unit. Dashed vertical line at P = 0.001 indicates the significance level.

The attributes for determining unit stability were chosen by considering their effectiveness as a marker for stability and the limitations they may impose on the results. MSW should be independent of the behavioral task. Therefore, grouping units across sessions on the basis of this attribute should not influence the analysis of a unit's long-term behavioral tuning. However, the MSW is not particularly specific since extracellular action potentials from different neurons can often have very similar shapes. The ISIH can modulate with behavior, but was used since it, in combination with the MSW, has been shown to identify units better than the MSW alone (Dickey et al. 2009). The tradeoff for this increased specificity was that it precluded an analysis of long-term, force-field–dependent changes in the ISIH. The PESR was defined by the unit's relationship to behavior in the baseline trials. This stability criterion excluded any units with day-to-day changes in mean activity during baseline trials, including any systematic changes that may have been due to experience with the altered movement dynamics. We considered this an acceptable tradeoff since the PESR provided a very specific identity to each unit. Furthermore, it did not preclude an analysis of day-to-day directional tuning changes during baseline trials since only the average activity across all target directions was used in calculating the PESR.

Second, after computing the three attributes of each unit, we computed the similarity between attributes of each pair of units across all electrodes and sessions. Pearson's correlation coefficient (CC) was used to judge the similarity of MSWs and PESRs. The Kolmogorov–Smirnov (KS) statistic (i.e., the maximum absolute deviation between two cumulative probability distributions) was used to judge similarity between ISIHs.

Third, the similarity statistics were compiled for all pairs of units recorded on different electrodes (Fig. 1B, black). Since the same unit could not be recorded on multiple electrodes, this gave an empirical distribution of CCs and KS statistics for “true negatives” (i.e., pairs that were not the same unit).

Fourth, for each pair of units recorded on the same electrode, we computed the probability that they were the same unit (Fig. 1, B and C, gray). Assuming statistical independence of the three attributes, the probability (P) was defined as the product of the proportions of the three “true negative” distributions that were greater than (CC) or less than (KS) the similarity statistics of the tested unit pair. Finally, pairs of units that were significantly similar (P < 0.001) were grouped to determine the final number and duration of units recorded on each electrode.

In this procedure, the significance of similarity between pairs of units may have been overestimated. The “true negative” distribution, from which the similarity significance was derived, was based on units recorded on different electrodes. However, different units recorded on the same electrode may be more similar than different units recorded on different electrodes (Liu et al. 2006). Nevertheless, we found that results of the stability analysis were quite insensitive to the significance level (α). Choosing a lower or higher α, from 0.0001 to 0.01, simply changed the number of significant pairs within a group (e.g., sessions 1–2, 2–3, 3–4 vs. 1–2, 2–3, 3–4, 1–3, 2–4, 1–4) but not the group itself (e.g., sessions 1, 2, 3, 4).

Analysis.

Only successful (i.e., rewarded) trials were included in the behavioral and neuronal analyses. Behavioral performance on each trial was quantified by a position-based measure and a velocity-based measure. The former was the signed deviation area between the hand path and a straight line between the center and peripheral target (Richardson et al. 2008; Rokni et al. 2007). The latter was the correlation between the hand velocity vector and the average baseline velocity vector for a given target direction (Shadmehr and Mussa-Ivaldi 1994). The hand path and velocity vectors were composed of the first second of data after movement onset. Movement onset (denoted as mvt in the figures) was defined as the first time in which the hand speed exceeded 5 cm/s.

The neuronal database was treated in three different ways throughout the analyses: either as 35 stable units, 281 unit × sessions, or 2,248 unit × session × directions. Each of the 35 units was recorded over a variable number of sessions (Fig. 2). Unit × sessions refers to analyzing each daily recording of each unit separately, such that 281 is the number of nonunique sessions in which the 35 units were recorded. Unit × session × directions is the same as unit × sessions, but further separating trials to each of the eight target directions (281 × 8 = 2,248).

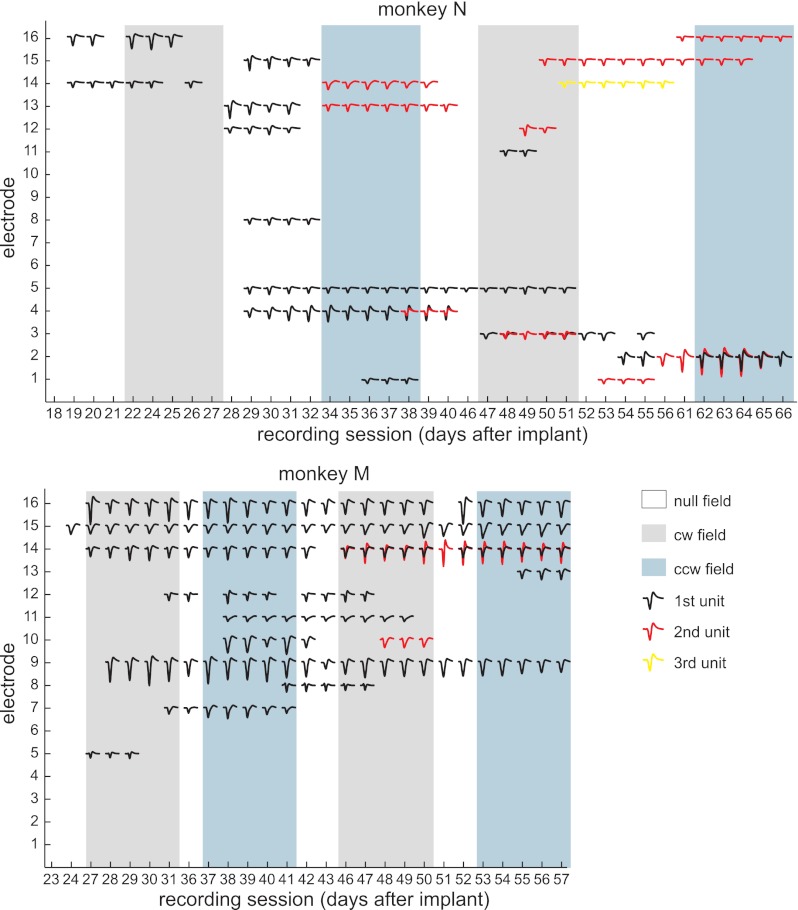
Fig. 2.

Neuronal database. The sessions in which each of the 35 stable units were recorded are indicated by the unit's MSW. Different colored waveforms on the same electrode indicate different units. The force field presented during each session is also indicated (null field = control sessions, cw field = clockwise force-field sessions, ccw field = counterclockwise force-field sessions).

Neuronal activity was quantified by the spike rate within a particular time window. The significance of unimodal directional tuning of the spike rate was assessed by two criteria. First, there had to be a significant difference in mean spike rate across directions (ANOVA, P < 0.05). Second, a von Mises function fit to the data had to have a coefficient of determination, r² > 0.75. The r² assessed the goodness of fit (Amirikian and Georgopoulos 2000). The von Mises tuning function was defined as r(θ) = a + b exp[κ cos (θ − μ)], where r was the spike rate, θ was the target direction, and μ was the preferred direction (PD). Tuning depth was defined as the maximum minus minimum of the fitted function. Tuning width was defined as the half-width at half-maximum of the fitted function.

Within-session neuronal activity was classified by the pattern of significant PD changes between the three epochs (Li et al. 2001). Significance of PD changes was determined by computing the 95% bootstrap confidence interval (CI) on the angular difference (Sergio et al. 2005). A PD change was significant if 0° fell outside the 95% CI of the distribution of bootstrapped angular differences. The pattern of PD changes was defined by three significance tests: the force-baseline change, the washout-force change, and the washout-baseline change. The corresponding cell classification based on these patterns of PD changes is described in the following text (see results).

RESULTS

We recorded chronically from the primary motor cortex (M1) of two macaques, N and M, for 5 to 7 weeks as they made reaching movements that were repeatedly perturbed by velocity-dependent forces. Only units that were stable for 2 or more days were included in the analyses. Figure 2 presents all the stable units along with the schedule of applied force fields. Although only mean spike waveforms (MSWs) are shown, the identity of a unit from one session to the next was additionally based on similarities in the interspike interval histogram (ISIH) and baseline perievent spike rate (PESR; see methods and Fig. 1 for the stability analysis). Over the course of the experiment, zero to three different stable units were recorded on each of the 16 electrodes in the array. Overall, we recorded 35 stable units and 281 unit × sessions.

Within-session adaptation.

We first analyzed the behavioral and neuronal changes that occurred within each daily session, treating the 281 unit × sessions independently. This analysis provided a foundation to understand across-day changes and was comparable to analyses performed in our prior work.

Each session was composed of three sequential trial epochs: 160 trials without forces (baseline epoch), 160 trials with forces (force-field epoch), and 160 trials without forces (washout epoch). Baseline trials were characterized by relatively straight hand paths and single-peaked hand speed profiles (Fig. 3A, blue). The sudden introduction of velocity-dependent forces on trial 161 caused an initial perturbation, characterized by curved paths and multipeaked speed profiles, followed by adaptation (Fig. 3A, red). The sudden removal of forces on trial 321 revealed an adaptation aftereffect (i.e., curved paths in the opposite direction), followed by deadaptation back toward baseline values (Fig. 3A, green). We quantified hand path changes with the signed deviation area and hand velocity changes with the velocity correlation coefficient (Fig. 3A, bottom row; see methods).

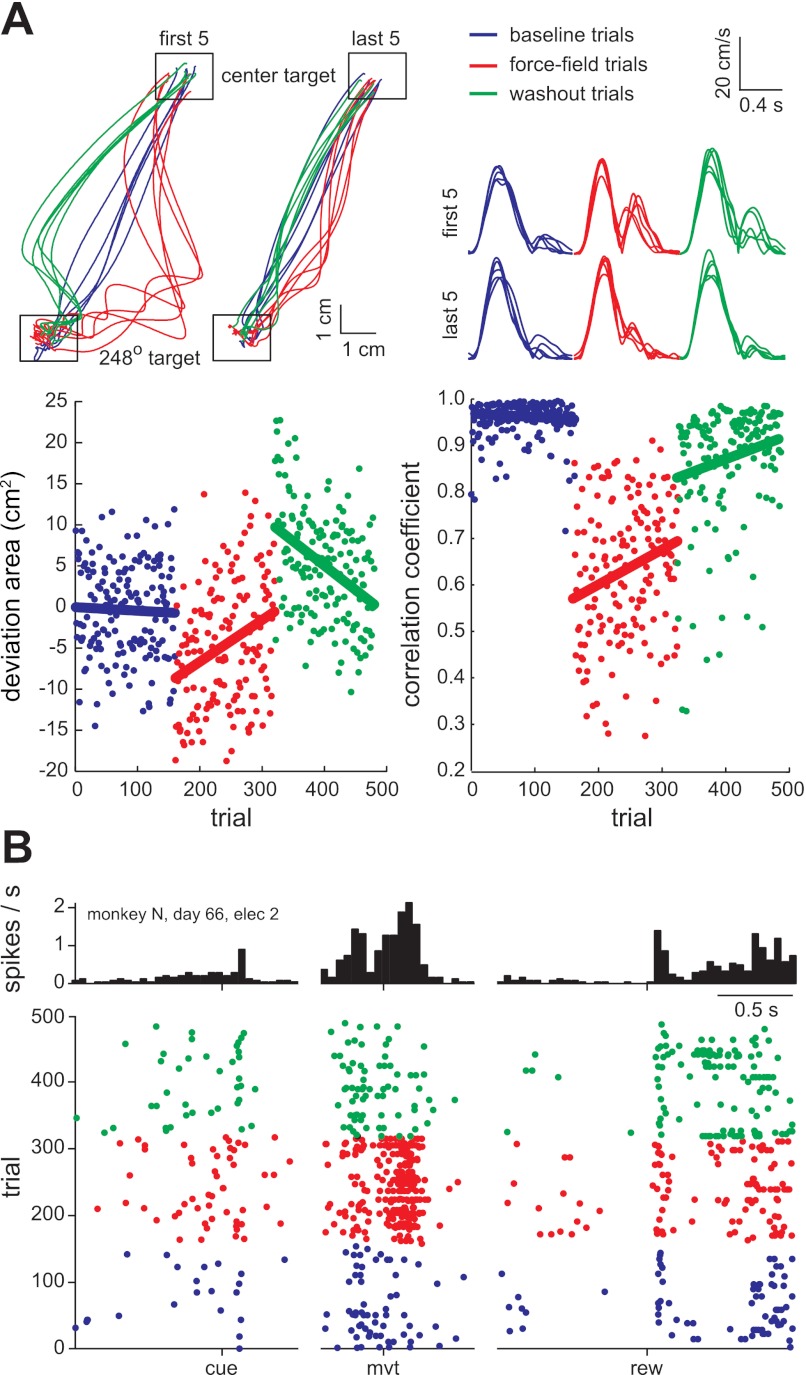
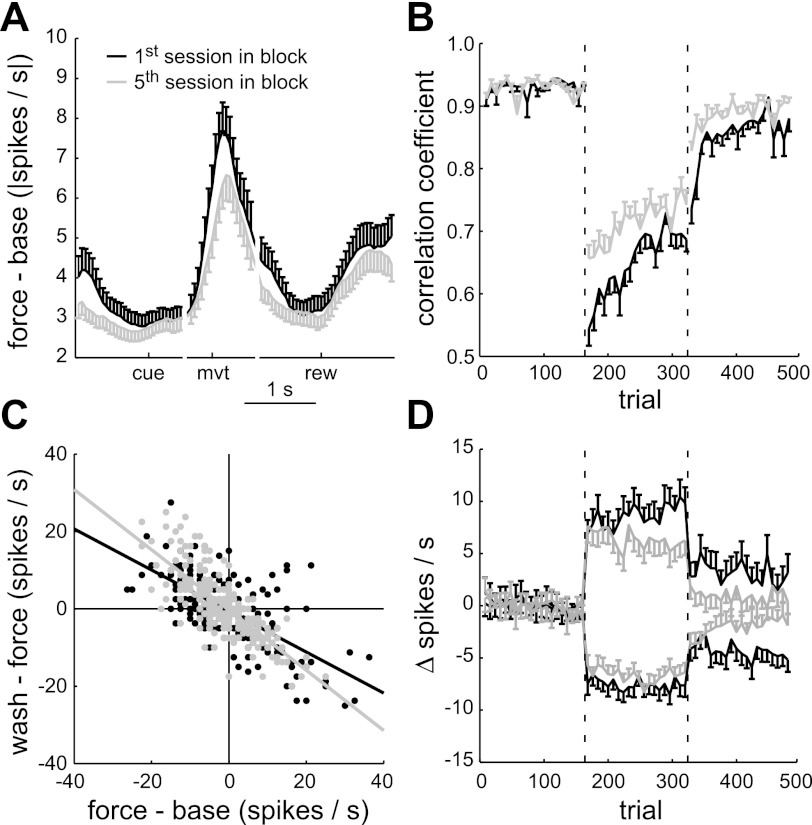
Fig. 3.

Typical within-session behavioral and neuronal changes. A: hand position (top left) and hand speed (top right) for an example session in which counterclockwise forces were applied on force-field trials (red). The position and speed are shown for the first five and last five trials in the 248° target direction of each epoch. Performance on each trial was quantified by path deviation area (bottom left) and velocity correlation coefficient (bottom right). The linear regression lines highlight the field-induced perturbation (red, line offset), adaptation (red, line slope), aftereffect (green, offset), and deadaptation (green, slope). B: perievent raster plot and histogram of the activity of an example unit. The unit had transient cue-related, movement-related, and reward-related activity. During force-field trials, the movement-related activity increased.

An example of force-field–related neuronal activity changes is shown in Fig. 3B. A threefold increase in spike rate, relative to baseline trials, occurred after movement onset during the force-field epoch. The spike rate at other trial times, including after the visual cue, before movement, and after the reward, was relatively unchanged across the three epochs. The same was generally true for the population (Fig. 4A). For each of the unit × sessions, we computed the PESR for baseline trials, as in the stability analysis, and the PESR for force-field trials. The absolute value of the difference between these two spike rate profiles is shown in Fig. 4A. The difference and modulus were taken for trials in each of the eight target directions separately and averaged to capture directional tuning changes in addition to mean rate changes. The activity changes were mostly confined to periods of movement, either outward (after movement onset event, mvt) or inward (after reward delivery, rew) because these were also the only times the velocity-dependent forces were present. Inward movements were relatively uncontrolled in this paradigm, often involving multiple pauses and direction changes, and therefore were not analyzed further. Thus the subsequent analyses evaluated neuronal activity in a 400-ms window following onset of the outward movements (Fig. 4A, interval between the two arrows).

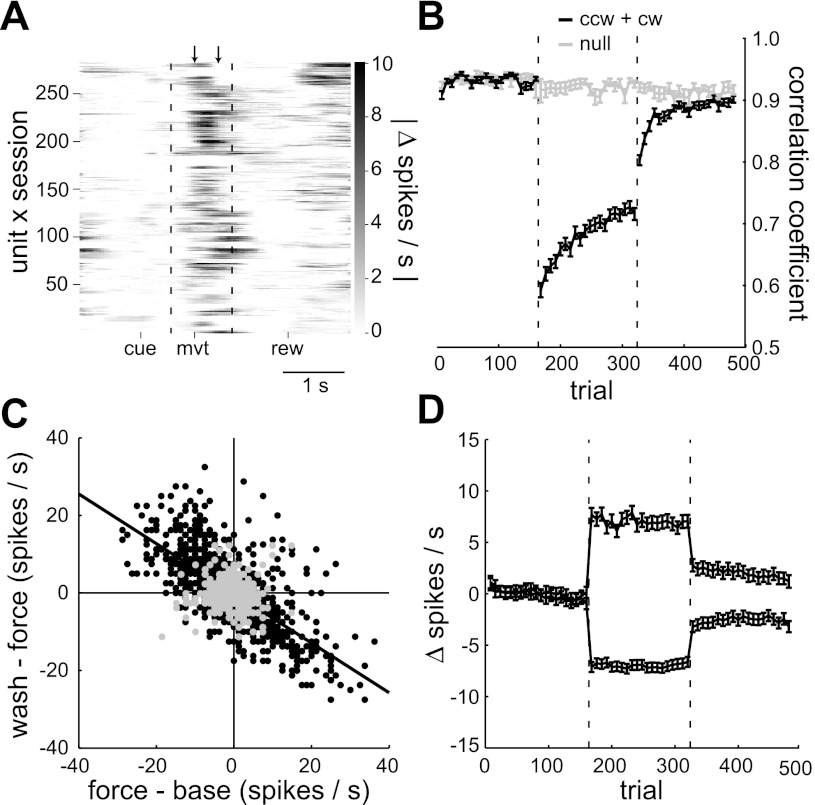
Fig. 4.

Population results: force-field vs. control sessions. A: absolute difference in perievent spike rate between the baseline and force-field epochs for each of the 281 unit × sessions. Arrows indicate the first 400 ms after movement onset in which most of the spike rate changes occurred. The vertical dotted lines divide the three perievent time windows. B: mean, within-session performance profile for all force-field sessions (black) and control sessions (gray). Performance was quantified by the velocity correlation coefficient. C: interepoch mean spike rate changes for each unit × session × direction in force-field sessions (black, N = 1,544) and control sessions (gray, N = 704). The black regression line indicates the significant anticorrelation between the interepoch changes in force-field sessions. D: within-session profile of spike rate changes in force-field sessions relative to mean baseline rate. Profiles were averaged separately depending on whether the mean rate change between the baseline and force-field epochs was positive (N = 654/1,544) or negative (N = 890/1,544). Error bars in B and D indicate SE values. The vertical dotted lines in B and D divide the baseline, force field, and washout trials.

Next, we quantified how the mean spike rate in this movement window changed within each session. The movement-related spike rate was often strongly modulated by target direction. For simplicity, we first looked for rate changes in each of the eight target directions separately, using a total population of 2,248 unit × session × directions with 60 observations of spike rate each (20/epoch). In clockwise (cw) and counterclockwise (ccw) force-field sessions (1,544 of the 2,248 unit × session × directions), spike rate changes from baseline to force-field trials were anticorrelated with changes from force-field to washout trials (Pearson's r = −0.70; Fig. 4C, black circles). In other words, the rate increases or decreases were relatively transient, returning back toward baseline levels once the forces were removed, similar to the example in Fig. 3B. However, the rate changes did persist to some degree in the washout epoch. The slope of the regression line in Fig. 4C was −0.64 ± 0.03 (95% CI), significantly less than unity. Correspondingly, in 27% of the cases (417/1,544) there was a significant difference between the baseline and washout epoch mean spike rate (Mann–Whitney, P < 0.01). This difference could be seen clearly in the average profile of spike rate changes across trials (Fig. 4D), provided excitatory and inhibitory force-field responses were averaged separately. The persistence of rate changes in the washout epoch may be evidence of an early memory trace of the altered dynamics (Arce et al. 2010b). On the other hand, deadaptation in the washout epoch was not complete (Fig. 4B). Comparing performance in baseline trials to late (last 80) washout trials, the mean velocity correlation coefficient significantly differed in 30/40 (75%) of the force-field sessions (Mann–Whitney, P < 0.01). Thus we cannot rule out the possibility that the persistent spike rate changes were related to persistent kinematics changes. Finally, not all rate changes were specific to the force fields. The gray circles in Fig. 4C indicate the interepoch changes for control sessions in which no forces were applied (i.e., null-field sessions; 704 of the 2,248 unit × session × directions). For these sessions, baseline, force field, and washout epochs were simply the first, second, and third block of 160 trials, respectively. There was no linear relationship between the two interepoch rate changes in control sessions, indicating that the anticorrelated changes in force-field sessions were truly related to adaptation.

Within-session directional tuning changes.

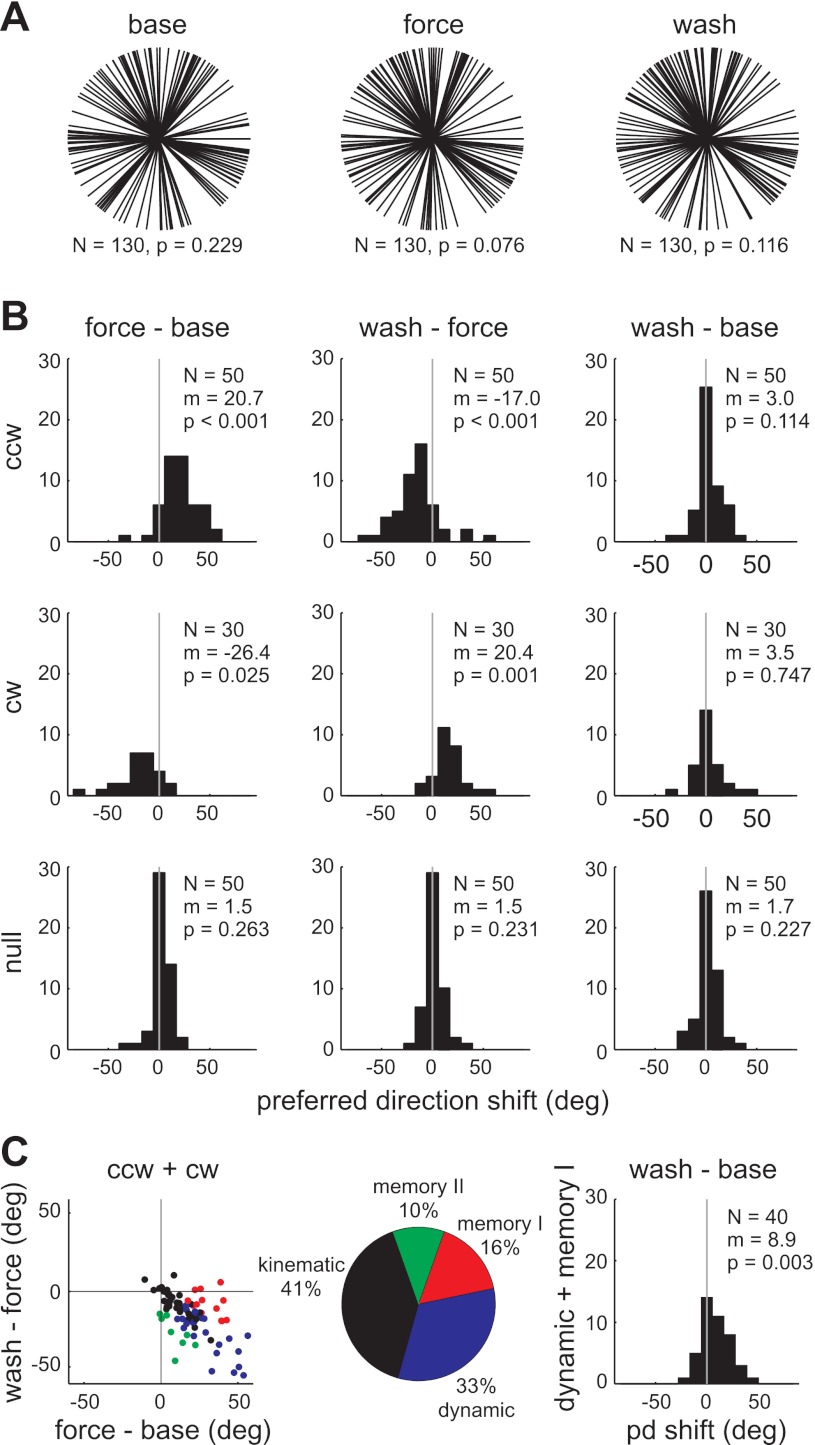
Similar force-field–related changes could be seen at the level of direction tuning curves. For this analysis, we included only those unit × sessions with significant, unimodally tuned spike rates (von Mises fit, r² > 0.75) in all three epochs (N = 130/281). Figure 5A summarizes, for each epoch, the distribution of preferred directions (PDs) for this tuned population. For each epoch, the null hypothesis of a uniform distribution could not be rejected (Rayleigh test, P > 0.05). As seen in our prior studies, the mean PD shifted in the direction of the force field (ccw shift = 20.7°; cw shift = −26.4°) and then shifted back in the washout (ccw shift = −17.0°; cw shift = 20.4°; Fig. 5B). This pattern of tuning curve changes has been shown previously to mirror muscle activity changes in this task (Li et al. 2001; Thoroughman and Shadmehr 1999). There was no evidence of persistent changes at the population level; the mean shift between the baseline and washout epoch was not significant (t-test, P > 0.05). Also, there were no significant PD shifts in null-field sessions, again confirming the changes in force-field sessions were related to the altered dynamics. Tuning depth and tuning width did not change as systematically as PD at the population level (data not shown).

Fig. 5.

Within-session directional tuning changes. A: preferred direction (PD) distributions for unit × sessions significantly tuned in all three epochs (N = 130/281). B: distributions of change in PD between each pair of epochs and for each type of force field. C: classification of all unit × sessions recorded in force-field sessions (N = 80/281) based on interepoch PD changes. Kinematic units (black) had no significant changes between epochs. Dynamic units (blue) had a significant PD change between baseline and force-field trials and an opposite PD change from force-field to washout trials. Memory I units (red) had a significant PD change between baseline and force-field trials, but no change from force-field to washout trials. Memory II units (green) had no change from baseline to force-field trials, but a significant change from force-field to washout trials. The distribution of baseline-to-washout PD changes for only dynamic and memory I units (N = 40/281) is shown on the right. N = number of unit × sessions; P = P value for Rayleigh test (A) or t-test (B, C); m = mean PD in degrees.

Although the mean population PD shift from baseline to washout was not significant, we have previously identified persistent tuning changes in specific subpopulations. Following Li et al. (2001), we classified the neurons based on the pattern of significant PD changes between epochs (Fig. 5C, left; see methods for details). Neurons were classified as kinematic if there were no significant PD changes (black), dynamic if the PD shifted in the force-field epoch, and shifted back in the washout epoch (blue), memory I if a force-field shift was retained in the washout (red), and memory II if there was no force-field shift but there was a significant PD change between baseline and washout (green). In Fig. 5C, PD changes were inverted for neurons in clockwise field sessions so that positive changes were always in the direction of the force field. The classification percentages, shown in Fig. 5C (middle) for the tuned unit × sessions, excluding the 50 recorded in null-field sessions, were similar to those found in our previous work (Li et al. 2001).

A recent study, using a reaching task in which velocity-dependent forces were applied in only one direction rather than all eight, found a significant shift in PD between baseline and washout trials for the subpopulation of neurons that were “force-field modulated” (Arce et al. 2010b). This sustained PD shift during the washout trials was interpreted as a correlate of motor memory. Cells were classified as force-field modulated if the spike rate in the one “learned” direction differed significantly between baseline and force-field trials (Arce et al. 2010a). In our experiment, forces were applied in all eight reaching directions. If we defined force-field–modulated cells as those that showed a significant baseline to force-field epoch change in spike rate in at least one direction, then nearly all units × sessions, 269/281, were force-field modulated (Mann–Whitney tests, P < 0.0063 for Bonferroni-corrected familywise error rate of 0.05). This appeared to be too liberal a definition for force-field modulation in our paradigm. However, if instead we defined this subpopulation by a PD shift between the baseline and force-field epochs (i.e., a coordinated change in spike rate across the eight directions), then force-field–modulated cells were equivalent to the dynamic and memory I cells described earlier. When only these two classes of cells were included, there was a significant population shift in PD from baseline to washout (Fig. 5C, right), analogous to the results of Arce et al. (2010b).

Across-session adaptation.

The movement-related activity of M1 neurons was clearly modulated by the force fields. Next, we looked at how the behavioral and neuronal changes evolved across sessions. Again for simplicity, we began with an analysis of spike rate changes in each of the eight target directions separately. The force fields were presented in blocks of five daily sessions (Fig. 2). In the same manner that we compared force-field session changes to control session changes (Fig. 4), here we compared changes from the first to the fifth sessions of the force-field blocks (Fig. 6).

Fig. 6.

Population results: first vs. fifth force-field sessions. A: mean absolute difference in perievent spike rate between the baseline and force-field epochs for the first sessions (black, N = 73 of the 281 unit × sessions) and fifth sessions (gray, N = 41). B: mean performance profile for the first sessions (black) and fifth sessions (gray). Performance was quantified by the velocity correlation coefficient. C: interepoch mean spike rate changes for the first sessions (black, N = 208 of the 2,248 unit × session × directions) and fifth sessions (gray, N = 232). Linear regression lines show the significant anticorrelated, interepoch changes. D: profile of spike rate changes relative to mean baseline rate in the first sessions (black, N = 208) and fifth sessions (gray, N = 232).

On average, the performance improved from the first to fifth sessions (Fig. 6B). In both the force-field epoch and washout epoch, the mean velocity correlation coefficient was significantly higher in the fifth sessions compared with the first sessions (Mann–Whitney, P < 0.001). The significant improvement in the fifth sessions was seen at the beginning of the force-field and washout epochs, after which the rates of adaptation and deadaptation were similar to those of the first sessions (t-test on the least-squares estimates of slope for first sessions vs. fifth sessions, P > 0.05). A performance improvement was also seen in the hand path deviation area, movement duration, and trial success rate (data not shown). Thus long-term learning occurred with repeated force-field experience (Padoa-Schioppa et al. 2004).

We next looked for population spike rate changes commensurate with these long-term performance changes. We considered the possibility that the force-field–related changes would shift earlier relative to movement onset, as has been demonstrated for force-field–related muscle activity (Thoroughman and Shadmehr 1999). However, using the analysis described previously for Fig. 4A, the timing of mean activity changes relative to baseline trials for the first sessions (black) and fifth sessions (gray) was similar (Fig. 6A). The largest changes in both cases were in the 400-ms window after movement onset. There was, however, a difference in amplitude of the mean activity changes. This difference was evident in the average profile of spike rate changes across trials (Fig. 6D), where again excitatory and inhibitory force-field responses were averaged separately. The mean absolute spike rate changes, relative to baseline, significantly decreased for both excitatory and inhibitory responses in both the force-field and washout epoch (t-tests, P < 0.01). Figure 6C shows how force-field experience modified the anticorrelated interepoch changes seen previously in Fig. 4C. The slope of the regression line was significantly closer to unity for the fifth sessions (−0.78 ± 0.08) compared with the first sessions (−0.53 ± 0.07). Therefore, long-term experience with the force fields decreased not only the force-field–related rate changes but also the persistent rate changes of the washout epoch.

It is important to note that the foregoing analysis relied on the schedule of applied force fields, not on stable units. Since units were not stable for all force-field blocks (Fig. 2), the neuronal populations in the combined first sessions and combined fifth sessions were different. We assumed, however, that these random neuronal sampling differences could not entirely account for the differences in force-field–related activity observed in Fig. 6.

Across-session directional tuning changes.

Finally, we investigated how force-field–related directional tuning changes evolved across sessions for the 35 stable units. Units recorded only during control sessions or only during one force-field session were excluded (N = 6). There was insufficient data to examine changes in tuning across multiple force-field blocks. Units recorded across multiple force-field blocks were treated independently, yielding a total of 50 unit × force-field blocks (25 clockwise, 25 counterclockwise) for the population analysis. Although this sample size was relatively small, because of the low yield of stable recording, there was a significant pattern of tuning changes, as exemplified for each monkey and type of force field in Figs. 7 and 8 and summarized for the population in Fig. 9.

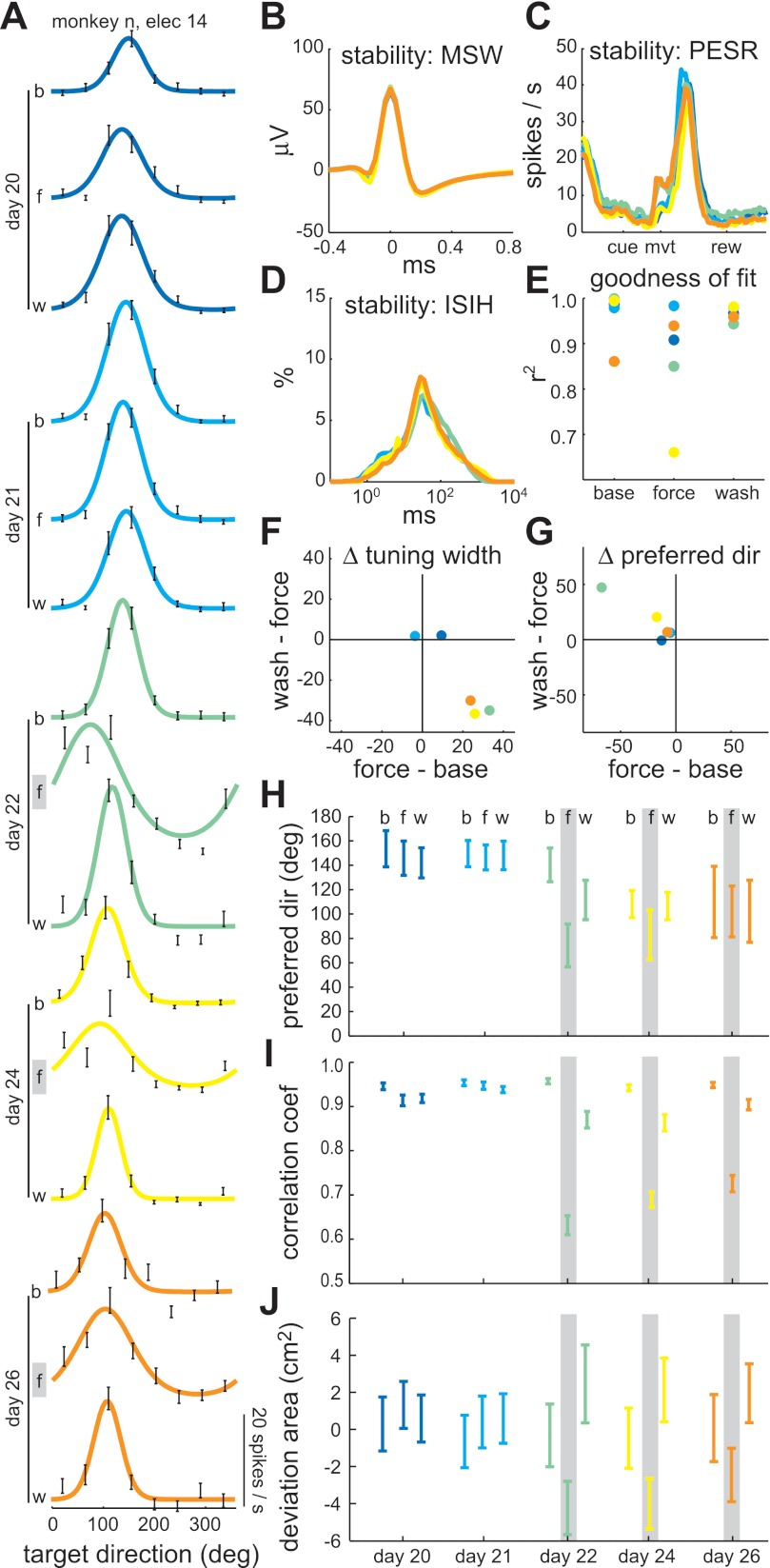
Fig. 7.

Evolution of directional tuning across sessions: example 1 (monkey N). A: fitted, von Mises tuning curves for each epoch (b, baseline; f, force-field; w, washout) of five consecutive sessions. Days 20 and 21 were control sessions. Days 22, 24, and 26 were clockwise force-field sessions. No recording session was performed on day 23. Noise on electrode 14 precluded unit isolation on day 25. Black error bars indicate spike rate mean ± SE in each target direction. B: mean spike waveform (MSW) for each of the five sessions. C: baseline perievent spike rate (PESR) for each of the five sessions. D: interspike interval histogram (ISIH) for each of the five sessions. E: coefficient of determination for the von Mises tuning curve fits, indicating the goodness of fit. F: interepoch changes in tuning width (degrees). G: interepoch changes in PD (degrees). H: PD for each epoch and session with 95% bootstrap confidence intervals. I: mean velocity correlation coefficient for each epoch and session with 95% Student's t confidence intervals. J: mean hand path deviation area for each epoch and session with 95% Student's t confidence intervals. Gray lines indicate the epochs in which a clockwise force field was present.

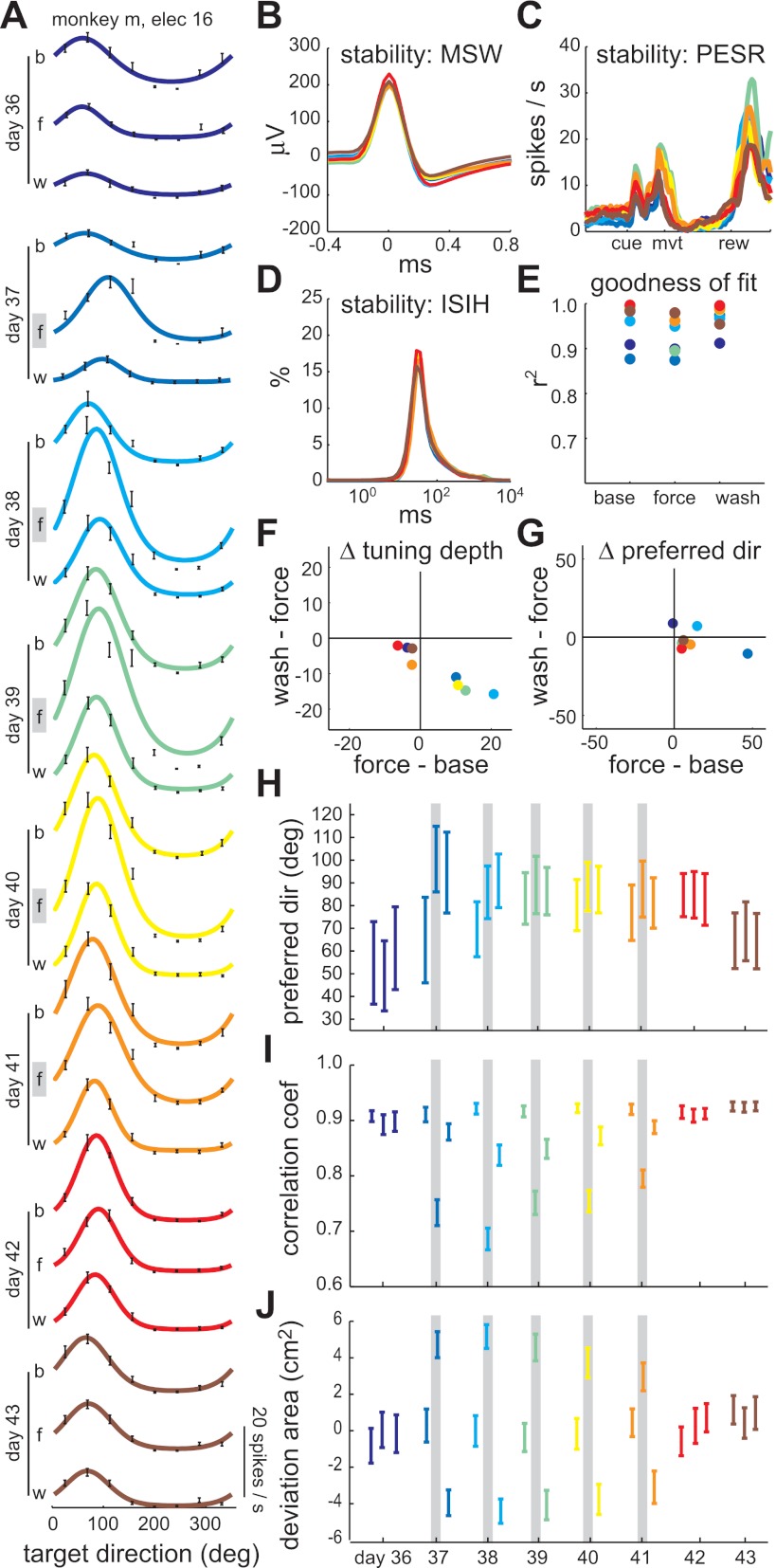
Fig. 8.

Evolution of directional tuning across sessions: example 2 (monkey M). A: fitted, von Mises tuning curves for each epoch (b, baseline; f, force-field; w, washout) of eight consecutive sessions. Days 36, 42, and 43 were control sessions. Days 37–41 were counterclockwise force-field sessions. Black error bars indicate spike rate mean ± SE in each target direction. B: mean spike waveform (MSW) for each of the eight sessions. C: baseline perievent spike rate (PESR) for each of the eight sessions. D: interspike interval histogram (ISIH) for each of the eight sessions. E: coefficient of determination for the von Mises tuning curve fits, indicating the goodness of fit. F: interepoch changes in tuning depth (spikes/s). G: interepoch changes in PD (degrees). H: PD for each epoch and session with 95% bootstrap confidence intervals. I: mean velocity correlation coefficient for each epoch and session with 95% Student's t confidence intervals. J: mean hand path deviation area for each epoch and session with 95% Student's t confidence intervals. Gray lines indicate the epochs in which a counterclockwise force field was present.

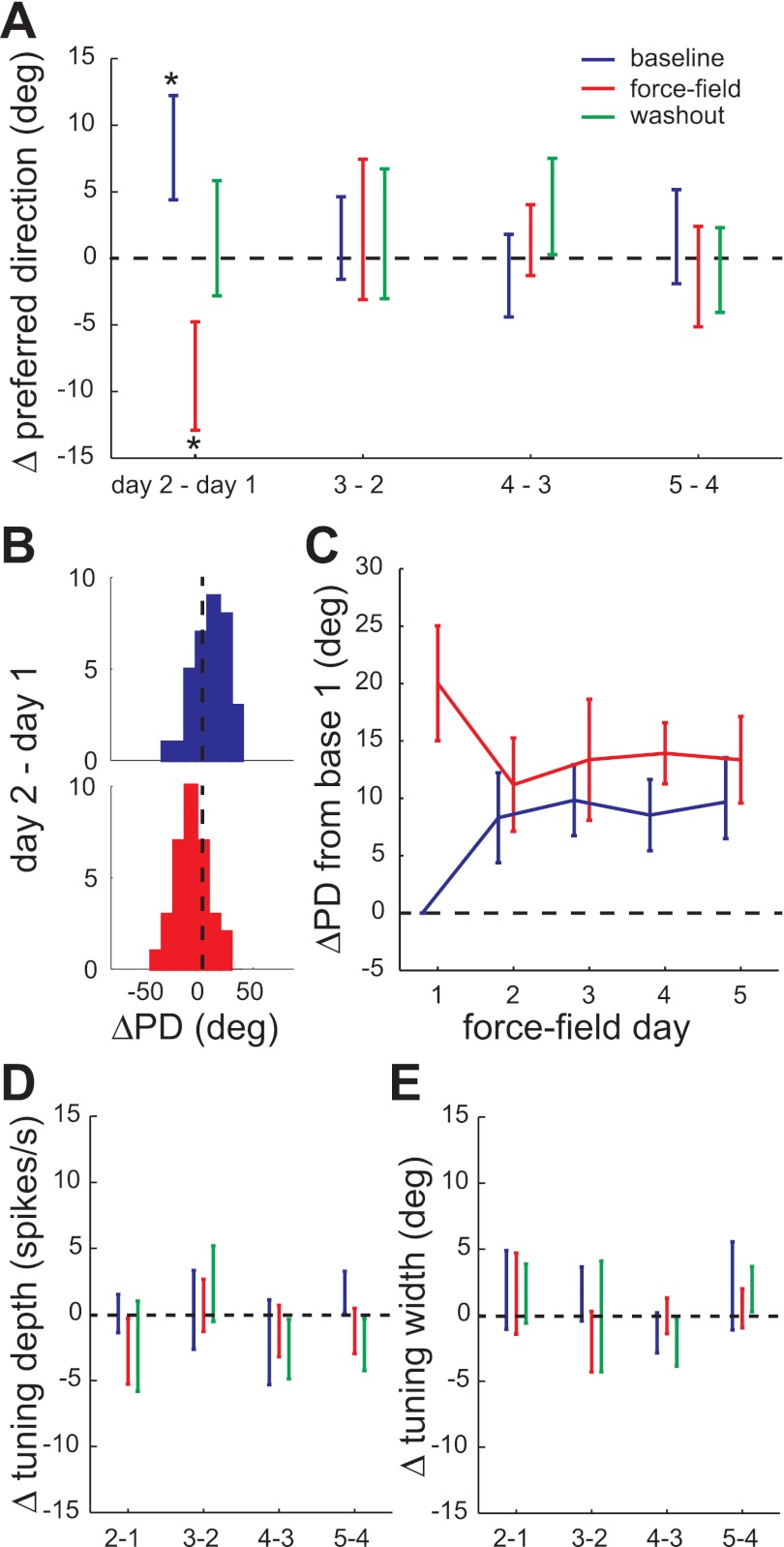
Fig. 9.

Evolution of directional tuning across sessions: population. A: PD changes (mean ± SE) between consecutive force-field sessions for the 50 unit ×force-field blocks. An asterisk indicates the sample mean was significantly different from zero (t-test, P < 0.05). B: histograms of significant PD changes shown in A: baseline epoch PD increase from day 1 to day 2 (top) and force-field epoch PD decrease from day 1 to day 2 (bottom). C: PD changes relative to the baseline PD on day 1 for the baseline and force-field epochs. D: tuning width changes (mean ± SE). E: tuning depth changes (mean ± SE) between consecutive force-field sessions.

For the first example unit (from monkey N), movement-related tuning curves are shown for two control sessions and three clockwise force-field sessions, spanning 7 days (Fig. 7A). The unit was quite stable across these 7 days, as evidenced by the similarity in MSW (Fig. 7B), baseline PESRs (Fig. 7C), and ISIH (Fig. 7D). Furthermore, the directional modulations in spike rate were well fit by von Mises functions, with r² > 0.85 in all but one epoch of 1 day (Fig. 7E). The most obvious within-session change in the three clockwise sessions was a transient increase in tuning width during the force-field epoch, an effect not seen in the two control sessions (Fig. 7F). There was also a field-appropriate, interepoch shift in PD in the first clockwise session, but this effect grew smaller in the second and third clockwise sessions (Fig. 7G). Interestingly, the smaller interepoch shifts in days 24 and 26 were due to the baseline PD shifting relative to its value prior to experiencing the clockwise field (Fig. 7H). This change in baseline PD could not be explained by differences in kinematics, because the baseline velocity correlation coefficient (Fig. 7I) and hand path deviation area (Fig. 7J) did not differ from that of the control sessions. These baseline PD changes were correlated with a performance improvement across the three clockwise sessions (Fig. 7, H–J). Thus the field-appropriate baseline PD shift may be evidence of a memory trace of the altered dynamics.

The second example unit (from monkey M) displayed a similar pattern of PD shifts. Tuning curves for one control session, followed by five counterclockwise sessions, followed by two control sessions are shown (Fig. 8A). The unit activity was stable (Fig. 8, B–D) and well fit by von Mises functions with r² > 0.87 (Fig. 8E). There were transient within-sessions changes in tuning depth, rather than width, in all counterclockwise sessions except the last one (Fig. 8F). As in the first example, a within-session PD shift was evident in only the first counterclockwise session (Fig. 8G). In subsequent sessions, the baseline PD shifted in the direction of the field (Fig. 8H). This shift remained through the first postfield control session (day 42), but then started to revert back by the last control session, perhaps indicating the temporal limits of the memory trace. Again the performance in the baseline was consistently high throughout all these sessions and the force-field performance improved, although not monotonically, over the counterclockwise sessions (Fig. 8, I and J).

The evolution of population PD changes is summarized in Fig. 9. The difference in PD for each epoch on consecutive force-field days was computed for the 50 unit × force-field blocks, excluding instances of insignificant tuning (Fig. 9A). Clockwise PD changes were inverted such that positive changes were in the direction of the force field. The mean PD change was significantly different from zero in two cases (t-test, P < 0.05): the baseline epoch PD significantly increased (Fig. 9B, top) and the force-field epoch PD significantly decreased from day 1 to day 2 (Fig. 9B, bottom). Thus, as in the two examples, the population baseline PD shifted in the direction of the field by the second session and this shift was maintained, although not increased, through the remainder of the force-field block. This can be seen more clearly (and compared with Figs. 7H and 8H) by plotting the PD change relative to the baseline PD on day 1 prior to force-field exposure (Fig. 9C). The evolution of force-field epoch PD changes show a maximum rotation (∼20°) in the direction of the field on day 1, with significantly smaller rotations (∼10°) on subsequent days. There were no significant washout epoch PD changes for the population (Fig. 9A); their cumulative change was omitted from Fig. 9C for clarity. Also, there were no significant changes in tuning depth (Fig. 9D) or tuning width (Fig. 9E) in any epoch at the population level (t-tests, P > 0.05). The combination of baseline and force-field epoch PD shifts led to smaller interepoch tuning changes on days 2–5 compared with day 1 of the force-field block. This result is consistent with the previously described decrease in interepoch spike rate changes in the fifth sessions compared with the first sessions (Fig. 6, A and D). Thus, as learning progressed, the population of stable units maintained a field-appropriate tuning shift, on average, rather than transiently shifting PD only when the field was encountered.

DISCUSSION

In this experiment, we studied M1 neuronal activity while reaching movements were repeatedly perturbed by the same force fields. Within each session the force fields modulated movement-related M1 activity, causing a population shift in direction tuning that was appropriate to compensate for these types of perturbations. Long-term learning was evident across multiple force-field sessions as performance errors decreased. Correlated with this long-term performance improvement, the population of stable M1 cells maintained the field-appropriate directional tuning shift learned on the first force-field exposure.

Neuronal correlates of early memory formation in force field learning have been described previously. Using the same paradigm but more conventional, single-session recording methods, we previously identified two classes of so-called memory cells. Here we consider only classifications based on the PD of movement-related activity because they are the most relevant to the present study. Memory I cells had a PD shift from baseline to force-field epoch, in the direction of the field, that was maintained in the washout epoch. Memory II cells showed no significant shift from baseline to force-field epoch, but then shifted in the opposite direction of the field in the washout epoch. These two types of memory cells were identified in M1 (Gandolfo et al. 2000; Li et al. 2001), in the supplementary motor area (Padoa-Schioppa et al. 2004), in the premotor cortex (Xiao et al. 2006), and again in M1 in the present study.

However, two issues challenged the interpretation that the persistent PD changes seen in our prior studies were correlates of memory formation. First, as in the present study, adaptation and deadaptation were often not completed by the end of the 160 trials of the force-field and washout epoch, respectively. Thus there were kinematic differences that might explain the tuning changes. To address this challenge, it was previously argued that although the actual kinematics were different, the desired kinematics did not change since the adaptation and deadaptation trends were to converge back toward the baseline level given enough trials (Padoa-Schioppa et al. 2004). Furthermore, it was argued, the desired kinematics were most relevant to the directional tuning, since the PD of a cell that reflected the actual kinematics would shift in the direction opposite to the force field in the case of incomplete adaptation. This is contrary to what was observed. Rather than invoking these arguments, others have simplified the paradigm to learning the force field in only one, rather than eight, movement directions such that adaptation and deadaptation are completed in each session (Arce et al. 2010a). With identical kinematics in the baseline/prelearning and washout/postlearning epochs, persistent direction tuning changes consistent with memory I cells were observed in M1 neurons (Arce et al. 2010b). Although the present study suffered from the same lack of complete adaptation and deadaptation as our previous studies, the field-appropriate persistent shifts in preferred direction across sessions were seen in the baseline epochs where kinematics were the same from day to day. This substantiates the claim that the across-session tuning changes were indeed related to memory formation.

The second issue related to interpretation of memory cells was that the distribution of baseline-to-washout PD changes was similar in force-field sessions and control sessions. This has been observed in a number of studies (Arce et al. 2010b; Padoa-Schioppa et al. 2004; Rokni et al. 2007), include the present one. We previously put forward the hypothesis that these baseline-to-washout changes were the result of noisy plasticity mechanisms that led to unstable neural representations (Rokni et al. 2007). The implication was that memory I and memory II cells were not truly related to memory of the force field, but simply two tails of a zero-mean distribution of behaviorally irrelevant tuning changes that occur even in the absence of learning. However, Arce et al. (2010b) found that if they included only “force-field–modulated” cells (i.e., cells with significant modulation of the learned direction spike rate from the baseline to force-field epoch) then the distribution of baseline-to-washout PD changes had a nonzero mean in the direction of the force field. The authors suggested that nonmodulated cells masked this ensemble correlate of memory formation in previous studies. In our task, with forces applied in all directions, an appropriate definition of “force-field–modulated” cells is that of those with significant PD shifts from the baseline to force-field epoch. By this definition, force-field–related cells are equivalent to the dynamic and memory I cell classes described previously. We showed that, similar to Arce et al. (2010b), the baseline-to-washout PD changes for only these units had a nonzero mean in the direction of the force field. This is not surprising since it specifically leaves out the memory II cells that made up the other tail of the zero-mean distribution described by Rokni et al. (2007). Thus, this is not an overly convincing correlate of memory formation in this task. Our across-session analysis, on the other hand, found systematic, field-specific PD shifts that were not seen in control sessions, leaving little doubt that they were related to long-term, force-field learning.

However, the persistent population PD shift observed in our study is somewhat surprising from the point of view of subsequent performance in the normal, null-field environment. To support both motor performance and motor learning, Li et al. (2001) proposed the memory I and memory II responses balanced each other in the postlearning washout trails, permitting a memory trace while maintaining the same overall M1 output as in the baseline trials. The present data apparently did not have this balance. This may simply be due to a sampling bias. The within-session analysis indicated a larger proportion of memory I cells (16%) than memory II cells (10%). Alternatively, the memory I/memory II hypothesis may be incorrect (Rokni et al. 2007). Persistent PD shifts in M1 could be compensated elsewhere, by the myriad other cortical and subcortical areas driving motor output, or could themselves represent an optimal solution to reaching in both normal and modified environments. It is worth noting that memory II responses were not observed by Arce et al. (2010b). However, as alluded to earlier, their focus on force-field–modulated cells may have specifically excluded memory II cells.

The Arce et al. paradigm of one-direction force-field learning was recently used, in conjunction with chronic recording arrays, to study correlates of long-term adaptation across five daily sessions (Mandelblat-Cerf et al. 2011). Although recordings of the same neurons across sessions were not specifically sought out or analyzed, the chronic ensemble results of Mandelblat-Cerf et al. are certainly relevant to our study. They found sudden increases or gradual decreases in M1 spike rates across the five sessions depending on the angle between the neuron's PD and the one target direction to which forces were applied. The spike rate dependence on relative angle between the PD and learned direction was consistent with what was described previously in their within-session paradigm (Arce et al. 2010a). Differences in task design make it difficult to compare this interesting across-trial evolution of activity to our results. However, of more relevance, they found that these rate changes resulted in a change in PD of the directional tuning curves only if the direction was defined by the target or observed hand direction. If instead direction was defined by the “motor plan” (difference between the hand direction and applied force vector), no PD shift was observed. Their analysis makes an important point regarding the interpretation of PD shifts in the present study, which were calculated using target directions (using observed hand directions yielded nearly identical results). The PD shifts do not necessarily imply any change intrinsic to the M1 neurons being recorded or their effect on motor output. As we have noted earlier, the tuning curve changes more likely reflect changes in how the M1 neurons were being recruited by upstream circuits to execute the reaching task in a modified environment (Rokni et al. 2007).

The unique results of the present work were made possible by chronic, stable recordings. The primary advantage of this technique was to allow the study of single-cell correlates of behavioral processes, such as motor memory formation, which evolve over timescales longer than a typical daily recording session. An inherent disadvantage of this type of recording is the low yield. Therefore many questions remain, including how long the persistent directional tuning shifts last. An intriguing, yet anecdotal, finding was that the persistent shifts in tuning may last only a few days beyond training (Fig. 8F). Even during the 5-day training blocks, the persistent rate changes in the washout epoch at the population level decreased (Fig. 6, C and D). We could speculate that M1 plays a greater role in early motor memory formation, after which the memory is stored in other areas, analogous to the role of the hippocampus in episodic memory (Squire et al. 2004). Prior evidence for this hypothesis has come from noninvasive stimulation and imaging (Muellbacher et al. 2002; Shadmehr and Holcomb 1997). Our results provide an initial view of this process at the single-cell level. Although additional data are needed, it is clear from the present study that task-specific M1 neuronal activity changes during development of a motor skill.

GRANTS

This research was supported by National Institute of Neurological Disorders and Stroke Grant NS-044393.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

A.G.R. and E.B. conception and design of research; A.G.R. and T.B. performed experiments; A.G.R. and T.B. analyzed data; A.G.R. and E.B. interpreted results of experiments; A.G.R. prepared figures; A.G.R. drafted manuscript; A.G.R. and E.B. edited and revised manuscript; A.G.R., T.B., and E.B. approved final version of manuscript.