The relationship between voltage-sensitive dye imaging signals and spiking activity of neural populations in primate V1

Abstract

Voltage-sensitive dye imaging (VSDI) is a powerful technique for measuring neural population responses from a large cortical region simultaneously with millisecond temporal resolution and columnar spatial resolution. However, the relationship between the average VSDI signal and the average spiking activity of neural populations is largely unknown. To better understand this relationship, we compared visual responses measured from V1 of behaving monkeys using VSDI and single-unit electrophysiology. We found large and systematic differences between position and orientation tuning properties obtained with these two techniques. We then determined that a simple computational model could explain these tuning differences. This model, together with our experimental results, allowed us to estimate the quantitative relationship between the average VSDI signal and local spiking activity. We found that this relationship is similar to the previously reported nonlinear relationship between average membrane potential and spike rate in single V1 neurons, suggesting that VSDI signals are dominated by subthreshold synaptic activity. This model, together with the VSDI measured maps for spatial position (retinotopy) and orientation, also allowed us to estimate the spatial integration area over which neural responses contribute to the VSDI signal at a given location. We found that the VSDI-integration area is consistent with a Gaussian envelope with a space constant of ∼230 μm. Finally, we show how this model and estimated parameters can be used to predict the pattern of population responses at the level of spiking activity from VSDI responses.

a fundamental feature of early sensory cortical areas is the representation of sensory information in two-dimensional (2-D) topographic maps across the cortical surface (e.g., Hubel and Wiesel 1963; Mountcastle 1957; Woolsey 1952). Within these maps, sensory stimuli elicit patterns of neural responses that are distributed across multiple square millimeters. Characterizing these patterns in space and in time is therefore a prerequisite to understanding sensory encoding and decoding.

Voltage-sensitive dye imaging (VSDI) provides a powerful tool for measuring 2-D patterns of population responses in the superficial cortical layers at high spatial and temporal resolution in vivo (reviewed in Grinvald and Hildesheim 2004). Furthermore, VSDI can be applied to behaving animals performing demanding perceptual tasks, where sensory encoding and decoding can be studied most directly (e.g., Chen et al. 2006). However, the interpretation of VSDI findings is complicated by open questions regarding the quantitative relationship between the average VSDI-measured neural signals and the average patterns of population responses at the level of spiking activity.

Specifically, two key questions regarding the relationship between VSDI signals and spiking activity in vivo remain open. First, what is the relative contribution of subthreshold and suprathreshold neural responses to VSDI signals? Whereas in single neurons, VSDI signals are directly proportional to membrane voltage across the entire physiological dynamic range (e.g., Salzberg et al. 1973), at the level of neural populations, factors such as spiking activity in nonmyelinated axons and back-propagation of action potentials from the cell body into the dendrites could lead to a significant contribution of spikes to the VSDI signal. A central goal of the current study is to estimate the relative contribution of these factors to VSDI signals in vivo.

Second, what is the size of the neural population that contributes to the VSDI signal at a given cortical location? This VSDI integration area depends on the horizontal spread of dendrites and axons in the cortex, on the light scattering properties of the cortical tissue, and on the optical properties of the imaging system, but the relative contribution of these factors and the final value of this integration area are unknown. A second goal of the current study was to provide an estimate of the VSDI integration area.

To begin to address these open questions, we measured neural responses from V1 of behaving monkeys using a combination of VSDI and extracellular electrophysiology. Specifically, we compared the average tuning properties of VSDI signals and single-unit (SU) spiking activity across two stimulus dimensions: orientation and spatial position.

Because subthreshold membrane potentials are generally less selective and more broadly tuned than spiking activity (reviewed in Priebe and Ferster 2008), the relative contribution of subthreshold vs. suprathreshold responses to the VSDI signal must affect the relationship between the tuning properties of signals measured with these two techniques. A larger contribution of subthreshold responses to the VSDI signals will necessarily lead to broader tuning and decreased selectivity of the VSDI-measured responses relative to the spiking activity of single V1 neurons. By taking into account the known relationship between average membrane potential and average spiking activity in single V1 neurons, our first goal was to obtain an estimate of the relative contribution of sub- and suprathreshold responses to the VSDI signal.

In addition, the tuning properties of the VSDI-measured neural responses depend on the size of the neural population that contributes to the VSDI signal at a given location. V1 contains topographic maps of spatial position, i.e., retinotopy (Adams and Horton 2003; Daniel and Whitteridge 1961; Talbot and Marshall 1941; Tootell et al. 1982, 1988; Van Essen et al. 1984) and orientation (Blasdel and Salama 1986; Bonhoeffer and Grinvald 1991; Hubel and Wiesel 1963, 1968; Obermayer and Blasdel 1993). Consider, for example, tuning for orientation. Intuitively, an increase in the VSDI integration area will lead neurons with different preferred orientations to contribute to the VSDI signal at a given location. This, in turn, would lead to broadening of the orientation tuning of the VSDI-measured responses relative to the average tuning of individual V1 neurons. In addition, an increase in the VSDI integration area will lead to an increase in the component of the response that is not orientation selective (untuned component). VSDI allows us to measure both the retinotopic map (see Fig. 2) (Yang et al. 2007) and the orientation map (see Fig. 6) with high precision and reliability in the awake monkey. Therefore, we can use these maps to estimate how different VSDI integration areas are expected to affect the average tuning properties of the VSDI-measured responses for orientation and position. By comparing these predictions with the observed VSDI tuning curves, our second goal was to obtain an estimate of the VSDI integration area.

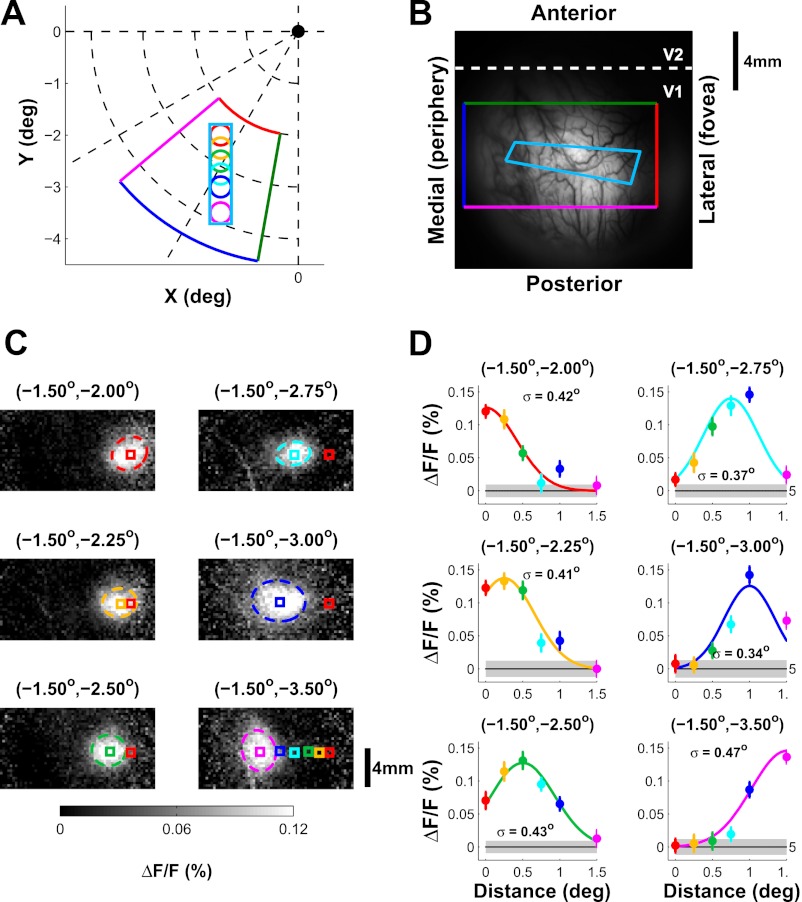
Fig. 2.

Example position tuning of voltage-sensitive dye imaging (VSDI) signal. A: stimulus position (same format as in Fig. 1A). Colored wedge shape shows the region in visual space that is approximately represented by the corresponding rectangle area in B. B: image of cortical vasculature with the approximate retinotopic mapping. The rectangle with 4 colors corresponds to the wedge-shaped area in A, whereas the elongated cyan rectangle corresponds to the predicted trajectory of the stimuli along the cortical surface. C: spatial distributions of responses to stimuli at different positions. Responses were averaged during a 200-ms interval starting 36 ms after stimulus onset. Ellipsoids show contour of the 2-D Gaussian fit to the response at one σ. Colored squares (0.75 × 0.75 mm²) denote the center of the 2-D Gaussian functions. The center position for the most foveal position (red) is shown in all panels for reference. All centers are shown in bottom right panel. ΔF/F, fractional change relative to average fluorescence. D: position tuning curves for the 6 locations in C. Different colors represent different positions. The solid curve shows a 1-D Gaussian fit. Estimated tuning width σ is indicated in each panel.

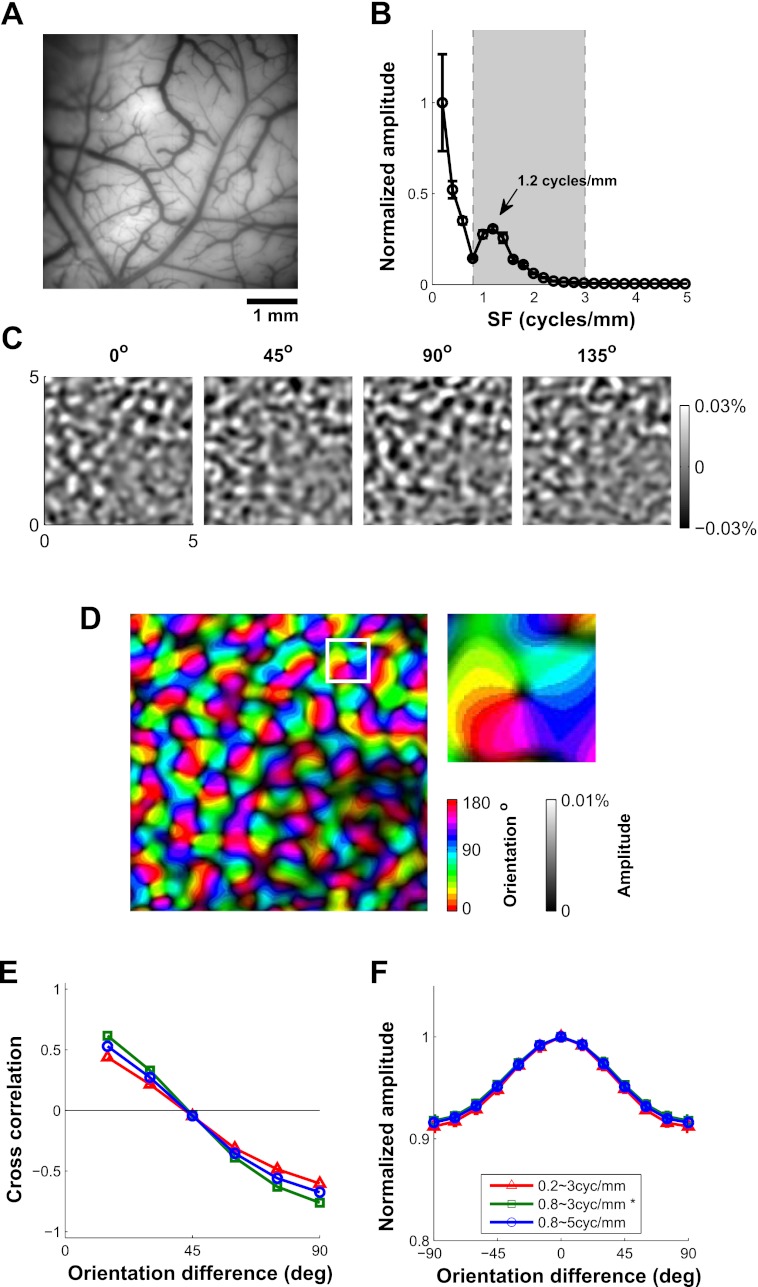
Fig. 6.

Orientation tuning of VSDI signal. A: image of the cortical vasculature; V1/V2 border is parallel to the top of the image. B: spatial 1-D amplitude spectrum of the single-orientation response maps. The 2-D amplitude spectrum of each map was averaged radially and then averaged across the 12 orientations. The peak at 1.2 cycles/mm is due to orientation columns with a corresponding peak period of ∼0.83 mm. C: average response maps to 4 of 12 orientations. Only the components with spatial frequency between 0.8 and 3 cycles/mm, indicated by the shaded area between the dashed vertical lines in B, are shown. The spatial filtration removes components with periods larger than 1.25 mm and smaller than 0.33 mm. D: orientation map computed on the basis of the vector sum of the responses. Hue represents preferred orientation, and saturation represents tuning amplitude. The white square corresponds to the magnified region (0.7 × 0.7 mm²) inset at right. E: correlations between all pairs of response maps as a function of the orientation difference. Different colors indicate different ranges of spatial filtration. Adding lower or higher spatial frequencies causes the correlation functions to flatten, suggesting that the added frequencies contribute components that are less orientation selective. F: normalized VSDI orientation tuning curve including the untuned component. Different colors indicate different ranges of spatial filtration. In E and F, SE values are smaller than symbols.

To address these goals, we developed a simple computational model that attempts to predict the pattern of population responses at the level of spiking activity from the VSDI signals, and vice versa. The model includes two free parameters, one for the relative contribution of sub- and suprathreshold responses to the VSDI signals and one for the VSDI integration area. We then used our measured tuning curves, together with the VSDI-measured topographic maps for spatial position and orientation, to constrain our model. The results of this analysis show that VSDI signals are dominated by subthreshold synaptic activity and that the space constant of the Gaussian-shaped VSDI integration area is ∼230 μm. Because a single set of parameters accounts for our results across the two stimulus dimensions, our study raises the possibility that for a wide range of visual stimuli, the average pattern of population responses at the level of spiking activity could be predicted from the VSDI signals.

METHODS

Subjects and surgery.

Results from a total of eight monkeys (Macaca mulatta) were included in this study: six contributed to position tuning measurements (3 for electrophysiology and 3 for VSDI); six contributed to orientation tuning measurements (3 for electrophysiology, 1 for VSDI, and 2 for both); four contributed to both position and orientation tuning measurements. Surgical procedures for VSDI and electrophysiological recordings from behaving monkeys have been described in detail elsewhere (Chen et al. 2006, 2008; Palmer et al. 2007). All surgical procedures were performed under deep anesthesia, using strictly sterile techniques, in a dedicated surgical suite. All procedures were approved by the University of Texas Institutional Animal Care and Use Committee and conformed to National Institutes of Health standards.

Task.

Each trial began when the animal achieved fixation in a small window (<2° full width) around a 0.1 × 0.1° central fixation point displayed against a uniform gray background. After initial fixation, a visual stimulus (either Gabor patch or sinusoidal grating, see details below) was presented parafoveally to both eyes for 1–2 s. The monkey received a reward at the end of the stimulus presentation interval provided it did not break fixation.

Visual stimulus for position tuning.

For position tuning (electrophysiology and VSDI), the visual stimulus was a small Gabor patch (a sinusoidal grating in a Gaussian envelope). The Gabor patch was presented two to four times at 2 Hz (200 ms on and 300 ms off). The position of the Gabor patch varied pseudorandomly from trial to trial among a total of five to eight positions extending from receptive field (RF) center (or a location within the imaging chamber close to the representation of the fovea in the case of the VSDI experiments) to a peripheral location that elicited a response indistinguishable from the baseline. In different experiments, stimulus position was changed along horizontal, vertical, or iso-eccentric directions (for electrophysiology only). The contrast of the Gabor patch was 100%, and it was in sine phase. In electrophysiological recordings, the spatial frequency and orientation of the Gabor patch were adjusted to match the preferred parameters of the recorded neuron [mean RF eccentricity, 2.57°; range across experiments, 2.01–3.17°; mean spatial frequency, 2.73 cycles per degree (cpd); range, 2–4.2 cpd; no orientation bias] while the space constant (σ) of the Gabor patch was kept constant at 0.167°. In VSDI experiments, only the position of the Gabor patch varied across experiments (mean eccentricity, 2.55°; range across experiments, 1.8–3.35°); the parameters of the Gabor patch were kept constant (σ, 0.167°; spatial frequency, 2.76 cpd; orientation, 0°).

Visual stimulus for orientation tuning.

For orientation tuning, the visual stimulus was either a small Gabor patch (electrophysiology) flashed two to four times at 2 Hz (200 ms on and 300 ms off) or a larger sinusoidal grating (VSDI) flashed at 5 Hz (60 ms on and 140 ms off) for 1 s. The 5-Hz stimulus presentation helped us obtain an improved signal-to-noise ratio necessary for VSDI measurements of high-resolution orientation maps (see Fig. 5 and results, Orientation tuning of VSDI signals in V1). The orientation of the stimulus varied from 0° to 180° in steps of 15° or 30°. In electrophysiological recordings, the position, spatial frequency, and size of the Gabor patch were adjusted to match the preferred parameters of the recorded neuron. The grating stimulus used in the VSDI experiments always fully covered the portion of the visual field corresponding to the V1 area in the imaging chamber, and the spatial frequency and size of the grating were kept constant at 2 cpd and 6°, respectively.

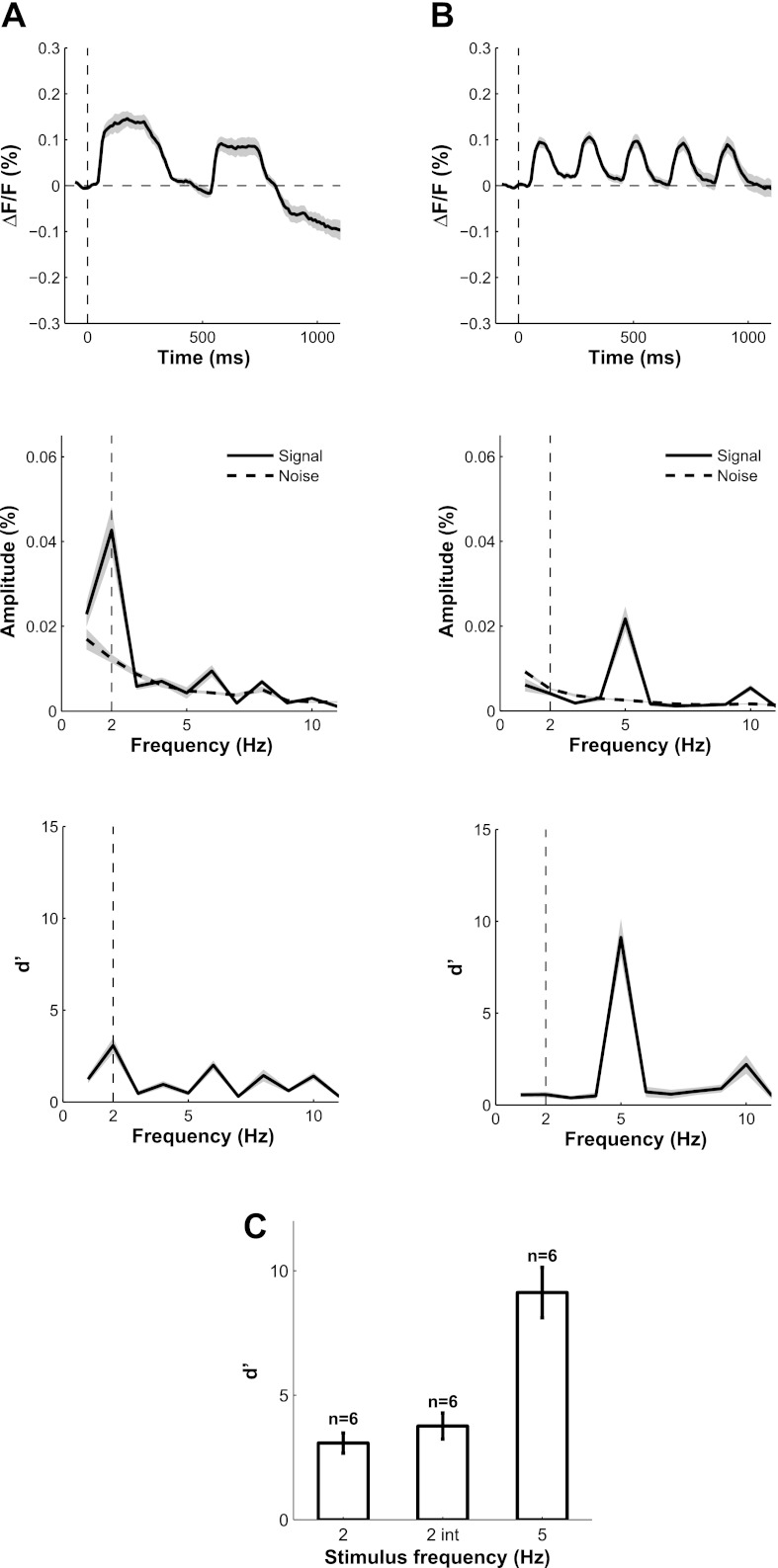
Fig. 5.

Temporal dynamics of VSDI responses and signal-to-noise ratio (S/N) as a function of stimulus frequency. Response to grating flashed at 2 Hz (A) or 5 Hz (B) was integrated over a cortical area of 1 × 1 mm². Top: mean and SE (shaded area) of time course of V1 responses in 6 separate experiments at each stimulus frequency. The mean response in blank trials was subtracted from each trace. Middle: amplitude spectrum of the average evoked response (solid) and average amplitude spectrum of the VSDI noise (dashed). The noise amplitude spectrum was computed from the residual time courses (single-trial minus mean time course) and averaged across all blank trials. Bottom: S/N computed as the d′ or z score from the middle panel. C: summary of average S/N at stimulus frequency across experiments. 2 int indicates the average d′ for 2-Hz presentation when the response is integrated over 200 ms, as in the analysis of the position tuning.

Visual stimuli were presented on a gamma-corrected high-end 21-in. color display at a fixed mean luminance of 30 cd/m². The display subtended 20.5° × 15.4° at a viewing distance of 108 cm, pixel resolution of 1,024 × 768, 30-bit color depth, and a refresh rate of 100 Hz.

Electrophysiology.

Our electrophysiological recording techniques have been described previously (Palmer et al. 2007). Briefly, electrodes (FHC, Bowdoinham, ME) were advanced using a guide tube through a rubber gasket that sealed a small hole in the transparent plastic cover sealing the recording chamber. A dual slope/height window discriminator (Bak Electronics, Germantown, MD) was used to isolate spikes from single neurons. Only waveforms that were well separated from the background noise were considered SUs.

After isolation, we used a custom software package (courtesy of G. DeAngelis, University of Rochester, Rochester, NY) to qualitatively analyze the RF properties of the recorded neuron. The software allowed interactive variation of the parameters (location, spatial frequency, orientation, and size) of a sinusoidal grating while graphically monitoring neural responses. Based on the initial analysis of the RF properties, we performed an additional quantitative assessment using a Gabor presented for 200 ms for a minimum of 5 trials per condition to identify the preferred orientation of the neuron. We also quantitatively assessed the preferred size (at a fixed spatial frequency of 3 cpd) and spatial frequency (with size fixed at the preferred value) of some of the recorded neurons.

Voltage-sensitive dye imaging.

The experimental techniques for VSDI in awake, behaving monkeys have been described elsewhere (Arieli and Grinvald 2002; Arieli et al. 2002; Seidemann et al. 2002; Slovin et al. 2002). Briefly, in the current study we used the voltage-sensitive dyes RH1838 or RH1691 (Shoham et al. 1999) and a high-speed camera (Imager 3001; Optical Imaging) to image any changes in membrane potentials in an area of up to 16 × 16 mm² over the occipital lobe of macaque monkeys. Results from the two dyes were combined because no systematic differences between signals obtained with these two dyes were observed. The camera collected 512 × 512 pixels at 110 Hz. For position tuning measurements, imaging area was 16 × 16 mm² with a pixel size of ∼32 × 32 μm². For orientation tuning measurements, imaging area was 5 × 5 mm² with pixel size of ∼10 × 10 μm².

Behavior monitoring and data acquisition.

Behavior monitoring and data acquisition were performed by a computer running software for real-time neurophysiological recordings from alert animals (Tempo; Reflective Computing, St. Louis, MO). This computer interfaced with an infrared eye-tracker (Dr. Bouis Devices, Karlsruhe, Germany) for high-quality analog eye position monitoring. Eye position signals were sampled with 16-bit resolution at 1 kHz. Electrophysiological signals were sampled at 1 kHz. The data acquisition computer also interfaced with the systems used to acquire electrophysiological data (Bak Electronics, Mount Airy, MD) and optical imaging data (Optical Imaging, Germantown, NY). In addition, this computer controlled a dedicated personal computer with a high-end graphics card that was used for stimulus presentation.

Experiment database for position tuning.

The results are based on 19 SU recordings and 68 VSDI recording sites from 13 VSDI experiments (2 of which were performed simultaneously with electrophysiology). All electrophysiological recordings had to meet three criteria to be included in our analysis: 1) a minimum of eight repetitions per condition; 2) peak stimulus-evoked response >5 spikes/s; and 3) eccentricity of RF center between 1.8° and 3.4°. Of the 37 single neurons that were initially screened, 6 were excluded because isolation was not maintained for long enough to collect the minimum number of repeats, 1 was excluded due to the weak peak stimulus-evoked response, and 11 were excluded because their RF centers were outside the required eccentricity range.

For VSDI recordings, we usually had eight sites (corresponding to 8 stimulus positions) in each experiment. Three criteria were applied to these sites: 1) peak d′ > 3 (where d′ is equal to the mean response over its SD); 2) spatial response had to be fully within the imaged V1 area and sufficiently far from V2; and 3) stimulus eccentricity between 1.8° and 3.4°. Of the total 102 sites tested, 15 were excluded due to a low peak d′, 4 due to proximity to V2, and 15 because they were outside the required eccentricity range.

Experiment database for orientation tuning.

The results are based on 44 SU recordings and 8 VSDI experiments. All electrophysiological recordings had to meet two criteria to be included in our analysis: 1) a minimum of eight repetitions per condition; and 2) a peak stimulus-evoked response >5 spikes/s. Of the 73 single neurons we initially recorded, 17 were excluded because the number of repetitions per condition was too low, and 12 were excluded due to the weak stimulus-evoked response.

For VSDI recordings, the criterion was that d′ was greater than 8 for >90% of the 8 × 8 binned pixels within a rectangular area larger than one-quarter of the entire imaged area.

Analysis of electrophysiological data.

For both position tuning and orientation tuning, SU responses (spikes) were averaged during a 200-ms interval starting 36 ms after stimulus onset. The results were essentially identical when averaging the responses in 100-ms intervals starting at 36 or 136 ms after stimulus onset (data not shown). Responses for a given trial were then averaged across the two to four stimulus presentations.

Analysis of the voltage sensitive dye imaging.

For position tuning, VSDI analysis followed eight steps: 1) remove outlier trials (see below) from each block, usually fewer than 1% of trials; 2) normalize to fractional change relative to the average fluorescence at each location across all trials; 3) average signals across all trials for each stimulus condition; 4) subtract the mean blank condition; 5) subtract from the responses in each condition the average response in the 100-ms interval before response onset; 6) average the VSDI response during the integration period (36–236 ms after stimulus onset); 7) fit the averaged VSDI response with a 2-D Gaussian function with DC; and 8) remove the fitted DC component. The VSDI spatial position tuning curves were slightly narrower when the responses were averaged in a 100-ms interval starting at 36 ms than when the responses were averaged in a 100-ms interval starting at 136 ms after stimulus onset, but this difference had negligible effect on our results (data not shown). Effective pixel size for position tuning experiments (after 8 × 8 binning) was ∼250 μm. Steps 2–6 were done independently for each 8 × 8 binned pixel. VSDI responses were averaged across the two stimulus presentations per trial. To remove outliers (step 1), we first divided each frame into four quadrants and averaged the gray level in each quadrant. Outliers were trials whose average gray level at any quadrant during any frame exceeded 5 standard deviations (SD) from the mean across all trials. Generally, outliers were caused by excessive movements of the animal. Normalization (step 2) and anchoring (step 5) were helpful for eliminating the effect of uneven illumination in the recording chamber or uneven dye penetration and for eliminating the effect of slow drift in the VSDI response across trials. All data analysis was performed in Matlab (MathWorks).

For orientation tuning, VSDI analysis followed eight steps. The first four steps were identical to the ones in the analysis of position tuning (see above). The additional steps were as follows: 5) extract the Fourier transform (FT) amplitude at 5 Hz at each pixel for each condition; 6) perform 2-D spatial FT on the 5-Hz amplitude map for each condition and extract the components at spatial frequencies between 0.8 and 3 cycles/mm by removing all other frequencies and applying the inverse FT to the filtered data (these components correspond to the VSDI signals shown in Fig. 6C); 7) use a vector summation method to calculate the orientation map (see Fig. 6D); and 8) calculate the orientation tuning curve (see Fig. 6F) by averaging orientation tuning across space and adding the average DC components of the 2-D spatial FT. Step 5 significantly enhances the VSDI signal-to-noise ratio as shown in Fig. 5; step 6 can help to reduce the corruption of the orientation map by low spatial frequency noise and high-frequency shot noise (see Fig. 5).

Correcting for the effect of stimulus size on the estimated position tuning widths.

Our position tuning width measurements depend on the RF size of the recorded neurons as well as on the stimulus size. To correct for the effect of stimulus size, we used the following equation: ${\sigma }_{\text{RF}}=\sqrt{{\sigma }_{\text{Pos}}^2-{\sigma }_{\text{Stim}}^2}$, where σ_Stim is the Gabor stimulus' space constant (0.167°), σ_RF is the receptive field space constant, and σ_Pos is the space constant of the position tuning curve (e.g., Fig. 1C, 2D) (for additional details, see Palmer et al. 2012).

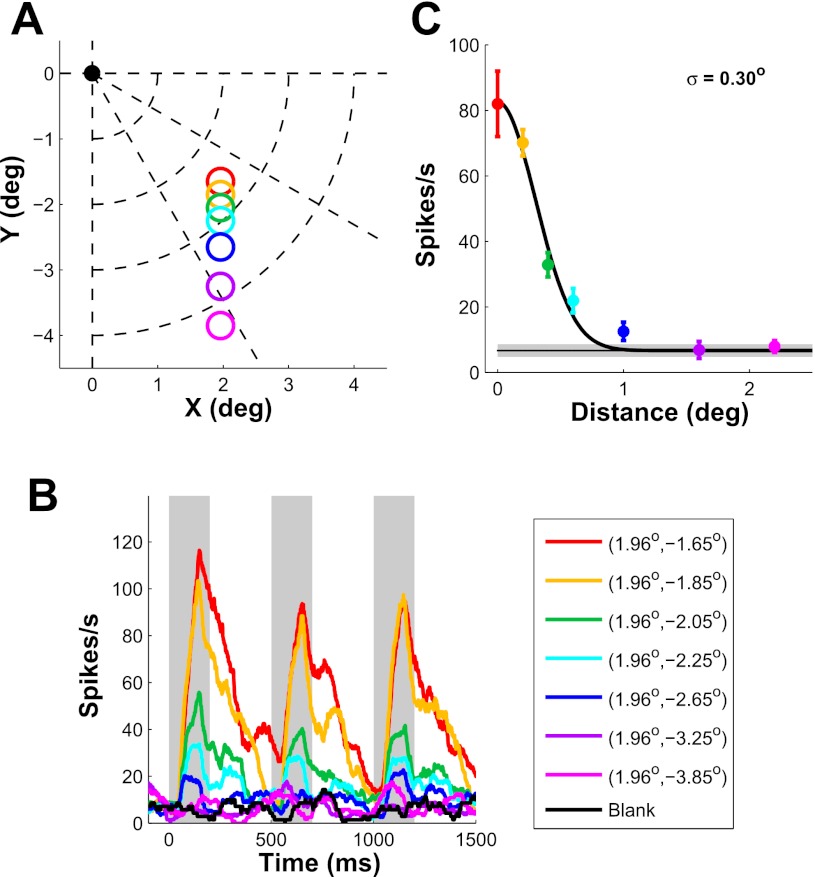
Fig. 1.

Position tuning properties of an example V1 neuron. A: stimulus position. Fixation point is at the origin. Colored circles indicate stimulus positions with circle radius equal to stimulus σ (0.167°). B: peristimulus time histogram (PSTH) of a V1 neuron as the distance between stimulus center and receptive field (RF) center is varied. Shaded areas show periods in which mean firing rate was computed. C: position tuning curve obtained from B. The solid curve shows a 1-dimensional (1-D) half-Gaussian fit. Estimated tuning width (σ) is indicated at top right. Horizontal line shows spontaneous activity ± SE (shaded area). Error bars represent ±SE.

Estimating the parameters of the transfer function and integration function.

A detailed description of the model is given in results. Briefly, the model includes a transfer function that describes the nonlinear relationship between average spiking activity and average VSDI signal in a small cortical region, and an integration (or blurring) function that describes the region over which neural responses contribute to the VSDI signals at a given location. The transfer function was assumed to be a power function with an exponent N, and the integration function to be a Gaussian with a space constant σ_Int.

For position tuning, both SU and VSDI signals were assumed to follow a Gaussian function over space. Therefore, there is a constant relationship between the power N of the transfer function that relates VSDI signals and spiking activity (see results) and the σ values of the Gaussians: ${\sigma }_{\text{VSDI}}=\sqrt{N}\times {\sigma }_{\text{SU}}$. To estimate N and its variability, we bootstrapped σ_VSDI and σ_SU from our measured data sets. As will be shown later, because the spatial scale of σ_Int is much smaller than the spatial scale of the population RF, σ_Int could not be reliably estimated from the measured position tuning data (see results).

For orientation tuning, we adopted a curve fitting method to estimate the two parameters. We first obtained the average orientation tuning curve of SU by bootstrapping the SU data set. We then randomly picked an orientation map from the eight VSDI experiments and assigned the average orientation tuning curve of SU to each pixel in the map. Specifically, we aligned the peak of the curve to the preferred orientation at each pixel and then used the tuning amplitude at that pixel to scale the tuning amplitude of the curve. This allowed us to mimic the orientation response of SU over the cortex while ensuring that the average orientation tuning was the same as the one obtained from the SU recordings. Next, we applied the inverse of the transfer function (Eq. 2) to convert these cortical orientation responses of SUs to membrane potentials and integrated the membrane potentials with a Gaussian function to obtain the predicted VSDI signals at each pixel. Finally, the orientation tuning curve was calculated from the simulated VSDI signals using the method applied to the real VSDI recordings. The curve-fitting method adjusted the power N of the transfer function and the space constant σ_Int of the integration function to minimize the least square error between the model's prediction and the measured average VSDI tuning curve.

In addition, to verify that our estimated model parameters do not depend on the assumption that all V1 neurons have identical tuning curve widths, we repeated the analysis described above but allowed the orientation tuning width at each location to be a random sample from a Gaussian distribution with a mean of 23° and SD of 10°. The estimated parameters in this analysis were indistinguishable from those in the previous analysis.

RESULTS

We begin our results section by describing the average spatial and orientation tuning properties of V1 responses measured with VSDI and SU spiking activity. We then develop a simple computational model that predicts the expected VSDI tuning curves for position and orientation from the average tuning curves of individual V1 neurons and from the retinotopic and orientation maps. By comparing the model's predictions with the observed VSDI tuning curves, we obtain estimates of the relative contribution of sub- and suprathreshold responses to the VSDI signals and of the VSDI integration area.

Position tuning of single V1 neurons.

To measure the position tuning of V1 neurons, we systematically varied the position of a small Gabor patch (σ, 0.167°; optimal orientation and spatial frequency; contrast, 100%) relative to the center of the neuron's RF. Stimulus position was varied along a linear trajectory (horizontal, n = 2; vertical, n = 14) or an iso-eccentric trajectory (n = 3), starting at the neuron's RF center (n = 16) or extending in both directions from RF center (n = 3). Figure 1B shows the responses of one V1 neuron to seven stimulus positions that varied along a vertical trajectory (Fig. 1A). The response dropped rapidly as stimulus position shifted away from RF center. We plotted the average firing rate as a function of the distance between stimulus center and RF center to obtain the position tuning curve (Fig. 1C). To estimate position tuning width, we fitted the position tuning data with a half-Gaussian. The space constant (σ) of the Gaussian in this case was 0.30°. The position tuning curve is closely related to the neuron's RF profile. Because RF size of V1 neurons depends on eccentricity (e.g., Hubel and Wiesel 1974; Van Essen et al. 1984), we restricted our analysis to a narrow range of eccentricities (1.8°–3.4°).

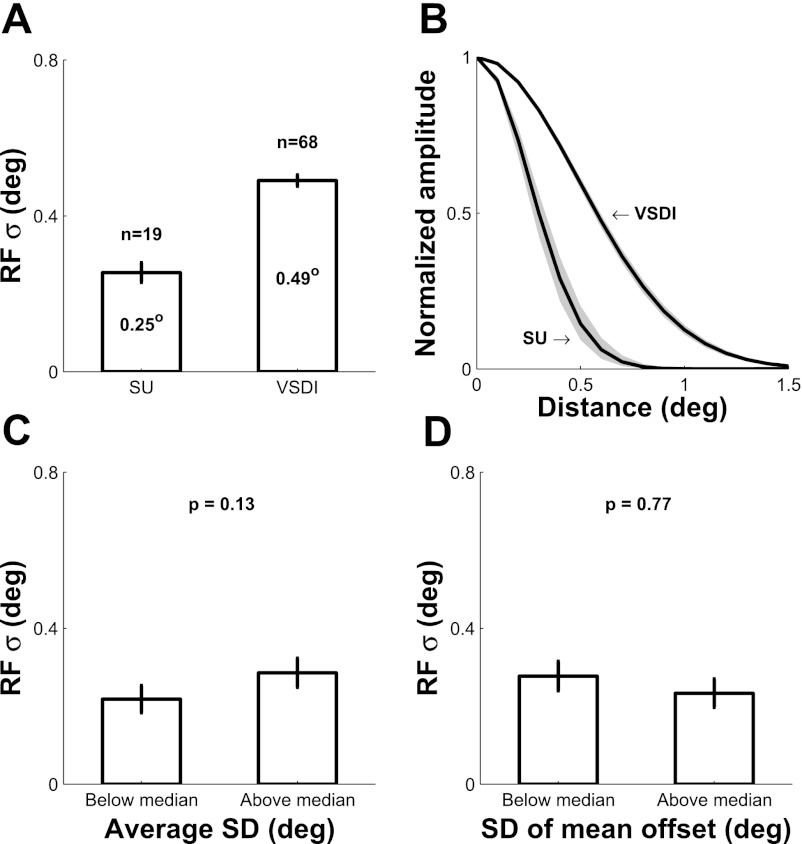
Figure 3A (left bar) shows the average position tuning space constants across all recorded neurons after correction for the effect of stimulus size (see methods). The average position tuning width of our single V1 neurons is 0.25° ± 0.03 (mean ± SE), comparable to previous measurements at similar eccentricities (e.g., Levitt and Lund 2002; Nienborg and Cumming 2006; Read and Cumming 2003).

Fig. 3.

Summary of position tuning width for single V1 neurons and for VSDI signals, and analysis of the possible effect of variations in fixational eye position on position tuning width of single V1 neurons. A: bar plot of average position tuning widths for single units (SUs) and VSDI. B: average normalized position tuning curves. Shaded areas represent ±SE. C: for each SU we computed the SD of eye position (within trial) during stimulus presentation. The bar plot shows the mean position tuning widths for SUs with below-median (left) and above-median (right) eye position SD. P = 0.13; 1-tailed t-test. D: same format as in C, but based on the SD (across trials) of the mean eye position offset from fixation point. P = 0.77; 1-tailed t-test.

Position tuning of VSDI signals in V1.

To obtain analogous position tuning curves for VSDI signals, we measured the VSDI response maps to Gabor stimuli that varied in position along a linear trajectory (horizontal, n = 34; vertical, n = 34). Figure 2 shows the response to Gabor stimuli at six positions (Fig. 2A) imaged over an area of ∼16 × 16 mm² (Fig. 2B) in one VSDI experiment. Each Gabor stimulus elicited an ellipsoidal cortical response that was well fitted by a 2-D Gaussian (Fig. 2C), consistent with our previous findings (Chen et al. 2006, 2008; Palmer et al. 2012). The position of the active region shifted along the cortical surface as predicted by the retinotopic map in V1 (Fig. 2B). To obtain a position tuning curve, we picked a cortical location corresponding to the center of one stimulus and measured the responses at this fixed cortical location to stimuli at all possible positions along the trajectory. By plotting the VSDI response as a function of the distance of each stimulus from the center location, we obtained a position tuning curve analogous to the position tuning curves of single V1 neurons. We repeated this analysis for each stimulus position that fell within our limited eccentricity range. Figure 2D shows the position tuning curves obtained at all six stimulus locations. Similar to the SU data, the position tuning curves were fitted with a Gaussian. The space constants obtained with VSDI tended to be larger than the space constants of single V1 units at similar eccentricities.

Figure 3A (right bar) shows the average position tuning space constants for all VSDI sites after correction for the effect of stimulus size (see methods). The average VSDI position tuning width is 0.49 ± 0.02°, significantly larger than the tuning width of single V1 neurons (P < 0.001; t-test). Therefore, average position tuning space constants obtained with VSDI are about twice those obtained with SU electrophysiology (Fig. 3B).

Possible effect of fixational eye movements on position tuning.

Because of the proximity of the recorded V1 area to the fovea, small fixational eye movements could lead to significant biases in our estimates of the position tuning data. To test for such an effect in our SU measurements, we computed two eye movement metrics: 1) to capture eye movements within trials, we computed the SD of the eye position during the stimulus presentation interval and averaged this value across trials; and 2) to capture the scatter in the average eye position across trials, we measured the distance of the mean eye position during the stimulus presentation interval from the fixation point in each trial and then computed the SD of this offset across trials. The average values of the “within-trial” metric (0.13 ± 0.04°, n = 19) and the “across-trials” metric (0.27 ± 0.08°, n = 19) were small. Furthermore, some of this variability is likely to be due to noise in our eye position measurements, rather than to poor fixation. Nevertheless, to determine whether the small amount of variability in eye position had an impact on our results, we compared the average position tuning width in neurons in which the within-trial or across-trials metrics were above and below their median value across all neurons. The position tuning widths were not significantly different in these two groups for the within-trial metric (1-tailed t-test, P = 0.13; Fig. 3C) and the across-trials metric (1-tailed t-test, P = 0.77; Fig. 3D), demonstrating that our monkeys maintained tight fixation and that fixational eye movements had a negligible impact on our results.

We used the same approach to examine possible effects of fixational eye movements on position tuning in our VSDI measurements. These results, which are presented in a separate study (Palmer et al. 2012), showed no significant effects of eye movement on our VSDI position tuning estimates.

Orientation tuning of single V1 neurons.

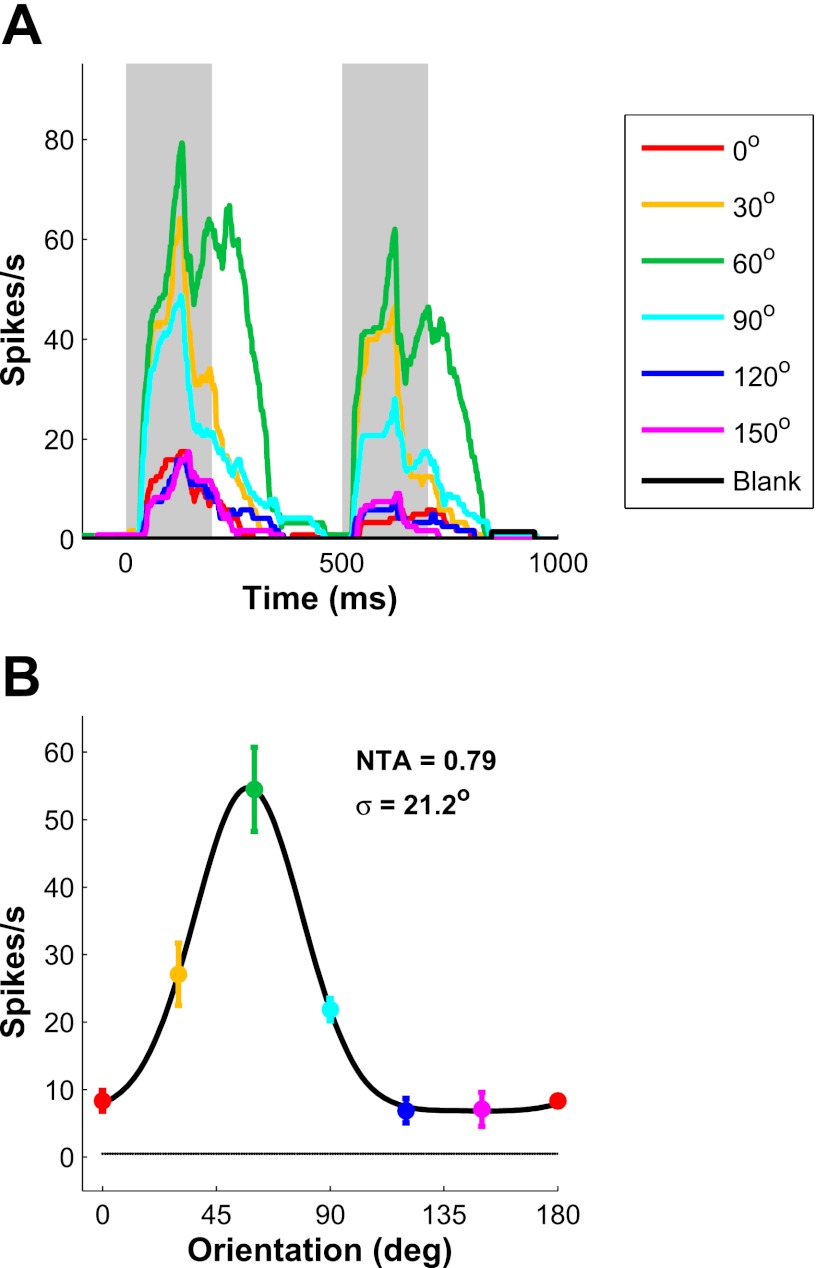
To estimate the orientation tuning curves of single V1 neurons, we measured SU responses to small Gabor patches (optimal size and spatial frequency; contrast, 100%) at 6 or 12 evenly spaced orientations. Figure 4A shows the response of an example V1 neuron. The neuron responded most strongly to a 60°-oriented Gabor, and the response decreased as stimulus orientation differed from the preferred orientation. The orientation tuning curve (Fig. 4B) was fitted with a circular Gaussian to obtain an orientation tuning width (the SD of the circular Gaussian) of 21.2° and a normalized tuning amplitude[NTA = (R_pref − R_orthogonal)/R_pref] of 0.79.

Fig. 4.

Orientation tuning properties of an example V1 neuron. A: PSTH of a V1 neuron responding to a Gabor stimulus at 6 different orientations and in blank trials. Shaded areas show periods in which mean firing rate was computed. Spontaneous firing rate was near zero. B: orientation tuning curve obtained from A. The solid curve shows a 1-D circular Gaussian fit. Estimated normalized tuning amplitude (NTA) and tuning width σ are indicated at top right.

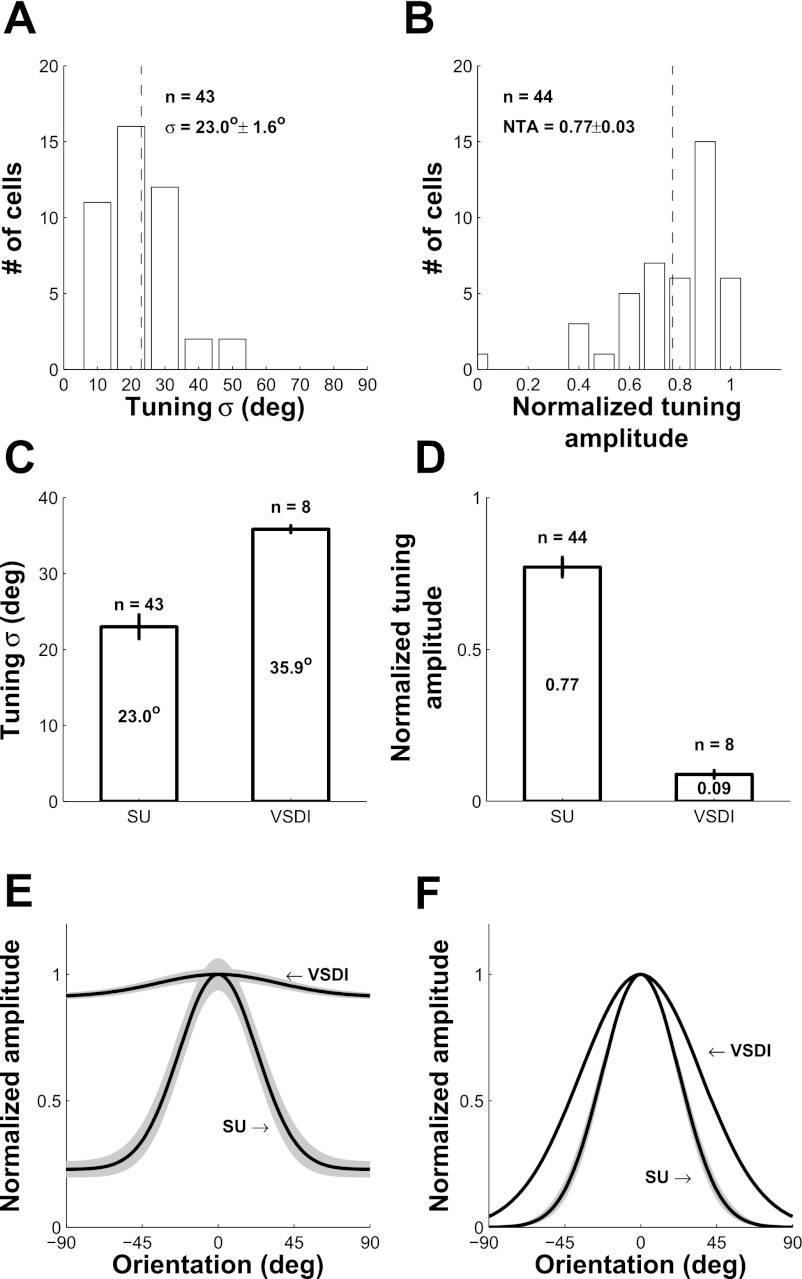
The distributions of the orientation tuning widths and normalized tuning amplitudes across the 44 recorded V1 neurons are shown in Fig. 7, A and B (1 neuron with a flat orientation tuning curve for which the estimated tuning width was ∼90° was excluded from the histogram of orientation tuning widths). The average orientation tuning width of single V1 neurons is 23.0 ± 1.6° (Fig. 7C, left bar), consistent with previous studies (De Valois et al. 1982; Nauhaus et al. 2008; Vogels and Orban 1990). The average normalized tuning amplitude is 0.77 ± 0.03 (Fig. 7D, left bar).

Fig. 7.

Average orientation tuning properties of SU and VSDI responses in V1. A and B: histogram of tuning width σ and normalized tuning amplitude, respectively, for single V1 neurons. One unit was untuned (NTA ∼ 0; σ ∼ 90°) and was removed from A. C and D: bar histogram of average tuning width σ and average NTA, respectively, for SU and VSDI. E: average normalized orientation tuning curves for SU and VSDI including the untuned response. Shaded area represents ±SE. F: same as E but with untuned responses removed.

Orientation tuning of VSDI signals in V1.

Our next goal was to estimate the average orientation tuning curve of VSDI signals. To measure reliable VSDI signals from orientation columns in behaving monkeys, we made two changes to the experimental protocol we used for measuring position tuning with VSDI. First, to measure signals at the submillimeter scale of orientations columns, we zoomed in to a cortical area of 5 × 5 mm² (Fig. 6A), using a magnification that is about three times higher than for position tuning measurements (where our goal was to have a large field of view; Fig. 2B). Second, to measure the weaker orientation-specific VSDI signals, we changed our visual stimulation protocol from 2-Hz stimulus presentation (200 ms on and 300 ms off) to 5-Hz stimulus presentation (60 ms on and 140 ms off).

Increasing the temporal frequency of the visual stimulation from 2 to 5 Hz provided a dramatic increase in the signal-to-noise ratio (S/N) of the VSDI signals. Figure 5 shows a comparison of VSDI responses to stimuli flashed at 2 and 5 Hz. The VSDI signals display clear response modulations at stimulus frequency (Fig. 5, A and B, top) as expected for flashed stimuli, with a clear peak at 2 Hz (Fig. 5A, middle) and at 5 Hz (Fig. 5B, middle). The amplitude of the response tended to be lower in the 5-Hz presentation. However, because the noise in the VSDI signal decreases with frequency (see dashed line in Fig. 5, A and B, middle) (see also Benucci et al. 2007), the d′, or S/N, for 5-Hz presentation was about three times higher than for 2-Hz presentation (Fig. 5, A and B, bottom, and Fig. 5C). In the following analysis of VSDI orientation tuning, we computed the 5-Hz Fourier amplitude at each pixel to obtain the spatial response map for each orientation condition. As shown below, the higher magnification and improved S/N allowed us, for the first time, to measure reliable orientation selective signals with VSDI in behaving monkeys.

To estimate the average orientation tuning curve of VSDI signals, we calculated the spatial response maps to sine-wave gratings at 12 evenly spaced orientations (spatial frequency, 2 cpd; contrast, 100%). To determine the spatial scale of the orientation selective signals, we first computed the 1-D amplitude spectrum of the response maps to single orientations by radially averaging the 2-D amplitude spectrum of each orientation map and then averaging the 1-D amplitude spectra across the 12 orientations (Fig. 6B). Orientation-selective signals produced a clear peak at ∼1.2 cycles/mm (corresponding to a peak period of ∼0.83 mm), consistent with previous studies of orientation maps in macaque V1 (Blasdel and Salama 1986; Hubel and Wiesel 1968; Obermayer and Blasdel 1993). To focus on the spatial scale of the orientation columns, we selected a range of spatial frequencies based on the average 1-D amplitude spectrum (dashed vertical lines in Fig. 6B) of 0.8–3 cycles/mm, corresponding to elements with a period of 0.33–1.25 mm. Figure 6C shows the pattern of V1 responses elicited by gratings at 4 of the 12 orientations after spatial filtration. The maps display small submillimeter patches, with bright patches responding above average to the given orientation and dark patches responding below average. To determine whether these patches reflect orientation columns, we computed the correlation between pairs of maps as a function of their stimulus orientation difference (Fig. 6E). If these maps reflected filtered noise rather than orientation columns, the correlations between pairs of maps should be close to zero and independent of the orientation difference. Instead, the correlations between two maps drop systematically as the orientation difference increases, reaching a near-zero value when the two orientations differ by 45° and a maximally negative value of −0.76 for an orientation difference of 90°. These results demonstrate that the obtained response maps capture the systematic representation of orientation across the cortical surface in V1. The function relating orientation difference to map correlations (Fig. 6E) becomes flatter when lower (0.2–3 cycles/mm; red) or higher spatial frequencies (0.8–5 cycles/mm; blue) are included in the response maps, indicating that most orientation-selective signals in macaque V1 are represented at the scale of 0.8–3 cycles/mm.

Next, we used a vector summation method (Ts'o et al. 1990) to obtain a complete orientation map from these single-orientation response maps (Fig. 6D). In this map, color indicates the preferred orientation at each location, whereas saturation indicates the strength of orientation tuning. A small inset shows the typical pinwheel organization of orientation columns (Bonhoeffer and Grinvald 1991). To the best of our knowledge, these are the first high-quality orientation maps obtained with VSDI in behaving monkeys.

To estimate the average orientation tuning of the VSDI signal from these orientation maps, we computed the orientation tuning curve at each cortical location, aligned all curves to peak at zero, and then averaged these curves across all locations. Figure 6F shows the average orientation tuning curve for the VSDI signal in this example experiment. The orientation tuning width (σ = 35.7°) is broader than the average value for single V1 units, and the NTA (0.09) is much smaller than the average NTA value for single V1 units. The average VSDI orientation tuning curve was not sensitive to the specific spatial filtration range (Fig. 6F, different line color).

Figure 7, C and D (right bars), show the average tuning width and average normalized tuning amplitude across all eight VSDI experiments. As with the example experiment, the average VSDI tuning width (σ = 35.9°) is significantly larger than for single V1 neurons (P = 0.03; t-test), whereas the average NTA is much smaller than for single V1 neurons (P < 0.001; t-test). Figure 7E shows the average normalized orientation tuning curves of VSDI and single V1 neurons, whereas Figure 7F shows the average normalized tuning curves after removal of the untuned response. Overall, the average tuning curves of VSDI signals and single V1 neurons are dramatically different.

Computational model of the relationship between VSDI signals and spiking activity of neural populations.

Our results show large and systematic differences between the average tuning properties of SU spiking activity and VSDI signals in V1. As discussed above, two factors are likely to contribute to these differences. First, because membrane potential tends to be more broadly tuned and less selective than spiking activity in single neurons, any contribution of subthreshold responses to VSDI signals will lead to broader and less selective VSDI responses. Second, the spatial integration area of VSDI signals could lead to broader and less selective VSDI responses.

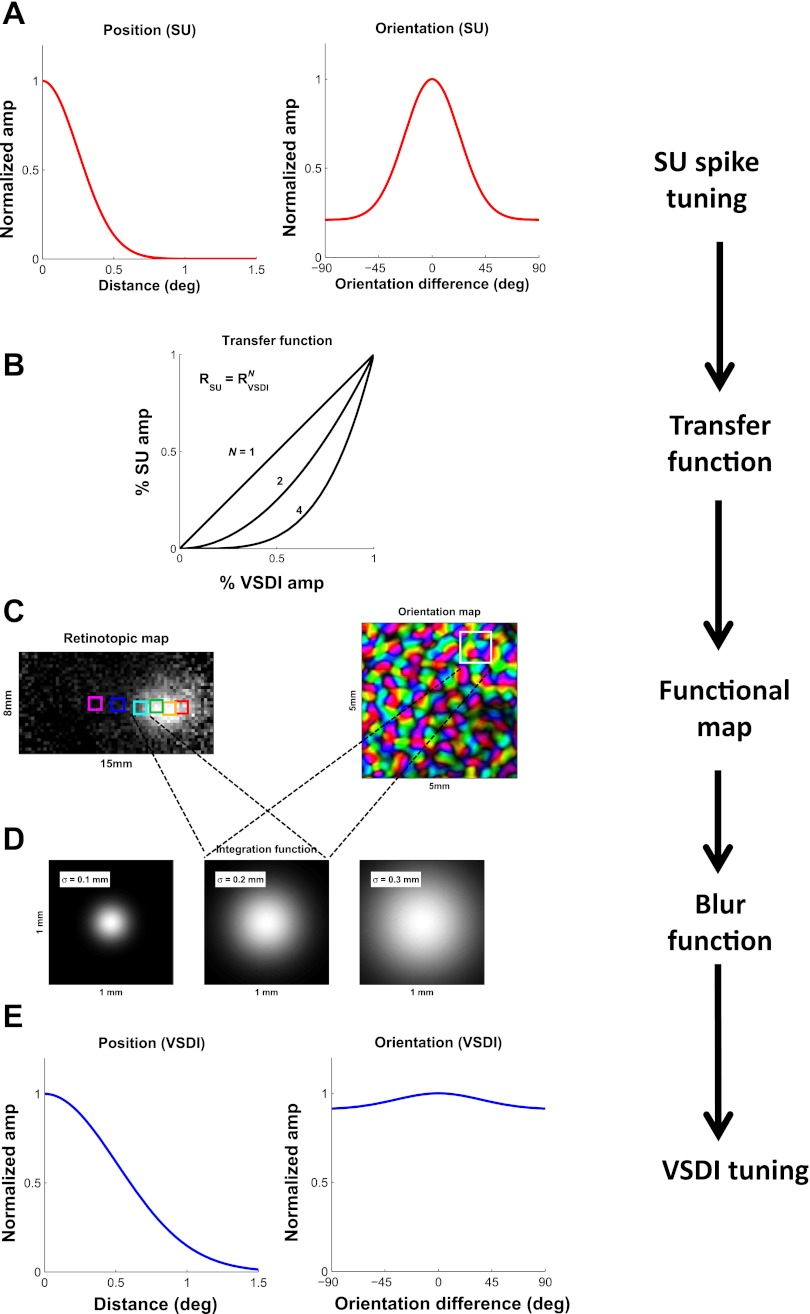
To understand how these two factors are expected to influence the tuning properties of VSDI signals, we developed a simple computational model that describes the relationship between spiking activity of neural populations and VSDI signals in V1. The model, which is illustrated schematically in Figure 8, starts with the average spiking activity tuning curves of single V1 neurons (A) and ends with the predicted average VSDI tuning curves (E). It takes into account the structure of the V1 topographic maps for space and orientation (Fig. 8C). Finally, the model allows one to vary parametrically (as described below) the assumptions regarding the relative contribution of sub- and suprathreshold responses to VSDI signals (Fig. 8B) and the VSDI integration area (Fig. 8D) and to examine how these two factors influence the predicted average VSDI tuning properties.

Fig. 8.

Schematic representation of our model of the relationship between average VSDI signals and average spiking activity. A: the model starts with the average SU tuning curve for position (left) and orientation (right). B: the local VSDI responses at each cortical location are obtained based on the nonlinear relationship between average SU spiking activity and local VSDI signals. This relationship is assumed to be consistent with a power law. The exponent N is the 1st of the 2 free parameters of the model. The graph shows 3 possible values for N: N = 1, a linear relationship, consistent with VSDI being dominated by spiking activity; N = 4, similar to the relationship between average membrane potential and spike rate in single V1 neurons, consistent with VSDI being dominated by subthreshold membrane potential; and N = 2, intermediate between the 2 extremes. C: the predicted spatial pattern of VSDI responses before spatial integration is computed based on the functional maps for position (retinotopy; left) and orientation (right). The squares in each map represent a reference area of 1 × 1 mm². D: to model the effect of the VSDI spatial integration, the predicted VSDI response at each location is computed as the weighted sum of the responses at neighboring locations, with Gaussian weights having a space constant σ_Int. σ_Int is the 2nd free parameter of the model. Three values of σ_Int are indicated schematically by the 3 Gaussians. Note that the size of the squares in D is 1 × 1 mm², the same as the squares in C. The 1 × 1 mm² is small relative to the scale of the retinotopic map (C, left) but large relative to the scale of the orientation map (C, right). E: predicted average VSDI tuning curve for position (left) and orientation (right) is obtained by aligning the predicted tuning curves from all locations to peak at 0 and averaging across locations.

We start by considering the expected effect of the relative contribution of spikes vs. subthreshold responses to VSDI signals. Intracellular recording experiments have demonstrated that the relationship between average membrane potential and firing rate in individual cortical neurons can be described by a power law of the form

$$R_{\text{SU}}=k{\left[V_m-V_0\right]}_{+}^N$$ (1)

where R_SU is the average firing rate in a short temporal interval, k is a constant, V_m is the average membrane potential, V₀ is the average membrane potential below which the neuron does not spike, [ ]₊ represents rectification, and N is an exponent (typically in the range of 3–4 for single V1 neurons) (Anderson et al. 2000; Priebe et al. 2004). This relationship provides a convenient way to model the contribution of spikes vs. subthreshold responses to VSDI signals. Thus, in our model, the transfer function that relates average firing rate and average VSDI signal is given by

$$R_{\text{SU}}=k{\left(R_{\text{VSDI}}\right)}^N$$ (2)

where R_VSDI is the average normalized VSDI signal. In other words, the model assumes that the average firing rate of a population of neurons in a short temporal interval is proportional to the average VSDI signal in the corresponding region to the power of N. If the VSDI signal reflected only spikes, the relationship between the VSDI signal and spiking activity would be linear (Fig. 8B, N = 1). If, on the other hand, the VSDI signal reflected only subthreshold membrane potential, the relationship of the VSDI signal to spiking activity would match the average relationship between membrane potential and spikes in single neurons (Fig. 8B, N = ∼4). Different relative contributions of spiking vs. subthreshold responses to the VSDI signal can therefore be approximated by the exponent N of the power function, which is the first of the two free parameters of our model.

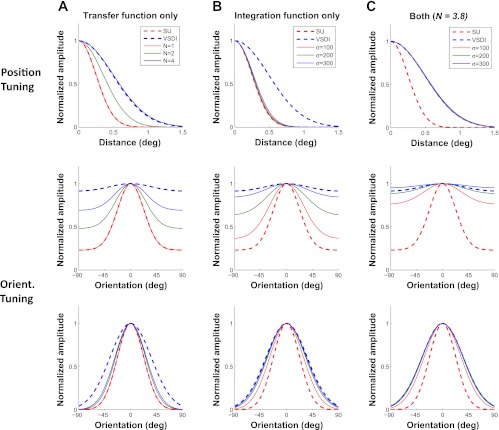
To show how this relative contribution is expected to affect the tuning properties of VSDI responses, Fig. 9A, top, shows the expected width of the VSDI position tuning curve for different values of the exponent of the VSDI-to-spikes transfer function. As the exponent increases from 1 (i.e., dominant spikes) to 4 (i.e., dominant subthreshold synaptic activity), the expected VSDI position tuning curve becomes wider. Specifically, for an exponent N = 4, the expected VSDI position tuning curve is twice as wide as the curve for spiking activity, as observed in our VSDI measurements (Fig. 3A).

Fig. 9.

Model predictions. A: tuning curves for SUs (dashed red) and VSDI (dashed blue) and predicted VSDI tuning curves based on the nonlinear transfer function with 3 possible values of the exponent N (solid curves). Top, position tuning; middle, orientation tuning with the untuned response; bottom, orientation tuning with the untuned response removed. B: same as A, but showing predicted VSDI tuning functions for 3 different values of the VSDI integration area. C: same as B, but showing predicted VSDI tuning curves after assuming that VSDI signals are dominated by subthreshold responses (N = 3.8) while varying the VSDI integration area.

Similarly, as the exponent N increases from 1 to 4, the predicted VSDI orientation tuning amplitude drops (Fig. 9A, middle), but even for a value of 4, the predicted orientation tuning amplitude is much higher than the observed VSDI tuning amplitude. Finally, to better examine the orientation tuning width, Fig. 9A, bottom, shows the normalized orientation tuning curves after the untuned response has been removed. As the exponent N increases from 1 to 4, the predicted VSDI orientation tuning curve becomes wider (Fig. 9A, bottom), but it remains far narrower than the observed VSDI orientation tuning curve. The exponent has a weaker effect on orientation tuning width than on position tuning width because the average orientation tuning curve of single V1 neurons has a significant untuned component (Fig. 7E). These results show that although a dominant contribution of subthreshold responses to VSDI signals could account for the observed VSDI position tuning curve (Fig. 9A, top), it is insufficient, by itself, to account for the observed VSDI orientation tuning curve (Fig. 9A, middle and bottom).

We next consider the effect of the VSDI integration area. Two factors contribute to the size of this area. First, due to light-scattering properties of cortical tissue and blurring introduced by the optics, some of the fluorescent signal arriving to the camera at a given pixel originates from cortical locations corresponding to nearby pixels. Computational analysis (Polimeni et al. 2005) and experimental measurements (Petersen et al. 2003) suggest that this spread has a space constant of ∼0.1 mm. A second, and probably more dominant, contribution comes from the horizontal spread of dendrites and axons in the cortex (e.g., Lund 1988).

To capture the effect of the VSDI integration area on the tuning of VSDI responses, we modeled the VSDI signals at a given location as the sum of responses of a population of nearby neurons, weighted by a 2-D Gaussian with a space constant σ_Int centered at that location (as in Katzner et al. 2009). Therefore, the second free parameter of our model is the space constant σ_Int. We start by examining the effect of the VSDI integration area in isolation, initially ignoring the possible contribution of subthreshold responses to VSDI signals (i.e., assuming that N = 1). We later combine these two factors.

To estimate the expected VSDI tuning curve for a given stimulus feature, say orientation, as a function of σ_Int, we first computed the expected spatial pattern of spiking responses to each stimulus orientation. To do this, we applied the average SU orientation tuning curve at each location, adjusting the preferred orientation based on the corresponding orientation map (Fig. 8C). The spiking response to a given stimulus orientation at each location was assumed to depend only on the difference between stimulus orientation and the preferred orientation at this location. To obtain the expected pattern of VSDI response following spatial integration, we applied the Gaussian weights at each location, assuming a particular value for σ_Int (Fig. 8D). By combining the predicted responses to all stimulus orientations, we obtained an orientation tuning curve at each location. Finally, we aligned the tuning curves to peak at zero and averaged across all locations to obtain the predicted VSDI orientation tuning curve (Fig. 8E).

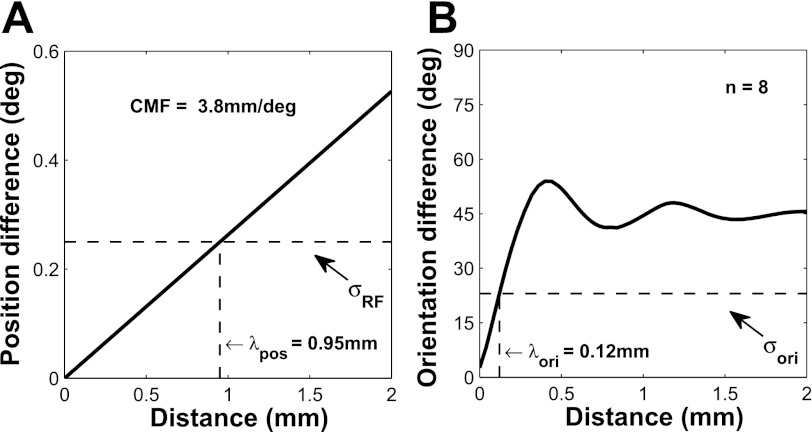
Before examining the effect of the VSDI integration area, we investigated more quantitatively the spatial scales of the position and orientation maps in macaque V1. Because VSDI signals at each location represent the integrated activity across a population of neurons, and because the preferred parameter of V1 neurons changes systematically across the cortical surface, VSDI signals from each location receive contributions from neurons with different preferred parameters. This spatial integration, or blurring, is expected to lead to changes in the tuning properties of the VSDI signals relative to the average tuning of individual V1 neurons. The extent to which a given integration area will affect the relative tuning of VSDI responses and SU activity depends on the rate at which the preferred parameter changes across the cortical surface. This rate can be characterized by a length constant, λ_map (in mm), which is equal to the average horizontal distance that one has to travel in order for the preferred parameter (either orientation or position) to shift by one tuning width.

To estimate λ_position, we computed from our position tuning VSDI measurements the average slope of the curve that relates distance in visual space to distance in the cortex (Fig. 10A). This slope is equal to the average cortical magnification factor (3.8 mm/°) at eccentricities of 1.8°–3.4°. We then estimated λ_position as the cortical distance that corresponds to the average SU position tuning width and obtained a value of 0.95 mm. Recent results from our laboratory indicate that λ_position, which is related to the size of the cortical point image (McIlwain 1986), is invariant with eccentricity in parafoveal V1 (Palmer et al. 2012).

Fig. 10.

Change in preferred parameters as a function of cortical distance for position (A) and orientation (B) in macaque V1. Note that in A, the y-axis is in degrees of visual angle, whereas in B it is in degrees of polar angle. The dashed horizontal line indicates the corresponding average tuning width of V1 neurons, whereas the dashed vertical line indicates the corresponding cortical distance λ, which is the length constant of each map. CMF, cortical magnification factor; ori, orientation; pos, position.

To estimate λ_orientation, we computed the average difference in preferred orientation between all pairs of points in our orientation maps as a function of their cortical distance (Fig. 10B). We then estimated λ_orientation as the cortical distance that corresponds to the average SU orientation tuning width. In the case of the orientation map, λ_orientation is ∼0.12 mm (Fig. 10B), almost an order of magnitude smaller than λ_position. Therefore, a VSDI integration area of σ_Int = 0.2 mm will cause neurons with very different preferred orientations to contribute to VSDI responses at a given location, whereas the same integration area will cause neurons with nearly identical position tuning curves to contribute to VSDI responses at the same location.

These results suggest that the average VSDI orientation tuning curve should be strongly affected by spatial integration areas with σ_Int in the range of 0.1–0.3 mm, whereas the average VSDI spatial tuning curve should be nearly invariant to integration areas within this range. Consistent with these predictions, the VSDI integration area has a large impact on the predicted VSDI orientation tuning curve (Fig. 9B, middle and bottom) but has negligible impact on the predicted VSDI position tuning curve (Fig. 9B, top). Specifically, increasing σ_Int from 0.1 to 0.3 mm leads to a large broadening of the predicted VSDI orientation tuning curve and a large reduction in the VSDI orientation tuning amplitude, but even an integration area with σ_Int of 0.3 mm is not sufficient to account for the observed VSDI orientation tuning curve.

So far, we had considered the effects of the VSDI integration area and the relative contribution of spikes vs. subthreshold responses to VSDI signals separately. To consider the combined effect of both factors, we performed a bootstrap analysis on our experimental results (see methods), estimating simultaneously the two free parameters, N and σ_Int. We applied this analysis independently to our orientation and position tuning data. The results are shown in Table 1. Across the two stimulus dimensions, VSDI tuning curves are consistent with an exponent that is close to 4. These results suggest that VSDI signals are dominated by subthreshold synaptic activity. In addition, the analysis shows that the VSDI orientation tuning curves are consistent with a VSDI integration area with σ_Int of ∼230 μm. As discussed above, because the spatial scale of the retinotopic map is much larger than the VSDI integration area, our position tuning results do not constrain the estimate of the VSDI integration area but provide a highly constrained estimate of the power function exponent. Figure 9C shows that, using N = 3.8 and σ_Int between 200 and 300 μm, the predicted VSDI tuning properties are consistent with the observed ones.

Table 1.

Estimated model parameters

	Power Function Exponent N	Integration Area σ, μm
Position tuning	3.9 ± 1.0
Orientation tuning	3.8 ± 1.0	233 ± 36

DISCUSSION

The goal of the current study was to address two fundamental questions regarding the nature of VSDI signals and their relation to the average spiking activity of local populations of cortical neurons. To address these questions, we developed a simple computational model that allows one to predict the tuning properties of VSDI signals from the average tuning properties of single cortical neurons and from the underlying functional maps. To constrain this model, we measured VSDI signals and spiking activity of single neurons from V1 of behaving monkeys and compared the tuning properties of these two signals across two stimulus dimensions: orientation and spatial position. Our results suggest that VSDI signals in the cortex are dominated by subthreshold synaptic activity and receive little contribution from spiking activity. In addition, our results suggest that VSDI signals at a given cortical location are equal to a weighted sum of neural responses at neighboring locations, with Gaussian weights with radius (σ_Int) of ∼230 μm centered at that location. These results help interpret a large body of work that used VSDI to measure neural population responses in the cortex in vivo (e.g., Arieli et al. 1996; Benucci et al. 2007; Chen et al. 2006, 2008; Grinvald et al. 1994; Huang et al. 2010; Jancke et al. 2004; Kenet et al. 2003; Petersen et al. 2003; Seidemann et al. 2002; Sharon and Grinvald 2002; Sit et al. 2009; Slovin et al. 2002; Tsodyks et al. 1999; Yang et al. 2007; for review, see Grinvald and Hildesheim 2004). In addition, our findings could help in designing future VSDI experiments.

We found that VSDI signals are substantially less selective than the average spiking activity of single V1 neurons across the two stimulus dimensions. The difference in position tuning width between VSDI signals and SU spiking activity is comparable to differences between RF size of sub- and suprathreshold responses in individual V1 neurons (e.g., Bringuier et al. 1999; Nowak et al. 2010). With respect to orientation tuning, VSDI signals are more broadly tuned and contain a much larger untuned component than spiking activity of single V1 neurons. Although membrane potential in single V1 neurons is also more broadly tuned and contains a larger untuned component than spiking activity (for review, see Priebe and Ferster 2008), VSDI signals are substantially less orientation selective than SU membrane potentials. The additional reduction in orientation selectivity of VSDI signals relative to membrane potential of single neurons can be attributed to the spatial integration of VSDI, which combines neural signals from a population of neurons with different preferred orientations at each cortical location.

Our results suggest that the VSDI integration area has a σ_Int of ∼230 μm. Recent studies used a similar approach to estimate the integration area of local field potentials (LFP) (Katzner et al. 2009; Xing et al. 2009). Whereas the results of Katzner et al. (2009) suggest that the LFP signals have an integration radius of <100 μm and are therefore substantially more local than the VSDI signals, the results of Xing et al. (2009) suggest that the LFP integration radius is comparable to that of the VSDI signals. Additional studies are necessary to better understand the relationship between the VSDI and LFP signals.

Our results show that the relationship between VSDI signals and spiking activity is well captured by a power function with an exponent of ∼4. Similar power functions with comparable exponents have been obtained when examining the relationship between average membrane potential and average spike rate in single V1 neurons (Anderson et al. 2000; Priebe et al. 2004). Several studies, however, have demonstrated that the relationship between membrane potential and spike rate in single neurons depends on stimulus contrast (Anderson et al. 2000; reviewed in Priebe and Ferster 2008). Specifically, for SUs, the exponent of the power function tends to decrease at low contrast, consistent with an increase in response gain at low contrast. Therefore, one would predict a similar change with contrast in the power function that relates VSDI signals to spiking activity. Previous results regarding the spatial spread of SU responses and VSDI signals are consistent with this prediction. Specifically, our previous work demonstrated that the spatial spread of VSDI responses to a small oriented stimulus is largely invariant to stimulus contrast (Chen et al. 2006, 2008; Sit et al. 2009). In contrast, multiple studies have demonstrated that the size of the suprathreshold RF of single V1 neurons increases substantially at low contrast relative to high contrast (e.g., Cavanaugh et al. 2002; Sceniak et al. 1999). These results imply that the difference in response spread between VSDI signals and spiking activity is likely to become smaller at lower contrast, consistent with a reduction in the exponent of the power function that relates VSDI signals to spiking activity.

VSDI is a powerful technique that allows one to measure neural population responses simultaneously over large cortical regions with millisecond temporal resolution. The integration area of VSDI reported here affects its spatial resolution. However, it is important to note that the integration area does not imply an inability of this technique to resolve neural signals at a much finer spatial scale. Our previous study of the retinotopic map in macaque V1 (Yang et al. 2007) and the detailed orientation maps reported here (Fig. 6) demonstrate that one can use VSDI in behaving animals to resolve neural responses that vary at a spatial scale of ∼100 μm.

VSDI has several advantages over multiple-electrode electrophysiological techniques as a tool for measuring neural population responses. First, in contrast to the sparse sampling afforded by electrode arrays, VSDI provides a complete and dense coverage of the imaged area. Second, in contrast to the rigid nature of electrode arrays, the field of view of VSDI and the pixel size can be easily adjusted by changing the lens combination on the imaging camera, therefore providing high flexibility in studying responses from an entire population of neurons over regions from several square millimeters to several square centimeters. A major limitation of VSDI has been the lack of understanding of the relationship between VSDI signals and neural population responses at the spiking activity level. The current study provides a first step in addressing this important question.

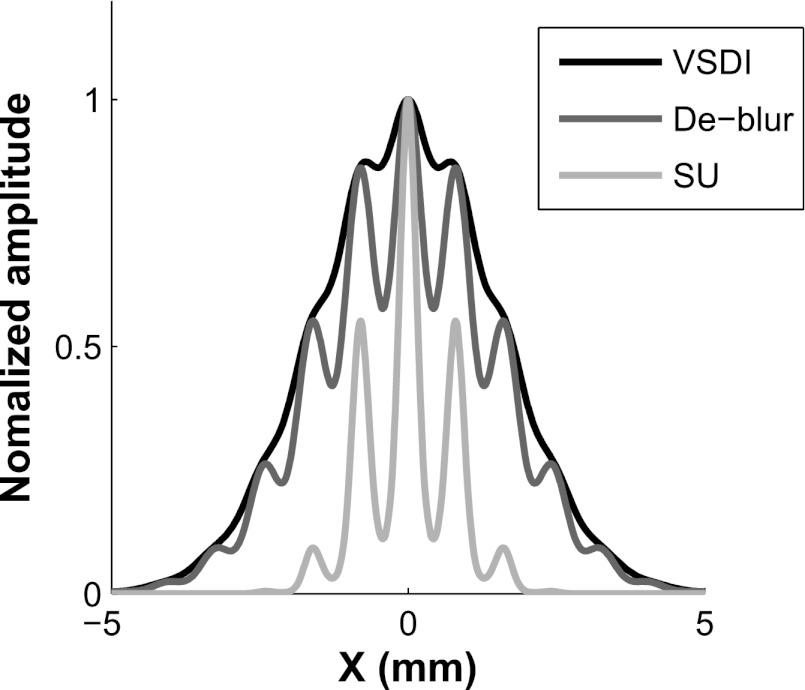
Our finding that the same model parameters can account for the differences between tuning properties of VSDI and SU spiking activity across two different stimulus dimensions (position and orientation) raises the possibility that, across a range of stimulus parameters, one could use our computational model and estimated model parameters to predict the average pattern of population responses at the spiking level from the VSDI signals, and vice versa. To illustrate the potential of this approach, Fig. 11 shows a 1-D slice through a simulated pattern of VSDI signals in response to a small oriented Gabor patch (black curve). Using our model, we can remove the effect of VSDI spatial integration (by deconvolving the VSDI signals with the proper kernel) to obtain the predicted pattern of neural responses at the level of membrane potentials (dark gray curve). Compared with the VSDI signals, the predicted response at the level of membrane potential has a substantially smaller orientation untuned component but a similar spatial extent. Finally, by applying the power function describing the relation between VSDI signals and spiking activity (Eq. 2), we obtain an estimate of the population response at the spiking level (light gray curve). This step leads to a substantial reduction in the spread of the population response and an additional decrease in the orientation untuned component of the population response relative to the VSDI signals. This analysis demonstrates the potential utility of applying this model to VSDI signals (see also Fig. 7 in Chen and Seidemann 2012). An important goal for future experiments is therefore to test the validity of this model for other stimulus dimensions in V1, and for other cortical areas where information is organized topographically.

Fig. 11.

A synthetic example illustrating how our model could be used to predict V1 population responses at the spiking activity level from the measured VSDI responses. The black curve shows a simulated 1-D slice through VSDI responses to an oriented Gabor stimulus centered at position 0 at the preferred orientation for that location. The cortical response has 2 components, a large Gaussian envelope component representing the contrast envelope of the Gabor stimulus (σ = 1.5 mm) and a higher spatial frequency pattern representing the cortical columns (∼1.2 cycles/mm). The predicted pattern of responses before the spatial integration can be obtained by deblurring the VSDI response with the proper kernel (dark gray curve). Note that the overall width of the response remains the same, but the magnitude of the modulations at the columnar scale increases severalfold. The predicted pattern at the level of spiking activity (light gray curve) can be obtained by applying the nonlinear transfer function relating VSDI signals to spiking activity (Eq. 2). Note that the response spread is reduced by a factor of 2, and the modulations at the columnar scale increase even further.

GRANTS

This work was supported by National Eye Institute Grants EY-016454 and EY-016752.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: Y.C., C.R.P., and E.S. conception and design of research; Y.C., C.R.P., and E.S. performed experiments; Y.C., C.R.P., and E.S. analyzed data; Y.C., C.R.P., and E.S. interpreted results of experiments; Y.C., C.R.P., and E.S. prepared figures; Y.C., C.R.P., and E.S. drafted manuscript; Y.C., C.R.P., and E.S. edited and revised manuscript; Y.C., C.R.P., and E.S. approved final version of manuscript.