Abstract
When saccades systematically miss their visual target, their amplitude adjusts, causing the position errors to be progressively reduced. Conventionally, this adaptation is viewed as driven by retinal error (the distance between primary saccade endpoint and visual target). Recent work suggests that the oculomotor system is informed about where the eye lands; thus not all “retinal error” is unexpected. The present study compared two error signals that may drive saccade adaptation: retinal error and prediction error (the difference between predicted and actual postsaccadic images). Subjects made saccades to a visual target in two successive sessions. In the first session, the target was extinguished during saccade execution if the amplitude was smaller (or, in other experiments, greater) than the running median, thereby modifying the average retinal error subjects experienced without moving the target during the saccade as in conventional adaptation paradigms. In the second session, targets were extinguished at the start of saccades and turned back on at a position that reproduced the trial-by-trial retinal error recorded in the first session. Despite the retinal error in the first and second sessions having been identical, adaptation was severalfold greater in the second session, when the predicted target position had been changed. These results argue that the eye knows where it lands and where it expects the target to be, and that deviations from this prediction drive saccade adaptation more strongly than retinal error alone.
Keywords: saccade, plasticity, eye movements
we observe the world by making saccadic eye movements, which bring the fovea onto the object of interest. Because saccades are too rapid to be guided by vision, their accuracy is maintained by saccadic adaptation. When saccades systematically miss their visual target, as in subjects with extraocular muscle impairments, saccade amplitude adapts and the targeting errors diminish progressively over days (Abel et al. 1978; Kommerell et al. 1976; Optican and Robinson 1980; Scudder et al. 1998). In the laboratory, saccadic adaptation can be evoked within minutes by displacing the saccade target during movement execution, so that when the saccade lands the fovea is not on the target. Although such intrasaccadic target steps are usually not noticed (Bridgeman et al. 1975), repetition of these trials results in a progressive modification of saccadic amplitude such that it eventually becomes appropriate to the postsaccadic target position (McLaughlin 1967; reviewed by Hopp and Fuchs 2004 and Pélisson et al. 2010).
The error signals guiding saccadic adaptation have been the object of some debate. Because forward intrasaccadic steps cause saccade amplitude to increase whereas backward intrasaccadic steps cause saccade amplitude to decrease, the most obvious candidate error signal is the retinal distance of the target from the fovea from after each saccade (“retinal error”). This attribution is supported by the fact that saccade amplitude reaches an asymptote as adaptation brings the eyes close to the new target position. Consequently, retinal error has been widely considered to be the primary or the only error signal guiding saccadic adaptation (Havermann and Lappe 2010; Hopp and Fuchs 2004; Noto and Robinson 2001; Wallman and Fuchs 1998). Implicit in the designation of retinal error as the driver of saccadic adaptation is the presumption that the oculomotor system does not know, or does not care, where exactly the saccade lands, but only cares how far it is from the target. A complication with regarding retinal error as the sole error signal is the fact that normal saccades usually are hypometric (undershoot their target), and if this is corrected by manipulating the target to be on the fovea after saccades, the saccade amplitude is reduced, as though the goal state of saccade adaptation is to maintain this small retinal error (Henson 1978; Robinson et al. 2003; but see Havermann and Lappe 2010).
Alternatively, motor-related information could provide an error signal if the oculomotor system kept track of the direction and amplitude of corrective saccades that followed the primary saccade. Thus if primary saccades were consistently followed by a corrective saccade in the opposite direction, the oculomotor system could infer from this “motor error” that the saccadic gain (the ratio of primary saccade amplitude to target eccentricity) was too high. However, eliminating such corrective saccades does not prevent adaptation (Noto and Robinson 2001; Wallman and Fuchs 1998), demonstrating that motor error is neither necessary nor sufficient to drive adaptation.
Another possible error signal is prediction error, in which the predicted postsaccadic image is compared with the actual postsaccadic image. Differences between the predicted and actual postsaccadic images could drive the system to adapt to eliminate future errors. Several findings argue in favor of saccade adaptation being driven by prediction error, rather than simply by the postsaccadic visual error (“visual comparison model”; Bahcall and Kowler 1999, 2000). Deubel (1991) showed that an intrasaccadic shift of a large random grating, containing a transient target that could not be identified after the saccade, resulted in saccade adaptation, suggesting that there was a low-level mechanism for visual comparison across a saccade. More directly, when subjects were instructed to make saccades 75% of the way to a target and the target was stepped back by <25%, the saccade amplitude decreased, even though the target lay beyond the fovea after the saccades (Bahcall and Kowler 2000), a result similar to that of Wong and Shelhamer (2010). Furthermore, adaptation occurs when subjects make saccades to the center of a circular array of dots that makes an intrasaccadic step, even though there is no single stimulus near the fovea (Bahcall and Kowler 2000). Finally, the temporal characteristics of the postsaccadic image are crucial to adaptation. Optimal adaptation occurs when the postsaccadic visual information is available within 150 ms after primary saccade end and for at least 80 ms (Bahcall and Kowler 2000; Shafer et al. 2000). Such a time window would not be expected if only the retinal characteristics of the error were important.
The goal of the present study was to directly compare a prediction error signal to a retinal error signal.
We propose that the oculomotor system knows where the saccade lands (Collins 2010; Collins et al. 2009; Ostendorf et al. 2010; Sommer and Wurtz 2004), either from proprioception or from efference copy, and that it is thus able to predict the postsaccadic location of the target. We suggest that adaptation is driven weakly by retinal error and is driven more strongly by prediction error—a difference between actual retinal error and the predicted retinal error, which is exactly what the intrasaccadic target step in the saccadic adaptation paradigm causes.
Several computational models have also suggested that prediction error may play a role in saccadic adaptation (Chen-Harris et al. 2008; Dean et al. 1994). Prediction plays a central role in computational models of motor learning by providing the desired state the system is to learn based on deviations from it. In the computational frameworks, forward models generate predictions about the sensory consequences of our movements (Miall and Wolpert 1996; Wolpert and Flanagan 2009). Such internal predictions have been proposed to explain a wide range of phenomena, such as why we cannot tickle ourselves (Blakemore et al. 2000) and the escalation of tactile force that occurs when a subject tries to match the force experienced (Shergill et al. 2003). By generating an internal prediction of the consequences of a movement, forward models may also participate in learning by providing the desired consequences to be compared with the actual postmovement state of the world. Any discrepancy between the desired and actual states (prediction errors) could then constitute the basis for adapting future behavior.
The present work compares the potency of retinal error and prediction error as guides for saccadic adaptation. In the first of two experimental sessions we produced postsaccadic retinal error without prediction error by turning off the target during saccades larger than the median amplitude, such that the target provided postsaccadic visual feedback only after saccades smaller than the median (“Small-On” experiments). In this situation, the target was most often beyond the fovea (“positive retinal error”), as would occur with a forward intrasaccadic step. In a complementary experiment, during the first session we extinguished the target only after saccades smaller than the median amplitude, such that the target provided postsaccadic visual feedback only after saccades larger than the median (“Large-On” experiments), producing retinal errors much like those that would occur with a backward intrasaccadic step (Fig. 1A). Thus, at the end of the first session, we had a list of retinal errors in the order subjects experienced them. In the second session, days later, for each subject we reproduced his/her retinal errors of session 1, trial by trial, but this time retinal errors were obtained by stepping the target relative to the saccade endpoint. Thus retinal error was identical between the two sessions, but in the first session there was no prediction error (the target never stepped) while in the second session there was prediction error because of the target steps. If retinal error alone drives adaptation, then the amount of adaptation should be equivalent for sessions 1 and 2. Any difference between the two sessions would be attributable to prediction error.
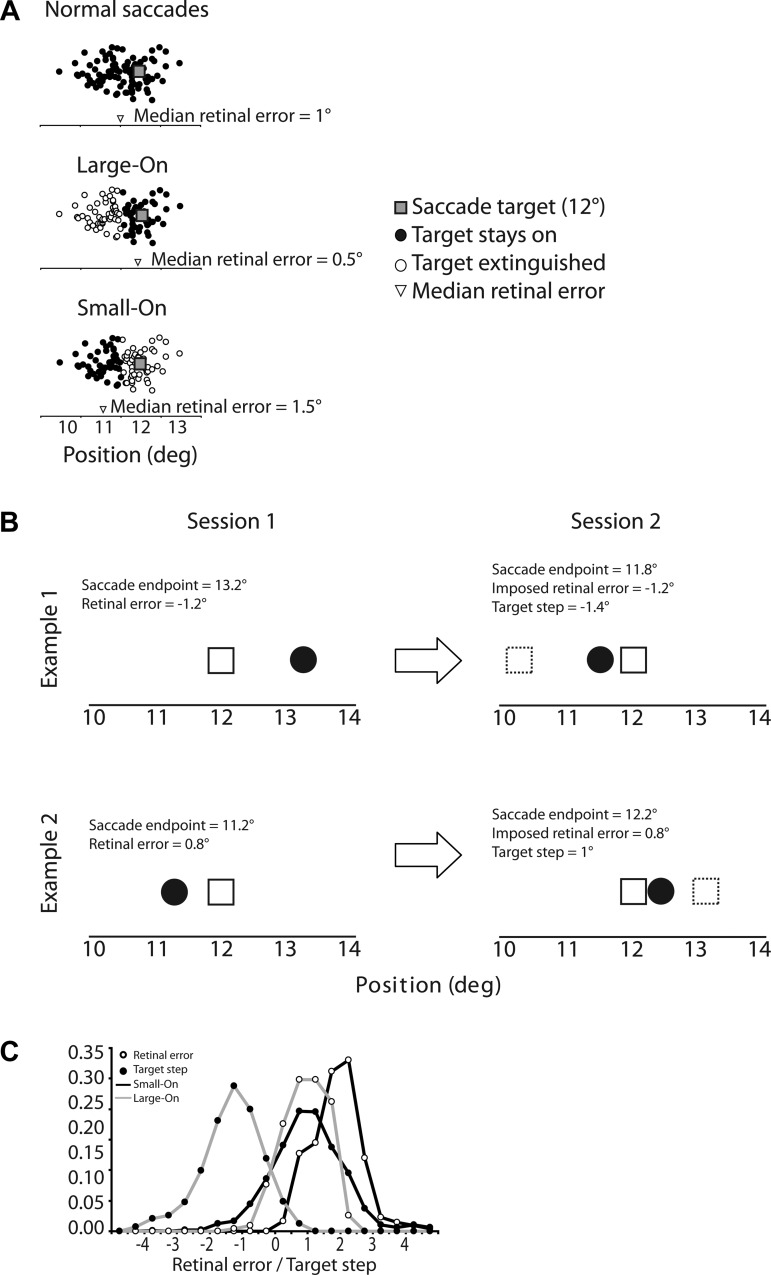
Fig. 1.
A: schematic illustration of amplitude-dependent visual feedback. In normal saccades (top), endpoints tend to undershoot the visual target. Thus the median retinal error tends to be positive. In the “Large-On” condition (middle), the visual target was available after the primary saccade only when its amplitude was larger than the median. Thus the distribution of retinal errors experienced by the subject was smaller than usual. In the “Small-On” condition (bottom), the visual target was available after the primary saccade only when its amplitude was smaller than the median. The distribution of retinal errors experienced by the subject was larger than usual. B: 2 examples of corresponding trials during the 2 sessions. The saccade target (open square) was always at 12°. In the first example (top), in session 1 the saccade endpoint (black dot) on trial n was 13.2°, which corresponds to a retinal error of −1.2°. In session 2, the saccade endpoint on trial n was 11.8°. To obtain a retinal error of −1.2°, the target had to be stepped back to position 10.6° (dashed square), a step of −1.4°. In the second example (bottom), in session 1 the saccade endpoint was 11.2° and retinal error was 0.8°. In session 2, since the endpoint was 12.2°, obtaining a retinal error of 0.8° required stepping the target forward by 1°. C: distribution of retinal errors and target steps in Large-On and Small-On conditions, pooled over all subjects. The zero mark on the x-axis corresponds to the target location; thus a step of 0 means that the target did not step, and a retinal error of 0 means that the saccade endpoint was at the same location as the postsaccadic target.
METHODS
Subjects.
Nine subjects participated in the experiment. Four naive subjects received course credit in exchange for their participation, four volunteered, and one was an author (T. Collins); all gave their informed consent. Five subjects participated in both Large-On and Small-On conditions and four participated in only one, resulting in there being seven subjects in each condition. These experiments were covered by a protocol approved by the Institutional Review Board of the City College of New York.
Stimuli.
Subjects viewed stimuli in a darkened room at a distance of 57 cm while on a chin rest to minimize head movements. Stimuli were generated on a computer running VisionWorks (Vision Research Graphics, Durham, NH) and displayed on a 21-in. monochrome CRT display with a fast phosphor and a vertical refresh rate of 200 Hz (Image Systems, LaFox, IL). Stimuli were 1° × 1° red crosses (3.3 cd/m2) presented on a black background (<0.5 mcd/m2). This setup minimized the potential detection of target steps by subjects, in accordance with saccadic suppression of displacement (Bridgeman et al. 1975). The subject fixated a cross located at horizontal coordinates chosen randomly from −6° to 0° (screen center) and vertical coordinates between −3° (below screen center) and 3° (above). After ∼500 ms, the cross stepped 12° to the right.
Eye movement recording and analysis.
Binocular movements were monitored with an Eyelink 1000 (SR Research, Kanata, ON, Canada) at a 1,000-Hz sampling rate. The Eyelink was calibrated at the beginning of a session. Stimulus presentation and data collection were controlled by a LabVIEW program. On-line saccade detection was based on a 30°/s velocity threshold maintained for two consecutive above-threshold samples; saccade offset was defined as five consecutive below-threshold samples. On-line gain was calculated based on the eye position measured in the final sample. Eye movement traces were subsequently analyzed off-line (saccade onset and offset marked as the first and last points, respectively, above a 10°/s velocity threshold and adjusted by the experimenter). Compared with these more accurate off-line measurements, the on-line saccade amplitudes were 10 ± 2% lower. However, because we used the on-line measurements from session 1 for calculating the retinal error to be presented in session 2, this discrepancy did not bias our results. Saccades with amplitudes smaller than 5.0° and latencies <80 or >500 ms were excluded.
Procedure.
Subjects fixated a red cross. After ∼500 ms, the cross jumped to the target position 12° to the right. Subjects were instructed to follow the cross with an eye movement. Upon saccade onset detection, the cross was extinguished. Upon saccade offset detection, the target either remained off or reappeared depending on the on-line measure of saccade amplitude and condition.
Each subject participated in two sessions. In session 1, subjects ran 50 practice trials in which the target always reappeared and then 50 baseline trials in which the target reappeared on a random 50% of trials. This was followed by 300 test trials in which the extinction/reappearance of the target depended on the on-line median primary saccade amplitude calculated on a 50-sample sliding window. In the Small-On condition, the target reappeared if the on-line gain on that trial was less than the on-line median (all saccades with amplitude greater than the median received no postsaccadic visual feedback). Conversely, in the Large-On condition, the target reappeared if the on-line gain on that trial was greater than the on-line median (all saccades with amplitude smaller than the median received no postsaccadic visual feedback). Target reappearance was ∼12 ms after the saccade ended [a delay too short to interfere with adaptation (Bahcall and Kowler 2000; Bonnetblanc and Baraduc 2007) or to suppress saccadic suppression of displacement (Deubel et al. 1996)]. The 300 test trials were followed by 50 posttest trials in which the target never reappeared. These trials assessed the final adaptation level while minimizing the decay of adaptation (Ethier et al. 2008). Finally, 100 trials in which the target always reappeared were run, whose function was to return amplitude to baseline.
In session 2, 50 practice trials and 50 pretest trials were run as in session 1. In the test epoch (300 trials), reappearance of the target no longer depended on the on-line median. Instead, we reproduced the retinal errors of session 1 trial by trial: In a given test trial n of session 2, we stepped the target relative to the on-line measure of saccade amplitude in that trial by an amount that exactly equaled the retinal error of test trial n of session 1 (Fig. 1B). Thus, in session 2, the order and magnitude of retinal errors experienced in test trials were the same as those produced by the subject in session 1. Test trials were followed by 50 posttest trials as before. The two sessions were separated by at least 48 h.
Because in session 1, on about half the trials (45%), the target did not reappear after the saccade, we arranged for the same to occur on the corresponding trials of session 2. In addition, a small percentage (<1%) of session 1 trials could not be analyzed because of blinks or because the primary saccade was of very small amplitude; therefore, in the corresponding trials of session 2, the targets did not reappear.
Retinal error and target step characteristics.
In the Small-On condition, visual feedback was obtained only after saccades smaller than the median. Because normal saccades tend to be hypometric (i.e., positive retinal error), this means that the retinal errors that were experienced tended to be larger than normal (retinal error went from 1.71 ± 0.54° in the baseline epoch to 1.80 ± 0.51° in the test epoch). In session 2, to reproduce these larger-than-usual errors, the target usually had to be stepped forward, and indeed forward steps occurred in 77 ± 3% of trials (average step size 0.73 ± 0.44°). In the Large-On condition, visual feedback was obtained only after saccades larger than the median, and thus the experienced retinal errors tended to be smaller than usual (closer to the target). Retinal error went from 1.45 ± 0.49° in the baseline epoch to 0.69 ± 0.50° in the test epoch. Therefore, in session 2, to reproduce these smaller-than-usual errors, the target almost always (97 ± 3% of trials) had to be stepped back (average step size −1.66 ± 0.31°). However, despite this difference in the direction of target steps between Small-On and Large-On conditions, because of normal undershoot retinal errors in both tended to be positive (Small-On: 96 ± 3% retinal errors were positive, average 1.8 ± 0.5°; Large-On: 84 ± 17% retinal errors were positive, average 0.69 ± 0.5°). Figure 1C illustrates the distribution of retinal errors and target steps.
Our adaptation procedure differed from conventional adaptation in that it included trials in which the target turned off during the saccade. Bonnetblanc and Baraduc (2007) showed that repeating target-off trials had no effect on saccade gain to target at the eccentricity employed here (12°), although they resulted in amplitude-increasing adaptation for larger saccades (20–30°). Even if the target-off trials had affected the amount of adaptation, our aim was to compare adaptation between session 1 (retinal error only) and session 2 (both retinal and prediction errors); because there was an equivalent number of target-off trials in each session, the potential influence of these trials on adaptation does not affect our findings.
RESULTS
Average saccade latency was normal for visually guided saccades (164 ± 13 ms in the Large-On condition; 169 ± 15 in the Small-On condition). A repeated-measures ANOVA with factors Epoch (baseline vs. posttest) and Session showed no significant effects or interactions in either condition (all F < 1).
In general, we found significant saccadic adaptation both in the sessions in which only retinal error was available (the first sessions) and in those in which the same degree of retinal error was accompanied by a prediction error (the second sessions, in which the target stepped during the saccade). However, the degree of adaptation was severalfold greater when the prediction error was present. Figure 2 shows example adaptation courses of individual subjects. Across subjects, this trend for more adaptation in session 2 was notable (Fig. 3).
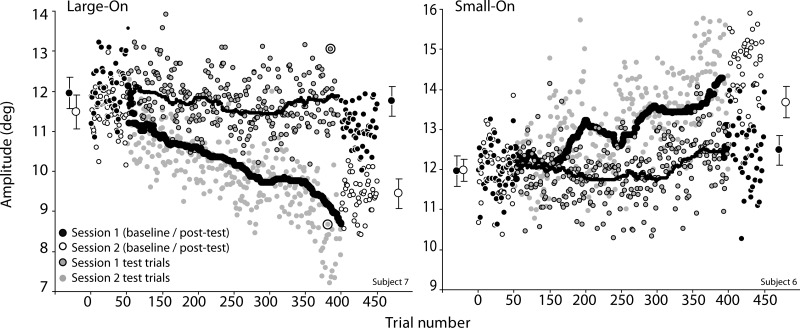
Fig. 2.
Example time courses of adaptation (amplitude as a function of trial). Each point is 1 saccade. Larger symbols with standard deviation error bars on left and right correspond to the mean endpoint in baseline and posttest epochs, respectively. Curves represent the sliding median (n = 50). Recall that in session 1 only saccades below (in the Small-On condition) or above (in the Large-On condition) this median received visual feedback. Note that at trial ∼400 in the Large-On condition (upper circled data point) saccade amplitude in session 1 was 13.1°; because the target was at 12°, this resulted in a retinal error of −1.1°. In session 2 at the same trial number (lower circled data point), the saccade amplitude was 8.7°, so we moved the target to 7.6° to replicate the retinal error seen on session 1.
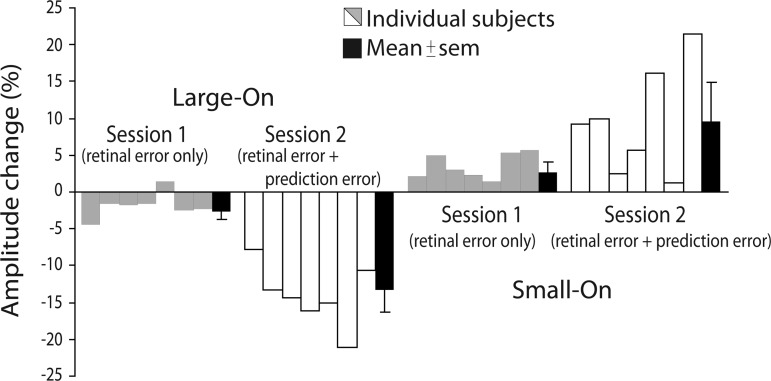
Fig. 3.
Percent amplitude change over the course of adaptation in Large-On (left) and Small-On (right) conditions. The data plotted are the difference between the posttest and baseline open-loop trials (target extinguished upon saccade onset and no reappearance). Gray and white bars are individual subjects; black bars are means ± SE. Percent amplitude change was calculated as % amplitude change = (posttest amplitude − baseline amplitude)/baseline amplitude.
Specifically, in the Large-On condition, the saccade amplitude in session 1 decreased by 2.6% (from 11.82 ± 0.12° to 11.51 ± 0.15°; mean ± SE) between the baseline and posttest epochs [paired t-test, t(6) = 3.9, P < 0.005]. In session 2, the amplitude decreased by 13.3% [from 11.65 ± 0.12° to 10.11 ± 0.12°; t(6) = 9.0, P < 0.001]. This was confirmed by a significant interaction between Epoch and Session [F(1,6) = 30.7, P < 0.001]. Both Epoch and Session main effects were also significant [F(1,6) = 149.8, P < 0.001 and F(1,6) = 26.3, P < 0.003, respectively].
Similarly, in the Small-On condition, the saccade amplitude in session 1 increased by 2.6% (from 11.28 ± 0.29° to 11.58 ± 0.32°) between the baseline and posttest epochs [t(6) = 3.7, P < 0.01], whereas in session 2 the amplitude increased by 9.5% [from 11.65 ± 0.21° to 12.76 ± 0.40°; t(6) = 3.2, P < 0.02]; the interaction between Epoch and Session was significant [F(1,6) = 6.8, P < 0.04]. Both Epoch and Session main effects were also significant [F(1,6) = 12.8, P < 0.015 and F(1,6) = 7.3, P < 0.035, respectively].
To compare the amount of adaptation relative to the magnitude of the error signal, we need to estimate the two error signals being compared. In our experiment, we know the exact value of the retinal error because it was fixed by design (in session 2). Although we cannot know the exact prediction error, if we assume that the prediction is good (Collins et al. 2009) then the back-step is a proxy for prediction error size. In the Small-On condition, retinal error was 1.80 ± 0.51° and prediction error was 0.73 ± 0.44° (see methods and Fig. 1C). If retinal error and prediction error were equally good at evoking adaptation, then in session 2 we would expect ∼40% more adaptation than in session 1; in fact, we found ∼270% more adaptation. Specifically, in session 1 the difference between baseline and test was 0.30° (from 11.28 ± 0.29° to 11.58 ± 0.32°); thus every degree of retinal error evoked a 0.17° change in saccade amplitude (0.30°/1.80°). In session 2 amplitude change was 1.11° (from 11.65 ± 0.21° to 12.76 ± 0.40°). If we attribute the same amount of amplitude change in session 2 to retinal error, then there is 0.81° change left over for prediction error to explain (1.11–0.30°). Here every degree of prediction error evoked 1.1° amplitude change (0.81°/0.73°). In the Large-On condition, retinal error was 0.69 ± 0.50° and target step size was −1.66 ± 0.31°. Again, granting that small positive retinal errors cause amplitude-decreasing adaptation (Wong and Shelhamer 2010), if both errors were equally effective at evoking adaptation there should be ∼40% more adaptation in session 2 relative to session 1; instead, we found 200% more adaptation in session 2. Specifically, the amplitude decrease was 0.31° in session 1 (from 11.82 ± 0.12° to 11.51 ± 0.15°) and 1.54° in session 2 (from 11.65 ± 0.12° to 10.11 ± 0.12°). In this condition every degree of retinal error evoked 0.45° amplitude change, and every degree of prediction error evoked 0.77° amplitude change.
Therefore in both conditions, in session 2, in which there was both prediction and retinal error, it appears that prediction error was more powerful in evoking amplitude changes.
DISCUSSION
We contrasted two different sources of error information that could drive saccadic adaptation, retinal error, the distance between the saccade endpoint and the visual target, and prediction error, which occurs whenever there is a difference between the predicted postsaccadic retinal error and the observed postsaccadic retinal error. This difference is equivalent to the target step in test trials of session 2. The use of target step as a proxy for the prediction error assumes that the oculomotor system has relatively good knowledge about where the saccade lands, so that it can predict nonfoveal postsaccadic target positions (Collins et al. 2009). This assumption is supported by several studies on the double-step task in which subjects have to update remembered retinal information with intervening movements (Hallett and Lightstone 1976); their performance suggests that the system possesses good extraretinal knowledge (Bock et al. 1995; Collins 2010; Ditterich et al. 1998; Joiner et al. 2010; Munuera et al. 2009; Sommer and Wurtz 2004; Sparks and Mays 1983). Thus the oculomotor system would expect a retinal error of a particular size, but the target step makes the actual postsaccadic retinal error different from the prediction. This discrepancy is prediction error. The source of the prediction error is likely to be a forward model that uses an efference copy of the saccade motor command to predict the sensory consequences of the upcoming movement (Miall and Wolpert 1995). Although in principle proprioception could contribute to the prediction, Lewis et al. (2001) showed that proprioception probably does not play a role in adaptation, as normal adaptation was unaffected in two monkeys with deafferentiation of the extraocular muscles.
In our experiments, subjects experienced the same retinal error but different prediction errors during the two sessions. In session 1, we manipulated retinal error without introducing prediction error by extinguishing the visual target during the primary saccade to it, depending on the amplitude of that saccade. By reilluminating targets when the amplitude was larger than the median, we created a situation in which the eyes landed most frequently on or beyond the target, creating a mean retinal error smaller than the baseline; this caused saccade amplitude to decrease. By reilluminating targets when the amplitude was smaller than the median, mean retinal error was larger than the baseline; this caused saccade amplitude to increase. These results show that retinal error alone can drive amplitude changes. To test the role of prediction error, in the subsequent session 2 the retinal errors experienced during session 1 were presented to the same subjects by measuring saccade amplitude on-line and stepping the visual target during the saccade to the appropriate position. Thus, while the retinal errors between the two sessions were identical, the second session in addition had prediction errors. In these sessions, saccade amplitude adapted to a much larger extent than previously. It therefore appears that while retinal error can evoke a small change in amplitude, prediction error has a substantially larger effect.
Our results are therefore in agreement with previous reports that retinal error is not the sole determinant of saccade adaptation and that prediction plays an important role (Bahcall and Kowler 2000). In their paradigm, retinal error was intentionally modified by the subjects and prediction error by means of a target step. Here we altered the distributions of retinal error by removing the target on selected trials. Wong and Shelhamer (2010) took advantage of the fact that large saccades tend to fall short of the target and displaced the target during the saccade to a position about midway between its initial position and the mean saccade landing position. This situation created a mean positive retinal error, which would be expected to cause an increase in saccade amplitude. However, the backward target step introduced a prediction error in the opposite direction. Because they found that saccade amplitude decreased under these conditions, the implication is that prediction error plays a larger role than retinal error. This is similar to studies in which the target is made to land on average on the fovea, thereby eliminating retinal error. This situation causes saccade amplitude to decrease, as if to actively maintain the expected undershoot in saccade amplitude (Henson 1978; Robinson et al. 2003). All of these results could also be explained without invoking prediction error by postulating a mechanism that maintains the postsaccadic retinal error at a small positive goal state (saccadic undershoot). In this way, positive postsaccadic retinal errors could still by themselves evoke amplitude-decreasing adaptation.
One caveat we must consider about our conclusion is that if reinforcement processes play an important role in the control of saccade gain, this could mitigate our conclusion about retinal error per se being relatively unimportant. Consider whether it was rewarding to see the target after a saccade or, alternatively, it was punitive to have the target disappear upon a saccade. In our session 1 Small-On condition, the larger-than-usual retinal error might be driving the saccade amplitude to increase, while seeing the target only after smaller saccades might be driving the saccade amplitude to decrease. The result of such a conflict might be incorrectly interpreted as retinal error playing a weaker role than was the case.
Finally, if prediction error drives saccadic adaptation, the question arises as to why, during conventional saccadic adaptation, amplitude change tends to asymptote at a level close to the postsaccadic target location. Adaptation may stop once the predicted retinal error matches the actual retinal error, i.e., when the amplitude change exactly matches the target step. However, the fact that adaptation develops in a nonlinear fashion suggests this may not be the only determinant. An alternative view proposes that the prediction error itself adapts (by adapting the forward model that provides the predictions) or that retinal error becomes more effective in this situation, because of an interaction between the two error mechanisms. The updating of internal predictions synchronous to (Synofzik et al. 2008) or even preceding (Flanagan et al. 2003) changes in motor behavior has been shown for hand movements. Alternatively, a difference in dynamics of saccade adaptation based on prediction error and retinal error may be responsible for the gain asymptote. According to Körding et al. (2007), motor adaptation is the combination of fast-state and slow-state gains. Fast-state gains change and decay rapidly, such that early in the adaptation epoch almost all motor behavior is due to the fast-state gain. Slow-state gains change and decay slowly and can contribute to motor behavior only at the end of the adaptation epoch. This computational framework has been shown to explain some behavioral characteristics of saccadic adaptation such as retention and memory effects (Kojima et al. 2004; Robinson et al. 2006). We can explain the asymptote if we assume that prediction error influences motor behavior early in the adaptation epoch (i.e., influences the fast-state gain) and that retinal error drives the slow-state gain. If prediction error was negative (because of a back-step of the target as in our Large-On condition), early changes would cause amplitude to decrease. As the adaptation epoch unfolded, however, these early adaptive changes would tend to return the retinal error back to zero. If retinal error influences motor behavior at the end of the adaptation epoch (via the slow-state gain), then amplitude changes should asymptote as the weight of the fast-state gain decreases and that of the slow-state gain increases.
GRANTS
This work was supported by National Institutes of Health Grants EY-019508 and RR-03060.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: T.C. and J.W. conception and design of research; T.C. performed experiments; T.C. analyzed data; T.C. and J.W. interpreted results of experiments; T.C. prepared figures; T.C. and J.W. edited and revised manuscript; T.C. approved final version of manuscript.
ACKNOWLEDGMENTS
The idea of testing saccade adaptation without intrasaccadic steps arose from discussions with Axel Lindner, to whom we are indebted. We are also grateful to Mark R. Harwood and James P. Herman for generous assistance in the design of the experiment and in the analysis of the data.
REFERENCES
- Abel L, Schmidt D, Dell'Osso L, Daroff R. Saccadic system plasticity in humans. Ann Neurol 4: 313–318, 1978 [DOI] [PubMed] [Google Scholar]
- Bahcall D, Kowler E. Illusory shifts in visual direction accompany adaptation of saccadic eye movements. Nature 26: 864–866, 1999 [DOI] [PubMed] [Google Scholar]
- Bahcall D, Kowler E. The control of saccadic adaptation: implications for the scanning of natural visual scenes. Vision Res 40: 2779–2796, 2000 [DOI] [PubMed] [Google Scholar]
- Blakemore SJ, Wolpert DM, Frith CD. Why can't you tickle yourself? Neuroreport 11: 11–15, 2000 [DOI] [PubMed] [Google Scholar]
- Bock O, Goltz H, Bélange S, Steinback M. On the role of extraretinal signals for saccade generation. Exp Brain Res 104: 349, 1995 [DOI] [PubMed] [Google Scholar]
- Bonnetblanc F, Baraduc P. Saccadic adaptation without retinal postsaccadic error. Neuroreport 18: 1399–1402, 2007 [DOI] [PubMed] [Google Scholar]
- Bridgeman B, Hendry D, Stark L. Failure to detect displacement of the visual world during saccadic eye movements. Vision Res 15: 719–722, 1975 [DOI] [PubMed] [Google Scholar]
- Chen-Harris H, Joiner WM, Ethier V, Zee DS, Shadmehr R. Adaptive control of saccades via internal feedback. J Neurosci 28: 2804–2813, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins T, Rolfs M, Deubel H, Cavanagh P. Post-saccadic location judgments reveal remapping of saccade targets to non-foveal locations. J Vis 9: 1–9, 2009 [DOI] [PubMed] [Google Scholar]
- Collins T. Extraretinal signal metrics in multiple-saccade sequences. J Vis 10: 7, 2010 [DOI] [PubMed] [Google Scholar]
- Dean P, Mayhew J, Langdon P. Learning and maintaining saccade accuracy: a model of brainstem-cerebellar interactions. J Cogn Neurosci 6: 117–138, 1994 [DOI] [PubMed] [Google Scholar]
- Deubel H. Adaptive control of saccade metrics. In: Presbyopia Research, edited by Obrecht G, Stark LW. New York: Plenum, 1991 [Google Scholar]
- Deubel H, Schneider W, Bridgeman B. Postsaccadic target blanking prevents saccadic suppression of image displacement. Vision Res 36: 985–996, 1996 [DOI] [PubMed] [Google Scholar]
- Ditterich J, Eggert T, Straube A. Fixation errors and timing in sequences of memory-guided saccades. Behav Brain Res 95: 205–217, 1998 [DOI] [PubMed] [Google Scholar]
- Ethier V, Zee DS, Shadmehr R. Spontaneous recovery of motor memory during saccadic adaptation. J Neurophysiol 99: 2577–2583, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan JR, Vetter P, Johansson RS, Wolpert DM. Prediction precedes control in motor learning. Curr Biol 13: 146–150, 2003 [DOI] [PubMed] [Google Scholar]
- Hallett PE, Lightstone AD. Saccadic eye movements towards stimuli triggered by prior saccades. Vision Res 16: 99–106, 1976 [DOI] [PubMed] [Google Scholar]
- Havermann K, Lappe M. The influence of the consistency of postsaccadic visual errors on saccadic adaptation. J Neurophysiol 103: 3302–3310, 2010 [DOI] [PubMed] [Google Scholar]
- Henson DB. Corrective saccades: effects of altering visual feedback. Vision Res 18: 63–67, 1978 [DOI] [PubMed] [Google Scholar]
- Hopp J, Fuchs A. The characteristics and neuronal substrate of saccadic eye movement plasticity. Prog Neurobiol 72: 27–53, 2004 [DOI] [PubMed] [Google Scholar]
- Joiner WM, FitzGibbon EJ, Wurtz RH. Amplitudes and directions of individual saccades can be adjusted by corollary discharge. J Vis 10: 1–12, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima Y, Iwamoto Y, Yoshida K. Memory of learning facilitates saccadic adaptation in the monkey. J Neurosci 24: 7531–7539, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kommerell G, Olivier D, Theopold H. Adaptive programming of phasic and tonic components in saccadic eye movements. Investigations in patients with abducens palsy. Invest Ophthalmol 15: 657–660, 1976 [PubMed] [Google Scholar]
- Körding K, Tenenbaum JB, Shadmehr R. The dynamics of memory as a consequence of optimal adaptation to a changing body. Nat Neurosci 10: 779–786, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis RF, Zee DS, Hayman MR, Tamargo RJ. Oculomotor function in the rhesus monkey after deafferentation of the extraocular muscles. Exp Brain Res 141: 349–358, 2001 [DOI] [PubMed] [Google Scholar]
- McLaughlin S. Parametric adjustment in saccadic eye movements. Percept Psychophys 2: 359–362, 1967 [Google Scholar]
- Miall RC, Wolpert DM. Forward models for physiological motor control. Neural Netw 9: 1265–1279, 1995 [DOI] [PubMed] [Google Scholar]
- Munuera J, Morel P, Duhamel JR, Deneve S. Optimal sensorimotor control in eye movements. J Neurosci 29: 3026–3035, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noto C, Robinson F. Visual error is the stimulus for saccadic gain adaptation. Brain Res Cogn Brain Res 12: 301–305, 2001 [DOI] [PubMed] [Google Scholar]
- Optican L, Robinson D. Cerebellar-dependent adaptive control of primate saccadic system. J Neurophysiol 44: 1058–1076, 1980 [DOI] [PubMed] [Google Scholar]
- Ostendorf F, Liebermann D, Ploner CJ. Human thalamus contributes to perceptual stability across eye movements. Proc Natl Acad Sci USA 107: 1229–1234, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pélisson D, Alahyane N, Panouillères M, Tilikete C. Sensorimotor adaptation of saccadic eye movements. Neurosci Biobehav Rev 34: 1103–1120, 2010 [DOI] [PubMed] [Google Scholar]
- Robinson FR, Noto C, Bevans S. Effect of visual error size on saccade adaptation in monkey. J Neurophysiol 90: 1235–1244, 2003 [DOI] [PubMed] [Google Scholar]
- Robinson FR, Soetedjo R, Noto C. Distinct short-term and long-term adaptation to reduce saccade size in monkey. J Neurophysiol 96: 1030–1041, 2006 [DOI] [PubMed] [Google Scholar]
- Scudder CA, Batourina EY, Tunder GS. Comparison of two methods of producing adaptation of saccade size and implications for the site of plasticity. J Neurophysiol 79: 704–715, 1998 [DOI] [PubMed] [Google Scholar]
- Shafer J, Noto C, Fuchs A. Temporal characteristics of error signals driving saccadic gain adaptation in the macaque monkey. J Neurophysiol 84: 88–95, 2000 [DOI] [PubMed] [Google Scholar]
- Shergill SS, Bays PM, Frith CD, Wolpert DM. Two eyes for an eye: the neuroscience of force escalation. Science 301: 187, 2003 [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz R. What the brain stem tells the frontal cortex. II. Role of the SC-MD-FEF pathway in corollary discharge. J Neurophysiol 91: 1403–1423, 2004 [DOI] [PubMed] [Google Scholar]
- Sparks D, Mays L. Spatial localization of saccade targets. I. Compensation for stimulation-induced perturbations in eye position. J Neurophysiol 49: 45–63, 1983 [DOI] [PubMed] [Google Scholar]
- Synofzik M, Lindner A, Thier P. The cerebellum updates prediction about the visual consequences of one's behavior. Curr Biol 18: 814–818, 2008 [DOI] [PubMed] [Google Scholar]
- Wallman J, Fuchs A. Saccadic gain modification: visual error drives motor adaptation. J Neurophysiol 80: 2405–2416, 1998 [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Flanagan JR. Forward models. In: The Oxford Companion to Consciousness, edited by Bayne T, Cleermans A, Wilken P. Oxford, UK: Oxford Univ. Press, 2009, p. 294–296 [Google Scholar]
- Wong AL, Shelhamer M. Sensorimotor adaptation error signals are derived from realistic predictions of movement outcomes. J Neurophysiol 105: 1130–1140, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]