High-performance GPU-based rendering for real-time, rigid 2D/3D-image registration and motion prediction in radiation oncology

Abstract

A common problem in image-guided radiation therapy (IGRT) of lung cancer as well as other malignant diseases is the compensation of periodic and aperiodic motion during dose delivery. Modern systems for image-guided radiation oncology allow for the acquisition of cone-beam computed tomography data in the treatment room as well as the acquisition of planar radiographs during the treatment. A mid-term research goal is the compensation of tumor target volume motion by 2D/3D registration. In 2D/3D registration, spatial information on organ location is derived by an iterative comparison of perspective volume renderings, so-called digitally rendered radiographs (DRR) from computed tomography volume data, and planar reference x-rays. Currently, this rendering process is very time consuming, and real-time registration, which should at least provide data on organ position in less than a second, has not come into existence. We present two GPU-based rendering algorithms which generate a DRR of 512 × 512 pixels size from a CT dataset of 53 MB size at a pace of almost 100 Hz. This rendering rate is feasible by applying a number of algorithmic simplifications which range from alternative volume-driven rendering approaches – namely so-called wobbled splatting – to sub-sampling of the DRR-image by means of specialized raycasting techniques. Furthermore, general purpose graphics processing unit (GPGPU) programming paradigms were consequently utilized. Rendering quality and performance as well as the influence on the quality and performance of the overall registration process were measured and analyzed in detail. The results show that both methods are competitive and pave the way for fast motion compensation by rigid and possibly even non-rigid 2D/3D registration and, beyond that, adaptive filtering of motion models in IGRT.

1 Introduction

Radiation therapy is a common and indispensable method of treatment in the management of many malignant diseases including cancer of the lung, breast and prostate. A dose of 50 – 80 Gy is applied, destroying all cells in the tumor target volume. Given these circumstances a precise irradiation plan and the subsequent monitoring of dose escalation is mandatory. The basic principles of radiation biology require that the dose has to be delivered in fractions, which are applied on a more or less daily basis. Periodic as well as aperiodic motion and changes in anatomy complicate this task obviously; therefore, it is necessary to include large safety margins around the target volume, imperilling surrounding healthy tissue. Sometimes, tumor location and shape render radiation therapy treatment even unfeasible.

It is the aim of image-guided radiation therapy (IGRT) to increase the precision of irradiation utilizing additional information from intra-fractional imaging [1-5]. Methods for retrieving this additional image information range from ultrasound [6,7], magnetic resonance imaging [8] and, most important, kilovoltage and megavoltage x-ray imaging, either by means of planar radiography [9,10] or 3D modalities [11,12]. Non-rigid registration [13] techniques can be employed to simulate the deformation of the tumor [14,15] between treatment sessions. A common feature of most of the presented techniques is the fact that these are methods for patient setup–therefore, they are used for positioning the patient properly prior to each treatment session, and not for motion compensation.

For intrafractional motion compensation, modelling of breathing motion [16-18] is a topical field of research. Here, a typical patient-specific motion pattern is applied to simulate the motion of the tumor target volume (usually the lung or the liver) during irradiation. The identification of fiducial markers implanted into the tissue neighboring the tumor with planar x-ray imaging [9,10] or the implantation of passive electromagnetic transponders [19] is an alternative method to achieve motion monitoring. The increase in dose delivery precision is, however, accompanied by additional clinical effort and trauma caused by the implantation. Furthermore, metallic material such as the passive transponders or markers renders magnetic resonance imaging problematic due to extinction artifacts [20].

Real-time non-invasive tumor motion compensation and modelling is an open research challenge. While patient-specific motion models provide a good starting point, it is of course necessary to monitor the correctness of the modelled tumor trajectory; in lung cancer therapy, this can be accomplished by the aforementioned invasive methods, or by optical tracking of extrinsic landmarks attached to [21] or intrinsic features on the patients surface [22]. A classic approach from control theory towards driving a motion model with minimum latency would be the application of a predictive Kalman filter where a prediction value is provided by the model, whereas tracking of the tumor target value adds the corrector part.

2D/3D registration [23-29], the derivation of six degrees of rigid body motion from an iterative comparison of perspective volume renderings simulating x-ray images (also called digitally rendered radiographs or DRRs) and real x-ray data taken during irradiation might provide a non-invasive method to track tumor motion. However, the massive computational effort connected to DRR rendering does still result in typical runtimes of 30 to 100 seconds until the registration process is completed [28]. It is therefore straightforward to use the computational power of a modern graphics processor unit (GPU) to increase algorithm performance. A possible goal is a typical registration time of 0.2 s, which corresponds to the image update rate from modern x-ray units directly attached to the linear accelerator (LINAC) delivering the treatment beam. In [30], we presented a GPU-based implementation of an already efficient volume-driven splat rendering method [31]. In [30], a rendering time of approximately 25 ms was achieved. We have refined this method using a more efficient implementation, and it was compared against a further development of the sparse raycasting method presented in [25].

2 Materials and Methods

2.1 Wobbled Splat Rendering

The wobbled splat rendering algorithm was first proposed by in [31] as a high-performance variance of splat rendering. It achieves anti-aliasing by stochastic modification of the focal spot’s or every voxels position instead of using footprints to simulate the splatting of three-dimensional kernels [31,32].

Wobbled splat rendering iterates over all voxels of a volume and performs a geometric projection of the form

$${\overrightarrow{x}}_p=P\cdot V\cdot \overrightarrow{x}.$$ 1

where $\overrightarrow{x}$ is the original voxel and ${\overrightarrow{x}}_p$ is the projected voxel. P is projection matrix, and V is a volume transform given in homogeneous coordinates. In order to avoid discretization artifacts and the considerable computational effort of footprint computation as used in conventional splat rendering, a stochastic motion of the virtual focal spot is introduced. Further details about wobbled splat rendering are given in [30,31].

The direct implementation of the wobbled splat rendering suffers from two major problems. First, the random number generation for introducing wobbling is a deterministic process and the memory is not used in an efficient way. To initiate the processing of the voxel data, this data is transferred once for each rendering from the CPU to the GPU. For datasets consisting of several millions of voxels, this can easily result in an overhead of several milliseconds just for the data transfer. By utilizing the OpenGL concept of vertex buffer objects, it is possible to skip this retransferring. The voxel data that do not change in the course of registration are stored directly in the video memory of the graphics card and only changing parameters like transformation matrices are retransferred for every rendering.

For efficient wobbling of the focal spot, precalculated Gaussian distributed random numbers are stored in a three dimensional texture to be used as a lookup table. Because one texture for the whole volume would require too much memory, we used a smaller texture which is applied to several parts of the volume. This texture can then be fetched during the DRR generation to access the random numbers.

2.2 Ray Casting

Ray casting is the most popular algorithm for volume rendering in general and DRR generation in particular [26,29,33]. One widespread used implementation of ray casting for the GPU is to utilize a bounding structure – a simple geometric body that encloses the voxel volume – to generate rays that are used to traverse and sample a volume in form of a texture. By using a special color encoding, it is possible to calculate the ray for every pixel of the DRR with this structure. In a first pass, the back faces of the volume are rendered. In a second pass, the corresponding front faces are rendered and the faces are used to calculate the ray by subtracting the colors, which are represented by single precision numbers – therefore, the distance between front and back faces can be directly derived from the color coding. This ray is then used to traverse the volume data that is stored in a three-dimensional texture. Along the rays, the volume data is sampled in certain intervals and composed to the final intensity for the current pixel.

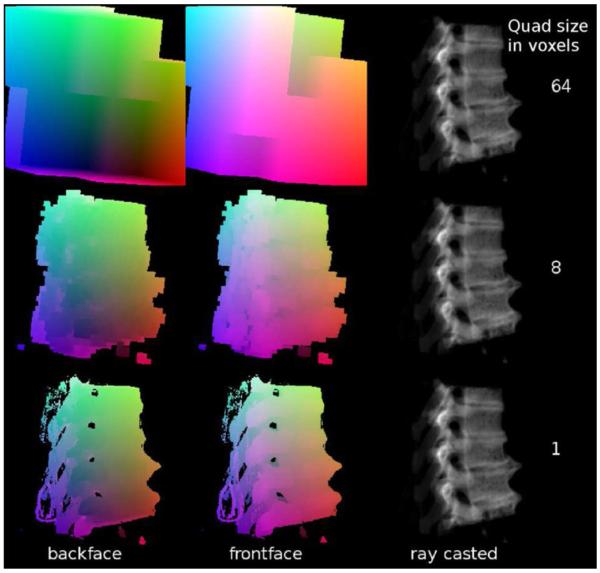
One concept for improving the performance of GPU based ray casting is the use of bounding structures that are as small as possible [33], which implies that these bounding structures are more or less surface representations of the volume data. To generate such refined bounding structures, a volume to surface transformation is required. The most known algorithm for this purpose is marching cubes, which has proved to produce models of too high complexity for the use as bounding structures. Therefore, the simpler cuberille method was utilized in this work [34]. For every voxel that contains data above a threshold, quads representing the voxels sides are generated to all neighboring voxels that do not contain data above the threshold. This allows to fast generate a closed surface of the volume. This surface is blocky, but since the surface is not rendered itself, this does not influence the quality of the DRRs. To produce more coarse grained bounding structures, it also possible to only transform groups of voxels to surface cubes. Examples of cuberille refined bounding structures of different granularity are shown in Fig. 1.

Fig. 1.

Illustrations of the bounding structure generated using the cuberille method for volume to surface transformation. The relative distance of the bounding surface with respect to the rendering plane is encoded by color. Therefore it is possible to compute the effective path of the ray when passing the relevant image data by a subtraction of the numerical values representing the color.

2.3 Optimizing DRR rendering for fast 2D/3D registration

The strengths of wobbled splat rendering are evident. First, it is a very simple method that can be easily parallelized on a GPU since it consists of subsequent matrix computations. The introduction of perspective is easily achieved by modifying the projection matrix and does not cause additional computational effort. Second, being a volume-based rendering technique, it is possible to reduce the number of voxels to be rendered in a similar manner to the aforementioned cuberille method by introducing a minimum rendering threshold.

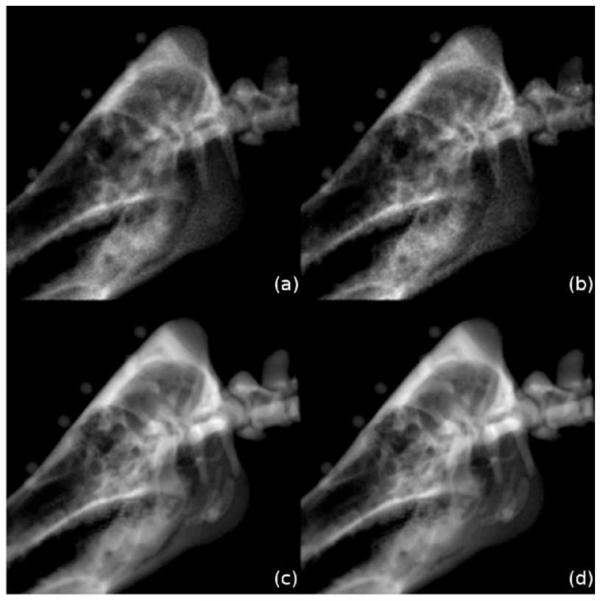
Another concept for improving the performance of GPU based ray casting is sparse sampling. For 2D/3D-image registration using intensity based merit functions, it is possible to calculate the similarity measure on only a subset of the image content, as long as this subset was chosen stochastically [25]. In [25], only a small number of rays with randomly chosen endpoints in the DRR was used to sample a joint histogram, which was used to compute a mutual information (MI) merit function. Another recently introduced merit function named stochastic rank correlation (SRC) [28] also allows for the computation of a similarity measure from a subset of the rendered DRR; as opposed to MI type merit functions, it is not suitable for multimodal image fusion but is invariant to monotonous shifts in image intensity and gives more robust and accurate results compared to other merit functions. For this series of experiments, we have adopted a ray casting algorithm utilizing bounding structures and sufficient GPU use. Examples for sparsely sampled DRRs with a different amount of image content are shown in Fig. 2.

Fig. 2.

Sparsely sampled DRRs with different amounts of image content. (a) shows a complete DRR, and (b) – (d) show the same DRR with 50, 25 and 5% image content.

2.4 Evaluation and Implementation

Evaluating the performance of the rendering approaches was done by rendering two test datasets of CT and x-ray data provided with known gold standard positions. These gold standard parameters were modified in the interval [−180° … 180°] for all three axes with a step size of 12°. The used datasets were a section of a human spine [35] and a pig skull including the soft tissue [37]. Both CT and x-ray datasets were reduced to 8 bit depth after appropriate windowing for reducing the amount of data to be transferred to the GPU and back, and were rendered with a low and a high threshold to extract additional properties. The mean rendering times and their standard deviations for these measurements are shown in Table 1. The test system was an Intel(R) Core(TM)2 Duo T7700 CPU @2.40 GHz with 4 GB Ram running Kubuntu 9.10 ×64, which uses the 2.6.31 Linux kernel. A NVIDIA Quadro FX 570M graphics card with 512 MB video memory was used with the NVIDIA 190.18 driver for all rendering procedures.

Table 1.

Mean rendering times (in ms) and their standard deviations (SD) for 27000 renderings using GPU based wobbled splat rendering and GPU based ray casting including several optimization techniques for them. Two reference datasets available to the public [36,37] were used for this validation.

Rendering Method (all GPU based)	Rendering Times and Standard Deviation in ms for
	Spine Dataset with Threshold 20	Spine Dataset with Threshold 70	Pig Dataset with Threshold 10	Pig Dataset with Threshold 60
Wobbled Splatting
basic	58.1±1.4	15.0±0.2	68.9±1.6	46.1±0.9
noise texture	57.0±0.6	15.3±0.4	68.0±0.5	45.0±0.296
vertex buffer objects	29.5±2.7	8.4±0.7	34.5±2.6	23.0±1.5
Ray Casting
basic	14.1±2.0	13.0±1.9	22.2±4.3	21.8±4.4
Cuberille (64 voxels)	20.9±3.4	17.9±2.8	24.7±6.2	24.2±4.8
Cuberille (8 voxels)	17.9±3.4	10.0±3.0	38.3±16.5	20.5±6.5
Sparse Sampling (50%)	12.0±1.8	11.0±1.6	15.3±2.9	15.3±3.0
Sparse Sampling (25%)	9.8±1.4	9.0±1.2	13.4±2.1	13.3±2.0
Cuberille (8 voxels) and Sparse Sampling (25%)	11.9±2.0	7.3±2.1	22.1±8.8	12.8±4.1

3 Results and Discussion

Fig. 3 presents some DRRs rendered with the different rendering methods compared by this work for visual analysis. These images show that wobbled splat rendering produces DRRs containing more noise than ray casting, which is a direct consequence of the stochastic routines that avoid aliasing artifacts in this volume-driven method. Also the contours of ray casting are sharper and overall image blur is lower. Therefore, in general, ray casting seems to produce DRRs of better quality. However, since the DRRs are not used for visualization, it is questionable whether an influence on registration performance is evident.

Fig. 3.

Identical perspective renderings of a porcine skull created with (a) wobbled splat rendering, (b) wobbled splat rendering using a precalculated texture for random number generation, (c) ray casting and (d) ray casting with a bounding structure refined by the cuberille method.

Table 1 shows rendering time measurements for the different rendering approaches with differing optimization techniques. These values represent the mean and the standard deviation of 27000 renderings created with differing rotational parameters.

Several properties of the different rendering approaches can be extracted from Table 1. For wobbled splatting, the most important improvement in rendering time is achieved by utilizing vertex buffer objects to optimize the memory management. This technique allows for an acceleration of the algorithms by a factor of 2 in comparison to the implementation by [30]. Furthermore, it can be shown that using precalculated textures with random numbers instead of the deterministic approach of [30] for introducing stochastic motion to the splat rendering do not improve the rendering time significantly.

In this implementation, ray casting is faster than wobbled splat rendering for almost all setups. Only if the volume to render contains a very sparse distribution of non-zero voxels, wobbled splat rendering performs considerably better than ray casting. The refinement of the bounding volume has proved to not always accelerate the rendering. Depending on the used dataset, the threshold and the pose and the size of the cuberille generation kernel, this method can result in large improvements (see Table 1 for the spine dataset with a threshold of 70) or to a increase of the rendering time (see Table 1 for the pig dataset with a threshold of 10). The problem is that using a more detailed bounding structure requires more processing by the graphics hardware. Table 2 also shows that sparse sampling of the DRR allows to speed up the whole rendering process for all datasets and any threshold. The results illustrate that the introduction of a rendering threshold is of crucial influence on both methods: in the case of splat rendering, the number of voxels to be rendered depends directly on the threshold [30,31] since it is a volume driven method; in the case of the proposed raycasting method, the shape of the bounding structure and therefore also the computational effort is determined by the same threshold.

Table 2.

Measured times including standard deviations for the overall registration process. In addition, the number of required iterations until the optima was found as well as the mean mPD and mTRE errors are shown as a measure of overall registration quality. Every registration was carried out 150 times.

Rendering Method (all GPU based)	Reg. Time and SD in s	Number of Iterations	mPD Error ± SD in mm	mTRE Error ± SD in mm
Wobbled Splatting with Vertex Buffer Objects	11.722±3.202	102.03±22.4	10.85±1.88	9.71±2.00
Ray Casting	8.195±1.955	134.05±34.1	10.19±2.81	9.66±2.86
Ray Casting Cuberille (8 voxel)	9.922±2.934	112.27±28.5	6.86±1.36	6.53±1.92
Ray Casting Cuberille (8 voxel) and Sparsely Sampling (25%)	6.230±1.250	99.49±25.8	5.72±1.60	5.69±2.03

The results of registrations utilizing different rendering methods from Table 2 revealed the different properties of the investigated approaches. While using ray casting allows to reduce the overall registration time, it shows that the quality of registration does not increase in comparison to wobbled splat rendering. Refining the bounding structure for ray casting using the cuberille approach can reduce the performance, but seems on the other hand to improve the quality of the registration. Sparse sampling of the rendering process has proved to not only improve the rendering time, but also the registration time and the quality of the overall process. The image data were acquired by using a rather large gold standard dataset for 2D/3D registration featuring CT as well as x-ray data with known ground truth registration parameters [37]; the CT scan of this dataset, for instance, features 67 MB. Therefore the registration time became quite considerable, especially for the purpose of realtime tumor motion compensation. However, in a recent series on clinical data, the appropriate choice of the region-of-interest for registration yielded registration times in the range of 0.5 seconds. The registration experiments were carried out after a random displacement of 25 mm from a known ground truth position defined by fiducial markers using a local optimization routine. A rendering threshold of -540 HU was chosen, which is known from an extensive series of experiments to give good results without sacrificing too much information on soft tissue [38]. Details on the evaluation procedure can be found in [38]. It turned out that the DRR rendering – which was considered a major source of computational labor in older publications [23-25] – only requires 23 – 43% of the computation time for a single iteration. It is therefore evident that in a next step, the merit function evaluation should also be carried out on the GPU in order to further improve registration performance.

4 Conclusion

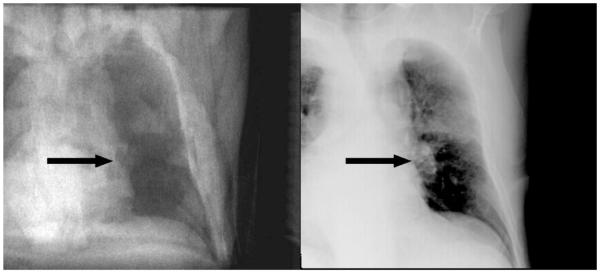
It is shown that modern programming techniques, alongside with efficient implementation of rendering paradigms and similarity function evaluations, allow for generation of DRRs suitable for high-speed 2D/3D registration. The combination of sparse ray sampling and SRC or MI based similarity measures is, however, specific to this specific registration problem. Still, we see a merit for the application of lung cancer motion compensation; in many cases, the tumor can be identified even on MV images from electronic portal imaging [27]. The introduction of kV imaging units attached to the linear accelerator does even provide a source of better quality images in real time. An example is shown in Fig. 4.

Fig. 4.

A comparison of a registered DRR (left) and the matching X-ray (right) of a patient suffering from bronchial carcinoma. The tumor is marked with an arrow. Despite the fact that X-ray only provides poor soft tissue contrast, structures usable for registration can be identified in the target volume.

In current LINAC-setups, parallel acquisition of perpendicular kV and MV image data is feasible. It is therefore an straightforward further development to utilize the most important intrinsic property of rank-correlation based measures like SRC – its independence from variations in the histogram of the DRR and the kV or MV data – together with the sparse sampling raycasting method presented. The use of this method to other areas where driving a soft tissue model using X-ray data is, however, imaginable but depends on the boundary conditions in a specific clinical application field. Due to the fact that ionizing radiation is to be used, we assume that organ motion monitoring in this setup is confined to radiotherapy, where the comparatively small dose from X-ray imaging is marginal with respect to the dose delivered by the LINAC. Beyond lung motion, another potential application includes liver motion since at least parts of the organ surface – namely the part next to the diaphragm – give a clear contrast in X-ray.

The rendering results presented mainly show bony tissue, which is certainly a weakness of the chosen evaluation with respect to driving soft tissue models. It is however mandatory that new algorithms are tested on reference datasets, and unfortunately a reference motion sequence with known gold standard parameters is not yet available. For the given purpose – the evaluation of specialized DRR rendering algorithms – this drawback of the available phantoms appears acceptable. The next open research challenge to be tackled is the further refinement of a time-critical registration routine to achieve a further improvement of the already very efficient registration algorithm and fusion of registration results and motion models using adaptive filters.