Oscillatory dynamics in the hippocampus support dentate gyrus–CA3 coupling

Abstract

Gamma oscillations in the dentate gyrus and hippocampal CA3 show variable coherence in vivo, but the mechanisms and relevance for information flow are unknown. We found that carbachol-induced oscillations in rat CA3 have biphasic phase-response curves, consistent with the ability to couple with oscillations in afferent projections. Differences in response to stimulation of either the intrinsic feedback circuit or the dentate gyrus were well described by varying an impulse vector in a two-dimensional dynamical system, representing the relative input to excitatory and inhibitory neurons. Responses to sinusoidally modulated optogenetic stimulation confirmed that the CA3 network oscillation can entrain to periodic inputs, with a steep dependence of entrainment phase on input frequency. CA3 oscillations are therefore suited to coupling with oscillations in the dentate gyrus over a broad range of frequencies.

Many brain areas, including the dentate gyrus and hippocampal CA3, show prominent gamma oscillations whose inter-region coherence varies during awake activity^1,2. Structures of gamma-oscillatory activity in the temporal lobe are modulated by both brain state³ and task demands^4,5. Such changing patterns of coherent oscillatory activity may be involved in controlling information flow among connected networks^6–8. The dynamical mechanisms underlying the emergence of coherence among anatomically coupled networks are, however, poorly understood.

During gamma oscillations, individual neurons spike irregularly^1,2,9–11, but the collective dynamics of the local network are oscillatory. Thus, the emergence of phase coherence between regions is a process of synchronization between local network oscillators. Important determinants of the synchronization properties of systems of coupled oscillators are the phase-response curves (PRCs) of the constituents^12–14. Synchronization through excitatory connections is strongly promoted by biphasic PRCs, in which the same input can either advance or delay the phase of oscillation depending on when the perturbation occurs during the oscillatory cycle. Such PRCs allow oscillators to entrain to periodic inputs at both higher and lower frequencies than the unperturbed oscillation frequency. Although the mechanisms generating gamma oscillations in local networks have been extensively studied^9,11,15,16, the phase response dynamics of the resulting network oscillators have not been measured, nor have their entrainment properties in response to periodic inputs been examined. We found that gamma band oscillations in the hippocampal CA3 subfield exhibit dynamical properties that make them suitable to entrain to periodic output from the dentate gyrus across a range of frequencies.

RESULTS

CA3 gamma oscillations exhibit biphasic PRCs

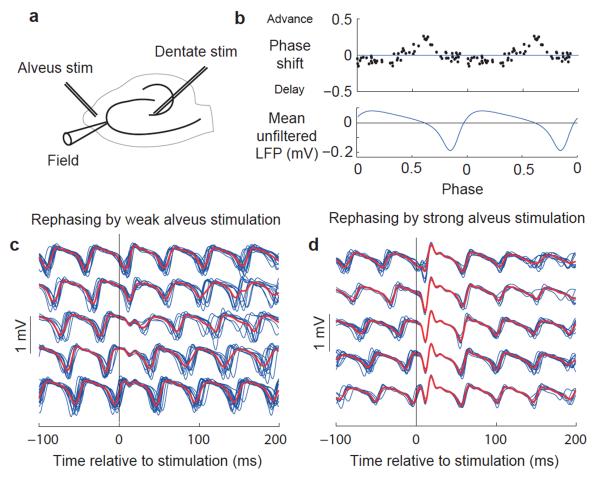
We characterized PRCs of carbachol-induced oscillations in the rat CA3 hippocampal subfield in vitro to determine whether they exhibit regions of phase advance and delay (Fig. 1a–c). A weak extracellular stimulus in the alveus indeed elicited a biphasic PRC (Fig. 1b). Stimuli arriving shortly before the trough of the local field potential (LFP) oscillation caused a phase advance, whereas stimuli arriving during the rest of the cycle delayed the oscillation. Because the LFP trough corresponds to the phase of maximum pyramidal cell activity⁹, stimuli that caused a phase advance arrived in the rising phase of excitatory activity.

Figure 1.

Measurement of network PRCs in the hippocampal CA3 subfield. (a) Schematic indicating positions of recording and stimulating electrodes. (b) PRC with weak stimulation, aligned with average unfiltered LFP over two cycles. (c) Filtered LFP traces (blue) around weak alveus stimulation in a representative experiment, sorted into five groups by phase of stimulation with group averages superimposed (red). (d) Data obtained and plotted as in c, but with strong alveus stimulation.

When the stimulation strength was increased, a discontinuity emerged in the PRC such that the oscillation was reset to a narrow range of phases, irrespective of the phase of stimulation (Figs. 1d and 2, and Supplementary Fig. 1a). This range of new phases narrowed with further increase in the stimulation strength until the phase after stimulation was largely independent of the phase before.

Figure 2.

A neural mass model reproduces rephasing behavior. (a) Schematic illustrating the Wilson-Cowan model (top), with activity of excitatory (E) and inhibitory (I) populations in the absence of noise or perturbation (below). (b) Phase plane diagram showing the limit cycle (blue), nullclines (black: dashed, excitatory; solid, inhibitory; see Online Methods) and isochrons (red). (c) Rephasing by stimuli of four different strengths in one hippocampal slice. Points indicate the troughs of the filtered LFP, with the last trough before stimulation and 3–4 troughs after stimulation shown for each trial. Times of successive troughs (sequences of points running vertically) are arranged on the x axis by phase of stimulation. Diagonal lines indicate the expected positions of troughs in the absence of stimulation, calculated from the time of the final trough before the stimulus and the mean unperturbed period duration. (d) Rephasing behavior of Wilson-Cowan model in response to perturbations of different intensities, plotted as in c. (e,f) Rephasing phase plane diagrams. Colored squares show positions at the time of stimulation for 100 simulations, equally spaced in phase. Correspondingly colored circles show the state 6 ms after the stimulus. Colored lines show trajectories of ten of these simulations from the time of stimulation until their return to the limit cycle. Arrows indicate the direction (ratio of inhibitory to excitatory stimuli) and strength of the input pulse (also see Supplementary Movie 1a,b).

Rephasing is reproduced in a neural mass model

To understand the mechanisms underlying the biphasic shape of the PRC and the highly structured transition from weak perturbation to complete resetting, we turned to the Wilson-Cowan equations, a highly simplified neural mass network model¹⁷ (Fig. 2a). The dynamical state of the network is represented in the model by only two variables, representing the excitatory and inhibitory population activities. These activity levels evolve under their synaptic interactions and oscillatory dynamics emerge for appropriate sets of parameter values (Fig. 2a). In the oscillating state, the trajectory of the excitatory and inhibitory activity forms an anti-clockwise limit cycle in the model’s phase space (Fig. 2b). Perturbing the model with an exponentially decaying transient input produced an excellent match to the experimentally observed PRCs across a broad range of stimulus intensities (Fig. 2c,d).

The simplicity of the model gives a mechanistic insight into the rephasing behavior through consideration of the perturbed trajectories of activity following stimulation (Fig. 2e,f and Supplementary Movie 1a,b). The transient input pulse perturbs the system away from the limit cycle, after which it relaxes back, returning to the limit cycle with a phase that is, in general, different from what it would have had in the absence of perturbation. To understand whether a given perturbation will advance or delay the oscillation, it is therefore necessary to consider the latent phase of points away from the limit cycle^14,18. The latent phase of point a off the limit cycle is defined as the phase of point b on the limit cycle, for which trajectories starting from points a and b will converge as t → ∞. Lines connecting points with the same latent phase make up the model’s isochrons, which radiate outward from the unstable fixed point, pass through the limit cycle and continue out to the edge of the phase plane (Fig. 2b). The effect of a transient stimulus on the oscillation phase is determined by the direction that it pushes the system relative to the local isochrons. An impulse that pushes the system perpendicular to the isochrons in the direction of increased (decreased) latent phase will advance (delay) the oscillation, whereas a perturbation that pushes the system parallel to the isochrons will have little effect on the phase.

The effects of alveus stimulation were reproduced in the model by a transient input that preferentially targeted the inhibitory population over the excitatory population. This corresponds to an impulse vector in the phase plane that is close to vertical (Fig. 2e,f). Shortly before the peak excitatory firing rate in the unperturbed limit cycle, the isochrons cross the cycle approximately horizontally, with increasing latent phase in the upward direction (Fig. 2b). Stimulation at this phase therefore advances the oscillation. The same stimulus delivered during the falling phase of excitatory activity pushes the system in the direction of decreasing latent phase, delaying the oscillation.

Both the model and our experimental data reveal a qualitative change in the rephasing behavior as the stimulation strength is increased. For weak stimulation, the PRC is continuous and, as the phase at stimulation is varied through a whole cycle, the phase reached after stimulation also varies through a whole cycle (following the nomenclature in ref. 18, rephasing is type 1 by winding number). For strong stimulation, the PRC is discontinuous and the phase reached after stimulation is largely invariant of the phase before stimulation (type 0 by winding number). The mechanism of this transition can be visualized in the model by considering the positions reached at the end of stimulation by trajectories starting at points evenly spaced on the limit cycle at stimulus onset (Fig. 2e,f). For weak stimulation, these positions encircle the fixed point and therefore span the full range of latent phases (Fig. 2e). For strong stimulation, the loop defined by these positions is displaced so much that it no longer encircles the fixed point and therefore only subtends a fraction of the range of latent phases (Fig. 2f). The transition between these regions occurs for a stimulus intensity just strong enough that the loop touches the fixed point at the end of stimulation.

Alveus and dentate gyrus stimulation yield different PRCs

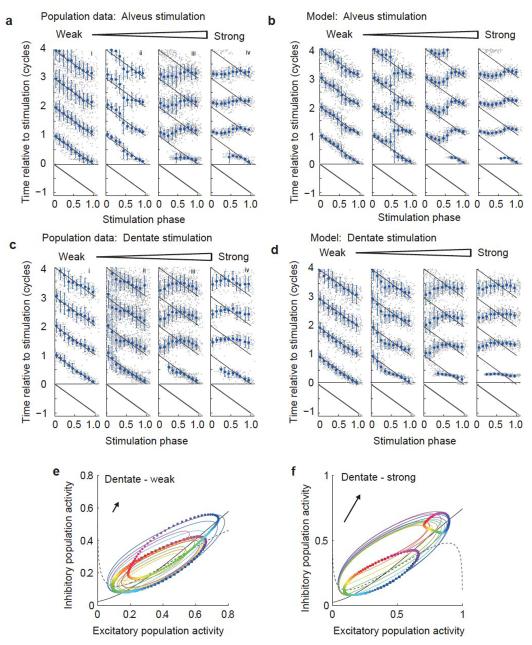
The response to alveus stimulation was consistent across slices (Fig. 3a and Supplementary Fig. 1b), with the scatter accounted for by differences in stimulus intensity and noise, and could be reproduced in the Wilson-Cowan model (Fig. 3b). Do these results shed light on the ability of CA3 to couple with gamma oscillations in the dentate gyrus? Mossy fibers carry the entire signal from dentate granule cells to CA3 and innervate both pyramidal neurons and feed-forward interneurons¹⁹. Stimulation of the dentate gyrus produced the same overall structure of rephasing behavior as stimulation in the CA3 alveus, with a biphasic PRC in response to weak stimulation, giving way to complete resetting for strong stimuli (Fig. 3c and Supplementary Fig. 1c). The biphasic PRC is therefore consistent with gamma oscillations in CA3 entraining with periodic input from the dentate over a wide range of frequencies and with the emergence of coherence between these synaptically coupled regions².

Figure 3.

Population data and model behavior. (a–d) Population rephasing data for alveus (a,b) and dentate stimuli (c,d). Experimental data are shown in a and c, and simulation results are shown in b and d. Gray dots indicate times of troughs in individual traces, plotted as in Figure 1c, but combining data across experiments. Blue symbols indicate the circular mean trough position for data binned by phase of stimulation (error bars indicate circular variance). (e,f) Rephasing phase plane diagrams for dentate stimulation, plotted as in Figure 2e,f. Note the difference in stimulation angle (indicated by arrow) compared with alveus stimulation.

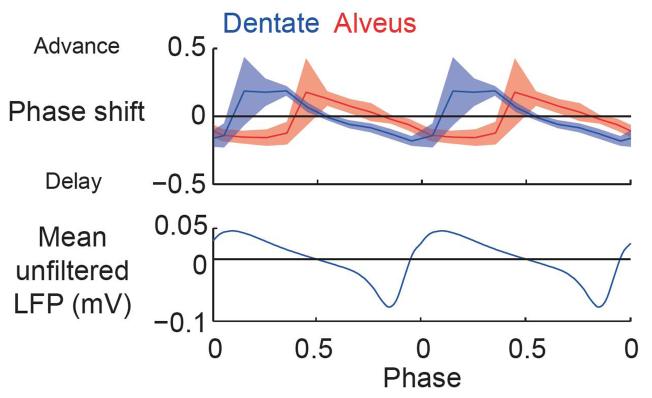
Notably, the phases of stimulation that resulted in phase advance and delay were different for stimulation of either CA3 alveus or dentate gyrus (Figs. 3 and 4), and 20–30% of this difference, at most, could be accounted for by conduction delay (see Online Methods). The detailed structure of the resetting at intermediate and strong stimulation intensities also differed between the two stimulus types (Fig. 3a,c). To date, the nature of the signal carried by mossy fibers has been considered from the point of view of excitation versus inhibition in a quiescent system²⁰. However, the dynamic analysis presented here gives additional insight into the nature of the dentate-CA3 interaction.

Figure 4.

Population PRCs for weak dentate and alveus stimulation with circular 95% confidence interval, and the cycle-averaged unfiltered LFP shown for reference.

The only modification to the Wilson-Cowan model that was needed to reproduce the difference between stimulation in the CA3 alveus and the dentate was a change in the relative strength of the input pulse to the excitatory and inhibitory populations (Figs. 2 and 3). Stimulation of CA3 alveus was best reproduced by an input to the inhibitory population that was approximately sixfold stronger than the input to the excitatory population (Fig. 2e,f and Supplementary Movie 1a,b). This represents the net effect on each population of spikes elicited by the stimulus in excitatory and inhibitory neurons, and is consistent with the synaptic strengths of the local connections in the model; both populations received strong and approximately balanced excitatory and inhibitory local inputs, but the net input to the inhibitory population was somewhat more excitatory. Dentate stimulation, on the other hand, was best reproduced by an input that targeted the inhibitory population ~1.7-fold more strongly than the excitatory population (Fig. 3d–f and Supplementary Movie 1c,d).

The mechanism by which this difference in the stimulus shifts the PRC can again be understood by considering the effect of the perturbation in the model’s phase plane. Changing the relative strength of the stimulus to the excitatory and inhibitory populations corresponds to a change in the direction of the impulse vector in the phase plane. The alveus stimulation corresponds to an angle of 85° (measured counter-clockwise from a horizontal rightward vector), whereas the dentate stimulation corresponds to an angle of 60°. This change in direction means that the dentate stimulus acts in the direction of increasing latent phase (and therefore advances the oscillation) at an earlier phase of the limit cycle than the alveus stimulation.

To quantify the goodness of model fit, we evaluated the circular correlation across stimulation intensities and phases of stimulation between experimental and modeled LFP trough times (Supplementary Fig. 2). This revealed a strong correlation between experimental data and the model for both stimulation loci (correlation coefficients: dentate, 0.85; alveus, 0.79). Correlations were much weaker between experimental data for one locus of stimulation and modeled data for the other locus (0.18 and 0.27).

To further test the correspondence between the model and experimental data, we performed voltage clamp recordings from CA3 pyramidal neurons, while holding them at either the GABA_A or the ionotropic glutamate receptor reversal potential, simultaneously with the LFP recordings. Membrane currents fluctuated substantially from cycle to cycle of the unperturbed oscillation (Supplementary Fig. 3a,b). However, in all slices (n = 12), when the cycle-averaged inhibitory and excitatory currents were plotted against each other the trajectory formed an ellipsoidal anti-clockwise cycle (Supplementary Fig. 3c), consistent with the model. Current trajectories following stimulation were also highly variable from trial to trial. Given the number of stimulation events that we were able to record, the averaged trajectories during weak rephasing were too noisy to resolve their fine structure. We were, however, able to resolve the larger current excursions that occurred during strong rephasing (Supplementary Fig. 3d,e). To compensate for changes in holding current and access resistance during recordings, we normalized the trajectory post-stimulation for each trace by the cycle-averaged pre-stimulation current (see Online Methods). In all slices in which we recorded such current trajectories (n = 4), the perturbed trajectories moved away from the average cycle in the direction of increasing excitatory and inhibitory currents, turned in an anti-clockwise direction and returned to the average cycle in the lower left corner (Supplementary Fig. 3d,e and Supplementary Movies 2a,b). This excursion was again consistent with the model’s activity trajectories. Also consistent with the modeling, the initial trajectories following alveus stimulation were tilted anti-clockwise, that is, oriented toward a relatively greater increase in inhibition than excitation, than those for dentate stimulation. We quantified this difference in the direction of the trajectories by evaluating the angle, in normalized current space (see Online Methods), between the mean current during the unperturbed cycle and the average position reached 0.3 cycles after stimulation (alveus, 61.4 ± 0.4°, mean ± s.d., n = 2; dentate, 35.5 ± 9.2°, n = 2).

Overall, the membrane current recordings provide an internal validation of the highly reduced model and, although the sample size is small, are consistent with the prediction that the phase difference in PRCs for dentate and alveus stimulation relates to differences in the relative input to excitatory and inhibitory populations. We, however, note an important caveat. In the model, the effect of the stimulus on each population is represented by a transient input pulse corresponding to the net (that is, excitatory minus inhibitory) input resulting from spikes directly evoked by the stimulus. A small net excitatory input could be a result of a small excitatory current in isolation or of large and approximately balanced excitatory and inhibitory currents. These distinct possibilities are indistinguishable in the model, but predict different intracellular current trajectories. The measured current trajectories are therefore a compound of currents resulting from the activity trajectory following stimulation and those resulting from spikes directly elicited by the stimulus, whose relative contributions to the trajectory cannot be dissociated.

Optogenetic rephasing and entrainment

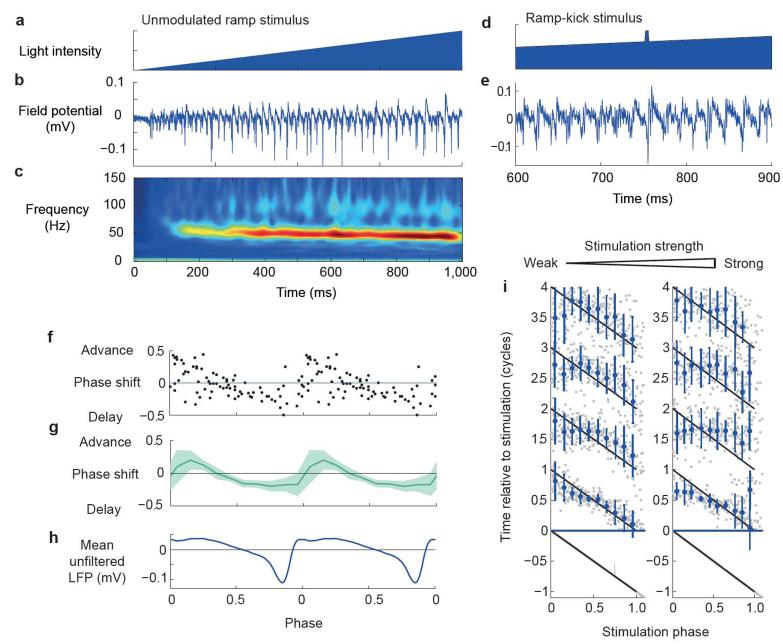
To test the generalizability of the measured PRCs of the CA3 network, we examined the phase response properties of gamma band oscillations evoked by optogenetic stimulation. Channelrhodopsin-2 (ChR2) was expressed under the Camk2a promoter in the CA3 region of the dorsal hippocampus using stereotaxic injection of adeno-associated virus. Consistent with a recent study in cortical layer 2/3 (ref. 21), a slowly increasing ramp of blue light lasting 1 s, delivered to the CA3 region, evoked robust gamma frequency oscillatory activity in the LFP (n = 7; Fig. 5a–c). The frequency of the oscillation was higher than that elicited by carbachol (52.6 ± 5.1 versus 22.2 ± 4.6 Hz, P < 0.001), consistent with involvement of metabotropic glutamate receptors in oscillogenesis²².

Figure 5.

Optogenetic rephasing. (a–c) Example of oscillatory activity evoked by 1-s light ramp showing light intensity (a), LFP (b) and average wavelet transform amplitude (c; 12 traces from 1 slice). (d,e) Example of rephasing using a ramp-kick stimulus showing light intensity time course (d) and field potential (e) during a 400-ms window around the kick. (f–h) PRC for single slice (f) and population (g) (n = 4, shaded area indicates 95% circular confidence interval) aligned with mean unfiltered LFP response (h). (i) Population rephasing data for weak (left) and strong (right) stimuli, plotted as in Figure 3.

We first examined the effect of a transient (5 ms) increase in light intensity riding on top of the light ramp (Fig. 5d,e). This ‘ramp-kick’ stimulus evoked a clearly biphasic continuous PRC (Fig. 5f–h), implying that this is a general feature of perturbing gamma oscillations in CA3 and does not depend on the specific stimulus type or mechanism used to induce the oscillation. Stronger kicks generated discontinuous PRCs (type 0 by winding number), which is again consistent with the data obtained using carbachol and electrical stimulation (Fig. 5i and Supplementary Fig. 1d).

The region of phase in which optogenetic stimulation advanced the oscillation was earlier, relative to the trough of the unfiltered LFP, when compared with electrical stimulation of either the dentate gyrus or alveus during carbachol-induced oscillations. This shift is consistent with that predicted by the model’s isochron portrait when the stimulus is biased further toward the excitatory population. Perturbing the model with a stimulus pulse targeting only the excitatory population produced a PRC with a region of phase advance similar to that observed experimentally, albeit spanning a somewhat larger fraction of the cycle (Supplementary Fig. 4a,b).

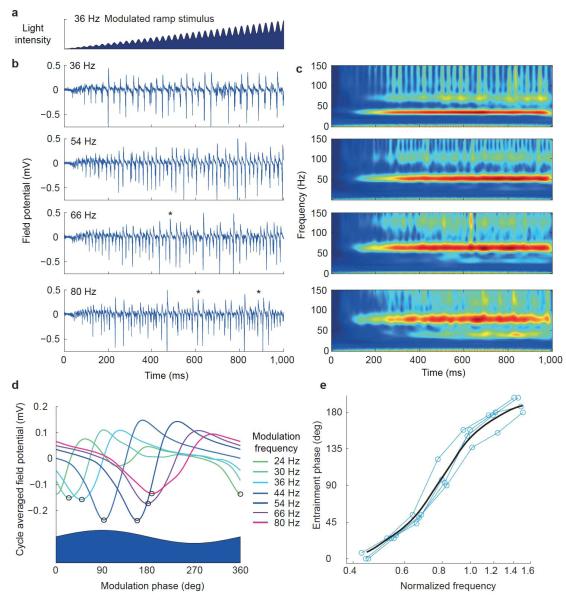
Biphasic PRCs in response to pulse inputs predict that an oscillator will entrain to periodic inputs at a range of frequencies spanning the unperturbed oscillation frequency. To test this prediction directly, we used a stimulation protocol in which the ramp used to induce the oscillation was multiplicatively modulated by a shallow sinusoid (Fig. 6a). LFP oscillations indeed entrained to the modulation over a wide range of frequencies spanning the unperturbed oscillation frequency (Fig. 6b,c).

Figure 6.

Entrainment demonstrated with modulated light ramps. (a) Example of modulated ramp stimulus light intensity. (b) Example LFP traces elicited by modulated ramp stimuli at a range of modulation frequencies (frequency indicated by each panel). Asterisks indicate cycles with 1:2 entrainment. (c) Corresponding average wavelet transform amplitudes (n = 4). (d) Example average LFP responses as a function of phase of the sinusoidally modulated stimulus, for a range of frequencies indicated by trace color. Black circles indicate troughs used to evaluate entrainment phase. (e) Entrainment phase plotted as function of normalized modulation frequency; blue lines show individual slice data and black curve shows Gaussian weighted moving average.

Given that the CA3 population oscillation can be entrained by an afferent input, we expect the entrainment phase to vary as a function of the driving frequency. To evaluate the phase of entrainment, we averaged the LFP across multiple cycles of the modulation to generate a cycle-averaged LFP for each modulation frequency (Fig. 6d). This showed a strong dependence of the phase of entrainment, estimated from the time of occurrence of the trough of the LFP relative to the sinusoidal modulation cycle, on the frequency of the modulation. To compare entrainment phase across slices, we normalized the sinusoidal modulation frequency by the unperturbed oscillation frequency evoked with an unmodulated ramp for each slice. This revealed a consistent frequency-phase relationship across slices (n = 4), in which the entrainment phase varied through 180° as the modulation frequency varied from 0.4-fold to 1.6-fold that of the unperturbed oscillation frequency (Fig. 6e). The amplitude of the cycle-averaged LFP also varied with the modulation frequency (Supplementary Fig. 4c). Although the frequency-amplitude relationship was less consistent across slices than the frequency-phase relationship, the largest-amplitude LFP response occurred for modulation frequencies close to the unperturbed oscillation frequency.

We asked whether the Wilson-Cowan model showed similar entrainment behavior when the excitatory population was driven with a sinusoidal input (Supplementary Fig. 4d). The phase of peak excitatory activity for the model showed a frequency dependence similar to that of the experimentally measured LFP trough phase, with both lagging approximately 45° behind the peak of the sinusoidal input when the input frequency was the same as the unforced oscillation frequency.

At the highest modulation frequencies, we observed occasional epochs of 1:2 entrainment in which one cycle of network oscillation occurred for two cycles of the stimulus modulation. This could be seen in the raw LFP traces as interspersed normal and double length cycles (Fig. 6b) and in the emergence of a subharmonic in the wavelet transform at half the modulation frequency (Fig. 6c). At the lowest modulation frequencies, the LFP response often showed a double trough (Fig. 6d), indicating a type of 2:1 entrainment, but with the two troughs tightly grouped in phase rather than evenly spaced.

DISCUSSION

We characterized the response of gamma-oscillating CA3 networks to perturbation by single pulse and sinusoidal inputs. We observed biphasic PRCs to three different types of stimulation, using two different means to induce oscillations, suggesting that this is a general property of gamma oscillations in this system. Such PRCs predict that the network oscillation can entrain to periodic inputs over a wide frequency range spanning the unperturbed frequency. This was confirmed using sinusoidal optogenetic stimulation, revealing a strong frequency-dependent phase relationship between stimulus and response.

Measurements of how oscillating local networks respond to simple temporally structured inputs provide a building block for understanding the complex dynamic patterns of inter-region coherence observed in vivo. Coherence between dentate and CA3 gamma oscillations varies in the awake state^1,2 and is enhanced during REM sleep³, although precise behavioral correlates remain unclear. Increased coherence between these regions may reflect changes in the input to CA3, which facilitate entrainment to dentate oscillations, specifically an increase in gamma frequency input from the dentate, or a decrease in gamma frequency fluctuations in other input pathways that will compete with the dentate to influence CA3 phase. Alternatively, changes in the dynamical state of the CA3 network itself may affect its entrainment properties. Such changes could include shifts in intrinsic frequency or along the axis of network states from asynchronous to strongly oscillatory.

The correspondence between our experimental data and model supports the use of coupled neural mass models and their spatially continuous counterpart, neural fields²³, to study large-scale coherence dynamics. Further work is required to identify the extent to which the observations generalize to other network oscillations. We anticipate that the basic finding of biphasic PRCs will generalize widely to sparsely synchronized oscillations in different systems. Such PRCs are a general feature of oscillations arising through supercritical Hopf bifurcations²⁴, which are thought to underlie the transition between asynchronous and sparsely synchronized states^25,26.

Our results extend recent findings of a correlation between the amplitude of a given gamma cycle and the interval to the next cycle²⁷, which led to the proposal that larger cycles recruit more inhibition, resulting in longer-lasting hyperpolarization and delay of the next cycle. Although a correlation between cycle amplitude and duration occurs in both our experimental data and the noisy Wilson-Cowan model (data not shown), our results suggest a somewhat more complex picture of how excitation and inhibition interact to determine cycle duration. Specifically, our results suggest that a perturbation that excites inhibitory cells may either advance or delay the next cycle of the oscillation, depending on the phase at which it is delivered. A perturbation that drives excitatory cells alone can also either advance or delay the next cycle, although the regions of advance and delay are shifted in phase. We argue that to understand the effects of external perturbations or intrinsic fluctuations on phase, and hence instantaneous frequency, it is useful to consider the direction of perturbation relative to local isochrons in a two-dimensional phase plane defined by the excitatory and inhibitory activity levels.

Much recent interest in coherence patterns in vivo stems from the hypothesis that they may have a functional role in controlling signal flow between networks. Our results do not speak directly to this, as they do not address the critical question of what effect local circuit and inter-region synchronization has on the gain for propagation of population-coded signals⁸. They do, however, demonstrate that the dynamics of the oscillating local circuit are well suited to generating inter-region synchronization, a necessary prerequisite for such mechanisms. In addition, our results provide an insight into how the relative phase of coupled oscillating networks may be controlled, which is a potentially powerful mechanism for controlling the gain of functional interactions. First, the strong dependence of entrainment phase on driving frequency indicates that varying the relative intrinsic frequency of coupled networks can control their phase relationship. Indeed, we previously found that differences in intrinsic frequency in a feed-forward pathway can generate phase offsets that can be exploited for selective gain control⁸. Second, phase relationships could be controlled by exploiting the shift in the PRC that occurs as the relative coupling of an input to the excitatory and inhibitory populations is varied. As this does not require driving oscillators away from their intrinsic frequency, it may be more stable at large phase offsets and permit coupling through weaker connections than mechanisms exploiting differences in natural frequency.

Finally, understanding how oscillating networks respond to temporally structured inputs can facilitate the design of experiments that seek to test the functional relevance of oscillations by manipulating them in vivo²⁸. The observed biphasic PRCs indicate that intrinsic oscillations will entrain readily to periodic stimulation, particularly around the natural frequency, where very weak perturbation may be sufficient to substantially bias the phase. Optogenetic stimulation using sinusoids or sinusoidally modulated ramps of light intensity offer potential advantages over pulse trains in this context, as they minimize harmonics and sharp onset transients on each cycle. Such stimuli may therefore allow control of oscillation phase while minimizing aberrant excessive synchronization and other disruption of the temporal structure of activity.

METHODS

Methods and any associated references are available in the Supplementary Data.