Chain entropy: Spoiler or benefactor in pattern recognition?

Although how life began on our planet will always be of intrigue, polymers must have certainly existed before the beginning of life, because life as we now know it requires replicating polymers. There is little doubt (1) that replication of polymers, e.g., DNA, involves complexation among molecules consisting of complementary specific chemical sequences. Such processes of recognition of chemical patterns occur even within one macromolecule leading to tertiary structures (2–6) originating from patterned primary structures, e.g., protein folding. Thus macromolecular recognition of specified chemical patterns, mediated through a combination of coulombic, hydrogen bonding, hydrophobic and hydrophilic, and van der Waals forces, has manipulated evolution of humans and other organisms in this planet over three and half billion years. Yet, little progress has been made in this problem of tremendous significance.

The most straightforward approach to this problem is to directly solve a specific example with appropriate details of potentials between all pairs of atoms in the system. But this computational methodology, in its present status, cannot address the large-scale aspects of macromolecular recognition, as seen overwhelmingly in biological contexts (1). The alternate method is to coarse-grain nonessential microscopic details and consider only the bare essentials of potential interactions and accompanying entropy of self-assembled complexes. Only recently, general principles guiding the macromolecular pattern-recognition process were addressed (7–9). The most important principle of pattern recognition by polymers is the entropic frustration leading to topological dereliction (7–9). According to this principle, the entropy associated with different ways of cooperatively arranging various moieties of macromolecular complexes leads to rugged and hilly free-energy landscapes such that the unavoidable presence of lowest free-energy states at intermediate stages of pattern recognition can actually make the approach to the final fully recognized state much delayed, and that the distance between different paths diverges with time. It is therefore necessary to temporally modify the free-energy landscape to guide the pattern recognition to be successful and efficient. By using dynamic Monte Carlo simulations of a two-component heteropolymer bearing statistical patterns of sequences in the proximity of a heterogeneous surface bearing statistical patches of chemistries with short-range interaction toward the polymer, a vivid demonstration of the above-mentioned theme of pattern recognition is reported in this issue of PNAS by Golumbfskie et al. (10).

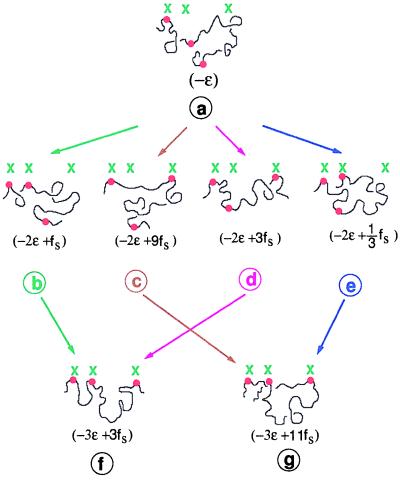
Consider the following simple but exact argument, which illustrates entropic frustration and the devastating role it plays in pattern recognition. Let us imagine a scenario of recognition of a pattern imprinted on a surface by a polymer containing chemical groups complementary to the surface pattern. Somewhere intermediate in the evolution of this process, many pairings would have occurred and many other pairings remain to be made. At this intermediate juncture, let us follow the details of sequentially making three new pairs in the immediate future (Fig. 1). Consider only three units (labeled i = 1, 2, 3, and green) making up a linear pattern with spacing between i = 1 and i = 2 being b (in units of polymer segment length), and that between i = 2 and i = 3 being 2b in three- dimensional space. (The shape of the pattern, chosen here to illustrate the argument for a specific case, can be generalized to any situation). Let us proceed to monitor the recognition of this pattern by a portion of a polymer with three special groups (labeled i_p = 1, 2, 3, and red) complementary to green groups. For specificity, we assume that there are m segments between i_p = 1 and i_p = 2 and 2 m segments between i_p = 2 and i_p = 3. Also i_p = 1 segment complexes with i = 1, as shown in Fig. 1a. Assuming that the polymer obeys Gaussian statistics, and the gain in energy per pairing is −ɛ, the free-energy F corresponding to the configuration of Fig. 1a is −ɛ. The second contact between the polymer and the pattern can take place in four possible ways. Each of i_p = 2 and i_p = 3 can be paired with either i = 2 or i = 3. These are shown in Fig. 1 b–e. When i_p = 2 is paired with i = 2, the end-to-end distance of the polymer spacer with m segments is b, and the entropy of the loop in Fig. 1b is −3k_Bb²/2m, apart from uninteresting constants, where k_B is the Boltzmann constant. Therefore, the free energy of the topological state of Fig. 1b is −2ɛ + f_s, where f_s = 3k_BTb²/2m is the free energy associated with the loop arising from entropy. Similarly, the complexes with contacts (i_p = 2; i = 3), (i_p = 3; i = 3), and (i_p = 3; i = 2) have free energies −2ɛ + 9f_s, −2ɛ + 3f_s, and −2ɛ + f_s/3, respectively. It must be noted that the topological state of Fig. 1e (i_p = 3; i = 2) is the most stable as far as two-contact complexes are considered (and for b²/m > 2 ln 3, if we keep track of all numerical prefactors).

Figure 1.

Topological dereliction caused by loop entropy.

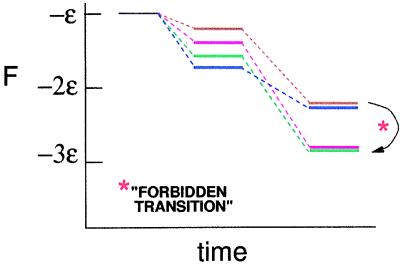
Proceeding now to consider the three-contact complexes, there are only two such complexes, as shown in Fig. 1 f and g, with respective free energies −3ɛ + 3f_s and −3ɛ + 11 f_s. Assuming sequential pairing, the complex with full registry given in Fig. 1f can arise only from Fig. 1 b and d. The complex of Fig. 1g can arise from Fig. 1 c and e. This free-energy landscape is sketched in Fig. 2, where free energies F of various topological states in the present specific example are plotted against time, which is proportional to the number of sequential pairings. Although the most stable complex with only two contacts is that of Fig. 1e, its further evolution to the three-contact state is to a state with higher free energy and not to the lowest free-energy state. It is obvious from the configurations of the complexes shown in Fig. 1 f and g that these configurations cannot be directly converted to each other, marked as a forbidden transition in Fig. 2. The only way the complex of Fig. 1g can relax to that of Fig. 1f is to trace its trajectory backward to its original state and try again to avoid the free-energy minimum state at an intermediate time. Thus any effort to minimize the free energy of the system at intermediate times can make the trajectory further away from the proper trajectory leading to the fully registered state of the complex.

Figure 2.

Spontaneous achievement of most-favored state in the immediate future leads to an unfavorable state at later times.

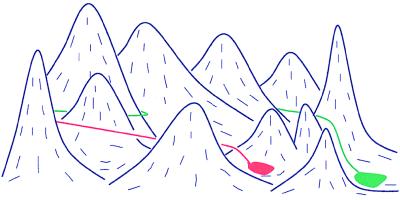
This situation then forces the system to explore only parts of the phase space leading to its dereliction, arising from entropy associated with possible topological states. The above exact argument for the formation of only three pairings can readily be generalized to M (≫1) pairings with chosen sequences for the surface pattern and polymer with the same major conclusion as above. Typical landscape of free energy (sum of energy gain and entropy of a collection of chain loops) for a large system of pattern recognition is sketched in Fig. 3, where the green trail is the necessary path for full recognition, and the red trail is the path taken by minimizing the free energy of the system at every time step of evolution. This illustrates the necessity of optimized temporal tampering of free-energy landscapes by using external fields to achieve efficient and full pattern recognition. The same qualitative arguments are valid for the recognition process involving patterns even within a single-polymer chain.

Figure 3.

Divergence of distance between paths with time.

The measurable consequences of such landscapes are profound. Returning to the example of only three pairings, we know the free energies of all seven (j = 1–7) topological states and various allowed pathways connecting these, as indicated in Fig. 2. Therefore, using methods in chemical kinetics, we can calculate the time evolution of the population in a particular topological state. If k_pq is the “reaction” rate constant for going to qth state from pth state, the time dependence of concentration of the system in the jth state is given by ρ_j = Σ_μ=1⁷ α_μ exp(−t/τ_μ), where τ_μ and α_μ are the relaxation time and amplitude, respectively, for the μth normal mode. For a pattern recognition involving M (>>1) pairings, 7 in the above sum is to be replaced by a very large number. This result cannot be distinguished from a stretched exponential, ρ_j ≃ exp[−(t/τ)^β], where the parameters τ and β measure the extent of topological dereliction. Furthermore, because the free energies of various states are known, the temperature dependence of entropy of the whole system can be calculated. It has been shown (7–9) that total entropy of a pattern-recognizing system gradually decreases as the temperature is reduced and then smoothly crosses over to that of a fully recognized state without encountering any catastrophe. The stretched exponential nature of time evolution and the above-mentioned temperature dependence of entropy are typical properties of glasses (11) and other frustrated systems (12), where the origins of frustrations are different from loop entropy.

The simulations of Golumbfskie et al. (10) beautifully illustrate all of the above-discussed features of entropic frustration, as originally enunciated (7–9). The dynamics of a partially pattern-recognized complex consisting of many loops is demonstrated to be highly cooperative leading to stretched exponential correlations in various properties. The behavior of complexed polymer is also shown to be dramatically different from that of a complexed single particle. The difference is because of the necessary navigation through entropic barriers arising from polymer loops. One of the key results of this report is the argument that by matching the statistics of the polymer sequence and site distributions on the polymer, the loop fluctuations are suppressed and probability of polymer binding is higher. This argument has a strong potential to formulate new separation protocols. Simulations of simple models of the type studied by Golumbfskie et al. (10) need to be extended further. We mention only a few issues here. How do we learn about recognition of unique patterns such as those in biology from studies on statistical patterns (10)? What is the role of long-range interactions in self assembly (7–9, 13, 14)? How do fluctuations in the preparation of statistical patterns influence the efficiency of binding? What is the relationship between the relaxation time of loops and the degree of recognition? How does the pattern recognition proceed in a crowded environment consisting of many chains, each with a unique sequence?

The multitude of diverging kinetic pathways present in pattern recognition between complementary pairs of polymers or a polymer and a surface occurs even for intrapolymer recognition, as in the problem of protein folding (2–6). Indeed, concepts and results discussed here resonate with issues in understanding how proteins fold (15, 16).

The model discussed above clearly establishes that the chain entropy associated with loops in the intermediate stages of pattern recognition is a spoiler of efficient recognition. The availability of a whole spectrum of topological states (e.g., Fig. 1 b–e) for the complex is responsible for the dereliction. To get rid of this frustration, we need to eliminate the possibility of occurrence of chain loops. This elimination of chain loops can be accomplished by tightening the sequence of the polymer, thus reducing the occurrence of entropically favored loops. Another strategy to reduce the ruggedness of the free-energy landscape is to keep the interaction energy ɛ very weak, so that mistakes can be readily erased and correct matching can follow immediately. These strategies are precisely those followed in biological contexts by DNA, RNA, and proteins. In these polymers, we rarely encounter a long contiguous sequence of only one kind of monomer (except for kinetic control in replication machinery), and energetics for a complementary pair of monomers are mild.

The precision and elegant complexity of pattern recognition at local length scales of biological phenomena such as signaling, formation of nucleosome, etc., are too rich to be addressed by statistical mechanics tools discussed in this Commentary. Nevertheless, there exists a class of biological problems where loop entropy plays as a benefactor in stabilizing large-scale structures derived from complementary macromolecules and controlling their lifetimes. One important example is the chromosome where chromatin loops are distributed differently with regulation during various stages of the cell cycle (1, 17, 18). A quantitative assessment of the relation between loop entropy and relative stabilities of macromolecular assemblies is a challenge.

The role of pattern recognition in the context of controlled fabrication of mesoscopic assemblies is clear. Here, chain entropy is a benefactor for designing a desired level of pattern recognition and achieving a wide range of structures and functions. The basic principle (19, 20) behind formulating self-organizing materials (involving liquid crystals, block copolymers, and hydrogen- and π-bonded complexes) is the same as discussed in Figs. 1–3. By playing with the spacer length (loop entropy), there is a great opportunity to fabricate a variety of self-organized structures with controllable lifetimes. In bulk polymer systems, the time associated with topological dereliction can be so long that fabrication of a particular desired morphology is impossible. Under these circumstances, it is necessary to alter the free-energy landscape by using external fields, such as chemical potential gradients through solvent evaporation or magnetic/electric or flow fields to quickly annihilate defects. Such strategies are analogous to the chaperons for biological molecules and patterned surfaces for artificial catalysis and sensors. One of the challenges that has not received adequate attention is the effect of simultaneous application of several external fields in guiding pattern recognition and self assembly.

Finally, we remark on a suggestion by Golumbfskie et al. (10), who attempt to connect the binding of a heteropolymer at a heterogeneous surface with the NK model (21) (where a system consists of N parts and each part is coupled to K other parts) of how populations evolve through a competition between self organization and selection. Although such highly questionable models of evolution and analogies to other models can be merely exciting games, macromolecular manipulations of pattern recognition have yet to have humans evolve to be sufficiently intelligent about such manipulations. However, the above discussion should convince the reader that there is a tremendous opportunity to make new materials by playing the game of loop entropy somewhere between that of Mother Nature designing human functions and that of a contemporary synthetic chemist formulating advanced plastics.