Unified Framework for Robust Estimation of Brain Networks From fMRI Using Temporal and Spatial Correlation Analyses

Abstract

There is a rapidly growing interest in the neuroimaging field to use functional magnetic resonance imaging (fMRI) to explore brain networks, i.e., how regions of the brain communicate with one another. This paper presents a general and novel statistical framework for robust and more complete estimation of brain functional connectivity from fMRI based on correlation analyses and hypothesis testing. In addition to the ability of examining the correlations with each individual seed as in the standard and existing methods, the proposed framework can detect functional interactions by simultaneously examining multiseed correlations via multiple correlation coefficients. Spatially structured noise in fMRI is also taken into account during the identification of functional interconnection networks through noncentral F hypothesis tests. The associated issues for the multiple testing and the effective degrees-of-freedom are considered as well. Furthermore, partial multiple correlations are introduced and formulated to measure any additional task-induced but not stimulus-locked relation over brain regions so that we can take the analysis of functional connectivity closer to the characterization of direct functional interactions of the brain. Evaluation for accuracy and advantages, and comparisons of the new approaches in the presented general framework are performed using both realistic synthetic data and in vivo fMRI data.

I. Introduction

Functional magnetic resonance imaging (fMRI) is a powerful technique that noninvasively measures and characterizes brain functions in humans under various cognitive and behavioral tasks. A thorough understanding of the neural mechanisms not only requires the accurate delineation of activation regions (“functional segregation or specification”) but demands precise description of function in terms of the information flow across networks of areas (“functional integration”). Various approaches have been proposed to extract association information from fMRI datasets, most of which rely on either functional or effective connectivity [1]. Functional connectivity has been identified as “temporal correlations between spatially remote neurophysiological events” [2]. In this work, motivated by the following four factors, we present a novel and general statistical framework for robust and more complete estimation of functional connectivity or interactivity. In addition, we provide comprehensive comparisons of the proposed methods in our framework, including using multiple and partial correlation analyses of fMRI data, and the single-seed based method using marginal correlation, with and without accounting for the spatial noise correlations.

First, for functional connectivity studies, a common approach is to calculate the temporal correlation coefficients of a fMRI signal from a selected voxel or region (so-called “seed,” or “seed region”) in a region of interest with all other voxels in the brain [3]. Different strategies have been developed in the literature to select the seed voxel or region [4]. Each correlation map is resulting from the cross correlation of only one seed region. However, when areas with quite different time series patterns are used as seed regions for brain connectivity inference, they should not be grouped as a single region; in some applications, functional co-activation to multiple seeds rather than a single one would be of particular interest. Multiple seeds can be chosen to calculate multiple correlation maps to separately discover the functional connectivity to different seeds. But how to reasonably integrate multiple connectivity maps for brain function inference is still unresolved and ambiguous. Furthermore, it is often unrealistic to examine all pair-wise correlations. Therefore, it is desirable to have a single correlation map resulting from the cross correlation of two or more seed regions simultaneously. A related goal is achieved in [5], which studies hippocampal connectivity in the brain by using a multiple regression analysis. However, in addition to accounting for the spatial correlation of the fMRI data through the postprocessing of multiple comparison correction as in the typical univariate analysis (for example, through Gaussian kernel smoothing and random field theory based multiple testing correction [6]), we are also interested in accounting for the spatial correlations of the noise while we estimate the functional connectivity at each voxel through temporal correlation analyses.

Second, when investigating effective connectivity, the first level of information required concerns the regions involved in the process and forming the spatial support of the network, which is in fact nontrivial. Functional connectivity developed in this work can serve as a technique for such purpose. Compared to existing approaches such as principal or independent component analysis, or correlation maps [2], [7]–[9], the advantage of the present methods is that the identified functionally connected regions can then be used as additional new seed regions for recursive and further connectivity exploration due to a major feature of our method—the ability to handle multiple seed regions simultaneously. Using one seed region to identify functional connectivity may detect only a subset of a specific neural system, and would not recover co-activation networks or regions to multiple seeds due to the fact that the correlations to only one of the seeds may not be high enough to be shown as significant. Also, it may underestimate the size and number of areas involved in a task performance. Our functional connectivity framework offers the possibility of more complete and powerful detection of specific neural systems by allowing one and multiple regions as seed(s).

The third motivation of the present work is related to the spatial correlations of the noise in the fMRI data. Dynamic connections in fMRI are thought to be reflected by high temporal correlations of the time series. The strong correlation between the time series of each region in the network with that of another distant region implied by the functional interactions may be related to the spatially structured noise in fMRI [10]. The spatial correlations of the noise must therefore be taken into account when dealing with sensitive and reproducible estimation of the network. Recently, an approach for large-scale network identification in fMRI was proposed in [11] by considering the noise structure in the data. However, this method is again entirely restricted to connectivity detection between pair-wise (one to one) brain areas through regular Pearson's linear correlation (i.e., marginal correlation) analysis and can not handle multiple regions simultaneously [12]. Other efforts in modeling the spatial dependencies in fMRI [13], [14] are successful in activation detection but have yet been incorporated into brain connectivity studies.

Finally, brain functional connectivity based on marginal correlation can be dominated by the stimulus-locked responses. For example, if visual and auditory stimuli are presented concurrently, the stimulus-locked neural responses would cause increases in the BOLD signal in the primary auditory cortex (A1) and the primary visual cortex (V1) simultaneously. Correlation between A1 and V1 would thus be high, though not due to any intrinsic task-induced functional couplings but due to the responses in both regions to externally driven stimuli. Partial correlation is the conditional correlation which estimates any remaining correlation between time series after taking into account the relationship of each to one or more reference time series. The stimulus-locked responses can then be accounted for by choosing the reference functions to model the external stimuli. This allows us to measure any additional task-induced, but not stimulus-locked relation over brain regions. Recently, methods using partial correlation (or coherence) have been proposed [15], [16], though they are for pair-wise correlation (or coherence) analysis and not applicable to multiple seeds. In addition, the partial correlation in [16] is for subtracting and removing mutual dependencies on common influences from other brain areas rather than from stimulus-locked responses. How to apply the partial correlation concept to multiple seed regions to brain connectivity study while considering spatial partial correlations in noise to those seed regions is challenging and has not yet been pursued in the literature. Here, we propose a novel procedure to achieve this as one of the goals of this work.

The objective of the present paper is to develop new and general statistical framework to estimate brain networks based on multiple correlations and partial multiple correlations of fMRI data. To the best of our knowledge, this work shows for the first time an innovative application of multiple and partial multiple correlation analyses to study brain connectivity caused by multiple seed regions. Note that a special case of our multiseed framework is the single-seed method. The remainder of the paper is organized as follows. In Section II, we describe our strategy of determining seed regions. The novel methods and our mathematical formulations for functional connectivity estimation based on multiple seeds using multiple correlations and partial multiple correlations are proposed in Sections III and IV, respectively. Experiments and results on both simulated and real fMRI data are presented in Sections V and VI, followed in Section VII by conclusions and discussions for this work.

II. Determining Multiple Homogeneous Seed Regions

We select multiple seed regions based on their respective functional homogeneity as well as their known involvement in the functional or behavioral task and our interest in characterizing their interactions with other regions of the brain. The functional homogeneity is achieved with a region growing algorithm, and the related techniques have been applied in [11] for finding homogeneous brain regions. More specifically, in this work, through the standard general linear model analysis [17] using contrasts of interest (i.e., categorical comparisons), we can identify activation regions of interest by thresholding the parametric t statistic maps. Among the activation regions, we can have the approximate locations of the seed regions based upon their known involvement in characterizing brain networks of interest. For example, we might be interested in using the hippocampus or the primary visual cortex (V1) as the seed. For each of the activation regions that we use as a seed, we determine its precise location or choose the voxels (among those above the threshold), whose time series will be utilized as seeds for the connectivity analysis, with the following technique. Starting from a peak activation voxel (i.e., the maximum t statistics voxel), we let the seed region grow by merging with other neighboring voxels based on a similarity criterion, such as the Pearson's linear correlation between the time series of the peak voxel and the candidate voxel considered to be merged. The procedure is repeated for each of the activation regions to be used as seeds so that we can precisely localize the seed regions (i.e., the associated voxels for each of the seed regions). Let the identified seed regions be denoted as S₁, S₂, …, S_P, where P is the total number of regions. For subsequent statistical analysis, the mean time series of any seed region (i.e., the average time course for all time courses of the voxels within a seed region) is utilized as the time series of that seed region, and the centroid of the region is considered to be the position of the corresponding seed region. Using the mean time series can make the results more robust to the imprecise localization of the seed regions.

III. Functional Connectivity Using Multiple Correlations

A. Estimating Temporal/Sample Multiple Correlations

The temporal or sample multiple correlation coefficient considers the fMRI time series correlation between a given voxel X and a combination of seed regions, S₁, S₂, …, S_P. Its estimation is based on the variance–covariance matrix

$$\begin{array}{cc}\hfill {\widehat{\Sigma }}_{\text{tem}}& =\left[\begin{array}{cccc}\hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,S_P}\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,X}\hfill & \hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_{S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,S_P}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,X}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_{S_P}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}^{\prime }\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{SS}}\hfill \end{array}\right]\hfill \end{array}$$

where var_X and var_SP are the time series variances for voxel X and seed S_P(p = 1, 2, …, P), respectively; and cov_{X, Sp} is their covariance. Their estimation can be achieved through

$$\mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X=\frac{1}{T-1}\sum _{i=1}^T{(y_X\left(i\right)-{\stackrel{‒}{y}}_X)}^2$$

$$\mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_{S_p}=\frac{1}{T-1}\sum _{i=1}^T{(y_{S_p}\left(i\right)-{\stackrel{‒}{y}}_{S_p})}^2$$

$$\begin{array}{cc}\hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,S_p}& =\mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_p,X}\hfill \\ \hfill & =\frac{1}{T-1}\sum _{i=1}^T(y_X\left(i\right)-{\stackrel{‒}{y}}_X)(y_{S_p}\left(i\right)-{\stackrel{‒}{y}}_{S_p})\hfill \end{array}$$

where T is the total number of time points; y_X(i) and y_Sp(i) (for i = 1, 2, …, T) are, respectively, the time series for voxel X, and seed S_p (i.e., the mean time series of seed region S_p); and ${\stackrel{‒}{y}}_X$ and ${\stackrel{‒}{y}}_{S_p}$ are the corresponding averages over T. The temporal multiple correlation coefficient ${\widehat{R}}_{\mathrm{tem}}$ between voxel X and the multiple seeds [S₁, S₂, …, S_P]′ can be calculated as [18]

$${\widehat{R}}_{\text{tem}}=\sqrt{\frac{\mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}^{\prime }\cdot {\widehat{\Sigma }}_{\mathrm{SS}}^{-1}\cdot \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}}{\mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X}}.$$

B. Estimating Spatial Multiple Correlations in Noise

The main factors contributing to the spatial correlation of the noise include fMRI data preprocessing, the point spread function, which causes data from an individual voxel to contain some signal from the tissue around that voxel, an effect compounded by motion correction techniques, and the smoothness introduced by interpolation in motion correction [19]. Despite the strategies and efforts to reduce such structured noise [20], [21], some residual and further corrections are still essential for robust fMRI data analysis.

1) Voxel-Based Spatial Correlograph of Noise

We assume the spatial noise is stationary and has a multivariate Gaussian distribution with variance–covariance matrix $\Sigma ={\left({\sigma }_{i,j}\right)}_{i,j}^M$, where M is the total number of voxels; σ_i and σ_j are positive standard deviations for voxels X_i and X_j. The spatial correlations in noise then depend only on the spatial distance between voxels: σ_ij = σ_iσ_jρ(∥i − j∥), where ∥i − j∥ denotes the spatial distance or lag between X_i and X_j; and ρ is the spatial correlogram, a real-valued function that satisfies ρ(0) = 1 and is bounded by − 1 and 1. Such a spatial model is valid if and only if the resulting variance–covariance matrix Σ is positive-definite [22].

Since it is unknown what voxels or regions are predominantly influenced by the noise, the entire set D_h = {(X_i, X_j)|∥i − j∥ = h} of pairs of voxels at lag h over the whole brain area is considered for the nonparametric estimate based on the median: $\widehat{\rho }\left(h\right)=\mathrm{median}\{r_{ij},(X_i,X_j)\in D_h\}$, where r_ij is the Pearson's linear correlation between the time series of the two voxels. As in general the empirical estimator $\widehat{\rho }$ of the correlogram does not provide a positive-definite correlation matrix, we focus on a parametric class of valid matrices, based on the empirical values $\widehat{\rho }$ estimated from the fMRI data. The rational-quadratic model ρ_θ(h) in [22] is utilized for such purpose

$$\{\begin{array}{c}{\rho }_{\theta }\left(0\right)=1,\hfill \\ {\rho }_{\theta }\left(h\right)=1-{\theta }_1-{\theta }_2\frac{h^2}{1+\frac{h^2}{{\theta }_3}},\forall h>0\hfill \end{array}\phantom{\}}$$ (1)

where θ = (θ₁, θ₂, θ₃) is a parameter vector of three nonnegative real values with θ₁ + θ₂θ₃ < 1. The derived spatial correlogram of noise, ρ_θ(h), decreases rapidly from a correlation level between nearby voxels, ρ₀₊, towards an asymptotic correlation, ρ_∞. A critical distance $h_{\infty }^{\epsilon }$ can be determined beyond which the correlogram is almost equal to the asymptote, with a tolerance of ε. The parameterization of the rational-quadratic model using ρ₀₊, ρ_∞, $h_{\infty }^{\epsilon }$ is given as below [11]

$$\{\begin{array}{c}{\rho }_{0+}=1-{\theta }_1\hfill \\ {\rho }_{\infty }=1-{\theta }_1-{\theta }_1{\theta }_2\hfill \\ {\left(h_{\infty }^{\epsilon }\right)}^2=(\frac{{\theta }_2{\theta }_3}{\epsilon }-1){\theta }_3\hfill \end{array}\phantom{\}}.$$

Note that the Bartlet interval argument [23] could potentially be utilized as an alternative way to determine $h_{\infty }^{\epsilon }$.

2) Spatial Multiple Correlations in Noise

The spatial multiple correlations of the noise consider the correlations between any voxel X and a combination of multiple seeds S₁, S₂, …, S_P. As shown in Fig. 1, suppose the distances between the voxel X and the seeds S₁, S₂, …, S_P are, re-spectively, h₁, h₂, …, h_P and the distances between any pair-wise seeds are h_ij(for S_i and S_i, h_ij = h_ji). The noise spatial correlation matrix for [X, S₁, S₂, …, S_P]′ can then be constructed as

$$\begin{array}{cc}\hfill {\Lambda }_{\text{spa}}& =\left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\rho }_{\theta }\left(h_1\right)\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }\left(h_P\right)\hfill \\ \hfill {\rho }_{\theta }\left(h_1\right)\hfill & \hfill 1\hfill & \hfill \hfill & \hfill {\rho }_{\theta }\left(h_{1P}\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\rho }_{\theta }\left(h_P\right)\hfill & \hfill {\rho }_{\theta }\left(h_{P1}\right)\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\rho }_S^{\prime }\hfill \\ \hfill {\rho }_S\hfill & \hfill {\Lambda }_{\mathit{SS}}\hfill \end{array}\right]\hfill \end{array}$$

where ρ_θ(h) is the correlogram estimated above. Let ${\sigma }_X^2$ and ${\sigma }_{S_p}^2$, respectively, denote the noise variance for voxel X, and seed S_p p = 1, 2, …, P (see the Appendix for their estimation). Then the corresponding variance–covariance matrix, Σ_spa is shown in the equation at the bottom of the page. The spatial multiple correlation coefficient of the noise between any voxel X and the seeds [S₁, S₂, …, S_P]′ is computed as $R_{\mathrm{spa}}=\sqrt{{\sigma }_{XS}^{\prime }\cdot {\Sigma }_{SS}^{-1}\cdot {\sigma }_{XS}∕{\sigma }_X^2}$, and can be reformulated to

$$R_{\text{spa}}=\sqrt{{\rho }_{\mathrm{S}}^{\prime }\cdot {\Lambda }_{\mathrm{SS}}^{-1}\cdot {\rho }_{\mathrm{S}}}.$$ (2)

Fig. 1.

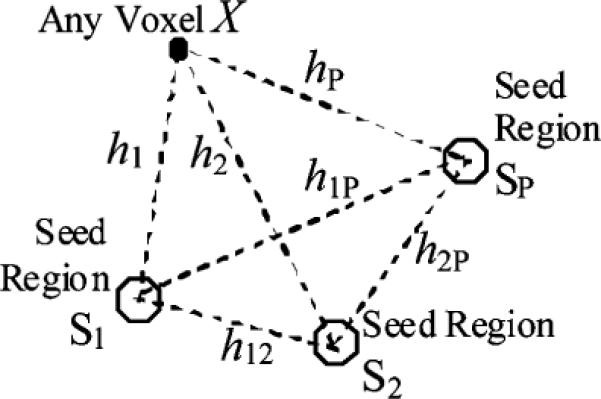
Configuration diagram for the P seed regions and a random voxel X.

C. Identifying Functional Connectivity of Brain

Given the estimation of multiple correlations in noise, we use hypothesis testing to search for significant correlations between any voxel and the seed regions that are statistically unlikely to be due to noise.

1) Statistical Hypothesis Testing

We would like to test whether the temporal multiple correlation ${\widehat{R}}_{\mathrm{tem}}$ is likely to be found only by chance from the noise correlation. The hypothesis is

$$H_0:R_{\text{tem}}=R_{\text{spa}}\text{vs}\cdot H_1:R_{\text{tem}}>R_{\text{spa}}.$$

Under the null hypothesis that the temporal multiple correlation, ${\widehat{R}}_{tem}$, arises from a population whose multiple correlation equals the spatial multiple correlation of the noise, R_spa, the following quantity is a noncentral F [18, p. 153–154]

$$F=\frac{{{\widehat{R}}^2}_{\text{tem}}}{1-{{\widehat{R}}^2}_{\text{tem}}}\cdot \frac{T-1-P}{P}.$$ (3)

Here, the degrees-of-freedom are P and T − 1 − P, and the noncentrality parameter is $(T-1){\sigma }_{X\mathrm{S}}^{\prime }{\Sigma }_{\mathrm{SS}}^{-1}{\widehat{\Sigma }}_{\mathrm{SS}}{\Sigma }_{\mathrm{SS}}^{-1}{\sigma }_{X\mathrm{S}}∕\left((1-R_{\mathrm{spa}}^2){\sigma }_X^2\right)$, where we condition on the seeds' time series. In the present work, due to the reformulated R_spa in (2), the noncentrality parameter can be shown to be: $(T-1){\rho }_{\mathrm{S}}^{\prime }{\Lambda }_{\mathrm{SS}}^{-1}\Psi {\widehat{\Sigma }}_{\mathrm{SS}}\Psi {\Lambda }_{\mathrm{SS}}^{-1}{\rho }_{\mathrm{S}}∕(1-{\rho }_{\mathrm{S}}^{\prime }\cdot {\Lambda }_{\mathrm{SS}}^{-1}\cdot {\rho }_{\mathrm{S}})$, where Ψ is a P × P diagonal matrix with diagonal element $1∕{\sigma }_{S_p}^{\ast }$, for p = 1, 2, …, P. In this way, the p-value for each voxel can be calculated from this noncentral F distribution. A

$$\begin{array}{cc}\hfill {\Sigma }_{\text{spa}}& =\left[\begin{array}{cccc}\hfill {\sigma }_X^2\hfill & \hfill {\rho }_{\theta }\left(h_1\right)\cdot {\sigma }_X\cdot {\sigma }_{S_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }\left(h_P\right)\cdot {\sigma }_X\cdot {\sigma }_{S_P}\hfill \\ \hfill {\rho }_{\theta }\left(h_1\right)\cdot {\sigma }_{S_1}\cdot {\sigma }_X\hfill & \hfill {\sigma }_{S_1}^2\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }\left(h_{1P}\right)\cdot {\sigma }_{S_1}\cdot {\sigma }_{S_P}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\rho }_{\theta }\left(h_P\right)\cdot {\sigma }_{S_P}\cdot {\sigma }_X\hfill & \hfill {\rho }_{\theta }\left(h_{P1}\right)\cdot {\sigma }_{S_P}\cdot {\sigma }_{S_1}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{S_P}^2\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill {\sigma }_X^2\hfill & \hfill {\sigma }_{X\mathrm{S}}^{\prime }\hfill \\ \hfill {\sigma }_{X\mathrm{S}}\hfill & \hfill {\Sigma }_{\text{SS}}\hfill \end{array}\right]\hfill \end{array}$$

voxel shall be included in the functional connectivity network if the corresponding p-value is smaller than a prechosen type I error α (note: α = 0.05 is used in this paper).

It can also be shown that under the null hypothesis of the population multiple correlation, R_spa, is zero (i.e., our hypothesis becomes: H₀ : R_tem = 0 vs · H₁ : R_tem > 0), the F in (3) is a central F[18, p. 149–150], with P and T − 1 − P degrees-of-freedom. In fact, this is equivalent to multiple correlation analysis of multiseed functional connectivity but without taking the spatial correlations of the noise into consideration.

2) Effective Degrees-of-Freedom for Temporal Autocorrelation

A departure from the temporally independent and identically distributed (i.i.d.) assumption due to the temporal autocorrelation will result in a decrease in the degrees-of-freedom in the above hypothesis testing. To correct such possible bias, we estimate the effective degrees-of-freedom T_eff. This can be achieved through the context of the general linear model [24]. Note that the T_eff estimated this way assumes voxelwise spatial independence, which can be considered as an upper-bound estimation of our effective degrees-of-freedom. More relaxed or more precise estimation accounting for the spatial correlation can be a future work. In this paper, we approximate the effective degrees-of-freedom as T_eff, and use the estimated T_eff to replace the T − 1 in the F statistic's calculation in (3).

3) Multiple Testing Using Noncentral F Random Field

We need to perform numerous tests equal to the total number of voxels over the brain area. In order to correct this multiple testing problem, different strategies can be potentially applied, such as Bonferroni correction, cluster-size thresholding, random field theory or false discovery rate control [25]–[30].

The Random field theory (RFT) correction on the t-field, Hotelling's T² field, χ² field, central F field, and the correlation field has been developed by Worsley et al. [6], [31]. RFT estimates the number of independent statistical tests based upon the spatial correlation, or smoothness, of the experimental data. With even small to moderate amounts of smoothness in the data, the number of resels (resolution elements) will be much less than the original number of voxels. From the number of resels, one can estimate how many clusters of activity should be found by chance at a given statistical threshold. This number is known as the Euler characteristic of the data. RFT correction is less conservative than the Bonferroni correction. Recently, Hayasaka et al. [32] has derived the noncentral F RFT for the calculation of power and sample size. In this paper, we use the noncentral F RFT to correct the multiple comparison problems.

Suppose α is the type I error (false–positive rate) of the whole procedure

$$\alpha =\mathrm{P}(\max F>tf)\approx \sum _{d=0}^3{\text{Resels}}_{d}E{C}_d\left(tf\right)$$

where F is noncentral F test statistics, Resels_d is the number of d-dimensional resels in the region and EC_d(tf) is the d-dimensional Euler characteristic density. The above approximation is based on the fact that left-hand side is the exact expectation of Euler characteristic of region above the threshold tf. The formulas for the calculation of Resela_d are given in [3]. The EC₀, EC₁, EC₂ and EC₃ for a noncentral F-random Field have recently been derived in [32]. Based on the desired α, Resels_d and α, we can find the threshold tf for the noncentral F random field given by our (3) for multiple comparison correction.

IV. Functional Interactivity Using Partial Multiple Correlations

Based on our multiple correlation formulations in Section III, we describe in this section our multiseed method and mathematical formulations using partial multiple correlations.

A. Estimating Temporal Partial Multiple Correlations

The temporal partial multiple correlation coefficient considers the fMRI time series correlation between a given voxel and a combination of seed regions S₁, S₂, …, S_P conditioned on fixed stimuli (experimental paradigms or reference functions, i.e., the convolution functions of the hemodynamic response with the 0–1 boxcar stimulus functions in the case of the block-design experiments), V₁, V₂,…, V_N. Its estimation is based on the matrix the equation shown at the bottom of the page, where var_Vn is the time series variances of the stimulus V_n (n = 1,2,…, N); cov _X,Vn is the covariance between voxel X, and V_n, and cov S_p, V_n is the covariance between the seed S_p and V_n. Their estimation can be achieved through time series and reference function samples of size T (as the one for var _X, var_Sp and cov_X,Sp Lgiven in Section III-A), though here they are

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccccccc}\hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{x}}_X\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,S_1}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,V_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X,V_N}\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,X}\hfill & \hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_{S_1}\hfill & \hfill \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,S_P}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,V_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_1,V_N}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,X}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_{S_P}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,V_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{S_P,V_N}\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_1,X}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_1,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_1,S_P}\hfill & \hfill {\text{var}}_{V_1}\hfill & \hfill \cdots \hfill & \hfill {\mathrm{cov}}_{V_1,V_N}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_N,X}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_N,S_1}\hfill & \hfill \cdots \hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{V_N,S_P}\hfill & \hfill {\text{cov}}_{V_N,V_1}\hfill & \hfill \cdots \hfill & \hfill {\text{var}}_{V_N}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}\hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{V}}^{\prime }\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{SS}}\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{SV}}^{\prime }\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{V}}\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{SV}}\hfill & \hfill {\Sigma }_{\mathrm{VV}}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill {\widehat{\Sigma }}_{\left\{X\mathrm{S}\right\}\left\{X\mathrm{S}\right\}}\hfill & \hfill {\widehat{\Sigma }}_{\left\{X\mathrm{S}\right\}\mathrm{V}}^{\prime }\hfill \\ \hfill {\widehat{\Sigma }}_{\left\{X\mathrm{S}\right\}\mathrm{V}}\hfill & \hfill {\Sigma }_{\mathrm{VV}}\hfill \end{array}\right]\hfill \end{array}$$

not technically variances and covariances because the V_n are fixed stimuli. With the assumption that the conditional distribution (X, S₁,…, S_p|V₁ = v₁,…, V₂ = v₂…, V_N = v_N)′ is a multinormal distribution [18], its variance-covariance matrix can be calculated as

$${\widehat{\Sigma }}_{\text{tem}}={\widehat{\Sigma }}_{\left\{XS\right\}\left\{XS\right\}}-{\widehat{\Sigma }}_{\left\{XS\right\}\mathrm{V}}^{\prime }\cdot {\Sigma }_{\mathrm{VV}}^{-1}\cdot {\widehat{\Sigma }}_{\left\{XS\right\}\mathrm{V}}.$$

Let the components of ${\widehat{\Sigma }}_{\mathrm{tem}}^{\ast }$ be divided into four groups

$$\left[\begin{array}{cc}\hfill \mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X^{\ast }\hfill & \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}^{\ast \prime }\hfill \\ \hfill \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{X\mathrm{S}}^{\ast }\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{SS}}^{\ast }\hfill \end{array}\right]$$

where ${v\widehat{a}r}_X^{\ast }$ and ${\widehat{\Sigma }}_{\mathrm{SS}}^{\ast }$ are variances of volex X and the seeds holding the reference functions (stimuli) fixed, ${c\widehat{o}v}_{XS}^{\ast }$ is their corresponding covariance under the same condition. Based on Section III-A, the temporal partial multiple correlation is thus

$${\widehat{R}}_{\text{tem}}\cdot \mathrm{V}=\sqrt{\frac{\mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{XS}^{\ast \prime }\cdot {\widehat{\Sigma }}_{SS}^{\ast -1}\cdot \mathrm{c}\widehat{\mathrm{o}}{\mathrm{v}}_{XS}^{\prime }}{\mathrm{v}\widehat{\mathrm{a}}{\mathrm{r}}_X^{\ast }}}$$

B. Estimating Spatial Partial Multiple Correlations in Noise

In Section III-B, we estimate the voxel-based spatial correlograph of noise using the median of Pearson's linear correlation, i.e., marginal correlation. Here, we take the similar approach but replace the marginal correlation with partial correlation because the stimuli are now considered to be fixed, i.e., $\widehat{\rho }\ast \left(h\right)=\mathrm{median}\{r_{ij\cdot \mathrm{V}},(X_i,X_j)\in D_h\}$ where r_ij·V is the partial correlation coefficient between voxels X_i and X_j holding V₁, V₂,…, V_N fixed, and its calculation is as below. Let the variance–covariance matrix of (X_i, X_j, V₁, …, V_N)′ be

$$\left[\begin{array}{cc}\hfill {\widehat{\Sigma }}_{\mathrm{XX}}\hfill & \hfill {\widehat{\Sigma }}_{\mathrm{XV}}^{\prime }\hfill \\ \hfill {\widehat{\Sigma }}_{\mathrm{XV}}\hfill & \hfill {\Sigma }_{\mathrm{VV}}\hfill \end{array}\right]\cdot (X_i,X_j\mid V_1=v_1,V_2=v_2,\dots ,V_N=v_N)\prime$$

is assumed to be multinormal and its variance–covariance matrix is calculated as

$$\begin{array}{cc}\hfill {\widehat{\Sigma }}_{\mathrm{X}\cdot \mathrm{V}}& ={\widehat{\Sigma }}_{\mathrm{XX}}-{\widehat{\Sigma }}_{\mathrm{XV}}^{\prime }\cdot {\Sigma }_{\mathrm{VV}}^{-1}\cdot {\widehat{\Sigma }}_{\mathrm{VX}}\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill {\widehat{\sigma }}_{i\cdot \mathrm{V}}^2\hfill & \hfill {\widehat{\sigma }}_{ij\cdot \mathrm{V}}^{\prime }\hfill \\ \hfill {\widehat{\sigma }}_{ij\cdot \mathrm{V}2}\hfill & \hfill {\widehat{\sigma }}_{j\cdot \mathrm{V}}^2\hfill \end{array}\right].\hfill \end{array}$$

The partial correlation coefficient is thus given by [18]

$$r_{ij\cdot \mathrm{V}}=\frac{{\sigma }_{ij\cdot \mathrm{V}}}{{\sigma }_{i\cdot \mathrm{V}}\cdot {\sigma }_{j\cdot \mathrm{V}}}.$$

The corresponding parametric correlogram ${\rho }_{\theta }^{\ast }\left(h\right)$ based on r_ij·V can then be estimated as in Section III-B.

The noise spatial partial correlation matrix for [X, S₁, S₂, …, S_P]′ holding V₁, V₂, …, V_N fixed can be constructed as

$$\begin{array}{cc}\hfill {\Lambda }_{\text{spa}}^{\ast }=& \left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\rho }_{\theta }^{\ast }\left(h_1\right)\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }^{\ast }\left(h_P\right)\hfill \\ \hfill {\rho }_{\theta }^{\ast }\left(h_1\right)\hfill & \hfill 1\hfill & \hfill \hfill & \hfill {\rho }_{\theta }^{\ast }\left(h_{1P}\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\rho }_{\theta }^{\ast }\left(h_p\right)\hfill & \hfill {\rho }_{\theta }^{\ast }\left(h_{P1}\right)\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right]\hfill \\ \hfill =& \left[\begin{array}{cc}\hfill 1\hfill & \hfill {\rho }_{\mathrm{S}}^{\ast \prime }\hfill \\ \hfill {\rho }_{\mathrm{S}}^{\ast }\hfill & \hfill {\Lambda }_{\mathrm{SS}}^{\ast }\hfill \end{array}\right]\hfill \end{array}$$

where ${\rho }_{\theta }^{\ast }\left(h\right)$ is the correlogram estimated above. Let ${\sigma }_{S_p}^{\ast }$ denote the residual standard deviation of the noise for seed S_p, p = 1, 2,…, p, holding V₁, V₂, …, V_N fixed (see the Appendix for its estimation). As in Section III-B, the spatial partial multiple correlation coefficient of the noise between any voxel and the seeds [S₁, S₂,…, S_P]′ holding the stimuli fixed is computed as

$$R_{\text{spa}\cdot \mathrm{V}}=\sqrt{{\rho }_{\mathrm{S}}^{\ast \prime }\cdot {\Lambda }_{\mathrm{SS}}^{\ast -1}\cdot {\rho }_{\mathrm{S}}^{\ast }}.$$

C. Identifying Conditional Functional Connectivity of Brain

We would like to test whether the temporal partial multiple correlation $\widehat{R}\mathrm{tem}{\cdot }_{\mathrm{V}}$ is likely to be found only by change from the noise correlation. The hypothesis is

$$H_0:R_{\text{tem}\cdot \mathrm{V}}{R}_{\text{spa}\cdot \mathrm{V}}\mathrm{VS}\cdot H_1:R_{\text{tem}\cdot \mathrm{V}}>R_{\text{spa}\cdot \mathrm{V}}\cdot$$

Here, we can show that the following quantity is a noncentral F

$$\frac{{\widehat{R}}_{\text{tem}\cdot \mathrm{V}}^2}{1-{\widehat{R}}_{\text{tem}\cdot \mathrm{V}}^2}\cdot \frac{(T-1)-N-P}{P}$$ (4)

with the degrees-of-freedom and P and the T − 1 − N − P, and the noncentrality parameter

$$(T-1){\rho }_{\mathrm{S}}^{\ast \prime }{\Lambda }_{\mathrm{SS}}^{\ast -1\prime }\Psi \ast {\widehat{\Sigma }}_{\mathrm{SS}}^{\ast }\Psi \ast {\Lambda }_{\mathrm{SS}}^{\ast -1}{\rho }_{\mathrm{S}}^{\ast }∕(1-{\rho }_{\mathrm{S}}^{\ast \prime }{\Lambda }_{\mathrm{SS}}^{\ast -1}{\rho }_{\mathrm{S}}^{\ast }),$$

where we condition on the seeds' time series; Ψ* is a P × P diagonal matrix with diagonal element $1∕{\sigma }_{S_p}^{\ast }$ for p = 1,2,…, P. Note that the temporal autocorrelation can be handled in a similar way as in the multiple correlation case by computing the associated effective degrees-of-freedom (see Section III-C); the multiple testing correction is similarly based on noncentral F random field theory as described in details in Section III-C.

Similar to the multiple correlation case (Section III-C), under the null hypothesis of the population partial multiple correlation, R_spa·V, is zero (i.e., our hypothesis becomes: H₀ : R_spa·V = 0 vs · H₁ : R_spa·V > 0) the F in (4) is a central F with P and T − 1 − N − P degrees-of-freedom. This is then equivalent to partial multiple correlation analysis of multiseed functional connectivity but without taking the spatial partial correlations of the noise into consideration.

V. Simulated Data Results

In the absence of any ground truth about the functional connectivity in the human brain, the validation of a new method for the analysis of fMRI data is always problematic. We propose therefore to first validate our approach with realistic simulated data in this section. We then proceed to the evaluation of our method using in vivo data in Section VI.

A. Data Generation

The simulated time series were composed of time- and space-correlated noise (see below for the detailed generation strategies), added on a base 3-D brain image with size 64 × 64 × 20. First, the space correlation was simulated based on a rational-quadratic parameter model described in Section III-B, with ρ₀+ = 0.4, ρ_∞ =0.001, and $h_{\infty }^{\epsilon }=20\mathrm{mm}$ (ε = 0.01). The parameters θ = (θ₁, θ₂, θ₃) of (1) were determined through the following equations [11]:

$$\{\begin{array}{ccc}\hfill {\theta }_1\hfill & \hfill =\hfill & \hfill 1-{\rho }_{0+}\hfill \\ \hfill {\theta }_3\hfill & \hfill =\hfill & \hfill \frac{\epsilon }{{\rho }_{0+}-{\rho }_{\infty }-\epsilon }{\left(h_{\infty }^{\epsilon }\right)}^2\hfill \\ \hfill {\theta }_2\hfill & \hfill =\hfill & \hfill \left(\frac{{\rho }_{0+}-{\rho }_{\infty }}{h_{\infty }^{\epsilon }}\right)\left(\frac{{\rho }_{0+}-{\rho }_{\infty }-\epsilon }{\epsilon }\right)\hfill \end{array}\phantom{\}}$$

The space correlation matrix was then derived by calculating ρ_θ(h) according to (1) and at the desired h lags. Temporally independent Gaussian data sets with this space correlation were generated as described in [22, p. 201–203] using a Cholesky decomposition of the space correlation matrix and Gaussian random samples generated using Matlab¹. Next, the time series were added with the autoregressive moving average ARMA(1,1) temporal noise [33], [34] to simulate the block-design fMRI(T =128). In addition, some randomly selected regions were further summed with different types of signal time series (boxcar functions convolved with the hemodynamic response function as defined by the SPM5 software package²; signal amplitude: 3%~ 5%) to simulate functional networks with multiple seed regions. We generated the data at four different noise levels, with the signal-to-noise ratios (SNR), respectively, 0.0 dB, −0.5 db, −1.0 db, −1.5 db. The SNR is defined as: SNR(dB) = 10log₁₀ (Var_signal/Var_noice), where Var_signal and Var_noice are the empirical variances of the signal and noise.

B. Validation of Our Multiseed Method Using Multiple Correlations (Fig. 2)

Fig. 2.

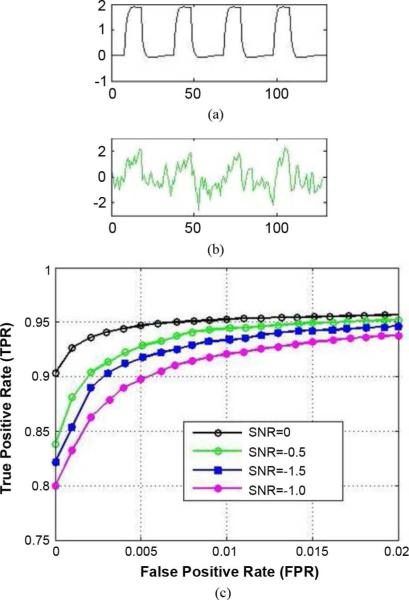
(a) Ground truth of a simulated seed. (b) Normalized time series of an associated connectivity voxel at SNR = −0.5 dB. (c) ROC curves at SNR (in dB) = 0.0, −0.5, −1.0, −1.5 (top to bottom).

In this experiment, two types of networks were simulated, highly correlated with the two types of seed regions, respectively. We used receiver operating characteristic (ROC) analysis for evaluation. The essence of ROC analysis is the comparison of true positive rates (TPR) (proportion of voxels correctly detected as significant to all voxels with added connectivity) obtained with different analysis techniques for a given false positive rate (FPR) (proportion of voxels incorrectly detected as significant to all voxels without added connectivity). The ROC curves in Fig. 2 indicate that our multiple correlation method can robustly detect the true multiseed connectivity when the SNR is greater than or equal to −1.5 dB, though the performance increases for increased SNR.

C. Comparison of Our Multiseed Method and the Single-Seed Method (Figs. 3 and 4)

Fig. 3.

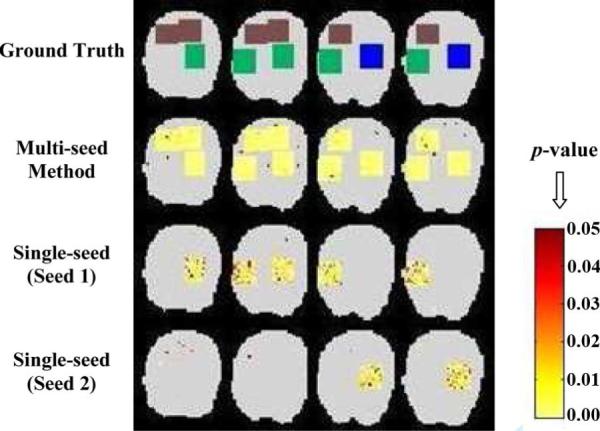
Identified functional connectivity (color maps) for simulated data (SNR = −1.0 dB): Comparison of our multiseed method (multiple correlation) and the single-seed method (with spatial noise considered, too).

Fig. 4.

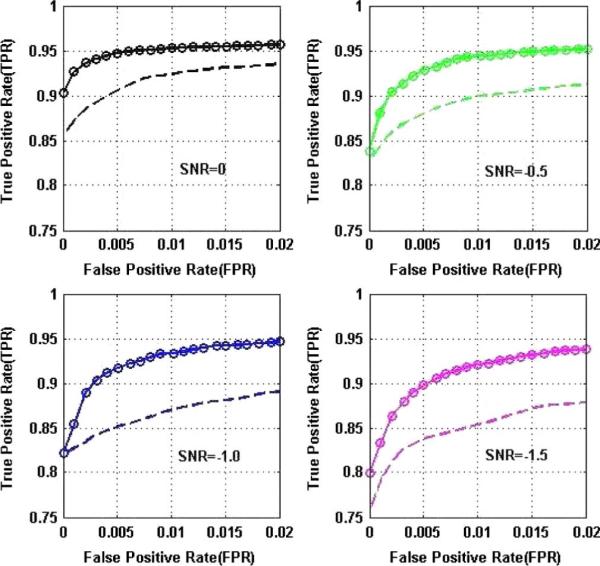
Comparison of ROC curves for our multiseed method (solid lines with circles) and the single-seed method (with spatial noise also considered, dashed lines) at different SNRs, showing significantly improved performance using multiple seeds. Note: The TPR and FPR for the single-seed case are computed as below: M is the total number of voxels; Let i = 1, 2 be the seed index. Suppose: ni (i = 1, 2) is the number of voxels correctly detected as significant; Ni (i = 1, 2) is the number of voxels with added type i connectivity; mi (i = 1, 2) is the number of voxels incorrectly detected as significant. Therefore, the combined TPR and FPR used in the ROC plots for the single-seed case are: TPR = (n₁ + n₂)/(N₁ + N₂) and FPR = (m₁ + m₂)/(M − N₁ − N₂)

In Fig. 3, three types of networks were simulated, with the green region highly correlated to seed 1, the blue region highly correlated to seed 2, and the brown having medium (relatively low) correlation to both of the two seed regions. Fig. 3 shows that the identified connectivity (at α = 0.05, corrected) by our multiseed method and by the single seed method (spatial correlations in noise also considered using the technique in [11]): 1) With our multiseed method using multiple correlations, all three types of connectivity are detected, both the highly correlated ones to the seeds (green and blue) and the medium correlated one (brown). 2) Using any one seed alone, only the corresponding one type of highly correlated connectivity is detected in each case; in addition, compared to our multiseed method, the significance level is lower, and there are more false negatives and false positives; the correlation over the brown region is not high enough in either of the cases to be shown as significant when using any single seed alone.

With the data generated in Section V-A, quantitative performance comparison with the single-seed method using ROC curves at different SNRs are shown in Fig. 4, demonstrating that besides being able to identify all underlying networks, our approach is more robust and powerful in detecting functional connectivity and the improvements increase when SNR decreases.

D. Comparison of Our Methods: Multiple Versus Partial Multiple Correlations (Fig. 5)

Fig. 5.

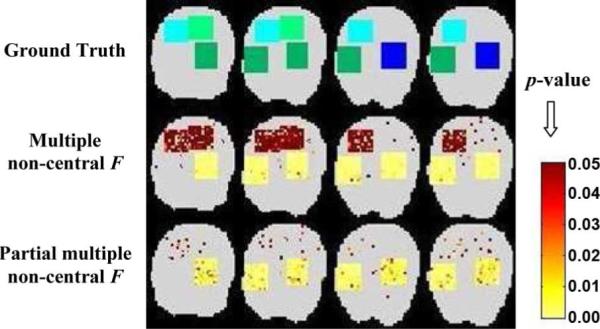
Identified functional connectivity (color maps) for simulated data (SNR = −1.0 dB): Comparison of our multiseed methods using multiple and partial multiple correlations.

We also generated simulated data with four different types of connectivity (see Fig. 5): light green and light blue denote the stimulus-locked activation regions to the type 1 and type 2 seeds, respectively; dark green and dark blue denote the stimulus-locked activation plus the task-induced functional coupling to the type 1 and type 2 seeds, respectively. With the multiple correlations, all four types of regions are shown as significant, though at different significance levels. However, using partial multiple correlations, only the regions imbedding task-induced functional coupling (dark green and dark blue) are identified as significant because the partial correlation analysis is able to adjust for the stimulus-locked effects.

VI. Real Fmri Data With Visual Motion Task

A. Data Description

The real fMRI data (single-subject) was obtained from the SPM data site³ with the detailed description in [35]. The subject was scanned during four runs, each lasting 5 min 22 s. One hundred image volumes were acquired and the first ten was discarded in each run. Each condition lasted 32.2 s, giving 10 multi-slice volumes per condition. The fMRI data size was 53 × 63 × 46 × 360. Four conditions—“fixation,” “attention,” “no attention,” and “stationary”—were used. Electrophysiological and neuroimaging studies have shown that attention to visual motion can increase the responsiveness of the motion-selective cortical area V5 and some other areas, and an occipito-parieto-frontal network is involved in the visual pathway modulation by attention. The structural model for the dorsal visual pathway is shown in Fig. 6, including primary visual cortex (V1), visual cortical area MT (V5), posterior parietal cortex (PP), and modulatory interaction term involving dorsolateral prefrontal cortex (PFC).

Fig. 6.

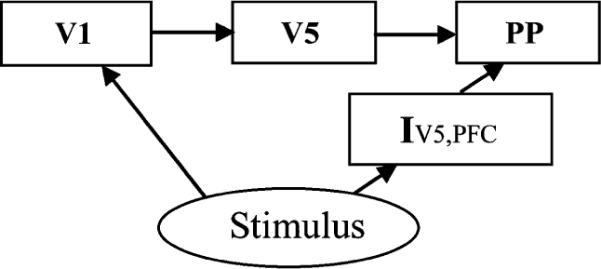
Structural model for the dorsal visual stream (modified from [35]), including primary visual cortex (V1), visual cortical area MT (V5), posterior parietal cortex (PP), and modulatory interaction term involving dorsolateral pre-frontal cortex (PFC).

B. Determining Activation and Seed Regions

The activation regions were identified by categorical comparisons using the SPM5 software package, contrasting “attention” and “no attention” and contrasting “no attention” and “stationary.” The involvement of V1 and V5 were predicted with a stimulus consisting of rapidly moving dots. The location of V1 was in accord with the calcarine fissure [36], and that of V5 was consistent with previous functional imaging studies [35], [37]. The location of the posterior parietal regions was similar to that in previous PET and fMRI studies of attention [35], [38], [39]. Fig. 7 shows the location of the activation regions for a single individual, with each region centered around the most significant (α = 0.05, corrected) voxel as revealed by the categorical comparison.

Fig. 7.

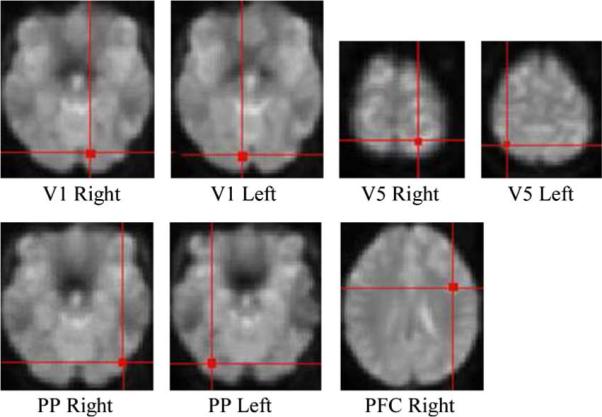
Spatial location of the activation regions identified from SPM5 for a single subject real fMRI data.

Here we examine the functional interactions by using the different seed regions: V1, or V5 or both V1 and V5, and by using different methods. The seed regions were determined through the procedures described in Section II, i.e., starting with the peak activation voxels in the corresponding V1 and V5 activation regions identified above, we used the region growing strategy based on the functional homogeneity. Note that it might also be interesting to investigate the functional connectivity by using other seed regions in addition to V1 and V5, such as PP. However, based on the structural model in Fig. 6, using PP is not quite justifiable from the neural networking or information flow point of view. Unlike studying the effective connectivity [1], [40], our method examines the functional connectivity without inferring or being constrained by the causal relationship (i.e., the directionality) among spatially separated brain regions. Thus, the results from our framework are usually not sensitive to the improper placing of seeds.

C. Partial Correlation Effects–Multiple Versus Partial Multiple Correlations (Figs. 8 and 9)

Fig. 8.

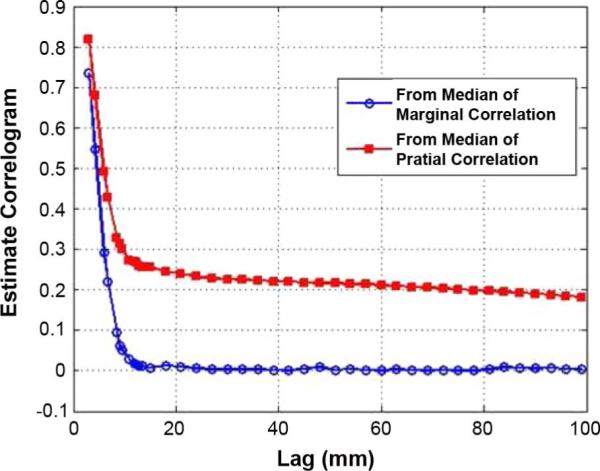
Estimated correlograms from the real fMRI data, showing the asymptotic correlation, ρ_∞, in ρ_θ(h) (marginal correlation) is lower than the one in ${\rho }_{\theta }^{\ast }\left(h\right)$(h) (partial correlation). This might be related to the fact that a baseline condition of brain function exhibits decreases during performance of a cognitive task [41].

Fig. 9.

Comparison and results of functional interaction maps for the real fMRI data. (a) Seeds: Left and right VI. (b) Seeds: Left and right V5. (c) Seeds: Right V1 and Right V5.

Estimated correlograms using marginal correlation (Section III-B) and partial correlation (Section IV-B) are shown in Fig. 8, which indicates that the correlations between time series with visual motion task (equivalent to performance of cognitively demanding processing) are lower than the remaining correlations after taking into account the relationship of each time series to the reference functions (here two were used, one for “attention” and the other for “no attention”). This might be related to the fact that a baseline condition of brain function exhibits decreases during performance of a cognitive task [41].

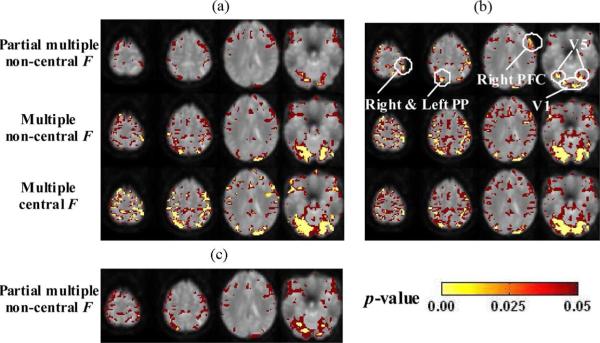
From Fig. 9(a) and (b), we can see that using multiple correlation (second row), both stimulus-locked and task-induced networks are identified, with all the involved regions in Fig. 6 shown as highly significant (yellow). However, using partial multiple correlation (first row), since the stimulus-locked effects are accounted for, the network regions and their sizes are considerably reduced. Specifically: 1) with V1 as seed regions [Fig. 9(a), first row], mainly the low level visual network is identified as highly significant implying task-induced coupling among the visual areas, such as V1–V5 and 2) withV5 as seed regions [Fig. 9(b), first row], the two PP and the right PFC regions are still shown as highly significant, suggesting the involved task-induced coupling of attention to motion modulation described in Fig. 6, after taking account of the stimulus-locked effects.

D. Effects of Multiple Seeds—Comparison Using Both V1 and V5 as Seeds (Fig. 9)

The partial multiple correlation results using V1 or V5 [Fig. 9(a) and (b), first row] as seed regions have been illustrated in the above section. With a combination of a V1 and a V5 as seed regions [Fig. 9(c)], using partial multiple correlation, we can not only detect the highly significant low level visual network regions (as in Fig. 9(a) and (b), first row, last slice), but also identify the highly significant attention to motion modulation PP areas [as in Fig. 9(b), first row; also compare to Fig. 9(a), first row], achieving the combined effects of multiple seed regions involving both V1 and V5. Note that since only one V5 is used here, the region sizes and significance levels for the PP and right PFC are not as large as the ones using both V5 regions in Fig. 9(b) (first row).

E. Effects of Spatial Noise–Comparison of Noncentral and Central F-Tests (Fig. 9)

The results without taking the spatial noise correlations into consideration (central F-test) are shown in Fig. 9(a) and (b), third row, with many unjustified areas identified as functionally correlated with the V1 and/or V5 seed regions due to the spatial structured noise in the fMRI data.

VII. Conclusion and Discussion

This paper presents a novel and general statistical framework for sensitive and reproducible estimation of brain networks from fMRI based on multiple and partial multiple correlation analyses and multiple seed regions, with the standard single-seed region analysis as the degenerate and a special case. The networks of functional interconnections are found by comparing the temporal multiple (and/or partial multiple) correlations against a model of the spatial multiple (and/or partial multiple) correlations in the noise. Compared with using only a single seed, using multiple seeds can not only lead to more robust estimation of functional connectivity, but also more sensitive identification of functional co-activation networks or regions to multiple seeds that may not be detected in the single-seed method. The use of the partial multiple correlation has the interesting features of providing a convenient summary of conditional independences and hence of being more closely related to the direct functional interactions (i.e., effective connectivity) of the brain than marginal correlation. Experimental results from both simulated and real fMRI data demonstrate that the proposed approaches can robustly and sensitively detect and differentiate brain functional networks caused by stimulus-locked and/or task-induced responses.

Note that our method/framework can degenerate to the single seed case with spatial noise accounted for. A reasonable way of utilizing the present approaches is to test different combinations of seeds, including single and multiple seeds based on prior literature and the goal of the specific research. The multiseed methods can provide valuable information regarding co-activation to multiple seed regions that is not achievable in the conventional single-seed analysis. However, employing individual seeds separately in a subsequent analysis would help us better understand the different individual networks. Utilizing multi-seed in conjunction with the single-seed analyses based on our framework can provide complementary and comprehensive information of brain interactions.

Analyzing the connectivity from fMRI data can also be achieved through alternative approaches, such as Granger causality mapping (GCM) [42], dynamic causal modeling (DCM) [40], partial least-squares (PLS) [43], independent component analysis (ICA) [9], [44], principal component analysis (PCA) [2], and conventional correlation analysis [3], [45], etc. Among these methods, GCM and DCM aim for the effective connectivity which refers to a causal relationship between spatially separated brain regions; PLS, ICA, and PCA are multivariate analysis techniques for detecting functional connectivity through modeling relations between sets of observed variables by means of latent variables (PLS), or identifying the spatial or temporal components which are either uncorrelated (PCA) or independent (ICA); and the conventional correlation analysis of a signal from a selected voxel or region is a univariate approach for functional connectivity study. The proposed methods in this paper provide a hybrid version of multivariate and univariate analyses for functional connectivity detection and estimation by modeling the temporal and spatial correlations to multiple seed regions, which may be interpreted as a regional multivariate analysis though with the univariate one seed region as the degenerate case.

In addition to fMRI, other noninvasive techniques such as electroencephalography (EEG) and magnetoencephalography (MEG), provide spatio-temporal information about the ongoing neural activity in the cortex, and can be used for brain effective and functional connectivity studies. The associated analysis techniques of such data typically involve the identification of foci of activity such as single- or multiple-dipole localization in a 3-D volume [46]. More ambitious techniques not only decompose the spatio-temporal dynamics into meaningful patterns, but also identify equations governing the dynamics of these patterns [47]. Despite the successes, the simplifications made in the approaches do not take into account the detailed physiological and anatomical interpretation of the identified dynamic systems. Jirsa et al. [48] define a spatio-temporal neural field dynamics on a spherical geometry. The neuronal dynamics is mapped onto the unfolded cortical surface, and then on the folded cortical surface, and finally on the EEG and MEG patterns on the scalp.

The spatio-temporal noise modeling in fMRI has been investigated in some literature. For example, a spatially independent temporal noise modeling approach was introduced by Bullmore et al. [49] within a null hypothesis testing general linear model framework. This was also tackled in an empirical Bayesian framework [50], which avoided problems due to the estimation of the temporal autocorrelation from the residuals of the model fit. In these methods, the parameters associated with the correlation structure of the noise are assumed to be known exactly; the uncertainty associated with these parameters is not taken into consideration, resulting in potentially biased statistical inference. To overcome this limitation, a full Bayesian framework was proposed by Genovese [51] to model the fMRI time series with deterministic drift in the data using cubic splines. Woolrich et al. [19] model short scale statistical spatial and temporal noise using autoregressive (AR) processes, after taking away the large scale deterministic temporal fluctuation in a preprocessing step using temporal high-pass filtering.

There are some assumptions in our methods and the simulated data generation. First, we assume the spatial noise is stationary and has a multivariate Gaussian distribution. In addition, separable space and time models are used. The stationarity of noise and the separability of space and time are simplifications for computational feasibility; which have been used in the literature for fMRI modeling and analysis [52]. More general and complicated noise model such as the time-varying [53] and Ricean [54] noise, and a nonseparable spatio-temporal model [19], [55] can possibly be considered for the corresponding derivations. However, the main contribution of this paper is to demonstrate the ideas, methods, and advantages of the unified framework for brain connectivity study; comprehensively modeling the fMRI noise is beyond the scope of this work and could be pursued further in the future. Second, in our simulated data experiments, we generated the block-design experimental paradigm data with an ARMA(1,1) process modeling the temporal autocorrelations. But the proposed framework can be applied to the event-related paradigm as well, in which case, the temporal autocorrelations can be modeled as a more general autoregressive (AR) process. The time series modeling of ARMA, AR, and their variations have been developed and tested for fMRI analysis in [24], [49], and [56].

One of our major future directions is to generalize the method to multisubject study. In this paper, the approach was applied on single-subject fMRI data. One way to extend it to group level analysis is as following: First perform our single-subject correlation analyses by computing $\widehat{R}={\widehat{R}}_{\mathrm{tem}}-{\widehat{R}}_{\mathrm{spa}}$ based on Sections III-A and III-B for the multiple correlation case and computing $\widehat{R}={\widehat{R}}_{\text{tem}}\cdot \mathrm{v}-R_{\mathrm{spa}}\cdot \mathrm{v}$ based on Sections IV-A and IV-B for the partial multiple correlation case. Second, perform the corresponding second-level group analyses using permutation tests, for example, using our newly developed hybrid and efficient permutation tests [30] or the standard random permutation tests [57]. One advantage of utilizing the nonparametric permutation tests instead of any parametric tests (such as the t-test or F-test) is that no data distribution assumption is required. In this case, the cluster-size thresholding or the false discovery rate control [25]–[28], [30], [58] could be potentially applied for the multiple testing problem given that the parametric statistic field/image is not explicitly available for the random field theory to be applied for correction.

Appendix

Estimation of Noise Variance

Let σ² denote the noise variance for each individual voxel, in the fMRI data. It can be estimated using an ARMA(1,1) model, as in [33], [34]. Let the time series for a voxel be y. After using the general linear model to take away the part of y related to neural activity, the residual noise error is $\widehat{\mathrm{e}}=\mathrm{y}-\mathrm{G}\cdot \widehat{\beta }$, where e = [e(1), …, e(t), …, e(T)]′, for t = 1,2, …, T. With the assumption of the ARMA(1,1) model, we have e(t) − φ · e(t − 1) = z(t) + ϑ · z(t − 1), where z = [z(1), z(2), …, z(T)]′ is temporally independent and identically distributed Gaussian noise, i.e., z ~ i.i.d. N(0, σ²). For each voxel, three parameters: variance σ², autoregressive coefficient φ, and moving average coefficient ϑ, can be estimated as following. Suppose the variance–covariance matrix for e is

$${\left[\begin{array}{cccc}\hfill \gamma \left(0\right)\hfill & \hfill \gamma \left(1\right)\hfill & \hfill \cdots \hfill & \hfill \gamma (T-1)\hfill \\ \hfill \gamma \left(1\right)\hfill & \hfill \gamma \left(0\right)\hfill & \hfill \cdots \hfill & \hfill \gamma (T-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \gamma (T-1)\hfill & \hfill \gamma (T-2)\hfill & \hfill \cdots \hfill & \hfill \gamma \left(0\right)\hfill \end{array}\right]}_{T\times T}.$$

Then

$$\gamma \left(1\right)={\sigma }^2\left[1+\frac{{(\vartheta +\phi )}^2}{1+{\vartheta }^2}\right]$$

$$\gamma \left(1\right)={\sigma }^2\left[\vartheta +\phi +\frac{{(\vartheta +\phi )}^2\phi }{1-{\vartheta }^2}\right]$$

$$\gamma \left(t\right)={\vartheta }^{t-1}\gamma \left(1\right),\text{fot}2\le t\le T.$$

Also, the estimation for γ(t) is

$$\widehat{\gamma }\left(t\right)=\frac{1}{T-1}\sum _{i=0}^{T-t}(\widehat{e}(i+t)-\text{mean}\left(\mathrm{e}\right))\cdot (\widehat{e}\left(i\right)-\text{mean}\left(\mathrm{e}\right)),0\le t\le T.$$

The parametric fitting will lead to the estimation of ${\widehat{\sigma }}^2$, which is the estimated noise variance at each individual voxel.

Let ${\sigma }_S^2$ denote the noise variance for a seed region S (i.e., the noise variance for the mean time series of this seed region). Suppose there are $\mathcal{w}$ voxels in S, and the voxels within this region are correlated rather than independent. In order to estimate ${\sigma }_S^2$, we first calculate the $\mathcal{w}\times \mathcal{w}$ variance-covariance matrix, A. The diagonal elements in A are ${\sigma }_i^2(i=1,2,\dots ,\mathcal{w})$, the variance of the noise at voxel estimated above; and the off diagonal elements in A are ρ_θ(d_ij) · σ_i · σ_j (i, j = 1,2, …, $\mathcal{w}$), where ρ_θ(d_ij) is the correlogram estimated in Section III-B for lag d_ij the spatial distance between voxel i and j. That is

$$A=\left[\begin{array}{cccc}\hfill {\sigma }_1^2\hfill & \hfill {\rho }_{\theta }\left(d_{12}\right)\cdot {\sigma }_1\cdot {\sigma }_2\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }\left(d_{1w}\right)\cdot {\sigma }_1\cdot {\sigma }_2\hfill \\ \hfill {\rho }_{\theta }\left(d_{21}\right)\cdot {\sigma }_1\cdot {\sigma }_2\hfill & \hfill {\sigma }_2^2\hfill & \hfill \cdots \hfill & \hfill {\rho }_{\theta }\left(d_{2w}\right)\cdot {\sigma }_1\cdot {\sigma }_w\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\rho }_{\theta }\left(d_{w1}\right)\cdot {\sigma }_w\cdot {\sigma }_2\hfill & \hfill {\rho }_{\theta }\left(d_{w2}\right)\cdot {\sigma }_w\cdot {\sigma }_2\hfill & \hfill \cdots \hfill & \hfill {\sigma }_w^2\hfill \end{array}\right].$$

Let the entries in matrix A be a_ij. We then have: ${\sigma }_S^2={\Sigma }_{i=1}^{\mathcal{w}}{\Sigma }_{j=1}^{\mathcal{w}}{a}_{ij}∕{\mathcal{w}}^2$, which is used as the noise variance of the seed region S, needed in the F statistic's calculation in Section III-C (multiple correlation case). If we replace the ρ_θ(d_ij) with ${\rho }_{\theta }^{\ast }\left(d_{ij}\right)$ (see Section VI-B) in matrix A, using the same procedure, we can estimate ${\sigma }_S^{\ast }$, the residual standard deviation of the noise for seed region S holding the stimuli fixed, which is needed in the F statistic's calculation in Section VI-C (partial correlation case).