Abstract
β2-syntrophin, a dystrophin-associated protein, plays a pivotal role in insulin secretion by pancreatic β-cells. It contains a PDZ domain (β2S-PDZ) that, in complex with protein-tyrosine phosphatase ICA512, anchors the dense insulin granules to actin filaments. The phosphorylation state of β2-syntrophin allosterically regulates the affinity of β2S-PDZ for ICA512, and the disruption of the complex triggers the mobilization of the insulin granule stores. Here, we investigate the thermal unfolding of β2S-PDZ at different pH and urea concentrations. Our results indicate that, unlike other PDZ domains, β2S-PDZ is marginally stable. Thermal denaturation experiments show broad transitions and cold denaturation, and a two-state model fit reveals a significant unfolded fraction under physiological conditions. Furthermore, Tm and Tmax denaturant-dependent shifts and noncoincidence of melting curves monitored at different wavelengths suggest that two-state and three-state models fail to explain the equilibrium data properly and are in better agreement with a downhill scenario. Its higher stability at pH >9 and the results of molecular dynamics simulations indicate that this behavior of β2S-PDZ might be related to its charge distribution. All together, our results suggest a link between the conformational plasticity of the native ensemble of this PDZ domain and the regulation of insulin secretion.
Introduction
Cellular functions are mediated by protein-protein interactions, and PDZ domains are remarkable examples of universal adaptors used for protein-specific recognition. These domains, which have a central role in a variety of signaling mechanisms, recognize short linear sequences and are present singly or in several copies in numerous proteins. β2-syntrophin is a PDZ-containing protein first identified as a part of the dystrophin-associated protein complex (1). It is a mediator between several proteins and actin filaments (2,3), and recently, its central role in the regulation of insulin secretion has been unveiled (2,4–6). In the pancreatic β-cells, β2-syntrophin forms a supramolecular complex through interactions mediated by its PDZ (β2S-PDZ) and SU domains. The former domain binds protein-tyrosine phosphatase ICA512 (also known as IA-2), a type I membrane protein of the insulin granule, whereas the latter interacts with utrophin, an actin-binding protein. Disrupting the complex between β2S-PDZ and the intracellular domain of ICA512 is the key molecular event associated with mobilization of the stores of insulin secretory granules. Moreover, the affinity of this complex is regulated by the phosphorylation state of β2-syntrophin in regions flanking the PDZ domain (6).
The crystal structure of the isolate β2S-PDZ shows that it shares the fold observed in other PDZ domains. In the context of the whole protein, β2S-PDZ is inserted in a loop of the first PH domain, splitting it into two halves (1). The NMR structure of PHN-PDZ-PHC of α1-syntrophin shows that there is no interaction between the PDZ and PH domains, which remain connected by two long, disordered intervening arms (7).
Numerous studies on the binding of isolated PDZ domains gave rise to a sequence-based classification of their ligands (8–10), although promiscuous binding is a feature of these domains (11). In all cases, the interaction involves a few ligand residues, one of which must have a carboxylate C-terminal group or, much less frequently, a side chain with a carboxylate. On the other hand, there is also a large body of research devoted to the study of thermodynamics of PDZ domains. Investigations of the three PDZ domains from PSD-95 and the second PDZ from tyrosine phosphatase PTP-BL suggest that PDZ domains share a common three-state folding mechanism (12). However, variations have been observed in the transition states of different PDZ domains (13), and even the formation of intriguing oligomeric intermediates was ultimately reported, arguing in favor of a complex relationship between folding and sequence (14,15). Moreover, it has been reported that conformational changes in the native state constitute a mechanism to regulate the affinity of the PDZ5 domain of the INAD scaffold in Drosophila (16). Together, these investigations strengthen the idea that PDZ domains exhibit allosteric behavior and dynamical changes that are domain- and or ligand-specific (17,18).
Here, we present a thermodynamic characterization of β2S-PDZ. The untagged, wild-type recombinant protein was produced in Escherichia coli and purified to homogeneity. This allowed us to perform chemical and thermal denaturation experiments monitored by circular dichroism. Our results demonstrate that this domain is significantly less stable than other PDZ domains studied so far. In addition, some distinguishing characteristics of the unfolding of this PDZ domain might bear relevance to its function and could be caused by its peculiar sequence features.
Materials and Methods
Protein cloning, expression, and purification
The DNA sequence of β2S-PDZ (residues 113–195) was amplified by polymerase chain reaction from the β2-syntrophin cDNA (a generous gift from Dr. S. C. Froehner, University of Washington, Seattle, WA) using primers containing target sequences for NdeI and BamHI restriction enzymes and cloned into pET-9b (Novagen, Madison, WI) expression vector (pET-PDZ). For protein expression, E. coli BL21(DE3) pLyS transformed with pET-PDZ were grown in Terrific Broth at 37°C to DO600 of 1–1.5 and, after supplementation with 0.5 mM IPTG, the culture was incubated for 16–20 h at 18°C. Next, the bacteria were harvested by centrifugation, resuspended in lysis buffer (25 mM Tris-HCl, pH 8, 25 mM NaCl, and 0.5 mM EDTA) supplemented with 1 mM PMSF, and lysed using a French Press (Thermo Fisher Scientific, Milwaukee, WI). After centrifugation at 13,000 × g, the supernatant, containing ≈90% of β2S-PDZ, was subjected to two consecutive precipitations at 47% and 80% ammonium sulfate saturation, respectively: in the first, β2S-PDZ remained soluble, and in the second, it precipitated. Then, the protein redissolved and extensively dialyzed against 30 mM sodium phosphate, pH 6.5, was loaded in a cationic exchange column (MonoS, GE Healthcare, Waukesha, WI) attached to a Jasco (Easton, MD) 2089i-Plus pump system. The protein was eluted by increasing NaCl concentration, and fractions containing purified β2S-PDZ were buffer-exchanged. Size-exclusion chromatography was carried out using a Superose 12 column (GE Healthcare). Since β2S-PDZ lacks tryptophan and tyrosine residues, protein concentration in pure samples was estimated by absorbance at 214 nm (19) using a molar extinction coefficient of This method was consistent with estimations by SDS-PAGE.
Circular dichroism spectroscopy
Circular dichroism (CD) experiments were carried out in a Jasco J-810 spectropolarimeter thermostatized with a Peltier system. For chemical denaturation at constant temperature (20°C), at least six spectra between 180 and 250 nm were averaged and, after baseline correction, smoothed using a Savitzky Golay filter. Thermal denaturation experiments were carried out monitoring ellipticity at 220 or 200 nm between 4°C and 90°C, with a change rate of 2°C min−1. The protein concentration was between 3.6 and 8 μM, and a cell with a pathlength of 1 mm was used. Unless otherwise stated, all experiments were carried out in 50 mM sodium phosphate, pH 7.5. Urea concentration was determined by refractometry and all reagents were analytical grade. Temperature-dependent spectra from 200 to 240 nm were taken every 2° from 4°C to 90°C, with a temperature slope of 2° min−1 and an equilibration time of 30 s.
Data analysis
In all cases, ellipticity was converted to mean residue molar ellipticity. The equilibrium denaturation curves were fitted to a two-state model and the observable (S) was calculated as , where SN and SU are the pre- and posttransition temperature-dependent baselines, respectively. fN and fU, the molar fractions of the native and unfolded states, respectively, were related by the unfolding equilibrium constant:
| (1) |
| (2) |
For the chemical denaturation experiments at 20°C, the denaturant dependence of KU was fitted through the equation
| (3) |
where is the free energy of unfolding in the absence of denaturant. For the thermal denaturation experiments, the temperature dependence of KU was predicted according to the equation:
| (4) |
where is the difference between native and unfolded heat capacities and is the enthalpy at the melting temperature, Tm. The values of the temperature of highest stability, Tmax, and at this temperature, , were calculated from Eq. 4 using the fitted values.
Pretransition baselines were considered linearly related to temperature and denaturant, whereas a global polynomial posttransition baseline was used for all the denaturant-dependent melting curves, as follows:
| (5) |
| (6) |
Temperature-dependent variations of the CD spectra were analyzed by singular value decomposition (SVD). A matrix of components was calculated as U × D, where the columns of the rectangular matrix U, embodying spectral information, were weighted by the singular values (SVs) contained in the diagonal matrix D. Only the first two components were relevant; the rest were noise. A matrix of phenomenological melting curves can be calculated as D × VT, where V is a square matrix comprising the temperature variations of each component of U. The first two columns of this matrix, which were the only relevant vectors, were summed up to compose a melting curve.
Computer simulations
Simulations with all-atom, structure-based force fields (20) were carried out with the GROMACS package (21). Topologies for the β2S-PDZ structure (residues 113–195, PDB code 2VRF) were built applying the shadowmap method (22). Basically, these force fields consider solely attractive interaction between pairs of heavy atoms in close proximity in the native structure. In the crystal structure, the charged side chains of Arg-113, Arg-157, Lys-120, and Lys-188 are very close and form several repulsive pairs, which were disrupted in preliminary simulations using the empiric gromos-G43a1 force field (23) and explicit SPCE water. Thus, these pairs were disregarded in building the structure-based force field. In addition, electrostatic effects were explored adding 0.1 charge units to every ionizable side chain. Several simulations were carried out in a range of constant temperatures, ensuring that the structure remained fully folded and unfolded at the lower and higher temperatures, respectively. Bidimensional energy maps were obtained with the weighted-histogram analysis method (24).
Data fit and SVD were carried out using the R package and graphs drawn with Xmgrace. Structure images and adaptive Poisson-Boltzmann continuum electrostatic models (25) were performed with VMD (26).
Results and Discussion
Thermodynamic characterization
We overexpressed the wild-type PDZ domain of human β2-syntrophin in E. coli without tag sequences. Its purification, consisting of two successive precipitations and a chromatographic step, yielded a protein sample >95% pure as judged by SDS-PAGE. The identity and integrity of β2S-PDZ was confirmed by mass spectrometry and its monomeric state in solution by analytical size-exclusion chromatography (not shown).
Since the lack of tryptophan and tyrosine residues in β2S-PDZ made it difficult to apply fluorescence techniques, and because it was sought to monitor the overall topology of β2S-PDZ rather than local details, the unfolding was monitored by far-ultraviolet (UV) CD. The CD spectrum of β2S-PDZ is as expected for an α/β protein (Fig. 1 A). Thermal transitions are fully reversible: heating to 90°C produces a spectrum with a negative minimum at 200 nm, typical of a random-coil conformation, which is transformed into the fully native spectrum after cooling to room temperature.
Figure 1.
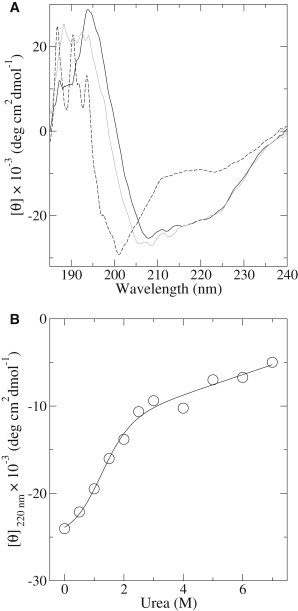
CD analysis of β2S-PDZ. (A) Far-UV spectra at 20°C (black line), 4°C (gray line), and 90°C (dashed line). (B) Mean molar ellipticity at 220 nm (circles). A two-state fit to the data (Eqs. 1 and 3) is shown as a solid line.
Chemical denaturation of β2S-PDZ at pH 7.5 shows that concentrations of urea above 3 M completely unfold the protein (Fig. 1 B). A two-state fit yields at least 5% of unfolded state in the absence of denaturant, with and m values of 1.36 ± 0.36 and 1.18 ± 0.28, respectively. The absence of a clear pretransition is a major source of uncertainty, and the fitted parameters should be taken instead as upper limits.
To further characterize the equilibrium folding of β2S-PDZ, urea-dependent thermal denaturation experiments were performed following ellipticity at 220 nm. As shown in Fig. 2 B, the transitions are broad and marginally cooperative, posing difficulties in the fitting procedure. Usually, when fitting narrow transitions to a two-state model, baselines are regarded as temperature-induced linear shifts of each state signal rather than as conformational changes, and are straightforwardly identified by simple inspection. In the case of β2S-PDZ, the broadness of the transitions makes such confident identification impossible.
Figure 2.
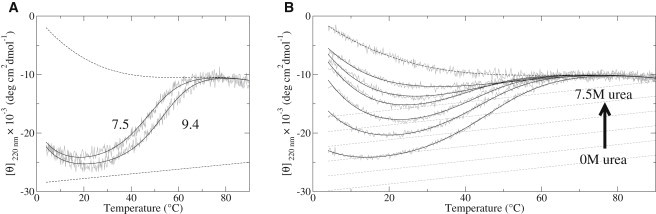
Thermal denaturations of β2S-PDZ monitored by ellipticity at 220 nm. Two-state fits and baselines are shown as heavy solid and dashed lines, respectively. The fit procedure and considerations for the baselines are explained in the text. (A) Transitions at different pH (solid lines). (B) Thermal denaturations of β2S-PDZ at different urea concentrations (solid lines) of (bottom to top) 0, 0.4, 0.8, 1.2, 1.6, 2, and 7.5 M. In both panels, two-state fits and baselines are shown as heavy solid and dashed lines, respectively. The fit procedure and considerations for the baselines are explained in the text.
Therefore, we estimated the unfolded baseline experimentally, considering the information from chemical denaturation experiments (Fig. 1 B), where β2S-PDZ is completely unfolded at urea concentrations above 3 M at 20°C. Thus, a better estimation of this baseline is a melting curve of β2S-PDZ at 7.5 M urea that, far from linearity, was better fit to a polynomial equation (Eq. 6), as in several other works (27,28). On the other hand, to obtain a better estimate of the native baseline, we searched for more stabilizing conditions. Variation in the salt concentration from 0 to 1 M NaF or sodium phosphate, or pH changes in the range 5.8–8.5 had no noticeable effects. However, the thermal stability of β2S-PDZ was increased at pH 9.4 (Fig. 2 A). In this condition, the two-state fit yields a folded fraction of ∼95% at the temperature of maximal stability (Tmax) and allows a better distinction between transition and pretransition regimes. Thus, the linear, temperature-dependent pretransition baseline of this thermogram was considered a good estimation for more physiological pH conditions.
With this baseline scheme, attempts to globally fit the curves with a two-state model (Eq. 4) using a linear urea dependence of (Eq. 3) failed, since the fit systematically deviated from the experiments at low temperature and at the minima of the curves (not shown). We also attempted a global three-state model fit with linear urea dependence of , which was also unsatisfactory, because it yielded multiple solutions and nonconvincing values for the parameters. A much better result was obtained using a two-state model with independent thermodynamic parameters for each melting curve and baselines following Eqs. 5 and 6 for the pre- and posttransitions, respectively (Fig. 2 B). Equation 5 establishes a linear dependence of the signal with both temperature and urea, whereas the unfolded signal depended only on the temperature (Eq. 6). The temperature parameters in Eqs. 5 and 6 were derived from the fits at pH 9.4 (native baseline in Fig. 2 A) and at 7.5 M urea, pH 7.5 (Fig. 2 B) respectively, and globally applied to all the urea-dependent curves.
This approach has been applied by Felitsky and Record (27) with a two-state, low-stability protein, and by Muñoz (29), Sanchez-Ruiz (30), and others to study downhill proteins. In our case, the two-state fit rendered a strong dependence of , Tm, and on the denaturant concentration (Table 1 and Fig. 3) that is characteristic of proteins that unfold through low or negligible energy barriers.
Table 1.
Thermodynamic parameters for the thermal transitions of β2S-PDZ
| Urea (M) | (kcal mol−1) | Tm (°C) | (kcal mol−1 K−1) | Tmax (°C) | (kcal mol−1) |
|---|---|---|---|---|---|
| 0.0 | 17.33 ± 0.11 | 39.88 ± 0.07 | 0.551 ± 0.008 | 9.95 ± 0.55 | 0.84 ± 0.02 |
| 0.4 | 16.25 ± 0.14 | 36.51 ± 0.08 | 0.814 ± 0.010 | 17.16 ± 0.32 | 0.51 ± 0.01 |
| 0.8 | 15.08 ± 0.19 | 34.42 ± 0.11 | 1.038 ± 0.013 | 20.23 ± 0.29 | 0.35 ± 0.01 |
| 1.2 | 11.47 ± 0.27 | 30.77 ± 0.19 | 1.137 ± 0.017 | 20.84 ± 0.35 | 0.19 ± 0.01 |
| 1.6 | 9.69 ± 0.36 | 31.80 ± 0.30 | 1.014 ± 0.018 | 22.39 ± 0.51 | 0.15 ± 0.01 |
| 2.0 | 0.00 ± 1.05 | 23.69 ± 1.40 | 0.755 ± 0.019 | 23.69 ± 1.97 | 0.00 ± 0.00 |
Figure 3.
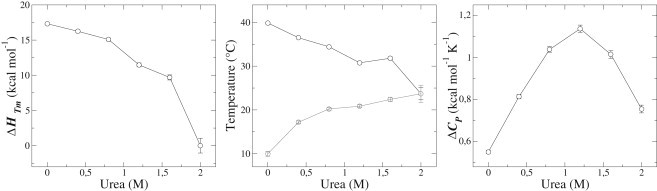
Thermodynamic parameters obtained from two-state fitting of the melting curves at different urea concentrations. (left), Tm (middle, black), Tmax (middle, gray), and (right).
In the absence of urea, is somewhat lower than predicted for a protein of this size ( (31)) and may indicate an incomplete unfolding transition in a two-state context. Cold denaturation is also evident in the melting curves, even in the absence of urea (Fig. 2 B), with a significant unfolded fraction that varies with the temperature. As discussed below, these observations, which are considered diagnostic of small-barrier or downhill unfolding (29,32), may suggest limitations of the two-state model in the case of β2S-PDZ. Moreover, and are low compared to proteins of the same size or to other PDZ domains. For instance, in the works of Chi et al. (12) and those of others (33–35), values in the range 2.9–4.7 kcal mol−1 were reported for the three PDZ domains of PSD-95, and the PDZ domains of nNOS and PTP-BL.
To further characterize the unfolding process, temperature-dependent CD spectra were recorded at 2° intervals. Fig. 4 A shows that the spectra evenly span the transition from folded to random coil, and no isodichroic point is observed. The figure also shows that the thermograms monitored at 204, 208, and 220 nm are noncoincident. The first wavelength senses random-coil structure and corresponds to the minimum in the CD spectra of β2S-PDZ at 90°C, whereas the others are more responsive to β-strands and α-helices. The noncoincidence between denaturation curves at several wavelengths is considered a strong suggestion of small-barrier or downhill unfolding and has been associated to local structural changes in proteins whose conformational ensemble varies gradually and noncooperatively along the melting curve (30,36,37).
Figure 4.
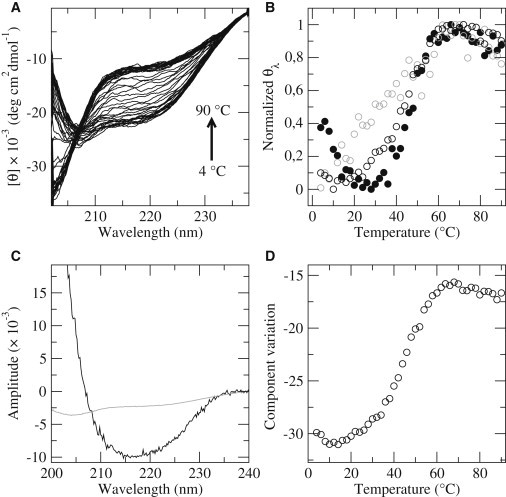
Spectral analysis of the temperature transitions. (A) CD spectra taken at 2° intervals. (B) Normalized temperature-dependent CD signal monitored at 204 nm (black solid circles), 208 nm (gray open circles), and 220 nm (black open circles) obtained from the spectra in A. (C) Amplitude of the two significant components, A (gray line) and B (black line), obtained by SVD of the spectra in A and weighted by their singular values. (D) Melting curve obtained by addition of the variation of the principal components. Calculations are described in the text.
In addition, SVD of temperature-dependent CD spectra yielded two significant components that comprise almost all the CD information at all temperatures (Fig. 4 C). These components should not be ascribed to specific conformational species, since they may represent instead combinations of spectral features from different species. The first two columns of the matrix D × VT (Fig. 4 D) capture the spectral variation of the components as a function of temperature, solving the ambiguities implied in the single-wavelength measurements. Individually, these vectors show that each relevant component varies independently, as reflected in the lack of an isodichroic point. Their summation, which gives the final melting curve in Fig. 4 D, is very informative, because it reveals a gradual drift at low temperature preceding a more cooperative transition. The drift is due mostly to component A, whereas component B is responsible for the second transition at higher temperatures. In this light, the unfolding reaction of β2S-PDZ may be interpreted as the gradual change of the initial state followed by a more cooperative transition leading to the fully unfolded state through a major conformational change. A similar skewness of the SVD curve observed for the downhill protein BBL was ascribed to a gradual loss of helical structure (29).
β2S-PDZ exhibits some characteristics of proteins with low stability or low cooperativity, such as the helix-turn-helix domain (HTH) of the lacI repressor (27), which has been extensively studied with an approach similar to the one applied in this work. Namely, for β2S-PDZ is low compared to proteins of its size, and significant cold denaturation is observed due to poor enthalpic compensation. In addition, a lower-than-predicted value would be consistent with an incomplete unfolding.
Furthermore, β2S-PDZ shows some distinguishing features, such as a significant denaturant dependence of Tmax, Tm, and , noncoincidence between curves monitored at different wavelengths, and a low value. These observations have been considered diagnostic for marginal-barrier or downhill unfolding (30,32,36,37). In equilibrium, these proteins populate one thermodynamic state that varies gradually with temperature through local structural changes. Downhill proteins show no preferred secondary structure, are able to crystallize, and have well defined tertiary structures, as exemplified by the fast-folder mutants of WW domain of the hPin in the context of the whole protein (38) and by a variant of the fragment of the λ-repressor (39), which has a size similar to β2S-PDZ. In fact, the structure of the variant presents B-factors that indicate a higher rigidity in crystal packing than is observed in its wild-type variant. It is worth mentioning that β2S-PDZ has been crystallized as a dimer of a chimeric variant fused to a PDZ-ligand peptide at the C-end. In the crystal, each partner interacts through its PDZ-ligand, and thus, an effect of binding on the protein structure or stability cannot be ruled out.
At this point, it is worth mentioning the works of Gruebele and co-workers with a significant collection of mutants of the WW (40) and (39) domains. The authors show that some variants turn into a downhill regime at temperatures near Tmax, far from the cold (Tcd) and heat-denaturation midpoints, and only in the instances where Tm exceeds certain empirical and protein-dependent cutoffs. These results would support the general idea that a high native-state bias is necessary for a protein to fold downhill (41). Although barrierless folding has been observed in proteins with Tm values comparable to that of β2S-PDZ, our results show that this domain presents significant cold unfolding, characteristic of poor enthalpic compensation, and that it would not fulfill the requisite of a high native-state bias. Thus, β2S-PDZ constitutes an interesting case in which to survey this hypothesis, as well as the scope of the downhill diagnostic techniques in solution.
Equilibrium denaturation experiments of PDZ domains are analyzed satisfactorily using two-state models. Yet, hydrogen-exchange experiments with PDZ-3 of PSD-95 in native conditions (33) revealed on-pathway intermediates in equilibrium with the native states. This was corroborated using destabilized mutants (34) or under mildly denaturing conditions (12) where the intermediates are more populated and become evident in kinetic studies. From these works, a conserved three-state folding mechanism has been proposed for PDZ topology. We failed to fit the urea-dependent melting curves to a three-state model. However, if this conserved mechanism applies to β2S-PDZ, our results could suggest that the native state is in equilibrium with highly populated intermediate states in native conditions. Moreover, a low transition barrier between these states could explain the uncooperative drift observed by SVD between 20°C and 40°C, whereas the more abrupt transition between 40°C and 60°C agrees with the global unfolding step. In this sense, β2S-PDZ agrees with PDZ-3 in their m-value being lower than expected for a protein of this size.
Computational studies
Structural alignment of a sequentially diverse set of PDZ domains, including β2S-PDZ, reveals at once the high level of conservation between the structures (not shown). In the PDZ domains, α-helix B and its connecting loop to C-terminal β-strand F contain major determinants for ligand recognition. α-helix B flanks the binding pocket and harbors a highly conserved positive residue (Lys-120 in β2S-PDZ) crucial for binding (9). Nearby, the loop connecting β-strands A and B is another functionally relevant positive residue (Lys-184 in β2S-PDZ).
β2S-PDZ exhibits some distinguishing features in its charge distribution. The electrostatic potential of several PDZ domains, simulated with a Poisson-Boltzmann continuum electrostatic model (25), showed that β2S-PDZ presents a more dense distribution of positive charges around the binding loop (Fig. S1 in the Supporting Material), which is associated with the presence of extra, nonconserved positive side chains. Two of these, likely relevant for function, are located at the C-end of α-helix B (Figs. 5 and 6). Thus, in a stretch of five residues, β2S-PDZ has three positively charged residues (Lys-184, Arg-185, and Lys-188), which, together with Lys-120, configure a region of high positive potential. It is worth mentioning that this charge distribution is characteristic of the PDZ domains of syntrophins (1). Nevertheless, β2S-PDZ possesses three additional arginine residues compared to the PDZ domain of α1-syntrophin (α1S-PDZ). In the work of Harris et al. (9), two chemical unfolding curves at different ionic strength conditions are described. The results of that work are consistent with a higher stability of α1S-PDZ compared with β2S-PDZ and with a charge effect on the thermodynamic stability of these domains.
Figure 5.
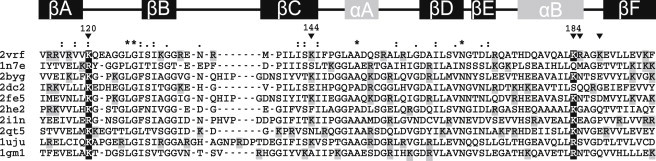
Structural alignment of a low-redundancy set of PDZ domains. Boxes indicate the position of canonical structure elements. Triangles point to basic amino acids relevant for function or present only in β2S-PDZ. Only basic amino acids were highlighted: the most conserved residues appear in black and the less conserved in gray background. The left column lists the pdb codes of each structure included in the alignment: β2S-PDZ (2vrf), sixth PDZ and PDZ12 domains of glutamate-receptor-interacting protein 1 (1n7e and 2qt5, respectively), fourth PDZ domain of 2 scribble protein (1uju), second and third PDZ domains of disc large homolog 2, PSD-93 (2byg and 2he2, respectively), Golgi-associated PDZ domain (2dc2), first and second PDZ domains of DLG3 (2fe5 and 2i1n, respectively), and PDZ2 of PTP-BL (1gm1).
Figure 6.
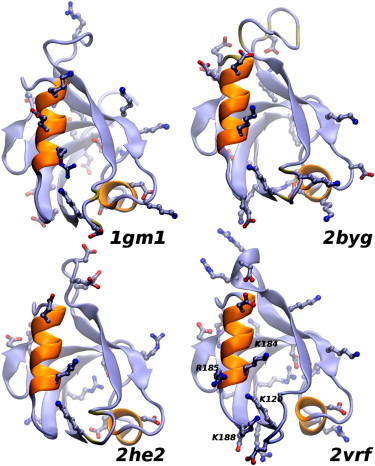
Ribbon representation of four PDZ-domain structures. PDZ2 of PTP-BL (1gm1), second and third PDZ domains of disc large homolog 2, PSD-93 (2byg and 2he2, respectively) and β2S-PDZ (2vrf). In the foreplane are α-helix B and the protein-binding pocket. The side chains of charged residues are shown in all four structures. The amino acids in the characteristic cluster of arginine and lysine residues in β2S-PDZ are labeled.
A Cβ contact map of four PDZ domains (Fig. 7) shows the presence of more positive repulsive contacts in β2S-PDZ. These contacts involve residues of the binding loop, the loop between β-strands A and B, and the interaction between Arg-114 and Arg-158. Interestingly, Gianni et al. (42) reported for the PDZ2 domain of PTP-BL that the loop between β-strands A and B forms a cluster of native interactions in the early folding transition state.
Figure 7.
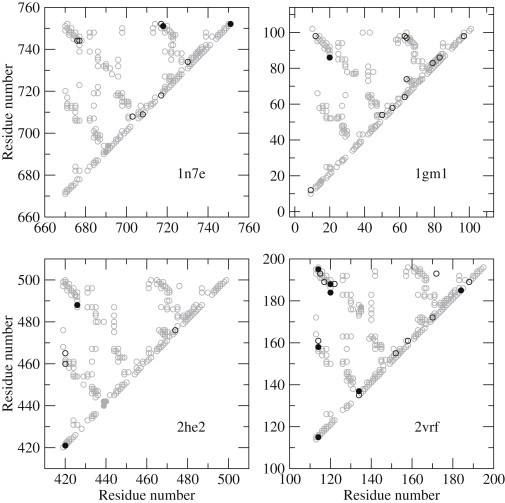
Cβ contact maps of four PDZ domains. The circles correspond to positive repulsive contacts (black solid circles), negative repulsive contacts (gray solid circles), attractive contacts (black open circles), and nonionic contacts (gray open circles). PDB codes are indicated in each panel and correspond to the sixth PDZ domain of glutamate-receptor interacting protein 1 (1n7e), PDZ2 of PTP-BL (1gm1), the third PDZ domain of postsynaptic density protein PSD-93 (2he2), and β2S-PDZ (2vrf).
To gain further insight into the electrostatic effects on the folding reaction, we performed molecular dynamics simulations using structure-based force fields. Fig. 8 shows the energy maps obtained by weighted-histogram analysis (24) from simulations with and without charges, using the fraction of native contacts as folding coordinate. In both cases, a single barrier is observed between broad basins corresponding to folded and unfolded ensembles, but the inclusion of electrostatics produced a lower energy barrier. This is consistent with a role of electrostatics in the stabilization of the transition state and/or in populating partly folded intermediates.
Figure 8.
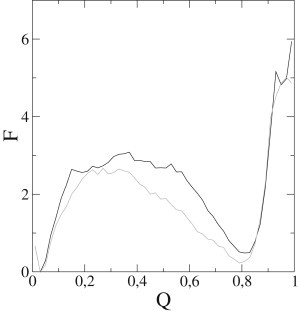
Energy diagrams of molecular dynamics simulations using structure-based force fields. The energy (F) of each conformation is represented as a function of the fraction of native contacts (Q). The black line was obtained using a plain structure-based force field, whereas the gray line is the result of including the electrostatic effects in the force field.
Sequence analysis and molecular dynamics suggest a link between this behavior and the presence of repulsive electrostatic interactions in the surface of this domain, in accordance with the observation that in small proteins, the contribution from surface charges to enthalpy is more relevant. The presence of repulsive electrostatic interactions in the surface of α-lactalbumin explains the differences with hen-egg-white lysozyme (43). Despite their high structural homology, the first one folds through a marginal barrier and presents a high extent of structure in the denatured states, whereas the second folds according to a two-state model. Also, Desai and co-workers demonstrated with the downhill protein BBL that surface electrostatic interactions have a strong impact on folding cooperativity (44).
By means of its interactions with ICA512 and utrophin, β2-syntrophin anchors the dense secretory granules to the actin cytoskeleton and plays a pivotal role in insulin secretion. Solimena et al. clearly demonstrated that the association between β2S-PDZ and ICA512 is regulated by the phosphorylation of two serine residues (2,4,6). These modifications occur not in the PDZ domain but in an adjacent disordered segment between the PDZ domain and the first PH hemidomain. Furthermore, phosphorylation has a paradoxical effect on each site: on Ser-75, it impairs the binding, whereas on Ser-90, it enhances the affinity for ICA512. Based on our results, we hypothesize that the nearby charged phosphate groups might regulate the affinity of β2S-PDZ for its ligand by modulating the degree of structure in the conformational ensemble populated physiologically. It has been proposed that proteins showing complex unfolding behaviors similar to that of β2S-PDZ, especially those folding through marginal barriers, could act as rheostats whose conformational ensemble sensitively responds to environmental regulation (32,45). Characterizing the thermodynamic behavior of β2S-PDZ will allow testing this and other hypotheses regarding the function of this protein.
Concluding Remarks
In recent years, intrinsic structural disorder has been found to be a relevant feature of many proteins. Some of these proteins show low stability, but their unfolding still can be explained under discrete-state scenarios (27); other proteins, which challenge simple models, fold through marginal energy barriers (38,46) or in a downhill fashion (36,37,47–49). In all cases, thermodynamic features play a key role in their function. They show remarkable conformational adaptability to different ligands or can behave as rheostats sensitive to environmental regulation (32,45).
Our results from orthogonal urea-temperature denaturations and temperature-dependent spectra demonstrate that β2S-PDZ is less cooperative than other PDZ domains investigated so far. Two- and three-state models cannot explain satisfactorily the folding equilibrium of this domain, which has some features that characterize marginal-barrier folding. The results demonstrate that the conformational ensemble of β2S-PDZ varies sensitively in a physiologic temperature range. Moreover, computational analyses indicate that this behavior might be ascribed to the presence of additional positive charges that are absent in most PDZ domains.
Thermodynamic analysis is crucial to understanding the biological behavior of a protein. The conformation of stable proteins is relatively resilient to changes in the milieu, but the ensemble of marginally stable proteins can readily sense the environment in normal conditions. In light of our results, it is conceivable that conformational plasticity of the conformational ensemble of β2S-PDZ in native conditions constitutes an important mechanism in the regulation of insulin secretion.
Acknowledgments
We acknowledge support from the National Agency for Science and Technology Promotion (ANPCyT) (M.S) and the National Scientific and Technical Research Council (CONICET) (M.E. and M.S.).
Supporting Material
References
- 1.Adams M.E., Dwyer T.M., Froehner S.C. Mouse α1- and β2-syntrophin gene structure, chromosome localization, and homology with a discs large domain. J. Biol. Chem. 1995;270:25859–25865. doi: 10.1074/jbc.270.43.25859. [DOI] [PubMed] [Google Scholar]
- 2.Ort T., Maksimova E., Solimena M. The receptor tyrosine phosphatase-like protein ICA512 binds the PDZ domains of β2-syntrophin and nNOS in pancreatic β-cells. Eur. J. Cell Biol. 2000;79:621–630. doi: 10.1078/0171-9335-00095. [DOI] [PubMed] [Google Scholar]
- 3.Lumeng C., Phelps S., Chamberlain J.S. Interactions between β2-syntrophin and a family of microtubule-associated serine/threonine kinases. Nat. Neurosci. 1999;2:611–617. doi: 10.1038/10165. [DOI] [PubMed] [Google Scholar]
- 4.Ort T., Voronov S., Solimena M. Dephosphorylation of β2-syntrophin and Ca2+/μ-calpain-mediated cleavage of ICA512 upon stimulation of insulin secretion. EMBO J. 2001;20:4013–4023. doi: 10.1093/emboj/20.15.4013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Trajkovski M., Mziaut H., Solimena M. Regulation of insulin granule turnover in pancreatic β-cells by cleaved ICA512. J. Biol. Chem. 2008;283:33719–33729. doi: 10.1074/jbc.M804928200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schubert S., Knoch K.-P., Solimena M. β2-syntrophin is a Cdk5 substrate that restrains the motility of insulin secretory granules. PLoS ONE. 2010;5:e12929. doi: 10.1371/journal.pone.0012929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yan J., Wen W., Zhang M. Structure of the split PH domain and distinct lipid-binding properties of the PH-PDZ supramodule of α-syntrophin. EMBO J. 2005;24:3985–3995. doi: 10.1038/sj.emboj.7600858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Harris B.Z., Hillier B.J., Lim W.A. Energetic determinants of internal motif recognition by PDZ domains. Biochemistry. 2001;40:5921–5930. doi: 10.1021/bi010142l. [DOI] [PubMed] [Google Scholar]
- 9.Harris B.Z., Lau F.W., Lim W.A. Role of electrostatic interactions in PDZ domain ligand recognition. Biochemistry. 2003;42:2797–2805. doi: 10.1021/bi027061p. [DOI] [PubMed] [Google Scholar]
- 10.Kozlov G., Gehring K., Ekiel I. Solution structure of the PDZ2 domain from human phosphatase hPTP1E and its interactions with C-terminal peptides from the Fas receptor. Biochemistry. 2000;39:2572–2580. doi: 10.1021/bi991913c. [DOI] [PubMed] [Google Scholar]
- 11.Basdevant N., Weinstein H., Ceruso M. Thermodynamic basis for promiscuity and selectivity in protein-protein interactions: PDZ domains, a case study. J. Am. Chem. Soc. 2006;128:12766–12777. doi: 10.1021/ja060830y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chi C.N., Gianni S., Jemth P. A conserved folding mechanism for PDZ domains. FEBS Lett. 2007;581:1109–1113. doi: 10.1016/j.febslet.2007.02.011. [DOI] [PubMed] [Google Scholar]
- 13.Calosci N., Chi C.N., Jemth P. Comparison of successive transition states for folding reveals alternative early folding pathways of two homologous proteins. Proc. Natl. Acad. Sci. USA. 2008;105:19241–19246. doi: 10.1073/pnas.0804774105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Murciano-Calles J., Cobos E.S., Martinez J.C. An oligomeric equilibrium intermediate as the precursory nucleus of globular and fibrillar supramacromolecular assemblies in a PDZ domain. Biophys. J. 2010;99:263–272. doi: 10.1016/j.bpj.2010.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sicorello A., Torrassa S., Chiti F. Agitation and high ionic strength induce amyloidogenesis of a folded PDZ domain in native conditions. Biophys. J. 2009;96:2289–2298. doi: 10.1016/j.bpj.2008.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mishra P., Socolich M., Ranganathan R. Dynamic scaffolding in a G protein-coupled signaling system. Cell. 2007;131:80–92. doi: 10.1016/j.cell.2007.07.037. [DOI] [PubMed] [Google Scholar]
- 17.Petit C.M., Zhang J., Lee A.L. Hidden dynamic allostery in a PDZ domain. Proc. Natl. Acad. Sci. USA. 2009;106:18249–18254. doi: 10.1073/pnas.0904492106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gianni S., Haq S.R., Jemth P. Sequence-specific long range networks in PSD-95/discs large/ZO-1 (PDZ) domains tune their binding selectivity. J. Biol. Chem. 2011;286:27167–27175. doi: 10.1074/jbc.M111.239541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Buck M.A., Olah T.A., Cooperman B.S. Protein estimation by the product of integrated peak area and flow rate. Anal. Biochem. 1989;182:295–299. doi: 10.1016/0003-2697(89)90597-6. [DOI] [PubMed] [Google Scholar]
- 20.Whitford P.C., Noel J.K., Onuchic J.N. An all-atom structure-based potential for proteins: bridging minimal models with all-atom empirical forcefields. Proteins. 2009;75:430–441. doi: 10.1002/prot.22253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lindahl E., Hess B., van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 2001;7:306–317. [Google Scholar]
- 22.Noel J.K., Whitford P.C., Onuchic J.N. SMOG@ctbp: simplified deployment of structure-based models in GROMACS. Nucleic Acids Res. 2010;38(Web Server issue):W657–W661. doi: 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Scott W.R.P., Hünenberger P.H., van Gunsteren W.F. The GROMOS biomolecular simulation program package. J. Phys. Chem. A. 1999;103:3596–3607. [Google Scholar]
- 24.Kumar S., Rosenberg J.M., Kollman P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 25.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 27.Felitsky D.J., Record M.T.J., Jr. Thermal and urea-induced unfolding of the marginally stable lac repressor DNA-binding domain: a model system for analysis of solute effects on protein processes. Biochemistry. 2003;42:2202–2217. doi: 10.1021/bi0270992. [DOI] [PubMed] [Google Scholar]
- 28.Liu J., Campos L.A., Muñoz V. Exploring one-state downhill protein folding in single molecules. Proc. Natl. Acad. Sci. USA. 2012;109:179–184. doi: 10.1073/pnas.1111164109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oliva F.Y., Muñoz V. A simple thermodynamic test to discriminate between two-state and downhill folding. J. Am. Chem. Soc. 2004;126:8596–8597. doi: 10.1021/ja048309w. [DOI] [PubMed] [Google Scholar]
- 30.Naganathan A.N., Perez-Jimenez R., Muñoz V. Robustness of downhill folding: guidelines for the analysis of equilibrium folding experiments on small proteins. Biochemistry. 2005;44:7435–7449. doi: 10.1021/bi050118y. [DOI] [PubMed] [Google Scholar]
- 31.Robertson A.D., Murphy K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1268. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 32.Naganathan A.N., Doshi U., Muñoz V. Dynamics, energetics, and structure in protein folding. Biochemistry. 2006;45:8466–8475. doi: 10.1021/bi060643c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Feng H., Vu N.-D., Bai Y. Detection of a hidden folding intermediate of the third domain of PDZ. J. Mol. Biol. 2005;346:345–353. doi: 10.1016/j.jmb.2004.11.040. [DOI] [PubMed] [Google Scholar]
- 34.Gianni S., Calosci N., Travaglini-Allocatelli C. Kinetic folding mechanism of PDZ2 from PTP-BL. Protein Eng. Des. Sel. 2005;18:389–395. doi: 10.1093/protein/gzi047. [DOI] [PubMed] [Google Scholar]
- 35.Murciano-Calles J., Cobos E.S., Martinez J.C. A comparative analysis of the folding and misfolding pathways of the third PDZ domain of PSD95 investigated under different pH conditions. Biophys. Chem. 2011;158:104–110. doi: 10.1016/j.bpc.2011.05.018. [DOI] [PubMed] [Google Scholar]
- 36.Garcia-Mira M.M., Sadqi M., Muñoz V. Experimental identification of downhill protein folding. Science. 2002;298:2191–2195. doi: 10.1126/science.1077809. [DOI] [PubMed] [Google Scholar]
- 37.Muñoz V., Sanchez-Ruiz J.M. Exploring protein-folding ensembles: a variable-barrier model for the analysis of equilibrium unfolding experiments. Proc. Natl. Acad. Sci. USA. 2004;101:17646–17651. doi: 10.1073/pnas.0405829101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jäger M., Zhang Y., Kelly J.W. Structure-function-folding relationship in a WW domain. Proc. Natl. Acad. Sci. USA. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liu F., Gao Y.G., Gruebele M. A survey of lambda repressor fragments from two-state to downhill folding. J. Mol. Biol. 2010;397:789–798. doi: 10.1016/j.jmb.2010.01.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liu F., Du D., Gruebele M. An experimental survey of the transition between two-state and downhill protein folding scenarios. Proc. Natl. Acad. Sci. USA. 2008;105:2369–2374. doi: 10.1073/pnas.0711908105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Akmal A., Muñoz V. The nature of the free energy barriers to two-state folding. Proteins. 2004;57:142–152. doi: 10.1002/prot.20172. [DOI] [PubMed] [Google Scholar]
- 42.Gianni S., Geierhaas C.D., Brunori M. A PDZ domain recapitulates a unifying mechanism for protein folding. Proc. Natl. Acad. Sci. USA. 2007;104:128–133. doi: 10.1073/pnas.0602770104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Halskau O.J., Jr., Perez-Jimenez R., Sanchez-Ruiz J.M. Large-scale modulation of thermodynamic protein folding barriers linked to electrostatics. Proc. Natl. Acad. Sci. USA. 2008;105:8625–8630. doi: 10.1073/pnas.0709881105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Desai T.M., Cerminara M., Muñoz V. The effect of electrostatics on the marginal cooperativity of an ultrafast folding protein. J. Biol. Chem. 2010;285:34549–34556. doi: 10.1074/jbc.M110.154021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Muñoz V. Conformational dynamics and ensembles in protein folding. Annu. Rev. Biophys. Biomol. Struct. 2007;36:395–412. doi: 10.1146/annurev.biophys.36.040306.132608. [DOI] [PubMed] [Google Scholar]
- 46.Dhar A., Girdhar K., Gruebele M. Protein stability and folding kinetics in the nucleus and endoplasmic reticulum of eucaryotic cells. Biophys. J. 2011;101:421–430. doi: 10.1016/j.bpj.2011.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yang W.Y., Gruebele M. Folding lambda-repressor at its speed limit. Biophys. J. 2004;87:596–608. doi: 10.1529/biophysj.103.039040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fung A., Li P., Muñoz V. Expanding the realm of ultrafast protein folding: gpW, a midsize natural single-domain with α+β topology that folds downhill. J. Am. Chem. Soc. 2008;130:7489–7495. doi: 10.1021/ja801401a. [DOI] [PubMed] [Google Scholar]
- 49.Zwanzig R. Simple model of protein folding kinetics. Proc. Natl. Acad. Sci. USA. 1995;92:9801–9804. doi: 10.1073/pnas.92.21.9801. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


