Abstract
We put forward a modified Zipper model inspired by the statics and dynamics of the spontaneous reconstitution of rodlike tobacco mosaic virus particles in solutions containing the coat protein and the single-stranded RNA of the virus. An important ingredient of our model is an allosteric switch associated with the binding of the first protein unit to the origin-of-assembly domain of the viral RNA. The subsequent addition and conformational switching of coat proteins to the growing capsid we believe is catalyzed by the presence of the helical arrangement of bound proteins to the RNA. The model explains why the formation of complete viruses is favored over incomplete ones, even though the process is quasi-one-dimensional in character. We numerically solve the relevant kinetic equations and show that time evolution is different for the assembly and disassembly of the virus, the former exhibiting a time lag even if all forward rate constants are equal. We find the late-stage assembly kinetics in the presence of excess protein to be governed by a single-exponential relaxation, which agrees with available experimental data on TMV reconstruction.
Introduction
Arguably, virology as a field of study in biology started in 1898 with a publication of Beijerinck on a communicable disease afflicting tobacco plants, causing lesions in and curling of the leaves detrimental to crop yields (1–3). He showed that the disease was caused by neither a bacterium nor any other microscopic organism but by a contagious fluid that reproduces itself in diseased plants. This contagious fluid contains what we now know to be tobacco mosaic virus particles. Tobacco mosaic virus (TMV) is a rod-shaped virus consisting of a single-stranded RNA molecule of 6395 nucleotides and 2130 identical protein subunits. The latter are helically arranged around the RNA molecule, 16 1/3 proteins per turn, producing a particle that measures ∼300 nm in length and 18 nm in width (4). It has a characteristic cylindrical cavity ∼4-nm wide that runs through the entire length of the rod; the RNA is locked in the protein body of the cylinder ∼2 nm from the cavity. Each coat protein binds to three nucleotides via a combination of hydrogen-bonding, hydrophobic, and electrostatic interactions (5).
Although superficially TMV perhaps appears like a simple virus consisting of only two components, coat protein and single-stranded RNA, the processes involved in its reconstitution from its constituents are far from that even in vitro (6,7). Despite half a century of intense research there are still many open questions and we refer to recent reviews of the assembly kinetics by Caspar and Namba (7), Butler (4), and Klug (6). Under conditions similar to those where in infected tobacco cells assembly occurs, a 20S coat protein aggregate is known to be required for efficient nucleation (4,6,8). Still under debate is the precise nature of this 20S aggregate structure, that is, whether it constitutes a disk or a short helix and therefore two nucleation pathways have been put forward. See Fig. 1.
Figure 1.
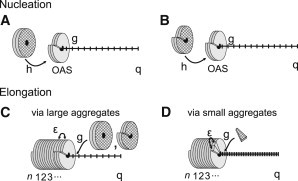
Schematic representation of our kinetic zipper model for the assembly of Tobacco Mosaic Virus from coat proteins onto RNA templates with q binding sites. Nucleation of the assembly of the rodlike virus particles starts at the origin of assembly (OAS) region and is speculated to occur by either of two mechanisms: (A) by conformational switching of the 20S disk aggregate to a helix, which requires an energy h, to the OAS. (B) Alternatively, nucleation takes place by binding of the 20S helical aggregate with the RNA and ordering of the inner loops of the proteins making up the aggregate, which requires an energy h. Subsequent elongation happens by binding of (C) larger units such as the disk or the helical 20S protein aggregate or (D) the much smaller A-protein. Binding of the protein units to the RNA yields a binding free energy g, and the binding between two protein disks is associated with an interaction free energy ϵ. This guarantees sequential assembly commencing at the OAS.
In both cases the adsorption of the first 20S protein aggregate at the origin-of-assembly sequence (OAS) of the RNA requires a conformational change of the 20S aggregate, either from a disk to a proto-helix (9,10) or from a disordered to an ordered state of the inner loops of the helical aggregate (7,11–13). The subsequent elongation of the virus is currently viewed to involve a bidirectional process originating from the OAS on, with a much more rapid elongation toward the 5′ terminus than toward the 3′ terminus. The latter probably occurs by the addition of single subunits (14,15), whereas the elongation toward the 5′ tail may take place by the addition of disks, helices (4,9,16), and/or smaller protein aggregates (17–19). See Fig. 1. Despite the controversies surrounding the nucleation and elongation of TMV, there is little doubt that the initial conformational switching is crucial to an efficient and successful assembly of the virus. Indeed, the concept of autosteric control, in which conformational switching is used as a regulatory control mechanism in biology, and which was put forward by Caspar 30 years ago, was inspired by assembly studies on TMV (20). Strong support for the importance of conformational switching for self-assembly of viruses is not restricted to TMV and other rodlike viruses such as papaya mosaic virus (21), but extends to icosahedral viruses (22), e.g., hepatitis B virus (23), the plant virus CCMV (24), and the phage MS2 (25).
Here, we argue that some sort of allosteric conformational switching is not only advantageous to the assembly of viruses but may in fact even be a necessity if only to prevent empty viral shells from self-assembling in solution. For linear viruses, the additional reason is that the self-assembly of molecular building blocks (coat proteins) onto the linear template molecule (a single-stranded RNA molecule) is dominated by fluctuations, as this in essence constitutes a quasi-one-dimensional process (26). Fluctuations imply imperfect coverage of the template molecule, which is detrimental to the survival of the virus as the coat protects the genome from, e.g., the attack of nucleases. Indeed, recent experiments on the reversible, Langmuir-type adsorption of naphthalene derivatives to single-stranded, homopolymeric DNA molecules support this: for this kind of system, full coverage is virtually impossible to attain (27).
We base our conclusions on the application of a model inspired by the well-known zipper model originally devised to describe the melting of DNA (28). We specifically model the self-assembly of the virus from the OAS in the 5′ direction and for simplicity ignore the finalization of it in the 3′ direction. The latter process is slow and it involves a relatively small portion of the RNA (4). We find that allosteric regulation necessitating the sequential binding of coat proteins starting at the OAS strongly favors either complete assembly toward the 5′ end or no assembly at all. The strong suppression of incompletely covered RNAs we believe is of evolutionary advantage to the virus. A kinetic version of the zipper model is proposed to describe the kinetics of reversible assembly. We find that conformational switching introduces nucleation-type kinetics, and an inherent asymmetry in the assembly and disassembly kinetics. Although highly idealized, our model describes the limited available experimental data on the encapsulation of TMV RNAs by coat proteins reasonably well. From comparison with these data, we learn that the precise determination of the start time of assembly, as well as knowledge about the thermodynamic state at the starting and end-points of an experiment, are crucial to infer quantitative predictions from the model such as the size of the basic protein-building units.
Equilibrium Assembly Model
To describe the assembly of TMV virus particles in a solution containing single-stranded RNAs and 20S aggregates, we apply a model that, in essence, is equivalent to the well-known zipper model for the melting of DNA (28). In our case it is used to describe the elongation of the virus capsid from the OAS onwards to the 5′ end of the RNA. The model does not allow for random adsorption onto different sites of the template, for this is not seen in nature and in fact constitutes a cooperative binding that in itself strongly promotes complete coverage of the RNA (16,29). This is in contrast to the also well-known model of McGhee and von Hippel (26,30), in which random adsorption is allowed, and therefore also in contrast to the equivalent one-dimensional Ising model of ferromagnetism as well as the Bragg-Zimm model for the helix-coil transition (31–33).
Binding of the first protein to the template necessitates a conformational change of the proteins to accommodate a helical structure if the nucleating agent is indeed a disk (9,10), or, if it is a short helix, to induce a helix-coil transition in the so-called flexible loop involved in the locking in of the RNA (7,11–13). The helical aggregate taking part in the binding with the OAS we presume to be a high-energy structure, otherwise it would already form in free solution—that is, without binding to the RNA. This is plausible, as elongation of this structure in the absence of bound RNA is prevented, either by the closed structure of the disk, or the electrostatic repulsion between the carboxylate pairs and steric hindrance of the flexible-loop structures within the short helices (7). Of thermodynamic importance for our model is the required conformational switching and the associated free energy cost h(n) > 0 that this implies for n = 1. We thus need not specify the precise structure of the nucleating agent.
We assume that the switching of subsequent protein units is catalyzed by the presence of the previous protein unit and costs much less free energy than that of the first. For simplicity, we put this free energy cost equal to zero, so we put h(n) = 0 for n > 1 (note that, formally, this contribution can be absorbed in the free energy gain of binding). This way, allosteric binding enters in our model in two ways: first to enforce sequential binding of protein units, and second through a nucleation barrier that will further increase the level of cooperativity of the self-assembly. Binding of the first 20S aggregate and of each subsequent coat protein aggregate after that, shown schematically in Fig. 1, liberates free energy. This free energy is in part needed to allow for the conformational switching of the first 20S aggregate (and/or the proteins therein) upon binding. There are two obvious sources of binding free energy: that of the interaction of the proteins with the RNA, and that of the protein-protein contacts in the growing helix. The former is relative to that associated with the self-basepairing of the RNA in free solution, whereas the latter is taken relative to that between the proteins in the aggregates in free solution. Given these assumptions, we can now make the model more explicit.
Let each viral RNA strand present in the solution act as a template that can accommodate a maximum of q protein units. Considering a total of N RNA strands in the system therefore corresponds to Nq binding sites for protein material. If the total amount of protein material present in the solution corresponds to M protein units, we can define the stoichiometry between available binding sites and protein aggregates as λ ≡ Nq/M. It turns out useful to work not in a canonical but grand canonical ensemble, in which case N and M are expectation values. Later on we return to the canonical ensemble. The quantity of interest describing the thermodynamic state of the solution is, in that case, the grand potential. Adsorption of the protein onto the RNA liberates a binding free energy, g < 0, presumed equal for all units. This parameter also implies any helicase activity the protein might have on the RNA. Furthermore, sequential binding of protein to previously adsorbed ones produces an additional protein-protein interaction free energy, ϵ < 0.
Let Ω denote a dimensionless grand potential density (note that the grand potential is scaled by the thermal energy, and multiplied by the ratio of a molecular volume and the system volume) of coat protein aggregates, RNA molecules, and partially assembled viruses in an ideal solution of volume V. The only interactions we account for are those involved in the binding of protein aggregates onto the RNA binding sites. The grand canonical potential then consists of contributions from the translational entropy of protein units in solution—the RNA strands with n adsorbed protein units, the chemical potentials of RNA molecules, μR, and that of the free and adsorbed protein aggregates, μP. There is also a contribution accounting for the different configurations of n bound protein units on an RNA, expressed in an intrachain partition function Z (n). If the dimensionless number densities of the coat proteins and partially assembled viruses (i.e., RNA molecules with n adsorbed protein units (0 ≤ n ≤ q)) are defined as ρP and ρR (n), we have
| (1) |
In thermodynamic equilibrium, the optimal number densities of the RNA molecules and the free protein units minimize the grand potential. Hence, we set
| (2) |
and find that the number density of chains that have n bound protein aggregates is given by
| (3) |
and the number density of free protein units by ρP = exp(μP). Given the above assumptions, the dimensionless free energy F (n) of n protein aggregates adsorbed to one RNA can be written as
| (4) |
Here, h(n = 1) > 0 is the conformational free energy cost of the first 20S aggregate upon adsorption onto the OAS, and for the subsequently adsorbed protein units we set h(n > 1) = 0. The expression ϵ < 0 is the protein-protein interaction free energy and g < 0 is the free energy associated with the binding of the protein units to the RNA. We take all energies to be in units of the thermal energy, kBT.
It turns out useful not to focus on the canonical partition function Z(n), but rather on the semigrand canonical partition function
| (5) |
that is, the sum over all possible configurations of bound coat protein aggregates onto RNA. Here, F(n) = −ln Z(n). The quantity Ξ is easily calculated using Eq. 4 and reads
| (6) |
where we have defined the parameters s ≡ exp(−ϵ −g + μP) = ρP exp(−ϵ −g) and σ ≡ exp(−h + ϵ). The quantity s is a measure for the affinity of proteins for RNA molecules, combining the binding free energy between the proteins and that to the RNA with the number density of free protein aggregates. The effect of nucleation and allostery is captured in the quantity σ, a measure for the net free energy cost of adsorption of the first 20S aggregate as described in the introduction. If s·σ is small, then the binding of the first 20S aggregate to the template constitutes a high-energy state.
From the semigrand partition function of the RNA molecules, we can now calculate the average level of their coverage by the coat proteins,
| (7) |
and find
| (8) |
Equation 8 shows that increasing the affinity of the protein for the RNA, that is, increasing the value of s, e.g., by changing the pH or the concentration of free protein aggregates in solution (5), can only lead to full encapsidation of the viral RNA and 〈θ〉 → 1 if s ≫ 1. For s ≪ 1, 〈θ〉 → 0 and RNA molecules and protein aggregates then remain freely dispersed in solution. For s = 1, we have 〈θ〉 = 1/2 σ(q + 1)/(1 + q), which is equal to one-half if qσ ≫ 1 or to 1/2 σ(q + 1) if qσ ≪ 1.
From the plots of 〈θ〉 in Fig. 2, C and D, it is apparent that the transition from free RNA and protein aggregates to fully functional TMV particles occurs for values close to s = 1 and becomes sharper with increasing template length. The required sequential binding implies long-range correlations between bound protein units, which is why the adsorption transition becomes a true phase transition in the limit q → ∞ despite the model being one-dimensional. For templated assembly models such as that based on the one-dimensional Ising model (26), there is no phase transition even in the infinite-chain limit. Allostery causes the point where half of the RNA molecules are, on average, covered with coat protein (the adsorption transition point) to shift toward larger values of s, while at the same time sharpening the transition (see Fig. 2, C and D).
Figure 2.
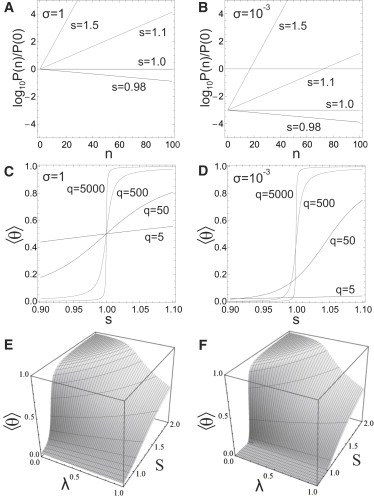
Ratio of probabilities P(n)/P(0) for an RNA molecule to be coated by n protein units as a function of the affinity s (A) in the absence of allostery (σ = 1), and (B) in the presence of allosteric effects (σ = 10−3). The average fraction of binding sites occupied by protein aggregates, 〈θ〉, for (C) σ = 1 and (D) σ = 10−3 also as a function of the affinity s. For the number of binding sites on each polymeric template we set q = 63. (E and F) The average level of coverage of RNA strands by coat proteins 〈θ〉 as a function of the bare affinity s (E) in the absence of allostery (σ = 1), and (F) in the presence of allosteric effects (σ = 10−3). The effective number of binding sites equals q = 63.
We now investigate whether the mean coverage applies to all individual RNA molecules or whether there are great differences in coverage between different ones. From the equilibrium distribution of RNAs occupied by n protein aggregates, defined as
| (9) |
we find
| (10) |
From Fig. 2, A and B, we conclude that allostery plays an important role in strongly favoring fully, over partially, covered RNA molecules. For σ = 1, that is, in the absence of allosteric effects, RNA molecules coated with n protein units obey an exponential distribution in n, leading to partially covered TMV particles of all intermediate lengths n for s > 1 albeit favoring the completely filled one for n = q. When allostery does come into play and σ ≪ 1, the probability for coverage of RNA with coat proteins below a critical value 0 < n∗ = −ln σ/ln s is much lower than that of the empty RNAs (with n = 0). Only above n∗, substantial coverage of RNA with coat protein occurs, producing either empty or almost fully covered viruses, in particular if σ is sufficiently small. Nucleated virus capsids with n < n∗ are thus high-energy structures that do not form free in solution in appreciable concentrations and are thermodynamically unfavorable.
We now come back to the issue of linking the affinity, s, to an experimentally controllable quantity and return from a grand canonical to a canonical description in which the amount of material in solution is fixed rather than the chemical potentials. Let ϕP denote the overall (dimensionless) concentration of proteins present in the solution. From the condition of the conservation of mass of the protein aggregates, we have
| (11) |
where is the dimensionless RNA concentration. Hence,
| (12) |
with λ = qρR/ϕP the earlier defined stoichiometric ratio and S ≡ ϕP exp(−ϵ−g) a bare affinity. The bare affinity is the product of the overall protein concentration ϕP, which is a known quantity, and a binding constant K ≡ exp(−ϵ − g). Clearly, Eq. 12 is an implicit expression that needs to be solved for s. For the case of excess protein λ → 0 we obviously have the identity s = S. In the other limit, for concentrations of RNA binding sites far in excess of that of protein units in the solution, λ → 0 and s → 0, implying low average RNA coverage.
Perhaps not entirely surprisingly, we conclude that to fully cover all the RNA molecules present in the solution such that 〈θ〉 = 1, we need an amount of protein far in excess of the number of binding sites, qN. This can also be deduced from Fig. 2, E and F, where we plot the mean fraction of occupied sites as a function of the bare affinity, S, and of the stoichiometry, λ. Apparently, the level of cooperativity of the binding of the proteins to the RNA strongly decreases with increasing stoichiometry. It is in this context not quite clear why so many experimental studies focus on stoichiometric ratios close to unity (13,17,34,35).
Kinetic Model
To extend our equilibrium model toward a description of the dynamics of the assembly and disassembly of the rodlike virus particles, we consider a reversible sequential association or dissociation of coat proteins, with adsorption rates k+ (n) and desorption rates k− (n) that depend on how many protein units n are bound onto the RNA. From this, we obtain a set of kinetic equations for the probabilities P (n, t) that RNA molecules are occupied by n protein aggregates at time t. Our approach is similar in spirit, yet not directly comparable, to that of recent work describing the assembly and disassembly kinetics of capsids of spherical viruses (36–38), and approaches to describe the helix-coil transition kinetics in polypeptides (31–33).
For convenience, we imply the time dependence of the occupation probabilities by writing P (n) = P (n,t), and distinguish these from the equilibrium distribution written as Peq (n). The set of kinetic equations is
| (13) |
| (14) |
| (15) |
where the first and last equation involve the empty and fully bound RNAs, respectively. In time, the system evolves toward its equilibrium state as discussed in the previous section, and hence and . With these conditions, the disassembly rates k−(n) can be expressed by the assembly rates k+(n) and the equilibrium probabilities Peq(n) as k−(n) = k+(n − 1) Peq(n − 1)/Peq(n), where the equilibrium distribution Peq(n) is given by Eq. 10.
After the adsorption of the first 20S aggregate onto the OAS with a rate k+(0), the adsorption kinetics of subsequent protein aggregates should not differ significantly from each other. We therefore presume that the on-rates are independent of the number of previously adsorbed protein units, so k+(n) = k+, at least for n > 1. Then, it makes sense to relate the on-rate of the first protein aggregate to that of the others, k+(0) ≡ κk+. Here, κ is a measure for how much faster or slower binding of the first 20S aggregate is relative to that of the subsequent protein units. Clearly, if κ ≪ 1, we expect assembly to be slowed down drastically as the binding of the first aggregate will become rate-limiting. However, as we shall see below, for the viruses to assemble, we need to pass a free energy barrier if σ ≪ 1. The reason is, of course, that assemblies of size 0 < n < n∗ are high-energy structures, as discussed in the preceding section. This implies that in practice it will be difficult to distinguish between kinetic and thermodynamic nucleation, although their effect on the disassembly kinetics turns out to be quite different.
If, in addition, we substitute and , we obtain the kinetic equations
| (16) |
| (17) |
| (18) |
| (19) |
where we see that the second equation depends on the ratio of κ and σ. The former is a measure for the importance of kinetic nucleation and the latter for thermodynamic nucleation. Note that κ occurs in the first equation independently of σ, yet the ratio of κ and σ occurs in the kinetic equation of RNA molecules with one bound protein aggregate. For the matrix notation, see the Supporting Material.
We employed a classical fourth-order Runge-Kutta method to numerically solve the kinetic equations for protein concentrations in excess of the number of binding sites, i.e., λ → 0 or S = s, and investigate the characteristics of assembly and disassembly of our model. We need not focus on the case of excess protein, of course. Subunit depletion can be taken into account by calculating 〈θ〉 at every time step τ and calculating from Eq. 11 the corresponding value of s that becomes a function of τ. The physics is not appreciably different, which is why we focus our discussion on the numerically much simpler case λ → 0.
Assembly from nearly empty to fully covered RNA molecules requires a deep quench in the affinity S, for example by a sudden change in pH or temperature, or by a sudden addition of proteins to a solution of RNA molecules. Upon a quench from, say, conditions where 〈θ〉 = 1.0 × 10−4 to those with 〈θ〉 = 0.99, assembly occurs via unstable intermediates toward the stable equilibrium distribution. See Fig. 3, C and D. In this case, the majority of RNA molecules, roughly 95%, is covered with >60 protein 20S assemblies after assembly has completed, if we presume q = 63 (note that q = 63 corresponds to full coverage of the RNA if we presume the adsorbing protein units to consist of 20S assemblies consisting of ∼17 coat proteins; we chose this value of q only for discussing the model and do not imply that the building blocks have to be 20S units) and σ = 0.01. For these values of σ and q, the affinities s = 0.35 and s = 2.6 correspond to the values for the initial and final coverage.
Figure 3.
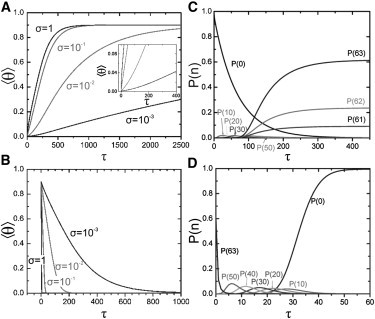
(A) Assembly and (B) disassembly kinetics of TMV as modeled by a kinetic zipper for different values of the allosteric parameter σ presuming 63 binding sites for each RNA molecule. The quenches are between average surface coverages 〈θ〉 = 0.001 → 〈θ〉 = 0.9 and 〈θ〉 = 0.9 → 〈θ〉 = 0.001. (A, Inset) Expanded view of the onset of assembly, to point out the lag time introduced by the allosteric factor σ. (C) Assembly after a sudden quench from affinities s1 = 0.35 → s2 = 2.6 and (D) disassembly after the quench s2 = 2.6 → s1 = 0.35. Shown are the probabilities P(n) of n protein units on RNA molecules consisting of 63 binding sites as a function of the dimensionless time τ. Here, s1 = 0.35 and s2 = 2.6 correspond to a coverage of 〈θ〉 = 10−4 and 〈θ〉 = 99, respectively, and the allosteric parameter σ = 0.01. All on-rates are equal, implying κ = 1.
The rate-determining step for assembly is the adsorption and conformational switching of the first 20S protein aggregate, as indicated by the slow decrease in concentration of empty RNA molecules, P(0). See Fig. 3 C. After nucleation has occurred and the highly unfavorable intermediate states are populated temporarily, assembly occurs quickly toward fully assembled virus particles. If allosteric effects were not important and σ = 1, P(0) decreases significantly more quickly than if σ ≪ 1. So, although allostery helps to completely cover the RNAs, it does so at the cost of slowing down the assembly kinetics.
Not surprisingly, the disassembly is not delayed by a sluggish nucleation process and therefore the fraction of fully assembled viruses quickly decreases upon a downward quench of the affinity s. According to our model, disassembly is quite a bit swifter than assembly. Still, σ influences the disassembly kinetics, although subtly (see Fig. 3 B). Unfortunately, we have not been able to find in vitro disassembly studies in the literature, so whether this prediction holds any water remains unclear. It is true that in the in vivo experiments, disassembly from the 5′ to the 3′ end occurs rapidly in 2–3 min (39–41). In vitro assembly into full viruses occurs on the timescale of 6–10 min, which would support our prediction (4). However, disassembly in vivo is thought not to proceed via spontaneous processes but rather by cotranslational disassembly (42,43) so this observation does not lend actual support for our model.
Decreasing the value of the allostery parameter σ increases the influence of allosteric effects on the binding of protein to the RNA and thus the dynamics. As can be seen from Fig. 3 A, the average coverage by coat proteins shows a lag time in the early-stage kinetics due to the nucleation step that strongly influences the overall rate of assembly. The rate of disassembly is decreased as well by a stronger allosteric effect, as is shown in Fig. 3 B. Here, assembly and disassembly were chosen between a coverage of 〈θ〉 = 0.001 and of 〈θ〉 = 0.9. It implies that different quench depths Δs were employed because the coverage depends on σ, as discussed in the previous section.
The disassembly rates for deep quenches of equal quench depth are essentially equivalent for different values of σ, except for the very late stages (see Fig. S1 in the Supporting Material). For shallow quenches in the affinity s, the rates are indeed different and the late-stage assembly can be described by a single exponential relaxation (see Fig. S2). We quantify the rates by evaluating the half-coverage time τ1/2, i.e., the time required to achieve 50% coverage (see the Supporting Material for extended discussion). We find for shallow quenches that the nucleation step predominates over the overall rate of assembly, and less so for disassembly. As a consequence, disassembly rates are always larger than assembly rates. This qualitatively different behavior for shallow and deep quenches originates from the variation of mean coverage 〈θ〉 with the affinity s. For deep quenches in s, 〈θ〉 does not significantly change with different σ. For shallow quenches, 〈θ〉 varies strongly as a function of σ, which translates itself in different rates of assembly and disassembly.
In Fig. 3, the assembly rates for adsorption of the first and subsequent protein units were taken to be equal, i.e., κ = 1 so k+ (0) = k+. The observed nucleation-type assembly kinetics originates solely from the costly conformational switching of the first adsorbed protein aggregate and the melting of the RNA strand. By taking a different assembly rate for the adsorption of the first protein unit, implying κ ≠ 1, or, in other words, k+(0) ≠ k+, we find an even stronger delay of the assembly the smaller κ is, and the slower the first step is in comparison with subsequent steps. See Fig. S3 A. The disassembly kinetics of the removal of all but the last coat protein unit is unaffected by the parameter choice of κ ≪ 1 (see the Supporting Material for details, and Fig. S3 B). Setting κ > 1 does not influence the assembly and disassembly kinetics to any discernible level. This, we believe is caused by the presence of the high-energy intermediates, and hence to be an effect of the allostery. As the assembly kinetics is already well captured by the introduction of the allosteric factor σ, it seems sensible to set κ = 1 for comparison with experiments in the following section.
Comparison with Experimental Data
From comparison with experiments we ideally would not only confirm the validity of our model but also determine the correct model parameters and thus be able to distinguish, for example, between the contested building blocks involved in TMV assembly, that is, the template length q, as well as the cooperativity σ. Although the model describes the dynamics of the assembly quite accurately as we shall see, the determined parameters are of limited precision due to several experimental challenges, not least the fact that RNA extracted from TMV-infected plants often contains shorter RNA pieces, presumably due to the presence of nucleases in solution. As a result, the observed length distribution of assembled virus particles contains a significant fraction of short virus particles, which are indistinguishable from incompletely assembled viruses. Furthermore, because the allostery parameter σ in particular influences the initial stages of the virus particle growth, determination of the starting time of the experiment is crucial yet not always clearly stated in experiments. Lastly, knowledge of the phase diagram of the virus assembly and thus the experimentally employed quench depth would limit the number of freely adjustable parameters significantly. Without knowledge of the quench details, the parameter space is considerable and requires one to guess for at least some of the parameters.
To compare our model with available experimental data, we presume that the addition rate of the first protein unit is equal to that for all subsequent protein aggregates and set κ = 1. Even if this is not quite true and, say, κ < 1, the nucleation-type of kinetics that this produces cannot easily be distinguished from that resulting from the effects of allostery as we have seen previously. We thus absorb potential kinetic effects into the thermodynamics of allostery, i.e., into the value of σ that becomes an effective one.
The most detailed experimental data we confront our theory with are those of Butler and Finch (44), who, in 1973, studied the reconstitution of TMV particles. In these experiments, solutions of protein disks were added to the RNA molecules in excess of the number of binding sites on the RNA with a stoichiometry of λ = 0.45. The length distribution of the assembled structures was recorded as a function of time and corrected for the effects of the degradation of RNA molecules. Partially assembled rods shorter than 20 nm were ignored due to limitations of the electron microscopy that was used to determine the size distribution. We set the length of the template equal to the effective number of binding sites per protein unit on the viral RNA. We now presume that such a protein unit is equivalent to a 20S aggregate, i.e., either a disk or a proto-helix, as the authors have claimed to have used 20S protein aggregates. Thus, we set q = 63.
The best fit to the data, presented in Fig. 4 A, we found by setting σ = 0.001, and presuming a quench from an affinity of s = 0.84 to that of s = 2.6. This corresponds to bare values of the affinities of S = 0.84 and S = 4.7 and average coverage 〈θ〉 = 5 × 10−4 and 〈θ〉 = 0.99. Following the experiments, we left out partially assembled rods shorter than 20 nm, equivalent to 0 ≤ n ≤ 4, from the analysis, and we renormalized the probabilities. The timescale τ = 15t [min] we set equal to the actual time in minutes t [min] to obtain the best fit, giving an add-on rate of k+ = 15 [min−1]. Here, we presumed that the experimental data at t = 0 [min] indeed corresponds to the beginning of the assembly process, that is, t0 = 0 [min] ignoring any delay time between the moment the sample was taken from the protein RNA solution, and the time at which the assembly was actually stopped. A somewhat different choice of zero-time may lead to a smaller value for σ than we estimated from our curve fitting.
Figure 4.
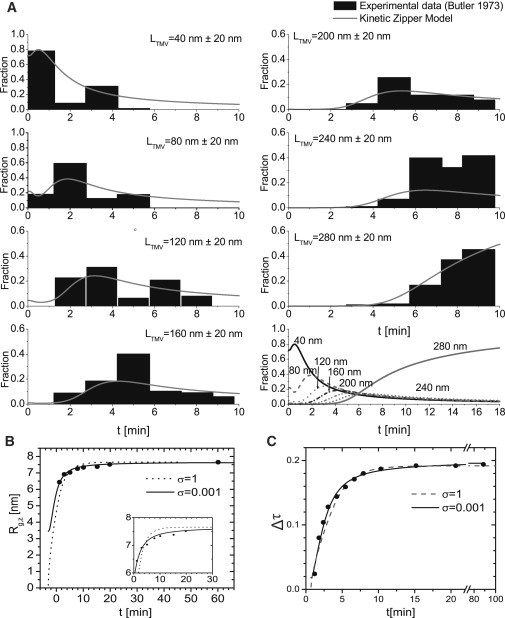
Comparison of the predictions of the kinetic zipper model with experimental data. (A) Experiments of Butler and Finch (44) on the reconstitution kinetics of TMV. Shown are fractions in percentile units of binned length ranges as a function of dimensionless time τ. To obtain a good fit, we set the model parameters described in the main text at σ = 0.001 and κ = 1, and presumed a quench from s1 = 0.84 to s2 = 2.58. (B and C) Comparison between experimental results probing some average of the size of the growing virus particles in TMV assembly experiments and the kinetic zipper model. (B) Radius of gyration R,g,z, as obtained by SAXS versus time. (Symbols) Experimental data (35). (Drawn line) Theory (k+ (σ = 1) = 40[min−1], k+ (σ = 0.001) = 65[min−1]). (Inset) Enlarged part of the same plot. (C) Assembly kinetics followed by the increase in turbidity upon mixing TMV protein disks with TMV RNA. (Symbols) Experimental data (45). (Drawn line) Theory (k+ (σ = 1) = 60[min−1], k+ (σ = 0.001) = 112[min−1]). Model parameters for panels B and C were set to σ = 0.001, κ = 1. A quench from 〈θ〉 = 0 to 〈θ〉 = 0.9 was presumed.
Butler and Finch (44) divided the experimental data for the time evolution of the various levels of completion of the encapsulation of the RNA into bins of multiples of 40-nm particle lengths. As is clear from Fig. 4 A, our kinetic zipper model describes the time dependence of the entire population of TMV particles of different states of completion reasonably well. In the late stages, i.e., after 10 min, still a very large fraction of almost complete TMV particles with an average length of 240 ± 20 nm remains, which does not quite agree with our predictions as is evident from Fig. 4 A.
Although Butler and Finch did correct their data for growth termination due to degraded RNA, it is reasonable to assume that, in the late assembly stages, distinguishing discontinued growth of the 240 ± 20 nm particles for thermodynamic reasons from that due to broken RNA molecules is not possible. The latter is of course not accounted for in our model. From the best fit to the experimental data, we conclude that the assembly has not completed at the point when the experiments halted (Fig. 4 A, bottom right).
Another explanation for the discrepancy may be that the elongation of the virus is bidirectional: assembly from the origin of assembly region on toward the 5′ end of the viral RNA completes much more rapidly than the assembly in the direction of the 3′ end. If the assembly in the 5′ direction is completed, the virus particles are roughly 260 nm in length, which is in good agreement with the large fraction of almost fully complete viruses 240 ± 20 nm in length seen in experiments. Similar experiments by Fukuda et al. (14) with a higher resolution in the particle length observed this slower assembly toward the 3′ end. Although a different TMV strain (namely, the Japanese common strain OM) and higher salt concentrations were used, the length distributions during the reconstitution reaction closely resemble the ones from Butler and Finch.
We compare the evolution of the particle distribution obtained from our model for various values of σ and quench depths in Fig. S4 and show the best fit we could find for a template length q = 400 corresponding to a smaller protein unit (A-protein, with 4–6 proteins per unit) in Fig. S5. From comparing the best fits for q = 63 in Fig. 4 A and q = 400 in Fig. S5, we find that our model is not capable of distinguishing between the two values for the template length and hence the building block size given the noise in the experimental data. To be able to infer the type of building blocks from similar experiments, one would need a higher resolution of the virus particle-length distribution as well as a reasonably accurate zero-time to obtain a correct value for σ.
Despite all this, it seems that our model captures the main elements of the assembly kinetics of TMV, certainly of that in the direction of the 5′ end. As a further test, we compared our model with reconstitution data obtained by means of small-angle x-ray scattering (SAXS) (35) and turbidity measurements (45). In both these studies, experiments were conducted with just as many coat proteins as RNA binding sites available, implying that λ = 1. Strictly speaking, our numerical model does not apply for this stoichiometric ratio as we presumed λ ≪ 1, except in the initial stages when the solution concentration of protein units remains close to its initial value, and thus our predictions for the late stages may be more tenuous.
The mean radius of gyration, R,g,z, of the assembling virus particles, extracted from (time-resolved) static-radiation-scattering experiments is a so-called z average of all particles in the population and related to the z-averaged particle length, 〈Lz〉, via
| (20) |
where L(n) = 1 × n obviously depends on how many protein units n of length l have adsorbed onto the RNA (46) and 〈…〉z denote z averages. In Fig. 4 B, we fit the theory to the SAXS data of Sano et al. (35), where we set q = 63, l = 4.76 [nm], σ = 0.001, and k+ = 65 [min−1] and presume a quench from 〈θ〉 = 0 to 〈θ〉 = 0.9. The value of the add-on rate k+ that we now find is larger by a factor 4 than the one we found previously, but this may of course be due to different solution conditions. For comparison we plot the numerical results for σ = 1 and k+ = 40 [min−1]. As the zero-time is not precisely known in these experiments either, we set the assembly to commence at t0 = −3 [min] in our model to obtain good agreement with the experimental data.
Quite similar results for the size of the growing rods may be obtained from turbidity measurements. The turbidity is proportional to the scattered total intensity that within the Rayleigh-Debye-Gans approximation scales as the weight average of the rod length (47),
| (21) |
By setting σ = 0.001, k+ = 112 [min−1], t0 = 0.7 min, and presuming the assembly proceeds from a coverage of 〈θ〉 = 0 to that of 〈θ〉 = 0.9, we find good agreement between the experimental data, as is shown in Fig. 4 C. We also compare the data to the best fit for σ = 1.0, k = 60 [min−1], t0 = 0.7 min. For short timescales, the theoretical values for σ = 1 diverge slightly from the experimental data.
Because the parameters associated with the best fit are somewhat ambiguous due to the experimental uncertainties, the question as to which building blocks may be involved in the assembly of TMV remains unanswered at this point. New experiments could improve the accuracy of the measurements and thus of the extracted parameters, and might allow us to distinguish between the contested assembly paths.
Conclusions
In summary, we have presented a kinetic zipper model to describe the statics and dynamics of the assembly and disassembly of tobacco mosaic virus particles in solutions containing coat protein units and RNA molecules. The key ingredient of our theory is the integration of allostery: only the binding of the first 20S aggregate and concomitant conformational switching is penalized by a free energy cost. The conformational switching of subsequent aggregates (or single proteins) bound to the RNA is in our model catalyzed by the already present helical arrangement of proteins.
The model, although admittedly crude, does explain the main features of the in vitro reconstitution of TMV particles as observed in experiments. We find that allostery, if sufficiently strong, leads to all-or-nothing behavior in the assembly. This means that rather than incompletely encapsulating all RNAs in the solution, there is a strong driving force to (nearly) completely cover a fraction of RNAs, while keeping the remainder naked. Arguably, this all-or-nothing coverage enhances the survival probability of the virus, because the exposed (i.e., naked) RNA of an incomplete viruses is susceptible to attack, e.g., by nucleases.
We find that the cooperative assembly of fully covered RNA molecules, i.e., intact virus particles, is strongly influenced by the stoichiometric ratio that is proportional to the number of nucleotides and proteins in the solution. Only for the case where protein is available vastly in excess of the total number of nucleotides, full coverage can be achieved.
If allostery is indeed an important mechanism in virus assembly, as we believe is the case, then our calculations show that the assembly kinetics must occur via high-energy intermediate states that are present only in low concentrations. This makes the nucleation process the rate-limiting step. The associated lag time before assembly commences seems to be influenced by both the relative rate of adsorption of the first 20S aggregate and the extent of allostery. For disassembly of the virus, these parameters only influence desorption of the last protein unit and hence not the overall rate of disassembly. The combination of conformational switching and template-assisted self-assembly is not specific to the in vitro assembly of tobacco mosaic virus, and our model hence may apply to other viruses and protein-macromolecule binding processes as well. The late-stage assembly and the early-stage disassembly kinetics we find to be governed by a single-exponential relaxation, at least for the situation of excess protein.
Comparison of our quite simple model with available experimental data shows remarkably good agreement. From our curve fitting, we obtain estimates for the allostery parameter of σ ≈ 0.001. However, this value may be somewhat ambiguous related to the difficulty of establishing zero time and/or a stoichiometry ratio that is not sufficiently small as well as to experimental difficulties involving partially broken RNA pieces. Thus, to draw reliable conclusions new experiments are required, ideally conducted with the now available high-resolution electron microscopy techniques at well-controlled conditions, e.g., pH and salt concentration, and possibly varying stoichiometry. Good control over the starting time t0 is crucial for extracting an accurate value for σ.
An ideal testing ground for the model would be experiments employing poly-A nucleic acid containing the origin of assembly region of TMV. These experiments could distinguish between ideal assembly kinetics and any issues related to the tertiary structure of the RNA or the bidirectional assembly of TMV. Variation of the length of the poly-A molecule allows us to investigate the influence of the template length and if conducted under controlled conditions may resolve the controversy on the primary building block for assembly. Clearly, more experiments are needed to resolve these issues, as is an analysis of the kinetic model that deals with more realistic stoichiometries. The latter is left for future work.
Footnotes
Daniela Kraft's present address is Center for Soft Matter Research, New York University, New York, NY.
Contributor Information
Daniela J. Kraft, Email: d.j.kraft@uu.nl.
Paul van der Schoot, Email: p.vanderschoot@phys.tue.nl.
Supporting Material
References
- 1.Beijerinck M. About a contagium vivum fluidum as the cause of the mottling of tobacco leaves [Over een contagium vivum fluidum als oorzaak van de vlekziekte der tabaksbladen] Verhandelingen der Koninklijke Nederlandse Akademie van Wetenschappen. 1898;65:3–21. [Google Scholar]
- 2.Scholthof K., Shaw J., Sindelar L. APS Press; St. Paul, MN: 1999. Tobacco Mosaic Virus: One Hundred Years of Contributions to Virology. [Google Scholar]
- 3.Scholthof K.B. Tobacco mosaic virus: a model system for plant biology. Annu. Rev. Phytopathol. 2004;42:13–34. doi: 10.1146/annurev.phyto.42.040803.140322. [DOI] [PubMed] [Google Scholar]
- 4.Butler P.J. Self-assembly of tobacco mosaic virus: the role of an intermediate aggregate in generating both specificity and speed. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1999;354:537–550. doi: 10.1098/rstb.1999.0405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kegel W.K., van der Schoot P. Physical regulation of the self-assembly of tobacco mosaic virus coat protein. Biophys. J. 2006;91:1501–1512. doi: 10.1529/biophysj.105.072603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Klug A. The tobacco mosaic virus particle: structure and assembly. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1999;354:531–535. doi: 10.1098/rstb.1999.0404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Caspar D.L., Namba K. Switching in the self-assembly of tobacco mosaic virus. Adv. Biophys. 1990;26:157–185. doi: 10.1016/0065-227x(90)90011-h. [DOI] [PubMed] [Google Scholar]
- 8.Butler P.J.G., Klug A. Assembly of the particle of tobacco mosaic virus from RNA and disks of protein. Nat. New Biol. 1971;229:47–50. doi: 10.1038/newbio229047a0. [DOI] [PubMed] [Google Scholar]
- 9.Butler P.J., Finch J.T., Zimmern D. Configuration of tobacco mosaic virus, RNA during virus assembly. Nature. 1977;265:217–219. doi: 10.1038/265217a0. [DOI] [PubMed] [Google Scholar]
- 10.Butler P.J. The current picture of the structure and assembly of tobacco mosaic virus. J. Gen. Virol. 1984;65:253–279. doi: 10.1099/0022-1317-65-2-253. [DOI] [PubMed] [Google Scholar]
- 11.Shalaby R.A., Lauffer M.A. Hydrogen ion uptake upon tobacco mosaic virus protein polymerization. J. Mol. Biol. 1977;116:709–725. doi: 10.1016/0022-2836(77)90267-4. [DOI] [PubMed] [Google Scholar]
- 12.Namba K., Stubbs G. Structure of tobacco mosaic virus at 3.6 Å resolution: implications for assembly. Science. 1986;231:1401–1406. doi: 10.1126/science.3952490. [DOI] [PubMed] [Google Scholar]
- 13.Raghavendra K., Kelly J.A., Schuster T.M. Structure and function of disk aggregates of the coat protein of tobacco mosaic virus. Biochemistry. 1988;27:7583–7588. doi: 10.1021/bi00420a002. [DOI] [PubMed] [Google Scholar]
- 14.Fukuda M., Ohno T., Takebe I. Kinetics of biphasic reconstitution of tobacco mosaic virus in vitro. Proc. Natl. Acad. Sci. USA. 1978;75:1727–1730. doi: 10.1073/pnas.75.4.1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lomonossoff G.P., Butler P.J. Assembly of tobacco mosaic virus: elongation towards the 3′-hydroxyl terminus of the RNA. FEBS Lett. 1980;113:271–274. doi: 10.1016/0014-5793(80)80607-7. [DOI] [PubMed] [Google Scholar]
- 16.Lebeurier G., Nicolaieff A., Richards K.E. Inside-out model for self-assembly of tobacco mosaic virus. Proc. Natl. Acad. Sci. USA. 1977;74:149–153. doi: 10.1073/pnas.74.1.149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shire S.J., Stegkert J.J., Schuster T.M. Mechanism of tobacco mosaic virus assembly: incorporation of 4S and 20S protein at pH 7.0 and 20°C. Proc. Natl. Acad. Sci. USA. 1981;78:256–260. doi: 10.1073/pnas.78.1.256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schuster T.M., Scheele R.B., Potschka M. Studies on the mechanism of assembly of tobacco mosaic virus. Biophys. J. 1980;32:313–329. doi: 10.1016/S0006-3495(80)84959-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fukuda M., Okada Y. Elongation in the major direction of tobacco mosaic virus assembly. Proc. Natl. Acad. Sci. USA. 1985;82:3631–3634. doi: 10.1073/pnas.82.11.3631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Caspar D.L. Movement and self-control in protein assemblies. Quasi-equivalence revisited. Biophys. J. 1980;32:103–138. doi: 10.1016/S0006-3495(80)84929-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Erickson J.W., Bancroft J.B. Melting of viral RNA by coat protein: assembly strategies for elongated plant viruses. Virology. 1981;108:235–240. doi: 10.1016/0042-6822(81)90542-0. [DOI] [PubMed] [Google Scholar]
- 22.Zlotnick A., Mukhopadhyay S. Virus assembly, allostery and antivirals. Trends Microbiol. 2011;19:14–23. doi: 10.1016/j.tim.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zlotnick A., Johnson J.M., Endres D. A theoretical model successfully identifies features of hepatitis B virus capsid assembly. Biochemistry. 1999;38:14644–14652. doi: 10.1021/bi991611a. [DOI] [PubMed] [Google Scholar]
- 24.Liepold L.O., Revis J., Douglas T. Structural transitions in Cowpea chlorotic mottle virus (CCMV) Phys. Biol. 2005;2:S166–S172. doi: 10.1088/1478-3975/2/4/S11. [DOI] [PubMed] [Google Scholar]
- 25.Dykeman E.C., Twarock R. All-atom normal-mode analysis reveals an RNA-induced allostery in a bacteriophage coat protein. Phys. Rev. E. 2010;81:031908. doi: 10.1103/PhysRevE.81.031908. [DOI] [PubMed] [Google Scholar]
- 26.Jabbari-Farouji S., van der Schoot P. Competing templated and self-assembly in supramolecular polymers. Macromolecules. 2010;43:5833–5844. [Google Scholar]
- 27.Janssen P.G.A., Jabbari-Farouji S., Schenning A.P. Insights into templated supramolecular polymerization: binding of naphthalene derivatives to ssDNA templates of different lengths. J. Am. Chem. Soc. 2009;131:1222–1231. doi: 10.1021/ja808075h. [DOI] [PubMed] [Google Scholar]
- 28.Kittel C. Phase transition of a molecular zipper. Am. J. Phys. 1969;37:917–920. [Google Scholar]
- 29.Gallie D.R., Plaskitt K.A., Wilson T.M. The effect of multiple dispersed copies of the origin-of-assembly sequence from TMV RNA on the morphology of pseudovirus particles assembled in vitro. Virology. 1987;158:473–476. doi: 10.1016/0042-6822(87)90225-x. [DOI] [PubMed] [Google Scholar]
- 30.McGhee J.D., von Hippel P.H. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogeneous lattice. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- 31.Zimm B.H., Bragg J.K. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 1959;31:526–535. [Google Scholar]
- 32.Jernigan R., Ferretti J., Weiss G. Helix lifetimes within the conformational transition region. A random walk model. Macromolecules. 1973;6:684–687. [Google Scholar]
- 33.Brooks C.L. Helix-coil kinetics: folding time scales for helical peptides from a sequential kinetic model. J. Phys. Chem. 1996;100:2546–2549. [Google Scholar]
- 34.Sano Y., Inoue H., Kajiwara K. Solution x-ray scattering study of reconstitution process of tobacco mosaic virus particle using low-temperature quenching. Biophys. Chem. 1995;55:239–245. doi: 10.1016/0301-4622(95)00003-g. [DOI] [PubMed] [Google Scholar]
- 35.Sano Y., Inoue H., Hiragi Y. Differences of reconstitution process between tobacco mosaic virus and cucumber green mottle mosaic virus by synchrotron small angle x-ray scattering using low-temperature quenching. J. Protein Chem. 1999;18:801–805. doi: 10.1023/a:1020689720082. [DOI] [PubMed] [Google Scholar]
- 36.Endres D., Zlotnick A. Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys. J. 2002;83:1217–1230. doi: 10.1016/S0006-3495(02)75245-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Morozov A.Y., Bruinsma R.F., Rudnick J. Assembly of viruses and the pseudo-law of mass action. J. Chem. Phys. 2009;131:155101. doi: 10.1063/1.3212694. [DOI] [PubMed] [Google Scholar]
- 38.Hagan M.F., Elrad O.M. Understanding the concentration dependence of viral capsid assembly kinetics—the origin of the lag time and identifying the critical nucleus size. Biophys. J. 2010;98:1065–1074. doi: 10.1016/j.bpj.2009.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wu X., Xu Z., Shaw J.G. Uncoating of tobacco mosaic virus RNA in protoplasts. Virology. 1994;200:256–262. doi: 10.1006/viro.1994.1183. [DOI] [PubMed] [Google Scholar]
- 40.Wu X., Shaw J. Bidirectional uncoating of the genomic RNA of a helical virus. Proc. Natl. Acad. Sci. USA. 1996;93:2981–2984. doi: 10.1073/pnas.93.7.2981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shaw J.G. Tobacco mosaic virus and the study of early events in virus infections. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1999;354:603–611. doi: 10.1098/rstb.1999.0412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mundry K.W., Watkins P.A., Wilson T.M. Complete uncoating of the 5′ leader sequence of tobacco mosaic virus RNA occurs rapidly and is required to initiate cotranslational virus disassembly in vitro. J. Gen. Virol. 1991;72:769–777. doi: 10.1099/0022-1317-72-4-769. [DOI] [PubMed] [Google Scholar]
- 43.Culver J.N. Tobacco mosaic virus assembly and disassembly: determinants in pathogenicity and resistance. Annu. Rev. Phytopathol. 2002;40:287–308. doi: 10.1146/annurev.phyto.40.120301.102400. [DOI] [PubMed] [Google Scholar]
- 44.Butler P.J., Finch J.T. Structures and roles of the polymorphic forms of tobacco mosaic virus protein. VII. Lengths of the growing rods during assembly into nucleoprotein with the viral RNA. J. Mol. Biol. 1973;78:637–649. doi: 10.1016/0022-2836(73)90285-4. [DOI] [PubMed] [Google Scholar]
- 45.Schön A., Mundry K.W. Coordinated two-disk nucleation, growth and properties, of virus-like particles assembled from tobacco-mosaic-virus capsid protein with poly(A) or oligo(A) of different length. Eur. J. Biochem. 1984;140:119–127. doi: 10.1111/j.1432-1033.1984.tb08074.x. [DOI] [PubMed] [Google Scholar]
- 46.van der Schoot P. Structure factor of a semidilute solution of polydisperse rodlike macromolecules. Macromolecules. 1992;25:2923–2927. [Google Scholar]
- 47.Flory P.J. Cornell University Press; Ithaca, NY: 1953. Principles of Polymer Chemistry. [Google Scholar]
- 48.Zandi R., van der Schoot P., Reiss H. Classical nucleation theory of virus capsids. Biophys. J. 2006;90:1939–1948. doi: 10.1529/biophysj.105.072975. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


