Discharge properties of motor units during steady isometric contractions performed with the dorsiflexor muscles

Abstract

The purpose of this study was to record the discharge characteristics of tibialis anterior motor units over a range of target forces and to import these data, along with previously reported observations, into a computational model to compare experimental and simulated measures of torque variability during isometric contractions with the dorsiflexor muscles. The discharge characteristics of 44 motor units were quantified during brief isometric contractions at torques that ranged from recruitment threshold to an average of 22 ± 14.4% maximal voluntary contraction (MVC) torque above recruitment threshold. The minimal [range: 5.8–19.8 pulses per second (pps)] and peak (range: 8.6–37.5 pps) discharge rates of motor units were positively related to the recruitment threshold torque (R² ≥ 0.266; P < 0.001). The coefficient of variation for interspike interval at recruitment was positively associated with recruitment threshold torque (R² = 0.443; P < 0.001) and either decreased exponentially or remained constant as target torque increased above recruitment threshold torque. The variability in the simulated torque did not differ from the experimental values once the recruitment range was set to ∼85% MVC torque, and the association between motor twitch contraction times and peak twitch torque was defined as a weak linear association (R² = 0.096; P < 0.001). These results indicate that the steadiness of isometric contractions performed with the dorsiflexor muscle depended more on the distributions of mechanical properties than discharge properties across the population of motor units in the tibialis anterior.

attempts to identify the mechanisms that limit the ability of an individual to maintain a constant muscle force during a steady contraction have focused on the properties and activation characteristics of motor units (2, 12, 20, 23, 27–29, 31, 34, 36, 38). A key finding of this work is that it is often misleading to extrapolate from the recordings of a few motor units to the net output of all active motor units (27, 36). This limitation in determining the association between motor unit activity and muscle force can be circumvented either by increasing the number of motor units recorded during a contraction (28) or by importing experimental data into a computational model of motor unit recruitment and rate coding (10). The latter strategy was used to demonstrate that the number of motor units, the distribution of twitch forces, and the discharge variability of the population of motor units in the first dorsal interosseus were critical in approximating the simulated and experimental measures of the variability in abduction force exerted by the index finger during steady isometric contractions (2, 27).

Due to the influence of motor unit properties and motor unit number on the fluctuations in force during steady contractions (2, 12, 13, 27), the extent to which the results for the first dorsal interosseus generalize to other muscles remains to be determined. One other muscle, for which there are sufficient data for comparison with the first dorsal interosseus, is the tibialis anterior (6, 9, 11, 19a, 22, 25, 29, 37, 39). This muscle differs from the first dorsal interosseus in that it has ∼50% more motor units (9, 18, 25), fewer direct corticospinal inputs onto its motor neuron pool (5), a greater proportion of type I muscle fibers (19a), greater peak twitch forces (26, 39), and a greater motor unit recruitment range (7, 22, 27, 39).

The purpose of this study was to record the discharge characteristics of tibialis anterior motor units over a range of target forces and to import these data, along with previously reported observations, into a computational model to compare experimental and simulated measures of torque variability during isometric contractions with the dorsiflexor muscles. As the coefficient of variation (CV) for torque during steady contractions is less for the dorsiflexor muscles (33) than that for the first dorsal interosseus (12), we hypothesized that a different set of motor unit properties would be required to approximate the experimental measures of dorsiflexion torque variability. Some of these data have been presented in abstract form (19).

METHODS

The data were acquired in two experimental sessions to minimize the influence of muscle fatigue: the discharge characteristics of tibialis anterior motor units were measured in one session, and the variability in the torque exerted by the foot during steady isometric contractions performed with the dorsiflexor muscles at several target forces was recorded in the other session. The discharge times of 44 motor units were recorded from 10 individuals (32.9 ± 6.75 yr; nine men), and the variability of ankle dorsiflexion torque was measured from 11 volunteers (30.0 ± 4.71 yr; nine men). Eight subjects participated in both sessions. The ethics committee of the medical faculty of the Free University of Brussels (Belgium) approved the experimental protocol. None of the subjects had any known neurological disorders.

Torque measurement.

Subjects were seated in a chair in a slightly reclined position with the left foot strapped to a footplate, which was inclined at 0.785 rad relative to the floor. The angle between the foot and lower leg was 1.57 rad, and that between the lower and upper leg was 1.92 rad. The force exerted by the foot during isometric contractions was measured by connecting a footplate to a strain gauge force transducer (TC 2000-500, Kulite, Basingstoke, UK), which was attached under the footplate at the level of the metatarsophalangeal joint of the big toe. A moment arm of 17 cm was used to convert force to torque about the ankle joint. The signal from the strain gauge was amplified by a custom-made amplifier, low-pass filtered at 300 Hz (AM 502, Tektronix, Beaverton, OR), and sampled at 2 kHz. The sensitivity of the force transducer was 30 mV/N (linear range, 0–2,200 N).

Electromyogram measurement.

Single motor unit action potentials were recorded from the tibialis anterior muscle with a needle electrode, which comprised two 50 μm diamel-coated nichrome wires glued into the lumen of a 30-gauge hypodermic needle (8). The needle was inserted into the middle of the muscle and was moved to various depths and angles to improve the quality of the recording. No subject complained of discomfort during contractions due to the needle. A reference surface electrode for the single motor unit recordings was placed on the skin over the tibia. The single motor unit recording was amplified with a custom-fabricated differential amplifier (×2,000), filtered (100 Hz-10 kHz) prior to being sampled at 12,500 samples/s with AcqKnowledge version 3.7 (Biopac Systems, Goleta, CA), and stored on a computer.

To monitor whole-muscle activity during the prescribed tasks, the surface electromyogram (EMG) of the tibialis anterior (agonist) and soleus (antagonist) muscles was recorded with two silver disk electrodes (8 mm diameter) attached to the skin over each muscle in a bipolar configuration. Ground electrodes for the surface EMG were placed on the skin over the tibia. Surface EMG signals were amplified (×1,000) and filtered (10 Hz-1 kHz) with a custom-fabricated differential amplifier.

Experimental protocol.

Each experimental session began with the subjects performing two to three maximal voluntary contractions (MVC) to determine the maximal dorsiflexion and plantarflexion torques exerted by the foot. Subjects increased torque from rest to maximal in 1–2 s and maintained the maximal torque for ∼3 s. Participants were provided with verbal encouragement during the MVC task. Visual feedback of the torque was provided for the subjects, and the subject's leg and foot were monitored to ensure that the task was performed correctly. The greatest mean torque over a 1-s period was defined as the MVC torque. The mean value of the rectified surface EMG over the same time period was used to normalize EMG activity during the submaximal contractions.

Motor unit recordings.

Single motor unit action potentials were recorded during brief isometric contractions performed with the dorsiflexor muscles to match several different target torques. The subject increased torque gradually until a candidate motor unit was identified from the intramuscular recording (ramp task). Once a suitable motor unit was identified, its recruitment threshold was estimated across two to three ramp contractions. The recruitment threshold was defined as the torque at which the motor unit began to discharge action potentials repetitively (27).

The subject was then provided with several target torques, ranging from just below the recruitment threshold torque of the motor unit to the maximal torque at which the motor unit could be identified (target-matching task). Target torques (∼4) near recruitment threshold torque for the motor unit were increased in small increments to determine the torque at which the motor unit began to discharge action potentials repetitively. Subjects increased torque from rest to the target torque in ∼0.5 s and held the torque for 2–5 s. An example of data obtained during the target-matching task at recruitment and the maximal torque at which the motor unit could be identified are shown in Fig. 1. The electrode was then moved to a different location to identify another motor unit, and its discharge characteristics were recorded. Successive trials from different electrode locations were separated by at least 1 min of rest. Furthermore, subjects performed a maximal ramp contraction after recording from a single motor unit and before attempting to record from a new motor unit. Once the subject could not achieve a torque that was within 15% of the initial MVC torque recorded at the beginning of the session, the experiment was terminated to ensure that the protocol involved minimal fatigue.

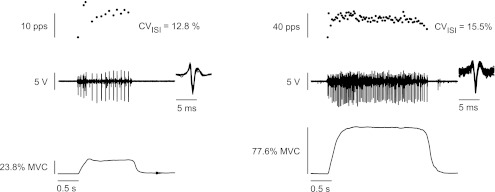
Fig. 1.

Sample data for 1 motor unit recorded during the target-matching task at its recruitment threshold torque [22.3% maximal voluntary contraction (MVC) torque] and the maximal torque (77.6% MVC torque) at which the motor unit could be identified. CV_ISI, coefficient of variation for interspike interval; pps, pulses per second.

Torque steadiness task.

Eleven subjects performed brief isometric contractions with the dorsiflexor muscles to match eight target torques. Each subject practiced the task at two randomly chosen target torques to become familiar with the requirements of the task. The target torques (2%, 5%, 15%, 30%, 50%, 70%, 85%, and 90% MVC torque) were presented in a random order, and the subject performed a brief, isometric contraction to match each target torque twice. The task involved increasing ankle dorsiflexion torque from rest to the target in ∼1 s and then exerting a steady torque for 4–6 s. Visual feedback of the target torque and the torque exerted by the foot were provided for the first 3 s of the contraction, once the target had been reached and was then removed for the remainder of the contraction. Visual feedback of ankle dorsiflexion torque was provided on a 17-in. monitor, located in front of subjects at eye level. The gain of the torque display was adjusted so that the target line was always in the middle of the screen, and the zero torque line was always at the top of the screen. Subjects were provided with at least 30 s of rest between trials, with longer rest periods for greater target torques.

Motor unit model.

A computational model of motor unit recruitment and rate coding, originally developed by Fuglevand et al. (10) and later modified by Moritz et al. (27) and Barry et al. (2), was used to simulate the isometric torque produced by a pool of motor units innervating the tibialis anterior muscle (9, 22, 25, 37, 39). The model, which was implemented in MATLAB R2009b (MathWorks, Natwick, MA), has been described in detail previously (2, 10, 27, 31, 32).

The model is comprised of a pool of motor units with systematic variation in recruitment threshold, minimal and peak discharge rates, and twitch torques. Motor unit recruitment was controlled by an excitation function that acted on the entire motor unit pool. Each motor unit generated a twitch torque in response to the discharge of a single action potential and a summation of twitch torques in response to trains of action potentials. The amplitude of the summed twitch torques was defined by a gain function that comprised two regions: 1) a gain of one was assigned for motor unit discharge rates normalized by motor unit contraction times, which were ≤0.4, and 2) the gain increased as a sigmoidal function for normalized discharge rates >0.4 (10). The simulated muscle torque about the ankle joint was generated by linearly summing the torques generated by the active motor units. Muscle torque at each level of excitation was normalized to the muscle torque at 100% excitation, when all motor units were active and discharging action potentials at peak rates.

The model was modified from previous versions that simulated the pool of motor units for the first dorsal interosseus muscle by increasing the number of motor units from 180 to 250, which is less than the value for the tibialis anterior, estimated by Feinstein et al. (9) and Van Cutsem et al. (39), but greater than that determined by McNeil et al. (25). Furthermore, the recruitment range was expanded from 60% to ∼85% MVC torque (22, 39), and the twitch torques were modified so that motor unit 1 had a twitch contraction time of 79.6 ms, and twitch torque of 1.02 mN·m, and motor unit 250 had values of 20.0 ms and 120 mN·m, respectively (39). The recorded minimal and peak discharge rates were imported into the model with the values increasing as a function of recruitment threshold torque. Minimal discharge rates ranged from 6.1 to 18.0 pulses per second (pps), and peak discharge rates ranged from 15.3 to 31.0 pps. The CV for interspike interval (CV_ISI) at motor unit recruitment was positively related to the recruitment threshold torque and declined exponentially for each motor unit as torque increased above recruitment threshold torque. The CV_ISI was defined as a function of the recruitment threshold of motor units in excitatory units (RTE_i; i = 1–250), the excitatory input to the pool (Ein), the excitatory drive above the recruitment threshold of each motor unit (ΔE), and a constant (A), which set the lower limit for the CV_ISI

$${\text{CV}}_{\text{ISIi}}=\text{A}+\left({\text{RTE}}_{\text{i}}/25\right)+\left(\text{Ein}/4\right)e^{\left(-\Delta {\text{E}}_{\text{i}}\right)}$$ (1)

The variation in contraction times and peak twitch torques across the motor unit pool was implemented with three different schemes. 1) Contraction time was matched to motor unit peak twitch torque, as in previous versions of the model (2, 10, 27, 31, 32), so that motor unit 1 had the longest contraction time and lowest peak torque, and motor unit 250 had the shortest contraction time and greatest peak torque. 2) Variability was added to the assignment of peak twitch torques (P_i) and contraction times (T_i) by adding a random number from a normal distribution. The random number for the twitch torques had a SD of 3.9 and was added to the exponential equation for peak twitch torques from Fuglevand et al. (10), but the values were constrained between 1 and 120 mN·m. The random number for the twitch contraction times had a SD of 10 and was added to the power law equation for twitch contraction times (note that the twitch torque values without variability were used for this scheme), which reduced the nonlinear least squares value (R²) for the power relation between motor unit twitch contraction time and peak torque from 1 to 0.57. 3) The association between motor unit peak twitch torque and contraction time was changed from a power function to a linear function to approximate the association reported in Van Cutsem et al. (39) (Eq. 2). This third scheme was accomplished by first adding variability to the assignment of motor unit twitch torques, as in the second scheme, and then adding variability to contraction times with a random number from a normal distribution and a SD of 10 to Eq. 2, which resulted in a linear relation (Eq. 3) with a coefficient of determination (R²) between motor unit peak twitch torque and contraction time of 0.096 (P < 0.001). The model parameters for the simulations are listed in Table 1.

$${\text{T}}_{\text{i}}=-0.13{\text{P}}_{\text{i}}+48.9$$ (2)

$${\text{T}}_{\text{i}}=-0.11{\text{P}}_{\text{i}}+50.5$$ (3)

Table 1.

Summary of parameters used for simulating the tibialis anterior motor unit pool

Model Parameters	Simulation 1	Simulation 2	Simulation 3
Motor unit number	250	250	250
Recruitment range, % MVC	80.4	85.7	87.6
Average twitch torque, mN·m	25.1	25.8	25.8
Twitch torque range, mN·m	1.02–120	1.06–117	1.02–117
Average contraction time, ms	44.5	46.6	47.5
Contraction time range, ms	20.0–79.6	20.1–86.6	21.2–73.8
Minimal DR range, pps	6.41–18.0	6.41–18.0	6.41–18.0
Peak DR range, pps	15.5–31.0	15.5–31.0	15.5–31.0
Minimum CVISI, %	3.04	5.04	5.04
MVC, mN·m	22.5	33.0	45.2

MVC, maximal voluntary contraction; DR, discharge rate; pps, pulses per second; CV_ISI, coefficient of variation for interspike interval.

Data analysis.

Single motor unit action potentials were discriminated offline using the template-matching features of Spike2 (Version 5.02; Cambridge Electronic Design, UK) and were verified by visual inspection. ISIs >250 ms (4 pps) or <10 ms (100 pps) were excluded from the data set, which corresponded to 0.13% of the total number of discharges (n = 3,868). The region of the force trace, over which the discharge characteristics were determined, corresponded to the 1-s period, in which the SD of force was minimal. The minimal discharge rate of each motor unit was defined as the discharge rate at which the motor unit began to discharge action potentials repetitively during the target-matching task. Peak discharge rate corresponded to the discharge rate at the greatest force at which the motor unit could be discriminated during the target-matching task. The average slope of the relation between discharge rate and torque was calculated for each motor unit by fitting a linear regression to the data for at least three target torques.

Recruitment threshold during the target-matching task was defined as the minimal target torque at which the motor unit discharged action potentials repetitively. When possible, this torque was compared with the recruitment threshold torque of the motor unit during the ramp task, which was defined as the force corresponding to the first discharge within a 0.5-s window in which the CV_ISI was <50%. Only seven of the 44 motor units did not have an identifiable recruitment threshold during a ramp contraction for comparison with the threshold determined during the target-matching task.

The CV for the torque exerted by the foot during the two steady contractions at each target torque was determined for a 1-s period beginning 0.5 s after visual feedback of the torque trace was removed. The trial, in which the torque was closest to the target torque, was used to calculate the CV for torque. The torque was linearly detrended (1-s period) before the CV was determined. The data reported in Moritz et al. (27) were reanalyzed using the above criteria and used to compare the CV for the abduction force exerted by the index finger with the CV for the foot torque. The rectified surface EMG for the tibialis anterior and soleus was averaged for the same 1-s period when the torque was analyzed and normalized to the MVC value.

Statistical analysis.

Linear regression analyses were used to determine the relations between recruitment threshold torque and 1) the minimal and peak discharge rates, 2) the slope of the relation between discharge rate and torque, 3) the CV_ISI at recruitment during the brief constant-torque contractions, 4) the range of target torques over which each motor unit was recorded, and 5) the greatest target torque at which each motor unit could be identified.

Two-factor repeated-measures ANOVAs were used to compare the simulated and experimental measures of the CV for dorsiflexion torque (between-subjects factor) across the eight target torques (within-subjects factor). Similarly, a two-factor repeated-measures ANOVA was used to compare the CVs for the abduction force exerted by the index finger and the dorsiflexion torque (between-subjects factor) across the eight target torques (within-subjects factor). Independent sample t-tests with a modified Bonferroni correction were used to determine the torques at which there were significant differences between the experimental and simulated CVs for dorsiflexion torque and index finger abduction force.

Regression analysis was also used to quantify the correlation, expressed as the coefficient of determination or the nonlinear least squares value (R²), between the experimental and simulated data, and independent sample t-tests compared the MVC torques of the three versions of the model with the experimental data. Statistics were performed with SPPS versions 16.0 and 17.0 (SYSTAT Software, Chicago, IL), nonlinear regression analysis was performed in MATLAB R2009b (MathWorks), and an α-level of 0.05 (α = 0.007, modified Bonferroni) was considered significant. Values are reported as means ± SD.

RESULTS

Discharge characteristics were obtained from 44 motor units in the tibialis anterior and tracked at an average of 5.9 ± 3.1 target torques. The torques ranged from recruitment threshold to an average of 22 ± 14.4% MVC torque (range: 2.23–74.4% MVC torque) above recruitment threshold. The average decline in MVC torque at the end of each motor unit experiment was 16.8% (P < 0.001). The simulated CVs for dorsiflexion torques did not differ from the experimental measurements at each of the eight targets once the model was updated with previous and current measurements of motor unit properties. The updates also produced simulated MVC torques (46.0 ± 0.050 mN·m), which did not differ statistically (P ≥ 0.383) from experimental values (48.8 ± 9.95 mN·m).

Recruitment threshold.

The torques at which motor units were recruited during the target-matching task were statistically indistinguishable (P = 0.691) from the recruitment threshold torques identified during the ramp task (Table 2). Although seven of the 44 motor units could not be tracked during the ramp task, the average difference in torque, at which these seven motor units either did or did not discharge action potentials during the target-matching task, was 2.17 ± 1.61% MVC torque.

Table 2.

Motor unit (MU) characteristics recorded during the target-matching contractions

MU No.	Recruitment Torque (% MVC)	Peak Torque (% MVC)	Torque Range (% MVC)	Minimum DR (pps)	Peak DR (pps)	Recruitment CVISI (%)	Peak Torque CVISI (%)
1	3.72	13.2	9.43	9.88	16.4	18.7	5.90
2	4.67	19.1	14.4	8.86	14.6	9.30	9.71
3	5.85	51.2	45.3	8.95	23.6	11.2	17.9
4	6.90	26.1	19.2	8.16	14.3	7.07	6.69
5	9.14	43.0	33.9	5.89	19.4	28.1	11.8
6	9.38	15.2	5.90	8.22	13.9	8.03	7.71
7	9.90	16.4	6.50	5.76	8.60	20.5	9.95
8	11.3	29.4	18.0	9.18	15.3	5.81	9.03
9	13.1	34.5	21.4	9.39	19.5	11.0	8.42
10	13.1	24.2	11.1	7.80	12.2	3.70	10.7
11	13.4	20.3	6.9	8.21	12.8	7.89	8.99
12	13.8	53.0	39.2	6.72	15.8	3.96	9.18
13	13.9	39.8	26.0	10.1	19.4	12.0	12.6
14	16.3	32.2	15.9	10.8	19.6	8.33	7.91
15	16.9	38.1	21.2	9.86	13.5	8.17	3.95
16	17.9	29.5	11.6	10.9	17.4	9.37	6.76
17	18.3	24.8	6.50	17.7	21.9	5.34	15.1
18	18.7	47.4	28.7	9.98	17.5	6.67	6.93
19	19.7	30.2	10.6	9.26	15.1	12.1	4.61
20	20.0	94.5	74.4	9.87	37.5	12.8	15.5
21	22.3	37.9	15.7	8.79	19.5	20.9	13.2
22	24.1	64.5	40.3	8.88	27.2	19.6	15.9
23	24.5	44.0	19.5	8.44	22.9	18.7	16.7
24	25.5	35.4	9.90	9.10	17.0	24.5	14.1
25	26.1	62.6	36.5	10.8	29.7	14.7	15.8
26	27.7	48.9	21.2	10.7	20.3	14.7	9.90
27	27.7	61.5	33.8	9.49	15.2	3.75	8.86
28	28.3	65.2	36.9	10.5	22.8	6.37	12.1
29	28.9	68.1	39.2	10.8	33.0	18.2	15.0
30	30.2	37.5	7.28	9.05	16.9	9.97	10.6
31	32.3	54.6	22.3	10.8	24.1	19.2	8.61
32	34.0	50.1	16.1	8.83	20.1	19.0	13.1
33	35.1	49.3	14.3	12.0	23.6	20.9	14.7
34	38.9	65.4	26.5	12.0	22.1	16.1	12.5
35	39.0	41.2	2.23	13.9	17.0	10.3	13.8
36	42.3	87.8	45.5	11.3	33.0	36.7	17.5
37	42.5	55.8	13.2	14.0	18.2	11.3	9.93
38	44.9	54.4	9.52	14.4	23.5	9.39	10.2
39	45.8	83.4	37.5	19.8	31.4	27.3	16.0
40	46.4	77.5	31.1	10.8	28.9	31.5	17.1
41	57.2	77.6	20.4	16.1	30.4	27.8	25.7
42	61.3	67.3	6.00	11.7	17.0	39.2	21.6
43	66.6	82.5	15.9	13.1	31.3	34.3	16.2
44	68.6	90.5	21.9	13.6	24.3	34.2	17.2
Mean	26.7	48.8	22.0	10.6	20.9	15.9	12.2
SD	16.6	21.8	14.4	2.82	6.5	9.61	4.55
Min	3.72	13.2	2.23	5.76	8.60	3.70	3.95
Max	68.6	94.5	74.4	19.8	37.5	39.2	25.7

Peak Torque and Peak DR, maximum torque and discharge rate at which motor unit was discriminated, respectively.

Discharge rate.

Motor unit discharge rate measured during the target-matching task increased with ankle dorsiflexion torque for all motor units. The slope of the relation between discharge rate and torque (0.55 ± 0.26 pps/% MVC torque; range: 0.15–1.21 pps/% MVC torque) exhibited a weak, positive relation with recruitment threshold torque (R² = 0.169; P = 0.006).

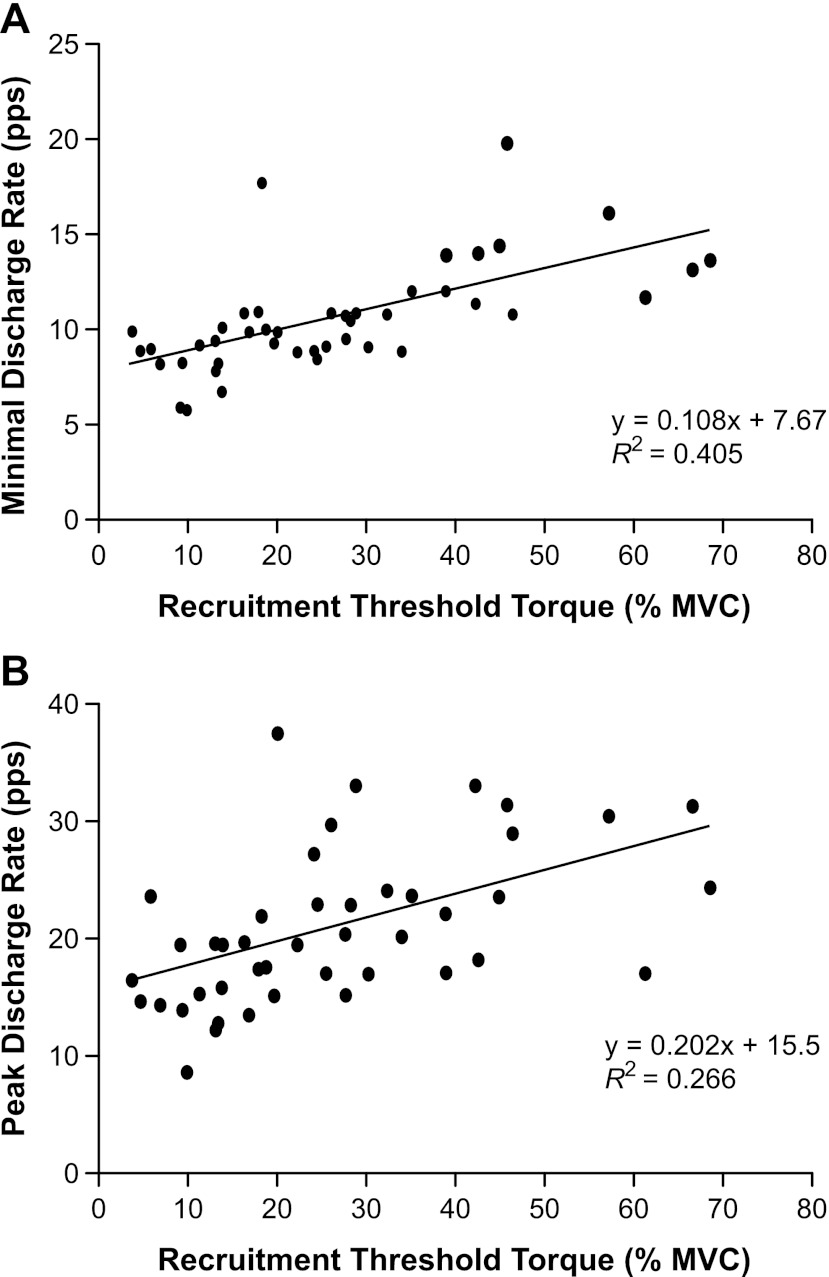
The minimal discharge rates of those motor units that were tracked during both tasks were significantly greater during the ramp task (11.6 ± 4.08 pps) than during the target-matching task (10.6 ± 2.73 pps; P = 0.05). The minimal and peak discharge rates measured during the target-matching task increased linearly as recruitment threshold torque increased. Minimal discharge rates increased from 8.1 to 15.1 pps as recruitment threshold torque increased (R² = 0.405; P < 0.001; Fig. 2A). Similarly, peak discharge rates increased from 16.2 to 29.3 pps, as recruitment threshold torque increased (R² = 0.266; P < 0.001; Fig. 2B). There was no significant association between recruitment threshold torque and the range of torques over which motor units could be identified (R² ≤ 0.001; P = 0.910). However, there was a significant association between recruitment threshold torque and the peak torque at which motor units could be identified (R² ≥ 0.564; P < 0.001).

Fig. 2.

The minimal and peak discharge rates of motor units as a function of recruitment threshold torque during the target-matching task. A: motor unit discharge rate at recruitment increased linearly as a function of the recruitment threshold force (R² = 0.405; P < 0.001). B: motor unit discharge rate at the peak target torque, at which the motor unit could be clearly identified, increased linearly as a function of recruitment threshold torque (R² = 0.266; P < 0.001).

Discharge variability.

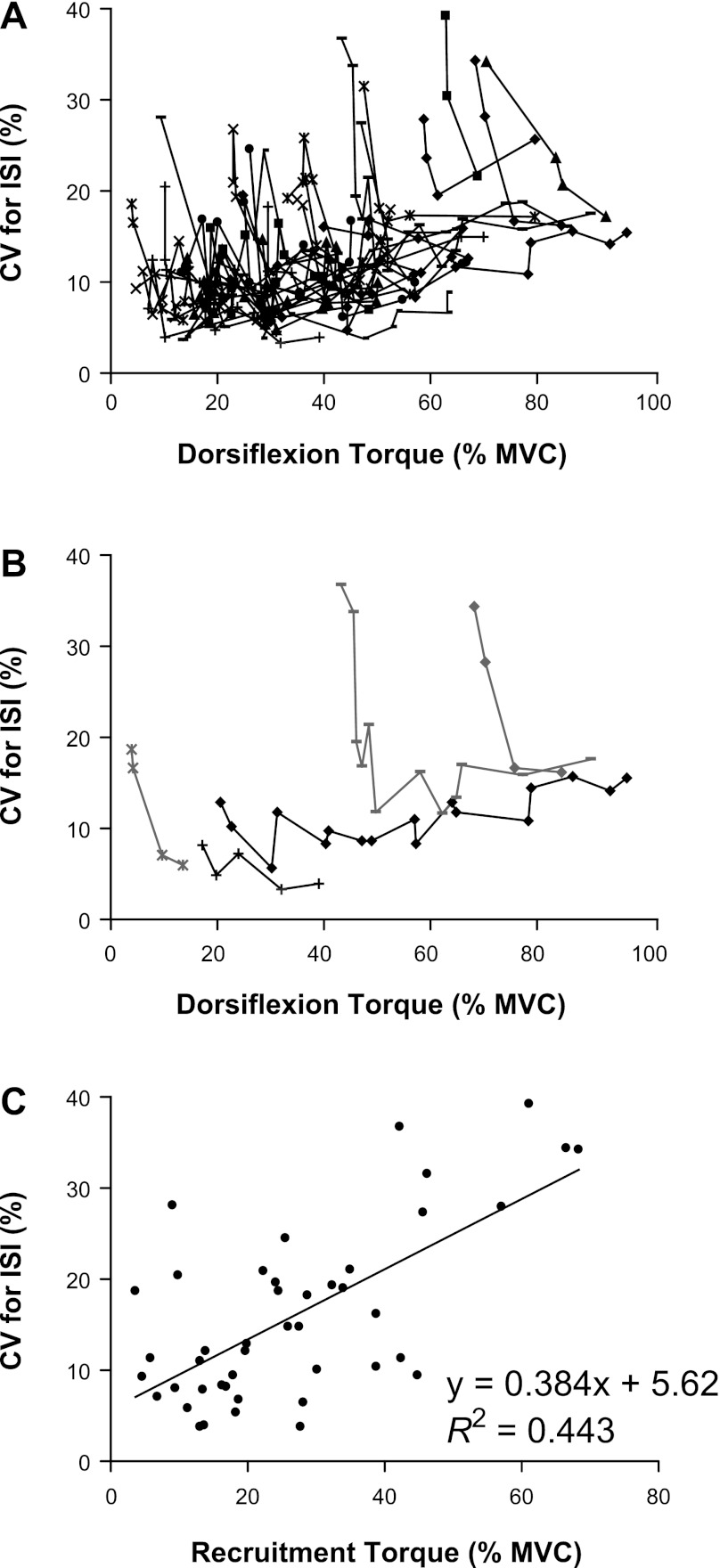
The CV_ISI for 24 of the 44 motor units declined exponentially as torque increased above recruitment (R² = 0.635 ± 0.245; nonlinear least squares value), whereas it remained relatively constant for 17 motor units (R² = 0.187 ± 0.292; P ≥ 0.060; Fig. 3, A and B), increased linearly for two motor units (R² = 0.556 ± 0.292; P ≤ 0.022), and varied nonmonotonically for one motor unit (R² = 0.489; nonlinear least squares value). The CV_ISI at recruitment increased linearly with recruitment threshold torque (R² = 0.443; P < 0.001; Fig. 3C). The mean CV_ISI for all motor units was 15.9 ± 9.61% at recruitment and 12.2 ± 4.55% at the greatest torque at which motor units could be identified.

Fig. 3.

The CV_ISI for the 44 motor units identified during the target-matching task. A: each symbol and line represents a different motor unit, and each data point corresponds to the mean CV_ISI over the steadiest 1-s period of the force trace at 1 target force. B: an example of the 2-principal patterns observed for the relation between the CV_ISI and dorsiflexion torque. The gray data points are examples of motor units for which the CV_ISI was high at recruitment and then decreased exponentially as torque increased above recruitment threshold torque. The black data points are examples of motor units for which the CV_ISI was low at recruitment and remained relatively constant as torque increased above recruitment threshold. C: the relation between the CV_ISI of each unit at recruitment and recruitment threshold torque (R² = 0.443; P < 0.001).

Torque variability and simulations.

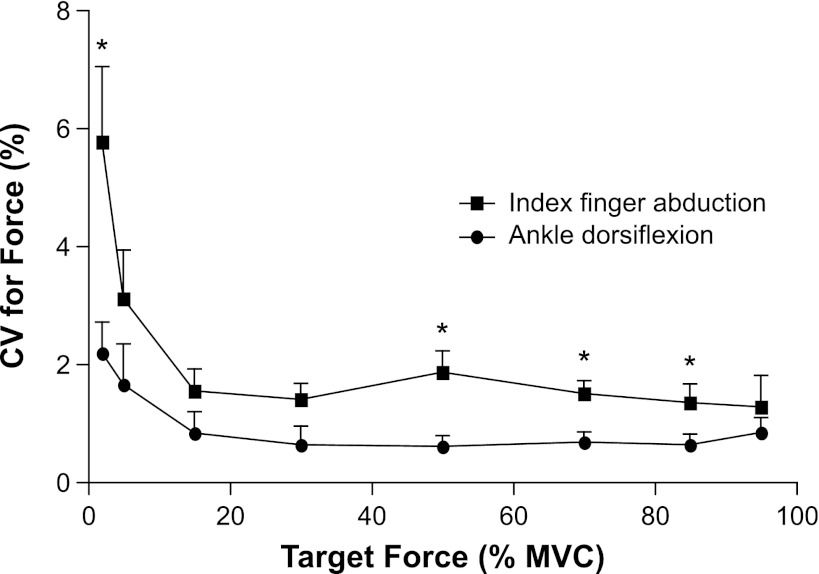
The CV for the torque exerted by the dorsiflexors was greatest at the two lowest target torques (2% and 5% MVC torque) and decreased to a relatively constant value for the remaining target torques. The CV for dorsiflexion torque was significantly less than that for the force exerted by the index finger abduction at targets of 2%, 50%, 70%, and 85% of MVC torque (P ≤ 0.001, modified Bonferroni; Fig. 4).

Fig. 4.

The CV for ankle dorsiflexion torque and for index finger abduction force plotted as a function of the target value. The index finger data are from Moritz et al. (27). The CV for ankle dorsiflexion torque was less than that for index finger abduction force at targets of 2%, 50%, 70%, and 95% MVC force (P ≤ 0.001, modified Bonferroni). Data are plotted as mean ± SE; *P ≤ 0.007 (modified Bonferroni) for the CV for force between the ankle dorsiflexion torques and index finger abduction forces.

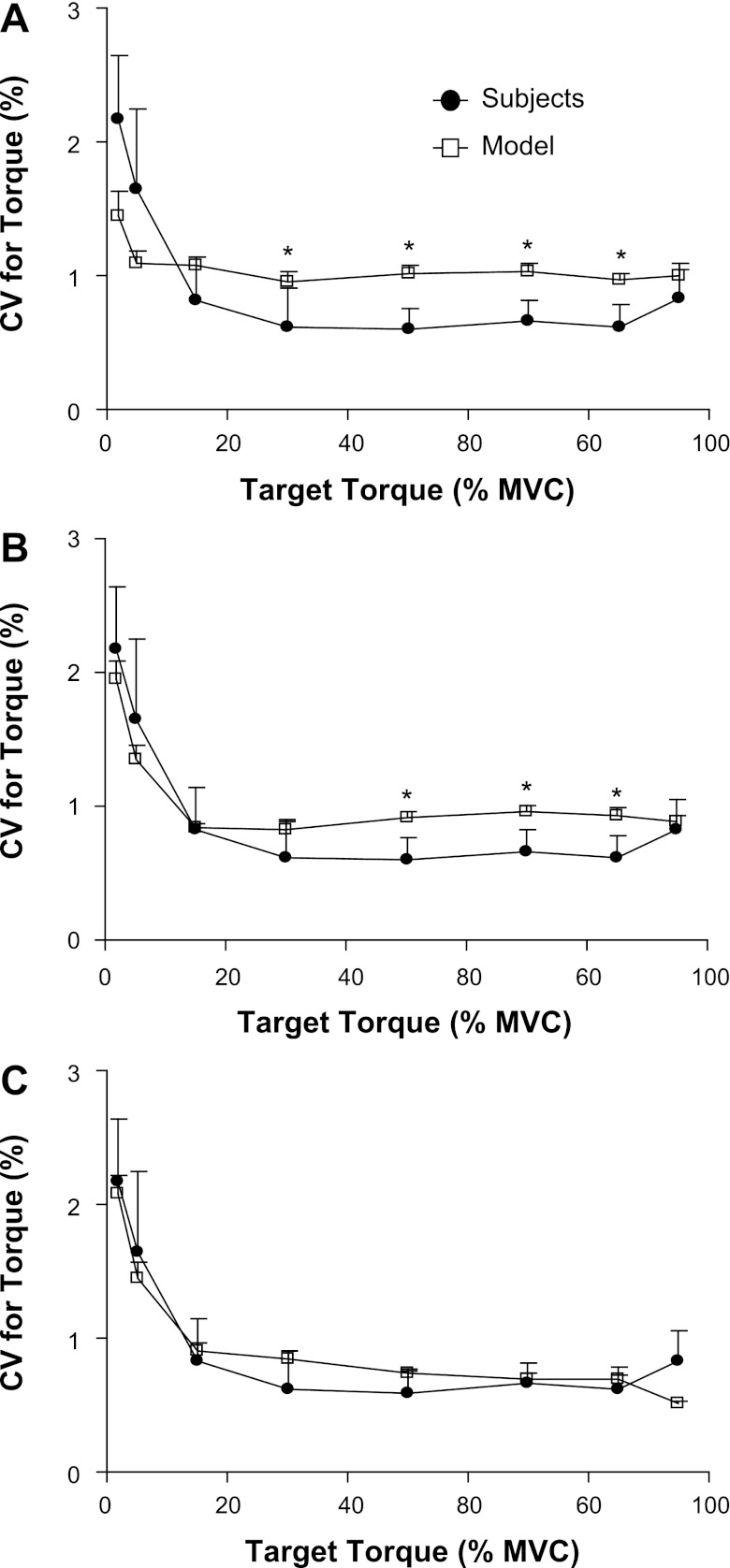
The first simulation scheme, in which the motor unit twitch torque varied as a function of contraction time, produced CVs for dorsiflexion torque, which were least successful in approximating the experimental CVs for torque (Table 1, Simulation 1). The simulated CV for torque matched the values observed experimentally at target torques of 2%, 5%, 15%, and 95% MVC torque (P ≥ 0.013, modified Bonferroni; Fig. 5A). Although the simulated MVC torque for the tibialis anterior (22.5 ± 0.04 mN·m) was significantly less than the experimental dorsiflexion MVC torque (48.8 ± 9.95 mN·m; P < 0.001), there was a strong linear association between the simulated and experimental CVs for force (R² = 0.823; P = 0.002).

Fig. 5.

The measured and simulated CVs for dorsiflexion torque. Each panel represents the difference between the experimental measurements and 1 of the models of motor unit recruitment and rate coding for the tibialis anterior. A: the model reported by Moritz et al. (27) was revised to include an upper limit of motor unit recruitment at 80% MVC force and a minimal CV_ISI for motor units of 3%. B: the upper limit of motor unit recruitment was set at 85.7% MVC torque, the minimal CV_ISI was assigned to be 5%, and variability was added to the association between motor unit peak twitch torques and contraction times. C: the association between motor unit peak twitch torques and contraction times was changed to a linear relation (y = −0.11× + 50.5; R² = 0.096; P < 0.001). Data are plotted as mean ± SE; *P ≤ 0.007 (modified Bonferroni) between the simulated and experimental measurement of CV for torque.

The second simulation scheme (Table 1, Simulation 2) included an increase in the upper limit of motor unit recruitment to 85.7% MVC torque (39), an increase in the lower limit of the CV_ISI to 5%, approximating the average CV_ISI, which was predicted to be recorded from subjects' lowest threshold tibialis anterior motor unit (Fig. 3C), and the addition of variability to motor unit twitch contraction times and peak torques. Although the modifications increased the simulated MVC torque of the tibialis anterior to 32.3 ± 0.050 mN·m, the MVC torque remained significantly less than that observed experimentally (P < 0.001). With these modifications, however, the simulated CV for torque did not differ from the experimental values at target forces of 2%, 5%, 15%, 30%, and 95% MVC torque (P ≥ 0.185, modified Bonferroni; Fig. 5B), and there was a stronger association between the simulated and experimental CVs for torque (R² = 0.916; P < 0.001).

The third simulation scheme imposed a change in the association between motor unit peak twitch torques and contraction times from a power function (10) to a linear relation (39) (Table 1, Simulation 3). These adjustments further increased the simulated MVC torque of the model to 46.0 ± 0.050 mN·m, which was not significantly different from the experimental dorsiflexion MVC torques (P ≥ 0.383). With these adjustments, the simulated CVs for torque did not differ from the experimental values at each of the eight target torques (P ≥ 0.019, modified Bonferroni), and there was a strong association between the simulated and experimental CVs for torque (R² ≥ 0.907; P ≤ 0.001; Figs. 5C).

DISCUSSION

The main findings of this study were that the relative discharge variability of most (55%) motor units of the tibialis anterior decreased exponentially as force increased above recruitment threshold force and that the relative discharge variability at recruitment was positively related to the recruitment threshold force. Although these associations were somewhat similar to those reported for the first dorsal interosseus, the CV_ISI of tibialis anterior motor units was not the main factor contributing to a close approximation between the simulated and experimental CVs for dorsiflexion force, especially at the moderate-to-higher target forces. The ability of the model to approximate the experimentally observed torque variability over the operating range of the dorsiflexors was achieved only after variability was added to the assignment of motor unit twitch contraction times and peak twitch torques, and the association between the two motor unit twitch properties was changed from a power to a linear relation. The implementation of a linear association between motor unit twitch torque and contraction time increased the proportion of higher threshold motor units with longer contraction times, which increased motor unit twitch fusion and thereby, reduced the force fluctuations.

Minimal and peak discharge rates.

The rate at which motor units discharged action potentials at recruitment during the ramp task in the current study was slightly but significantly greater than that during the target-matching task. This difference in initial discharge rate for the two tasks contrasts with previous results for the first dorsal interosseus, in which there was no difference in the minimal discharge rate of motor units during the two tasks (2, 27). These findings suggest that the minimal and peak discharge rates of motor units can vary depending on the specifics of the task, the method used to analyze the train of motor unit action potentials, and the test muscle.

The minimal and peak discharge rates of motor units in the tibialis anterior, measured during the target-matching task, increased linearly with motor unit recruitment threshold torque. These findings are similar to those observed for motor units of the first dorsal interosseus (2, 27) and the tibialis anterior (14) during comparable contractions. In contrast, the finding in the current study of a positive association between peak discharge rate and recruitment threshold torque for motor units in the tibialis anterior differs from an earlier report on the same muscle (39). Although the torque range over which motor units were identified in the current study was not related to recruitment threshold torque, the peak torque at which motor units could be identified was related to the recruitment threshold torque. Thus it seems unlikely that the relation between peak discharge rate and recruitment torque, observed in the current study, is influenced by possible differences in the torque range over which motor unit discharges were recorded.

In general, however, peak discharge rates, observed in the current study (Table 2), were less than those reported by other investigators (30–65 pps) (6, 14, 29, 39). The lower peak discharge rates observed in the current study were likely due to an inability to determine maximal motor unit discharge rates, largely due to signal interference from the recruitment of additional motor units and significant electrode movement during stronger contractions. However, the ability of the model to approximate the experimental dorsiflexion torque data was not impaired with the lower peak firing rates observed in the current study. This finding is similar to that of Barry et al. (2), who found that the assignment of motor unit peak firing rates is not critical for approximating the force fluctuations observed in experimental measures of index finger abduction force with those simulated with a model. Despite this limitation, the model did not differ from the experimental CV for torque observed for the dorsiflexors.

Discharge variability.

The CV_ISI for 55% of the motor units was greater at recruitment and decreased exponentially as torque increased above recruitment. These results are similar to those observed for motor units of the first dorsal interosseus muscle (2, 27). The average CV_ISI at recruitment for motor units in the tibialis anterior, however, was 15.9 ± 9.6% compared with 30.0 ± 3.5% for the first dorsal interosseus (27). Furthermore, the exponential decrease in the CV_ISI was not observed in all motor units recorded from the tibialis anterior. The CV_ISI, at recruitment for 39% of the motor units, was relatively low (10.7 ± 6.43%) and remained constant as dorsiflexion torque increased above recruitment threshold torque. The CV_ISI for tibialis anterior motor units at recruitment was also positively related to the recruitment threshold torque. These results are similar to those reported by Hannerz (14), in which motor units, recruited at higher forces, displayed greater discharge variability compared with motor units recruited at lower forces. The lower discharge variability for tibialis anterior motor units than for those in the first dorsal interosseus may be the result of fewer synaptic inputs onto the alpha motor neurons that project to the tibialis anterior (5), due to the association between conductance noise and the quantity of synaptic inputs onto a neuron (3, 4). Although the reduced discharge variability for tibialis anterior motor units may have contributed to the lower values for the CV for force compared with the first dorsal interosseus (27), the results of Negro et al. (28) indicate that differences in the low-frequency oscillations of motor unit discharge rates between these muscles may explain the differences in force variability. Furthermore, the seemingly weaker association between motor unit twitch contraction times and peak forces for the tibialis anterior, rather than the first dorsal interosseus motor units, may have also contributed to the differences in CV for force values between the two muscles (13, 34, 35).

Torque variability.

The CV for dorsiflexion torque was greatest at the two lowest target torques (2.5% and 5% MVC torque) and then decreased to a relatively constant value for the remaining target torques. The lesser CV for dorsiflexion torque relative to that for the index finger abduction force (27) is consistent with previous observations that larger muscles with more motor units produce submaximal forces with lesser relative force fluctuations than smaller muscles with fewer motor units (13, 34, 35). The CVs for torque observed in the current study, however, are less than those reported previously for the dorsiflexors, in which the CV for torque ranged from 5% at a target torque of 2% MVC torque to 2.5% at a target torque of 80% MVC torque (33). These greater CVs for torque in the latter study are likely related to the use of visual feedback during the steady contractions, which has been shown to increase the CV for torque (34).

The ability of the model to approximate the observed CVs for ankle dorsiflexion torque was improved by adding variability to the assignment of motor unit twitch contraction times and peak twitch forces. Further improvement in the approximation was accomplished by changing the association between motor unit peak twitch torque and contraction time from a power to a linear function, similar to that observed experimentally by Van Cutsem et al. (39). The improvement was primarily due to a reduction in the CV for torque values at the moderate and high target torques (Fig. 5). The reduced CVs for torque may be due to an increase in the proportion of higher threshold motor units with longer contraction times, which increased motor unit twitch fusion and thereby reduced the torque fluctuations.

This result emphasizes that the association between the contraction times and peak twitch torque of motor units in the tibialis anterior is likely linear (1, 6, 39), rather than a power function, as modeled by Fuglevand et al. (10), for the first dorsal interosseus muscle (30). Furthermore, the results indicate that the association between motor unit twitch torques and contraction times may be relatively weak in a large muscle such as the tibialis anterior, despite the moderate linear association observed by Andreassen and Arendt-Neilsen (1) when motor units were activated by electrical stimulation (R² = 0.66; n = 27). The linear association (R² = 0.15) and large number of motor units recorded (n = 528) by Van Cutsem et al. (39) support the existence of a relatively weak association between twitch torques and contraction times. These findings highlight the critical contribution of motor unit mechanical properties to muscle force fluctuations, especially at moderate-to-higher forces when discharge variability is relatively consistent across active motor units (24).

A number of investigators have emphasized that a match between the mechanical and discharge properties of motor units is necessary to maximize the force capacity of the muscle (15, 16, 21). However, the simulation that modeled a weak linear association between motor unit twitch contraction times and motor unit number also produced the greatest MVC torques, which did not differ significantly from the experimental values and were similar to those reported previously for the tibialis anterior (22, 39). In contrast, those simulations that had a closer match between peak twitch torque and contraction times had lower MVC forces than that observed experimentally in this study and by others (22, 39). Measurements of the physiological cross-sectional areas of the dorsiflexor muscles, however, indicate that the tibialis anterior contributes ∼60% to the total dorsiflexion torque (11); therefore, the lack of a significant difference between the simulated and experimental MVC torques indicates that the third version of the model may have overestimated the dorsiflexion torque contributed by the tibialis anterior. Although other dorsiflexor muscles were not included in the model, neither was the opposing action of the antagonist muscles. Coactivation of antagonist muscles likely limited the maximal dorsiflexion torque observed in the experimental data, as mean EMG activity of the soleus muscles increased progressively from 4.02 ± 2.4% to 34.7 ± 28.3% MVC and as dorsiflexion torque increased from 2% to 95% of MVC torque. The simulated values for the tibialis anterior dorsiflexion torque, therefore, were likely not too dissimilar from the absolute values generated during the MVC task.

Conclusion.

The relative variability in the torque exerted by the dorsiflexor muscles during steady contractions was only modestly related to the distribution of discharge variability across the population of motor units in the tibialis anterior. This result contrasts with observations on the first dorsal interosseus, in which discharge variability has a greater influence on the more substantial force variability, especially at low torques. Rather, the findings for the dorsiflexors indicate that there was a stronger association between experimental and simulated values for the CV for the dorsiflexor torque when the relation between motor unit twitch torques and contraction times was changed from a power function to a weak linear relation. The results of this study indicate that the discharge variability of tibialis anterior motor units is of lesser significance in influencing torque variability of the dorsiflexors.

GRANTS

Support for this work was provided by awards by the Fonds National de la Recherche Scientifique of Belgium (to J. Duchateau) and the National Institute on Aging AG009000 (to R. M. Enoka).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: M.K., J.D., and R.M.E. conception and design of research; M.J. and M.K. performed experiments; M.J. and M.K. analyzed data; M.J., M.K., J.D., and R.M.E. interpreted results of experiments; M.J. prepared figures; M.J. drafted manuscript; M.J., M.K., J.D., and R.M.E. edited and revised manuscript; M.J., M.K., J.D., and R.M.E. approved final version of manuscript.