Abstract
To measure spatial variations in mechanical properties of biological materials, prior studies have typically performed mechanical tests on excised specimens of tissue. Less invasive measurements, however, are preferable in many applications, such as patient-specific modeling, disease diagnosis, and tracking of age- or damage-related degradation of mechanical properties. Elasticity imaging (elastography) is a nondestructive imaging method in which the distribution of elastic properties throughout a specimen can be reconstructed from measured strain or displacement fields. To date, most work in elasticity imaging has concerned incompressible, isotropic materials. This study presents an extension of elasticity imaging to three-dimensional, compressible, transversely isotropic materials. The formulation and solution of an inverse problem for an anisotropic tissue subjected to a combination of quasi-static loads is described, and an optimization and regularization strategy that indirectly obtains the solution to the inverse problem is presented. Several applications of transversely isotropic elasticity imaging to cancellous bone from the human vertebra are then considered. The feasibility of using isotropic elasticity imaging to obtain meaningful reconstructions of the distribution of material properties for vertebral cancellous bone from experiment is established. However, using simulation, it is shown that an isotropic reconstruction is not appropriate for anisotropic materials. It is further shown that the transversely isotropic method identifies a solution that predicts the measured displacements, reveals regions of low stiffness, and recovers all five elastic parameters with approximately 10% error. The recovery of a given elastic parameter is found to require the presence of its corresponding strain (e.g., a deformation that generates ε12 is necessary to reconstruct C1212), and the application of regularization is shown to improve accuracy. Finally, the effects of noise on reconstruction quality is demonstrated and a signal-to-noise ratio (SNR) of 40 dB is identified as a reasonable threshold for obtaining accurate reconstructions from experimental data. This study demonstrates that given an appropriate set of displacement fields, level of regularization, and signal strength, the transversely isotropic method can recover the relative magnitudes of all five elastic parameters without an independent measurement of stress. The quality of the reconstructions improves with increasing contrast, magnitude of deformation, and asymmetry in the distributions of material properties, indicating that elasticity imaging of cancellous bone could be a useful tool in laboratory studies to monitor the progression of damage and disease in this tissue.
Keywords: elastography, anisotropy, nondestructive imaging, modulus, trabecular bone, inverse problems
1. Introduction
Many tissues, such as cancellous bone, tendon, and arterial walls, are anisotropic materials that can display substantial variations in material properties even within a single anatomic site. For example, spatial variations in the stiffness of cancellous bone throughout the proximal femur are thought to follow the distributions of principal stresses that arise during gait and other habitual activities [1,2]. Inhomogeneous distributions of material properties can also signal a pathology, as in the case of breast carcinomas, fibrosis, and arteriosclerosis. While spatial variations in elastic properties can be measured directly by excising multiple samples of tissue, there are many instances in which a less invasive measurement of the variation in properties is desired. These instances include disease diagnosis and monitoring of disease progression. They also include “patient-specific” finite element modeling in which computed tomography (CT) or magnetic resonance (MR) images of a bone or portion of the cardiovascular system are used to generate the model geometry. Moreover, in these patient-specific computational analyses, as well as in many experimental studies, the ability to quantify changes in the elastic properties, as well as changes in the spatial variations of these properties, that occur as the tissue sustains damage during loading, could provide important insight into mechanisms of damage and failure for both whole organs and excised specimens.
Elasticity imaging (or “elastography”) is a rapidly growing field of imaging science in which an image of the spatial variation in elastic properties within a region can be nondestructively or even noninvasively reconstructed (c.f. [3,4]). The method of elasticity imaging consists of two key ingredients: measurement of displacement fields that occur during deformation of a tissue and the formulation and solution of an inverse elasticity problem. Measurement of displacement fields can be carried out using digital volume correlation (DVC) or other methods [5–8]. The displacement fields are then used as input, along with an assumed form of the constitutive equation and the balance of linear momentum, to form an inverse problem for the elastic properties.
Early work in elasticity imaging [9] focused on simply presenting the distributions of axial strain produced by uniaxial quasi-static compression. The reciprocal of this strain distribution may be regarded as a reconstructed distribution of Young's modulus within the context of an isotropic, linear elastic, uniaxial-stress model of tissue deformation. We have analyzed and extended these techniques by broadening the scope and accuracy of the mathematical models used to model tissue deformation. In particular, we have analyzed and solved the plane strain [10–13] and plane stress cases [14], as well as cases of 3D linear elastic [14,15] and 2D hyperelastic behavior [16]. We have also demonstrated the feasibility of applying these methods to 2D [11] and 3D benchtop experimental data [15] and to in vivo data obtained in a clinical setting [17]. So far, however, these methods have all been based on an assumption of material isotropy and have therefore been limited in their applicability to anisotropic materials.
Extending these cases to include material anisotropy (e.g., transverse isotropy) is complicated in large part due to an increase in the number of parameters to be evaluated. Yet there is also a more subtle difference in the mathematical structure between inverse problems for anisotropic and isotropic cases. In an iso-tropic material, the elasticity (or stiffness) tensor is a linear function of the unknown elastic parameters. In an anisotropic material, however, the elasticity tensor is expressed in terms of products of elastic parameters and the direction vector. Thus the elasticity tensor for an anisotropic material is a nonlinear function of the problem unknowns. In the case of transverse isotropy, a reasonable approximation for cancellous bone in the human spine [18], five elastic parameters and a unit material direction vector must be evaluated at each point. Several studies have developed methods for anisotropic elasticity imaging of soft-tissues within the framework of 2-D analyses [19,20] and 3-D analyses of piecewise constant stiffness distributions [21]. The current study reports a method for 3-D, transversely isotropic elasticity imaging for the general case of continuously varying stiffness distributions and demonstrates the feasibility of its application to vertebral cancellous bone.
2. Methods
In this section, we pose the inverse problem for the 3-D, transversely isotropic case and present the optimization method that we use to solve this problem in general. We then describe the specific application of this method to human vertebral cancellous bone. Isotropic reconstructions of experimentally measured data are performed to demonstrate the feasibility of elasticity imaging of cancellous bone, and transversely isotropic reconstructions of simulated data are performed to investigate the effects of model mismatch, ill-conditioning, and measurement noise on reconstruction accuracy.
2.1. Formulation of the Transversely Isotropic Inverse Problem.
To formulate the inverse elasticity problem for the case of transverse isotropy, we start with the conservation of linear momentum. For a tissue undergoing quasi-static compression with negligible body forces, the momentum balance at a point reduces to the equilibrium equation
| (1) |
where Tij is the Cauchy stress tensor, summation over repeated indices is assumed, and a comma denotes partial differentiation in the indicated spatial direction. Assuming a linear, elastic anisotropic body, we invoke Hooke's law [22],
| (2) |
where Cijkl is the stiffness tensor and εkl is the linearized (infinitesimal) strain tensor
| (3) |
Combining Eqs. (1)–(3), and recalling the symmetry of the stress tensor in the absence of body torques, the equilibrium equation becomes
| (4) |
The stiffness tensor, Cijkl, which satisfies Eq. (4) is the solution to the inverse problem. In the examples that follow, we will have or we will assume we have the measured displacement ui at each point of interest. Thus ui is known in Eq. (4), which may be interpreted as three partial differential equations for the unknown entries in Cijkl. Additional measurements of ui from other loading experiments yield additional equations.
The degree of material anisotropy determines how many independent coefficients Cijkl contains and thus how many independent displacement measurements are needed. In the present study, we use a transversely isotropic form of the stiffness tensor, and we assume that the material direction vector is known a priori. In principle, with a sufficient number of measured displacements, Cijkl can be uniquely determined up to a multiplicative constant without the independent measurement of stress. If an insufficient number of displacements is available, the reconstructed solution could be just one of a family of solutions that all satisfy the equilibrium equation for the given loading and boundary conditions.
We observe that one deformation for each unknown parameter is sufficient to determine all the parameters in Cijkl uniquely. However, fewer deformations are often sufficient when additional information is available. For example, in some cases, if the traction is known on the boundaries of an isotropic specimen, only one deformation is required to determine both Lamé parameters [12]. As such, it is plausible to suppose that fewer than five deformations are required to uniquely determine the elastic parameters for a transversely isotropic material. However, an inadequate combination of deformations and boundary information can render the problem ill-conditioned and=or produce a solution that is nonunique. The loading conditions and initial information needed to produce a well-posed transversely isotropic inverse problem (i.e., a solution exists, is unique, and depends continuously on the given data) have not yet been fully determined.
2.2. Optimization Formulation.
Our method for solving the inverse problem posed in Sec. 1 for Cijkl(x, y, z) throughout the domain of interest is not to solve the equilibrium Eq. (4) directly, but rather to solve it indirectly through an optimization strategy. Given a distribution of measured displacements we seek a stiffness tensor distribution Cijkl(x, y, z) that minimizes
| (5) |
| (6) |
and ℛ(Cijkl) is a regularization term [10,11].
The “predicted” displacement field, , in the error term is obtained by solving Eq. (4) as a forward problem for a proposed Cijkl(x, y, z). This is done by creating a finite element mesh of the specimen using 3D, compressible, transversely isotropic, linear elastic elements, assigning boundary conditions and a distribution of elastic properties, and solving for the displacements. This result is then compared to the measured displacement field obtained from DVC to compute the error and objective function. This process is repeated within an optimization algorithm that updates Cijkl(x, y, z). By finding the Cijkl(x, y, z) that minimizes the objective function and predicts a displacement field that closely matches the measured displacement fields, we infer the stiffness distribution. We stabilize this optimization problem by exploiting the material symmetries in Cijkl to reduce the number of unknowns and by using several measured displacement fields to limit the number of possible solutions.
The boundary conditions for the forward problem are determined by the experimental setup that produced the measured displacements. Because displacement measurements made by DVC exist throughout the sample volume, measured values for the displacements are available on all boundaries of the sample. In some experimental configurations, the unloaded (zero-traction) surfaces can be known a priori. On such surfaces, we have the option of using either the measured displacement boundary conditions or the known, zero-traction boundary conditions. We choose the latter as this adds information to the inverse problem [12].
In the results that follow, we work in a coordinate system aligned with the principal material direction and assume this direction is known and is uniform in space. In this case, the five independent coefficients for the fourth-order stiffness tensor Cijkl are, in reduced Voigt notation, C11, C22, C55, C12, and C23, where 1 is the principal direction. We group these into a five dimensional elastic parameter vector, Cn, such that
| (7) |
In the current study, we use total variation diminishing (TVD) regularization to overcome two potential sources of error: ill-posedness of the inverse problem and the confounding effects of noise. Typically, regularization works by penalizing large gradients in the modulus distribution. However, with TVD regularization, high frequency oscillations are penalized while sharp jumps in the solution are allowed [23]. For TVD, the ℛ operator in the objective function is given by:
| (8) |
Here, βn is a numerically small constant introduced to smooth the singularity that would otherwise exist at ΔCn = 0. The constant αn is called the regularization parameter. It controls the relative importance of regularization in the optimization problem. Typically, the greater the level of noise in the measurement or the more ill-posed the problem, the more regularization is required.
The minimization of the objective function is driven by a quasi-Newton Broyden-Fletcher-Goldfarb-Shanno (BFGS) optimization algorithm that requires the evaluation of the functional and its gradient to determine new values for Cijkl(x, y, z). However, the straightforward evaluation of the gradient requires N + 1 solves of the forward problem for each optimization iteration, where N is the number of nodes in the finite element mesh. This can be computationally prohibitive for typical values of N ≥ 103. We avoid this problem by utilizing the adjoint elasticity operator, which requires only two forward solves per iteration, significantly decreasing the required computation time [10,11].
2.3. Application of Isotropic Elasticity Imaging to Measured Cancellous Bone Displacements.
As a prerequisite to exploring transversely isotropic reconstructions for the specific case of anisotropic vertebral cancellous bone, the feasibility of applying elasticity imaging to cancellous bone displacement fields is established in Experiment 1. To do so, we utilize a previously reported method for 3D, linear elastic, isotropic reconstructions [13,15] that has been successfully used with in vivo measurements of soft tissue from ultrasound [17].
2.3.1. Experiment 1: Isotropic Reconstruction of Measured Displacements.
In this experiment, an isotropic modulus distribution of a specimen of cancellous bone from the human lumbar vertebra is reconstructed from a single measured displacement field. This displacement field is obtained from a DVC analysis of micro-computed tomography (μCT) images (resolution = 36 μm/voxel) that were generated as part of a separate study [24]. In that study, the images were captured as a cylindrical specimen (8:0 mm diameter, 9:4 mm length) of human vertebral cancellous bone that was loaded in uniaxial compression to 2:0% strain (Fig. 1). Briefly, DVC involves subdividing the reference image (in this case, the 0% image) into many small, overlapping subregions and, typically, using spatial cross correlation to calculate the average displacement of the features within each subregion in response to the load increment [25]. In this experiment, the subregions are overlapping cubes with side lengths equal to 50 voxels (1:8 mm) and centroids spaced 10 voxels (0:36 mm) apart. The displacements are calculated for the central 5.7 × 5.7 × 9.4 mm3 parallelepiped of the specimen, resulting in a field of dimensions 11 × 11 × 22. We have estimated the precision of these displacement measurements to be 0.071 voxels (2.57 μm) [8].
Fig. 1.

Three dimensional μCT renderings at (a) 0% and (b) −2% strain
Several caveats of this experiment must be noted. First, the reconstruction is isotropic, and the results are thus used merely to investigate the feasibility of applying elasticity imaging to experimentally measured displacement fields in cancellous bone. Second, the result of the reconstruction is a distribution of secant modulus, rather than tangent modulus, because the applied deformation of −2.0% strain corresponds to more than twice the compressive yield strain of human vertebral cancellous bone (0.77%) [26]. Third, the reconstruction produces relative, rather than absolute, values of modulus, because no force data are used in this experiment. Finally, the size of each subregion used in the DVC calculations is less than the minimum length scale at which cancellous bone can be considered a continuum (≈5 mm or five inter-trabecular spacings) [27]. As such, the secant modulus obtained for a given subregion represents the secant modulus of a continuum that has the same secant stiffness as the cancellous micro-structure contained in that subregion.
2.4. Application of Isotropic and Transversely Isotropic Elasticity Imaging to Simulated Cancellous Bone Displacements.
In the remaining experiments, synthetic displacement fields from a finite element model of the forward problem are generated to demonstrate the utility and the accuracy of transversely isotropic reconstructions. The synthetic displacements are created by specifying a distribution of target elastic parameters, Cijkl(x, y, z), on a 20 × 20 × 20 finite element mesh and running a custom forward finite element solver for a given set of loading and boundary conditions. The results of the finite element model are scalable to any specimen size as long as the edge lengths of the cube are greater than the minimum continuum length (≈5 mm for cancellous bone). In this study, the dimensions of the cube are scaled by 1 mm to correspond to the typical size of a human lumbar vertebral body (≈20 mm). Therefore, the results of the forward problem are considered to represent displacements for ≈5 mm (i.e., continuum-scale), overlapping subregions spaced ≈1 mm apart.
To investigate the ability of our method to identify inhomogeneous regions in the specimen, a distribution of transversely isotropic elastic parameters that corresponds to a region of osteopenic cancellous bone surrounded by healthy cancellous bone is assigned to the finite element mesh. The elastic parameters for these two regions are determined using constitutive relationships [28] developed for cancellous bone that specify Cn as a function of volume fraction (ϕ), fabric eigenvalues (λi), and tissue modulus (Etiss):
| (9) |
where typical values of ϕ and λi are obtained from the literature [26] (Table 1). The osteopenic parameters are chosen to reflect the decreased volume fraction and increased anisotropy of the central region of vertebral bone that occurs with age [29]. We note that the constitutive model in Equation (9) treats Etiss as a multiplicative constant, and thus for simplicity we use a value of 1.0 GPa for both the osteopenic and healthy cases. We also assume that the principal material direction at every point in the volume is aligned with the vertical, x-axis (superior-inferior direction). This assumption is supported by evidence that the principal material direction is closely related to the principal structural direction in cancellous bone [30], that the principal direction of human vertebral cancellous bone is in the superior-inferior direction [31], and that the horizontal plane is isotropic when the vertebra is at peak bone mass (25–30 years of age) [18].
Table 1.
Transversely isotropic elastic parameters for healthy and osteopenic cancellous bone (Eq. (9))
|
Tissue parameters |
Elastic parameters |
|||||||
|---|---|---|---|---|---|---|---|---|
| ϕ | λi | Et | C11 | C22 | C55 | C12 | C23 | |
| Healthy | 0.15 | (1.0, 0.67, 0.67) | 1.0 | 0.0642 | 0.0192 | 0.0112 | 0.0097 | 0.0074 |
| Osteopenic | 0.08 | (1.0, 0.5, 0.5) | 1.0 | 0.0502 | 0.0017 | 0.003 | 0.002 | 0.0013 |
The degree of degradation between osteopenic and healthy regions is calculated as the ratio . For the values used in this study (Table 1), these contrast ratios are [Rn] = 1.3, 11, 3.7, 4.9, 5.7]. Therefore, the five reconstructed stiffness distributions reveal not only anisotropy in the healthy and osteopenic material properties, respectively, but also anisotropy in the extent of their degradation (e.g., R1 ≠ R2). For example, although the degradation of C22 in the osteopenic region is quite large, the elastic anisotropy is increased such that C11 is only slightly diminished.
The default applied loading conditions for Experiments 2–4 consist of three uniaxial compression cases of 1% strain: one in each of the principal material directions. Because of the assumption of linear elasticity, the magnitude of the applied strain is of no consequence except when evaluating the effect of signal (strain) on reconstruction accuracy. One percent strain is used simply for convenience in interpreting the results. For uniaxial compression, the plane parallel and opposite to the loaded plane is constrained in the direction of loading along the entire surface, and one edge is constrained in each perpendicular direction to prevent rigid body motion. In Experiment 3, 1–2 and 2–3 simple shear conditions are also considered. The 1–2 shear condition is approximated by prescribing lateral displacements in the 2-direction at every node across a 1-surface while the parallel surface is constrained in the 1- and 2-directions. The 2-3 shear condition is prescribed in an analogous manner on the 2-surface with displacements in the 3-direction. Other load conditions, such as bending, can also be prescribed but are not considered in this study. The elastic parameters corresponding to healthy cancellous tissue are used as a homogeneous initial guess for the optimization since these values are available in the literature (e.g., Ref. [26]).
The reconstructed distributions of elastic parameters are qualitatively evaluated by visual comparison to corresponding target distributions. The accuracy of a given reconstructed parameter is quantified by comparing the predicted value, Cpred, to the target values, Cback and Cinc, that correspond to the healthy and osteopenic values, respectively, in Table 1. Two measures of error in the reconstructions are calculated for each parameter and then averaged across parameters: inclusion L2 error and full-field L2 error. These measures are defined as
| (10) |
and
| (11) |
respectively, where ω is the inclusion subdomain, Ω is the full-field domain, and ∥ · ∥ is the L2 norm of values in the indicated domain. The L2 error between synthetic and predicted displacement fields, , is also calculated in some instances.
2.4.1. Experiment 2: Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to a Compliant Spherical Inclusion.
The purpose of the second experiment is to investigate the result of applying an isotropic reconstruction to a transversely isotropic data set. Displacement fields are generated from solving a forward problem in which the region of osteopenic bone is a centered, spherical inclusion of radius equal to 35% of the specimen's side length. The first case analyzed in this experiment consists of performing an isotropic reconstruction on displacements corresponding to a single, uniaxial load applied to an isotropic specimen. This is done to provide a basis for evaluating the change in accuracy due to model mismatch (i.e., isotropic reconstruction of anisotropic data). The background and spherical inclusion regions are assigned elastic parameters λ and μ that are the “closest isotropic equivalents” to the transversely isotropic properties of the healthy and osteopenic tissues, respectively [32].
These values and the corresponding primary Young's modulus (E1) and isotropic elastic parameter () are given in Table 2. Also, tailored regularization (α = 5e-9 and β = 5e-4), as determined by a trial-and-error approach in which error level comparisons are made between reconstructions with incrementally increasing levels of regularization, is applied.
Table 2.
Closest isotropic equivalents for transversely isotropic stiffness coefficients as defined by the minimum Riemann distance between stiffness matrices [32]
|
Tissue parameters |
Lamé parameters |
Stiffness and modulus |
|||||
|---|---|---|---|---|---|---|---|
| ϕ | λi | Et | λ | μ | C11 a | E1 b | |
| Healthy | 0.15 | (1.0, 0.67, 0.67) | 1.0 | 0.0102 | 0.00626 | 0.0227 | 0.0164 |
| Osteopenic | 0.08 | (1.0, 0.5, 0.5) | 1.0 | 0.00148 | 0.00091 | 0.0033 | 0.00238 |
C11 = 2μ + λ.
The second case in this experiment considers an isotropic reconstruction performed on displacements corresponding to a single, uniaxial load applied to a transversely isotropic specimen (λ: α = 1e-6, β = 5e-4; μ:α = 1e-5, β = 5e-4), and the third case is an isotropic reconstruction in which the number of loads is increased to the default (three separate orthogonal, uniaxial compressions) with the same regularization applied. In each case, distributions of primary Young's modulus (E1) and isotropic elastic parameter (C11) are calculated from the recovered distributions of Lamé parameters (Table 2).
2.4.2. Experiment 3: Transversely Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to a Compliant Spherical Inclusion.
The purpose of the third experiment is to demonstrate a transversely isotropic reconstruction of a transversely isotropic data set and to evaluate the effects of additional loading conditions and regularization on reconstruction accuracy. This experiment uses the same transversely isotropic, simulated cubic specimen with a spherical inclusion that was used in Experiment 2, but all reconstructions are transversely isotropic. The first case utilizes default loading conditions without regularization. The second case is the same as the first but with the addition of displacements from a 1-2 shear load in addition to those obtained from the default loading conditions. The third cases then adds a fifth load, 2–3 shear, to those applied in the second case while the fourth case applies regularization (α = 1e-9, β = 5e-4) instead of adding a 2–3 shear load.
2.4.3. Experiment 4: Transversely Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to a Compliant Band.
To investigate the effects of asymmetry in the distribution of material properties, the final experiment simulates a test with a compliant band of osteopenic tissue instead of a compliant spherical region. The band cuts obliquely at a 14 deg angle to the 2–3 plane with a thickness of approximately 1 = 3 the cube side length. The material properties from Table 1 are again assigned to the healthy and osteopenic regions of the sample, the default loading conditions are applied, and tailored regularization is utilized from the outset.
The compliant band model is also used to analyze the effect of noise in the measured displacements on the quality of the material property reconstructions. Noisy measured displacements are simulated by adding white Gaussian noise to synthetic displacement fields generated from the forward solver. The amount of noise added is determined by a chosen signal-to-noise ratio (SNR), defined as
| (12) |
where εo is the applied strain magnitude (signal) and σε is the strain precision. Reconstructions are performed on noisy data corresponding to six SNRs, ranging from 10 dB to 60 dB, and two signal levels, 0:5% and 1:0%. These levels correspond to applied strain magnitudes lower and higher, respectively, than the compressive yield strain for vertebral cancellous bone (0:77%) [26]. The full-field error of each reconstructed material parameter is then calculated and averaged to determine an accuracy for each combination of SNR and signal magnitude. Also, because the SNR and strain values are known for each reconstruction, the corresponding strain precision can be inferred from Eq. (12). Recalling that strain is calculated from two independent displacement measurements with equal variance, the displacement precision can be calculated from the strain precision for a known window size, W, according to [15]
| (13) |
In this way, the accuracy of transversely isotropic reconstructions for a specified level of signal (strain) can be related to the precision of the displacement data. All reconstructions are also performed without and with regularization (α = 1e-8, β = 1e-5) to evaluate the role of regularization in improving the accuracy of the reconstructions at different signal-to-noise ratios.
3. Results
3.1. Experiment 1: Isotropic Reconstruction of Measured Displacements.
The results for the first experiment are presented in Fig. 2. A visual comparison of a 2-mm-thick, longitudinal (x-z) section of the specimen at 0% (Fig. 2(a)) and −2% (Fig. 2(b)) shows regions of large deformation that are apparent to the eye. These correspond to regions of high strain in longitudinal (Fig. 2(c)) and shear (Fig. 2(d)) strain images generated from DVC. The reconstruction of the secant modulus distribution (Fig. 2(e)) likewise shows an area of high compliance that corresponds to the region of large strains. This correspondence among the μCT images, strains, and moduli indicates that with elasticity imaging, one can detect spatial variations in material stiffness from an experimentally measured displacement field in cancellous bone. However, it is important to emphasize that because the reconstruction assumed material isotropy, the accuracy of these results is questionable. This point will be addressed by the results of Experiment 2.
Fig. 2.
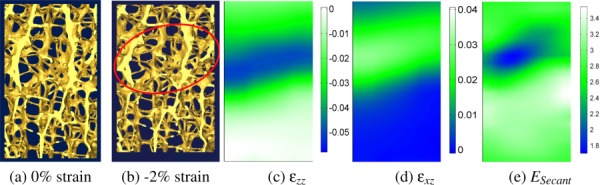
Renderings of a 2-mm-thick, longitudinal (x-z) section of the specimen in Fig. 1. Images taken at (a) 0% and (b) 2% compressive strain were used to generate longitudinal (c) and shear (d) strain images using DVC. The reconstructed distribution of secant modulus (e) shows a region of low modulus corresponding to the regions of high strain and of deformations large enough to be apparent to the eye (highlighted by a red circle). Secant modulus values are relative, rather than absolute, because no force data are used.
3.2. Experiment 2: Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to Compliant Spherical Inclusions.
Results for the second experiment are displayed in Figs. 4–6, according to the configurations shown in Fig. 3, and the full-field errors are tabulated in Table 3. For the first case (Fig. 4), the distributions of λ, μ, , and E1 are very accurately recovered as would be expected for an isotropic reconstruction of isotropic data. In contrast, in the second case (Fig. 5), although the shape and location of the inclusion are correctly identified for all parameters, the error is markedly increased. Moreover, vertical bands of moderately low values of μ, , and E1 appear in the reconstructions. For the third case (Fig. 6), in which three, orthogonal, uniaxial loads are applied, the isotropic model still does not yield an accurate reconstruction of any of the elastic parameters although the inclusion and background are each more homogeneously reconstructed than the first case. In both iso-tropic approximation cases (2 and 3), a higher level of regularization than that used for the first case (i.e., α = 1e-6 versus α = 5e-9) is required to correctly identify the location and shape of the inclusion, which may account for a portion of the error in the reconstructions.
Fig. 4.
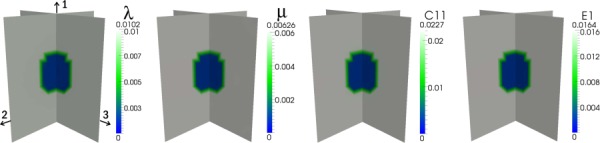
Isotropic reconstruction of synthetic data corresponding to an isotropic distribution of material properties with 1% applied strain in the 2-direction (see Fig. 3(b)). C11 and E1 are calculated from the independent λ and μ distributions.
Fig. 6.

Isotropic reconstruction corresponding to a transversely isotropic distribution of elastic parameters using three separate synthetic data sets with 1% applied compressive strain applied in each principal material direction
Fig. 3.
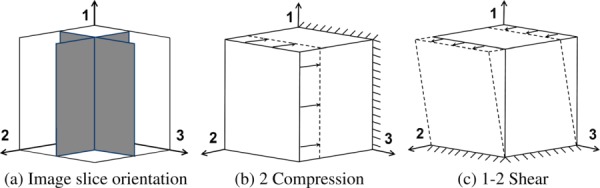
Positions of the reference images for the results presented in Experiments 2–4 (a) and schematics of the applied loadings for compression in the 2-direction (b) and shear in the 1–2 plane (c). The 1-axis is the principal material direction and the 2 and 3 axes define the transverse, isotropic plane.
Table 3.
Full-field error values for isotropic reconstructions in Experiment 2
| Target | Loads | λ | μ | C11 | E1 |
|---|---|---|---|---|---|
| Isotropic | 1 | 1.2% | 0.5% | 0.7% | 0.6% |
| Trans. Isotropic | 1 | 48% | 13% | 25% | 14% |
| Trans. Isotropic | 3 | 61% | 25% | 41% | 30% |
Fig. 5.
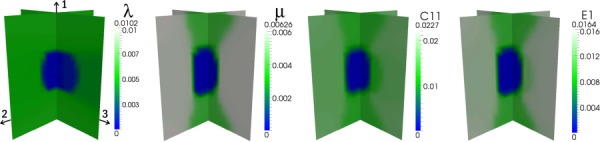
Isotropic reconstruction of synthetic data corresponding to a transversely isotropic distribution of elastic parameters with 1% applied strain in the 2-direction (see Fig. 3(b))
3.3. Experiment 3: Transversely Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to a Compliant Spherical Inclusion.
The third experiment demonstrates the ability of the optimization algorithm to recover the measured displacements with little error and illustrates the effects of ill-conditioning in the inverse problem. The distributions of each recovered elastic parameter for the first case, as compared to a target distribution (Fig. 7), are shown in Fig. 8. The reconstruction algorithm succeeds at recovering the shape of the inclusion within at least a portion of the inclusion for each parameter except C55. The inclusion errors are Eω = [8%, 13%, 56%, 15%, 13%] with an average of 21% and the full-field errors are EΩ = [2%, 3%, 10%, 4%, 4%] with an average of 4.6% (Table 4). The average error in the predicted displacement field, however, is less than 0.1% for the same reconstruction. This indicates that the model is able to identify an elastic parameter distribution that predicts a displacement field that closely matches the synthetic displacement field that was used as input. The discrepancy between the material property and displacement field accuracies is likely due to ill-conditioning of the inverse problem; only three independent loading conditions were provided to recover five unknown elastic parameters.
Fig. 7.

Target distributions for the five independent stiffness coefficients of a transversely isotropic specimen with a compliant spherical inclusion
Fig. 8.

Transversely isotropic reconstruction of a transversely isotropic distribution of elastic parameters with a uniaxial compressive strain applied in each (1-, 2-, 3-) principal material direction
Table 4.
Comparison of inclusion error (Eω), full-field error (EΩ), and displacement error () for the four cases in Experiment 3
| Shear Loads | Regularization | Eω | EΩ | |
|---|---|---|---|---|
| None | None | 21% | 4.6% | 0.091% |
| 1–2 shear | None | 8.8% | 2.6% | 0.058% |
| 1–2 and 2–3 shear | None | 9.8% | 2.8% | 0.062% |
| 1–2 shear | α = 1e-9, β = 5e-4 | 5.2% | 1.4% | 0.047% |
For the second case (Fig. 9), in which a 1–2 shear load is added to the default loads, all properties, including C55, are properly reconstructed and the inclusion error decreases significantly to 8:8% (Table 4), largely due to the recovery of C55. Through comparison of the results of these first two cases, the sensitivity of the reconstruction to the type of loading is apparent. In the first case, the shear strain, ε12, corresponding to C55, is negligible because no shear deformation is directly applied. As a result, the spherical inclusion in the distribution of C55 is not recovered. However, with the addition of the 1–2 shear load in the second case, the inclusion is clearly identified. This is evidence of the inverse problem becoming less ill-conditioned through the addition of a new, independent loading condition.
Fig. 9.

Transversely isotropic reconstruction of a transversely isotropic distribution of elastic parameters with a uniaxial compressive strain applied in each (1-, 2-, 3-) principal material direction and the addition of a 1–2 shear strain (see Fig. 3(c))
In contrast, the addition of a fifth load, 2–3 shear, in the third case does not improve the accuracy of the elastic parameters or the displacement fields. This is due to the fact that because this is a transversely isotropic material, the shear parameter in the iso-tropic plane, C44, is already determined by C22 and C23 [22]. For additional loads to be useful in improving the quality of the reconstruction, they must generate new strain components.
Though the average material property error decreases with the addition of a 1–2 shear load in the second case, some oscillatory inhomogeneities persist as a result of lingering ill-conditioning. The addition of regularization in the fourth case yields the results shown in Fig. 10. This level of regularization is successful in further reducing the inclusion error to 5:2%. We also note that the inclusion is more clearly identified in C22 than in C11, likely due to its larger contrast ratio (R2 > R1). Thus, C22 dominates the inhomogeneity of the material's response.
Fig. 10.

Transversely isotropic reconstruction of a transversely isotropic distribution of elastic parameters with a uniaxial compressive strain applied in each (1-, 2-, 3-) principal material direction and the addition of a 1–2 shear strain. In this case, regularization (α = 1e-9, β = 5e-4) is also applied.
3.4. Experiment 4: Transversely Isotropic Reconstruction of Transversely Isotropic Synthetic Data Corresponding to a Compliant Band.
The target material fields for Experiment 4 are given in Fig. 11. Figure 12 shows the reconstruction in the case of three uniaxial compressive loads (default). The same level of regularization (α = 1e-8, β = 1e-6), tailored for this reconstruction by trial and error, is applied for each property except C55 (α3 = 1e-9, β3 = 1e-5), which requires a smaller α. Qualitatively, the geometry of the band is recovered for each property, including C55, despite the absence of an applied shear load as was used in Experiment 2. For each elastic parameter, the inclusion errors are Eω = [7%, 13%, 14%, 16%, 16%] with an average of 13% and the full-field errors are EΩ [5%, 9%, 12%, 13%, 13%] with an average of 10%. We note that, compared to the first case in Experiment 3, the error in C55 is much closer to the error in the other parameters.
Fig. 11.

Target distributions for the five independent stiffness coefficients, Cn, of a transversely isotropic specimen with a compliant band
Fig. 12.

Transversely isotropic reconstruction of a transversely isotropic distribution of elastic parameters with a uniaxial compressive strain applied in each [1–3] principal material direction. Regularization: α = 1e-8, β = 1e-6 for all Cn except C55 (α3 = 1e-9, β3 = 1e-5).
Default loading conditions of three uniaxial compressions, one in each of the principal material directions (1,2,3), are applied in all cases.
It is interesting to note that the recovery of C55 without an applied shear load suggests the existence of secondary shear strains, possibly induced by the presence of the compliant band. Figure 13 is a comparison of the ε31 shear strain fields induced by a single uniaxial strain applied in the principal direction for two specimens with a compliant inclusion and a compliant band, respectively. A ratio of norms for all three shear strains over the principal longitudinal strain, defined by
Fig. 13.
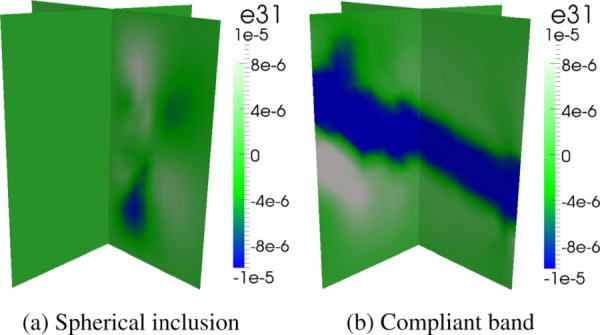
Shear strain (ε31) for (a) a specimen with a compliant spherical inclusion and (b) a specimen with a compliant band with an applied uniaxial compressive load in the 1 direction. Shear strains are not induced in the spherical inclusion whereas they are for the compliant band.
| (14) |
is used to compare the relative amounts of strain in each specimen. The ratio for the compliant-band specimen is 0.022, whereas the ratio for the compliant-sphere specimen, 0.0052, is nearly an order of magnitude lower. Also, for the compliant-sphere specimen, the location of the shear strains does not coincide with the location of the spherical inclusion. The distribution of strains in the band specimen, on the other hand, does coincide well with the compliant geometry.
The addition of noise to the displacement fields has a confounding effect on the reconstruction accuracy. A comparison of the average full-field errors across the range of signal-to-noise ratios reveals an increase in accuracy with increasing SNR (Figs. 14 and 15).
Fig. 14.
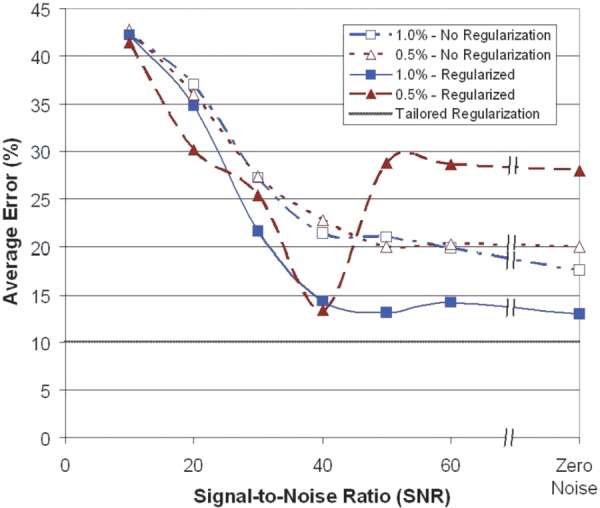
Change in reconstruction accuracy with increasing signal-to-noise ratio (SNR) at two levels of applied strain with and without regularization ( = 1e-8, β = 1e-5) for default loading conditions. The dotted line indicates the level of error for a reconstruction corresponding to zero-noise displacements using tailored regularization (α = 1e-8, β = 1e-6; C55: α = 1e-9, β = 1e-5).
Fig. 15.

Improvement in the qualitative fidelity of transversely isotropic reconstruction with increasing signal-to-noise ratio (SNR) for default loading conditions, 1:0% applied strain and regularization (α = 1e-8, β = 1e-5). Marked improvement is achieved at 40 dB.
Without regularization, errors drop below 23% at 40 dB for 1:0% applied strain and at 50 dB for 0:5% applied strain. For both curves, an elbow appears in the region between 40 dB and 50 dB, after which the rate of improvement in accuracy decreases with increasing SNR, trending toward 18–20% at zero noise. With the addition of regularization, errors at 10 dB are similar to the nonregularized results. However, accuracy improves much faster as SNR is increased to 40 dB, at which point the error drops to around 14% for both levels of applied strain. This approaches the 10% error obtained for the zero noise reconstruction with tailored regularization shown in Fig. 12. Beyond 40 dB, the reconstructions with regularization at 0:5% applied strain return to errors above 25%, while the 1:0%-strain reconstructions remain around 14%. The displacement precisions corresponding to an SNR of 40 dB and window size of 5 mm at 1:0% and 0:5% strain are 0:35 μm and 0:18 μm, respectively.
4. Discussion
In this study, elasticity imaging is extended to the case of trans-verse isotropy. Both experimentally measured and simulated displacements are analyzed that correspond to the specific application of human vertebral cancellous bone, although the methods that we employ in the reconstructions are not limited to this tissue. As illustrated by qualitative inspection of the deformed cancellous structure and the secant modulus field in Experiment 1, and as confirmed by the results of Experiment 2, isotropic elasticity imaging can successfully recover the location of a marked inhomogeneity in elastic parameters in an anisotropic material. However, the reconstruction is inaccurate with regard to the relative numerical values of the elastic parameters due to model mismatch. Use of a transversely isotropic algorithm, as was done in Experiments 3 and 4, reproduces the simulated measured displacement fields and greatly improves the quality of the reconstructions. The accuracy of a reconstruction for a particular elastic parameter depends on several factors, including the role of that parameter in the deformation response of the material to the applied loads and the choice of regularization constant. Further, noise in the displacement measurements is found to decrease the accuracy of the reconstruction, though, for signal-to-noise ratios of 40 dB or greater, proper application of regularization is found to greatly diminish this effect. In sum, these results indicate that elasticity imaging of a transversely isotropic material, such as cancellous bone, is both feasible and promising as a nondestructive measurement technique.
Our method of transversely isotropic elasticity imaging has several strengths. First, the optimization approach we use avoids the need to differentiate noisy displacement fields, which would introduce additional computational error, and it allows us to easily incorporate prior information (e.g., positivity of the material coefficients) by imposing constraints on the optimization space. Second, in contrast to methods of elasticity imaging that use only boundary data [21], our method can recover continuously varying distributions of material properties and does not require that the locations, shapes, or sizes of inclusions be known a priori. Third, as much displacement data as are available may be included in the objective function. The inclusion of additional sets of independent displacement data into the reconstruction not only stabilizes the optimization by improving the conditioning of the inverse problem but also provides a way to solve for complex distributions of material properties through the combination of simple loading states, such as compression, torsion and shear. We expect this feature to be valuable when designing loading experiments, as it will simplify the types of loading conditions required to obtain a complete reconstruction from experimentally measured displacements. Finally, the use of the adjoint method significantly improves the computational efficiency of our optimization algorithm. This improvement decreases the time required to complete the reconstructions to a few hours.
Our method also has several limitations to its general application. The first is its inability to model fully anisotropic stiffness distributions. As many biological materials, including cancellous bone, are most accurately described as orthotropic or fully anisotropic materials, a transversely isotropic representation is an inherent limitation as it assumes symmetry in the stiffness tensor Cijkl and isotropy in the transverse plane. However, many anisotropic materials exhibit a strong directional preference in architecture and mechanical properties. This includes cancellous bone in certain anatomic locations, such as the vertebra or proximal femur, that experience habitual loading. In these cases, a transversely isotropic approximation can differentiate the material properties in the principal and transverse directions that would otherwise be masked by an isotropic reconstruction. Another limitation of this method is that the optimal regularization constants are currently chosen by trial-and-error, and factors such as model mismatch, degree of ill-conditioning, and the signal-to-noise ratio all appear to require different levels of regularization. In fact, as demonstrated in Experiment 4, the wrong choice of regularization can actually significantly increase errors, even for high SNR levels. Currently, there is no agreed upon method for predetermining the best regularization constants for a specific situation.
Several barriers to the specific application of elasticity imaging to cancellous bone also exist. For in vivo measurements, these include an inability to obtain high-resolution images of the cancellous structure, lack of control over applied loads, and low physiological signal (strain). For example, although in vivo strains for cancellous bone have not been measured directly, Burr et al. reported strains in cortical bone around 2;000 με, or 0:2% strain, for the human tibia during vigorous activity [33]. Using the level of precision (σu = 2:75 μm) reported for current DVC capabilities with a window size of 1.44 mm [8], the SNR for a strain of 0:02% is approximately 0 dB, indicating the noise is as large as the signal. However, in a laboratory setting, strains of any magnitude up to the elastic limit could be applied in vitro to whole bones or excised specimens of cancellous bone. Various loading and imaging schemes may also be devised to obtain displacement estimates with higher precision. Also, if the bone is not loaded beyond yield, multiple loading experiments may be performed on the same sample. Because multiple displacement fields are necessary to solve for all five unknown material parameters, this ability could provide the conditions required for a unique solution.
As seen in the transversely isotropic reconstructions (Experiments 3 and 4), the clarity of the reconstructions improves with increasing contrast ratio. This is due to the larger difference between the two categories of tissue, healthy and osteopenic, in C22 as compared to C11, resulting in larger displacement magnitudes in the osteopenic region for C22. Also, in Experiment 4, C55 is recovered without the addition of a shear load. This is due to the asymmetry of the band inducing secondary shear deformations when loaded in uniaxial compression. Together, these results indicate that the inhomogeneity and asymmetry of the modulus distribution actually improves the ability to detect compliant regions. These findings bode well for potential application of elasticity imaging to detect changes in elastic properties of cancellous bone caused by aging, disease, or drug treatments. In addition, this method could be used in the laboratory to track the progression of damage, as defined by a change in elastic parameters, in the vertebral centrum as a vertebra is loaded beyond its elastic limit. As damage occurs, both the contrast ratio and inhomogeneity in Cn will increase, and the clarity of the compliant region in the the reconstruction will improve.
There are several avenues for future work in this area. Considering that the results of this study have established a link between the type or mode of loading and the accuracy of the reconstruction, it is possible that an optimum set of experimentally feasible loading cases can be found that would yield a well-posed problem with a minimum number of loading experiments. These conditions for uniqueness could be obtained through analytical methods similar to those previously reported for isotropic cases [12,13]. With these conditions known, an experiment to fully establish the efficacy of the current method could be developed to generate the required displacement fields from a transversely isotropic sample with a known distribution of material properties. Additionally, guidelines for preselecting the appropriate level of regularization need to be developed so that regularization can be used in reconstructions for specimens with an unknown distribution of elastic properties. The realization of these objectives would allow for the implementation of elasticity imaging to detect spatial variations in elastic properties of cancellous bone as well as for damage tracking in this tissue. As for now, we are confident that, given a sufficient set of displacement fields and the principal material direction, our method can fully and efficiently recover the relative inhomogeneous, three-dimensional distribution of elastic properties in a transversely isotropic material, without an independent measurement of stress.
Acknowledgment
Funding was provided by National Institutes of Health AR054620 (E.F.M.) and the International Osteoporosis Foundation Servier Research Award (E.F.M.). The micro-computed tomography images in Experiment 1 were generously provided by Dr. Ara Nazarian.
Contributor Information
Spencer W. Shore, Department of Mechanical Engineering, , Boston University, , 110 Cummington Street, , Boston, MA 02215 , e-mail: swshore@bu.edu
Paul E. Barbone, Department of Mechanical Engineering, , Boston University, , 730 Commonwealth Avenue, , Boston, MA 02446 , e-mail: barbone@bu.edu
Assad A. Oberai, Department of Mechanical, Aerospace, and , Nuclear Engineering, , Rensselaer Polytechnic Institute, , 4013 CII, 110 8th Street, , Troy, NY 12180 , e-mail: oberaa@rpi.edu
Elise F. Morgan, Department of Mechanical Engineering, , Boston University, , 110 Cummington Street, , Boston, MA 02215 , e-mail: efmorgan@bu.edu
Nomenclature
- Cn =
transversely isotropic vector of elastic parameters
- =
isotropic elastic parameter
- Cijkl =
elastic stiffness tensor
- Etiss =
tissue modulus
- E1 =
isotropic primary Young's modulus
- Eω =
error in the inclusion subdomain
- EΩ =
error in the full-field domain
- Tij =
Cauchy stress tensor
- ui =
displacement vector
- εkl =
infinitesimal strain tensor
- εo =
applied strain
- ϕ =
volume fraction
- λi =
fabric eigenvalues vector
References
- [1]. Wolff, J. , 1892, Das Gesetz der Transformation der Knochen, A. Hirschwald, Berlin. [Google Scholar]
- [2]. Brown, T. , and Albert Ferguson, J. , 1980. “Mechanical Property Distributions in the Cancellous Bone of the Human Proximal Femur,” Acta Orthop. Scand., 51, pp. 429–437. 10.3109/17453678008990819 [DOI] [PubMed] [Google Scholar]
- [3]. Ophir, J. , Cespedes, I. , Garra, B. , Ponnekanti, H. , Huang, Y. , and Maklad, N. , 1996. “Elastography: Ultrasonic Imaging Of Tissue Strain and Elastic Modulus In Vivo.” Eur. J. Ultrasound, 3(1), pp. 49–70. 10.1016/0929-8266(95)00134-4 [DOI] [Google Scholar]
- [4]. Gao, L. , Parker, K. J. , Lerner, R. M. , and Levinson, S. F. , 1996. “Imaging of the Elastic Properties of Tissue: A Review,” Ultrasound Med. Biol., 22(8), pp. 959–977. 10.1016/S0301-5629(96)00120-2 [DOI] [PubMed] [Google Scholar]
- [5]. Bay, B. K. , Smith, T. S. , and Fyhrie, D. P. , 1999. “Digital Volume Correlation: Three-Dimensional Strain Mapping Using X-Ray Tomography,” Exp. Mech., 39(3), pp. 217–226. 10.1007/BF02323555 [DOI] [Google Scholar]
- [6]. Smith, T. S. , Bay, B. K. , and Rashid, M. M. , 2002. “Digital Volume Correlation Including Rotational Degrees of Freedom During Minimization,” Exp. Mech., 42(3), pp. 272–278. 10.1007/BF02410982 [DOI] [Google Scholar]
- [7]. Verhulp, E. , van Rietbergen, B. , and Huiskes, R. , 2004. “A Three-Dimensional Digital Image Correlation Technique for Strain Measurements in Micro-structures,” J. Biomech., 37(9), pp. 1313–1320. 10.1016/j.jbiomech.2003.12.036 [DOI] [PubMed] [Google Scholar]
- [8]. Liu, L. , and Morgan, E. F. , 2007. “Accuracy and Precision of Digital Volume Correlation in Quantifying Displacements and Strain in Trabecular Bone,” J. Biomech., 40(15), pp. 3516–3520. 10.1016/j.jbiomech.2007.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Ophir, J. , Cespedes, I. , Ponnekanti, H. , Yazdi, Y. , and Li, X. , 1991. “Elastography:a Quantitative Method for Imaging the Elasticity of Biological Tissues,” Ultrason. Imaging, 13(2), pp. 111–134. 10.1016/0161-7346(91)90079-W [DOI] [PubMed] [Google Scholar]
- [10]. Oberai, A. A. , Gokhale, N. H. , and Feijoo, G. R. , 2003. “Solution of Inverse Problems in Elasticity Imaging Using the Adjoint Method,” Inverse Probl., 19(2), pp. 297–313. 10.1088/0266-5611/19/2/304 [DOI] [Google Scholar]
- [11]. Oberai, A. A. , Gokhale, N. H. , Doyley, M. M. , and Bamber, J. C. , 2004. “Evaluation of the Adjoint Equation Based Algorithm for Elasticity Imaging,” Phys. Med. Biol., 49(13), pp. 2955–2974. 10.1088/0031-9155/49/13/013 [DOI] [PubMed] [Google Scholar]
- [12]. Barbone, P. E. , and Bamber, J. C. , 2002. “Quantitative Elasticity Imaging: What Can and Cannot be Inferred From Strain Images,” Phys. Med. Biol., 47(12), pp. 2147–2164. 10.1088/0031-9155/47/12/310 [DOI] [PubMed] [Google Scholar]
- [13]. Barbone, P. E. , and Gokhale, N. H. , 2004. “Elastic Modulus Imaging: On the Uniqueness and Nonuniqueness of the Elastography Inverse Problem in Two Dimensions,” Inverse Probl., 20(1), pp. 283–296. 10.1088/0266-5611/20/1/017 [DOI] [Google Scholar]
- [14]. Barbone, P. E. , and Oberai, A. A. , 2007. “Elastic Modulus Imaging: Some Exact Solutions of the Compressible Elastography Inverse Problem,” Phys. Med. Biol., 52(6), pp. 1577–1593. 10.1088/0031-9155/52/6/003 [DOI] [PubMed] [Google Scholar]
- [15]. Richards, M. S. , 2007. “Quantitative Three-Dimensional Elasticity Imaging,” PhD thesis, Biomedical Engineering, Boston University, Boston, MA. [Google Scholar]
- [16]. Gokhale, N. H. , 2007. “Nonlinear Elasticity Imaging Using the Adjoint Method,” PhD thesis, Mechanical Engineering, Boston University, Boston, MA. [Google Scholar]
- [17]. Oberai, A. A. , Gokhale, N. H. , Goenezen, S. , Barbone, P. E. , Hall, T. J. , Sommer, A. M. , and Jiang, J. , 2009. “Linear and Nonlinear Elasticity Imaging of Soft Tissue In Vivo: Demonstration of Feasibility,” Phys. Med. Biol., 54(5), pp. 1191–1207. 10.1088/0031-9155/54/5/006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Mosekilde, L. , 1998. “The Effect of Modelling and Remodelling on Human Vertebral Body Architecture,” Technol. Health Care, 6(5), pp. 287–297. [PubMed] [Google Scholar]
- [19]. Raghupathy, R. , and Barocas, V. H. , 2010. “Generalized Anisotropic Inverse Mechanics for Soft Tissues,” ASME J. Biomech. Eng., 132(8), p. 81006. 10.1115/1.4001257 [DOI] [PubMed] [Google Scholar]
- [20]. Kroon, M. , and Holzapfel, G. A. , 2009. “Elastic Properties of Anisotropic Vascular Membranes Examined by Inverse Analysis,” Comput. Methods in Appl. Mech. Eng., 198(45), pp. 3622–3632. 10.1016/j.cma.2008.08.002 [DOI] [Google Scholar]
- [21]. Liu, Y. Sun, L. Z. , and Wang, G. , 2005. “Tomography-Based 3-d Anisotropic Elastography Using Boundary Measurements,” IEEE Trans. Med. Imaging, 24(10), pp. 1323–1333. 10.1109/TMI.2005.857232 [DOI] [PubMed] [Google Scholar]
- [22]. Lekhnitskii, S. G. , Theory of Elasticity of an Anisotropic Elastic Body (HoldenDay, San Francisco, CA, 1963). [Google Scholar]
- [23]. Vogel, C. , 2002, Computational Methods for Inverse Problems, Society for Industrial and Applied Mathematics, Philadelphia. [Google Scholar]
- [24]. Nazarian, A. , and Muller, R. , 2004. “Time-Lapsed Microstructural Imaging of Bone Failure Behavior,” J. Biomech., 37(1), pp. 55–65. 10.1016/S0021-9290(03)00254-9 [DOI] [PubMed] [Google Scholar]
- [25]. Sutton, M. A. , Wolters,W. J. , Peters, W. H. , Ranson, W. F. , and McNeill, S. R. , 1983. “Determination of Displacements Using an Improved Digital Correlation Method,” Image Vision Comput., 1(3), pp. 133–139. 10.1016/0262-8856(83)90064-1 [DOI] [Google Scholar]
- [26]. Morgan, E. F. , and Keaveny, T. M. , 2001. “Dependence of Yield Strain of Human Trabecular Bone on Anatomic Site,” J. Biomech., 34(5), pp. 569–577. 10.1016/S0021-9290(01)00011-2 [DOI] [PubMed] [Google Scholar]
- [27]. Harrigan, T. P. , Jasty, M. , Mann, R. W. , and Harris, W. H. , 1988. “Limitations of the continuum Assumption in Cancellous Bone,” J. Biomech., 21(4), pp. 269–275. 10.1016/0021-9290(88)90257-6 [DOI] [PubMed] [Google Scholar]
- [28]. Kabel, J. , van Rietbergen, B. , Odgaard, A. , and Huiskes, R. , 1999. “Constitutive Relationships of Fabric, Density, and Elastic Properties in Cancellous Bone Architecture,” Bone, 25(4), pp. 481–486. 10.1016/S8756-3282(99)00190-8 [DOI] [PubMed] [Google Scholar]
- [29]. Gong, H. , Zhang, M. , Yeung, H. Y. , and Qin, L. , 2005. “Regional Variations in Microstructural Properties of Vertebral Trabeculae With Aging,” J. Bone Miner. Metab., 23(2), pp. 174–180. 10.1007/s00774-004-0557-4 [DOI] [PubMed] [Google Scholar]
- [30]. Odgaard, A. , Kabel, J. , van Rietbergen, B. , Dalstra, M. , and Huiskes, R. , 1997. “Fabric and Elastic Principal Directions of Cancellous Bone are Closely Related,” J. Biomech., 30(5), pp. 487–495. 10.1016/S0021-9290(96)00177-7 [DOI] [PubMed] [Google Scholar]
- [31]. Smit, T. H. , Odgaard, A. , and Schneider, E. , 1997. “Structure and Function of Vertebral Trabecular Bone,” Spine, 22(24), pp. 2823–2833. 10.1097/00007632-199712150-00005 [DOI] [PubMed] [Google Scholar]
- [32]. Norris, A. N. , 2006. “The Isotropic Material Closest to a Given Anisotropic Material,” J. Mech. Mater. Struct., 1(2), pp. 223–238. 10.2140/jomms.2006.1-2 [DOI] [Google Scholar]
- [33]. Burr, D. B. , Milgrom, C. , Fyhrie, D. , Forwood, M. , Nyska, M. , Finestone, A. , Hoshaw, S. , Saiag, E. , and Simkin, A. , 1996. “In Vivo Measurement of Human Tibial Strains During Vigorous Activity,” Bone, 18(5), pp. 405–410. 10.1016/8756-3282(96)00028-2 [DOI] [PubMed] [Google Scholar]


