Abstract
OBJECTIVE
This study was designed to determine a cutoff point for identifying insulin resistance from hyperinsulinemic-euglycemic clamp studies performed at 120 mU/m2 ⋅ min in a white population and to generate equations from routinely measured clinic and blood variables for predicting clamp-derived glucose disposal rate (GDR), i.e., insulin sensitivity.
RESEARCH DESIGN AND METHODS
We assembled data from hyperinsulinemic-euglycemic clamps (120 mU/m2 ⋅ min insulin dose) performed at the Pennington Biomedical Research Center between 2001 and 2011. Subjects were divided into subjects with diabetes (n = 51) and subjects without diabetes (n = 116) by self-report and/or fasting glucose ≥126 mg/dL.
RESULTS
We found that 75% of individuals with a GDR <5.6 mg/kg fat-free mass (FFM) + 17.7 ⋅ min were truly insulin resistant. Cutoff values for GDRs normalized for body weight, body surface area, or FFM were 4.9 mg/kg ⋅ min, 212.2 mg/m2 ⋅ min, and 7.3 mg/kgFFM ⋅ min, respectively. Next, we used classification tree models to predict GDR from routinely measured clinical and biochemical variables. We found that individual insulin resistance could be estimated with good sensitivity (89%) and specificity (67%) from the homeostasis model assessment of insulin resistance (HOMA-IR) >5.9 or 2.8< HOMA-IR <5.9 with HDL <51 mg/dL.
CONCLUSIONS
We developed a cutoff for defining insulin resistance from hyperinsulinemic-euglycemic clamps. Moreover, we now provide classification trees for predicting insulin resistance from routinely measured clinical and biochemical markers. These findings extend the clamp from a research tool to providing a clinically meaningful message for participants in research studies, potentially providing greater opportunity for earlier recognition of insulin resistance.
There is substantial evidence that insulin resistance, typically defined as decreased sensitivity or responsiveness to the metabolic actions of insulin, is a precursor of the metabolic syndrome and type 2 diabetes. The gold standard for assessing insulin resistance in humans is the hyperinsulinemic-euglycemic clamp. Developed by DeFronzo et al. in 1979 (1), this procedure assumes that at high doses of insulin infusion (>80 mU/m2 ⋅ min), the hyperinsulinemic state is sufficient to completely suppress hepatic glucose production and that there is no net change in blood glucose concentrations under steady-state conditions. Under such conditions, the rate of glucose infused is equal to the rate of whole-body glucose disposal (GDR) or metabolizable glucose (M) and reflects the amount of exogenous glucose necessary to fully compensate for the hyperinsulinemia. GDR is expressed as a function of metabolic body size, such as body weight (kg), body surface area (m2; BSA), fat-free mass (kg; FFM), or metabolic size (kgFFM+17.7) (2).
Hyperinsulinemic-euglycemic clamps are used in cross-sectional studies and in prospective studies designed to test the effect of interventions (weight loss, weight gain, or pharmacological treatment) on insulin sensitivity. The question of what is a “normal” M value is largely unknown but is dependent on the dose of insulin infused. In 1985, Bergman et al. (3) examined M values across 18 independent clamp studies with an insulin infusion rate of 40 mU/m2 ⋅ min. For nonobese normal glucose-tolerant subjects, the mean M value was between 4.7 and 8.7 mg glucose per kilogram of body mass per minute. From these data, Bergman et al. (3) proposed a conservative definition for insulin resistance as an M value <4.7 mg/kg ⋅ min. To our knowledge, only one study has used a statistical approach to determine a cutoff point for identifying insulin resistance from the clamp (4). In this analysis, results from 2,321 (2,138 subjects without diabetes) euglycemic clamp procedures (40 mU/m2 ⋅ min) in an ethnically diverse population were assembled. It was found that insulin resistance was best predicted when subjects had a GDR (M value) <28 μmol/kgFFM ⋅ min (4). Together, these previous studies give a reasonable estimate of the distribution of GDR for clamps performed with an insulin infusion rate of 40 mU/m2 ⋅ min.
The question of what is a normal and clinically relevant M value derived from clamps using other insulin infusion doses, such as 120 mU/m2 ⋅ min (5–7), is unknown. As such, it is difficult for clinicians to explain the importance of the results from these clamps to research participants. The 120 mU/m2 ⋅ min insulin was chosen for this analysis for two major reasons: 1) endogenous glucose production is likely to be fully suppressed, and 2) a shorter time is needed to reach steady-state conditions with a higher infusion rate, thus making this insulin dose more cost-effective while also reducing participant burden. Moreover, although the clamp technique is the gold standard for directly assessing insulin resistance in humans, it is time-consuming, labor-intensive, and overall expensive. Therefore, the ability to predict results of the clamp from other clinical data, which are both easier to obtain and less expensive to measure, is important.
In the current study, we assembled data from clamp studies performed under standard operating procedures at the Pennington Biomedical Research Center (PBRC; Baton Rouge, LA), between 2001 and 2011, with an insulin infusion rate of 120 mU/m2 ⋅ min. Our aims were to 1) determine a cutoff point for identifying insulin resistance for hyperinsulinemic-euglycemic clamp studies performed at 120 mU/m2 ⋅ min in a white population and 2) generate equations from commonly measured clinic and blood variables for predicting insulin sensitivity (M values derived from the clamp).
RESEARCH DESIGN AND METHODS
The Pennington Center Longitudinal Study is an ongoing investigation of the effects of obesity and lifestyle factors on the development of chronic diseases such as type 2 diabetes and cardiovascular disease. The sample is comprised of volunteers who have participated in nutrition, weight loss, and other metabolic intervention and observational studies at the PBRC since 1992. The current cross-sectional analysis is limited to adult participants who had a single-step 120 mU/m2 ⋅ min hyperinsulinemic-euglycemic clamp before any intervention and a dual-energy X-ray absorptiometry (DXA) scan between 2001 and 2011 (n = 263). Subjects with fasting plasma glucose >180 mg/dL or a diagnosis of diabetes >5 years were excluded. Our cohort consisted of 167 whites, 94 African Americans, and two others. When euglycemic-hyperinsulinemic clamp studies were first established at PBRC by one of the authors (E.R.), the capability for measuring isotope tracers, and therefore hepatic glucose production, was unavailable. Therefore, clamps were performed at 120 mU/m2 ⋅ min as this insulin dose was considered high enough to completely suppress hepatic glucose production.
Diabetes status was defined by self-report or fasting plasma glucose concentrations ≥126 mg/dL. Subjects were classified as being diabetic if they 1) self-reported “yes” to having diabetes (n = 62) or 2) self-reported “no” to diabetes but had a fasting glucose ≥126 mg/dL (n = 4). Subjects were classified as being nondiabetic if they self-reported “no” and had a fasting glucose <126 mg/dL (n = 197). Furthermore, to verify diabetes status, we also obtained HbA1c data, which were available in 104 of 263 subjects. HbA1c levels were higher in subjects classified as having diabetes (6.1 ± 0.6%) compared with subjects classified as not having diabetes (5.4 ± 0.4%). All procedures were approved by the PBRC Institutional Review Board, and all participants provided written, informed consent.
Anthropometry and body composition
Height was measured with a wall-mounted stadiometer and metabolic weight with a digital scale. BMI was calculated as weight in kilograms divided by height in meters squared. Whole-body percent body fat was measured by DXA (Hologics QDR 4500A; Hologics, Bedford, MA), and fat mass (FM) and FFM were calculated from the percent body fat and body weight. BSA was calculated using the Du Bois equation (8).
Insulin sensitivity
In vivo insulin sensitivity was assessed with a hyperinsulinemic-euglycemic clamp with a primed continuous infusion of insulin at 120 mU/m2 ⋅ min to achieve endogenous steady-state insulin concentrations and to draw steady-state blood samples. An intravenous catheter was placed in an antecubital vein for infusion of insulin and glucose. A second catheter was placed retrograde in a dorsal vein of the contralateral hand for blood draws. The hand was placed in a heating box at 41°C for arterialization of venous blood. A 20% glucose solution was infused at a variable rate necessary to maintain plasma glucose concentrations between 90 and 100 mg/dL. For clamps performed at 120 mU/m2 ⋅ min, the duration was 2 h, and for clamps at 80 mU/m2 ⋅ min, the clamp duration was at least 3 h. The mean rate of exogenous glucose infusion during the last 30 min was defined as the GDR (1). First, GDR was adjusted for glucose concentrations during this steady-state interval (GDR × [average group steady-state glucose/individual steady-state glucose]) (3). Next, to adjust for metabolic size, GDR was normalized for weight, BSA, FFM, or FFM+17.7 (2).
Blood analysis
Plasma glucose was analyzed with a Yellow Springs Instruments 2300 STAT Glucose Analyzer (Yellow Springs Instruments Inc., Yellow Springs, OH). Plasma insulin was measured by chemiluminescent immunoassays on an Immulite 2000 Analyzer (Diagnostic Products), and lipid (FFA, total cholesterol, and HDL) concentrations were measured with a Beckman Coulter Synchron DXC 600 Pro. LDL was calculated with the Friedewald calculation.
Statistical methods
Descriptive data are presented as mean ± SD. Statistical analysis was performed with SAS version 9.2 (SAS Institute, Cary, NC). The χ2 test was used to test significance of group differences in sex. Independent sample t tests and Mann-Whitney U tests were used to test group differences for continuous variables. GDR determined from the hyperinsulinemic-euglycemic clamp and adjusted for weight, BSA, FFM, or FFM+17.7 was used as a biomarker for separating subjects who were insulin resistant (had type 2 diabetes mellitus) from those who were insulin sensitive (did not have type 2 diabetes). We defined the optimal cutoff point for discriminating insulin-resistant subjects from insulin-sensitive subjects as the GDR that provided both high sensitivity (ability to detect insulin-resistant subjects) and simultaneously provided high specificity (ability to detect insulin-sensitive subjects). Thus, sensitivity is the proportion of true positives (individuals known to be insulin resistant who were classified as insulin resistant based on their GDR), whereas 1 – specificity is the proportion of false positives (individuals known to be insulin sensitive who were classified as insulin resistant based on their GDR). We used a receiver-operating characteristic (ROC) curve, a plot of the sensitivity versus 1 – specificity, to display the trade-off between true positives and false positives across incremental choices of discriminating cutoff points for glucose disposal rate (9,10). The cutoff point corresponding to the optimal balance of true versus false positives indicates the best threshold for discriminating insulin-resistant individuals from insulin-sensitive individuals.
Principles of classification trees.
Classification trees were used to determine a specific set of rules (algorithm) for classifying subjects as insulin resistant or insulin sensitive from GDR (11). This method makes no assumptions about the underlying distribution of data and takes into account interactions among covariates and outcome variables. An advantage of the classification tree method is that it allows observations with missing values in a dataset, as opposed to traditional logistic regression analysis, which removes observations with missing predictor values. Tree-based methods recursively partition the predictor variables into a set of decision points or classification “nodes.” A binary decision tree is fully grown when classification rules are completely diagrammed. Without pruning, a large and complex tree can be built at the cost of overfitting the data (12). Thus, pruning the tree is implemented so that we can select a tree size that minimizes the cross-validated error and avoids overfitting.
Decision rules for classifying subjects can be obtained by assigning each terminal node a class label as either “1” (presence of insulin resistance) or “0” (absence of insulin resistance). The choice of a class label is based on a defined cutoff point and also the proportion of true event occurrences at that terminal node. For example, if “0.25” or above is chosen as a cutoff point, then only terminal nodes with true event occurrence proportion equal to or larger than “0.25” are classified as “insulin resistant” and the remaining are classified as “0” or insulin sensitive. The proportion displayed at each terminal node can be considered as a “risk score” for insulin resistance.
Single Classification Tree Method.
In order to select the best-performing models for exploring the relationship between insulin sensitivity and clinical variables, subjects were randomly split into a training subset for building the model (n = 125) and a testing subset for evaluating the performance of the model (n = 42) at a ratio of 3:1.
The Single Classification Tree Method was chosen as the statistical exploratory method because it outperformed other approaches such as logistic regression and boosting regression trees in terms of sensitivity, specificity, and area under the ROC curve, denoted aROC (10), on the testing dataset. Thus, aROC is used as a measure of average prediction performance of different classification algorithms. Because aROC represents area of a portion under a unit square, its value ranges between 0 and 1. Random guessing results in an aROC approximately equal to 0.5. A realistic classification method should have an aROC >0.5, and a classification rule with aROC >0.70 is generally considered adequate; aROC very close to 1 indicates exceptionally good performance. Our goal was to examine the selected decision trees for predicting insulin resistance to accommodate different clinical/research settings where values for all variables would not necessarily be available.
The tree analysis was performed with data from 167 whites. The main outcome variable used in this analysis was GDR adjusted for FFM+17.7 (GDRadj) because we believe that this adjustment is the best available method accounting for metabolic size (2). Covariates included sex, age, weight, height, BMI, BSA, FFM, self-reported family history of diabetes, fasting glucose, fasting insulin, cholesterol, HDL, LDL, triglycerides, FFA, and homeostasis model assessment of insulin resistance (HOMA-IR) [fasting insulin (μU/mL) × fasting glucose (mg/dL)/405]. Three classification tree models were developed to answer different questions. Model 1 was constructed with all available input variables, mimicking a clinical situation where body composition and blood markers were all included. Model 2 uses only fasting glucose and insulin concentrations, BMI, age, and sex as input variables. Model 3 is a minimalist model constructed using age, sex, and BMI.
RESULTS
Subject characteristics
Our white cohort comprised 51 subjects with diabetes and 116 subjects without diabetes (Table 1). Subjects with diabetes were significantly older (age 57.2 ± 8.6 vs. 44.2 ± 13.2 years, P < 0.001) and had higher LDL (P = 0.05) and glucose levels (by study design; P < 0.001) than subjects without diabetes. There were no significant sex differences between subjects with and without diabetes (P = 0.10).
Table 1.
Subject characteristics for whites undergoing hyperinsulinemic-euglycemic clamp studies at 120 mU/m2 ⋅ min
Distribution and optimal cutoff for determination of insulin resistance
The distribution of GDR, whether it was adjusted for weight, BSA, FFM, or FFM+17.7 was bimodal (summarized in Table 2). As expected, GDR was lower in subjects with diabetes compared with subjects without diabetes, regardless of how GDR was adjusted for metabolic size. For GDRadj, the mean was 7.4 ± 2.7 mg/kgFFM+17.7 ⋅ min in subjects without diabetes and 4.6 ± 1.7 mg/kgFFM+17.7 ⋅ min in subjects with diabetes. A cutoff of 5.6 mg/kgFFM+17.7 ⋅ min provided the maximum theoretical sensitivity (75%) and specificity (71%) with an aROC of 80% for defining insulin resistance. In other words, the optimal cutoff for identifying insulin-resistant individuals from the 120 mU/m2 ⋅ min clamp was 5.6 mg/kgFFM+17.7 ⋅ min. Using this criterion in the whole group, 44.3% of individuals fell below this cut point and could be considered insulin resistant. The same cutoff (5.6 mg/kgFFM+17.7 ⋅ min) was observed when this analysis was performed in the whole cohort (n = 267) (data not shown). When GDR was adjusted for body weight, BSA, or FFM, the cutoff value for insulin resistance was 4.9 mg/kg weight ⋅ min, 212 mg/m2 ⋅ min, and 7.3 mg/kgFFM ⋅ min, respectively (Table 2).
Table 2.
GDR values at 120 mU/m2 ⋅ min for subjects with and without diabetes adjusted for metabolic size, including body weight, BSA, FFM, and FFM+17.7 kg
As a subanalysis, we also compiled data from 86 hyperinsulinemic-euglycemic clamps performed at 80 mU/m2 ⋅ min. Similar to the 120-mU insulin dose, the distribution of GDR was bimodal with lower GDR in subjects with diabetes (n = 11) compared with subjects without diabetes (n = 75). The average data and cutoff points for GDR expressed by weight, BSA, FFM, or FFM+17.7, and the subject characteristics for this cohort are provided in Supplementary Tables 1 and 2. In subjects without diabetes, the mean GDRadj was 8.2 ± 3.0 mg/kgFFM+17.7 ⋅ min compared with 3.3 ± 0.7 mg/kgFFM+17.7 ⋅ min in subjects with diabetes, and the cutoff for defining insulin resistance was 4.1 mg/kgFFM+17.7 ⋅ min with a maximal sensitivity and specificity of 83 and 96%, respectively (aROC = 0.98). When GDR was adjusted for body weight, BSA, or FFM, the cutoff value for insulin resistance was 4 mg/kgweight ⋅ min, 192 mg/m2 ⋅ min and 5 mg/kgFFM ⋅ min, respectively (Supplementary Table 2). Tree model analyses were not performed at the 80-mU insulin dose because of the relatively small sample size and unbalanced proportion of subjects with and without diabetes.
Tree models for predicting insulin resistance using all predictors
As indicated in research design and methods, tree models and decision rules were developed to predict GDRadj based on a randomly selected training set (n = 125) followed by evaluating the performance of the models in the remaining testing set (n = 42).
Model 1: all predictors.
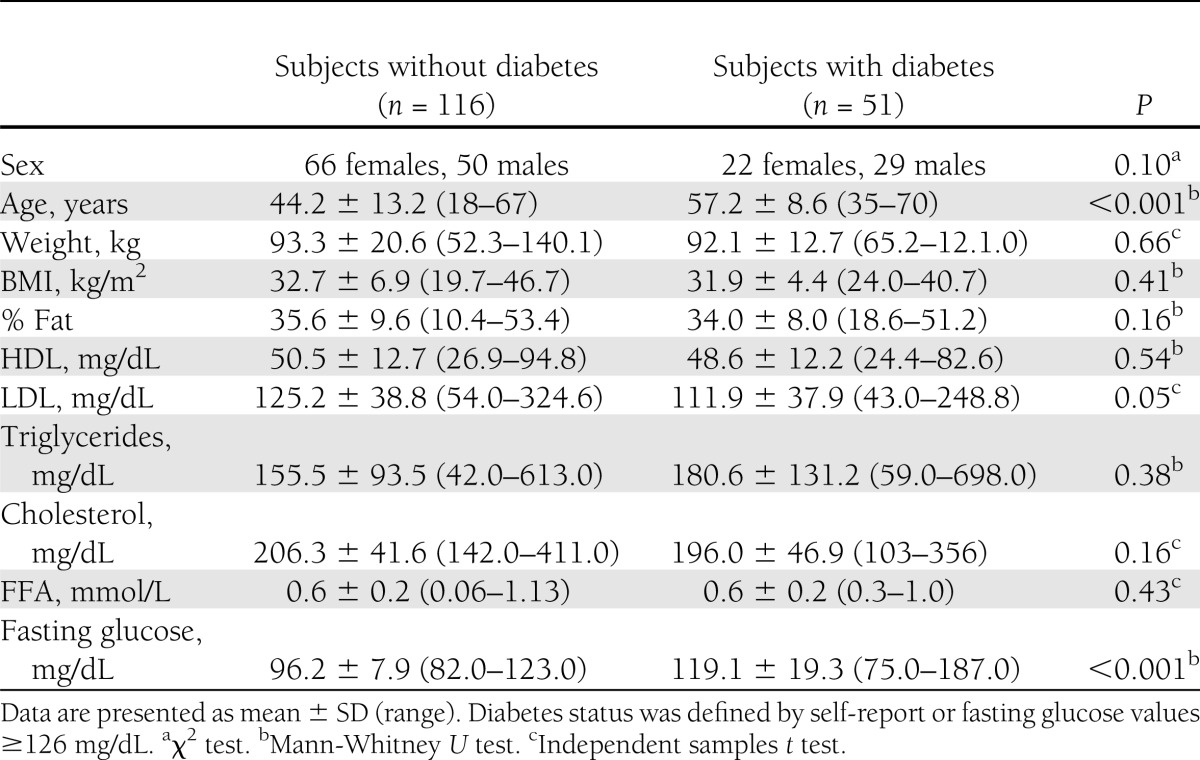
In the tree model based on all predictors (Model 1), the following predictors were statistically significant: HOMA-IR, HDL, and fasting glucose resulting in an aROC of 87%. Figure 1 depicts the classification tree model using these predictors. The number of insulin-resistant individuals and the number of insulin-sensitive individuals are shown in Fig. 1. Using an arbitrary cutoff of 0.25 as the “risk score” of having insulin resistance, nodes ≥25% (proportion of insulin-resistant individuals) predict insulin resistance and nodes <25% predict insulin sensitivity. Therefore, in Fig. 1, the associated decision rules for predicting an individual as being insulin resistant is either having the following: 1) a HOMA-IR >5.9 or 2) HOMA-IR = 2.8–5.9 and HDL <51 mg/dL. Use of other choices for the predictive cutoff value (e.g., 50%) yielded similar sensitivity (89%) and specificity (67%) results (data not shown).
Figure 1.
Tree model for insulin resistance determined using all available body composition and blood measures. HOMA-IR and HDL were the only significant determinants in this model. The model is built on a randomly selected training cohort of 125 subjects and tested in 42 subjects. An arbitrary risk score of 0.25 is calculated. Therefore, if a terminal node has a >25% proportion, those subjects are more likely to be insulin resistant (dashed lines). The decision nodes for being insulin resistant are as follows: 1) HOMA-IR >5.9 and 2) 2.8< HOMA-IR <5.9 and HDL <51 mg/dL.
Model 2: anthropometry, fasting glucose, and insulin measurements.
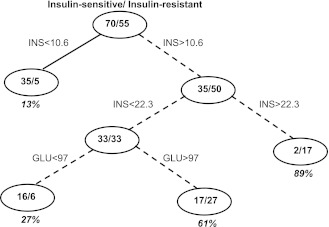
The next tree model was performed using only body composition, fasting glucose, insulin, and age and sex as predictor variables. Only fasting insulin and glucose were significant predictors in building the tree model with an aROC of 86% in the testing subset (Fig. 2). Similar to the above tree model using all predictors, we assigned an arbitrary cutoff of 0.25 as the “risk score” of being classified as insulin resistant. Therefore, in Fig. 2, the associated decision rule for predicting an individual to be insulin resistant is a fasting insulin concentration >10.6 μU/mL. This decision rule has an estimated sensitivity of 100% and specificity of 54%.
Figure 2.
Tree model for insulin resistance using only fasting glucose, insulin, age, sex, and BMI. Only fasting insulin was a significant determinant in the model. The model is built on a randomly selected training cohort of 125 subjects and tested on 42 subjects. An arbitrary risk score of 0.25 is calculated. Therefore, if a terminal node has a >25% proportion, those subjects are more likely to be insulin resistant (dashed lines). The decision node for being insulin resistant is having a fasting insulin >10.6 μU/mL.
Model 3: age, sex, and BMI.
The last tree model we tested for predicting insulin sensitivity from the clamp only used age, sex, and BMI as predictor variables. Again based on an arbitrary cutoff of 0.25% for detecting insulin resistance, the only significant predictor variable was BMI with an aROC of 61% and a BMI >24.7 kg/m2 predicting insulin resistance. As expected, as the number of predictor variables decreases, the aROC and sensitivity and specificity results worsen.
The same tree-based model analysis was also performed in a larger, more ethnically diverse cohort of 263 individuals (167 whites, 94 African Americans, one Hispanic, and one other). As expected, with a greater number of subjects, higher aROCs, and sensitivity and specificity results were obtained in the larger cohort (data not shown).
CONCLUSIONS
The hyperinsulinemic-euglycemic clamp technique is the gold standard for assessing insulin sensitivity in humans. This method is widely used in research studies to examine the effects of an intervention, such as low-calorie diet or pharmacological therapy. Unfortunately, few data exist on what is considered a “normal” glucose infusion rate, i.e., normal insulin sensitivity. Moreover, the ability to compare results from clamp studies is clouded by the fact that GDR results are expressed as a function of body weight, BSA, or FFM. The goal of the current study was to provide cutoff values for defining insulin resistance and insulin sensitivity in clamps performed at an insulin dose of 120 mU/m2 ⋅ min and to provide decision trees for predicting insulin resistance from routinely measured clinical and biochemical parameters. Similar to a previous study (4), we found that the distribution of whole-body glucose disposal rate is bimodal. This bimodality allowed us to use a statistical approach to determine a cutoff for defining insulin resistance or insulin sensitivity. We found that a GDR or M value of 5.6 mg/kgFFM+17.7 ⋅ min in whites gives an almost 80% probability of predicting insulin resistance. In other words, individuals with a GDR <5.6 mg/kgFFM+17.7 ⋅ min have an 80% chance of being insulin resistant. The same cutoff was found in a larger, more ethnically diverse cohort (data not shown).
In a smaller sample of clamps performed at 80 mU/m2 ⋅ min, a cutoff of 5.3 mg/kgFFM+17.7 ⋅ min (98% prediction probability) was determined for defining insulin resistance. That is, subjects with a GDR <5.3 mg/kgFFM+17.7 ⋅ min have a 98% probability of having insulin resistance. To expand the applicability of these findings to the investigators who do not measure body composition, we determined cut points for insulin resistance for GDR expressed by weight, BSA, or FFM. These data allow researchers performing hyperinsulinemic-euglycemic clamps at the 80 and 120 mU/m2 ⋅ min insulin infusion rates to gain valuable clinical information on a subject’s insulin sensitivity and translate findings from a primarily research setting to a clinically relevant message. A summary of our results at 80 and 120 mU/m2 ⋅ min and results from other studies at 40 mU/m2 ⋅ min (3,4) is provided in Supplementary Table 3.
Given the demanding nature, expense, and time involved in performing hyperinsulinemic-euglycemic clamps, we aimed to develop models for predicting insulin resistance by the clamp from routinely measured anthropometric, body composition, and biochemical markers. Our first classification model (Model 1) included all available variables (listed in research design and methods) and found that subjects with a 1) HOMA-IR >5.9 or 2) HOMA-IR between 2.8 and 5.9 and HDL <51 mg/dL predicted insulin resistance with good specificity and sensitivity. The finding that HOMA-IR was the strongest predictor of GDRadj is not surprising given the strong correlation between HOMA-IR and insulin sensitivity derived from the clamps demonstrated previously (13). In addition, our findings are similar to those from the study by Stern et al. (4) in which they generated classification trees from clamps performed at 40 mU/m2 ⋅ min. Stern et al. (4) found HOMA-IR, BMI, waist circumference, and LDL as significant predictors of insulin resistance, with similar sensitivity and specificity results (our study: aROC = 0.87; Stern et al.: aROC = 0.90). Model 2 used only anthropometry, fasting glucose, insulin, and age and sex. Similar to Model 1, we found that only fasting insulin was a significant predictor of GDRadj, with a fasting insulin >10.6 μU/mL defining insulin resistance. Model 3 used only age, sex, and BMI to predict GDRadj. This model gave poor specificity and sensitivity results that highlighted the well-known fact that insulin resistance is a heterogeneous disorder that is not only dependent on weight, sex, and age (14). Coupled with previous studies defining insulin resistance from clamps performed at 40 mU/m2 ⋅ min (3,4), our results at 80 and 120 mU/m2 ⋅ min insulin doses contribute substantially to the literature determining insulin resistance from clamps (Supplementary Table 3).
To account for the metabolic mass that uses insulin during a clamp procedure, GDR derived from the clamp must be adjusted for metabolic size. The majority of studies in the literature tend to use total body weight or kilograms of FFM with a smaller number of studies using BSA. However, total body weight is not a completely appropriate method for comparing individuals, because obese subjects have a greater proportion of low-metabolizing mass (adipose tissue) and females have a greater percentage of fat than men. BSA also poses a sex difference problem (2). From studies of metabolic rate in the Pima Indians, Lillioja and Bogardus (2) showed that metabolic rate is directly proportional to FFM+17.7 kg, suggesting that this measure can be equated to metabolic size. On the basis of this finding, we have chosen this normalization method in our classification analysis. However, we have also considered that not all researchers may have access to measuring body composition (DXA) and have also reported on these insulin resistance cutoffs normalized by weight and BSA. Finally, it needs to be noted that dividing GDRs during a clamp by resting metabolic rate would really represent the best way to compare values from people with different body sizes.
Limitations of this study may be the small sample size of clamp studies at 120 mU/m2 ⋅ min, and particularly at 80 mU/m2 ⋅ min. However, we were able to achieve good statistical sensitivity and specificity results (>80% prediction probability) in this cohort. We also demonstrated the same cutoff points in a larger, more ethnically diverse population. Another potential limitation may be that we did not use radiolabeled glucose tracers to quantify endogenous glucose production. However, the high insulin infusion doses reported in this study generally suppress most, if not all, the baseline splanchnic glucose output (15). We also acknowledge that there is considerable overlap in insulin sensitivity (M) between subjects with and without diabetes (2). An alternative approach would have been to divide our cohort into subjects with normal glucose tolerance, impaired glucose tolerance, or type 2 diabetes; however, this would have further diminished our sample size.
In conclusion, our study provides novel data for defining insulin resistance from hyperinsulinemic-euglycemic clamps performed at insulin doses of 120 and 80 mU/m2 ⋅ min. Moreover, we have provided classification trees for predicting insulin resistance from routinely measured biochemical markers. Together, our findings extend the hyperinsulinemic-euglycemic clamp from what is largely considered a research tool to providing clinically meaningful messages for patients, thus providing greater likelihood of earlier detection of insulin resistance.
Acknowledgments
This study was supported by funding from the National Institutes of Health (grants P30DK072476 and R01DK060412 and R00HD060762 and U01DK094418) to L.M.R.
No potential conflicts of interest relevant to this article were reported.
C.S.T. wrote the manuscript, contributed to discussions about the results, and reviewed and edited the final manuscript. W.X. performed the statistical analysis, contributed to discussions about the results, and reviewed and edited the final manuscript. W.D.J. performed the statistical analysis, contributed to discussions about the results, and reviewed and edited the final manuscript. W.T.C. contributed to discussions about the results and reviewed and edited the final manuscript. L.M.R. contributed to discussions about the results and reviewed and edited the final manuscript. E.R. contributed to discussions about the results and reviewed and edited the final manuscript. E.R. is the guarantor of this work and, as such, had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis.
We thank Dr. Frank Greenway for repeatedly asking us, what is a good (or bad) insulin sensitivity?
Footnotes
This article contains Supplementary Data online at http://care.diabetesjournals.org/lookup/suppl/doi:10.2337/dc11-2339/-/DC1.
References
- 1.DeFronzo RA, Tobin JD, Andres R. Glucose clamp technique: a method for quantifying insulin secretion and resistance. Am J Physiol 1979;237:E214–E223 [DOI] [PubMed] [Google Scholar]
- 2.Lillioja S, Bogardus C. Obesity and insulin resistance: lessons learned from the Pima Indians. Diabetes Metab Rev 1988;4:517–540 [DOI] [PubMed] [Google Scholar]
- 3.Bergman RN, Finegood DT, Ader M. Assessment of insulin sensitivity in vivo. Endocr Rev 1985;6:45–86 [DOI] [PubMed] [Google Scholar]
- 4.Stern SE, Williams K, Ferrannini E, DeFronzo RA, Bogardus C, Stern MP. Identification of individuals with insulin resistance using routine clinical measurements. Diabetes 2005;54:333–339 [DOI] [PubMed] [Google Scholar]
- 5.Stull AJ, Cash KC, Johnson WD, Champagne CM, Cefalu WT. Bioactives in blueberries improve insulin sensitivity in obese, insulin-resistant men and women. J Nutr 2010;140:1764–1768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Plaisance EP, Greenway FL, Boudreau A, et al. Dietary methionine restriction increases fat oxidation in obese adults with metabolic syndrome. J Clin Endocrinol Metab 2011;96:E836–E840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cefalu WT, Rood J, Pinsonat P, et al. Characterization of the metabolic and physiologic response to chromium supplementation in subjects with type 2 diabetes mellitus. Metabolism 2010;59:755–762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Du Bois D, Du Bois EF. A formula to estimate the approximate surface area if height and weight be known. 1916. Nutrition 1989;5:303–311; discussion 312–313 [PubMed] [Google Scholar]
- 9.Bewick V, Cheek L, Ball J. Statistics review 13: receiver operating characteristic curves. Crit Care 2004;8:508–512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bradley AP. The use of the area under the ROC curve in the evalution of machine learning algorithms. Pattern Recognit 1997;30:1145–1159 [Google Scholar]
- 11.Hastie T, Tibshirani R, Friedman J. Tree-based models. In The Elements of Statistical Learning, Second Edition Springer, New York, 2008, p. 305–316 [Google Scholar]
- 12.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Belmont, CA, Wadsworth International Group, 1984 [Google Scholar]
- 13.Matthews DR, Hosker JP, Rudenski AS, Naylor BA, Treacher DF, Turner RC. Homeostasis model assessment: insulin resistance and beta-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia 1985;28:412–419 [DOI] [PubMed] [Google Scholar]
- 14.Olefsky JM. Lilly lecture 1980. Insulin resistance and insulin action. An in vitro and in vivo perspective. Diabetes 1981;30:148–162 [DOI] [PubMed] [Google Scholar]
- 15.DeFronzo RA: Pathogenesis of type 2 diabetes mellitus. Med Clin North Am 88:787–835, ix, 2004 [DOI] [PubMed]