Measurement and simulation of myoplasmic calcium transients in mouse slow-twitch muscle fibres

Abstract

Non-technical summary

In voluntary muscle cells, the change in the intracellular concentration of calcium ions (ΔµCa²⁺½) controls the contractile cycle by controlling the binding of Ca²⁺ to the ‘regulatory’ sites on the troponin molecules attached to the myofilaments. ΔµCa²⁺½ is difficult to measure under physiological conditions, as indicated by the discrepancies in results from recent studies of ΔµCa²⁺½ on mouse slow-twitch muscle fibres. Here we examine some of the reasons underlying these discrepancies and argue that measurements made with membrane-impermeant Ca²⁺ indicators that are micro-injected into intact fibres are more accurate than those made with indicators introduced into enzyme-dissociated fibres by diffusion (“AM loading”). Using a computational model, we have analysed the ΔµCa²⁺½ measurements to estimate the kinetic rate constants that govern the reaction of Ca²⁺ with the troponin regulatory sites. To our knowledge, this is the first time such estimates have been deduced from physiological measurements in living slow-twitch muscle fibres.

Abstract

Bundles of intact fibres from soleus muscles of adult mice were isolated by dissection and one fibre within a bundle was micro-injected with either furaptra or mag-fluo-4, two low-affinity rapidly responding Ca²⁺ indicators. Fibres were activated by action potentials to elicit changes in indicator fluorescence (ΔF), a monitor of the myoplasmic free Ca²⁺ transient (ΔµCa²⁺½), and changes in fibre tension. All injected fibres appeared to be slow-twitch (type I) fibres as inferred from the time course of their tension responses. The full-duration at half-maximum (FDHM) of ΔF was found to be essentially identical with the two indicators; the mean value was 8.4 ± 0.3 ms (±SEM) at 16°C and 5.1 ± 0.3 ms at 22°C. The value at 22°C is about one-third that reported previously in enzyme-dissociated slow-twitch fibres that had been AM-loaded with mag-fluo-4: 12.4 ± 0.8 ms and 17.2 ± 1.7 ms. We attribute the larger FDHM in enzyme-dissociated fibres either to an alteration of fibre properties due to the enzyme treatment or to some error in the measurement of ΔF associated with AM loading. ΔF in intact fibres was simulated with a multi-compartment reaction-diffusion model that permitted estimation of the amount and time course of Ca²⁺ release from the sarcoplasmic reticulum (SR), the binding and diffusion of Ca²⁺ in the myoplasm, the re-uptake of Ca²⁺ by the SR Ca²⁺ pump, and ΔµCa²⁺½ itself. In response to one action potential at 16°C, the following estimates were obtained: 107 μm for the amount of Ca²⁺ release; 1.7 ms for the FDHM of the release flux; 7.6 μm and 4.9 ms for the peak and FDHM of spatially averaged ΔµCa²⁺½. With five action potentials at 67 Hz, the estimated amount of Ca²⁺ release is 186 μm. Two important unknown model parameters are the on- and off-rate constants of the reaction between Ca²⁺ and the regulatory sites on troponin; values of 0.4 × 10⁸m⁻¹ s⁻¹ and 26 s⁻¹, respectively, were found to be consistent with the ΔF measurements.

Introduction

Mammalian slow-twitch (‘type I’) fibres have both similarities and differences when compared with fast-twitch (‘type II’) fibres (e.g. Berchtold et al. 2000; Bottinelli & Reggiani, 2000)). Two notable differences are that slow-twitch fibres have a higher activity of oxidative enzymes and a slower contractile response when stimulated electrically. For example, in rat motor units studied in the whole animal at a physiological sarcomere length, the time of peak and full-duration at half-maximum (FDHM) of twitch tension are about 4-fold larger in slow-twitch units than in fast-twitch units (35°C; Close, 1967)). Similar differences in contractile parameters are seen in intact fibres of mouse muscle at long sarcomere length (∼3.6 μm), where the time of peak and FDHM of twitch tension are 3- to 4-fold larger in slow-twitch (soleus) fibres than in fast-twitch (extensor digitorum longus, EDL) fibres (16°C; Baylor & Hollingworth, 2003)). (Note: in this article, intact fibres refer to fibres or fibre bundles that have been obtained by dissection but have not otherwise been structurally modified; specifically, they have not been enzyme-dissociated, cut, skinned, or chemically permeabilized.)

Also differing in the two fibre types is the change in the myoplasmic free calcium concentration (ΔµCa²⁺½) during a twitch. In mouse intact slow-twitch fibres, the amplitude of ΔµCa²⁺½ elicited by an action potential is reported to be about half of that in fast-twitch fibres, 9.4 ± 1.0 vs. 18.5 ± 0.5 μm (mean ± SEM), while the FDHM of ΔµCa²⁺½ is about 60% larger, 7.7 ± 0.6 vs. 4.9 ± 0.3 ms (16°C; Table 1 of Baylor & Hollingworth, 2003)). These differences are best measured with a low-affinity rapidly responding Ca²⁺ indicator such as furaptra (Raju et al. 1989; Konishi et al. 1991)) but qualitatively similar differences have been measured in studies with other types of indicators (see Discussion in Baylor & Hollingworth, 2003)).

Fibre-type differences in ΔµCa²⁺½ have also been reported in mouse fibres isolated by enzyme-dissociation and studied with acetoxy-methyl ester (AM)-loaded mag-fluo-4, another low-affinity rapidly responding Ca²⁺ indicator (Calderón et al. 2009, 2010). While the tension response of fibres could not be measured in these studies, fibre types in one study were identified from their myosin heavy-chain isoforms (Calderón et al. 2010)). The properties of ΔµCa²⁺½ elicited by an action potential in these enzyme-dissociated slow-twitch fibres differ in some important respects from those mentioned above in intact slow-twitch fibres, even though the fibres were obtained from mice of similar age (young adult, 6–14 weeks) and from the same muscles (soleus). For example, in enzyme-dissociated slow-twitch fibres at 22°C, the FDHM of ΔµCa²⁺½ elicited by an action potential varied between 12.4 ± 0.8 ms (Calderón et al. 2009)) and 17.2 ± 1.7 ms (Calderón et al. 2010)). These values are substantially larger than the 7.7 ± 0.6 ms value mentioned above for intact fibres at 16°C, and an even larger relative difference would be expected if the measurements had been made at the same temperature (Baylor & Hollingworth, 2003)). A second difference is that, in enzyme-dissociated fibres, the rise time of ΔµCa²⁺½ is noticeably slower in slow-twitch fibres than in fast-twitch fibres (Calderón et al. 2010)), whereas, in intact fibres, essentially identical rise times are seen in the two fibre types (Baylor & Hollingworth, 2003)).

The work described in this article was undertaken with two goals in mind. First, new experiments were carried out on intact slow-twitch fibres of young-adult mice to examine possible reasons for the difference in the measured properties of ΔµCa²⁺½ in intact and enzyme-dissociated slow-twitch fibres and thereby to identify which results are most relevant to the functioning of these fibres in the whole animal. Second, a multi-compartment model was used to simulate the ΔµCa²⁺½ measurements in slow-twitch fibres. A successful simulation of this type permits estimation of the underlying Ca²⁺ movements that give rise to ΔµCa²⁺½, including the flux of Ca²⁺ through the Ca²⁺ release channels of the sarcoplasmic reticulum (SR), the binding and diffusion of Ca²⁺ within the myoplasm, and the re-sequestration of Ca²⁺ within the SR by the SR Ca²⁺ pump. The model employed is an adaptation of an analogous model that accurately simulates ΔµCa²⁺½ in mouse fast-twitch fibres and that appears to provide reliable estimates of these movements in fast-twitch fibres (Baylor & Hollingworth, 2007)).

Methods

Ethical approval

All animal procedures were approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania. The authors have read and the experiments comply with the policies and regulations of The Journal of Physiology given by Drummond (2009).

Solutions and fibre preparation

The methods were similar to those described previously (Hollingworth et al. 1996; Baylor & Hollingworth, 2003, 2007)). Experiments were carried out at 16 and 22°C on bundles of mouse soleus fibres that were bathed in an oxygenated Ringer solution that contained (in mm): 150 NaCl, 2 KCl, 2 CaCl₂, 1 MgCl₂ and 5 Hepes (4-(2-hydroxyethyl) piperazine-1-ethane-sulfonic acid) (pH, 7.4). Male Balb-C mice, aged 7–14 weeks, were used throughout; mice were obtained from Charles River Laboratories (Wilmington, MA, USA). On the day of an experiment, an animal was sedated with CO₂, then killed by rapid cervical dislocation. Both soleus muscles were removed by gross dissection. One muscle was used immediately for experimentation; the other was stored in Ringer solution at 4°C for later use, typically 2–3 h after the first. No significant differences in results were observed between fresh and stored muscles. A muscle was pared with forceps and scalpel to a bundle that contained 20–30% of the original muscle mass. Care was taken to avoid perturbing the superficial fibres on one side of the bundle, which contained the fibre used for experimentation. The bundle was mounted on an optical bench apparatus equipped for recording fibre fluorescence and twitch tension. To minimize movement artifacts in the optical signals, the bundle was stretched to a long sarcomere length (average value, 3.7 μm; range, 3.3–3.9 μm).

Ca²⁺ transient measurements

Furaptra (also called mag-fura-2) and mag-fluo-4 were obtained from Invitrogen Corp. (Carlsbad, CA, USA) in the membrane-impermeant (potassium salt) form. These indicators have a relatively low-affinity for Ca²⁺, with in vitro dissociation constants (K_D,Ca) of 44 and 70 μm, respectively (16–20°C; Konishi et al. 1991; Hollingworth et al. 2009)). The indicators also have some sensitivity to Mg²⁺, with in vitro dissociation constants (K_D,Mg) of 5.3 and 6.5 mm, respectively (16–20°C). Because these indicators have a low affinity for Ca²⁺ and because, in twitch muscle fibres, their fluorescence signals have little or no interference from components not related to metal binding (reviewed in Baylor & Hollingworth, 2011)), they can be used to accurately monitor the main time course of ΔµCa²⁺½ provided fibre movement can be minimized, for example, by stretch to a long sarcomere length (Konishi et al. 1991; Hollingworth et al. 1996, 2009).

A micro-pipette was filled with furaptra or mag-fluo-4 at a concentration of 10–40 mm in a 100 mm KCl solution and used to pressure-inject the indicator into one fibre within the bundle. Injections usually lasted 1–3 min. Indicator fluorescence was excited with visible radiation from a tungsten–halogen bulb that illuminated a ∼300 μm length of the bundle located near the injection site. The excitation wavelengths were selected by a wide-band interference filter that was positioned between the light source and the preparation. Fluorescence emission wavelengths were selected by a broad-band filter of longer wavelength positioned between the preparation and the photodetector. With furaptra, the excitation and emission wavelengths were 390–430 nm and 470–590 nm, respectively; with mag-fluo-4 they were 450–490 nm and 510–600 nm.

Fibre activity was elicited by 0.5 ms shocks from a pair of extracellular electrodes. The stimulus cathode was usually located 1–2 mm from the site of optical recording; thus the delay for propagation of the action potential to the optical recording site was usually 0.5–1 ms at 16°C (the starting temperature in the experiments). Fibres were studied only if they gave all-or-none changes in fluorescence intensity (ΔF) in response to stimulation. Experiments lasted tens of minutes to several hours after injection.

Indicator concentrations in myoplasm were not measured; however, in previous studies that used identical techniques, concentrations were estimated to be 0.03–0.3 mm (Hollingworth et al. 1996, 2009; Baylor & Hollingworth, 2003)). These values are sufficiently small that ΔµCa²⁺½ is expected to be perturbed in only a minor way by the Ca²⁺-buffering action of the indicator (Konishi et al. 1991; Baylor & Hollingworth, 2007)).

The resting fluorescence of the indicator (F_R) was calculated from the raw measurement of the resting fluorescence of the bundle (F_T) by subtraction of the non-indicator-related component of intensity, which was estimated from a region of the bundle that did not contain indicator. With furaptra, F_R was typically 5- to 10-fold larger than the non-indicator-related component; thus F_R could be accurately determined. This permitted an accurate estimation of furaptra's ΔF/F_R signal and thereby its conversion to ΔµCa²⁺½ (next paragraph). In contrast, with mag-fluo-4, the estimate of F_R was unreliable because the value of the non-indicator-related component of fluorescence was usually substantially larger than F_R. This situation arose because: (i) mag-fluo-4 injected less readily than furaptra, which resulted in concentrations of mag-fluo-4 in myoplasm that were usually smaller than those of furaptra; (ii) the non-indicator-related fluorescence of the bundles was substantially larger at the wavelengths of the mag-fluo-4 measurements than at those of the furaptra measurements; and (iii) the Ca²⁺-free form of mag-fluo-4, the predominant form in myoplasm in the resting state, is much less fluorescent than Ca²⁺-bound mag-fluo-4, whereas Ca²⁺-free furaptra is much more fluorescent than Ca²⁺-bound furaptra. Therefore the primary information available from the fluorescence measurements with mag-fluo-4 was the time course of ΔF. In two experiments, an indirect method was used to estimate the amplitude of the mag-fluo-4 signal in units of ΔF/F_R (see Results).

In the furaptra experiments, ΔµCa²⁺½ was estimated from ΔF/F_R with a two-step procedure, as previously described (Baylor & Hollingworth, 2003)):

1

2

Δf_CaD denotes the fraction of furaptra in the Ca²⁺-bound form and K′_D,Ca denotes the apparent value of K_D,Ca in the myoplasm. K′_D,Ca was assumed to be 96 μm, which is twofold larger than the value expected for furaptra in a simple salt solution at the approximate intracellular concentration of free Mg²⁺ (∼1 mm). Increases in the apparent values of both K_D,Ca and K_D,Mg are expected in the myoplasmic environment due to the binding of indicator to intracellular constituents, including soluble and structural proteins (reviewed in Baylor & Hollingworth, 2011)). As noted previously (e.g. Baylor & Hollingworth, 2007, 2011)), ΔµCa²⁺½ calculated with eqn (2) is only an approximation of (true) spatially averaged ΔµCa²⁺½. This situation arises because large differences in the amplitude of ΔµCa²⁺½ occur in different regions of the sarcomere, which results in different degrees of saturation of the indicator with Ca²⁺.

Tension recording

Isometric twitch tension during fibre activity was recorded by means of a tension transducer (AE801; Kronex Technologies Corp., Walnut Creek, CA, USA) attached to one tendon end of the bundle. The tension recordings were not calibrated in absolute force units; rather, their primary use was to monitor the time course of the twitch responses from one or several fibres near the surface of the bundle and thereby determine whether the recorded Ca²⁺ transient was from a fibre with a slowly developing and slowly decaying tension response, i.e. a slow-twitch fibre. In some experiments, the stimulus strength that was just sufficient to elicit an all-or-none twitch response from the bundle also elicited an all-or-none ΔF response from the injected fibre; in this case, it was likely that the tension response came from the injected fibre only. More typically, the stimulus strength required to elicit the ΔF response from the injected fibre was slightly larger than that required to elicit a detectable twitch response from the bundle. In this situation, the fluorescence and tension responses were recorded in response to stimuli whose strength was just below and just above that required to elicit the ΔF response. The ‘difference’ tension record, obtained by subtraction of the two tension responses, was used to estimate the twitch response of the injected fibre. Based on the twitch time course of the injected fibres, the principal results described in this article are thought to come only from slow-twitch (type I) fibres.

Statistics

Population measurements are reported as mean ± SEM (standard error of the mean). The statistical significance of a difference between means was evaluated with Student's unpaired two-tailed t test and considered significant if P < 0.05. Some tests at P < 0.01 were also carried out (see Results).

Simulations

The last part of Results describes simulations of Ca²⁺ movements within the sarcomere of slow-twitch fibres stimulated by action potentials (16°C). These simulations utilize a compartment model of the type that was first described by Cannell & Allen (1984) and that was used previously in the analysis of Ca²⁺ movements in mouse fast-twitch fibres (Baylor & Hollingworth, 2007)). The simulations yield estimates of the amount and time course of SR Ca²⁺ release, the binding of Ca²⁺ to the major myoplasmic Ca²⁺ buffers (troponin, ATP, the SR Ca²⁺ pump, and furaptra), the myoplasmic diffusion of free Ca²⁺ and of Ca²⁺ bound to the mobile Ca²⁺ buffers (ATP and furaptra), and the reuptake of Ca²⁺ into the SR by the Ca²⁺ pump. The multi-compartment simulations also yield a more accurate estimate of spatially averaged ΔµCa²⁺½ than that estimated with eqns (1) and (2) (see, e.g. Baylor & Hollingworth, 2007)).

The parameter values that define our slow-twitch model were taken from our fast-twitch model (Tables I–III of Baylor & Hollingworth, 2007)) but some changes were made to take into account several important anatomical, biochemical and physiological differences between slow-twitch and fast-twitch fibres. These changes, which are summarized in Table 1, are:

Table 1.

Changes to the fast-twitch model for the simulations in slow-twitch fibres

A. Spatially averaged concentrations of divalent-ion binding sites (μm)
Ca2+/Mg2+ binding sites:
ATP (one per molecule)	5000	(rather than 8000)
Parvalbumin (two per molecule)	0	(rather than 1500)
Ca2+ pump (two per molecule)	96	(rather than 240)
Troponin non-specific sites (two per molecule)	240	(rather than 0)
Ca2+-specific sites:
Troponin regulatory sites (one per molecule)	120	(rather than 240)

B. Troponin reaction kinetics (16°C)
	kon (108m−1 s−1)	koff (s−1)	KD (μm)
Ca2+ regulatory site:
Initial value	0.3	19.5	0.65
Final value	0.4	26.0	0.65
Non-specific sites:
Ca2+	1.61	0.322	0.002
Mg2+	5.36 × 10−4	1.07	20

The remaining parameter values in the slow-twitch model are identical to those in the fast-twitch model (Tables 1–III of Baylor & Hollingworth, 2007)). At µCa²⁺½_R= 0.05 μm, 7.1% of the troponin regulatory sites are occupied with Ca²⁺ at rest (8.6 μm/120 μm). The corresponding resting occupancies of the troponin non-specific sites are 32.9% with Ca²⁺ (78.9 μm/240 μm) and 65.8% with Mg²⁺ (157.9 μm/240 μm), with 1.3% of sites being metal free.

1. The concentration of ATP was reduced from 8 to 5 mm (Kushmerick et al. 1992)).

2. The concentration of parvalbumin was reduced from 0.75 mm to zero (Heizmann et al. 1982; Leberer & Pette, 1986)).

3. The concentration of SR Ca²⁺ pump molecules was reduced 2.5-fold, from 120 to 48 μm (Ferguson & Franzini-Armstrong, 1988; Leberer et al. 1988)); this corresponds to 96 μm metal-binding sites on the pump (two per molecule). No change was made to the kinetic scheme assumed for the pump molecules because the functional properties of the fast-twitch (‘SERCA1’) isoform of the pump are thought to be similar to those of the slow-twitch (‘SERCA2a’) isoform (Lytton et al. 1992)).

4. The concentration of troponin molecules (120 μm) was not changed but the metal reactions with troponin were changed in two ways based on the following considerations:

   1. Ca²⁺-specific sites (= Ca²⁺-regulatory sites). Each slow-twitch troponin C molecule has a single Ca²⁺ regulatory site (van Eerd & Takahasi, 1976; Potter et al. 1977)) whereas fast-twitch troponin has two. In the fast-twitch model, Ca²⁺ reacts with the two regulatory sites on each molecule with positive cooperativity (Hollingworth et al. 2006)); the steady-state level of free µCa²⁺½ that gives half-occupancy of the sites is 1.3 μm. With slow-twitch troponin, half-occupancy of the regulatory site probably occurs at a smaller free µCa²⁺½ level because the slow-twitch tension–pCa curve is left-shifted with respect to the fast-twitch curve (Kerrick et al. 1976; Stephenson & Williams, 1981)). For example, in rat skinned fibres, the µCa²⁺½ levels for half-activation of tension are ∼0.6 and ∼1.2 μm, respectively (Stephenson & Williams, 1981)). We thus assume in our slow-twitch model that troponin has a single regulatory site with a K_D,Ca of 0.65 μm (= (1.3 μm)/2). The on-rate constant of the site was estimated from the work of Davis et al. (2007), who studied the Ca²⁺-binding properties of ‘slow-skeletal’ troponin (which consisted of human recombinant cardiac/slow-skeletal troponin C + rat recombinant slow-twitch troponin I + human recombinant cardiac troponin T). The mean value of the on-rate constant of the regulatory site under several measurement conditions at 15°C is calculated to be 0.3 × 10⁸m⁻¹ s⁻¹ (Table 1 of Davis et al. 2007, excluding the rigor condition). The off-rate constant for the regulatory site in our model, 19.5 s⁻¹, was calculated from the product of K_D,Ca and the on-rate (0.65 μm× 0.3 × 10⁸m⁻¹ s⁻¹). As described in Results, these rate constants were modified slightly in the final version of the model (see also Table 1)).

   2. Non-specific sites (= Ca²⁺/Mg²⁺ sites). Each troponin C molecule also has two non-specific metal sites, so the total concentration of these sites is 240 μm (= 2 × 120 μm). The non-specific sites were ignored in our fast-twitch model because their kinetic properties are similar to those of the Ca²⁺/Mg²⁺ sites on parvalbumin (e.g. Robertson et al. 1981)) and the concentration of the parvalbumin sites in the fast-twitch model is large, 1.5 mm. Because parvalbumin is absent in slow-twitch fibres, it is relevant to include the troponin Ca²⁺/Mg²⁺ sites in the slow-twitch model. The on- and off-rate constants used for these sites are: 1.61 × 10⁸m⁻¹ s⁻¹ and 0.322 s⁻¹, respectively, for Ca²⁺ (K_D,Ca= 2 × 10⁻⁹m) and 5.36 × 10⁴m⁻¹ s⁻¹ and 1.07 s⁻¹ for Mg²⁺ (K_D,Mg= 2 × 10⁻⁵m). These values follow from those given by Robertson et al. (1981) if a Q₁₀ of 2 is used to convert rates from 25 to 16°C.

Figure 1 shows the compartment geometry of the model, which is identical to that in our fast-twitch model. The SR Ca²⁺ release flux enters the compartment in the outermost row that is one compartment removed from the z-line (downward arrow in Fig. 1)). This location is at the outer edge of the myofibril near the middle of the thin filament, the approximate location of the SR Ca²⁺ release channels in mammalian fibres (Smith, 1966; Eisenberg, 1983; Brown et al. 1998; Gomez et al. 2006)). The resultant increase in free µCa²⁺½ in this compartment drives Ca²⁺ complexation with the Ca²⁺ buffer sites there and also drives the diffusion of Ca²⁺ and the mobile Ca²⁺ buffers across the compartment's boundaries. Analogous changes occur subsequently in the other compartments of this reaction–diffusion model. As in the fast-twitch model, furaptra is included in all compartments at a concentration of 100 μm. As before, the adequacy of the simulation was assessed by a comparison of the simulated (spatially averaged) furaptra Δf_CaD waveform with the measured Δf_CaD waveform.

Figure 1. Compartment geometry of a half-sarcomere of a myofibril in the simulation of Ca²⁺ movements in mouse slow-twitch fibres.

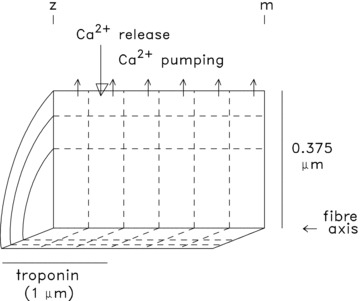
The myoplasmic volume is divided into 18 equal-volume compartments (6 longitudinal × 3 radial) at a half-sarcomere length of 2 μm. The large downward arrow denotes the location at which SR Ca²⁺ enters the myoplasm; the small upward arrows denote the location of Ca²⁺ pumping by the SR Ca²⁺ pump. Troponin is restricted to the 9 compartments located within 1 μm of the z-line (the region containing the thin filaments, average length ∼1 μm). Because the buffer concentrations in Table 1 represent averages over the full myoplasmic volume, the compartment concentration of Ca²⁺ pump molecules in the 6 pumping compartments is 3 times that in Table 1 (288 rather than 96 μm); similarly, the compartment concentration of troponin molecules in the 9 troponin-containing compartments is 240 rather than 120 μm. The vertical and horizontal calibrations are not to scale.

The SR Ca²⁺ release flux used to drive the simulations was calculated with an empirical equation defined by rising and falling exponentials (Baylor & Hollingworth, 2007)):

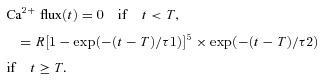3

The time-shift parameter T was set to 1.4 ms to simulate the delay between the external shock that generates the action potential and the onset of Ca²⁺ release. The value of R, which sets the amplitude of the release flux, is expected to be smaller in slow-twitch than fast-twitch fibres (Baylor & Hollingworth, 2003)). As before, R was adjusted until good agreement was observed between the peak amplitude of the simulated and measured furaptra Δf_CaD waveforms. The values of τ1 and τ2 were set to 1.4 and 0.55 ms, respectively (rather than 1.3 and 0.5 ms in the fast-twitch model). This gives a flux waveform whose FDHM is 1.7 ms (rather than 1.6 ms), which is the value estimated in the single-compartment version of the slow-twitch model.

Results

Experimental measurements

As mentioned in the Introduction, some of the properties of ΔµCa²⁺½ in mouse slow-twitch fibres stimulated by an action potential have been measured in three recent studies (Baylor & Hollingworth, 2003; Calderón et al. 2009, 2010), with the results differing in some important ways. These studies utilized fibres of soleus muscles from young adult mice and measured ΔµCa²⁺½ with a low-affinity, rapidly responding Ca²⁺ indicator. The differences in experimental conditions that might contribute to the different results include the choice of Ca²⁺ indicator (furaptra in Baylor & Hollingworth, 2003, vs. mag-fluo-4 in Calderón et al. 2009, 2010), the method by which the indicator was introduced into the fibre (micro-injection vs. AM loading, respectively), the method of fibre preparation (dissected bundles of intact fibres vs. enzyme-dissociated single fibres), and the temperature (16 vs. 22°C). The experiments described in the next four sections of Results were carried out to clarify the possible reason(s) for the difference in the reported properties of ΔµCa²⁺½, with a view to increasing confidence that the measurements of ΔµCa²⁺½ chosen for the simulations presented in the last two sections of Results are the relevant ones for understanding how slow-twitch fibres function in the whole animal.

Furaptra measurements at 16^oC

Figure 2 shows results from an experiment on a mouse soleus bundle at 16°C in which a fibre was injected with furaptra. In panel A, the lower superimposed pair of traces shows the twitch tension responses from the bundle to two different stimuli initiated at zero time, one that produced a small amount of tension but no detectable fluorescence response from furaptra (upper trace labelled ΔF/F_R in panel A) and one whose strength was 4% larger and elicited a larger tension response and an all-or-none fluorescence response (lower ΔF/F_R trace in panel A). In this experiment, the bundle had been sufficiently immobilized by stretch (sarcomere length = 3.6 μm) that neither the sub- nor supra-threshold ΔF/F_R responses appeared to be contaminated by a substantial movement artifact on the time scale shown. (At t > 200 ms, the supra-threshold ΔF/F_R trace crossed the baseline and became positive, indicative of the presence of a movement artifact at this time.) Although the supra-threshold ΔF/F_R response in panel A must have come from the fibre that was injected with furaptra, this fibre was clearly not the fibre in the bundle with the lowest action potential threshold. The additional tension response elicited by the supra-threshold stimulus is attributable to the twitch response from the injected fibre and from any other fibres with a similar threshold.

Figure 2. Ca²⁺ and tension transients elicited by an action potential in a soleus bundle that contained one fibre injected with furaptra.

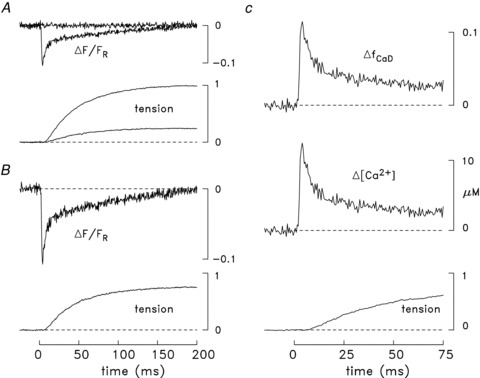
In all panels, zero time denotes the moment the bundle was stimulated by an external shock. A, the traces labelled ΔF/F_R are the fluorescence responses to sub- and supra-threshold stimuli for eliciting an all-or-none ΔF response from the injected fibre. The other pair of traces shows the sub- and supra-threshold tension responses from the bundle. The time of half-rise, time of peak and FDHM of the sub-threshold tension response are 42, 180 and 617 ms, respectively; the corresponding values for the supra-threshold response are 37, 189 and 827 ms. B, difference fluorescence and tension records obtained from the corresponding pairs of traces in A. Because the sub-threshold ΔF/F_R trace was virtually flat, it was heavily smoothed prior to subtraction from the supra-threshold ΔF/F_R trace, thereby avoiding an unnecessary increase in the noise level of the difference ΔF/F_R trace. Peak ΔF/F_R is –0.106. C, the Δf_CaD and ΔµCa²⁺½ traces were calculated from the ΔF/F_R trace in B with eqns (1) and (2); these traces, along with the tension trace from B, are shown displayed on a faster time base. The time of half-rise, time of peak, and FDHM of Δf_CaD are 2.6, 3.5 and 8.8 ms, respectively; the corresponding values for ΔµCa²⁺½ are 2.6, 3.5 and 7.3 ms. Peak Δf_CaD and peak ΔµCa²⁺½ are 0.113 and 12.2 μm, respectively. In all panels, the tension traces are shown relative to the maximum change elicited by the supra-threshold stimulus in A. The supra-threshold ΔF/F_R signal is an averaged response of 14 single sweeps, measured 11–27 min after injection. Fibre 042911.1; sarcomere spacing, 3.6 μm; 16°C.

Figure 2B shows the ‘difference’ traces related to the records in panel A, which were obtained by subtraction of the sub-threshold responses from the corresponding supra-threshold responses. The difference tension record was used as the estimate of the twitch time course of the fibre injected with furaptra. The time of half-rise, time of peak, and FDHM of this trace are 37, 194 and 974 ms, respectively. These values are close to the corresponding values observed for both the sub- and supra-threshold tension responses (see legend of Fig. 2)). This similarity suggests that all fibres that contributed to the tension responses in Fig. 2 were of the same type (e.g. slow-twitch). The temporal parameters of the difference tension record are also similar to the average values of these parameters measured in (i) a total of six similar experiments with furaptra at 16°C (row 3 of Table 2A, which includes the fibre of Fig. 2 plus the 5 fibres in Table 1 of Baylor & Hollingworth, 2003)) and (ii) eight similar experiments carried out with mag-fluo-4 (row 2 of Table 3A, described in detail in the next section). All the fibres that contributed to Tables 2A and 3A appear to be slow-twitch fibres because the temporal parameters of their twitch responses are all two- to fourfold larger than the corresponding values reported previously for mouse fast-twitch fibres at 16°C: 17.1 ± 0.4 ms for time of half-rise, 52 ± 2 ms for time of peak, and 197 ± 12 ms for FDHM (Table 2B; Hollingworth et al. 1996, 2008). The differences between these latter parameter values and those in Table 2A and Table 3A are all statistically highly significant (P < 0.01).

Table 2.

Properties of the furaptra Ca²⁺ signal and twitch tension elicited by an action potential in mouse fibres at 16°C

1	2	3	4	5
	Time of half-rise (ms)	Time of peak (ms)	FDHM (ms)	Peak amplitude
A. Slow-twitch fibres (n= 6)
Furaptra ΔfCaD	3.2 ± 0.2	4.5 ± 0.2	8.4 ± 0.5	0.092 ± 0.008
Furaptra ΔµCa2+½	3.3 ± 0.2	4.6 ± 0.2	7.6 ± 0.5	9.8 ± 0.9 μm
Twitch tension	37.8 ± 2.2	166 ± 12	766 ± 121	—
B. Fast-twitch fibres (n= 18)
Furaptra ΔfCaD	3.1 ± 0.1	4.4 ± 0.1	5.6 ± 0.3**	0.160 ± 0.004**
Furaptra ΔµCa2+½	3.2 ± 0.1	4.4 ± 0.1	4.9 ± 0.2**	18.4 ± 0.6 μm**
Twitch tension	17.1 ± 0.4**	52 ± 2**	197 ± 12**	—

The values in columns 2–5 are means ± SEMs measured from bundles of intact fibres in which one fibre was micro-injected with furaptra; the experiments in A and B were from 6 soleus bundles and 18 EDL bundles, respectively. The times of half-rise and peak are relative to the time of the external stimulus that generated an action potential. The furaptra Δf_CaD and ΔµCa²⁺½ waveforms were calculated from the furaptra ΔF/F_R signal with eqns (1) and (2). Fibre diameters and sarcomere lengths were 37 ± 3 μm (mean ± SEM) and 3.6 ± 0.1 μm, respectively, in A, and 41 ± 2 μm and 3.7 ± 0.1 μm in B. In B, twitch tension was not recorded in 2 of the 18 fibres and sarcomere length was not recorded in one fibre. An asterisk in B denotes that the value is significantly different from the corresponding value in A and in Table 3A (P < 0.05, single asterisk; P < 0.01, double asterisk).

Table 3.

Properties of the mag-fluo-4ΔF signal and twitch tension elicited by an action potential in mouse slow-twitch fibres at 16 and 22°C

1	2	3	4
	Time of half-rise (ms)	Time of peak (ms)	FDHM (ms)
A. 16°C (n= 8)
ΔF	3.5 ± 0.3	4.8 ± 0.4	8.3 ± 0.3
Twitch tension	37 ± 2	178 ± 13	900 ± 108
B. 22°C (n= 6)
ΔF	2.3 ± 0.1**	3.0 ± 0.1*	5.1 ± 0.3**
Twitch tension	27 ± 5*	119 ± 23*	457 ± 91*

The values in columns 2–4 are means ± SEMs from soleus bundles in which an intact fibre was micro-injected with mag-fluo-4. All experiments began at 16°C (n= 8); in 6 of these, measurements were also made at 22°C; in 3 of the latter experiments, measurements were made after return to 16°C. No significant differences in values were observed between the first and second measurements at 16°C, and these values were averaged for inclusion in part A. None of the values at 16°C is significantly different from the corresponding value in part A of Table 2 (P > 0.05). Fibre diameters and sarcomere lengths were 32 ± 2 μm (mean ± SEM; n= 5) and 3.7 ± 0.1 μm (n= 7), respectively; fibre diameter and sarcomere length were not recorded in 3 and 1 fibre, respectively. An asterisk in B denotes that the value is significantly different from the corresponding value in A (P < 0.05, single asterisk; P < 0.01, double asterisk).

Panel C of Fig. 2 shows the tension record of panel B displayed on a faster time base; also shown are the Δf_CaD and ΔµCa²⁺½ waveforms calculated from the ΔF/F_R record of panel B with eqns (1) and (2). Because eqn (1) involves a linear scaling of ΔF/F_R, the time course of the Δf_CaD waveform is identical to that of ΔF/F_R; in contrast, eqn (2) is non-linear and the time course of ΔµCa²⁺½ differs slightly from that of ΔF/F_R (see legend of Fig. 2)). The temporal parameters of these Ca²⁺-related traces are also consistent with those expected for a slow-twitch fibre (Baylor & Hollingworth, 2003; see also Fig. 5A described below); for example, the FDHM of Δf_CaD and ΔµCa²⁺½ are larger than expected for a fast-twitch fibre (Table 2B, which summarizes data from Hollingworth et al. 1996, 2008). Thus, the time courses of both the tension and ΔF/F_R records in the experiment of Fig. 2 indicate that the injected fibre in this experiment was a slow-twitch fibre.

Figure 5. Properties of the myoplasmic Ca²⁺ transient and twitch tension elicited by an action potential in mouse soleus and EDL fibres at 16°C.

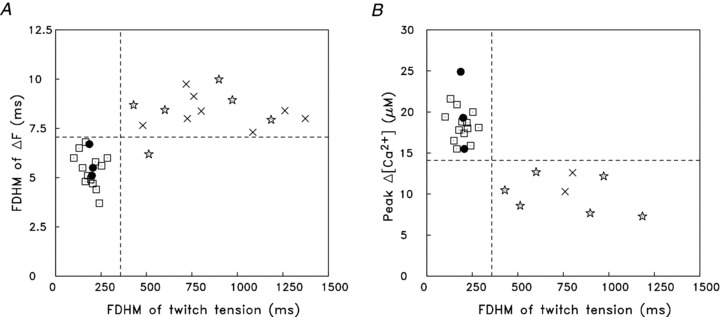
A, the FDHM of ΔF is plotted against the FDHM of twitch tension for 16 fibres from EDL muscles (open squares and filled circles) and 14 fibres from soleus muscles (stars and crosses). ΔF was measured with furaptra in all EDL fibres and in 6 of the soleus fibres (stars); ΔF in the remaining soleus fibres was measured with mag-fluo-4 (crosses). All data are from Balb-C (white) mice except for 3 of the EDL experiments, which are from BL/10 (black) mice (indicated by filled circles) (cf. Hollingworth et al. 2008)). B, plot similar to A except that the ordinate is peak ΔµCa²⁺½ calculated from the peak of furaptra's ΔF/F_R with eqns (1) and (2). Peak ΔµCa²⁺½ in the two mag-fluo-4 experiments (crosses) was calibrated indirectly under the assumption that, if the fluorescence measurement had been made with furaptra, peak ΔF/F_R would have been (minus) one-thirteenth of that measured with mag-fluo-4 (see text). Based on the FDHM of twitch tension, all EDL fibres appear to be fast-twitch fibres and all soleus fibres appear to be slow-twitch fibres (cf. dashed vertical line in each panel, the position of which clearly separates the fibres into two functional groups that match their muscle of origin). The values on the ordinates are also strongly correlated with the fibre types, as the positions of the horizontal dashed lines do almost as well at distinguishing the fibres according to their muscle of origin. (Note: tension was not recorded in two EDL experiments in Hollingworth et al. (1996, 2008), thus the indicator-related data from these experiments could not be included in the plots.)

Table 2A gives the average values of the time of half-rise, time of peak, FDHM, and peak amplitude of the Δf_CaD and ΔµCa²⁺½ traces in the six soleus experiments with furaptra. As expected, the FDHM of ΔµCa²⁺½ is slightly briefer than that of Δf_CaD because of the non-linearity in eqn (2).

In Table 2A, the FDHM of the furaptra fluorescence signal, 8.4 ± 0.5 ms, is substantially smaller than the values of FDHM reported at 22 ± 1°C in two studies of slow-twitch fibres that had been isolated from soleus muscle by enzyme dissociation and AM-loaded with mag-fluo-4 to measure ΔF: 12.4 ± 0.8 ms (Calderón et al. 2009)) and 17.2 ± 1.7 ms (Calderón et al. 2010)). An even greater relative difference would be expected between the FDHM values in intact and enzyme-dissociated fibres if the measurements had been made at the same temperature (Baylor & Hollingworth, 2003; see also below).

Mag-fluo-4 measurements at 16^oC

To investigate the possibility that the difference in time course of the Ca²⁺-related fluorescence signals in intact and enzyme-dissociated fibres noted in the previous section might be related to the use of different Ca²⁺ indicators, experiments similar to that illustrated in Fig. 2 were carried out with mag-fluo-4. Figure 3 shows results from one of these experiments. In this experiment, the initial fluorescence and tension measurements were made, as usual, at 16°C (panel A); this was followed by a similar set of measurements at 22°C (panel B) and a final set of measurements at 16°C (panel C). As noted in Methods, the measurements of F_R with mag-fluo-4 were generally unreliable, therefore the fluorescence records in Fig. 3 are shown displayed in (arbitrary) ΔF units rather than in normalized fluorescence units (ΔF/F_R). For the ΔF trace in Fig. 3A, the time of half-rise, time of peak and FDHM are 3.0, 4.0 and 9.5 ms, respectively; the corresponding values for the difference tension record are 31, 239 and 763 ms. As for the furaptra experiment of Fig. 2, these values indicate that the injected fibre was a slow-twitch fibre and not a fast-twitch fibre. Similar temporal parameters were observed in the second set of measurements at 16°C (panel C; see legend of Fig. 3)). (Note: the smaller amplitude of ΔF in panel C vs. panel A is expected because the concentration of indicator at the measurement site is expected to be smaller in panel C due to the diffusion of indicator along the fibre axis; see measurement times in the legend of Fig. 3.)

Figure 3. Fluorescence and tension transients elicited by an action potential in a soleus bundle that contained one fibre injected with mag-fluo-4.

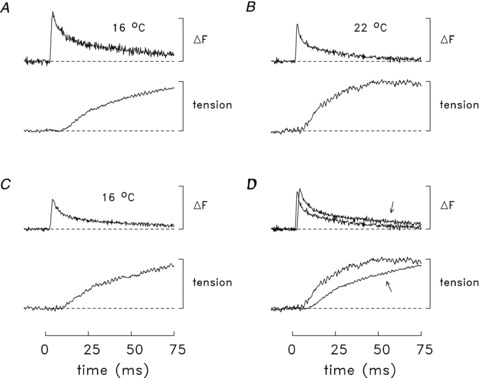
In all panels, the traces are difference fluorescence and tension records of the type shown in Fig. 2B. The sub-threshold ΔF responses (not shown) were not detectably different from baseline. The measurements were made at 16°C (A), then at 22°C (B) and finally at 16°C (C). The times of half-rise, time of peak, and FDHM of the ΔF responses are: 3.0, 4.0 and 9.5 ms (A), 2.2, 3.0 and 4.8 ms (B) and 3.4, 4.5 and 7.3 ms (C). The corresponding values for the tension responses are: 33, 171 and 760 ms (A), 18, 66 and 319 ms (B), and 36, 167 and 841 ms (C). The calibration bar for the ΔF traces is 20 arbitrary fluorescence units. In each panel, the tension traces are shown relative to their maximum value during the twitch. In D, the faster trace in each pair is a redisplay of the corresponding trace in B; the slower trace (arrowed) is the average of the corresponding traces in A and C. In A, B and C, the ΔF traces are averages of 4, 11 and 12 sweeps, respectively; the times of the measurements were 46–54, 58–65 and 68–87 min after injection, respectively. Fibre 063011.1; sarcomere spacing, 3.9 μm; fibre diameter, 28 μm.

Table 3A gives the mean values of the temporal parameters of the difference fluorescence and tension records in the eight experiments with mag-fluo-4 at 16°C. None of these values is significantly different statistically from the corresponding values in Table 2A (ΔF in Table 3Avs. Δf_CaD in Table 2A; tension in Table 3Avs. tension in Table 2A)). The similarity of the ΔF time courses with the two indicators is consistent with previous work on frog single fibres, which found that the time course of the ΔF of mag-fluo-4 during a twitch is the same as that of furaptra (Hollingworth et al. 2009)). Overall, our collective results on mouse soleus and EDL fibres support the conclusion that the fibres whose properties at 16°C are summarized in Tables 2A and 3A were slow-twitch fibres.

Mag-fluo-4 measurements at 22^oC

In 6 of the 8 mag-fluo-4 experiments, fluorescence and tension measurements were also made at 22°C (cf. Fig. 3B)). Table 3B gives the mean values of the temporal parameters of ΔF and twitch tension determined in these measurements. As expected from previous work on mouse fibres at different temperatures (e.g. Hollingworth et al. 1996; Baylor & Hollingworth, 2003)), all temporal parameters in Table 3 are smaller at 22°C than at 16°C. The percentage decreases vary from 30 to 50%, and all differences are statistically significant (P < 0.05). Figure 3D illustrates these differences in the experiment of Fig. 3A–C. The responses at 22°C, which are shown superimposed with the average of the responses at 16°C (arrowed traces), are clearly faster, consistent with their briefer temporal parameters.

The experiments described in this and the preceding section indicate that the differences in the temporal properties between the Ca²⁺-related ΔF signals reported in intact slow-twitch fibres (Baylor & Hollingworth, 2003)) and enzyme-dissociated slow-twitch fibres (Calderón et al. 2009, 2010) are not due to the temperature or the choice of Ca²⁺ indicator used for the measurements.

An indirect method for estimating the amplitude of the mag-fluo-4 ΔF/F_R signal

As noted in Methods, the standard procedure to estimate the indicator-related component, F_R, of the resting fluorescence of the bundle, F_T, was generally unreliable in the mag-fluo-4 experiments because the non-indicator-related component of F_T was usually much larger than F_R. Thus, the mag-fluo-4 fluorescence signals could not be routinely converted to units of ΔF/F_R, as was done in the furaptra experiments. In two mag-fluo-4 experiments (16°C), however, F_T and the ΔF signal from mag-fluo-4 were measured at different distances along the fibre axis, up to 800 μm from the site of indicator injection. In both experiments, F_T and ΔF decreased with distance from the injection site. This observation is consistent with a general feature of micro-injection experiments that, the further the distance from the injection site, the smaller is the indicator concentration and the smaller is the ΔF signal (e.g. Konishi et al. 1991)). Under the assumption that the non-indicator-related component of F_T in these experiments was approximately constant at the various measurement locations, the decrease in F_T would directly reflect the expected decrease in F_R due to the smaller concentration of indicator. Because non-buffering indicator concentrations were used in the experiments, ΔµCa²⁺½ is expected to be the same at all locations so that peak ΔF would be related linearly to F_T, with the slope of the line equal to the amplitude of ΔF/F_R.

In Fig. 4A and B, the symbols show the peak ΔF plotted vs. F_T in the two experiments; also shown is a least-squares line fitted to the data set from each experiment. The slopes of the lines, 1.42 (panel A) and 1.17 (panel B), give the estimated amplitude of ΔF/F_R in these experiments. The mean of these slopes, 1.30 (±0.12, SEM), is –15.1 times the mean amplitude of ΔF/F_R estimated with furaptra in the experiments described in the first section of Results, –0.086 (cf. peak Δf_CaD in Table 2A and its relation to furaptra's ΔF/F_R through eqn (1))). From this information, an estimate of the average peak ΔµCa²⁺½ in these two mag-fluo-4 experiments relative to that in the furaptra experiments can be made based on findings in experiments carried out previously in frog twitch fibres (Hollingworth et al. 2009)). In each of the frog experiments (n= 2), an intact single fibre was injected with both mag-fluo-4 and furaptra and the ΔF/F_R signals from the indicators were measured simultaneously from the same or nearby regions of the fibre; thus, in each experiment, these signals responded to the same underlying ΔµCa²⁺½. The ratio of the amplitude of the ΔF/F_R signal from mag-fluo-4 divided by that from furaptra averaged –13.0 (±2.5, SEM). The similarity of the mean values –13.0 and –15.1 suggests that the average peak ΔµCa²⁺½ in the mouse experiments with furaptra (Table 2A)) was similar to, although perhaps a little smaller than, that in the two experiments with mag-fluo-4 in Fig. 4. This similarity is expected because the experiments of Fig. 4 were slow-twitch fibres as judged from the temporal parameters of their ΔF and twitch responses (Tables 2A and 3; see also Fig. 5B, described below).

Figure 4. Indirect estimation of ΔF/F_R during a twitch in two experiments with mag-fluo-4.

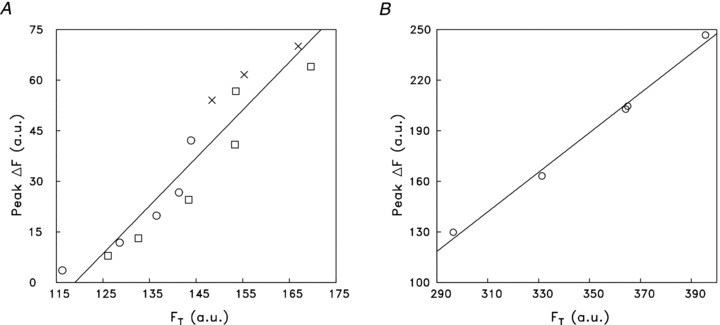
In each panel, the symbols show results from a slow-twitch fibre at 16°C in which a series of measurements of F_T (total resting fluorescence of the bundle, which includes indicator-related and non-indicator fluorescence) and ΔF were made at different distances from the site of mag-fluo-4 injection (–600 to +600 μm in A, 8–20 min after injection; 500–800 μm in B, 85–94 min after injection). Fluorescence intensities are given in arbitrary units (a.u.). Crosses denote measurements at the injection site; circles and squares denote measurements on opposite sides of the injection site. In each panel, the line is the least-squares fit of the data with the function: ΔF=aF_T+b. The fitted values of a and b are 1.42 and –169 in A and 1.17 and –222 in B. a gives the estimate of ΔF/F_R in the experiment (see text), whereas –b/a estimates the non-indicator-related fluorescence (119 in A; 189 in B), which is assumed to remain the same as measurement location is changed. Fibres 063011.1 (A) and 062811.2 (B).

The mean amplitude of the mag-fluo-4 ΔF/F_R signal estimated in the two intact slow-twitch fibres at 16°C, 1.30 ± 0.12, is approximately twice that reported for mag-fluo-4 in enzyme-dissociated slow-twitch fibres at 22°C, 0.59 ± 0.04 (n= 23; Table 2 of Calderón et al. 2010)), a difference that appears to be statistically highly significant based on the respective SEM values. It is likely that this difference is due in part to the method with which mag-fluo-4 was introduced into the fibres: micro-injection in intact fibres vs. AM-loading in enzyme-dissociated fibres (see Discussion).

Comparison of properties of ΔµCa²⁺½ and tension during a twitch in mouse slow-twitch and fast-twitch fibres

Figure 5 summarizes some differences between the myoplasmic Ca²⁺ signals and tension transients elicited by an action potential in intact slow-twitch (soleus) and fast-twitch (EDL) fibres at 16°C. Experiments with both furaptra and mag-fluo-4 are included in these comparisons. In Fig. 5A, the FDHM of ΔF is plotted vs. the FDHM of twitch tension; in Fig. 5B, peak ΔµCa²⁺½ is plotted vs. the FDHM of twitch tension. In both panels, the slow-twitch results with furaptra are shown as stars and those with mag-fluo-4 as crosses. All fast-twitch experiments (the results of which were reported previously; Hollingworth et al. 1996, 2008) were carried out with furaptra (squares and filled circles; see legend for symbol differences).

Figure 5 reveals that slow-twitch and fast-twitch fibres are well differentiated by the parameters selected for these plots (cf. dashed horizontal and vertical lines). The clearest distinction is observed in Fig. 5B, where all slow-twitch fibres had a FDHM of twitch tension that was greater than 360 ms and a peak ΔµCa²⁺½ that was less than 14 μm, and vice versa for fast-twitch fibres. Figure 5A shows that the fibre types are also well differentiated by the FDHM of ΔF, where slow-twitch fibres (with one exception) have a FDHM greater than 7 ms and fast-twitch fibres a FDHM less than 7 ms. Within each of the two major data clusters in Fig. 5A and B, there is no obvious indication of sub-groupings; if present, this might have been indicative of fibre sub-types (e.g. fast-twitch fibres of sub-type IIa vs. IIx/IIb; Bottinelli et al. 1991; Berchtold et al. 2000; see also Close, 1967)).

Figure 6 shows two summary comparisons of the time course of the ΔF and tension responses elicited by an action potential in intact mouse fibres at 16°C. The comparisons have several common features: (i) in each panel the ΔF and tension traces are displayed with their amplitudes normalized to a common peak value in order to facilitate the comparison of their time courses; (ii) results from several similar experiments were averaged to improve the signal-to-noise ratio of the traces; and (iii) the experiments selected for each comparison had ΔF records that appeared to have little or no contamination with movement artifacts on the time scale shown.

Figure 6. Comparison of normalized ΔF and tension time courses elicited by an action potential at 16°C.

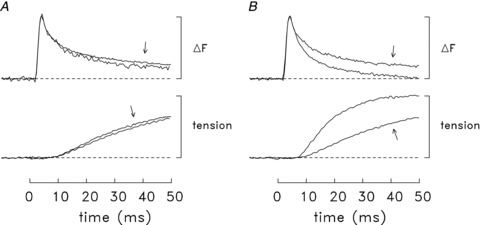
In all panels, the traces are averaged results from a number of similar experiments; fibres were included only if ΔF appeared to be unaffected or little affected by movement artifacts on the time scale shown. Traces of similar type are displayed normalized to the same peak amplitude. Prior to inclusion in the averages, the traces for any particular experiment were temporally shifted by up to 1 ms so as to bring the rising phase of its ΔF signal into alignment with that of the other ΔF traces; this shift allows for slight fibre differences in action potential timing. A, slow-twitch experiments with furaptra (n= 5) vs. those with mag-fluo-4 (arrows; n= 6). B, fast-twitch (EDL) fibres (n= 7) vs. slow-twitch (soleus) fibres (arrows; n= 11). The fast-twitch experiments utilized furaptra only; the slow-twitch experiments utilized furaptra (n= 5) and mag-fluo-4 (n= 6). Note that the average amplitude of ΔµCa²⁺½ itself is approximately twofold larger in fast-twitch fibres than in slow-twitch fibres (cf. Fig. 5B and column 5 of Table 2)).

Figure 6A concerns slow-twitch fibres only and compares results of experiments with furaptra and mag-fluo-4 (n= 5 and 6, respectively; the arrows point to the traces from the mag-fluo-4 experiments). As expected from the mean values in Tables 2 and 3 (16°C), the ΔF traces with furaptra and mag-fluo-4 have very similar time courses, as do the tension traces. The most likely explanation of the slight difference in the time course of the ΔF traces at time t > 10 ms is that, in spite of the selection criteria, the ΔF traces may still have been influenced by a small movement artifact and this influence may have differed slightly in the experiments with the two indicators. (Note that the tension response begins at t≍ 10 ms and that the ΔF signal from furaptra is a negative change whereas that from mag-fluo-4 is a positive change.)

Figure 6B shows a comparison of results in fast-twitch fibres (n= 7) and slow-twitch fibres (n= 11; traces with arrows). This comparison is similar to that shown in Fig. 3B of Baylor & Hollingworth (2003) except that (i) the upper records compare the time courses of ΔF rather than ΔµCa²⁺½, and (ii) it includes results from a larger number of slow-twitch fibres (11 vs. 4). As expected, twitch tension rises substantially more slowly in slow-twitch fibres than in fast-twitch fibres. In contrast, the normalized ΔF traces have essentially identical time courses through time of peak and the first ∼25% of the falling phases; at later times, ΔF decays more slowly in slow-twitch fibres. This observation in intact fibres about the similarity of the ΔF time courses through time of peak contrasts with the finding in enzyme-dissociated fibres that ΔF rises to peak substantially more slowly in slow-twitch fibres than in fast-twitch fibres (22°C; Fig. 3B of Calderón et al. 2010)).

Model simulations

Ca²⁺ movements in slow-twitch fibres stimulated by a single action potential at 16°C

Simulations with the compartment model described in Methods were carried out to estimate SR Ca²⁺ release and myoplasmic Ca²⁺ movements in slow-twitch fibres stimulated by action potentials. Based on the experimental measurements described in the preceding sections and in Baylor & Hollingworth (2003), we believe that the fluorescence measurements that we have made on intact fibres are the ones most relevant to the functioning of fibres in the whole animal and therefore that these results are the ones to use as an endpoint in the simulations. In all simulations, the value of R in eqn (3) was adjusted to give good agreement between the peak values of the simulated and measured furaptra Δf_CaD waveforms. A comparison between the time course of these waveforms was then used to evaluate the overall success of the simulation.

In Fig. 7A, the upper pair of traces shows two Δf_CaD waveforms. The trace with noise is the measured waveform, which was averaged from the slow-twitch experiments that were minimally influenced by movement artifacts; the noise-free trace is the simulated waveform calculated with the model parameters specified in Methods. The lower trace in Fig. 7A shows the SR Ca²⁺ release flux used to drive the simulation. The FDHM of the release waveform is 1.7 ms and its peak amplitude, if averaged over the 18 compartments of the model, is 52 μm ms^-1; the corresponding total amount of released Ca²⁺ is 97 μm. The Δf_CaD traces are in excellent agreement throughout their rising phases and during the first ∼20% of the falling phases (t≤ 6 ms). At later times, the simulated trace decays noticeably faster than the measured trace. Overall, the difference in the time course of the simulated and measured Δf_CaD traces at later times, while not large, is indicative of a deficiency in the model, for example, an error in one or more of the parameter values chosen for the myoplasmic Ca²⁺ buffers. Of these, an error in the kinetics of the troponin Ca²⁺ regulatory site is considered to be the most likely possibility as (i) this site is the dominant intracellular Ca²⁺ buffer on the time scale of Fig. 7, and (ii) uncertainty exists regarding the rate constants for this site under physiological conditions (Davis et al. 2007)).

Figure 7. Measured and simulated spatially averaged waveforms in mouse slow-twitch fibres stimulated by an action potential (16°C).

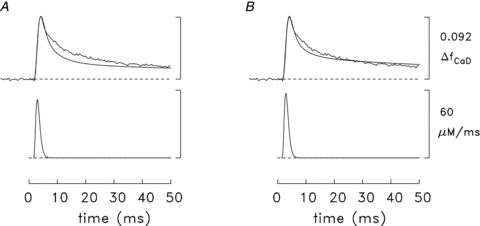
In each part, the upper pair of traces shows the measured Δf_CaD waveform (noisy trace) and a simulated version of Δf_CaD (noise-free trace, calculated with the multi-compartment model); the lower trace shows the SR Ca²⁺ release waveform used to drive the simulation. The noisy Δf_CaD trace is the same as the arrowed Δf_CaD trace in Fig. 6B but with its amplitude scaled to 0.092, the mean value measured with furaptra (column 5 of Table 2A)). In A, the model parameters described in Methods were used; in B, the model utilized slightly higher rate constants for the reaction of Ca²⁺ with the troponin regulatory sites (see text and ‘final values’ of the troponin regulatory-site rate constants in Table 1B)). The amplitude of each flux waveform was adjusted so that the peak of the simulated Δf_CaD waveform was 0.092, the same as the measured value. ΔµCa_T½, the simulated amount of released Ca²⁺, was 97 μm in A and 107 μm in B; the peak of the release flux was 51.9 μm ms^-1 in A and 57.4 μm ms^-1 in B. The calibration bars at the right apply to both panels.

This possibility was examined in additional simulations that considered altered rate constants for the troponin regulatory sites; the on- and off-rate constants were changed in the same proportion so that K_D,Ca would remain unchanged. These simulations indicated that a modest increase in the on- and off-rate constants of the troponin regulatory site reduced the discrepancy between the simulated and measured Δf_CaD waveforms. Figure 7B shows the result if both rate constants are increased by one-third, to 0.4 × 10⁸m⁻¹ s⁻¹ and 26 s⁻¹, respectively (Table 1, ‘final values’). The total amount of released Ca²⁺ in the simulation of Fig. 7B is 107 μm, which is 11% larger than that in Fig. 7A. The improved agreement between the simulated and measured Δf_CaD waveforms in Fig. 7Bvs. Fig. 7A supports the idea that the rate constants for the reaction of Ca²⁺ with the regulatory sites are faster than the initial rates assumed in the model (Table 1)).

It is likely that additional changes to the model could be identified that would further improve the agreement between the simulated and measured Δf_CaD waveforms. These changes were not pursued, however, as (a) the overall agreement in Fig. 7B is considered reasonable, and (b) it is not clear that further minor improvements in the agreement can be taken as evidence supportive of the associated changes.

Figure 8A shows additional details associated with the experiments and the simulation of Fig. 7B. The lowermost trace is the averaged twitch tension response measured in the experiments. The remaining traces are spatially averaged simulated traces, i.e. averaged over the 18 compartments of the model; thus the units of these traces are referred to the full myoplasmic water volume. The lowermost simulated trace is ΔµCa²⁺½, which has a peak and FDHM of 7.6 μm and 4.9 ms, respectively. The next trace shows the change in occupancy of the troponin Ca²⁺ regulatory sites (ΔµCaTrop½); the peak of this trace is 85.8 μm, which, in combination with the resting occupancy of the regulatory sites (8.6 μm), corresponds to a peak site occupancy of 79% (= 72 + 7%). The next two traces show the change in occupancy of the troponin non-specific sites (ΔµCaTNS½) and the transport sites on the SR Ca²⁺ pump (ΔµCaPump½). Ca²⁺ binding to both sites increases relatively slowly and by relatively small amounts on the time scale of the plot, attaining values of 9.3 and 10.1 μm, respectively, at t= 50 ms. Not shown is the concentration of Ca²⁺ returned to the lumen of the SR due to Ca²⁺ pumping (ΔµCaPumped½). ΔµCaPumped½ also increases slowly and by a small amount, attaining a value of 1.1 μm at t= 50 ms. While uncertainty exists regarding the selection of values of the parameters in the model, these simulated traces appear to supply reasonable estimates of the Ca²⁺ movements that take place on a time scale of 50 ms in slow-twitch fibres stimulated by an action potential at 16°C. The relative changes that occur in different regions of the sarcomere (i.e. in the different compartments of the model; not shown) are qualitatively similar to those shown previously for fast-twitch fibres (Baylor & Hollingworth, 2007)).

Figure 8. Additional details related to the simulations and measurements in slow-twitch fibres.

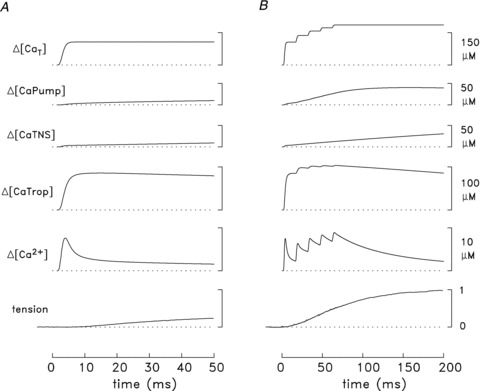
Responses to a single action potential are shown in A and to five action potentials at 67 Hz in B. The labels and calibration bars apply to both parts of the figure. The lowermost trace in each panel is an averaged tension response measured from several fibres (11 in A, 3 in B). The remaining traces are spatially averaged simulated traces obtained with the final values of the rate constants for the troponin regulatory sites (Table 1)), i.e. as in Figs 7B and 9. ΔµCa²⁺½ is the change in free µCa²⁺½; ΔµCaTrop½, ΔµCaTNS½, and ΔµCaPump½ are the changes in Ca²⁺ occupancy of the troponin regulatory sites, the troponin non-specific sites, and the transport sites on the SR Ca²⁺ pump, respectively; and ΔµCa_T½ is the total amount of Ca²⁺ released by the SR. ΔµCa_T½ due to one action potential is 107 μm in A and 106 μm in B; in B,ΔµCa_T½ due to all five action potentials is 186 μm. The value of 1.0 on the tension calibration corresponds to the average peak tension change elicited by the five action potentials. This was 2.8 ± 0.4 times that elicited by a single action potential in these three experiments; accordingly, the tension record in A has been scaled so that its peak value, which occurs at t= 192 ms (not shown), is 0.357 relative units (= 1/2.8).

Ca²⁺ movements in slow-twitch fibres stimulated by a high-frequency train of action potentials

As a further exploration of the model used for the simulation of Figs 7B and 8A, it was of interest to compare the simulated and measured Δf_CaD waveforms associated with a high-frequency train of action potentials. Figure 9 shows this comparison for five action potentials at 67 Hz (15 ms between action potentials). In this simulation, the function in eqn (3) was also used to specify the release due to each action potential after the first but, to do so, the time shift parameter T was progressively increased in 15 ms increments. As before, the amplitude of each of the fluxes was adjusted so that the peak of the simulated Δf_CaD waveform due to that action potential matched the corresponding peak of the measured Δf_CaD waveform. Figure 9 reveals that the overall time courses of the simulated and measured Δf_CaD waveforms are also in reasonable agreement for this high-frequency stimulus. This adds support to the conclusion that the slow-twitch model, modified as described in the previous section, provides an approximate description of the underlying Ca²⁺ movements in this fibre type.

Figure 9. Measured and simulated spatially averaged waveforms in mouse slow-twitch fibres stimulated by five action potentials at 67 Hz (16°C).

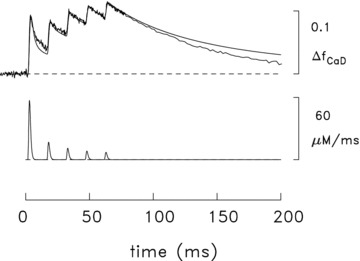
The noise-free traces are simulated traces of the type described in Fig. 7. The simulated amounts of SR Ca²⁺ release with the five action potentials are 106, 31, 21, 15 and 13 μm, respectively. The trace with noise is an averaged ΔF signal measured in three experiments, one with furaptra and two with mag-fluo-4; the amplitude of the waveform has been referred to Δf_CaD measured with furaptra. In the furaptra experiment (fibre 062597.1), the measured ΔF/F_R signal was converted to Δf_CaD with eqn (1). In one of the mag-fluo-4 experiments (fibre 063011.1), the measured fluorescence signal was indirectly calibrated in units of furaptra Δf_CaD as described in connection with Fig. 5B; in the other mag-fluo-4 experiment (fibre 062811.1), the signal amplitude was scaled so that peak Δf_CaD would be 0.091 in response to the first action potential, which is the average value determined for this peak in the other two experiments. The noise level in the measured trace changes at t≍ 78 ms due to a data-compression (averaging) routine in the data-taking program.

In Fig. 9, the amplitude of the release fluxes elicited by the second and subsequent action potentials are much smaller than that elicited by the first. Considered as a percentage of the first release, the values are 29.6, 19.3, 14.5 and 12.5%, respectively. These percentages are similar to those previously estimated in mouse fast-twitch fibres stimulated by five action potentials at 67 Hz: 25.5, 21.6, 18.3 and 15.4% (16°C; Fig. 3 of Baylor & Hollingworth, 2007)). In both fibre types, the large reductions in release in response to subsequent action potentials are thought to be due to the process of Ca²⁺ inactivation of Ca²⁺ release driven by the rise in µCa²⁺½ in response to the prior release(s) (Baylor et al. 1983; Schneider & Simon, 1988; Jong et al. 1995; Baylor & Hollingworth, 2007)).

Figure 8B gives additional information about the measurements and simulation of Fig. 9; the format is identical to that in Fig. 8A. The simulated (spatially averaged) ΔµCa²⁺½ waveform reveals that the peak of ΔµCa²⁺½ achieved with the second action potential is slightly smaller than that due to the first; thereafter the peaks increase modestly with subsequent action potentials, with the fifth peak being 18% larger than the first (8.9 and 7.5 μm, respectively). ΔµCaTrop½ during the train rises somewhat further toward full saturation, achieving a peak occupancy of the regulatory sites of 93% (= 86 + 7%) in response to the fifth action potential. As the regulatory sites become increasingly occupied with Ca²⁺, the ability of these sites to bind Ca²⁺ decreases and, concomitantly, there is a progressive decrease in the rate of decay of ΔµCa²⁺½ from its individual peaks during the train (Fig. 9 and Baylor & Hollingworth, 2003)). Because of the larger and longer lasting ΔµCa²⁺½ during the train, ΔµCaTNS½ and ΔµCaPump½ rise to severalfold higher levels than elicited by a single action potential, achieving values of 31 and 39 μm, respectively, at t= 200 ms. ΔµCaPumped½ (not shown) is 21 μm at t= 200 ms.

Discussion

ΔµCa²⁺½ in mouse slow-twitch fibres

The experiments described in this article support and extend the findings of Baylor & Hollingworth (2003) on the properties of the myoplasmic Ca²⁺ transient in mouse slow-twitch fibres activated by action potentials. The new findings include the observations that the time course of ΔF recorded with mag-fluo-4 in slow-twitch fibres is very similar to that recorded with furaptra (Tables 2A and 3A; Fig. 6A)) and that the temporal parameters of ΔF (and therefore ΔµCa²⁺½) are 35–40% smaller at 22°C than at 16°C (Table 3)). Supportive findings include the following: (i) the (normalized) time course of ΔF (and ΔµCa²⁺½) in slow-twitch fibres is similar to that in fast-twitch fibres through time of peak and early into the falling phase; (ii) at later times, ΔF (and ΔµCa²⁺½) decays substantially more slowly in slow-twitch fibres than in fast-twitch fibres; and (iii) the amplitude of ΔµCa²⁺½ in slow-twitch fibres is about half that in fast-twitch fibres. Regarding point (iii), we believe that the observation in enzyme-dissociated fibres that the amplitude of the mag-fluo-4 ΔF/F_R signal is essentially identical in fast-twitch and slow-twitch fibres (Calderón et al. 2010)) is likely to be an artifactual consequence of the AM-loading method used to introduce the indicator into the cytosol and should not be taken as evidence that the amplitude of ΔµCa²⁺½ is essentially identical in the two fibre types. For example, in frog intact fibres, a study of myoplasmic Ca²⁺ signals with a variety of indicators found that the amplitude of ΔF/F_R with AM-loading averaged about half that with micro-injection of the membrane-impermeant form (Zhao et al. 1997)). The explanation proposed was that not all of the indicator that contributes to F_R in AM-loaded fibres resides in the myoplasmic compartment and is able to respond to ΔµCa²⁺½.

Our new experimental results do not fully account for the substantial differences in the time course of ΔµCa²⁺½ in intact and enzyme-dissociated slow-twitch fibres as inferred from the measurements of ΔF (cf. Introduction). We have ruled out the possibility that these differences are due either to the choice of Ca²⁺ indicator or to the temperature of the measurements. One variable that has not been explored is the difference in the sarcomere lengths of the fibres: 1.7–2.1 μm (mean value, 1.9 μm) in Calderón et al. (2009, 2010) vs. 3.3–3.9 μm (mean value, 3.7 μm) in the current study and in Baylor and Hollingworth (2003). We have not explored this possibility in our studies with intact slow-twitch fibres because we are not able to make accurate measurements of ΔµCa²⁺½ at shorter sarcomere lengths due to the presence of large movement artifacts in ΔF. However, measurements in intact twitch fibres of frog muscle indicate that the FDHM of ΔµCa²⁺½ is smaller, not larger, at shorter sarcomere lengths; for example, FDHM is 6.4 and 9.9 ms at sarcomere lengths of 2.6 and 4.3 μm, respectively (Fig. 9 of Konishi et al. 1991)). Further, simulations of Δf_CaD also indicate that the FDHM of Δf_CaD is expected to be smaller at a shorter sarcomere length; for example, in mouse fast-twitch fibres, the FDHM of simulated Δf_CaD is 4.2 and 5.2 ms at sarcomere lengths of 2.4 and 4.0 μm, respectively (Fig. 12 of Baylor & Hollingworth, 2007)). Thus, in mouse slow-twitch fibres, adjustment for the expected effect of sarcomere length on the time course of ΔF would, if anything, exaggerate the difference between the FDHM of ΔF in intact and enzyme-dissociated fibres.

A second unexplored experimental difference that may influence the results concerns the selection of fibres for experimentation. Our studies on intact fibres have been limited to fibres at or near the surface of the soleus muscle whereas, with the enzyme-dissociation technique, a more random selection of surface and interior fibres probably occurs. At present, it is not possible to evaluate the effect of this difference. Nevertheless, the evidence is strong that the fibres identified as slow-twitch in both the intact and enzyme-dissociated studies are in fact slow-twitch fibres. With enzyme-dissociated fibres, the method relies on a biochemical identification of the myosin heavy chain I isoform via gel electrophoresis, which was determined in individual fibres after completion of the ΔF measurements (Calderón et al. 2010)); with intact fibres, the method relies on a defining functional property of the fibres, namely, that the time course of their twitch tension is much slower than that observed for fast-twitch fibres. We also note that, among the 14 intact fibres that we have identified as slow-twitch, there is no correlation between the values of FDHM of twitch tension and those of FDHM of ΔF (cf. Fig. 5A, data points to the right of the dashed vertical line). In these fibres, the sub-group with the seven largest values of FDHM of twitch tension (mean value, 1082 ± 77 ms) have a mean FDHM of ΔF of 8.4 ± 0.3 ms, which is not different from the mean ΔF of 8.3 ± 0.4 ms observed in the sub-group with the seven smallest values of FDHM of twitch tension (mean value, 604 ± 50 ms). This comparison supports the idea that, among fibres whose twitch tension response is slow, the FDHM of ΔµCa²⁺½ does not depend on the specific twitch duration. Although mouse soleus muscle is thought to contain a substantial proportion of fibres that are not slow-twitch/type I, we have no evidence of having sampled these fibres in our work, perhaps because we routinely work in a similar location on the muscle surface (see also Luff & Atwood, 1972)).

The most likely explanation for the differences between the time course of the ΔF signals in intact and enzyme-dissociated slow-twitch fibres is either an alteration of the properties of these fibres due to the enzyme treatment or some error in the measurement of ΔF associated with the AM-loading technique. In the study of Zhao et al. (1997) on frog twitch fibres, action-potential-evoked ΔF/F_R signals were recorded with a number of Ca²⁺ indicators and compared following either micro-injection or AM-loading. Although, as noted above, the amplitude of ΔF/F_R was generally smaller after AM-loading than after micro-injection, the time course of ΔF/F_R was not markedly different. If these results also apply to mouse fibres, then enzyme dissociation, rather than AM-loading, is a more likely cause of the 2.4- to 3.4-fold larger FDHM of ΔF of mag-fluo-4 measured in the studies of Calderon et al. (2009, 2010) than in the present study. If so, the long (50–60 min) incubation at 37°C used during the enzyme dissociation may be an important factor. In contrast to these results in slow-twitch fibres, in fast-twitch fibres, the FDHM of ΔF in enzyme-dissociated fibres AM-loaded with mag-fluo-4 is thought to be similar to that in intact fibres micro-injected with furaptra: 3.6 and 3.3 ms, respectively, at 22°C (Hollingworth et al. 2009)). Thus slow-twitch fibres appear to be more sensitive than fast-twitch fibres to the prolongation in the time course of ΔF. The larger fractional volume of the mitochondria in slow-twitch fibres might contribute to this sensitivity, perhaps through the generation of reactive oxygen species (Clanton, 2007)).

Overall, the differences noted in this article between both the amplitude and time course of ΔF/F_R in intact and enzyme-dissociated slow-twitch fibres indicate the need for caution when drawing physiological conclusions based on measurements in enzyme-dissociated fibres with AM-loaded indicators.

Simulation of Ca²⁺ movements in mouse slow-twitch fibres

The use of a multi-compartment model of the type employed in this article (Cannell & Allen, 1984; Baylor & Hollingworth, 1998, 2007)) is thought to give a more accurate estimation of ΔµCa²⁺½ and of the intracellular Ca²⁺ movements that take place in twitch fibres than is estimated with a single-compartment calculation and eqns (1) and (2) (e.g. Baylor & Hollingworth, 2003)). Our slow-twitch model is a direct adaptation of our fast-twitch model and takes into account known differences in the biochemical and anatomical properties of the two fibre types (Table 1)). While the simulations of the experimental furaptra Δf_CaD signal with our slow-twitch model does not appear to be quite as satisfactory as that with our fast-twitch model (Baylor & Hollingworth, 2007)), the overall agreement is nevertheless good (Figs 7B and 9)). Two important parameters in the model that have a strong effect on the results on the fast time scale of the simulations are the on- and off-rate constants of the Ca²⁺ regulatory site on troponin. These rate constants are not well known under physiological conditions (cf. Davis et al. 2007)) and our simulations indicate that a reasonable working hypothesis is that these constants are approximately 0.4 × 10⁸m⁻¹ s⁻¹ and 26 s⁻¹, respectively, at 16°C (‘final values’ in Table 1)).

Comparison of SR Ca²⁺ release in mouse fast-twitch and slow-twitch fibres

Our simulations in slow-twitch fibres with the (final) model indicate that the SR Ca²⁺ release flux elicited by a single action potential at 16°C has a peak amplitude of ∼57 μm ms^-1 and a FDHM of ∼1.7 ms, with the total amount of released Ca²⁺ being ∼107 μm (Fig. 7B)). The FDHM of release is similar to that estimated previously for mouse fast-twitch fibres, 1.6 ms, but the peak of the flux is only 0.3 times that estimated for fast-twitch fibres, 205 μm ms^-1 (Baylor & Hollingworth, 2007)). The smaller peak flux in slow-twitch fibres is consistent with the observation that the concentration of SR Ca²⁺ release channels (ryanodine receptors) in slow-twitch fibres is ∼0.4 times that in fast-twitch fibres (guinea-pig muscle; Franzini-Armstrong et al. 1988)). In both slow-twitch and fast-twitch fibres, the release amounts elicited during a high-frequency stimulus by action potentials after the first are of much smaller size than that elicited by the first action potential. With a 5-shock 67 Hz stimulus, the second release in slow-twitch fibres is ∼0.30 times the first release whereas the fifth release is ∼0.13 times the first release. These fractions are similar to those estimated for fast-twitch fibres, 0.26 to 0.15 (Baylor & Hollingworth, 2007)).

Possible role of Ca²⁺ uptake by mitochondria

The simulation in Fig. 7B indicates that the amplitude and time course of the furaptra Δf_CaD signal in slow-twitch fibres stimulated by an action potential is approximately explained with the (final) slow-twitch model. In Fig. 7B, the measured Δf_CaD waveform crosses the simulated waveform at t≍ 28 ms and thereafter declines more rapidly than the simulated waveform. This indicates that ΔµCa²⁺½ at this time is declining more rapidly than is predicted by the simulations. A similar but more marked effect in seen in Fig. 9, where, at t > 75 ms, the measured Δf_CaD waveform is declining more rapidly than the simulated waveform. These differences indicate that a Ca²⁺ buffer or uptake system functions on a relatively fast time scale in slow-twitch fibres to speed the decline of ΔµCa²⁺½ somewhat more rapidly than is accounted for by the model. Here we consider the possibility that Ca²⁺ uptake by the mitochondria might be important in this regard.

Mitochondrial Ca²⁺ uptake during activity of mouse fast-twitch fibres was estimated by Baylor & Hollingworth (2007) from biochemical and anatomical measurements (Eisenberg, 1983; Sembrowich et al. 1985; Schwerzmann et al. 1989)); the estimated uptake rate was small and not likely to significantly affect the time course of ΔµCa²⁺½ in fast-twitch fibres. In the case of slow-twitch fibres, this possibility deserves more scrutiny, as physiological experiments on skinned skeletal muscle fibres support the idea that the mitochondria can contribute significantly to the decline of ΔµCa²⁺½ in slow-twitch fibres (Gillis, 1997)). In those experiments, the kinetics of sarcomere shortening and re-extension were monitored in small fibre regions that were activated by a brief (sub-second) exposure to Ca²⁺ delivered locally from a Ca²⁺-filled pipette. The fibres studied included ‘red’ (mitochondrial-rich) fibres from rat soleus and rabbit masseter muscles as well as ‘white’ (mitochondrial-poor) fibres from frog sartorius and pigeon breast muscle. Interestingly, addition of 50 μm ruthenium red, a blocker of mitochondrial Ca²⁺ uptake, but not of the energetic state of the mitochondria nor of the SR Ca²⁺ pump, produced an obvious slowing of the kinetics of sarcomere re-extension in red fibres but not in white fibres. Controls were conducted to rule out effects of ruthenium red on the myofilament regulatory proteins (troponin and tropomyosin). It was concluded that, under normal circumstances, Ca²⁺ uptake by mitochondria contributes significantly to relaxation (re-extension) of red fibres, including rodent soleus fibres, by sequestering Ca²⁺ and speeding the decline of the myoplasmic Ca²⁺ transient (Gillis, 1997; but also see Bruton et al. 2003)).

Information in the literature also permits estimation of the rate of Ca²⁺ uptake by mitochondria in slow-twitch fibres. First, in vitro assays of Ca²⁺ uptake by mitochondria from red muscle of rat and rabbit reveal a maximal uptake rate of 145 nmol Ca²⁺ (mg protein)^-1 min^-1 at 37°C (Sembrowich et al. 1985)). If a Q₁₀ of 2 is assumed for this process, a rate of 34 nmol Ca²⁺ (mg protein)^-1 min^-1 at 16°C is calculated. Second, the protein content of mitochondria (in milligrams of protein per mitochondrial volume) is reported to be 0.38 g cm^-3 (Schwerzmann et al. 1989)). Together, this information predicts a maximal Ca²⁺ uptake rate by mitochondria in red (slow-twitch) fibres at 16°C of 0.214 nmol ms^-1 (cm³ mitochondria)^-1. Third, in mitochondrial-rich skeletal fibres, the mitochondrial volume as a percentage of fibre volume is reported to be between ∼6% (soleus fibres of guinea pig and cat; Eisenberg, 1983; Schwerzmann et al. 1989)) and ∼15% (rabbit masseter fibres, Gillis, 1997; mouse soleus muscle, Chen et al. 2001)). If the 15% value is assumed along with an SR volume of 3% in slow-twitch fibres (Eisenberg, 1983)), the non-mitochondrial, non-SR volume is 82%; of this, ∼80% consists of myoplasmic water (Baylor et al. 1983)). Thus, the proportion of the mitochondrial volume to the myoplasmic water volume is about 15:66, and the maximal mitochondrial Ca²⁺ uptake rate, if referred to the myoplasmic water volume (as in the simulations), is calculated to be 0.049 μm ms^-1. This is a substantial fraction of the rate of 0.11 μm ms^-1 that is required in the simulation of Fig. 9 for the decay of simulated Δf_CaD to match that of the measurement between t= 75 and 200 ms. This calculation, in conjunction with the striking experimental finding of Gillis (1997), indicates that the hypothesis that mitochondrial Ca²⁺ uptake contributes significantly to the decline of ΔµCa²⁺½ in slow-twitch/red fibres merits further investigation.

Glossary

Abbreviations

AM

acetoxy-methyl ester

µCa²⁺½_R

resting myoplasmic free µCa²⁺½

Δ

time-dependent change

EDL

extensor digitorum longus

FDHM

full-duration at half-maximum

F_R

indicator-related resting fluorescence

F_T

total resting fluorescence

SR

sarcoplasmic reticulum

TNS

troponin non-specific sites

Author contributions

Experiments were carried out in the laboratory of S. M. Baylor at the University of Pennsylvania. S.M.B. and S.H. contributed to all aspects of the work. M.M.K. contributed to data collection and analysis. All authors approved the final version of the manuscript.