The zoom lens of attention: Simulating shuffled versus normal text reading using the SWIFT model

Abstract

Assumptions on the allocation of attention during reading are crucial for theoretical models of eye guidance. The zoom lens model of attention postulates that attentional deployment can vary from a sharp focus to a broad window. The model is closely related to the foveal load hypothesis, i.e., the assumption that the perceptual span is modulated by the difficulty of the fixated word. However, these important theoretical concepts for cognitive research have not been tested quantitatively in eye movement models. Here we show that the zoom lens model, implemented in the SWIFT model of saccade generation, captures many important patterns of eye movements. We compared the model's performance to experimental data from normal and shuffled text reading. Our results demonstrate that the zoom lens of attention might be an important concept for eye movement control in reading.

How is attention allocated to the text during reading? This is one of the crucial questions driving experimental as well as theoretical research on eye movement control. Two classes of cognitive models can be distinguished based on the theory of attentional deployment that they incorporate. Serial attention shift models (SAS; e.g., E-Z Reader: Reichle, 2011; Reichle, Pollatsek, Fisher, & Rayner, 1998; Reichle, Rayner, & Pollatsek, 2003; see also Engbert & Kliegl, 2001) assume that an attention spotlight (Eriksen & Hoffman, 1972; LaBerge, 1983; Posner, 1980) focuses on a single word at a time (Inhoff, Pollatsek, Posner, & Rayner, 1989). In SAS models, the attentional spotlight shifts serially from one word to the next to move a reader's eyes through the text (for a recent overview see Reichle, 2011). Processing gradient models (PG; e.g., SWIFT: Engbert, Longtin, & Kliegl, 2002; Engbert, Nuthmann, Richter, & Kliegl, 2005; Glenmore: Reilly & Radach, 2006) propose that attention is allocated to a spatially extended region of the text to support parallel processing of several words at a time. In these models, the attentional gradient continuously drops off towards the visual periphery, where processing of visual stimuli is slowed (cf. Downing & Pinker, 1985; Shulman, Wilson, & Sheehy, 1985).

Both SAS and PG models of attentional deployment in reading can be combined with a prominent concept of selective visual attention formulated in the zoom lens model (Eriksen & St. James, 1986; LaBerge & Brown, 1989; Müller, Bartelt, Donner, Villringer, & Brandt, 2003). According to this model, the focus of visual attention can change in size, between sharply focusing on a narrow area and being widely distributed over a large part of the visual field. In reading, the zoom lens of attention is supported by the foveal load theory (Henderson & Ferreira, 1990), which postulates that the perceptual span (McConkie & Rayner, 1975; Rayner, 1975) is modulated by foveal processing difficulty. A key motivation for the development of a zoom lens model for reading is related to its prediction on effects of word frequency and word length on fixation durations. A modulation of the attentional span in a computational model can potentially decrease or even reverse these effects, since a broad span during a fixation on a high frequency word should slow foveal processing rate. Interestingly, such decreased and reversed effects of word frequency and word length have been found in a shuffled text reading paradigm (Schad, Nuthmann, & Engbert, 2010).

The perceptual span is the region of effective vision during reading and extends 3–4 letters to the left and about 14–15 letters to the right of fixation (McConkie & Rayner, 1975; Rayner, 1998). It has been studied in the moving window paradigm (McConkie & Rayner, 1975), where only the fixated part of the text is visible to the reader, while the remaining text is covered with a mask that moves with the eyes. The foveal load hypothesis postulates that the size of the perceptual span is modulated by foveal load or the processing difficulty of the fixated word (Henderson & Ferreira, 1990). If foveal load is low, then the perceptual span is wide and text processing during one fixation extends over several neighbouring words. In the case of high foveal load, the perceptual span is small and only the fixated word is processed during a fixation. Support for the foveal load hypothesis comes from studies using the boundary paradigm (Rayner, 1975), where effects of target-word preview were observed only when processing the preboundary word was easy, but not when it was difficult (Henderson & Ferreira, 1990; Kennison & Clifton, 1995; Schroyens, Vitu, Brysbaert, & d'Ydewalle, 1999; White, Rayner, & Liversedge, 2005). Foveal load effects can be explained based on zoom lens model of attention (Eriksen & St. James, 1986; LaBerge & Brown, 1989; Schad et al., 2010). Applying the model to reading, the assumption is that foveal processing controls the focus of the zoom lens.

First, we will review the main results from the recent study on shuffled text reading (Schad et al., 2010). In particular, Schad et al. (2010) discussed specific hypotheses about how a zoom lens model could account for differences in eye movement control between reading of shuffled and normal text. Second, we developed an advanced version of the SWIFT model (Engbert et al., 2002, 2005) incorporating a dynamically-modulated processing span (SWIFT 3). Third, the model is applied to experimental data during reading of shuffled and normal text. Finally, we will carry out further explorative simulations of the model to investigate its predictions on experimental data.

SHUFFLED VERSUS NORMAL TEXT READING

Schad et al. (2010) investigated eye movements during reading of normal and of shuffled text. To create shuffled text, words from the German Potsdam Sentence Corpus (PSC; Kliegl, Grabner, Rolfs, & Engbert, 2004; Kliegl, Nuthmann, & Engbert, 2006) were randomly shuffled. For each word list, words were drawn from the PSC without replacement such that different words in a list would normally stem from different original sentences in the PSC. This procedure was designed to reduce all local relations between words to chance level, e.g.,

Affen Vorschlag Armen schmale Giebel Kanzler dem besser.

Monkeys suggestion poor/arms narrow gable chancellor the better.

Jede ihrer Förster im Jahr Hunde meisten Gräfin Bauern.

Each [of her/their] foresters [in the] year dogs most countess countrymen.

To ensure that participants would read the words in the lists, they were occasionally given recognition probes for the words that had been contained in the last list.

Statistical analyses of eye movements revealed several interesting similarities and differences between normal and shuffled text reading. First, Schad et al. (2010) found reliable effects of spatially distributed word processing during reading of both normal and shuffled text. Specifically, word frequency and length of the upcoming word N+1 as well as of the preceding word N–1 affected fixation durations on the fixated word N, replicating successor- (word N+1) and lag- (word N–1) effects from normal text reading (Kliegl, 2007; Kliegl et al., 2006). Different from corpus analyses of normal text reading, in shuffled texts word neighbourhood is randomized. Therefore, effects of distributed word processing in shuffled text are of experimental nature and are not confounded with characteristics of the fixated region (Rayner, Pollatsek, Drieghe, Slattery, & Reichle, 2007; Schad et al., 2010).

Eye movements during shuffled and normal text reading also showed pronounced differences. As mentioned earlier, standard effects of current-word frequency and length were reversed during reading of shuffled text. During normal sentence reading, fixations are longer on long words than on short words (Just & Carpenter, 1980; Rayner, Sereno, & Raney, 1996). Likewise, readers usually look longer at low frequency than at high frequency words (Inhoff & Rayner, 1986; Just & Carpenter, 1980; Rayner & Duffy, 1986). For shuffled text, however, both of these standard effects were absent and even reversed. Surprisingly, fixation durations were longer for short words as compared to long words, and readers looked longer at high frequency words than at low frequency words. These effects are intriguing, as effects of word frequency belong to the most reliable and widely found effects in psycholinguistic and eye movement research (Rayner, 1998, 2009). Schad et al. (2010) did not have a good explanation for reversed effects of word length. Concerning word frequency effects, we discussed the hypothesis that word frequency might be reduced during shuffled text reading, because the signal to move the eyes is less affected by lexical word processing (cf. Rayner & Fischer, 1996). However, lexical influences were reliable as we found expected effects of word frequency, e.g., for the previous word N–1 (lag-frequency effects) and the upcoming word N+1 (successor-frequency effects), which suggested that lexical processing of these words affected eye movements. Moreover, word frequency effects were reversed in some conditions. Alternatively, Schad et al. argued that the new effects in shuffled text reading could be explained parsimoniously by a foveal load or zoom lens model: Based on analyses of statistical models, we derived the hypothesis that the perceptual span is more strongly dynamically modulated by foveal load for readers of shuffled text than for readers of normal text.

SWIFT 3: THE ZOOM LENS OF ATTENTION IN THE SWIFT MODEL

In the SWIFT model (Engbert et al., 2002; Engbert et al., 2005), a set of word-based activations controls saccade target selection, and commands to program saccades are generated by a random process. To adjust the processing time to the difficulty of the fixated word, an inhibitory control process, called foveal inhibition, was implemented (see also Engbert & Kliegl, 2011; Richter, Engbert, & Kliegl, 2006).

A key motivation to develop an activation-based model for the control of eye movements in reading was to derive an integrative framework for all types of saccades (i.e., forward, skipping, refixation saccades, and regressions). In close analogy to the dynamic field theory (Erlhagen & Schöner, 2002), the activation field determines probabilities for target selection at any point in time. This concept guarantees the existence of movement targets independent of the timing of upcoming saccade programs. Such a framework is essential for building models that implement the partial independence of spatial (“where” to move the eyes) and temporal (“when” to move the eyes) decisions on saccadic eye movements, conceptually required from models of the oculomotor physiology (Findlay & Walker, 1999).

For the simulation studies on the zoom lens of attention, we modified the processing span of the model. We assume that a letter-based processing rate is an inverse-parabolic function with two parameters that determine the extension of the processing span to the left and to the right. The processing span extends to – δ_L on the left and to δ_R on the right of the fixation point at the origin. Moreover, we assume that the asymmetry of the processing span is generated by a dynamical adjustment of the extension to the right, i.e.,

where a_k(t) denotes the time-dependent activation of word k at time t; A is the maximum of the activation reflecting the maximum possible word difficulty in the model. For the simulations, it turned out that an inverse-parabolic form of the processing span was necessary to constrain its spatial extent by experimental data during the simulations. Using such a functional form, the letter-based processing rate at an eccentricity ∊ was given by

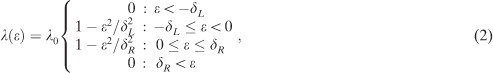where a normalization constant λ₀ = 3/(2(δ_L + δ_R)) is necessary to scale the total processing rate to one (independent of the values of δ_L and δ_R).

For the simulations, we implemented a fully stochastic framework proposed recently by Trukenbrod and Engbert (2011). In this framework, all dynamical variables are realized by independent, parallel discrete random walk processes (Figure 1).

Figure 1.

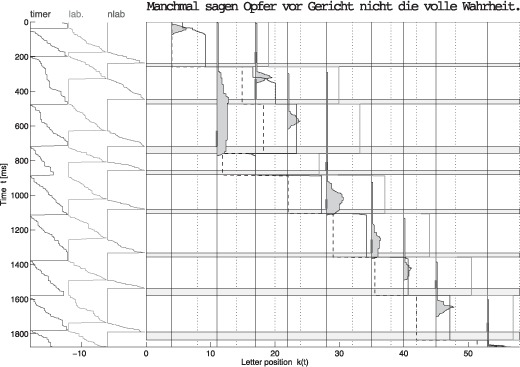
Simulated trajectory of the SWIFT model with attentional zoom lens. To view this figure in colour, please see the online issue of the Journal.

A typical numerical output of a single reading trajectory of the SWIFT model is displayed in Figure 1, by plotting the time evolution of several model states and processes along the vertical axis. In the main panel of Figure 1, vertical lines below each word represent the set of lexical activations {a_n(t)} and the thick dashed vertical line shows the fixation location k(t). The sequence of words fixated in this example is

{1, 3, 3, 2, 4, 5, 6, 7, 9}.

The blue and the green lines indicate the extension of the perceptual span to the right of fixation. The green line marks the extension of the perceptual span for nonlexical preprocessing of words, which has been estimated as extending 15 letters to the right of fixation (McConkie & Rayner, 1975; Rayner, 1998). The blue line represents the rightward extension of the lexical word processing span. During preprocessing of foveal words, that is, in the increasing phase of the lexical word activation, the word processing span is at a fixed minimum. After preprocessing of the foveal word is completed, however, then the lexical processing span is dynamically modulated by the lexical activation of the fixated word (Equation 1). Highly activated foveal words cause the processing span to be narrow in size. If foveal lexical word activation is reduced, however, then the span size dynamically increases up to its estimated maximum size.

The three lines in the left panel of Figure 1 display the states of sequentially coupled, directed random walk processes, which evolve over time. From the left to the right, the first random walk process displays the evolution of the random saccade timer and shows how evidence for a new saccade program accumulates over time. Note that the random oculomotor timer is subject to inhibition from foveal lexical word activations. Foveal activation temporarily inhibits the progression of the random walk and delays the onset of the next saccade program. Second, when the random oculomotor saccade timer reaches its threshold, a labile saccade program is triggered. At the end of the labile saccade program, a saccade target is determined and saccade programming enters into its stabile phase (red bars in the main panel of Figure 1 indicate the selected saccade target and their length represents the duration of the labile programming stage). Finally, a saccade is executed, during which visual input from the retina is suppressed (see Figure 1, the horizontal grey bars).

Additional new parameters were related to (1) a global inhibition (ppf) that slowed processing of words to the right as long as nonvanishing activations were to the left of the word considered (iota), (2) a partial reset of activation during the increasing part of processing during a saccade, and (3) a reduction of the processing rate by a constant factor (f) during postlexical processing, i.e., the decreasing part of the activation.

PREDICTIONS FOR SHUFFLED TEXT READING

Schad et al. (2010) proposed specific hypotheses about how eye movement control differs between shuffled and normal text reading. Here, we will test these qualitative predictions on a fully quantitative basis by estimating parameters of the SWIFT 3 model separately for normal and for shuffled text reading. Schad et al. (2010) hypothesized that the control of eye movements may be less affected by ongoing lexical processing when reading shuffled text. In the SWIFT model, the β parameter determines how strongly lexical processing (i.e., word frequency) influences word activations. We therefore predict that the β parameter should be reduced in the shuffled-SWIFT model as compared to the SWIFT model for normal text reading. Moreover, in the SWIFT model processing of foveal words influences eye movements via foveal inhibition of the autonomous saccade timer and we predict that this influence (captured in model parameter h) is reduced for shuffled-SWIFT. Moreover, we suggested that the perceptual span is more strongly modulated by foveal load during reading of shuffled text as compared to reading of normal text. In the SWIFT 3 model, the δ₁ parameter determines how strongly the processing span is modulated. We predicted that the δ₁ parameter should be larger for shuffled-SWIFT than for normal-SWIFT.

To test hypotheses, we defined a procedure and a set of criteria designed to avoid potential pitfalls associated with model fitting (see Appendix), including a split-half procedure to guard against overfitting, where independent data sets are used to (1) optimize model parameters (on a training set) and to (2) evaluate model predictions (on a test set).

RESULTS FROM PARAMETER ESTIMATION

When fitting the shuffled-SWIFT model to the training set, we defined measures of fixation times and probabilities separately for each subject (see Engbert et al., 2005, for the key principles of our procedure). Experimentally, the text had been randomly shuffled separately for each of the 30 subjects (Schad et al., 2010). For each subject, we thus computed word-based measures of fixation durations and probabilities for 850 words of the subject-specific version of the shuffled corpus (all words except for the first and the last word per list). This procedure represents eye movements at the level of individual fixations and saccades. The model produced averages over 20 model runs of single, first, second, and total fixation durations as well as probabilities for skipping, two fixations, three or more fixations, and the number of regressions for each word and for each subject separately. These simulations demonstrate that it is possible to fit a cognitive model of eye movement control (SWIFT 3) to data at the level of individual eye movements. This is an advantage compared to earlier simulation studies (e.g., Engbert et al., 2005).

Estimated parameter values from the training set for the normal-SWIFT and the shuffled-SWIFT model (see Figure 2 and Table 1) corresponded to our qualitative predictions. The lexical parameter β was smaller for shuffled-SWIFT than for normal-SWIFT. The β parameter approached zero for shuffled-SWIFT, indicating that lexical influences on word activities were strongly reduced for shuffled text readers. In addition, foveal inhibition was reduced for shuffled-SWIFT (smaller h parameter). Taken together, these results are compatible with the view that the influence of cognition on eye movements is reduced in shuffled text reading. Second, the δ₁ parameter was larger for shuffled-SWIFT than for the normal-SWIFT model. This indicates that the dynamical modulation of the processing span was stronger for shuffled than for normal text reading. In its current formulation (see Equation 1), the dynamical modulation of the processing span depends on the size of both, the δ₀ parameter and the δ₁ parameter. To get an estimate of how strongly the span differs between its focused and its defocused state, independent of the overall size of the span, we derived a new parameter δ_1additive. This parameter was calculated from the estimated values for the span-parameters δ₁ and δ₀, via

Figure 2.

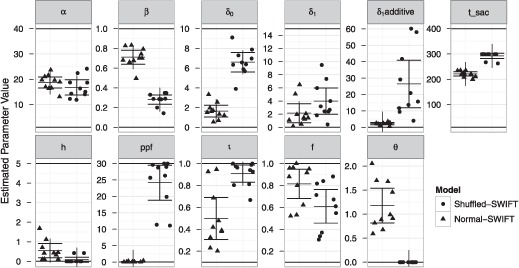
Results from the estimation of model parameters for the normal-SWIFT (triangles) and the shuffled-SWIFT (points) models. A genetic algorithm running for 13,000 generations was used to estimate individual sets of model parameters. This was repeated 10 times with random starting values for normal-SWIFT and for shuffled-SWIFT. Points/triangles show results from individual estimation runs; midlines indicate the average of the parameter estimates across 10 estimation runs; error bars indicate 95% confidence intervals.

TABLE 1.

SWIFT parameters for shuffled and normal text reading

			Shuffled text		Normal text		t-test (Welch)
	Parameter	Symbol	Ma	SEa	Ma	SEa	p-value	Rangeb	Equation
Lexical parameters	Frequency, intercept	α	16.8	1.3	18.7	0.97	.25	1–40
	Frequency, slope	β	0.28	0.02	0.71	0.03	.000	0–1
	Predictability	θ	0	—	1.18	0.16		0–4.6
	Global inhibition	ppf	24.16	2.36	0.069	0.047	.000	0–30
Visual processing	Visual span, constant	δ0	6.61	0.44	1.64	0.26	.000	0–10	1, 4
	Visual span, dynamic	δ1	3.98	0.88	2.15	0.64	.112	0–15	1, 4
	Visual span, dynamic—additivec	δ1additive	26.45	6.40	2.27	0.29	.004		3
	Visual span, preprocessing	pspan	15.0	—	15.0	—	—	—
	Word length exponent	η	0.3	—	0.3	—	—	—
	Preprocessing factor	f	0.609	0.068	0.814	0.059	.04	0.1–1
	Global decay	ω	0.01	—	0.01	—	—	—
	Transfer across saccades	ι	0.91	0.03	0.50	0.08	.001	0.1–1
	Eye–mind lag	pcd	30.0	—	30.0	—	—	—
Saccade timing	Random timing (ms)	tsac	292.5	4.6	221.2	3.8	.000	10–400
	Random timing—starting value	tsac0	0.8	—	0.8	—	—	—
	Inhibition factor	h	0.085	0.056	0.549	0.160	.02	0–5
	Target selection weight	γ	1.0	—	1.0	—	—	—
Saccade programs	Labile stage (ms)	τlab	100.0	—	100.0	—	—	—
	Refixation factor	refix	0.7	—	0.7	—	—	—
	Mislocated fixation factor	misfac	0.75	—	0.75	—	—	—
	Nonlabile stage (ms)	τ0nl	50.0	—	50.0	—	—	—
	Latency modulation	κ0	2.5	—	2.5	—	—	—
	Latency modulation	κ1	0.3	—	0.3	—	—	—
	Saccade execution (ms)	τex	30.0	—	30.0	—	—	—

^aMeans and standard errors over 10 independent runs of the genetic algorithm (for each run using the optimal parameter set from the last 500 generations). Other parameters were fixed for previous model versions or for theoretical reasons, and no standard errors are given for these parameters.

^bParameter boundaries used in fitting.

^cParameter was calculated from fitted values.

Substituting δ_1additive for δ₁ in Equation 1 yields,

The results showed that the zoom-lens response was much stronger in shuffled-SWIFT than in normal-SWIFT, even when controlling for task-differences in the (focused) size of the perceptual span. We also found a larger global inhibition in the shuffled-SWIFT model (larger ppf parameter). This result is highly plausible because words in a list are unrelated, and this should cause strong interference when multiple words are simultaneously processed. This stronger global inhibition may also cause stronger foveal load effects in shuffled text reading (Schad et al., 2010), as foveal processing difficulties inhibit processing of upcoming words.

We also obtained the following parameter differences between the shuffled-SWIFT and the normal-SWIFT model: For shuffled-SWIFT, the processing span was estimated to have an overall larger size, as reflected in a larger δ₀ parameter. Also, the average rate of the autonomous oculomotor timer, t_sac, was estimated to be larger in the shuffled-SWIFT model compared to normal-SWIFT. This effect is clearly related to the slower speed at which shuffled text is read, either due to a mindless eye movement control (Reichle, Reineberg, & Schooler, 2010; Vitu, O'Regan, Inhoff, & Topolski, 1995), because words cannot be predicted from the preceding context, or due to postlexical processing (e.g., memory encoding) of shuffled text. The latter interpretation is also supported by a smaller f parameter in shuffled-SWIFT, indicating that postlexical processing is slowed relative to lexical word processing. Thus, estimates for SWIFT parameters indicated that readers did engage in postlexical word processing when reading shuffled texts. Lastly, the f parameter was increased during shuffled text reading, suggesting that early visual representations were better transferred across saccades. It may be that this higher stability in visual input for shuffled texts results from the stronger global inhibition in this task. If processing of upcoming words succeeds against competing representations from other words, then the resulting representations may be more stable compared to normal reading, where global inhibition is small. Finally, the θ parameter determines influences of word predictability on eye movement control. We set the θ parameter to zero for the shuffled-SWIFT model because words cannot be predicted from their preceding context in shuffled text. The estimated value of θ for the normal-SWIFT model was consistent with estimates based on previous model versions.

SIMULATION RESULTS

To evaluate model performance, we compared model predictions to empirical data from the test set. The summary results are computed from 300 runs of the models. For normal text, we simulated 300 runs of the model for the Potsdam Sentence Corpus. The shuffled text corpus was randomly shuffled for each subject separately, such that each subject read a different corpus of shuffled text. The corpus of each single subject in the test sample was simulated with 20 runs of the model, yielding a total of 300 model simulations for 15 different versions of the shuffled corpus.

First, we investigated predictions of the SWIFT 3 model for normal and for shuffled text with respect to distributions of (1) fixation durations, (2) saccade lengths, and (3) within-word landing positions (effects on the preferred viewing location, PVL), and effects of within-word landing position on (4) refixation probabilities (optimal viewing position effect, OVP), and (5) fixation durations (inverted optimal viewing position effect, IOVP). Details of analyses and results are provided as Supplementary Information (available at http://read.psych.uni-potsdam.de/pmr2/). Overall, predictions of the SWIFT and the shuffled-SWIFT models were successful in reproducing standard effects on eye movements in normal and shuffled text reading, respectively. For distributions of fixation durations, model simulations were in good agreement with experimental results. The shuffled-SWIFT model captured the increase in mean and variance of fixation duration distributions during shuffled text reading. Likewise, distributions of forward- and backward-oriented saccade lengths were well reproduced by the SWIFT 3 model. For shuffled text reading, forward-directed saccades were clearly shortened for the experimental data and this effect was reproduced qualitatively by the shuffled-SWIFT model. The SWIFT 3 model also reproduced landing position distributions (including a leftward-shift in the preferred viewing location, PVL, for shuffled text), and the OVP effect on refixations. Moreover, SWIFT 3 successfully predicted stronger IOVP effects in shuffled text reading for single and first of multiple fixation durations, and these predictions are parameter free and arise from the model architecture.

WORD-BASED MEASURES: EFFECTS OF WORD LENGTH AND WORD FREQUENCY

We focused on summary statistics of how current word length and frequency affect diverse eye movement measures during normal and shuffled text reading (see Figure 3). We were interested to investigate whether simulations of the SWIFT model reproduce reversed effects of word length and frequency on fixation durations during shuffled text reading. Figure 3 demonstrates that the model simulations qualitatively reproduced task differences in measures of fixation durations and probabilities, as well as in effects of word length and frequency.

Figure 3.

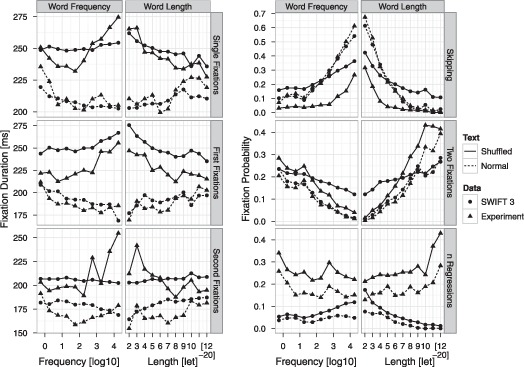
Effects of word length and frequency on different measures of fixation durations and probabilities for model simulations (points) and experimental data (triangles) of shuffled (solid lines) and normal (dashed lines) text reading. Left panel: Mean durations of single, first, and second fixations. Right panel: Mean probabilities for skipping and two fixations, and the mean number of between-word regressions.

Readers of shuffled text exhibit prolonged fixation durations on all measures, including single fixation durations, first of multiple fixation durations, and second fixation durations. The simulations of the model reproduced all of these differences. Moreover, SWIFT captured the influences of word frequency and length on fixation durations during normal text reading. As is usually found in reading studies, fixation durations in normal text were longer on long compared to short words and they were longer on low frequency words compared to high frequency words. These standard results were also present in the model simulations for all fixation duration measures. In experimental data on shuffled text reading, effects of word length and frequency were reversed for all measures of fixation durations. Readers looked longer at high frequency words than at low frequency words, and similarly, readers spent more time fixating short than long words in shuffled text. These effects were reproduced by simulations of the shuffled-SWIFT model: Simulated fixation durations showed reversed effects of word frequency and length for single and first fixation durations, but no effect for second fixation duration.

For measures of fixation probabilities, the model qualitatively reproduced experimental results. Experimentally, word skipping is at a very low rate for long and for low frequency words, but strongly increases for short and/or high frequency words (Brysbaert & Vitu, 1998; Rayner, 1998). This skipping pattern was present for both shuffled and normal text reading, and was also present in the simulation results. Skipping probability was strongly reduced for readers of shuffled text, which was basically driven by a strong reduction in skipping of short and high frequency words. Simulations of the shuffled-SWIFT model captured this task-effect: In the simulated eye movements, word skipping was also considerably reduced. Empirically, readers make more refixations on long and on low frequency words as compared to short and high frequency words, and the SWIFT models for both, normal and shuffled text reading, reproduced these effects. The refixation rate was also overall higher in shuffled text reading, and the shuffled-SWIFT model reproduced this effect. However, the model underestimated the amount of refixations on long and low frequency words, but overestimated refixations on short and high frequency words for shuffled text. Mismatches between model predictions and experimental data in skippings and refixations may have been caused by the large perceptual span in shuffled-SWIFT. The SWIFT model also generated regressive between-word saccades. The model, however, did not adequately capture the overall number of regressions and the effects of word length and frequency, suggesting that postlexical processes that are currently not implemented in the SWIFT model may contribute to regression behaviour. We conclude that the SWIFT 3 model qualitatively reproduced benchmark results on eye movements during first-pass reading of normal and of shuffled text, including reversed length and frequency effects for shuffled text.

DISTRIBUTED PROCESSING EFFECTS

Much research has been carried out under the immediacy assumption that primarily current word processing affects fixation durations during reading (Morrison, 1984; Rayner, 1998). However, several recent studies have found effects of spatially distributed word processing (Inhoff, Eiter, & Radach, 2005; Kennedy & Pynte, 2005; Kliegl, 2007; Kliegl et al., 2006; Kliegl, Risse, & Laubrock, 2007; Risse & Kliegl, 2011) and these effects and their interpretation have been subject to considerable debate (e.g., Pollatsek, Reichle, & Rayner, 2006; Rayner et al., 2007). Corpus analyses of normal text reading have found reliable effects of the upcoming word N+1 (successor effects) and the previous word N–1 (lag effects) on fixation durations on the fixated word N (Kliegl et al., 2006). The validity of these findings has been called into question by Rayner et al. (2007). In corpora of normal text, word neighbourhood is not under experimental control, making it difficult to control for potential confounds associated with neighbouring words. Different from normal text, word neighbourhood is under experimental (random) control in shuffled text. In this more highly controlled context, we have replicated effects of distributed word processing from normal reading (Schad et al., 2010), supporting the distributed processing assumption. Here, we investigate predictions of the SWIFT model for effects of distributed processing during shuffled and during normal text reading (Figure 4). Overall, the qualitative pattern of effects is well replicated by the model.

Figure 4.

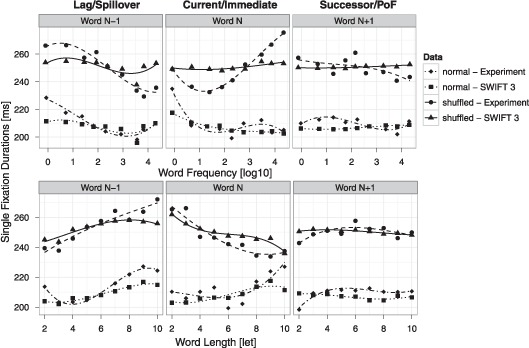
Analysis of distributed processing effects for model simulations of shuffled (triangles & solid lines) and of normal (squares & dotted lines) text and experimental data on shuffled (points & dashed lines) and normal (diamonds & dot-dashed lines) text reading. Top row: Average single fixation durations on word N as a function of word frequency of the previous word (word N–1, left column), the current word (word N, middle column), and the next word (word N+1, right column). Predictions from separate regression analyses involving cubic effects on averaged data for each condition are shown. Bottom row: Corresponding plots as a function of word length.

Lag effects

Empirically, the length of word N–1 exerts a very strong influence on single fixation durations on word N, such that single fixation durations are longer if word N–1 was long. Likewise, frequency of word N–1 strongly affects single fixation durations on word N, with longer fixations after low frequency words N–1. Both of these effects are consistent across tasks and similar for normal and for shuffled text reading. These strong lag effects are also present in data simulated by the SWIFT model for both reading tasks. Several mechanisms are responsible for producing the effects. First, a fixation on a long word N–1 will generate less preview for word N, and, consequently, prolong fixations on word N. Second, the processing span will be smaller on average during previous fixations if word N–1 is a low frequency word compared to the case when it is a high frequency word. This also reduces the amount of preview that is available and prolongs fixation durations on word N. Third, foveal inhibition slows the progress of the random saccade timer. Depending on whether a saccade program is already running, foveal inhibition can either affect the saccade timer for the current, or for the next saccade. If no saccade program is active, then slowing the autonomous saccade timer will prolong the current fixation duration. If a (labile or nonlabile) saccade program has already been started, then foveal inhibition will prolong the duration of the next fixation. Thus, lexical processing from word N–1 can spill over into longer fixation durations on word N.

Successor effects

The SWIFT model contains no explicit mechanism for modulating fixation durations as a function of processing upcoming words N+1. Interestingly, the model nevertheless shows effects of the upcoming word N+1, due to selection effects. Specifically, the likelihood for a refixation depends on lexical activation of the next word N+1. As the lexical activation of word N+1 is a function of the fixation duration on word N and lexical processing of word N+1, the durations of single fixations and of the first of multiple fixations can exhibit selection effects from word N+1 processing. In addition, the intended saccade length could generate small effects of parafoveal processing by influencing saccade programming time. For long words N+1, the intended saccade length may on average be larger, and saccade programming will be faster. This effect can cause longer fixation durations before short words (and before high frequency words, due to the correlation between word length and word frequency).

Current word effects

Interestingly, for shuffled text reading effects of distributed processing are dissociated from immediacy effects. Lag and successor effects are in the same direction as in normal text reading, while current word effects are reversed for shuffled text reading. In Figure 4, this is visible as the effects for words N–1 (Figure 4, left panel) and N+1 (Figure 4, right panel) are highly similar between normal and shuffled text reading. Effects for the current word, to the contrary, strongly differ between shuffled and normal text reading (see Figure 4, central panel).

MODEL PREDICTION: FIXATION DURATIONS BEFORE SKIPPING

In this section, we investigate model predictions for fixation durations before word skipping. In SWIFT 3, we presented a mechanism to explain the pattern of skipping costs and benefits observed in reading studies. It is a theoretically interesting question whether average fixation durations before word skippings are longer (skipping costs) or shorter (skipping benefits) compared to fixation durations before normal forward saccades to the next word N+1 (Drieghe, Brysbaert, Desmet, & De Baecke, 2004; Hogaboam, 1983; Kliegl, 2007; McConkie, Kerr, & Dyre, 1994; Pollatsek, Rayner, & Balota, 1986; Pynte, Kennedy, & Ducrot, 2004; Radach & Heller, 2000; Reichle et al., 1998; Risse & Kliegl, 2011). Kliegl and Engbert (2005) investigated this question and found reliable skipping benefits for short and for high frequency words in a highly controlled statistical analysis. Their results show that skipping costs are typical for long and low frequency words, whereas skipping benefits are reliable for short and high frequent words. Our present analyses for normal text reading are based on a subset of the data used by Kliegl and Engbert (2005) and we here replicate their basic findings (Figure 5).

Figure 5.

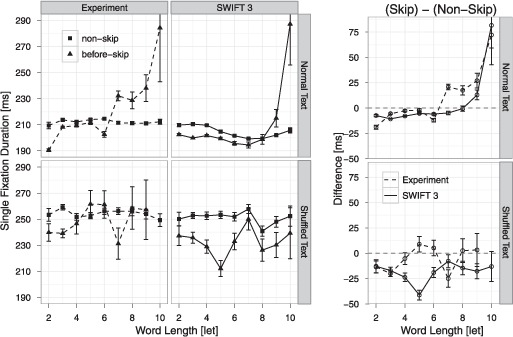
Single fixation durations before skipping (solid triangles) and nonskipping (solid squares) saccades as a function of word length of the skipped word for observed (left panel, dashed lines) and simulated (central panel solid lines) data during normal (upper panel) and shuffled (lower panel) text reading. The right panel displays the skipping difference in single fixation durations [SFD before skipping – SFD before nonskipping] for experimental (dashed lines) and simulated (solid lines) data, where positive difference values indicate skipping costs, and negative difference values indicate skipping benefits. Error bars are cell-based SEM.

Mathematical models of eye movement control have predicted skipping costs (e.g., E-Z Reader: Reichle et al., 1998), and this was also the case for previous versions of the SWIFT model (SWIFT 2: Engbert et al., 2005). Figure 5 shows that the SWIFT 3 model successfully produces skipping benefits for short words during normal text reading. Moreover, the model predicts skipping costs for long words, which is well in line with the observed data. For shuffled text, effects of word skipping on fixation durations were less stable due to the smaller amount of available data. To get a reliable estimate of skipping costs and benefits in shuffled text reading, we combined data from both sub-samples of the experimental data (training set and test set) for our analysis. Figure 5 shows that during shuffled text reading, skipping benefits are present for short words as has been observed for normal text reading. However, the effects for long words differed from those during normal text reading. For long words, we did not observe reliable skipping costs for readers of shuffled text.

The SWIFT 3 model also makes predictions about differences in skipping costs and benefits between tasks. For shuffled text reading, Figure 5 shows that the SWIFT 3 model successfully predicts the skipping benefits observed for short words. For long words in shuffled text, moreover, the model correctly predicts the absence of skipping costs. This prediction is quite surprising, given that we had no theoretical reason a priori to expect the effect and given that skipping costs and benefits were not explicitly included in fitting of model parameters. That the model simulations nevertheless predict the effect lends strong support to the mechanisms generating skipping benefits and costs in SWIFT 3. Next, we will investigate these model mechanisms in more detail.

HOW SPECIFIC ARE MODEL PREDICTIONS?

The previous analyses demonstrated that the SWIFT 3 model successfully reproduced key patterns of eye movements in shuffled and normal text reading. Based on the split-half procedure, we now investigate predictions for experimentally observed eye movements in a given test set by computing correlations between predicted and observed data. Predictions are based on (1) the SWIFT 3 model for the respective task, (2) experimental data observed in the other task, and (3) predictions from the SWIFT 3 model for the other task. As a minimal criterion for model validity, predictions based on the SWIFT model for the respective task (a) should be as good or better than predictions based on experimental data from the other task (b) or model predictions for the other task.

First, we used experimental data in normal text reading to predict data observed during shuffled text reading. For all measures of fixation probabilities correlations between predicted and observed values were very high (rs ≤ .85). These high correlations do not uncover clearly task-specific eye movement effects, and we therefore focus our analyses on fixation durations.

Figure 6 and Table 2 show correlations between predicted and observed data. Eye movements during normal text reading were best predicted by simulations of the normal-SWIFT model (Figure 6a, upper panel). Correlations between predicted and observed values were generally positive and high (rs ≥ .60, except for one slightly negative correlation). However, predictions for fixation durations during normal text reading failed when based on the shuffled-SWIFT model (Figure 6A, lower panel) or on experimental data observed during shuffled text reading (Figure 6C). For these cases, correlations between predicted and observed data were low (all rs ≥ .29, one exception: r = .58) or negative (8 out of 12 correlations). Likewise, fixation durations during shuffled text reading were best predicted by simulations of the shuffled-SWIFT model (Figure 6B, lower panel). Correlations between predicted and observed values were very high and positive for single and for the first of multiple fixation durations (rs ≥ .80). Only effects in second fixation durations were not well captured by the shuffled-SWIFT model (rs ≈ –.60). Again, predictions based on the normal-SWIFT model (Figure 6B, upper panel) or on experimental data observed for normal text reading (Figure 6C) were not successful. Correlations with model predictions were all negative, and correlations with experimental data were negative or low (rs ≤ .29).

Figure 6.

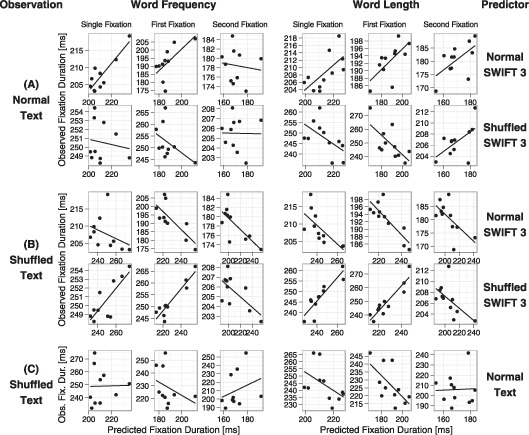
Shown are correlations between predicted and experimentally observed eye movement measures in the test data sets for normal and for shuffled text. Plotted at the ordinates are observed fixation durations from two tasks (indicated in the left-most column): Normal text reading (A), and shuffled text reading (B, C). Plotted at the abscissae are predicted fixation durations, where predictions are based on different sources (which are indicated in the right-most column): Predictions are based on simulations of the normal-SWIFT model [(A)-upper panel and (B)-upper panel], simulations of the shuffled-SWIFT model [(A)-lower panel and (B)-lower panel], and observed data from normal text reading (C). To compute correlations between observed and predicted data, word frequency (left panel) and length (right panel) were split into bins (the same bins used in Figure 3) and correlations were computed over average fixation durations per bin. Analyses were repeated for different measures of fixation durations, including the durations of single fixations (Panels 1+4, counted from left to right), first of multiple fixations (Panels 2+5) and second fixations (Panels 3+6).

TABLE 2.

Correlations between predicted and observed fixation durations in the test data sets for normal and shuffled text

	Single fixation duration		First of multiple fixation duration		Second fixation duration
Split by word	Length	Frequency	Length	Frequency	Length	Frequency
Experimental data (test set)
(a) Prediction by normal-SWIFT
Normal	.67	.87	.68	.65	.60	–.12
Shuffled	–.69	–.36	–.84	–.77	–.63	–.73
(b) Prediction by shuffled-SWIFT
Shuffled	.88	.80	.92	.93	–.59	–.67
Normal	–.56	–.14	–.68	–.48	.58	–.01
(c) Prediction by experimental data (normal text)
Exp. data (shuffled text)	–.50	.02	–.63	–.34	.04	.29

To compute correlations, word length and frequency were split into bins (cf. Figure 3) and correlations were computed over average fixation durations per bin.

We conclude that parameter estimates for both models, the normal-SWIFT model and the shuffled-SWIFT model, captured task-specific effects. Critically, they did not only fit eye movements in the two tasks. Additionally, models highly successfully predicted eye movements in the test sets from the split half-validation procedure.

SIMULATION EXPERIMENTS: HOW DOES THE DYNAMIC PROCESSING SPAN AFFECT EYE MOVEMENTS?

Next, we investigated the consequences of the zoom lens model for eye movements during reading. We had hypothesized that reversed effects of word length and frequency stem from a higher dynamic modulation of the processing span by foveal word activation, i.e., we had predicted that a larger δ₁ parameter reduces or reverses the influence of word frequency on first-pass fixation durations. To test this prediction in the SWIFT 3 model, we manually decreased the dynamic modulation of the processing span: The δ_1additive parameter for shuffled-SWIFT (estimated as 26.45) was set to the value estimated for the normal-SWIFT model (2.27) and 300 model simulations with this reduced modulation of the processing span were performed. We thus disenabled the stronger span-modulation in shuffled-SWIFT.

The results from these model simulations are displayed in Figure 7. As expected, the reversed effects of current-word frequency on single fixation durations were absent in the simulations. Moreover, the reversed effects of current-word length also disappeared, suggesting that a strong zoom-lens response can also explain reversed effects of current-word length. We conclude that the zoom lens model of attention, implemented as a dynamic processing span in the SWIFT model, can explain (1) variations in the effects of current-word frequency and length on fixation durations and (2) dissociations between immediacy effects and effects of distributed processing.

Figure 7.

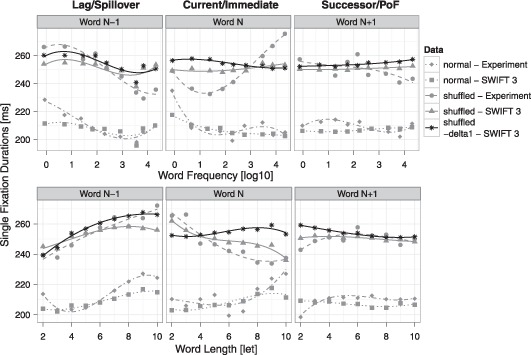
Effects of the dynamical processing span on spatially distributed word processing. Shown are the same results as in Figure 4 (grey), including model simulations of shuffled (triangles & solid lines) and of normal (squares & dotted lines) text and experimental data on shuffled (points & dashed lines) and normal (diamonds & dot-dashed lines) text reading. In addition, simulations of the shuffled-SWIFT model are presented, where the strong dynamic modulation of the processing span was disabled (black stars & solid lines, “shuffled – delta1”). Top row: Average single fixation durations as a function of word frequency of the previous word (word N–1, left column), the current word (word N, middle column), and the next word (word N+1, right column). Predictions from separate regression analyses involving cubic effects on averaged data for each condition are shown. Bottom row: Corresponding plots as a function of word length.

Next, we investigated the consequences of the zoom lens dynamic for skipping costs and benefits. We analysed fixation durations before skipping when the strong dynamic modulation of the processing span was disabled in shuffled-SWIFT. As a result, the model did not show the observed skipping benefits any more. Instead, it produced skipping costs across nearly all word lengths (see Figure 8). This result suggests that the dynamic modulation of the processing span is a key mechanism generating skipping benefits in the SWIFT 3 model.

Figure 8.

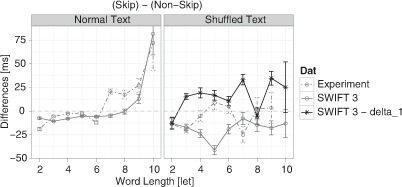
Effects of the dynamic processing span on skipping costs and benefits. Shown are the same results as in the right panel of Figure 5 (grey): Skipping- differences in single fixation durations (SFD before skipping – SFD before nonskipping) as a function of word length of the skipped word for normal (left panel) and shuffled (right panel) text reading for observed (dot-dashed lines & circles) and simulated (solid lines & circles). In addition, simulations of the shuffled-SWIFT model are presented, where the strong dynamic modulation of the processing span was disabled (black lines & stars, “SWIFT 3 – delta_1,” right panel).

A possible mechanistic analysis of the origin of skipping benefits in the zoom lens version of the SWIFT 3 model is beyond the current study and will be published elsewhere.

GENERAL DISCUSSION

In this paper, we developed and analysed a zoom lens version of the SWIFT model for eye movement control based on data from normal and shuffled text reading. We challenged the model with strong experimental eye-movement effects, like reversed effects of word length and frequency (Schad et al., 2010). Both models, the normal-SWIFT and the shuffled-SWIFT variants (differing in parameter values only), were in good agreement with data related to standard effects of eye guidance in reading. The models reproduced distributions of (1) fixation durations, (2) saccade lengths, and (3) within-word landing positions (including effects on the preferred viewing location, PVL; Rayner, 1979), as well as (4) effects of within-word landing positions on refixation probabilities (optimal viewing position effect, OVP; O'Regan & Lévy-Schoen, 1987), and (5) on fixation durations (inverted optimal viewing position effect, IOVP; Vitu, McConkie, Kerr, & O'Regan, 2001; Nuthmann, Engbert, Kliegl, 2005, 2007) (see Supplementary Information, available at http://read.psych.uni-potsdam.de/pmr2/). Critically, in a split half-procedure model predictions were evaluated on a data set that was independent from the one used for parameter fitting to guard against overfitting (see the Appendix for a procedure for model validation).

We found effects of word length and word frequency on fixation durations to be reversed in shuffled text reading, whereas the effects were in the standard direction in normal text reading, and these strong effects were well reproduced by the model simulations. For shuffled text, readers surprisingly looked longer at short words compared to long words, and they also looked longer at high frequency words than at low frequency words (Schad et al., 2010). The model simulations qualitatively reproduced these reversed effects, and a simulation experiment showed that a strong zoom-lens response in shuffled-SWIFT was responsible for the success. This finding supports our previous hypothesis (Schad et al., 2010) that SWIFT, as a parallel graded attention model, equipped with a zoom lens mechanism provides a theoretical framework that can explain reversed effects of word frequency. Moreover, it also uncovers a clear and strong, but previously unnoticed (Schad et al., 2010) influence of attention modulation on effects of word length, a result that may inspire future tests of the dynamic processing span in the SWIFT 3 model.

Effects of spatially distributed processing in the model were in agreement with the observed data. Earlier work by Kliegl et al. (2006) and Schad et al. (2010) reported spatially distributed effects of word frequency and length in experiments on normal and on shuffled text reading. It is important to note that these effects are of experimental nature for shuffled text because word neighbourhood is under experimental (random) control. Distributed processing effects were highly similar between shuffled and normal text reading, and at the same time immediacy effects of word length and frequency qualitatively differed between tasks. The SWIFT 3 model successfully reproduced this empirical dissociation of distributed processing effects from immediacy effects.

The SWIFT 3 model was successful in reproducing experimentally observed fixation probabilities. In shuffled text word skipping was reduced and refixations were increased compared to normal text and the shuffled-SWIFT model reproduced these findings at a qualitative level. Moreover, parameter variations between the normal-SWIFT and the shuffled-SWIFT models reproduced standard effects of word length and frequency on word skipping and refixations.

Model predictions

Kliegl and Engbert (2005) analysed fixation durations before word skipping using an advanced statistical bootstrapping approach and discovered the systematic effect that skipping costs occur for long and for low frequency (target) words, whereas skipping of short and high frequency words produces highly reliable skipping benefits. Our simulations demonstrated that SWIFT 3 is the first model that can explain skipping benefits; in particular, SWIFT 3 predicted experimental skipping benefits for short words and predicted skipping costs for long words in normal text reading. For shuffled text, we also found reliable benefits for skipping of short words. Skipping of long words, however, was not associated with the costs that had been observed in normal text reading. This finding is very interesting because it is novel, because there was no theoretical reason to predict such an effect a priori, and because skipping costs and benefits were not explicitly included in the procedure for parameter fitting. Nevertheless, the SWIFT 3 model reproduced the absence of skipping costs in shuffled text reading.

WHAT DO WE LEARN ABOUT SHUFFLED TEXT READING?

Randomly shuffling words in a corpus of text is a strong manipulation that may affect many different aspects of eye movement control during reading, including attentional, linguistic (lexical, syntactic, semantic), visual, and oculomotor processes. Here, we simultaneously investigated different control processes in a mathematical eye movement model. First, we tested the hypothesis (Schad et al., 2010) that readers’ eye movements are less strongly coupled to ongoing lexical word processing (see also Nuthmann et al., 2007; Rayner & Fischer, 1996; Reichle et al., 2010; Vitu et al., 1995) when reading shuffled text, and this hypothesis was supported by the simulation results. For shuffled-SWIFT, the influence of lexical processing on word activations was reduced, together with a reduced foveal inhibition of the autonomous saccade timer. We conclude that eye movements are less coupled to ongoing lexical processing during shuffled text reading, leading to a more autonomous or “mindless” control of eye movements.

What factors may cause this processing difference between reading tasks? First, readers may scan over the (boring) shuffled word lists in the first pass at a rather superficial level, accepting the risk that some long or low frequency words are not completely processed. This strategy may indeed be efficient for shuffled text, where words need to be encoded for later recognition: Low frequency words have a benefit in recognition memory (Reder et al., 2000), and processing low frequency words at a superficial level may therefore suffice to remember these words for the recognition probes. Alternatively, during reading of normal sentences, contextual (e.g., syntactic, semantic, or purely statistical) constraints ease the processing of individual words. This facilitation is not available in random lists of unrelated words. Therefore, lexical information may become available too late to reliably inform eye movement control.

Second, Schad et al. (2010) suggested that the perceptual span could be more strongly modulated by foveal load in readers of shuffled text as compared to readers of normal text, and our simulation results provided support for this prediction. If adaptive control of eye movements is reduced during reading of shuffled text (i.e., more autonomous control), we considered it surprising to find an increased adaptive control of the attentional focus (i.e., increased zoom-lens response). This result is interesting given that both mechanisms, attentional and behavioural control, share a common function during reading: They both provide means to adapt limited cognitive resources to local processing difficulties. Cognitive-saccadic coupling during normal reading allows for optimal control because reading proceeds fast for easy words, and difficult words are fixated long enough for sufficient processing. Similarly, focusing attention on low frequency words and defocusing attention for easy words also adapts processing to local needs. Based on this analysis, a strong dynamical modulation of the zoom lens during shuffled text reading may compensate for the mindless control of eye movements.

As an alternative, the strong modulation of the processing span in shuffled text may result from the serial nature of the shuffled text reading task. Shuffled text enforces a rather serial processing of words because none of the words can be predicted from the context. Accordingly, word skippings are strongly reduced and even very short and high frequency words are often fixated. When readers of shuffled text fixate on such words, which are processed easily, then it would be an optimal strategy to strongly widen the processing span to maximize preview of parafoveal words. The changed fixation patterns in shuffled text may therefore cause a stronger dynamical modulation of the processing span and a global increase in the size of the perceptual span, both of which were supported by our model simulations.

As a complementary finding, global inhibition was increased in the shuffled-SWIFT compared to the normal-SWIFT model, suggesting that inhibition is larger for unrelated words in a randomly shuffled list. This finding introduces a new and previously overlooked mechanism that may explain and contribute to foveal load effects when reading shuffled or normal text.

Third, despite the reduced cognitive-saccadic coupling in shuffled text reading, lexical and even postlexical processes seem to be intact, as was indicated by overall high word activations and a slowed deactivation of words in shuffled-SWIFT (see Lamme, 2003, for dissociations between awareness and attention). These results may indicate that readers attempt to memorize words for later recognition probes. Additionally, our simulation results suggest that visual and oculomotor processes in shuffled text reading may differ from normal text reading, as transfer of visual information across saccades was enhanced and the speed of the autonomous saccade timer was reduced in shuffled-SWIFT.

We developed a numerical simulation of eye movements during shuffled text reading based on the SWIFT model to capture important cognitive processes of eye guidance in this task. We take a parsimonious approach by using an existing model (SWIFT 3) to explain strong effects in a novel task (shuffled text reading) without adding post hoc assumptions about task-specific processes. An alternative strategy may be to introduce new task-specific assumptions to explain experimental results. For example, low frequency words have a benefit in recognition memory (the mirror effect; Reder et al., 2000) and readers of shuffled text may use this fact to save encoding time on low frequency words. Note, however, (1) that previous research has found mirror effects for retrieval but not for encoding (e.g., Diana & Reder, 2006) and (2) that it may be difficult to reconcile a mirror-effect account with specific aspects of our findings, like the strong standard lag- and successor-effects. It would be interesting to implement and test this and other alternative accounts in the future, of course. To support these investigations, we provide all data, analysis scripts, and the computer code of SWIFT 3 via an online repository (see link later). From an experimental perspective, our simulations make specific predictions that need to be investigated in future experimental work, for example, testing attention allocation using the boundary paradigm (Rayner, 1975) or the moving window paradigm (McConkie & Rayner, 1975).

THE ZOOM LENS MODEL OF SELECTIVE VISUAL ATTENTION

The SWIFT 3 model demonstrates that the zoom lens model of selective visual attention (Eriksen & St. James, 1986; LaBerge & Brown, 1989) can add to the understanding of eye movement control in reading. It combines the concept of the zoom lens with the idea of a processing gradient. The zoom lens in SWIFT 3 has been inspired as an account for the foveal load hypothesis, which states that parafoveal preview depends on the difficulty of the fixated word (Henderson & Ferreira, 1990). As one of our key results, we demonstrated with the development of SWIFT 3 that a zoom lens-type modulation of the processing span by foveal load could reduce and even reverse effects of foveal processing difficulty (Schad et al., 2010). Moreover, we showed that the zoom lens mechanism contributed to a mathematical explanation of systematic variations of skipping benefits and costs (Kliegl & Engbert, 2005).

SUMMARY

In the present research, we studied eye movement control during reading of normal and shuffled text using an advanced version of the SWIFT model (Engbert et al., 2005). Based on statistical analysis of eye movements, we previously (Schad et al., 2010) derived hypotheses on differences in eye guidance between both reading tasks. Here, we quantitatively investigated these hypotheses. Our results demonstrate that the SWIFT 3 model generalizes to explain specific aspects of eye movements during shuffled text reading. They further support our hypothesis that during shuffled text reading, readers reduce adaptive control of eye movements, but increase their adaptive control of attention. Thus, the implementation of a new mechanism, the dynamic modulation of the processing span, in the SWIFT model turned out to be a powerful mechanism to explain effects in experimental data.

APPENDIX: Using parameters of cognitive models for hypothesis testing

In this Appendix, we propose a minimum set of criteria for valid model comparisons. First, fitting models to experimental data always comprises the risk of overfitting error variance instead of capturing valid and reliable effects. This is particularly problematic for high-dimensional models containing many free parameters such as current models of eye movement control during reading. To guard against overfitting, we implement a cross-validation by splitting data into subsets containing half of the data. A training set is used for the estimation of model parameters. Estimated parameters are then used in Monte Carlo simulations to predict eye movements on a distinct and independent evaluation set (or test sample), where model predictions are compared to experimental results.

Second, we suggest that several basic eye movement phenomena should be checked for each estimated parameter set to ensure that model behaviour is reasonable for standard eye-movement effects. We suggest that it is particularly informative to investigate distributions of fixation durations, saccade lengths, and landing positions, as well as basic oculomotor effects like the optimal viewing position (OVP) effect on refixation probabilities and inverted optimal viewing position (IOVP) effects on fixation durations (Vitu et al., 2001). Moreover, effects of word length and frequency on various measures of fixation durations and fixation probabilities provide benchmark results for model evaluation.

Third, experimental results in different reading conditions are often quite similar in many respects. In our present analyses, several effects in eye movements were present in both shuffled and normal text conditions. For example, readers in both conditions exhibited Gaussian landing site distributions, an OVP effect on refixation probabilities, IOVP effects on measures of fixation durations, and effects of word length and frequency on fixation durations and fixation probabilities. Qualitatively replicating experimental effects in each task with numerical model simulations therefore does not guarantee that estimated model parameters capture variance that is specific to both tasks. We here suggest two ways how more specific model predictions can be tested. As a first step, we consider it critical to investigate effects that (1) specifically differ between tasks and (2) are meaningfully related to the estimated model parameters. In the present work, we are interested in specific differences in how word frequency and word length influence fixation durations during normal and shuffled text reading. We have previously proposed hypotheses about what cognitive processes may cause these effects, namely effects of foveal load on the perceptual span.

Fourth, an even closer model test should be performed before task differences in parameter estimates can be relied upon. Such a test provides evidence that parameter estimates for the SWIFT 3 model capture valid task-specific differences in eye movements. As a minimal criterion, we suggest deriving (1) model predictions for data observed in the test sample of a task. These predictions should be better than (2) predictions from the model for the other task and better than (3) predictions derived from the experimental data from the other task. For example, we predict experimental eye movement data in the test sample for shuffled text based on (1) simulations of the shuffled-SWIFT model, (2) simulations of the normal-SWIFT model, and (3) experimental data on normal text reading. When comparing these three predictions, one could postulate that predictions from the shuffled-SWIFT model must be as good or better than predictions from the normal-SWIFT model, and than predictions from experimental data on normal text reading. We will also test this criterion when predicting experimental data from normal text reading.