High-aspect ratio nanochannel formation by single femtosecond laser pulses

Abstract

Single femtosecond pulsed laser damage can be confined radially to regions smaller than the focus spot size due to the highly nonlinear mechanisms for energy absorption and ablation in transparent dielectrics. Along the propagation axis, however, we show that channels can be machined much deeper than the Rayleigh range of the laser focus. Using focused ion beam cross sections and acetate imprints, we analyze these channels and show that spherical aberration is not the primary source for this elongated damage, which is likely caused by microscale filamentation.

Machining using tightly focused femtosecond pulsed lasers is a precise and versatile method for producing micro and nanoscale features, with applications including fabrication of photonic devices, microelectromechanical systems (MEMS), and microfluidic devices [1–6]. Femtosecond laser machining allows very small regions of material removal or damage (~30 nm diameter) with minimal collateral damage in transparent dielectrics [7,8], and pulses can be overlapped to machine a variety of structures, including long, thin channels with aspect ratios as large as 1000 [1,2,9]. It has recently been shown that damage from a single pulse can produce thin channels that extend for several micrometers along the axis of laser propagation, despite a focal region with a significantly smaller Rayleigh length [10,11]. The processes underlying this phenomenon are not well understood, with suggested mechanisms including microscale filamentation, spherical aberration, and ablation by secondarily formed Bremsstrahlung x-rays [10–12]. In this paper we characterize nanochannels formed by single femtosecond laser pulses that extend several microns away from the surface of the sample, far beyond the calculated Rayleigh length of the laser focus. We quantify the scaling behavior and provide evidence that spherical aberration is not required for this phenomenon. We argue that nanochannels are produced by microscale filamentation during optical breakdown.

A Nd:glass laser (Intralase Corp., Irvine, CA) outputting 600 fs pulses at a wavelength of 1053 nm and a repetition rate of 150 Hz was focused into a KTP frequency doubling crystal. The infrared light was filtered out and single 527 nm pulses were selected using a shutter. The beam was brought into the epifluorescence light path of an inverted microscope and focused using the 0.65 NA/40x Achroplan objective lens (Carl Zeiss, Inc., Thornwood, NY) allowing simultaneous imaging and damage. A nanopositioning stage (Mad City Labs Inc., Madison, WI) mounted on the microscope was used to manipulate Corning 0211 glass cover slips (Fisher Scientific, Waltham, MA) used as targets. The objective lens compensates for the spherical aberration caused by passing through the cover slip so that the tightest focus and minimal aberration is achieved at the rear coverglass surface. We refer to the conditions when the laser is focused through the cover slip to the rear surface as back side machining; front side machining refers to when the focus is at the near surface of the cover slip (Fig. 1a ).

Fig. 1.

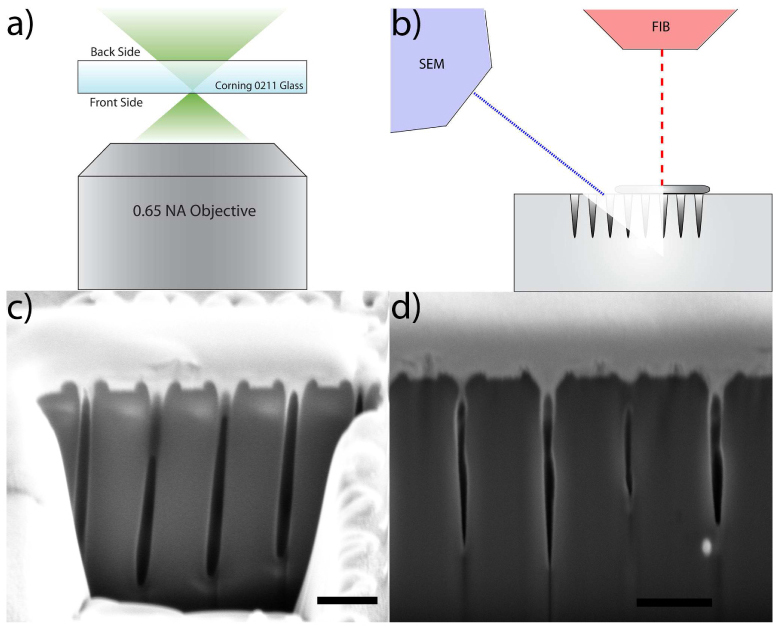
a) An illustration of the machining geometry, with the front and back side of the coverslip indicated. b) A damaged sample examined under a dual beam FIB/SEM. The FIB is placed perpendicular to the sample surface and the SEM is offset at a 52° angle. The sample is covered with a few hundred nanometers of platinum to protect the surface from unintended ion damage. The FIB removes a wedge from the sample, exposing the nanochannel cross section. c) An example cross section for back side machining. d) An example cross section for front side machining. Both images show damage at 67 J/cm². Irregularities along the axial dimension of these channels are presumably the result of variations in FIB milling such that channels are not uniformly bisected. Scale bars indicate 1 μm.

Samples were imaged using a Nova Nanolab DualBeam combined SEM and FIB (FEI Corp., Hillsboro, OR) at the University of Michigan Electron Microbeam Analysis Laboratory. After coating with ~4 nm of gold, the samples were placed in the electron microscope specimen chamber for imaging. The focused ion beam (FIB) was used to obtain cross sections of the laser damage by first coating the surface with a layer of platinum to protect the surface features, followed by FIB removal of the sample material until the full damage cross section was revealed (Fig. 1b).

Nanochannels are exposed in FIB cross sections of laser damage, allowing direct examination (Fig. 1). The channel profiles for both back and front side machining are shown in Fig. 1c and d respectively. In Fig. 1c, the longest channel is 4.06 μm deep and 240 nm wide; the longest channel in Fig. 1d is 3.12 μm by 157 nm. Under the optimal focusing conditions for the objective lens the confocal parameter has a length of 530 nm and a width at the beam waist of 344 nm. Thus these channels exhibit a void that is much longer than the calculated confocal parameter of the laser focus, and considerably smaller across than the diffraction limited beam waist. Additionally, one can observe a tapered profile extending into the material for channels fabricated using the front side technique, while those machined on the back side have a more rounded bottom (e.g. Figure 1c & d). Finally, these images show that channels are free from debris formed during the damage process. A small ring of melted and ejected material surrounds the channels, as previously observed [7,10].

In order to quantify the morphology of a larger number of channels, we performed acetate film surface replication. This process melts a film onto the surface which, when removed, provides an imprint of the sample. The molten acetate flows freely into the nanoscale channels, allowing measurements of channel length across an array of channels. A back side machining acetate replica is shown in Fig. 2 . This image shows replicas of the channels formed as the laser is focused progressively deeper into the bulk of the target. Most of the imprints stand perpendicularly off of the surface, while the deeper channel imprints sometimes topple and lay flat on the surface.

Fig. 2.

Back side machining sample showing single pulse laser damage at 74 J/cm² replicated using an acetate imprint. Pulses are focused 500 nm deeper with each row going from bottom to top in the vertical direction and 50 nm deeper with each pulse from right to left in the image. This image was taken at a sample tilt angle of 45°. The scale bar is 10 μm.

The length of the nanochannels increases as the laser focus moves deeper within the target. As shown in Fig. 3 , the length of the channels increases in direct proportion with the depth of the laser focus: within the error the slope of a regression line is one, demonstrating a close correspondence between the focal depth and the channel length. This correspondence indicates that during channel formation material removal begins at a fixed point along the beam relative to the beam waist, such that the length of the channel is determined by the location of this point relative to the surface. This relation holds until the channels approach a point at which channels are either no longer formed, are resealed by melt, or they may become too thin to allow imprint replication (e.g. see upper imprints in Fig. 2).

Fig. 3.

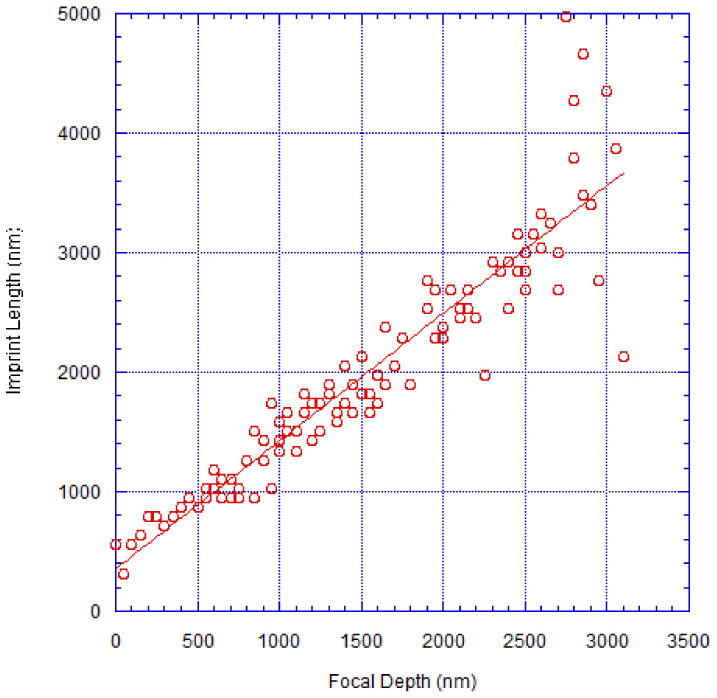
Back side machining sample measurements showing imprint length vs. focal depth, as measured from Fig. 2. The least-squares regression line is plotted on the figure as a solid line. The slope of this line is 1.07 ± 0.04. Because the precise location of the focus is difficult to determine with nanometer precision, the zero depth corresponds to the first observation of damage on the replica.

As shown in Fig. 4 , the relationship between the maximum channel length and the fluence exhibits two behaviors. At pulse fluences below ~80 J/cm², the channel length increases with fluence up to about 8 µm; thereafter the curve plateaus such that further increases in fluence have less effect on the channel length. Across all fluences the channel depth scales with the focal depth, with slopes for the regression lines fit to the data (e.g. Figure 3) close to 1 (1.05 ± 0.04).

Fig. 4.

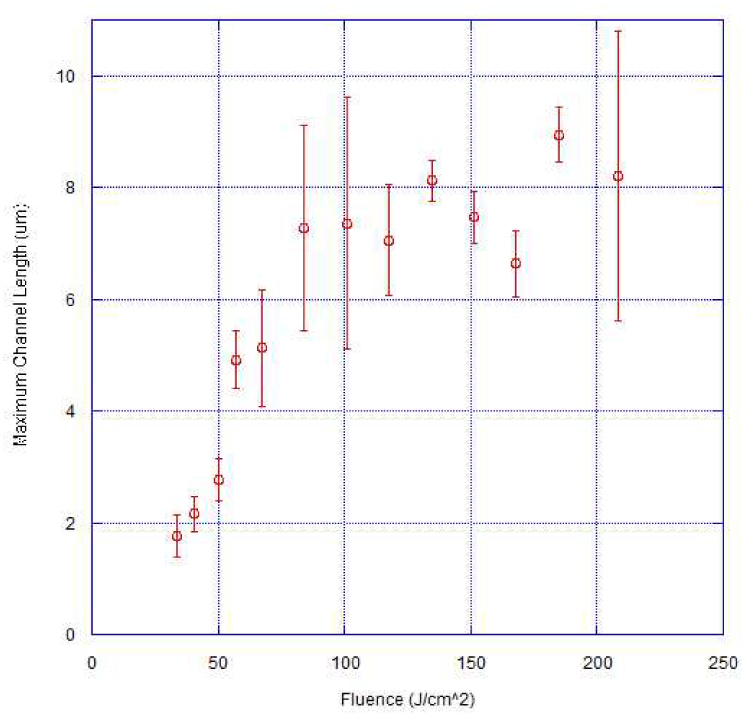
Back side machining sample measurements show that the maximum channel length increases with increasing fluence at low powers, but plateaus at ~8 µm for fluences above ~80 J/cm². The maximum channel length is obtained by taking the average of the four longest channels observed at each fluence.

Analysis of acetate replicas for front side machining similarly demonstrates that the channel length increases as the laser pulses are focused deeper into the glass. The tapering shape and thinner width of the front side channels is quite different than the more cylindrical shape of the channels formed during back side damage (Fig. 1d and 5 ). When the relationship between focal depth and channel length is examined, front side machining exhibits somewhat nonlinear scaling (Fig. 6 ). Additionally, as shown in Fig. 7 , we observe that in contrast with back side machining the maximum channel length does not plateau; instead the length increases linearly with fluence across the examined range.

Fig. 5.

Front side machining damage at 118 J/cm² replicated using an acetate imprint. Pulses are focused 500 nm deeper with each row going from bottom to top in the vertical direction and 50 nm deeper with each pulse towards the right side of the image. This image was taken at a sample tilt angle of 45°. The scale bar is 10 μm.

Fig. 6.

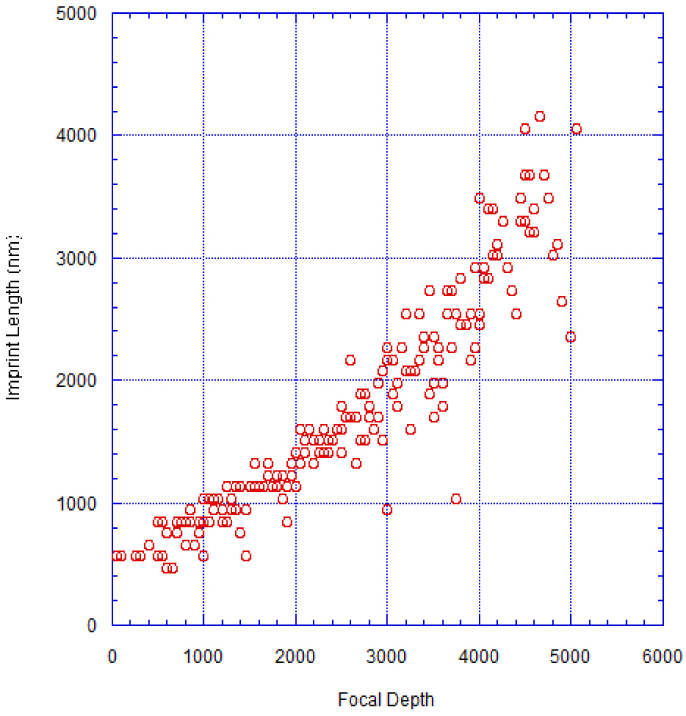
Front side machining imprint length vs. focal depth as measured from Fig. 5 at 118 J/cm².

Fig. 7.

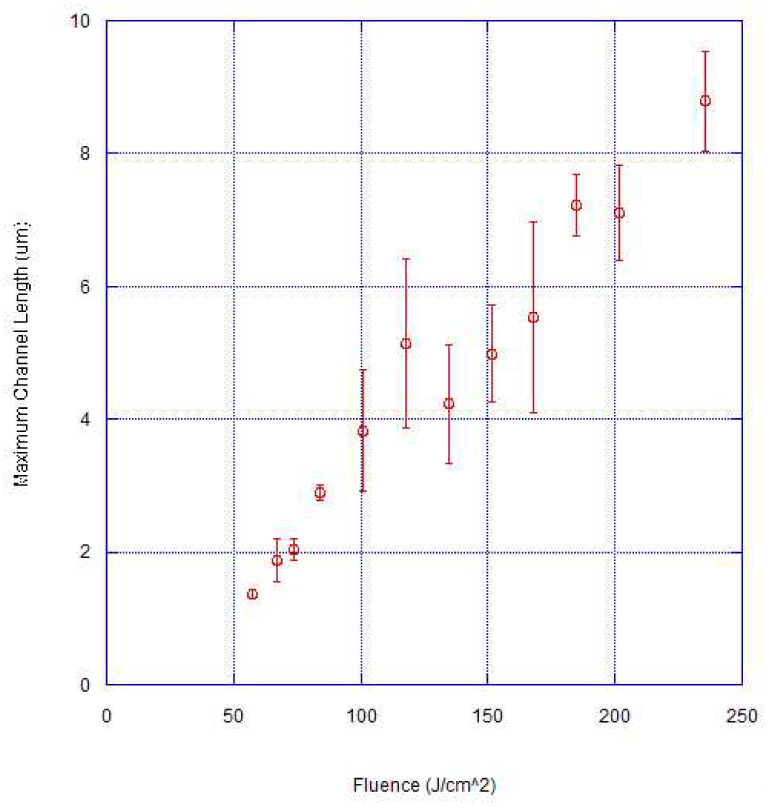
Front side machining maximum channel length vs. fluence. Maximum channel length is measured using the average of the four longest channels observed at each fluence.

These measurements demonstrate that for back side machining conditions, where spherical aberration is minimized, nanochannel formation occurs just as readily as in front side machining conditions, where substantial spherical aberration is expected. To quantify the degree of spherical aberration, we characterized the length of the focus using confocal microscopy at both the front and rear surfaces. This was accomplished by using the experimental objective lens to image with a confocal microscope and measuring the spatial extent of emission along the z-axis from a sub-resolution fluorescent microsphere. The back side showed an estimated confocal parameter of 2.0 ± 0.1 μm, while the front side exhibited a confocal parameter of 4.2 ± 0.2 μm. Thus, while spherical aberration may affect the shape of the channel, it is not required for the extremely elongated morphology of the damage; indeed, the channels were generally longer for back side machining, where spherical aberration is minimized (See Figs. 4 and 7).

A more general explanation for the formation of nanochannels in glass can be provided by nonlinear self-focusing and filamentation. Both theoretical predictions and previous studies of femtosecond laser damage using multiple pulses [13–16] incorporate self focusing and filamentation to show that with increasing pulse fluence the damage track will elongate and the initiation of damage will move upstream relative to the focus, as the converging beam reaches the critical fluence at an earlier position. The location relative to the focus where critical damage intensity is reached shifts upstream at most with the square root of the incident fluence. A larger extension of the damage track occurs due to continued ionization along the propagation axis from the self-focused laser pulse [14]. Consistent with this mechanism, for front side machining we observe a clear dependence of channel length on the incident pulse fluence (Fig. 7). The lengths of the nanochannels formed by back side machining show similar dependence on the laser fluence up to a plateau. The plateau exhibited in Fig. 4 may be the result of viscous resistance for extrusion of material, preventing clear channels above 8 μm in length, presenting the possibility of clearing longer channels with multiple pulses. The higher threshold for damage at the front side and limitations of the laser output prevent this plateau from being observed for front side damage. These results predict that a similar plateau would be observed for front side damage at higher fluences. Additionally, the effect of the increase in fluence may be mitigated by intensity clamping, where the balance of self-focusing and plasma defocusing set a limit on the peak intensity that occurs in the filament [17].

For back side damage at a particular fluence, the location at which critical fluence is reached and damage is initiated has homogeneous upstream conditions whether near the surface or several microns distant. Thus, the channel length depends only on the distance between the point where critical intensity is reached and the surface, up until this distance exceeds the maximum possible channel length, such that the surface is no longer breached, causing the linear dependence on the position of the focus. However, for front side machining the spot size of the focused beam on the glass surface where damage initiates depends on the position of focus relative to the surface. Thus the conditions where damage initiates change as the focus of the laser pulse is moved relative to the sample surface, creating conditions for a nonlinear extension of the channel presumably formed by laser filamentation seen in Fig. 6. Furthermore, the high directionality of the damage argues against the highly nonlinear generation of Bremsstrahlung x-rays as a source for this damage [10].

Regardless of the fundamental mechanism for the elongation of femtosecond laser damage, this phenomenon has a number of applications. The ability to form channels with single pulses addresses one of the fundamental disadvantages for industrial applications of laser machining; structures must be formed serially, rather than in parallel as with photolithographic techniques. With recent advances in laser technology allowing high repetition rate, high energy femtosecond lasers [18], formation of long channels using single pulses could allow fabrication speeds as high as 400 m/s. Thus femtosecond laser machining would approach rates comparable to photolithographic techniques, while enabling nanoscale and three-dimensional features to be formed outside of a clean room. This allows industrial applications ranging from large arrays of nanowells to both in-plane and out-of-plane modification of patterned structures to be performed entirely with a single optical machining device [19], and the high aspect ratio relaxes the requirements for nanoscale calibration between the laser focus and a surface when holes are drilled.