Abstract
Background
Optimizing a closed-loop insulin delivery algorithm for individuals with type 1 diabetes can be potentially facilitated by a mathematical model of the patient. However, model simulation studies that evaluate changes to the control algorithm need to produce conclusions similar to those that would be obtained from a clinical study evaluating the same modification. We evaluated the ability of a low-order identifiable virtual patient (IVP) model to achieve this goal.
Methods
Ten adult subjects (42.5 ± 11.5 years of age; 18.0 ± 13.5 years diabetes; 6.9 ± 0.8% hemoglobin A1c) previously characterized with the IVP model were studied following the procedures independently reported in a pediatric study assessing proportional–integral–derivative control with and without a 50% meal insulin bolus. Peak postprandial glucose levels with and without the meal bolus and use of supplemental carbohydrate to treat hypoglycemia were compared using two-way analysis of variance and chi-square tests, respectively.
Results
The meal bolus decreased the peak postprandial glucose levels in both the adult-simulation and pediatric-clinical study (231 ± 38 standard deviation to 205 ± 33 mg/dl and 226 ± 51 to 194 ± 47 mg/dl, respectively; p = .0472). No differences were observed between the peak postprandial levels obtained in the two studies (clinical and simulation study not different, p = .57; interaction p = .83) or in the use of supplemental carbohydrate (3 occurrences in 17 patient days of closed-loop control in the clinical-pediatric study; 7 occurrences over 20 patient days in the adult-simulation study, p = .29).
Conclusions
Closed-loop simulations using an IVP model can predict clinical study outcomes in patients studied independently from those used to develop the model.
Keywords: algorithm, artificial pancreas, automated, closed loop, diabetes, insulin delivery, mathematical model
Introduction
Metabolic modeling is widely believed to be essential to achieving a closed-loop insulin delivery system. As algorithms linking glucose-sensing and insulin-delivery components become more complex, the ability to optimize design parameters and evaluate changes in system components using animal or clinical studies becomes increasingly impractical. Even the simplest of closed-loop algorithms may have multiple parameters that need to be adjusted. Improvements in the insulin formulation or the means of insulin delivery resulting in a more desirable pharmacokinetic/pharmacodynamic (PK/PD) response may require adjustments in closed-loop parameters to capitalize on these developments. Glucose sensors have complex filtering/calibration routines that might also be optimized to effect an improve-ment in closed-loop performance. Closed-loop control parameters per se could potentially be optimized by empirical adjustments in much the same way as open-loop control parameters—e.g., glucose correction factors, carbohydrate-to-insulin ratios, basal rates, and insulin-on-board—are adjusted but changes in closed-loop parameters involve a putative higher risk. Animal studies can be conducted to mitigate some of this risk but animal models have limitations of their own. Insulin PK/PD profiles, meal absorption profiles, and the diurnal variation in metabolic parameters in any given animal model may not accurately reflect those observed in humans.
Generally, research groups seeking to develop closed-loop algorithms have developed model simulators in parallel with their closed-loop algorithms, with the models being used to make key decisions in the design process. Examples include metabolic models developed in Karlsberg,1 Cambridge,2 University of Virginia (UVA),3 and Medtronic4–6 that are paired with controllers developed at these same sites (Karlsburg,7 Cambridge,8,9 UVA,10 and Medtronic11–14). Of these, the Karlsburg model is now used primarily for optimizing open-loop insulin delivery;15,16 however, the UVA simulator3 is the only simulator accepted by the Food and Drug Administration as a replacement for animal studies.
The model used to aid in developing the Medtronicproportional–integral–derivative (PID) algorithm is itself composed of a set of submodels: the identifiable two-compartment model of subcutaneous insulin absorption proposed by Sherwin and colleagues,17 the so-called minimal model developed by Bergman and Cobelli,18–21 and a two-compartment model of glucose appearance following meals developed by Hovorka and colleagues.2 The combined model, termed identifiable virtual patient (IVP) model in this article, was shown to fit data obtained in the initial feasibility study of PID control with no significant residual error and with well-estimated parameters6 (with initial closed-loop study reported11). Although the ability to fit data is a necessary component of model validation, more stringent criteria can be developed.22,23 These include the ability of a model to reproduce results obtained in subjects that are independent from those used to develop the model. Ideally, the model should also be able to predict how a change in control parameters might impact an individual subject identified with the model and be able to predict regions of control stability (different combinations of control and patient parameters for which the closed-loop system provides acceptable control). In the present study, we evaluated the ability of the IVP model to satisfy the first of these additional criteria: the ability to reproduce closed-loop study results in subjects who are independent from those used to develop the model.
Methods
Ten virtual patients, 42.5 ± 11.5 years of age with diabetes for 18.0 ± 13.5 years, hemoglobin A1c (HbA1c) of 6.9 ± 0.8%, and metabolic model parameters reported in the literature6 were studied (i.e., simulated). Each subject was studied with the protocol and procedures reported in a clinical study of pediatric subjects assessing the impact of adding a meal insulin bolus to the Medtronic PID algorithm.11–14 Briefly, in the clinical pediatric study,12 closed-loop insulin delivery was started at 7 a.m. on day 1 and continued through until 3 p.m. on day 2. Breakfast, lunch, and dinner were served at 8 a.m., 12 p.m., and 5 p.m. each day. Eight subjects were studied without meal boluses [full closed-loop (FCL); subject age: 16.8 ± 1.6 years, duration of diabetes: 6.9 ± 4.6 years, HbA1c: 6.9 ± 0.8%]. Nine subjects were studied with a meal insulin bolus given 0–15 minutes in advance of the meal [hybrid closed-loop (HCL); subject age: 15.1 ± 1.0 years, duration of diabetes: 5.7 ± 2.9 years, HbA1c: 7.3 ± 0.9%; meal bolus about one-half that which would normally be given to the subject based on their carbohydrate-to-insulin ratio (CIR)]. These procedures were repeated in the simulation study with the exception that each of the 10 adult virtual subjects was studied once with FCL and once with HCL. For the simulation subjects, the CIR (g/Unit) was obtained as 500/DIR (daily insulin requirement in Units). Meal size was not changed from that reported in the clinical study used to identify the virtual patients.11
The IVP model is composed of five equations character-izing the subcutaneous (SC) insulin concentration at the catheter site (ISC), the concentration of insulin in plasma (IP), insulin’s effect (IEFF) to lower plasma glucose (G), and the rate of appearance of glucose following meals (RA):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Model parameters τ1 and τ2, (PK time constants, min); CI (insulin clearance, ml/min); p2, (time constant for insulin action, min-1); SI (insulin sensitivity, ml/µU/min); GEZI (glucose effectiveness at zero insulin, min-1); EGP (endogenous glucose production, mg/dl/min); VG (glucose distribution volume, dl); and τm (peak time of meal glucose appearance, one value for each meal) were identified during different time slots of varying length, with values in the first and third slots constrained to be identical (diurnal variation). Parameter values are reported in the original manuscript describing the identification procedure.6 A glucose sensor was assumed to be placed in a SC interstitial fluid (ISF) fluid compartment described by
| (6) |
where, GP(t) is defined as the glucose concentration in plasma and GISF(t) defined as the concentration of glucose in ISF. The ISF delay (τSEN) was fixed at 10 min.24 Sensor glucose (SG) values were obtained each minute and processed in the identical manner to the clinical study.12 SG was obtained by filtering the ISF signal with a seven-point, low-pass, finite impulse response (FIR) filter and the rate of change of SG (dSG/dt) estimated from an FIR filter, calculating the slope of SG versus time for the precious 15 min.24
The PID algorithm was also configured identical to that reported for the clinical study,12 with proportional (P), integral (I), and derivative (D) terms calculated at time points corresponding to minute-to-minute glucose values (time interval denoted as k):
| (7) |
| (8) |
| (9) |
| (10) |
and integral term (basal) constrained by a wind-up protection routine defined by
if SG > 80 mg/dl then IMAXA
else if SG ≥ 60 mg/dl then
| (11) |
IMAXA was set to the maximum overnight basal rate plus 2.4 U/h, and IMAXB was set to KP·(Gtarget – 60) to prevent the algorithm from delivering insulin with SG < 60 mg/dl and not increasing Gain KP was set in proportion to the subject’s daily insulin requirement: KP=DIR/135000 where DIR is in U/day and the resulting KP is in (U/min)/(mg/dl). Derivative and integration times TD and TI were set to 90 and 450 min during the day (6 a.m. to 10 p.m.), and 60 and 150 min otherwise (night). Target glucose was 100 mg/dl during the day and 120 mg/dl during the night. The integrator initial condition [I(k – 1)] was set to the subject’s basal rate at the start of closed-loop control and thereafter constrained to be greater than 0.
Although no changes were made in the virtual subject parameters or meal absorption parameters, the timing of each meal was modified to correspond to the timing in the clinical study. Breakfast, lunch, and dinner were moved from 8 a.m., 1 p.m. and 6 p.m. to 8 a.m., 12 p.m., and 5 p.m. Supplemental carbohydrate (15 g with a peak appearance time τm = 15 min) was given in the event SG fell below 60 mg/dl. One subject was excluded from the simulation analysis for breakfast on day 1 and dinner on day 2 as that subject, in the original closed-loop study, had requested to follow the Atkins diet routine during those meals (negligible carbohydrates with little or no meal response).
Statistical Analysis
Presentation of the simulation study results follows that used by Weinzimer and colleagues12 in the report of the pediatric clinical study results, with Figures 1 and 2 from that report reproduced here. Peak postprandial glucose level with and without meal bolus were compared using two-way analysis of variance (ANOVA) with study type (simulation vs clinical) and controller type (FCL vs HCL) as factors. Need for supplemental carbohydrate to treat hypoglycemia (SG < 60 mg/dl) was compared using a chi-square test. Results are reported as mean ± standard error of the mean unless otherwise noted. Simulations were performed using routines available in Matlab (Math Works, Natick, MA). Statistical analysis (two-way ANOVA, chi-square tests) was performed using GraphPad Prism version 5.04 for Windows (GraphPad Software, San Diego, CA). A posteriori power calculations were performed by Monte Carlo simulation using Mlab (Civilized Software, Silver Spring, MD).
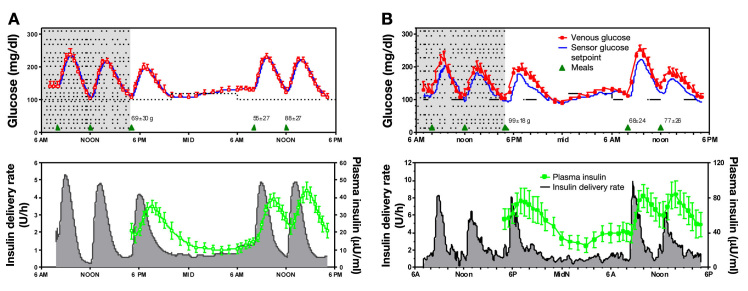
Figure 1.
(A) Left panels show closed-loop simulation results in 10 adult virtual patients. (B) Right panels, adapted from Figure 1 of Weinzimer and colleagues,12 show clinical data obtained in 8 pediatric subjects using the same protocol.
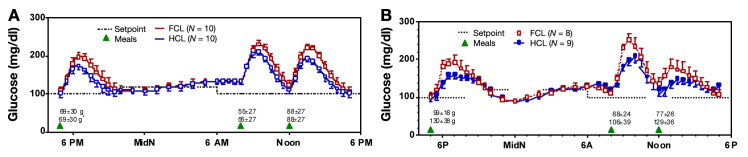
Figure 2.
(A) Left panel shows simulation of 24 h closed-loop control in 10 virtual adult subjects using FCL and the same algorithm modified by a meal bolus given by the subject 15 min in advance of a meal (HCL). Each subject was simulated twice with the same meal on both occasions. (B) Right panel shows results from a clinical study performed in pediatric subjects. Different patients (n = 8 and 9 for FCL and HCL, respectively) were studied with meals of their choosing (meal size shown in grams).
Results
Closed-loop control with meal bolus in the adult virtual patients (FCL; Figure 1A; Table 1) resulted in similar peak postprandial glucose values to closed-loop control in the pediatric clinical subjects (Figure 2B; Table 2). This result was obtained despite differences in meal sizes [55 ± 27 standard deviations (SD), 88 ± 36, 69 ± 28 for adult virtual subjects vs 68 ± 24, 77 ± 26, and 99 ± 18 for the pediatric subjects; overall amount not different, p = .078 but with interaction, p = .023]. Time between peak insulin delivery and peak plasma insulin concentration during each meal was similar in the simulation and clinical studies but with the magnitude of insulin-delivery and concentrations being about two-thirds that observed in the pediatric clinical study (compare y-axis in lower panels for both).
Table 1.
Insulin Delivery and Glycemic Control Parameters in FCL versus HCL Virtual Simulation Study
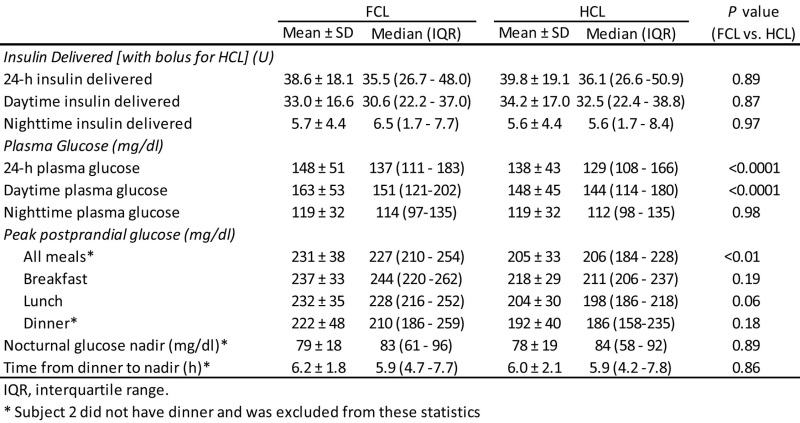 |
Table 2.
Glycemic Control Parameters in FCL and HCL Subjects from Pediatric Clinical Studya
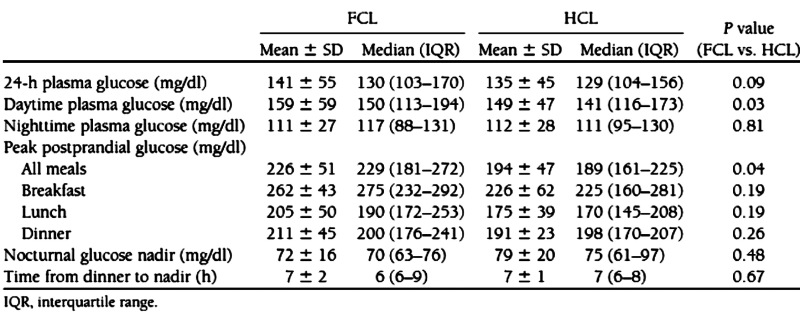 |
Reprinted with permission from Diabetes Care.12
Analyzed as independent studies, adding a meal bolus 15 min in advance of a meal lowered the peak post-prandial glucose from 231 ± 38 to 205 ± 33 mg/dl in the adult simulation study (p = .0081; Table 1), and from 226 ± 51 to 194 ± 47 mg/dl in the clinical pediatric study (p = .04; Table 2 reproduced from original publication). Combining the simulation and clinical studies together and reanalyzing the data by two-way ANOVA showed the effect of the meal bolus to be significant with p = .047 and with no difference between the simulation and clinical studies (p = .57; interaction, p = .83). There were 3 occurrences of supplemental carbohydrate over 17 patient days in the clinical study versus 7 occurrences over 20 patient days in the simulation study (not different; p = .29, chi-square test). Sensor glucose was in the target range 70–180 mg/dl 85% of the time in the clinical study versus 71% in the simulation. Mean absolute relative difference (MARD) introduced by the ISF delay and filter routine in the simulation study was 5.9%; MARD estimated from all sources of error was 13.9% in the pediatric clinical study.
Discussion
The present study showed that a low-order IVP simulator can reproduce clinical study results obtained in a population of subjects that are independent from those used to develop the model. Key observations made in the clinical study12 used for comparison were that (1) 85% of all sensor glucose levels were between 70 and 180 mg/dl, (2) there was large intersubject variability in peak post-prandial glucose levels, (3) the closed-loop algorithm did not respond until 15–20 min into the meal, (4) peak insulin concentrations did not occur until 120 min after the meal started, and (5) plasma insulin concentration did not return to basal level until 8–10 h after dinner. These observations were all reproduced in the simulation study with only minor differences noted.
Differences that were noted included a slightly lower percent of sensor glucose readings in target range (71 vs 85%, simulation vs clinical) and an increase in the use of supplemental carbohydrates (6 occurrences in 20 patient days vs 3 in 17). The difference in sensor values in the target range could potentially be attributed to the sensor underestimating glucose at high values in the clinical study.12 Underestimation of sensor glucose can be due to nonlinearities in the sensor response, intrinsic offset in sensor current, or delays in glucose equilibration with ISF.24 In our simulations, we included the delay in glucose equilibration with the SC ISF but did not simulate an offset in sensor current or nonlinearity in the sensor response. This resulted in a better MARD for the simulation than was reported in the pediatric study (5.1 vs 13.2%). Despite the better sensor, the virtual subjects still proved to be more difficult to control, with supplemental carbohydrate being used to correct hypoglycemia 7 times during 20 patient days of control in the simulation study and only 3 times in 17 patient days of real control. Although the difference was not statistically significant (p = .29), having a simulator that predicts the need for supplemental carbohydrate may be beneficial when testing algorithms for safety in advance of performing a clinical study.
Minor differences were also observed in the relative magnitude of the breakfast versus lunch glucose excursions within each study. The two excursions were of similar magnitude in the simulation study, whereas the lunch excursion was smaller than the breakfast excursion in the clinical study. This may have been due to differences in the meal sizes consumed in each study. The meal sizes in the clinical study used to identify virtual patient subjects11 and the pediatric study used for comparison12 were determined by the subjects, with the total amount of carbohydrate not different. However, while the total amount of carbohydrate consumed was not different, the distribution by meal was. Thus, to have the same ratio of breakfast to lunch carbohydrate in the two studies, the pediatric subjects would have had to consume 41% morecarbohydrate at lunch in the FCL control subjects and 31% more in the HCL subjects. Still, despite the differences in patient population and relative carbohydrate consumed at each meal, the average closed-loop glucose profiles obtained in the simulation closely matched that of the clinical study despite insulin delivery rates that were approximately one-third less in the virtual subjects. Similar glucose profiles with different insulin delivery rates can be expected for a closed-loop system that adjusts insulin delivery rates to achieve the same target at the same rate.
The inability to match all conditions in the simulation to those of the clinical study is nonetheless a limitation in the present study. The differences were, however, unavoidable, as IVP model parameters have not been published for pediatric subjects. Differences in the clinical versus simulation study design, population, and meals, may have masked our ability to detect differences between the simulation and clinical studies, or otherwise have affected the power of our statistical analysis. For example, in the simulation study, the difference in the peak postprandial glucose for breakfast on day 2 was significant [77 mg/dl with 95% confidence interval (CI) (55.12 to 99.16); FCL vs HCL], whereas the same comparison in the clinical study was not [32.43 ± 24.95 with 95% CI (-20.75 to 85.61)]. Effectively, the simulation study had more power to detect differences in peak postprandial glucose than the clinical study. However, rather than being an advantage, this suggests that there was an important component on variability that was not captured in the simulation. Conversely, the two-way ANOVA used to evaluate differences between the simulated and clinical results failed to detect differences in the peak postprandial glucose in the simulated and clinical data, raising the possibility that the comparison was underpowered. For the analysis performed, the peak postprandial values for breakfast, lunch, and dinner were combined leaving only study type (simulation vs clinical) and controller type (FCL vs HCL) as factors in the two-way ANOVA. However, combining breakfast, lunch, and dinner resulted in similar values [231 ± 35 (SD) vs 226 ± 51 for FCL, and 205 ± 38 vs 194 ± 47 for HCL]. As the difference was small, just 5 mg/dl for FCL, the power to detect significance was also low (13% estimated from Monte Carlo simulation). We estimate that to have detected a difference between simulated and clinical results, this difference would have needed to be at least 15% (~30 mg/dl) for both the FCL and HCL peak postprandial values (80% power). Given the limitations introduced by the nonmatched patient populations consuming different meals, further validation will be required to validate clinical closed-loop study results that can be reproduced with this simulator.
The IVP model represents one of several models that could have been used for the simulations performed here. Other models include the KADIS simulator,1 the Cambridge simulator,2 and the simulator developed at UVA.3 It is not clear if the simulators yield significantly different results. Generally, equations for all the simulators are known but model parameters for individual subjects are often proprietary. The exceptions to this are the parameters for the 10 adult IVP subjects used here (reported in Kanderian and colleagues)6 and the 10 patients in each of the adult, pediatric, and child groups described in the UVA patent.25 Equations for the different models differ primarily in number (model order) and the number of parameters. The trend has been to use high-order models for simulation,26 although the parameters of such models are unidentifiable from data that is routinely collected in clinical studies (meal information, insulin delivery, and insulin and glucose concentrations). Lower order models are still well accepted for measuring metabolic parameters or as components of model predictive control algorithms.26 However, low-order models do continue to be used as simulators. The KADIS model, for example, is identifiable from logbook or continuous glucose monitoring data. Once identified, the model is used to perform simulations to optimize open-loop therapy.27 Although IVP model parameters are identifiable from the same routine data collection, the model is not suited for predicting a single future meal excursion as the model parameters are time-varying. Time-varying parameters were chosen as a basis for the model as it is well known that individuals with type 1 diabetes can have high inter- and intraday variability in insulin requirements. As the IVP model is set up to capture this variability, it can only be used to predict average glucose responses that would be obtained by an individual on repeated days, or the average results obtained in a study involving multiple subjects. Results from the present study support its ability to predict results obtained across multiple subjects. The model has also been used as a guide in developing modifications to the PID controller,14 which have been tested and shown to work well in subsequent clinical studies.13 Nonetheless, given the limitations described earlier (nonmatched patient populations consuming different meals), further validation may still be required to assess its ability to reproduce other closed-loop clinical study results.
Components of the IVP model—specifically the two-compartment PK model described by Equations (1) and (2)—have been used as components of different control algorithms. The PID closed-loop insulin delivery algorithm developed by Medtronic13 and the MPC controller developed by Damiano and colleagues28 both incorporated this characterization of the PK insulin response to predict plasma insulin concentrations during closed-loop insulin delivery. Noteworthy is that in both of these cases,13,28 model parameters were preset to values obtained from the literature and no attempt was made to adjust or identify them in real time. In the study by Damiano and colleagues,28 the insulin profiles were not well predicted in some individual cases, leading to poor control. However, when the parameters were retrospectively identified and the subjects studied on a subsequent occasion, both the real-time prediction and resulting control were substantially improved. Generally, closed-loop controllers utilizing models as part of the control algorithm can be configured to identify the parameters of the model in real time; however, the ability of the real-time identification algorithms to track time-varying parameters needs to be carefully assessed. Subjects with parameters that differ substantially may need their parameters to be set off-line.
In summary, results presented in the original IVP model development and identification study6 showed that the IVP model can be identified from routine insulin, glucose, and meal data. The present study showed that once a population of virtual patients is identified, that population can be used to perform closed-loop studies with the expected result not statistically different from that which would be obtained in a clinical study. Additional validation of the model, however, is required to confirm that the model can be used to optimize control in an individual subject or identify regions of control stability for the individual.
Glossary
Abbreviations
- (ANOVA)
analysis of variance
- (CI)
confidence interval
- (CIR)
carbohydrate-to-insulin ratio
- (DIR)
daily insulin requirement
- (EGP)
endogenous glucose production
- (FCL)
full closed loop
- (FIR)
finite impulse response
- (GEZI)
glucose effectiveness at zero insulin
- (HbA1c)
hemoglobin A1c
- (HCL)
hybrid closed loop
- (ISF)
interstitial fluid
- (IVP)
identifiable virtual patient
- (MARD)
mean absolute relative difference
- (NIH)
National Institutes of Health
- (PID)
proportional–integral–derivative
- (PD)
pharmacodynamic
- (PK)
pharmacokinetic
- (SC)
subcutaneous
- (SD)
standard deviation
- (SG)
sensor glucose
- (UVA)
University of Virginia
Funding
This work was supported by National Institutes of Health (NIH) Grant #RO1-DK64701 (Garry Steil). Stuart Weinzimer is supported by NIH Grant #R01 DK085618 and Juvenile Diabetes Research Fund Grant #22-2009-799.
Disclosures
Garry Steil and Sami Kanderian were employed by Medtronic MiniMed during the performance of the clinical studies used to develop the IVP model and both have coauthored patents assigned to Medtronic.
References
- 1.Fischer U, Salzsieder E, Jutzi E, Albrecht G, Freyse EJ. Modelling the glucose-insulin system as a basis for the artificial beta cell. Biomed Biochim Acta. 1984;43(5):597–605. [PubMed] [Google Scholar]
- 2.Wilinska ME, Chassin LJ, Acerini CL, Allen JM, Dunger DB, Hovorka R. Simulation environment to evaluate closed-loop insulin delivery systems in type 1 diabetes. J Diabetes Sci Technol. 2010;4(1):132–144. doi: 10.1177/193229681000400117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kovatchev BP, Breton M, Dalla Man C, Cobelli C. In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J Diabetes Sci Technol. 2009;3(1):44–55. doi: 10.1177/193229680900300106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stocker D, Kanderian S, Cortina GJ, Nitzan T, Plummer J, Steil GM, Mastrototaro J. inventors; Medtronic MiniMed, Inc., assignee. Virtual patient software system for educating and treating individuals with diabetes. United States patent application US 2006/0272652. 2006 December 7.
- 5.Steil GM, Clark B, Kanderian S, Rebrin K. Modeling insulin action for development of a closed-loop artificial pancreas. Diabetes Technol. Ther. 2005;2(7(1):94–108. doi: 10.1089/dia.2005.7.94. [DOI] [PubMed] [Google Scholar]
- 6.Kanderian S, Weinzimer S, Voskanyan G, Steil GM. Identification of intraday metabolic profiles during closed-loop glucose control in individuals with type 1 diabetes. J Diabetes Sci Technol. 2009;3(5):1047–1057. doi: 10.1177/193229680900300508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rebrin K, Fischer U, von Woedtke T, Abel P, Brunstein E. Automated feedback control of subcutaneous glucose concentration in diabetic dogs. Diabetologia. 1989;32(8):573–576. doi: 10.1007/BF00285330. [DOI] [PubMed] [Google Scholar]
- 8.Hovorka R, Allen JM, Elleri D, Chassin LJ, Harris J, Xing D, Kollman C, Hovorka T, Larsen AM, Nodale M, De Palma A, Wilinska ME, Acerini CL, Dunger DB. Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: a phase 2 randomised crossover trial. Lancet. 2010;375(9716):743–751. doi: 10.1016/S0140-6736(09)61998-X. [DOI] [PubMed] [Google Scholar]
- 9.Elleri D, Allen JM, Nodale M, Wilinska ME, Mangat JS, Larsen AM, Acerini CL, Dunger DB, Hovorka R. Automated overnight closed-loop glucose control in young children with type 1 diabetes. Diabetes Technol Ther. 2011;13(4):419–424. doi: 10.1089/dia.2010.0176. [DOI] [PubMed] [Google Scholar]
- 10.Clarke WL, Anderson S, Breton M, Patek S, Kashmer L, Kovatchev B. Closed-loop artificial pancreas using subcutaneous glucose sensing and insulin delivery and a model predictive control algorithm: the Virginia experience. J Diabetes Sci Technol. 2009;3(5):1031–1038. doi: 10.1177/193229680900300506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Steil GM, Rebrin K, Darwin C, Hariri F, Saad MF. Feasibility of automating insulin delivery for the treatment of type 1 diabetes. Diabetes. 2006;55(12):3344–3350. doi: 10.2337/db06-0419. [DOI] [PubMed] [Google Scholar]
- 12.Weinzimer SA, Steil GM, Swan KL, Dziura J, Kurtz N, Tamborlane WV. Fully automated closed-loop insulin delivery versus semiautomated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care. 2008;31(5):934–939. doi: 10.2337/dc07-1967. [DOI] [PubMed] [Google Scholar]
- 13.Steil GM, Palerm CC, Kurtz N, Voskanyan G, Roy A, Paz S, Kandeel FR. The effect of insulin feedback on closed loop glucose control. J Clin Endocrinol Metab. 2011;96(5):1402–1408. doi: 10.1210/jc.2010-2578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kanderian S, Steil GM. inventors; Medtronic MiniMed, Inc., assignee. Apparatus and method for controlling insulin infusion with state variable feedback. United States patent US 7,806,886. 2010 Oct 5.
- 15.Augstein P, Vogt L, Kohnert KD, Heinke P, Salzsieder E. Translation of personalized decision support into routine diabetes care. J Diabetes Sci Technol. 2010;4(6):1532–1539. doi: 10.1177/193229681000400631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Salzsieder E, Vogt L, Kohnert KD, Heinke P, Augstein P. Model-based decision support in diabetes care. Comput Methods Programs Biomed. 2011;102(2):206–218. doi: 10.1016/j.cmpb.2010.06.001. [DOI] [PubMed] [Google Scholar]
- 17.Insel PA, Kramer KJ, Sherwin RS, Liljenquist JE, Tobin JD, Andres R, Berman M. Modeling the insulin-glucose system in man. Fed Proc. 1974;33(7):1865–1868. [PubMed] [Google Scholar]
- 18.Bergman RN, Ider YZ, Bowden CR, Cobelli C. Quantitative estimation of insulin sensitivity. Am J Physiol. 1979;236(6):E667–77. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
- 19.Bergman RN, Phillips LS, Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J Clin Invest. 1981;68(6):1456–1467. doi: 10.1172/JCI110398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bergman RN. Lilly lecture 1989. Toward physiological under-standing of glucose tolerance. Minimal- model approach. Diabetes. 1989;38(12):1512–1527. doi: 10.2337/diab.38.12.1512. [DOI] [PubMed] [Google Scholar]
- 21.Bergman RN. Minimal model: perspective from 2005. Horm Res. 2005;64(Suppl 3):8–15. doi: 10.1159/000089312. [DOI] [PubMed] [Google Scholar]
- 22.Steil GM, Reifman J. Mathematical modeling research to support the development of automated insulin-delivery systems. J Diabetes Sci Technol. 2009;3(2):388–395. doi: 10.1177/193229680900300223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Steil GM, Hipszer B, Reifman J. Update on mathematical modeling research to support the development of automated insulin delivery systems. J Diabetes Sci Technol. 2010;4(3):759–769. doi: 10.1177/193229681000400334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rebrin K, Sheppard NF, Steil GM. Use of subcutaneous interstitial fluid glucose to estimate blood glucose: revisiting delay and sensor offset. J Diabetes Sci Technol. 2010;4(5):1087–1098. doi: 10.1177/193229681000400507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kovatchev BP, Breton MD, Cobelli C, Dalla Man C. inventors; University of Virginia Patent Foundation, assignee. Method, system and computer simulation environment for testing of monitoring and control strategies in diabetes. United States patent application US 2010/0179768. 2010 July 15.
- 26.Cobelli C, Dalla Man C, Sparacino G, Magni L, De Nicolao G, Kovatchev BP. Diabetes: models, signals, and control. IEEE Rev Biomed Eng. 2009;2:54–96. doi: 10.1109/RBME.2009.2036073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Salzsieder E, Vogt L, Kohnert KD, Heinke P, Augstein P. Model-based decision support in diabetes care. Comput Methods Programs Biomed. 2011;102(2):206–218. doi: 10.1016/j.cmpb.2010.06.001. [DOI] [PubMed] [Google Scholar]
- 28.El-Khatib FH, Russell SJ, Nathan DM, Sutherlin RG, Damiano ER. A bihormonal closed-loop artificial pancreas for type 1 diabetes. Sci Transl Med. 2010;4(2(27)) doi: 10.1126/scitranslmed.3000619. 27ra27. [DOI] [PMC free article] [PubMed] [Google Scholar]