Abstract
Objective To evaluate the performance of the QRISK2-2011 score for predicting the 10 year risk of cardiovascular disease in an independent UK cohort of patients from general practice and to compare it with earlier versions of the model and a National Institute for Health and Clinical Excellence version of the Framingham equation.
Design Prospective cohort study to validate a cardiovascular risk score with routinely collected data between June 1994 and June 2008.
Setting 364 practices from the United Kingdom contributing to The Health Improvement Network (THIN) database.
Participants Two million patients aged 30 to 84 years (11.8 million person years) with 93 564 cardiovascular events.
Main outcome measure First diagnosis of cardiovascular disease (myocardial infarction, angina, coronary heart disease, stroke, and transient ischaemic attack) recorded in general practice records.
Results Results from this independent and external validation of QRISK2-2011 indicate good performance data when compared with the NICE version of the Framingham equation. QRISK2-2011 had better ability to identify those at high risk of developing cardiovascular disease than did the NICE Framingham equation. QRISK2-2011 is well calibrated, with reasonable agreement between observed and predicted outcomes, whereas the NICE Framingham equation seems to consistently over-predict risk in men by about 5% and shows poor calibration in women.
Conclusions QRISK2-2011 seems to be a useful model, with good discriminative and calibration properties when compared with the NICE version of the Framingham equation. Furthermore, based on current high risk thresholds, concerns exist on the clinical usefulness of the NICE version of the Framingham equation for identifying women at high risk of developing cardiovascular disease. At current thresholds the NICE version of the Framingham equation has no clinical benefit in either men or women.
Introduction
Cardiovascular disease is an important health concern, accounting for nearly one third of deaths worldwide in 2008.1 In the United Kingdom almost 200 000 deaths annually are attributed to diseases of the heart and circulatory system, with more than one in three deaths associated with cardiovascular disease (www.heartstats.org). Targeting interventions to reduce the risk of cardiovascular disease in high risk patients are now key components in national policies.2 3 Risk prediction models, including the Framingham risk score,4 the Reynolds risk score,5 6 and QRISK7 8 9 10 11 are tools used to identify people who are at high risk (≥20%)3 of developing (10 year) cardiovascular disease and could benefit from intervention.
In February 2010 the National Institute for Health and Clinical Excellence withdrew its recommendation that the Framingham risk equation be used to predict the risk of someone developing cardiovascular disease over the next 10 years.12 This was made in light of the emergence of a new cardiovascular risk prediction tool called QRISK,11 which was shown to have greater predictive ability than the Framingham risk equation.7 8 9 10 11 Despite increasing evidence to suggest that the Framingham equation is not well suited to the United Kingdom and that QRISK may be more suitably tailored, no firm recommendation exists on what model to use. Instead, NICE no longer recommends any single risk score, leaving healthcare professionals free to choose the model they consider the most appropriate.
Work has continued on QRISK since its introduction in 2007. In 2008, QRISK2 (QRISK2-2008) was developed, which was subsequently updated in 2010 (QRISK2-2010)13 and again in 2011 (QRISK2-2011) (www.qrisk.org) to capture improvements in data quality. QRISK2 (currently QRISK2-2011) now extends the age range to 30 and 84 years (from 35 to 74 years in QRISK2-2008). However, the most noticeable modification in QRISK2-2011 is the change in how smoking status is captured and included in the model. Earlier versions of QRISK2 included smoking status as a binary variable (current smoker versus not a current smoker), whereas QRISK2-2011 now defines smoking status as a five level category variable: non-smoker, former smoker, light smoker (<10 cigarettes/day), moderate smoker (10-19 cigarettes/day), and heavy smoker (≥20 cigarettes/day). Finally, the regression coefficients used to calculate the 10 year risk of developing cardiovascular disease using QRISK2 have been recalculated using more up to date and complete data in the QRESEARCH database (see www.qrisk.org for more details). QRISK2-2011 includes the risk factors of age (years), smoking status (non smoker, former smoker, light smoker, moderate smoker, and heavy smoker), self assigned ethnicity (white or not recorded, Indian, Pakistani, Bangladeshi, other Asian, black African, black Caribbean, Chinese, other including mixed race), systolic blood pressure (mm Hg), ratio of total serum cholesterol to high density lipoprotein, body mass index (kg/m2), family history of coronary heart disease in first degree relative, Townsend deprivation score, treated hypertension, and diagnosis of rheumatoid arthritis, atrial fibrillation, type 2 diabetes, and chronic renal disease. Table 1 provides a description of the predictors in the QRISK and Framingham risk scores. A major feature of QRISK2-2011 is the ability, using the web calculator (www.qrisk.org) and the recently developed iPhone app, to calculate an individual’s risk with one or more missing risk factors. QRISK2-2011 includes a mechanism that replaces missing data, with values from predefined reference values and predictor algorithms. Calculating the risk using the NICE version of the Framingham equation requires all information on all risk factors.
Table 1.
Summary of risk factors in QRISK2-2008, QRISK2-2011, and National Institute for Health and Clinical Excellence version of Framingham equation
| QRISK2-2008 | QRISK2-2011 | NICE Framingham equation |
|---|---|---|
| Age (continuous) (35-74 years) | Age (continuous) (30-84 years) | Age (continuous) (35-74 years) |
| Ratio of total serum cholesterol to high density lipoprotein (continuous) | Ratio of total serum cholesterol to high density lipoprotein (continuous) | Ratio of total serum cholesterol to high density lipoprotein (continuous) |
| Systolic blood pressure (continuous) | Systolic blood pressure (continuous) | Systolic blood pressure (continuous) |
| Smoking status (current smoker, non-smoker (including former smoker)) | Smoking status (non-smoker, former smoker, light smoker, moderate smoker, heavy smoker) | Smoking status (current smoker (or quit within past year), non-smoker) |
| Body mass index (continuous) | Body mass index (continuous) | Sex (male, female) |
| Family history of coronary heart disease in first degree relative <60 years (yes/no) | Family history of coronary heart disease in first degree relative <60 years (yes/no) | Left ventricular hypertrophy (yes/no) |
| Townsend deprivation score (output area level 2001 census data evaluated as continuous variable) | Townsend deprivation score (output area level 2001 census data evaluated as continuous variable) | Type 2 diabetes (yes/no) |
| Treated hypertension (diagnosis of hypertension and at least one current prescription of at least one antihypertensive agent) (yes/no) | Treated hypertension (diagnosis of hypertension and at least one current prescription of at least one antihypertensive agent) (yes/no) | Age×type 2 diabetes |
| Self assigned ethnicity (white/not recorded, Indian, Pakistani, Bangladeshi, other Asian, black African, black Caribbean, other included mixed) | Self assigned ethnicity (white/not recorded, Indian, Pakistani, Bangladeshi, other Asian, black African, black Caribbean, other included mixed) | Left ventricular hypertrophy×age |
| Type 2 diabetes (yes/no) | Type 2 diabetes (yes/no) | Age×sex |
| Rheumatoid arthritis (yes/no) | Rheumatoid arthritis (yes/no) | |
| Atrial fibrillation (yes/no) | Atrial fibrillation (yes/no) | — |
| Renal disease (yes/no) | Renal disease (yes/no) | — |
| Age×body mass index | Age×body mass index | — |
| Age×Townsend score | Age×Townsend score | — |
| Age×systolic blood pressure | Age×systolic blood pressure | — |
| Age×family history of cardiovascular disease | Age×family history of cardiovascular disease | — |
| Age×smoking current | Age×smoking current | — |
| Age×treated hypertension | Age×treated hypertension | — |
| Age×type 2 diabetes | Age×type 2 diabetes | — |
| Age×atrial fibrillation | Age×atrial fibrillation | — |
Any revisions and updates to a risk prediction model should be subject to continual evaluation (validation) to show that its usefulness for routine clinical practice has not deteriorated, or indeed to show that its performance has improved owing to refinements to the model.14 15 We describe the results from an independent evaluation assessing the performance of QRISK2-2011 on a large dataset of general practice records in the United Kingdom, comparing its performance with earlier versions of QRISK27 8 9 10 13 and the NICE adjusted version of the Framingham risk prediction model.3 4
Methods
Participants were patients registered between 27 June 1994 and 30 June 2008 and recorded on The Health Improvement Network (THIN) database (www.thin-uk.com). We excluded patients if they had a previous diagnosis of cardiovascular disease, were registered for less than 12 months with the general practice, had invalid dates, were aged under 30 years, were aged 85 years or over, had missing Townsend scores (social deprivation), or were prescribed statins at baseline.
Outcome measures
The primary outcome measure was the first diagnosis of cardiovascular disease (myocardial infarction, angina, coronary heart disease, stroke, and transient ischaemic stroke) recorded on the general practice’s clinical computer system.
Statistical analysis
To derive smoking status we combined two risk factors: whether the patient was a non-smoker, former smoker, or current smoker, and number of cigarettes smoked a day, defined as light (<10), moderate (10-19), or heavy (≥20).
We calculated the 10 year estimated risk of cardiovascular for every patient in the THIN cohort using the QRISK2-2011 risk score. Observed 10 year cardiovascular risks were obtained using the method of Kaplan-Meier by 10th of predicted risk and age group. To replace missing values for smoking status and body mass index we carried out multiple imputation using all predictors plus the outcome variable. This involves creating multiple copies of the data and imputing the missing values for each dataset with sensible values randomly selected from their predicted distribution. Ten imputed datasets were generated and we combined the results from analyses on each of the imputed values using Rubin’s rules to produce estimates and confidence intervals that incorporate the uncertainty of imputed values.16
We assessed the predictive performance of the QRISK2-2011 risk score on the THIN cohort by examining measures of calibration and discrimination. Calibration refers to how closely the predicted 10 year cardiovascular risk agrees with the observed 10 year cardiovascular risk. This was assessed for each 10th of predicted risk, ensuring 10 equally sized groups and each five year age band, by calculating the ratio of predicted to observed cardiovascular risk separately for men and for women. Calibration of the risk score predictions was assessed by plotting observed proportions versus predicted probabilities and by calculating the calibration slope.
Discrimination is the ability of the risk score to differentiate between patients who do and do not experience an event during the study period. This measure is quantified by calculating the area under the receiver operating characteristic curve statistic; a value of 0.5 represents chance and 1 represents perfect discrimination.17 We also calculated the D statistic and R2 statistic, which are measures of discrimination and explained variation, respectively, and are tailored towards censored survival data.18 19 Higher values for the D statistic indicate greater discrimination, where an increase of 0.1 over other risk scores is a good indicator of improved prognostic separation.19
We used decision curve analysis (accounting for censored observations) to describe and compare the clinical effects of QRISK2-2011 and the NICE Framingham equation.20 21 22 A model is considered to have clinical value if it has the highest net benefit across the range of thresholds for which an individual would be designated at high risk. Briefly, the net benefit of a model is the difference between the proportion of true positives and the proportion of false positives weighted by the odds of the selected threshold for high risk designation. At any given threshold, the model with the higher net benefit is the preferred model.
All statistical analyses were carried out in R (version 2.13.2)23 and the ICE (multiple imputation) procedure in Stata (version 11.2).24
Results
Between 27 June 1994 and 30 June 2008, 2 084 445 eligible patients, aged between 30 and 84 years, from 364 general practices in the United Kingdom were registered in the THIN database. These patients contributed 11 862 381 person years of observation, during which 93 564 incident cases of cardiovascular disease occurred. The median follow-up was 5.75 years (interquartile range 2.48-8.49) and 292 928 patients (14.1%) were followed up for 10 years or more. Table 2 details the characteristics of the eligible patients.
Table 2.
Characteristics of patients aged 30 to 84 years in The Health Improvement Network database. Values are numbers (percentages) of patients unless stated otherwise
| Characteristics | Women (n=1 066 127) | Men (n=1 018 318) |
|---|---|---|
| Mean (SD) age (years) | 49.6 (14.7) | 47.7 (13.4) |
| Mean (SD) body mass index (mg/kg2) | 26.0 (5) | 26.5 (4.1) |
| Body mass index not recorded | 220 012 (20.6) | 300 787 (29.5) |
| Mean (SD) systolic blood pressure (mm Hg) | 130.5 (21.3) | 134.3 (19.0) |
| Systolic blood pressure not recorded | 84 802 (8.0) | 183 852 (18.1) |
| Mean (SD) total cholesterol: HDL cholesterol ratio | 3.9 (1.2) | 4.5 (1.4) |
| Total cholesterol: HDL cholesterol ratio not recorded | 830 407 (77.9) | 791 281 (77.7) |
| Smoking status: | ||
| Non-smoker | 608 942 (57.1) | 440 245 (43.2) |
| Former smoker | 154 544 (14.5) | 180 952 (17.8) |
| Current smoker (cigarettes/day): | ||
| Light (<10) | 58 254 (5.5) | 56 176 (5.5) |
| Moderate (10-19) | 96 970 (9.1) | 92 200 (9.1) |
| Heavy (≥20) | 69 517 (6.5) | 102 955 (10.1) |
| Amount not recorded | 11 760 (1.1) | 29 072 (2.9) |
| Smoking status not recorded | 66 140 (6.2) | 116 718 (11.5) |
| Ethnic group: | ||
| White/not recorded | 1 041 209 (97.7) | 994 798 (97.7) |
| Indian | 5793 (0.5) | 5907 (0.6) |
| Pakistani | 1648 (0.2) | 1786 (0.2) |
| Bangladeshi | 520 (0.1) | 708 (0.1) |
| Other Asian | 2887 (0.3) | 2774 (0.3) |
| Black Caribbean | 2893 (0.3) | 2238 (0.2) |
| Black African | 4422 (0.4) | 3900 (0.4) |
| Chinese | 1142 (0.1) | 848 (0.1) |
| Other, including mixed race | 5613 (0.5) | 5359 (0.5) |
| Clinical condition: | ||
| Treated hypertension | 68 061 (6.4) | 45 079 (4.4) |
| Type 2 diabetes | 18 295 (1.7) | 22 056 (2.2) |
| Family history of early coronary heart disease | 46 974 (4.4) | 38 491 (3.8) |
| Atrial fibrillation | 6276 (0.6) | 7474 (0.7) |
| Chronic renal disease | 1579 (0.15) | 1467 (0.1) |
| Cardiovascular disease* | 42 224 | 51 340 |
| Person years of observation | 6 159 929 | 5 702 452 |
HDL=high density lipoprotein.
*Cardiovascular disease events before death and deaths due to cardiovascular disease.
In patients aged between 30 and 85 years the 10 year observed risk of cardiovascular in women (42 224 incident cases of cardiovascular disease) was 6.57% (95% confidence interval 6.50% to 6.64%) and in men (51 340 incident cases of cardiovascular disease) was 8.66% (8.58% to 8.75%).
Complete data on smoking status, number of cigarettes smoked daily, systolic blood pressure, total serum cholesterol to high density lipoprotein ratio, and body mass index were available for 19.6% of women (n=208 570) and 19.0% of men (n=193 825). Most patients (n=1 221 873; 58.6%) had no or only one missing risk factor (table 3). Considerably more data were missing for total serum cholesterol to high density lipoprotein ratio (77.9% for women and 77.7% for men) than for remaining risk factors. For other risk factors, 20.6% of women and 29.5% of men had missing data on body mass index, 8.0% and 18.1% on systolic blood pressure, 7.3% and 14.3% on smoking status, and 6.2% and 11.5% on number of cigarettes smoked daily.
Table 3.
Completeness of data
| No of risk factors not recorded (per patient) | No (%) of women (n=1 066 127) | No (%) of men (n=1 018 318) |
|---|---|---|
| 0 (complete data) | 208 570 (19.6) | 193 825 (19.0) |
| 1 | 635 626 (59.6) | 183 852 (49.2) |
| 2 | 127 290 (11.9) | 140 028 (13.8) |
| 3 | 33 791 (3.2) | 70 692 (6.9) |
| 4 | 16 568 (1.6) | 19 337 (1.9) |
| 5 | 44 282 (4.2) | 93 628 (9.2) |
The mean absolute difference between QRISK2-2011 and QRISK2-2010 was −0.16% for women and −0.38% for men. About 95.6% of women and 98.3% of men had QRISK2-2011 scores within 2% and 3% of the QRISK2-2010, respectively. The mean absolute difference between QRISK2-2011 and the original QRISK2-2008 predicted risks was −0.40% and −0.73% for women and men, respectively, and about 93% and 97% of all women and men will have QRISK2-2011 scores within 2% and 3% of the QRISK2-2008 scores, respectively.
Discrimination and calibration
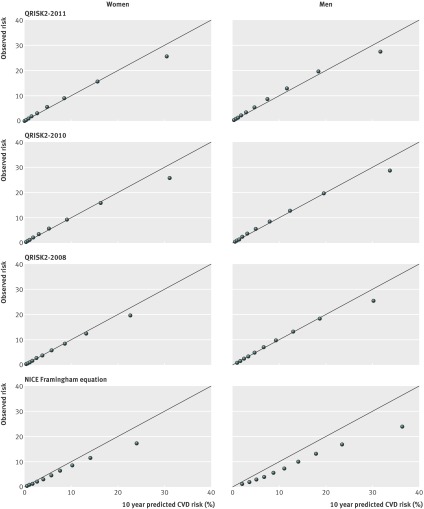
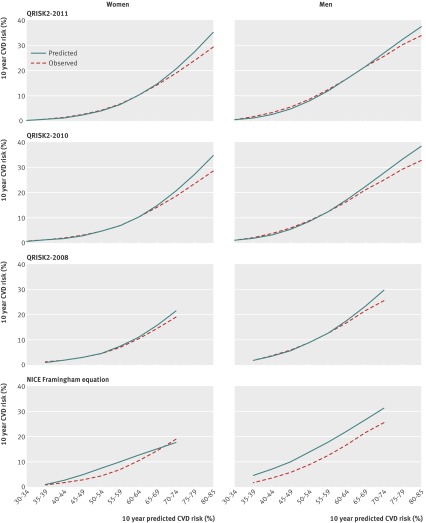
Figure 1 shows the calibration plots for the three versions of QRISK2 and the NICE version of the Framingham equation. The current version of QRISK2 and its predecessors show much better agreement between the observed risk and the predicted risk grouped by 10th of risk than does the NICE Framingham equation. All three versions of the QRISK2 prediction models show good calibration in all 10ths of risk, with the exception of the final 10th in both men and women (calibration slope, range 0.92-0.95). Similarly, Figure 2 shows the agreement between observed risk and predicted risk by age group for each of the QRISK2 prediction models and the NICE Framingham equation. All the QRISK2 prediction models show good agreement across the age groups, with a small divergence observed towards the latter age ranges (75 to 85 years). The NICE Framingham equation is, however, clearly miscalibrated, most noticeably for men, with a near constant over-prediction of about 5% across all age ranges (35-74 years). The observed risk across age groups in women shows a non-linear trend increasing with age, while the corresponding predicted risks exhibit a linear trend suggesting that age is not being adequately captured in this cohort of UK women.
Fig 1 Observed versus predicted 10 year risk of cardiovascular disease (CVD)
Fig 2 Observed and predicted 10 year risk of cardiovascular disease (CVD) by age group and sex
Table 4 presents performance data for the QRISK prediction models and the NICE Framingham equation. The R2 statistic (percentage of explained variation) is similar for QRISK2-2011 and QRISK2-2010 in men and women aged 30 to 84 years, indicating no change in performance of the newer QRISK2 model. Values for R2, restricted to those aged 35 to 74 years to enable comparison with the NICE Framingham equation, are about 4% to 5% higher for the QRISK2 models. The D discrimination statistic, where a higher score denotes better discrimination is higher (between 0.14 and 0.19 higher) for the QRISK2 models compared with the NICE Framingham equation, indicating improved prognostic separation. Finally, the area under the receiver operating characteristic curve is about 0.02 higher for QRISK2 in both men and women (restricted to those aged 35 to 74 years), whereas little difference is observed between QRISK2-2011 and QRISK2-2010 in those aged 30 to 84 years.
Table 4.
Performance data on QRISK2 and NICE Framingham equation on The Health Improvement Network
| Model | R2 (95% CI) | D statistic (95% CI) | AUROC (95% CI) |
|---|---|---|---|
| Women aged 30-84: | |||
| QRISK2-2011 | 48.3 (47.9 to 48.7) | 1.98 (1.96 to 1.99) | 0.835 (0.834 to 0.837) |
| QRISK2-2010 | 48.1 (47.7 to 48.6) | 1.97 (1.95 to 1.99) | 0.835 (0.833 to 0.837) |
| Men aged 30-84: | |||
| QRISK2-2011 | 41.6 (41.2 to 42.0) | 1.73 (1.71 to 1.75) | 0.809 (0.807 to 0.811) |
| QRISK2-2010 | 42.5 (42.0 to 42.8) | 1.76 (1.74 to 1.77) | 0.811 (0.809 to 0.812) |
| Women aged 35-74: | |||
| QRISK2-2011 | 40.1 (39.5 to 40.6) | 1.67 (1.65 to 1.69) | 0.802 (0.800 to 0.804) |
| QRISK2-2008 | 39.5 (36.6 to 42.4) | 1.66 (1.56 to 1.76) | 0.800 (0.798 to 0.803) |
| Men aged 35-74: | |||
| QRISK2-2011 | 33.1 (32.6 to 33.6) | 1.44 (1.42 to 1.46) | 0.771 (0.769 to 0.773) |
| QRISK2-2008 | 33.3 (28.9 to 37.8) | 1.45 (1.31 to 1.59) | 0.772 (0.769 to 0.774) |
| Women aged 35-74: | |||
| NICE Framingham equation | 34.2 (33.6 to 34.9) | 1.48 (1.46 to 1.50) | 0.776 (0.773 to 0.779) |
| Men aged 35-74: | |||
| NICE Framingham equation | 29.2 (28.7 to 29.7) | 1.31 (1.30 to 1.33) | 0.750 (0.747 to 0.752) |
AUROC=area under receiver operating characteristic curve.
Decision curve analysis
Table 5 shows how many of 1000 people would be identified as being at high risk (based on thresholds of 10%, 15%, and 20%) using either QRISK2-2011 or the NICE Framingham equation, and how many of these go on to experience a cardiovascular event compared with a strategy where all individuals are deemed at high risk. For women aged between 35 and 74 years there seems to be little difference between the two models, with both identifying similar numbers of women who experience a cardiovascular event. However, many more women would be incorrectly flagged as being at increased risk using the NICE Framingham equation. Table 5 also substantiates our earlier findings that in men aged between 35 and 74 years the NICE Framingham equation is currently over-predicting their risk of developing cardiovascular disease by about 5%. This table shows the similarity in the numbers of men who are identified at high risk and those who go on to experience a cardiovascular event if the NICE Framingham at 20% is compared with QRISK2-2011 at 15% or the NICE Framingham equation at 15% is compared with QRISK2-2011 at 10%.
Table 5.
Clinical outcomes basing treatment on varying high risk thresholds (5%, 10%, 15%, and 20%)
| Sexes per 1000 | No of people at risk | No of high risk cardiovascular events | |||
|---|---|---|---|---|---|
| High risk | Low risk | Identified | Not identified | ||
| Women aged 35 to 74 | |||||
| Treat all* | 1000 | 0 | 37 | 0 | |
| QRISK2-2011: | |||||
| ≥5% | 356 | 644 | 29 | 7 | |
| ≥10% | 194 | 806 | 22 | 15 | |
| ≥15% | 104 | 896 | 14 | 23 | |
| ≥20% | 48 | 952 | 8 | 29 | |
| NICE Framingham: | |||||
| ≥10% | 255 | 745 | 23 | 14 | |
| ≥15% | 128 | 872 | 14 | 22 | |
| ≥20% | 63 | 937 | 9 | 28 | |
| Women aged 30 to 85 | |||||
| Treat all* | 1000 | 0 | 40 | 0 | |
| QRISK2-2011: | |||||
| ≥5% | 344 | 656 | 34 | 6 | |
| ≥10% | 222 | 778 | 28 | 12 | |
| ≥15% | 156 | 844 | 23 | 17 | |
| ≥20% | 109 | 891 | 17 | 23 | |
| Men aged 35 to 74 | |||||
| Treat all* | 1000 | 0 | 54 | 0 | |
| QRISK2-2011: | |||||
| ≥5% | 504 | 496 | 47 | 7 | |
| ≥10% | 309 | 691 | 38 | 17 | |
| ≥15% | 191 | 809 | 27 | 27 | |
| ≥20% | 110 | 890 | 18 | 36 | |
| NICE Framingham: | |||||
| ≥10% | 494 | 506 | 45 | 9 | |
| ≥15% | 322 | 678 | 36 | 18 | |
| ≥20% | 206 | 794 | 27 | 27 | |
| Men aged 30 to 85 | |||||
| Treat all* | 1000 | 0 | 50 | 0 | |
| QRISK2-2011: | |||||
| ≥5% | 435 | 565 | 45 | 6 | |
| ≥10% | 284 | 716 | 37 | 13 | |
| ≥15% | 193 | 807 | 29 | 21 | |
| ≥20% | 129 | 871 | 22 | 28 | |
*All high risk people.
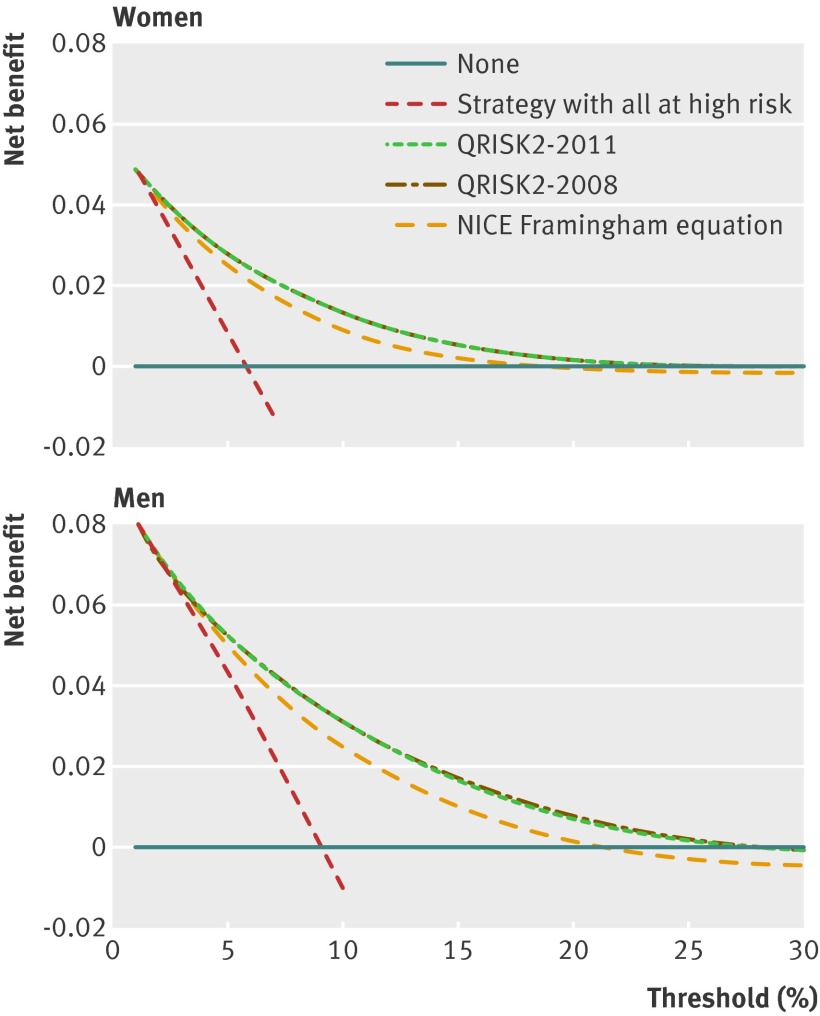
Figure 3 displays the net benefit curves for QRISK2-2011, QRISK2-2008, and the NICE Framingham equation for people aged between 35 and 74 years. At the traditional threshold of 20% used to designate an individual at high risk of developing cardiovascular disease, the net benefit of QRISK2-2011 for men is that the model identified five more cases per 1000 without increasing the number treated unnecessarily when compared with the NICE Framingham equation. For women the net benefit of using QRISK2-2011 at a 20% threshold identified two more cases per 1000 compared with not using any model (or the NICE Framingham equation). There seems to be no net benefit in using the 20% threshold for the NICE Framingham equation for identifying women who are at an increased risk of developing cardiovascular disease over the next 10 years. Both QRISK2 models perform similarly and clearly show greater net benefit across a range of thresholds compared with the NICE Framingham equation.
Fig 3 Decision curves for participants aged 34 to 75 years in The Health Improvement Network
Discussion
We carried out an independent evaluation of the performance of QRISK2-2011 on a large cohort of general practice patients using The Health Improvement Network (THIN) database, comprising two million patients contributing 11 862 252 person years of observation. The performance data presented in this article provide strong evidence for use of the updated QRISK2-2011 over the NICE Framingham equation. The performance of QRISK2-2011 is noticeably more impressive than the NICE version of the Framingham equation in discrimination, calibration, and clinical utility. The performance of QRISK2-2011 and its predecessor QRISK2-2010 are comparable, with no suggestion of deterioration in performance.
The NICE Framingham model for men is clearly miscalibrated, over-predicting the 10 year risk of developing cardiovascular disease by about 5%. For women, the equation seems to be performing poorly, with evidence to suggest that the model is inadequately capturing age. Furthermore, we have shown that the NICE Framingham equation has no clinical utility at the current threshold to identify those who are at an increased risk of developing cardiovascular disease. If the Framingham equation is to continue to be used and doctors advised to treat patients if their predicted risk is 20% or higher, then it is necessary for it to be recalibrated and updated to reflect current characteristics of the UK population. Without recalibration we urge caution in using the Framingham equation to identify high risk patients in the United Kingdom.
Strengths and limitations of the study
A major strength of this study is the size and the representativeness of the cohort, by including a large number of general practices using the EMIS computer system. A limitation of this study is the considerable amounts of missing data for total serum cholesterol to high density lipoprotein ratio both in the derivation and the external validation of QRISK2-2011. Despite the large amounts of missing data, information on all risk factors were available for 400 000 people, and 800 000 people had none or only one missing risk factor. However, we used current recommended approaches with multiple imputation to overcome the biases that occur when omitting people with incomplete data.25 26
Conclusions
We have provided an independent and external validation of QRISK2-2011 on a large cohort of general practice patients in the United Kingdom to predict the 10 year risk of developing cardiovascular disease. We have shown that the updated QRISK2-2011 model has not incurred any deterioration in performance and shows good potential clinical utility in predicting the risk of cardiovascular disease in those aged between 30 and 85 years. Furthermore, we have shown that QRISK2-2011 continues to be a considerable improvement over the NICE modification of the Framingham equation. For the Framingham equation to be even considered along side QRISK2-2011 for predicting the 10 year risk of developing cardiovascular disease, at a minimum we recommend that it should be updated and calibrated to the UK population. Finally, the current high risk threshold of 20% adopted by NICE to designate those at high risk of cardiovascular disease may need to be revisited, and there are likely to be different thresholds for women and men.
What is already known on this topic
Until recently cardiovascular risk prediction in the United Kingdom has been based on a NICE adjusted version of the US Framingham model, which has been shown to over-predict risk
QRISK2 was developed using a large cohort of UK patients and published in 2008 and updated in 2010 and 2011
Updated risk prediction models need to be independently and externally validated to objectively evaluate performance
What this study adds
Independent evaluation of QRISK2-2011 showed an improvement in performance over the NICE Framingham equation in a large external cohort of UK patients
Using current thresholds (20%) to designate those at high risk, the NICE Framingham equation has been shown to have no clinical usefulness in men or women
The NICE Framingham equation has been shown to consistently over-predict the 10 year risk of cardiovascular disease in men by about 5%
Contributors: GSC carried out the analysis and prepared the first draft, which was revised according to comments and suggestions from DGA. GSC is guarantor for the paper.
Funding: This research received no specific grant from any funding agency in the public, commercial, or not for profit sectors.
Competing interests: All authors have completed the ICMJE uniform disclosure form at www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: no support from any organisation for the submitted work; no financial relationships with any organisations that might have an interest in the submitted work in the previous three years; and no other relationships or activities that could appear to have influenced the submitted work.
Ethical approval: This study was approved by Trent multicentre research ethics committee.
Data sharing: No additional data available.
Cite this as: BMJ 2012;344:e4181
References
- 1.World Health Organization. Cardiovascular diseases (CVDs). Fact sheet No 317. WHO, 2011. www.who.int.
- 2.Department of Health. Putting prevention first—vascular checks: risk assessment and management. Department of Health, 2008.
- 3.National Institute for Health and Clinical Excellence. Lipid modification: cardiovascular risk assessment and the modification of blood lipids for the primary and secondary prevention of cardiovascular disease. 2008.http://guidance.nice.org.uk/CG67. [PubMed]
- 4.Anderson KM, Odell PM, Wilson PWF, Kannel WB. Cardiovascular disease risk profiles. Am Heart J 1991;121:293-8. [DOI] [PubMed] [Google Scholar]
- 5.Ridker PM, Buring JE, Rifai N, Cook NR. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: the Reynolds Risk Score. JAMA 1997;297:611-9. [DOI] [PubMed] [Google Scholar]
- 6.Ridker PM, Paynter NP, Rifai N, Gaziano JM, Cook NR. C-reactive protein and parental history improve global cardiovascular risk prediction: the Reynolds Risk Score for men. Circulation 2008;118:2243-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Collins GS, Altman DG. An independent external validation and evaluation of QRISK cardiovascular risk prediction: a prospective open cohort study. BMJ 2009;339:b2584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Collins GS, Altman DG. An independent and external validation of QRISK2 cardiovascular disease risk score: a prospective open cohort study. BMJ 2010;340:c2442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hippisley-Cox J, Coupland C, Vinogradova Y, Robson J, Brindle P. Performance of the QRISK cardiovascular risk prediction algorithm in an independent UK sample of patients from general practice: a validation study. Heart 2008;94:34-9. [DOI] [PubMed] [Google Scholar]
- 10.Hippisley-Cox J, Coupland C, Vinogradova Y, Robson J, Minhas R, Sheikh A, et al. Predicting cardiovascular risk in England and Wales: prospective derivation and validation of QRISK2. BMJ 2008;336:1475-82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hippisley-Cox J, Coupland C, Vinogradova Y, Robson R, May M, Brindle P. Derivation and validation of QRISK, a new cardiovascular disease risk score for the United Kingdom: prospective open cohort study. BMJ 2007;335:136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mayor S. Doctors no longer have to use Framingham equation to assess heart disease risk, NICE says. BMJ 2010;340:c1774. [Google Scholar]
- 13.Hippisley-Cox J, Coupland C, Robson J, Brindle P. Advantages of QRISK2 (2010): the key issue is ethnicity and extent of reallocation. Heart 2011;97:515. [DOI] [PubMed] [Google Scholar]
- 14.Moons KGM, Altman DG, Vergouwe Y, Royston P. Prognosis and prognostic research: application and impact of prognostic models in clinical practice. BMJ 2009;338:b606. [DOI] [PubMed] [Google Scholar]
- 15.Toll DB, Janssen KJM, Vergouwe Y, Moons KGM. Validation, updating and impact of clinical prediction rules: a review. J Clin Epidemiol 2008;61:1085-94. [DOI] [PubMed] [Google Scholar]
- 16.Rubin DB. Multiple imputation for nonresponse in surveys. Wiley, 1987.
- 17.Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA 1982;247:2543-6. [PubMed] [Google Scholar]
- 18.Royston P. Explained variation for survival models. Stata J 2006;6:83-96. [Google Scholar]
- 19.Royston P, Sauerbrei W. A new measure of prognostic separation in survival data. Stat Med 2004;23:723-48. [DOI] [PubMed] [Google Scholar]
- 20.Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology 2010;21:128-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vickers AJ, Cronin AM, Elkin EB, Gonen M. Extensions to decision curve analysis, a novel method for evaluating diagnostic tests, prediction models and molecular markers. BMC Med Inform Decis Mak 2008;8:53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making 2006;26:565-74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.R: a language and environment for statistical computing [program]. 2012. www.R-project.org.
- 24.StataCorp. Stata statistical software: release 11 [program]. StataCorp, 2009.
- 25.Burton A, Altman DG. Missing covariate data within cancer prognostic studies: a review of current reporting and proposed guidelines. Br J Cancer 2004;91:4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vergouwe Y, Royston P, Moons KGM, Altman DG. Development and validation of a prediction model with missing predictor data: a practical approach. J Clin Epidemiol 2010;63:205-14. [DOI] [PubMed] [Google Scholar]