Unraveling Metal-insulator Transition Mechanism of VO₂ Triggered by Tungsten Doping

Abstract

Understanding the mechanism of W-doping induced reduction of critical temperature (T_C) for VO₂ metal-insulator transition (MIT) is crucial for both fundamental study and technological application. Here, using synchrotron radiation X-ray absorption spectroscopy combined with first-principles calculations, we unveil the atomic structure evolutions of W dopant and its role in tailoring the T_C of VO₂ MIT. We find that the local structure around W atom is intrinsically symmetric with a tetragonal-like structure, exhibiting a concentration-dependent evolution involving the initial distortion, further repulsion, and final stabilization due to the strong interaction between doped W atoms and VO₂ lattices across the MIT. These results directly give the experimental evidence that the symmetric W core drives the detwisting of the nearby asymmetric monoclinic VO₂ lattice to form rutile-like VO₂ nuclei, and the propagations of these W-encampassed nuclei through the matrix lower the thermal energy barrier for phase transition.

Monoclinic/rutile vanadium dioxide VO₂ (M1/R), a model metal-insulator transition (MIT) material, displays a first-order transition from a monoclinic insulating phase to a tetragonal metallic phase at a critical temperature (T_C) of 341 K, accompanied by a reversible switch in optical transmittance/reflectance in the infrared range¹. This dramatic phase transition makes VO₂ potentially useful for ‘smart’ optical and electrical switches, which yet requires the regulation of T_C to around room temperature (RT)²,³,⁴,⁵,⁶. The most effective route for appreciable reduction of T_C is doping some donor impurity atoms, which could be easily realized by chemical substitution methods⁷,⁸,⁹,¹⁰. In particular, doping the V sublattice with W is very attractive since it yields a pronounced reduction in T_C by ~20 K/at.%W for the bulk and by ~50 K/at.%W for the nanostructure, and even metallic ground state is realized for W concentration of ≥8 at.%⁷,⁸. Therefore, W-doped VO₂ system has been widely used as key building blocks for some smart devices, such as thermochromics and variable-reflectance mirrors⁸,⁹. However, there are still many intriguing questions to be resolved: why such a small amount of W dopant could introduce so large a reduction in T_C and what is the underlying physical mechanism to drive the MIT transition when W is involved? Right answers to these questions would enrich our understanding on the exact interplay of electron and lattice of correlated materials during MIT mechanism.

Several experimental investigations have been carried out on the W_xV_1−xO₂ systems and attempted to present some structural and mechanistic explanations¹⁰,¹¹,¹². By using small-angle X-ray scattering and X-ray absorption methods, Tang et al. considered that the charger transfer from W ions weakens the V−V pairs, promoting the structural transformation from monoclinic to rutile¹¹. Also, Booth et al. found that a significant expansion in certain crystal axes induced by W dopants breaks the Peierls-paired V ions, leading to the reduction of T_C¹². However, these studies are limited to heavily-doped samples with relatively lower T_C, in which the VO₂ host lattice is close to rutile phase at RT. As a result, only the final state affected by W doping is obtained, which can be found from their stable and almost invariable local structure (LS) around W atoms. On the other hand, the interatomic distances of W dopants are short in heavily-doped samples; therefore the strong coupling effect between the neighboring W atoms makes it difficult to isolate the structure and contribution of a single W atom from its environment. Therefore, the real W local structure and its effect on the surrounding monoclinic VO₂ matrix, as well as its evolutions during MIT remain obscure. In order to attain physical insights into W-induced T_C reduction, one promising way is to conduct detailed structural characterizations on specimen with wide concentration gradients, which exhibits the reduction of T_C from several to dozens of degrees. For this purpose a rather suitable tool is X-ray absorption fine structure (XAFS) spectroscopy thanks to its element selectivity and good sensitivity to local structures¹³, which allows one to separately probe and compare the LS around V and W atoms in a same sample, even in the dilute doping case. In fact, the capability of XAFS has been demonstrated in a recent work that provides a very distinct, qualitative signature for the monoclinic-to-tetragonal transformation in VO₂¹⁴.

In this work, to completely understand the T_C reduction mechanism induced by W-doping, we study systematically the LS around W and V atoms in single crystals W_xV_1−xO₂ with a wide doping range from dilute to heavy concentrations (x = 0.54%, 0.95%, 1.45% and 2.38%) using the XAFS technique. These representative concentrations allow us to present for the first time: (i) a clear figure of LS around an isolated W dopant in the monoclinic VO₂ lattice, and (ii) the reconstruction of concentration-dependent evolutions of W and V structures across the VO₂ MIT.

Results

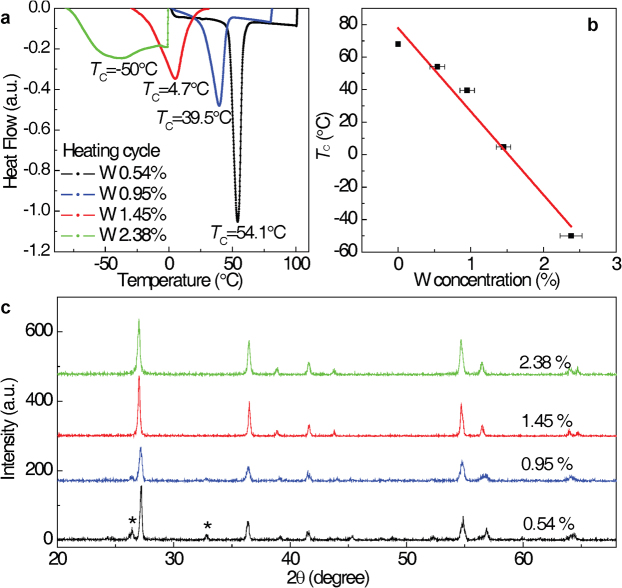
The T_C and the crystalline structures for the W_xV_1−xO₂ samples are determined by DSC and XRD as shown in Figure 1. DSC analysis indicates that increasing W content x from 0.54% to 2.38% significantly reduces T_C from 54.1 to −50°C (Figure 1a). The plot of T_C as a function of W concentration in Figure 1b shows an approximate linear relation with a slope of ~20 K/at.%W, comparable with that ~22 K/at. %W for thin films reported previously⁷. The RT XRD patterns displayed in Figure 1c exhibit two characteristic diffraction peaks (asterisks) assignable to the monoclinic phase for the x = 0.54% sample, suggesting the primary monoclinic VO₂ structure. At higher doping level (x≥1.45%), only the diffraction peaks corresponding to tetragonal phase can be observed¹⁵, demonstrating the complete transformation into rutile phase of VO₂. It should be noted that the magnitude of the phase transition is weakened with increasing W concentration, reflected by the peaks in DSC results, the phenomenon of which is well known in heavy atoms (W, or Mo) doped VO₂⁷,¹⁶. Although it is truly a practical problem, the W-doping is known as the most effective route to reduce T_C, and has been considered as the prototypical model in understanding the mechanism by which the T_C of VO₂ MIT could be manipulated.

Figure 1. The T_C and the overall structures for the prepared samples W_xV_1−xO₂.

(a) The DSC measurement results for samples with different W doping concentration. (b) The plot of transition temperature T_C as function of W composition x for W_xV_1−xO₂ single crystals. T_C values are effectively reduced by W doping at ~20 K/at.% W. (c) The XRD patterns measured at room temperature for W_xV_1−xO₂ samples. The diffraction peaks correspond to the rutile phase, while the additional peaks (indicated by asterisks) correspond to the monoclinic phase.

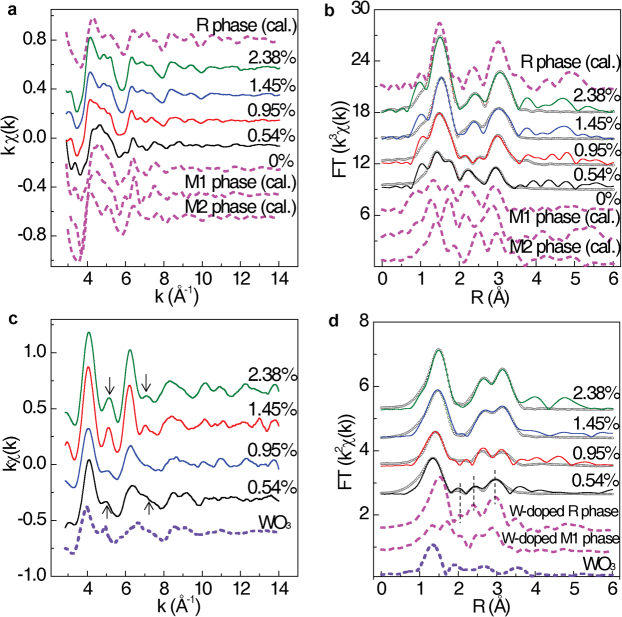
To obtain detailed structural information, we performed element-specific XAFS measurements on both host V and doped W atoms. Figures 2(a) and 2(b) show the V K-edge extended XAFS (EXAFS) oscillation χ(k) functions and their Fourier transforms (FTs), respectively, along with the calculated EXAFS data for VO₂ with monoclinic (M1, space group P21/c), rutile (R, space group P42/mnm) and another monoclinic (M2, space group C2/m) phases as the references. With increasing W content, the LS around V atoms gradually evolve into that in tetragonal phase, as indicated by the featured changes in the k range of 4–8 Å⁻¹ (Figure 2a)¹⁴. Correlated changes can be identified in FTs profiles (Figure 2b). The VO₂ lattice structure of 0.54% W doped sample remains in the monoclinic phase, because its FTs curve keeps the main features with that of pure monoclinic phase. When W content increases to 0.95%, the two V-O split peaks merge into a single peak at 1.48 Å and the V–V1 peak at 2.12 Å disappear, implying that the initial monoclinic VO₂ phase has been largely distorted towards tetragonal phase at RT. For the 1.45% and 2.38% W doped samples, the FTs curves match well with that of calculated tetragonal VO₂ phase. The structural transition from monoclinic to tetragonal phase with increasing W concentration clearly confirms the reduction of T_C, consistent with the XRD and DSC results.

Figure 2. XAFS results for W_xV_1−xO₂.

(a) The V K-edge EXAFS oscillations and (b) their Fourier transforms for W_xV_1−xO₂ samples, along with the VO₂ theoretical results of monoclinic (M1), rutile (R) and another monoclinic (M2) phases for references. (c) The W L₃-edge EXAFS oscillations and (d) their Fourier transforms, along with the reference WO₃ result, and the simulated curves for W-substituted monoclinic and tetragonal VO₂ phases. Fitting results are plotted as open circles.

Of note, the formation of the metastable M2 phase that has partial dimerization of the V–V chains was reported in the monoclinic to rutile phase transformation¹⁰,¹⁵,¹⁷,¹⁸,¹⁹,²⁰,²¹. However, metastable M2 phase is indeed tightly associated with the strains, and are nearly all found within the nanostructures that have strong surface-induced stress to stabilize M2 phase¹⁰,¹⁵,¹⁷, while there is no evidence for isolation of stable M2 phase for large VO₂ crystallites without apparent stresses and defects¹⁸. Even in doped bulk VO₂ crystallites, only the Al and Cr doping that could result in the increase of T_C are reported to stabilize the M2 phase¹⁹,²⁰. Compared with W ions, these dopants have smaller ionic radii and are acceptor impurities, which would lead to the differentiation of two types of V atoms, corresponding to the proposed M2 monoclinic phase²¹. Hence, we consider that the intermediate M2 phase can be precluded in our highly crystalline W-doped VO₂, in agreement with the previous reports¹²,²². This conclusion can be further confirmed by the significant differences in the oscillation χ(k) and FT curve between the calculated spectrum of M2 structure and our samples.

We further focus on the LS around W atoms that could be deduced from W L₃-edge XAFS data (Figures 2c and 2d). The LS around W atom should be symmetric in nature similar to the reference WO₃. This is inferred from the fact that these samples, like WO₃, also present two peaks at 4.0 and 6.2 Å⁻¹ in the low k region (3–8 Å⁻¹) of the kχ(k) oscillation curves (Figure 2c), and only one prominent W-O peak without splitting appears in the FTs curves (Figure 2d). It should also be noted that the symmetry around W core at the low concentration (< 1%) is distorted due to the significant compression of almost isolated W dopants by the overwhelmingly asymmetric monoclinic VO₂ lattices, which can be reflected by the missed fine features (marked by arrows) in the 3–8 Å⁻¹ region, as well as by the damped oscillations in the 8–14 Å⁻¹ region. Furthermore, we have also calculated the W L₃-edge FTs spectra for the W-substituted monoclinic and tetragonal VO₂ phases. Interestingly, the FT curve of low-doped (0.54%) sample is more similar to the calculated spectrum of the W-substituted tetragonal phase than that of W-substituted monoclinic phase which shows an obvious splitting for W–O peaks. Only a slight difference can be found for the position of W–O peaks which shifts from 1.35 Å of WO₃ toward 1.51 Å of W-substituted tetragonal phase with increasing W concentration. Although the host VO₂ is in monoclinic structure inferred by XRD results, the local environment of W dopant in the monoclinic VO₂ matrix has yet assembled the tetragonal-like structure with compressed W–O pairs, implying the W-doping induced structural transition of the neighboring host VO₂ lattice. Increasing x, the W–V1 and W–V2 peak positions (2.42 and 2.97 Å, respectively) increase to 2.67 Å and 3.13 Å, respectively, along with the enhancement of their intensities, implying the expansion of W local structures. The FT curves for highly doped samples (x≥0.95%), particularly the W-V peaks, are almost independent of the W concentration, and this trend continues until the heavy doping level of 5% ≤ x ≤33% as reported in Ref. 11. These indicate that the LS around W atoms would not undergo remarkable changes when the VO₂ host lattice is already in or near the rutile phase if the W concentration reaches a certain level, confirming the intrinsic and stable nature of symmetric W structure.

The quantitative structural information was extracted from EXAFS data fitting using the ARTEMIS module of IFEFFIT. The extracted parameters are summarized in Figure 3 and Table I and II. The obtained V–O and V–V distances show that the monoclinic VO₂ host lattice is largely distorted in the x = 0.95% sample, and has completely transformed into tetragonal rutile structure when x increases to 1.45%. Because of the slight distortion of W atoms by the surrounding VO₂ lattice, the EXAFS data for x = 0.54% sample were fitted using the monoclinic phase with degenerate W–O bonds. The rest three can be fitted well by using tetragonal rutile phase, due to their higher symmetric structures. The trend in Figure 2b shows steady increase of the average W–O and W–V bond distances, confirming the gradual expansion and relaxation of LS around W atoms with increasing W content. Here, we have found the expansion of both W–O and W–V1 pairs, which however are shown constant in Ref. 12, with the W concentration. The whole expansion observed here can be ascribed to the distinct W concentration gradient, thus reflecting the real evolution of LS of W dopants in monoclinic VO₂ across MIT.

Figure 3. The bond distances as a function of W concentration.

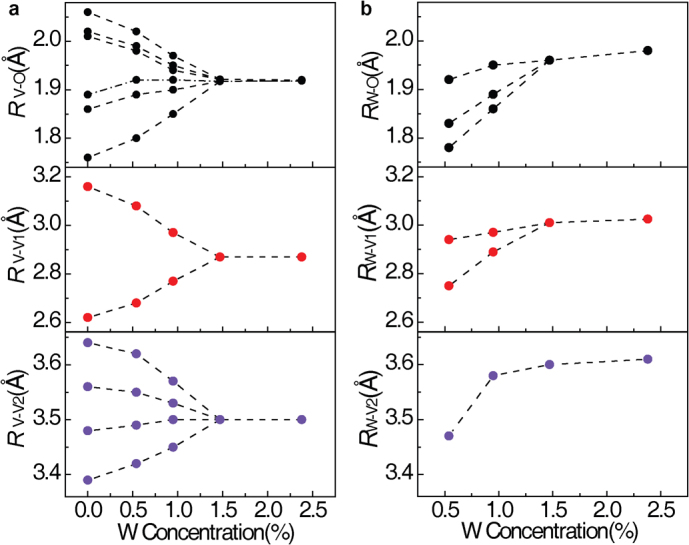
The bond distances of the nearest three shells of (a) V and (b) W as the center atom, based on the XAFS fitting results of each sample with different W doping concentration.

Table 1. EXAFS fitting results deduced from V K-edge spectra of W_xV_1−xO₂ samples.

W %	R-factor	V−O (Å) (±0.02)	σ2 (103 Å)	V−V (Å) (±0.02)	σ2 (103 Å)	ΔE0 (eV)
0.54	0.029	1.80/1.89/1.92	3.1 (±0.3)	2.68/3.08	2.9 (±1.7)	3.7 (±1.6)
		1.98/1.99/2.02	4.0 (±1.1)	3.42/3.49/3.55/3.62	4.0 (±2.1)
0.95	0.038	1.85/1.90/1.92	2.8 (±2.0)	2.77/2.97	3.7 (±2.3)	−5.5 (±2.3)
		1.94/1.95/1.97	3.7 (±1.9)	3.45/3.50/3.53/3.57	5.8 (±1.6)
1.54	0.032	1.92	8.2 (±3.5)	2.87	3.0 (±1.8)	−3.1 (±2.6)
				3.50	4.5 (±2.5)
2.38	0.027	1.92	8.5 (±4.1)	2.87	2.8 (±1.9)	4.3 (±1.1)
				3.50	3.6 (±2.7)

Table 2. EXAFS fitting results deduced from W L₃-edge spectra of W_xV_1−xO₂ samples.

W%	R-factor	V–O (Å) (±0.02)	σ2 (10−3 Å)	V–V (Å) (±0.02)	σ2 (10−3 Å)	ΔE0 (eV)
0.54	0.049	1.78/1.83/1.92	5.1 (±1.3)	2.75/2.94/3.47	9.2 (±2.6)	−3.1 (±1.6)
0.95	0.059	1.86/1.89/1.95	4.7 (±3.0)	2.89/2.96/3.57	3.7 (±2.3)	8.1 (±1.7)
1.54	0.023	1.96	3.6 (±1.3)	3.01/3.60	6.2 (±2.1)	−2.1 (±1.5)
2.38	0.028	1.98	3.2 (±1.1)	3.10/3.63	5.6 (±1.5)	−3.4 (±0.8)

Discussion

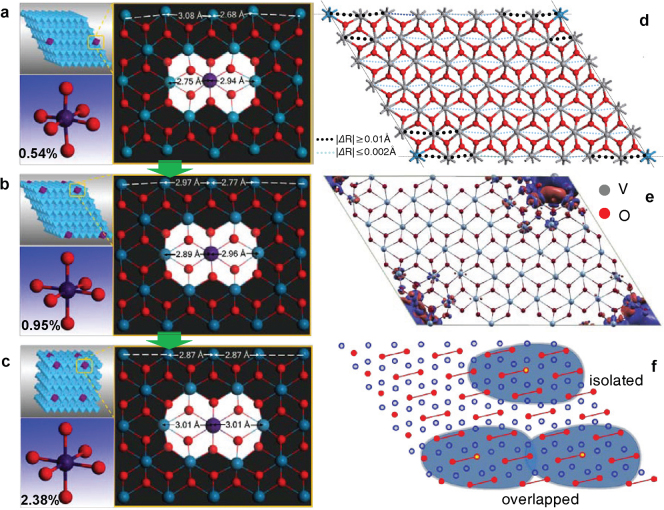
Summarizing our experimental results, we schematically show in Figures 4a~c the crystal structure variations for W–doped VO₂ samples with three representative concentrations (0.54%, 0.95% and 2.38%). For the purpose of clarity, we magnify the structural model around W atoms in a planar visual. At first sight, the LS around W atom highlighted in white exhibits two prominent features: the increased symmetry and the expanded volume. A point worth emphasizing is that several XAFS studies by Patridge et al.²³, Booth et al.¹², and Whittaker et al.¹⁰, as well as the static lattice calculations by Netsianda et al.²⁴, had suggested that dopants induce a local structural distortion towards high symmetry of rutile phase, which is generally accepted in the work of doping-induced phase transition of VO₂. Moreover, our results not only confirm this basic model, but also demonstrate a concentration-dependent evolution of LS of W atoms. We find that the LS of W atom at low concentration is tetragonal-like but distorted by surrounding asymmetric monoclinic VO₂ lattice; at high doping level, the repulsion of these distorted tetragonal units drives them to restore and stabilize the symmetric structure. This structural evolution of W atoms reflects the strong interaction between W and VO₂ structures that triggers the structural derivations of near VO₂ lattice from asymmetric monoclinic phase towards more symmetric.

Figure 4. Models and theoretical calculations.

Models of LS distortions of three representative doped concentrations (a) 0.54%, (b) 0.95%, and (c) 2.38%. The white area displays the LS evolutions around W atoms. The variations of average W-W distances and [WO₆] octahedral geometries are shown in the left top and bottom panel, respectively. (d) The relaxed structure projected along [010] axis and (e) the corresponding spatial redistribution of charge density of W doped VO₂ with about 0.6% concentration; |ΔR| (|ΔR| = |R_distorted−R_previous|) based on calculation results give a distinct pattern of doped effects. The blue and red isosurfaces correspond to charge densities of 0.005 e/Å⁻³ and −0.005 e/Å⁻³, respectively. (f) A schematic diagram of concentration scaled influences of W dopants in VO₂, in which shows the low concentration with isolated dopants and the high concentration with interactional dopants.

To reveal the reason why a small amount of W doping lowers the T_C, we performed density functional theory (DFT) calculations with Vienna Ab-initio Simulation Package (VASP) code based on the atomic structural parameters by XAFS. The calculations employed the projector augmented wave (PAW) method and the generalized gradient approximation (PBE-GGA) for electron exchange-correlation interaction²⁵,²⁶. A super large 4×3×5 supercell with 432 atoms containing 143 V atoms, 288 O atoms and 1 W atom, corresponding to ~0.6 % W concentration was used. At this concentration, the VO₂ lattice is of the monoclinic structure in the temperature range from 0 K to RT. We first considered the spatial extension of the influence on the atomic and electronic structures of VO₂ by W doping. Figure 4d shows the relaxed structure projected along [010], in which the distortion degree of VO₂ lattice is characterized by the difference of bond length |ΔR| (|ΔR| = |R_distorted−R_previous|). We can find that the structural change shows a dopant-centred nature, since |ΔR| near W dopants are all larger than 0.01 Å whereas those far away from W atoms are ≤0.002 Å. Furthermore, we examine the spatial redistribution of charge density upon doping W ions (Figure 4e). Also, the electron density pile-up is only significant in the neighborhood of W atoms along or cross the c axis. This is reasonable because the VO₂ structures away from W atoms remain in the insulating monoclinic phase which inhibits electron mobility²⁷. Importantly, the relaxed structures in the theoretic calculations confirm that W dopants could induce large variations in both atomic and electronic structures of nearby VO₂ lattice. In this sense, the corporation of local lattice disorder induced by the insert of W ions with larger volume, and the pile-up of itinerant electrons on the neighboring V-sites released by W ions with higher valence suppress the dimerized lattice distortion and destabilize insulating phase of VO₂.

On the basis of experimental and theoretical results, we consider that the W-doping effect is confined in a local area (covered by each blue area of W cores schematically illustrated in Figure 4f), in which the VO₂ has accomplished the phase transition, and can be seen as the nucleus for MIT. Due to the existences of these pre-MIT nuclei, the thermal energy needed to trigger MIT is lowered compared with that for pure VO₂ single crystals²⁸,²⁹. At the low doping concentration, the nucleus can be seen as isolated, while at higher concentration two neighboring nuclei could touch each other due to the increased average W-W distance (the overlapped area shown in Figure 4f). Meanwhile, the XAFS results of the steady expansion of W structures and significant phase transition of VO₂ lattices suggested the propagation of W-induced changes towards the farther V atoms. Therefore, the increased formation of nuclei, along with their percolation in the materials, will further lowers thermal energy to fulfill the whole phase transition as expected. This picture of concentration scaled influence of W dopants is somewhat like the “metallic nanopuddles” in thermal-induced pure VO₂ MIT process³⁰, in which Qazilbash et al. have revealed that nanoscale percolative MIT took place first with metallic puddles in insulating host, and subsequent heating drives its complete transformation to metallic phase.

In conclusion, the behavior of an isolated W dopant and its influence on the VO₂ host lattice are for the first time figured out by X-ray absorption spectroscopy coupled with the first-principle calculations, which helps us to unravel the mechanism of the reduction of MIT T_C induced by W-doping. A clear atomic structure of isolated W dopant has been unveiled, which possesses an intrinsically symmetric tetragonal-like structure, driving the detwisting of the nearby asymmetric monoclinic VO₂ lattice towards rutile phase. These W-encompassed rutile-like VO₂ regions in fact act as nuclei for the “metallic puddles” which propagate through the host matrix, thus lowering the thermal activation energy across phase transition. These results also provide a clear indication to modulate the T_C by doping impurity with symmetry corresponding to that of targeted structure, which has been noticed in some syntheses.

Methods

Synthesis and Characterization

Single crystals of W_xV_1−xO₂ used in this study were prepared by reacting vanadyl acetylacetonate (VO(acac)₂) with the required amount of sodium tungstate (Na₂WO₄) in aqueous solution at 200°C for 12 hours. The resultant products were calcined under argon at 700°C for 8 hours. The phase homogeneity and the reversible transition characteristics of the samples were confirmed by X-ray diffraction (XRD) and differential scanning calorimetry (DSC). XAFS data at the W L₃ and V K-edges were collected in fluorescence and transmission modes, respectively, at ambient temperature (25°C) on beam lines U7B and U7C of the National Synchrotron Radiation Laboratory, China. The storage rings of NSRL were operated at 0.8 GeV with the maximum current of 200 mA. The hard x-ray beam was from a three-pole superconducting Wiggler with a magnetic field intensity of 6 T. The fixed-exit Si(111) flat double crystals were used as monochromator. Ionization chambers filled with Ar/N₂, and a 7-element pure Ge solid-state detector were used for the transmission and fluorescence x-ray detection, respectively.

XAFS data analysis

The EXAFS signals, χ(k), were extracted from the absorption raw data, μ(E) from the averaged experimental spectra of four repeated scans, by using the ATHENA module³¹ implemented in the IFEFFIT package³² and the USTCXAFS software packages³³. The χ(k) data were weighted by k³ and k² for V and W, respectively. The normalized absorption data were Fourier transformed using a k-space range of 2.8–14 Å⁻¹. The theoretical scattering amplitude and phase shift functions for all the paths were calculated by using the FEFF7 code. The V K-edge XAFS spectra below and above 0.95% W concentration can be fitted well using the structural model of monoclinic VO₂ (P21/c) and tetragonal VO₂ (P42/mnm) based on ICSD #15889 and #4110, respectively. According to the T_C, W L₃-edge XAFS spectra below and above 0.95% concentration was fitted in the framework of monoclinic and tetragonal phase, respectively. The FEFF input files for the fitting of W L₃-edge XAFS spectra was altered by replacing the V core in the monoclinic and tetragonal FEFF input files with W. The fitting was done in the R range [0.8, 3.8] Å for all the data. In order to decrease the number of independent parameters, in the fitting procedure the coordination number was fixed to the nominal value for each scattering path, because the coordination numbers are not changed during MIT. For the monoclinic phase, the variation of M–O (M = V and W) bond distances in the range of 1.76–2.03 Å are classified into three groups, i.e., (1.76 Å), (1.86 Å, 1.87 Å), (2.00 Å, 2.01 Å and 2.04 Å) according to their contribution to the scattering paths, and four kind M–V2 bond distances (3.36 Å, 3.46 Å, 3.56 Å and 3.66 Å) are included in the fitting. For each shell, the interatomic distance R, the Debye-Waller factor σ², and the edge-energy shift ΔE₀ were allowed to vary.

Author Contributions

X.G.T. and T.Y. contributed equally to this work, performed the experiments, collected and analyzed the data, and wrote the paper; R.L., X.G.T. and C.Z.W. synthesized the samples; T.Y. Y.J.F. and H.C. performed XAFS experiments; Z.H.S. helped with data analysis; X.Y., W.Q.Z. and Q.H.L. performed theoretical calculations; Y.X. and S.Q.W. conceived the experiments, analyzed results, and wrote the paper.