The Original Michaelis Constant: Translation of the 1913 Michaelis-Menten Paper

Abstract

Nearly 100 years ago Michaelis and Menten published their now classic paper (Michaelis, L., and Menten, M. L. (1913) Die Kinetik der Invertinwirkung, Biochemische Zeitschrift 49, 333–369), in which they show that the rate of an enzyme-catalyzed reaction is proportional to the concentration of enzyme-substrate complex predicted by the Michaelis-Menten equation. Because the original text was written in German, yet is often quoted by English speaking authors, we undertook a complete translation of the 1913 publication, which we provide as an online supplement (http://pubs.acs.org). Here we introduce the translation, describe the historical context of the work, and show a new analysis of the original data. In doing so, we uncovered several surprises that reveal an interesting glimpse into the early history of enzymology. In particular, our re-analysis of Michaelis and Menten’s data using modern computational methods revealed an unanticipated rigor and precision in the original publication and uncovered a sophisticated, comprehensive analysis that has been overlooked in the century since their work was published. Michaelis and Menten not only analyzed initial velocity measurements, but they also fit their full time course data to the integrated form of the rate equations, including product inhibition, and derived a single global constant to represent all of their data. That constant was not the Michaelis constant, but rather, V_max/K_m, the specificity constant times the enzyme concentration (k_cat/K_m*E₀).

In 1913 Leonor Michaelis and Maud Leonora Menten published their now classic paper, Die Kinetik der Invertinwerkung (1). They studied invertase, which was so named because its reaction results in the inversion of optical rotation from positive for sucrose to a net negative for the sum of fructose plus glucose.

$$\text{Sucrose}\stackrel{\mathit{Invertase}}{\to }\text{Fructose}+\text{Glucose}$$

After receiving her M.D. degree in 1911 at the University of Toronto, Maud L. Menten (1879 – 1960) worked as a research assistant in the Berlin laboratory of Leonor Michaelis (1875–1949). She monitored the rate of the invertase-catalyzed reaction at several sucrose concentrations by careful measurement of optical rotation as a function of time, following the reaction to completion. Their goal was to test the theory that “invertase forms a complex with sucrose that is very labile and decays to free enzyme, glucose and fructose” leading to the prediction that “the rate of inversion must be proportional to the prevailing concentration of sucrose-enzyme complex.” Michaelis and Menten recognized that the products of the reaction were inhibitory, as known from prior work by Henri (2). Although most enzyme kinetic studies at the time had sought an integrated form of the rate equations, Michaelis and Menten circumvented product inhibition by performing initial velocity measurements where they would only “need to follow the inversion reaction in a time range where the influence of the cleavage products is not noticeable. The influence of the cleavage products can then be easily observed in separate experiments.” Michaelis and Menten performed initial velocity measurements as a function of variable sucrose concentration and fit their data based upon the assumption that the binding of sucrose was in equilibrium with the enzyme and the postulate that the rate of the reaction was proportional to the concentration of the enzyme-substrate complex. By showing that the sucrose concentration dependence of the rate followed the predicted hyperbolic relationship, they provided evidence to support the hypothesis that enzyme catalysis was due to formation of an enzyme-substrate complex, according to the now famous Michaelis-Menten equation, and obtained, “for the first time, a picture of the magnitude of the affinity of an enzyme for its substrate.” They also derived expressions for competitive inhibition and quantified the effects of products on the rates of reaction in order to get estimates for the dissociation constants for fructose and glucose. As a final, comprehensive test of their model, they analyzed full time course kinetic data based upon the integrated form of the rate equations, including product inhibition. Thus, as we describe below, they accomplished a great deal more than is commonly recognized.

Notes on the Translation

The style of the paper is surprisingly colloquial, making us realize how formal we are in our present writing. In translating the paper, which we provide here as a supplement, we have attempted to retain the voice of the original, while using terms that will be familiar to readers in the 21^st century. Michaelis and Menten referred to the enzyme as the “ferment,” but we adopt the word “enzyme” based upon contemporaneous papers written in English. Their reference to initial velocity literally translates as the “maximum velocity of fission” which we interpret to mean the maximum velocity during the initial phase of the reaction before the rate begins to taper off due to substrate depletion and product inhibition; and so, we have adopted the conventional “initial rate” terminology. The term Restdissoziationskurve, which is not commonly used, posed some problems in translation. We chose to rely upon the context in which it was used relative to mathematical expressions describing the fractional saturation of an acid as a function of pH, implying the meaning “association curve” in modern terms.

By modern standards there are a number of idiosyncrasies, including the lack of dimensions on reported parameters and some very loose usage of concepts. For example, on page 23 of our translation, the authors attribute the inhibitory effect of ethanol, with an apparent K_d = 0.6 M, as entirely due to a change in character of the solvent and accordingly assign K_alcohol = ∞; however, we now believe that for most enzymes a solution containing 5% alcohol is not inhibitory due to solvent effects. A general feature of the paper is an inexact use of the terms quantity, amount, and concentration. In most cases the authors mean concentration when they say amount. In the tables they used the unit “n” but in the text they generally used N to represent concentration. Throughout the translation, we have converted to the use of M to designate molar concentrations. Of course, Michaelis and Menten had no way of knowing the enzyme concentration in their experiments; so all references were to relative amounts of enzyme added to the reaction mixtures. Surprisingly lacking was any mention of the source of the enzyme or the methods used for its preparation.

We have tried to reproduce the overall feeling of the paper with approximately the same page breaks and layout of text and figures. We have retained the original footnotes at the bottom of each page and interspersed our own editorial comments. In general, we translated the paper literally, but corrected two minor math errors (sign and subscript), which were not propagated in subsequent equations in the original text. All of the original data for each of the figures was provided in tables, a useful feature lacking in today’s publications. Availability of the original data allowed us to redraw figures and reanalyze the results using modern computational methods. We have attempted to recreate the style of the original figures, with one exception. In Figs. 1–3, individual data points were plotted using a small x with an adjacent letter or number to identify the data set. In attempting to recreate this style, we found the labeling to be unreliable and ambiguous, so we have resorted to the use of modern symbols.

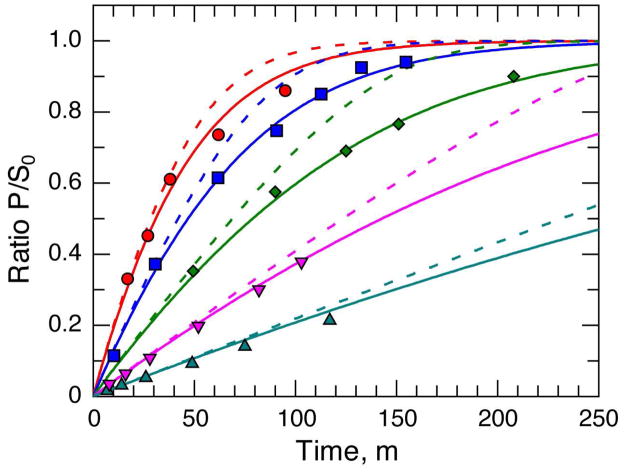
Fig. 1. Global fit to the data of Michaelis and Menten.

The data from Michaelis and Menten (reproduced in Table 1) were fit by simulation using KinTek Explorer software (9) with the only variable being k_cat*E₀ to get the smooth lines; an arbitrary, low enzyme concentration was chosen to perform the simulation. Data are for starting concentrations of sucrose of 20.8 (▴), 41.6 (▾), 83 (◆), 167 (■), and 333 (●) mM from Table 1. Data at times longer than 250 m were included in the fit but are not displayed in the figure. The dashed lines show the kinetics predicted if product inhibition is ignored.

Historical Perspective

Perhaps the unsung hero of the early history of enzymology is Victor Henri, who first derived an equation predicting the relationship between rate and substrate concentration based upon a rational model involving the formation of catalytic enzyme-substrate complex (2). However, as Michaelis and Menten point out, Henri made two crucial mistakes, which prevented him from confirming the predicted relationship between rate and substrate concentration. He failed to account for the slow mutarotation of the products of the reaction (equilibration of the α and β anomers of glucose) and he neglected to control pH. Thus, errors in his data precluded an accurate test of the theory. Otherwise, we would probably be writing about the Henri equation.

As they are usually credited, Michaelis and Menten measured the initial velocity as a function of sucrose concentration and derived an equation that approximates the modern version of the Michaelis-Menten equation:

$$\nu =C·\mathrm{\Phi }·\frac{[S]}{[S]+k}$$

• where C · Φ = V_max, Φ = total enzyme concentration, and k = K_S.

In this expression, C is k_cat multiplied by a factor to convert change in optical rotation to concentration of substrate converted to product.

Michaelis and Menten overlooked the obvious double reciprocal plot as a means to obtain a linear extrapolation to infinite substrate concentration. Rather, Michaelis relied upon his experience in analysis of pH dependence (although the term, pH, had not yet been defined). They re-plotted their data as rate versus the log of substrate concentration, in a form analogous to the Henderson-Hasselbalch equation for pH dependence, to be published four years later (3). Michaelis and Menten then followed a rather complicated procedure for estimating K_S from the data without knowing the maximum velocity of the reaction. They derived an expression defining the slope of the plot of initial rate against the log of the substrate concentration at V/2 (in their terminology V = v/(C·Φ), expressed as a fraction of the maximum velocity). They reasoned that the curve of V versus log [S] should be approximately linear at around V/2 with a slope of 0.576. The scale of the ordinate of a plot of rate versus log[S] was then adjusted to make the slope truly equal to 0.576, and since the adjusted curve should saturate at V=1, they could then read off the value of log[S] at V=0.5 to determine K_S. This lengthy procedure allowed normalization of their data to afford extrapolation to substrate saturation to estimate V_max and thus determine the K_S for sucrose. Having seen Michaelis’s mathematical prowess, which is evident in this paper and a subsequent book (4), we were surprised that he did not think of linearizing the equation to give:

$$\frac{1}{\nu }=\frac{1}{C·\mathrm{\Phi }}+\frac{k}{C·\mathrm{\Phi }·[S]}$$

Twenty years later Lineweaver and Burk (5) would discover the utility of the double reciprocal plot and their 1934 paper would go on to be the most cited in the history of the Journal of the American Chemical Society with greater than 11,000 citations (Lineweaver died in 2009 at the age of 101).

Michaelis and Menten assumed equilibrium binding of sucrose to the enzyme during the course of the reaction. Within a year Van Slyke and Cullen (6) published a derivation in which substrate binding to the enzyme and product release were both considered to be irreversible reactions, producing a result identical to the Michaelis-Menten equation. Their focus, like that of Michaelis and Menten, was on the integrated form of the rate equations and the fitting of data from the full time course of the reaction, and they noted some inconsistencies in their attempts to fit data as the reaction approached equilibrium. It was not until 12 years later when in 1925 Briggs and Haldane (7) introduced the steady state approximation and provided arguments supporting the validity of initial velocity measurements, thereby eliminating the need to assume that the substrate binding was in rapid equilibrium or irreversible. They reasoned that because the concentration of enzyme was negligible relative to the concentration of substrate, the rate of change in the concentration of the enzyme-substrate complex, “except for the first instant of the reaction,” must also be negligible compare with the rates of change in the concentrations of substrate and product. This provided the justification for the steady state approximation. Modeling sucrose binding as an equilibrium in the derivation published by Michaelis and Menten was probably correct for the binding of sucrose to invertase; although, in fitting steady state kinetic data to extract k_cat and k_cat/K_m values, the details regarding the intrinsic rate constants governing substrate binding need not be known and do not affect the outcome, a fact recognized by Briggs and Haldane. The Briggs and Haldane derivation based upon the steady state approximation is used in biochemistry textbooks to introduce the Michaelis-Menten equation. Perhaps our current usage of terms came into vogue after the reference by Briggs and Haldane to “Michaelis and Menten’s equation” and “their constant K_S”.

Product Inhibition and the Integrated Rate Equation

The analysis by Michaelis and Menten went far beyond the initial velocity measurements for which their work is most often cited. Rather, in what constitutes a real tour de force of the paper, they fit their full time-course data to the integrated form of the rate equation while accounting for inhibition by the products of the reaction. They showed that all of their data, collected at various times after the addition of various concentrations of sucrose, could be analyzed to derive a single constant. In their view, this analysis confirmed that their approach was correct, based upon estimates of the dissociation constants for sucrose, glucose, and fructose derived from the initial velocity measurements. In retrospect, their analysis can now be recognized as the first global analysis of full time course kinetic data! The constant derived by Michaelis and Menten provided a critical test of their new model for enzyme catalysis, but it was not the Michaelis constant (K_m). Rather they derived V_max/K_m, a term we now describe as the specificity constant, k_cat/K_m, multiplied by the enzyme concentration, which, of course, was unknown to them.

Here, we show a brief derivation of the rate equations published by Michaelis and Menten, but with terms translated to be more familiar to readers today, with the exception that we retain the term “Const” to describe their new constant, and we show how they analyzed their data globally to extract a single kinetic parameter from their entire data set. Moreover, we show that globally fitting their data using modern computational methods based upon numerical integration of rate equations gives essentially the same result produced by Michaelis and Menten nearly a century ago.

Michaelis and Menten tested the postulate that the rate of an enzyme-catalyzed reaction could be described by a constant term (c) multiplied by the concentration of the enzyme-substrate complex using the following model.

$$\begin{array}{l}E+S\stackrel{K_S}{\rightleftarrows }ES\stackrel{c}{\to }E+G+F\\ v=\frac{dG}{dt}=\frac{dF}{dt}=c·ES\\ E_0=E+ES\\ \nu =c·E_0·\frac{S}{S+K_S}=\frac{C·S}{S+K_S}\end{array}$$

Michaelis and Menten showed that the rate was proportional to the amount of enzyme (“ferment”) added to the reaction mixture, but they had no means to determine the molar enzyme concentration. Today, we recognize that c = k_cat and C = V_max, although each term contained a factor to convert concentration units to degrees of optical rotation in their measurements. Subsequently, they used a conversion factor to calculate the fraction of substrate converted to product in fitting their data to the integrated form of the rate equation, as described below. K_S is equal to K_m (the Michaelis constant), although it was defined as the equilibrium dissociation constant for sucrose. Michaelis and Menten went beyond this simple analysis and realized that the binding of the products of the reaction, fructose (F) and glucose (G) compete with the binding of sucrose and that a full analysis of the reaction time course would have to take product inhibition into account based upon a more complete model shown below.

$$\begin{array}{l}E+S\stackrel{K_S}{\rightleftarrows }ES\stackrel{c}{\to }E+F+G\\ E+F\stackrel{K_F}{\rightleftarrows }EF\\ E+S\stackrel{K_G}{\rightleftarrows }EG\end{array}$$

The dissociation constants for sucrose, fructose and glucose were estimated from initial velocity measurements treating fructose and glucose as competitive inhibitors to give:

$$\begin{array}{l}{K}_S=16.7mM\\ K_F=58.8mM\\ K_G=91mM\\ E=E_0-ES-EF-EG(\text{mass}\text{balance})\end{array}$$

Solving these equations simultaneously yielded:

$$ES=\frac{S·E_0}{S+K_S(1+F/K_F+G/K_G)}$$

where ES, S, F, and G represent the time-dependent concentrations of the enzyme-sucrose complex, sucrose, fructose and glucose, respectively. According to their postulate, the rate of reaction was proportional to the ES concentration:

$$\begin{array}{l}v=\frac{dF}{dt}=\frac{dG}{dt}=c·ES\\ v=\frac{C·S}{S+K_S(1+F/K_F+G/K_G)}\end{array}$$

• where C = c · E₀

This is the now familiar form of the equation for competitive enzyme inhibition, where the terms F/K_F and G/K_G in the denominator account for product inhibition. Although the concept of competitive inhibition had not yet been formally defined, it is clearly represented here mathematically.

Michaelis and Menten reasoned that if their postulate was correct, then they should be able to fit the full time dependence of the reaction at various sucrose concentrations to derive a single constant, C, based upon the known values of K_S, K_F and K_G. Integration of the rate equation requires including mass balance terms to reduce the equation to a form with a single variable for concentration of S, F or G.

$$\begin{array}{l}S=S_0-F\\ F=G\\ \frac{dF}{dt}=\frac{C·(S_0-F)}{S_0-F+K_S(1+F/K_F+G/K_G)}\\ \frac{dF}{dt}=\frac{C·(S_0-F)}{S_0+K_S-F·K_S·(1/K_S-1/K_F-1/K_G)}\end{array}$$

This differential equation was then integrated to yield:

$$\mathit{Const}=\frac{C}{K_S}=\frac{S_0}{t}\left(\frac{1}{S_0}+\frac{1}{K_F}+\frac{1}{K_G}\right)·ln\left(\frac{S_0}{S_0-F}\right)+\frac{F}{t}\left(\frac{1}{K_S}-\frac{1}{K_F}-\frac{1}{K_G}\right)$$

This equation allowed the constant term, Const = C/K_S, to be calculated from measurements of the concentration of product (F) as a function of time (t) at various starting concentrations of sucrose, S₀. Michaelis and Menten converted their optical rotation data to get the fraction of product formed relative to starting substrate concentration, [P]/[S₀], as illustrated in Table 1. They showed that, indeed, the constant term, C/K_S, was “consistent and, apart from slight fluctuations, shows no slant either with time or with sugar concentration, that we can consider it as a satisfactory constant.”

Table 1.

Michaelis-Menten Global Data Fitting ^a

Sucrose = 333 mM
Time (m)	[P]/[S0]	Const
7	0.0164	0.0496
14	0.0316	0.0479
26	0.0528	0.0432
49	0.0923	0.0412
75	0.1404	0.0408
117	0.2137	0.0407
1052	0.9834	[0.0498]

Sucrose = 41.6 mM
Time (m)	[P]/[S0]	Const
10.25	0.1147	0.0406
30.75	0.3722	0.0489
61.75	0.615	0.0467
90.75	0.747	0.0438
112.70	0.850	0.0465
132.70	0.925	0.0443
154.70	0.940	0.0405

Sucrose = 166.7 mM
Time (m)	[P]/[S0]	Const
8	0.0350	0.0444
16	0.0636	0.0446
28	0.1080	0.0437
52	0.1980	0.0444
82	0.3000	0.0445
103	0.3780	0.0454

Sucrose = 20.8 mM
Time (m)	[P]/[S0]	Const
17	0.331	0.0510
27	0.452	0.0464
38	0.611	0.0500
62	0.736	0.0419
95	0.860	[0.0388]
1372	0.990	[0.058]

Sucrose = 83 mM
Time (m)	[P]/[S0]	Const
49.5	0.352	0.0482
90.0	0.575	0.0447
125.0	0.690	0.0460
151.0	0.766	0.0456
208.0	0.900	0.0486

Const mean value = 0.0454/m

^aThis reproduces the data from the last (unnumbered) table in Michaelis and Menten (1). Michaelis and Menten analyzed these data using the integrated form of the rate equations to compute a single constant, Const = C/K_S, as described in the text. We fit these data globally based upon numerical integration of the rate equations to give the results shown in Fig. 1.

This extraordinary analysis enabled analysis of the full time course of product formation to the integrated form of the rate equation to extract a single unknown constant that accounts for all of the data. In doing so, Michaelis and Menten demonstrated that the variation in rate of turnover as a function of time and substrate concentration could be understood as a constant defining the rate of product formation based upon the calculated concentration of the ES complex. This is a remarkable contribution. However, it should be noted that the constant derived by Michaelis and Menten in fitting their data was not the Michaelis constant. Rather, in terms used today, they fit their data to the constant C/K_S = (k_cat/K_m)*E₀, the specificity constant times the enzyme concentration. This was as far as they could take their analysis, since they had no way of knowing the enzyme concentration; the exact nature and molecular weight of the enzyme where unknown at the time. Their data fitting provided an average value of C/K_S = 0.0454 ± 0.0032 m⁻¹, from which we can calculate $V_{\mathit{max}}=k_{\mathit{cat}}\ast E_0=0.76\pm 0.05\text{mM}/\text{m}$ based upon their reported value of K_S = 16.7 mM.

Computer Analysis

Today, we can fit the original Michaelis-Menten data globally based upon numerical integration of the rate equations and no simplifying assumptions. Fig. 1 shows the global fit of the data from the Michaelis-Menten paper (Table 1) obtained using the KinTek Explorer simulation program (8, 9). The data were fit to a model in which S, F, and G each bind to the enzyme in a rapid equilibrium reaction using dissociation constants reported by Michaelis and Menten. The data were fit to a single kinetic constant, k_catE₀ =0.80 ± 0.02 mM/m. The global (average) value achieved by Michaelis and Menten (0.76 ± 0.05 mM/m) equals what can be derived today with the most advanced computer simulation software and stands as a testament to the precision of Maud Menten’s and Leonor Michaelis’ measurements and their care in performing the calculations by hand.

Computer simulation can also be used to show how much product inhibition contributed to the time dependence of the reaction. The dashed lines in Fig. 1 show the predicted time course assuming no product inhibition. Clearly, the rebinding of product to the enzyme makes a significant contribution to the time course. Perhaps Michaelis and Menten recognized this fact when they first attempted to fit their data to the integrated rate equation based on a simpler model and then realized that they must include competitive product inhibition. Further analysis by numerical integration also supports the conclusion of Michaelis and Menten that there is no significant accumulation of a ternary E.F.G complex based upon the postulate of non-interacting sites, fast product release, and the measured K_d values.

In the past century, enzyme kinetic analysis has followed the use of the steady state approximation, allowing initial velocity data to be fit using simple algebraic expressions. Michaelis and Menten set a high standard for comprehensive data fitting and their pioneering work must now be considered a the forerunner to modern global data fitting. Work in enzymology during the first two decades of the twentieth century by Henri, Michaelis and Menten, and Van Slyke and Cullen was focused on finding the integrated form of the rate equations to account for the full progress curves of enzyme-catalyzed reactions. That approach is complicated by the assumptions necessary to derive a mathematical equation describing the full time course; namely, the assumption that the concentration of substrate was always much greater than the enzyme concentration, and the need for prior knowledge of the nature and K_I values for product inhibition. Michaelis and Menten and Briggs and Haldane provided the simple solution to the problem by showing how initial velocity measurements during a steady state that exists prior to significant substrate depletion can be used to derive k_cat and K_m for substrate turnover and K_I values for product inhibition. Lineweaver and Burk provided a simple graphical analysis to parse the kinetic data based upon a double-reciprocal plot. This type of analysis dominated enzymology for most of the twentieth century. Analysis by numerical integration of rate equations (a.k.a., computer simulation) has eliminated the need for simplifying assumptions to afford quantitative analysis of full progress curves, as pioneered by Carl Frieden (10). One can now derive steady state kinetic parameters and product inhibition constants by fitting full time course data directly using computer simulation (11), bypassing the laborious initial rate analysis. It is perhaps a testament to the early work in enzymology that only in the first decade of the 21^st century with the advent of fast personal computers and optimized algorithms that global data analysis of full progress curves has finally come of age.

It is also interesting to note that the original Michaelis constant, the one derived by Michaelis and Menten in analyzing their full time course data globally, was actually the specificity constant, k_cat/K_m, multiplied by the concentration of enzyme, which was unknown at the time. We now recognize the specificity constant as the most important steady state kinetic parameter in that it defines enzyme specificity, efficiency and proficiency (12). In contrast, the constant attributed to Michaelis, the K_m, is of lesser importance in enzymology and quite often is misinterpreted. It is perhaps the case that the use of K_m gained prominence because it could be measured without knowing the enzyme concentration and could be derived from any arbitrary rate measurements without the need to convert to units of concentration. Today, enzymologists generally regard k_cat and k_cat/K_m as the two primary steady state kinetic parameters and that K_m is simply a ratio of k_cat and k_cat/K_m. This view certainly generates less confusion than attempts to interpret K_m without additional mechanistic information (13). In terms of reduced errors in estimating the specificity constant and a more realistic representation of the kinetics of enzyme-catalyzed reactions, a better form of the Michaelis-Menten equation would be:

$$v=\frac{k_m·[S]}{1+\left(k_m/k_{\mathit{cat}}\right)·[S]}$$

where k_m is the specificity constant, using a lowercase k to designate a kinetic rather than a pseudo-equilibrium constant. We could perhaps refer to k_m to as the Menten constant.

Summary

Nearly a century after the original publication, the work of Michaelis and Menten stands up to the most critical scrutiny of informed hindsight. It is only unfortunate that the term Michaelis constant was not attributed to k_cat/K_m, which was derived as the constant in their “global” data analysis, rather than the K_m term. For the past century and certainly for the next, enzymologists continue to work toward the goal, stated by Michaelis and Menten in their opening paragraph, of “achieving the final aim of kinetic research; namely, to obtain knowledge of the nature of the reaction from a study of its progress.”