Generalised Linear Models Incorporating Population Level Information: An Empirical Likelihood Based Approach

Abstract

In many situations information from a sample of individuals can be supplemented by population level information on the relationship between a dependent variable and explanatory variables. Inclusion of the population level information can reduce bias and increase the efficiency of the parameter estimates.

Population level information can be incorporated via constraints on functions of the model parameters. In general the constraints are nonlinear making the task of maximum likelihood estimation harder. In this paper we develop an alternative approach exploiting the notion of an empirical likelihood. It is shown that within the framework of generalised linear models, the population level information corresponds to linear constraints, which are comparatively easy to handle. We provide a two-step algorithm that produces parameter estimates using only unconstrained estimation. We also provide computable expressions for the standard errors. We give an application to demographic hazard modelling by combining panel survey data with birth registration data to estimate annual birth probabilities by parity.

1 Introduction

In many statistical demographic applications, some information on the relationship of explanatory variable with the dependent variables is available from the population level data. Sources of population level data include a census, vital events registration systems, and other governmental administrative record systems. They contain too few variables, however, to estimate demographically interesting models. Thus in a typical situation the estimation is done using sample survey data alone, and the information from complete enumeration procedures is ignored. Sample survey data, however, are subjected to sampling error and bias due to non-response, whereas population level data are comparatively free of sampling error and typically less biased from the effects of non-response. It is not surprising, therefore, that the incorporation of population level information can lead to statistically more accurate estimates and better inference.

In many situations the population level information is independent of the model parameters. In this paper we show that the empirical likelihood approach of Qin and Lawless (1994) can be used to incorporate such auxilliary information by imposing additional moment conditions. We show that if there are “weights” that solve the empirical likelihood system for the population moment conditions, then these same weights can be used in the estimating equations of the model parameters. The number of such estimating equations can be equal to or even exceed the dimension of the model.

An alternative to the empirical likelihood approach is to express the population level information as (usually non-linear) functions of the model parameters and use them as constraints to the parametric likelihood (Handcock, Huovilainen, and Rendall, 2000). The constrained maximum likelihood estimates (CMLE) can then be obtained by maximising the likelihood function under these population level constraints. The methodology can be implemented using any of the widely available procedures for numerical optimisation with equality constraints. It is also known that the estimates are asymptotically normal and unbiased. An explicit form of the asymptotic variance-covariance matrix of the parameter estimate can also be obtained. Further, the standard errors of the parameter estimates are guaranteed to be at most those with no population constraints. The CMLE standard errors are typically much smaller for the intercept parameter and for those coefficient parameters relating to explanatory variables that are present also in the population data source (Handcock, Rendall, and Cheadle, 2005).

Even though the constrained maximum likelihood method uses intuitively straightforward procedures, it has its own limitations. Non-linear equality constraints are in general numerically difficult to handle and time-consuming to code in applications involving multiple population level constraints and even moderate numbers of regressors. Also, knowledge about the distribution of the explanatory variables is required.

Data combination is an active research area in econometrics. Imbens and colleagues explore the benefits of combining population with survey data, using economic data in a generalised method of moments (GMM) regression framework. Imbens and Lancaster (1994) consider the estimation of parameters in the regression model under moment restrictions on the data contributed by population data, and report large gains in efficiency by incorporating marginal moments from census data with sample-survey joint distributions. Imbens and colleagues (Imbens and Lancaster, 1994; Hellerstein and Imbens, 1999) develop a two-step procedure for combining population and survey data and derive some theoretical results in the GMM case, constraining to conditional moment information. For a review of recent developments see Ridder and Moffitt (forthcoming).

Chen and colleagues (Chen and Qin, 1993; Chen and Sitter, 1999) use empirical likelihood to incorporate available auxiliary information such as population mean, stratum mean or stratum size in finite population sampling. Qin and Lawless (1994) show that the empirical likelihood method can be used to estimate parameters of interest by solving sets of estimating equations involving them. They define a profile empirical likelihood of the parameters of interest and obtain estimates by maximising it directly. The same approach is taken by Qin (2000) to combine parametric and empirical likelihood for bivariate regression where the dependent variable is only partially observed.

In this article we connect the parametric likelihood approach when there is population level information to the empirical likelihood and GMM approaches. We generalise the two-step GMM method in Hellerstein and Imbens (1999) and use it to overcome the numerical and implementational difficulties of direct constrained maximisation. We develop a simple and computaionally efficient two-step method to estimate the parameters when the constraints imposed by the population information do not depend on the model parameters. We also show that if the sample is representative of the population then the estimates are asymptotically consistent and unbiased. Under the usual regularity conditions, the estimates are asymptotically normal. Through an explicit expression of the variance-covariance matrix of the parameter estimates, we show that the use of population level information reduces the standard errors. We provide a sandwich estimator for the variance-covariance matrix. This has the advantages of providing more accurate estimates of the standard errors and being computationally more feasible.

The methodology described in this article applies in general to the common situation where the population-level information is independent of the parameters in the model. We also develop the statistical theory and implementational methodology specifically for generalised linear models. Generalised linear models are the most popular class of statistical models used in the biological and social science applications (McCullagh and Nelder, 1989). For generalised linear models the parameters can be estimated by solving the score equations obtained by differentiating the likelihood with respect to each parameter. Thus the number of equations one needs to solve simultaneously equals the number of parameters. The estimates of the asymptotic standard errors of the parameter estimates can be expressed in analytic form. The methodology developed in this article can be implemented by easily extending existing algorithms, and we provide an R package to do this for the generalized linear model class.

The article is structured as follows. In Section 2 we discuss parametric estimation using empirical likelihood in the presence of population based information in full generality. This section also describes the relevant subsets of the n −1 dimensional simplex over which the non-parametric likelihood is maximised to estimate the parameters. We introduce and justify a two-step procedure to estimate the model parameters. This method generalises the two-step weighted least squared estimation described in Hellerstein and Imbens (1999). We further compare our empirical likelihood estimator with the CMLE. Section 3 introduces the notation and formulates the problem for a generalised linear model. In Section 4 we develop specific methods for estimating the model parameters for generalized linear models. Section 5 develops the asymptotic properties of the parameter estimates. As an illustrative example, in Section 6, the methodology is applied to combine panel survey data with birth registration data to estimate annual birth probabilities by whether the woman has previously given birth.

2 Parametric estimation using empirical likelihood in the presence of population level information

In this section we introduce a general methodology to estimate unknown parameters by maximising empirical likelihood subject to two kinds of constraints. The first kind of constraints depend on the parameters of interest. The second kind of constraints depend on the information known from the population where these constraints do not involve the model parameters.

2.1 Empirical likelihood

Suppose Z₁, Z₂, …, Z_n are i.i.d. univariate random variable with a common distribution F₀. Let ℱ be the set of all univariate distribution functions. In particular F₀ ∈ ℱ.

Definition 1

(Owen, 2001). Suppose F ∈ ℱ, then the non-parametric likelihood of F ∈ ℱ is defined as

$$L(F;Z)=\prod _{i=1}^n\{F(Z_i)-F(Z_i-)\},$$ (1)

where F (Z_i–) = lim_δ↓0 F (Z_i −δ).

In Definition 1 we use the word “likelihood” to mean that L (F; Z) in (1) is the probability of the sample Z₁, Z₂, …, Z_n from the distribution F. Also we note that, if F is continuous at Z_i, for some i, lim_δ↓0 F (Z_i −δ) = F (Z_i). So in particular if F is continuous L (F; Z) = 0. We estimate F₀ by an F maximising L(F; Z) in (1). Thus the estimate of F₀ places positive mass on every sample point Z₁, Z₂, …, Z_n and is discrete.

Note that F is identified only through the weight w_i = F (Z_i) − F (Z_i–), i = 1, 2, …, n it assigns to the observed sample point Z_i. Then (1) becomes

$$L(w,Z)=\prod _{i=1}^n{w}_i,$$ (2)

where w ≡ (w₁, …, w_n). From the properties of a distribution function it follows that

$$w\in {\mathrm{\Delta }}_{n-1}=\left\{w\in {\mathbb{R}}^n:w_i\ge 0,i=1,2,\dots ,n,\sum _{i=1}^n{w}_i=1\right\}.$$ (3)

Moreover for any w ∈ Δ_n−1, F_w ∈ ℱ is determined as

$$F_w(z;Z)=\sum _{i=1}^n{w}_i{1}_{\{Z_i\le z\}},-\infty <z<\infty .$$ (4)

Owen (2001) shows that the non-parametric likelihood in (2) (or equivalently in (1)) is maximised over Δ_n−1, when w_i = 1/n for all i = 1, 2, …, n. Thus with no other information on F₀ ∈ ℱ its estimate is the familiar empirical distribution function of the sample Z₁, Z₂, …, Z_n.

2.2 Parametric constraints and parameter estimation

Suppose that it is known that, for some unknown θ ∈ Θ, F₀ satisfies the parametric constraint

$$E_{F_0}[\psi (Z_1,\theta )]=0$$ (5)

where ψ is a known function. If the underlying true distribution F₀ depends on θ, it is well known that the score functions of parametric likelihoods satisfy (5). See, for example, Qin and Lawless (1994) for other examples.

Further suppose there is a known function, g, not depending on θ, for which

$$E_{F_0}[g(Z_1)]=\gamma .$$ (6)

with γ known. Knowledge of γ in (6) represents population-level information expressed as a constraint. Hence we refer to (6) as the population level constraint.

In this article we estimate θ by maximising the empirical likelihood in (1) subject to the constraints in (5) and (6).

For that purpose, for each θ ∈ Θ, we define

$${\mathcal{W}}_{\theta }=\left\{w\in {\mathrm{\Delta }}_{n-1}:\sum _{i=1}^n{w}_i\psi (Z_i,\theta )=0\right\},$$ (7)

$${\mathcal{W}}_P=\left\{w\in {\mathrm{\Delta }}_{n-1}:\sum _{i=1}^n{w}_{i}g(Z_i)=\gamma \right\},$$ (8)

$${\mathcal{W}}_{\mathrm{\Theta }}=\underset{\theta \in \mathrm{\Theta }}{\cup }{\mathcal{W}}_{\theta },\mathcal{W}=\underset{\theta \in \mathrm{\Theta }}{\cup }({\mathcal{W}}_{\theta }\cap {\mathcal{W}}_P).$$ (9)

Note that 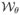is empty if 0 is not in the convex hull of ψ (Z₁, θ), ψ (Z₂, θ), …, ψ (Z_n, θ) and 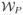may be similarly empty. However throughout this paper we assume that the set is non-empty.

If the vector of weights ŵ = (ŵ_i,.…, ŵ_n) maximises L(w, Z) over 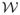, F_ŵ satisfies the constraint in (5) and (6). Thus F_ŵ is a constrained estimator of F₀.

The maximizer of (2) over 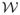also maximises the non-parametric likelihood in (1) over Θ, thus θ can be estimated as

$$\widehat{\theta }=\underset{\theta \in \mathrm{\Theta }}{\text{argmax}}\left\{\underset{w\in {\mathcal{W}}_{\theta }\cap {\mathcal{W}}_P}{max}\prod _{i=1}^n{w}_i\right\}.$$ (10)

Notice that the estimator θ̂ in (10) is exactly equal to the empirical profile likelihood estimator (EPLE) introduced by Qin and Lawless (1994). They express equation (2) as a function of unknown parameters and maximise it over the whole parameter space to obtain the estimate. Below we show that our representation of it leads to a two-step estimation procedure allowing for simpler computational and theoretical development.

2.3 A two-step procedure for estimating the model parameters

Even though the maximisation with respect to θ in (10) (and also in Qin and Lawless (1994)) is unconstrained, in general it is not a convex problem. From a computational perspective, it is difficult to implement compared to the two-step estimator described below.

The two-step procedure takes advantage of the fact that the population based constraints in (8) do not involve the parameters. This is a generalisation of the weighted estimator described in Hellerstein and Imbens (1999). The procedure can be described as follows:

In the first step we maximise (2) on the simplex, under the population level constraints. That is we compute

$$\widehat{w}=\underset{w\in {\mathcal{W}}_p}{\text{argmax}}\left\{\sum _{i=1}^{n}log({nw}_i)\right\}.$$ (11)

Here for computational purposes we maximise ${\sum }_{i=1}^{n}log({nw}_i)$ under the constraint that w ∈ 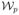. For an alternative interpretation of this product in terms of log-empirical likelihood ratio, see Owen (2001, Chapter 2).

In the second step we solve the parameter based constraints with ŵ_i as the weight for the ith sample point to compute the parameter estimate. That is we solve

$$\sum _{i=1}^n{\widehat{w}}_i\psi (Z_i,\theta )=0$$ (12)

for the parameter estimate θ̂.

The rationale for the two-step procedure can be outlined as follows. In the first step (11), we maximise ${\sum }_{i=1}^{n}log({nw}_i)$ over a larger set 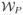. Clearly 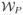is convex and ${\sum }_{i=1}^{n}log({nw}_i)$ is concave on 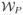. Thus there is a unique maximising ŵ in 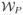. If ŵ ∈ 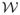, it is the intended maximising weight vector and θ̂ is a solution of (12) with ŵ as the sample weights. Note that neithe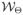r nor 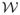needs to be convex.

However it is possible that there is no θ ∈ Θ satisfying the parametric constraints for the weights w, i.e. ŵ ∉ 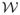(see for example Small and Wang 2003, Chapter 5 ). In that situation the two-step procedure fails and the nested maximisation (maximisation over 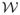) in (10) has to be done.

Empirical evidence suggests that the two-step procedure described above works for most cases. If the nested maximisation in (10) is required, the resulting procedure is same as in Qin and Lawless (1994).

The weights in the first step can be calculated using the Owen’s algorithm in Owen (2001, Chapter 3) or the algorithm described by Chen, Sitter, and Wu (2002). The second algorithm is guaranteed to converge but is slower than the first one. Once the weights are known the parameter estimates can be obtained using standard algorithms to solve the generalised estimating equations. See for example Small and Wang (2003) or Hardin and Hilbe (2003).

Note that the first step does not involve the parameters. Thus the objective functions maximised in this step cannot easily be expressed as a profile likelihood of the parameters as in Qin and Lawless (1994). However (11) provides a direct interpretation of the weights.

The asymptotic properties of the two-step estimator can be derived within the framework of Qin and Lawless (1994). It can be shown (by means of a comparatively easier argument) that the estimates are consistent and asymptotically normal. The asymptotic variance-covariance matrix is similar to the one in Qin and Lawless (1994). In Section 5 we discuss and provide explicit expressions for generalised linear models.

2.4 Comparison with the constrained maximum likelihood estimator

The properties of the EPLE depends on the choice of the constraints that define it. For finite sample sizes, DiCiccio, Hall, and Romano (1989) have shown that for a subclass of exponential families the parametric and empirical likelihoods are always maximised at the same point. For regular models it is well known that both estimators are consistent (Qin and Lawless, 1995). In many cases the efficiency of the EPLE and the CMLE are the same (Qin and Lawless, 1994). In general the EPLE is less efficient than the corresponding CMLE. However simulation results (not presented here) show that the loss is small and often negligible even in moderately large sample sizes and realistic models.

Sometimes, the CMLE is determined by the population level constraints only, ignoring the information in the sample. Thus it is vulnerable to error due to misspecification of the model. The EPLE has the advantage that one can always include the information in the sample in the estimator.

For our purpose we shall choose the parametric constraints which are solved by the MLE when no weighing is involved. The final parameter estimate will respect these constraints. In the following sections we consider inference for the parameters of generalised linear models with the likelihood represented by the score function constraints and the population level information represented by some additional constraints.

3 Generalised linear models with population level constraints

Suppose Y denotes the response variable dependent on the explanatory variables X = (X⁽¹⁾, X⁽²⁾, …, X^(p)). Suppose g_j (Y, X⁽¹⁾, X⁽²⁾, …, X^(p)), j = 1, 2, …, m be functions of the response and p explanatory variables such that the average value of each g_j over the population represented by Y,X⁽¹⁾, X⁽²⁾, …, X^(p) is known to be γ_j, for all j = 1, 2, …, m. Moreover as before assume that each γ_j is known without error.

Suppose we have an independent sample of size n. Denote the ith sample point by

$$(y_i,x_i)\equiv \left(y_i,x_i^{(1)},x_i^{(2)},\dots ,x_i^{(p)}\right)i=1,2,\dots ,n$$ (13)

We assume that the sample size n > p + m and there are no missing values.

Suppose we fit a generalised linear model ℳ to the data and incorporate the population level information in the known population mean of g_j, for all j = 1,2,.…, m. Suppose η_ℳ, μ _ℳ, and V_ℳ are respectively the linear predictor, the mean and the variance function of ℳ. The model is specified as

$${\mu }_i\equiv E(Y\mid X=x_i,\beta )={\mu }_{ℳ}(x_i\beta )\equiv {\mu }_{ℳ}({\eta }_i).$$ (14)

where β = (β₁, β₂, …, β_p)^T is the vector of regression coefficients and η_i = x_iβ. We assume that the marginal distribution of X does not depend on β.

By defining h_j (Y, X, γ_j) = g_j (Y, X) − γ_j, the population level constraints on the problem specify that

$$E[h_j(Y,X,{\gamma }_j)]=E[g_j(Y,X)-{\gamma }_j]=0.$$ (15)

The expectation in (15) is in general a nonlinear function of β.

One way to estimate the parameters constrained by the population level constraints is to directly maximise the likelihood corresponding to ℳ over the model parameters under these non-linear equality constraints. Though in practice computational tools are available for this purpose, optimisation with non-linear equality constraints usually creates several numerical and implementational difficulties (Handcock et al., 2005).

The general empirical likelihood based methodology described in Section 2 presents an alternative to the direct constrained maximisation method to estimate the model parameters. In this alternative method the parameters can be estimated by maximising the empirical likelihood under linear equality constraints. Furthermore in most cases it can be modified to a computationally efficient two-step estimation procedure.

From the discussion in Section 2, it is clear that the constraints specify the set 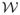. Once 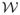is specified, one can maximise ${\sum }_{i=1}^{n}log({nw}_i)$ over 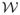and obtain the parameter estimates from (10).

The constraints imposed by the model are based on the score functions of the likelihood. It is well known (McCullagh and Nelder, 1989) that for any generalised linear model

$$E\left[\frac{X^{(k)}{\mu }_{ℳ}^{\prime }({\eta }_{ℳ})(Y-{\mu }_{ℳ}({\eta }_{ℳ}))}{V_{ℳ}({\mu }_{ℳ}({\eta }_{ℳ}))}\right]=0,k=1,2,\dots ,p,$$ (16)

where ${\eta }_{ℳ}={\sum }_{k=1}^p{\beta }_k{X}^{(k)},{\mu }_{ℳ}^{\prime }=\partial {\mu }_{ℳ}/\partial {\eta }_{ℳ}$.

Thus we can define the set of weights satisfying the score constraints as

$${\mathcal{W}}_S=\underset{\beta \in {\mathbb{R}}^p}{\cup }{\mathcal{W}}_{\beta },\text{where}{\mathcal{W}}_{\beta }=\underset{k=1}{\overset{p}{\cap }}\left\{w\in {\mathrm{\Delta }}_{n-1}:\sum _{i=1}^n{w}_i\frac{x_i^{(k)}{\mu }_i^{\prime }(y_i-{\mu }_i)}{V_i}=0\right\}.$$ (17)

where ${\mu }_i^{\prime }={\mu }_{ℳ}^{\prime }({\eta }_i)$ and V_i = V_ℳ (μ_i).

Similarly from (15) we define the set of weights satisfying the population constraints as

$${\mathcal{W}}_P=\underset{j=1}{\overset{m}{\cap }}\left\{w\in {\mathrm{\Delta }}_{n-1}:\sum _{i=1}^n{w}_i{h}_j(y_i,x_i,{\gamma }_j)=0\right\},$$ (18)

Now as before, the set 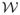is defined as

$$\mathcal{W}={\mathcal{W}}_S\cap {\mathcal{W}}_P.$$ (19)

Unlike the constrained MLE approach, the population level constraints in (18) do not explicitly depend on the model parameters β. However as the score constraints involve all the weights and the model parameters, the same constraints are imposed on the parameter estimation in both procedures.

4 Estimation of model parameters

Following (10) we estimate the model parameters β as

$$\widehat{\beta }=\underset{\beta \in {\mathbb{R}}^p}{\text{argmax}}\left\{\underset{w\in {\mathcal{W}}_P\cap {\mathcal{W}}_{\beta }}{max}\sum _{i=1}^{n}log({nw}_i)\right\}.$$ (20)

The parameter estimates maybe obtained from a nested maximisation procedure (following Qin and Lawless (1994)) and the model parameters only influence the estimation of weights through the score constraints in (17).

Note that in (20), the outer maximisation over β is unconstrained. The inner maximisation over w is constrained by linear constraints. So the use of empirical likelihood requires maximising over linear constraints only, which is numerically much easier to handle than maximisation over non-linear constraints.

4.1 Two-step procedure for estimating the model parameters

The two-step estimator has been described in Section 2. Since the population constraints do not depend on β, we can apply the procedure in this case.

The first step is just as in (11). That is we compute

$$\widehat{w}=\underset{w\in {\mathcal{W}}_P}{\text{argmax}}\left\{\sum _{i=1}^{n}log({nw}_i)\right\}.$$ (21)

The second step involves solving the score constraints with ŵ_i as the weight for the ith sample point to compute the parameter estimates. That is we solve

$$\sum _{i=1}^n{\widehat{w}}_i\frac{x_i^{(k)}{\mu }_{ℳ}^{\prime }(x_i\beta )\{y_i-{\mu }_{ℳ}(x_i\beta )\}}{V_{ℳ}({\mu }_{ℳ}(x_i\beta ))}=0,k=1,2,\dots ,p,$$ (22)

for the parameter estimates β̂ = (β̂₁, β̂₂, …, β̂_p)^T.

The rationale for the two-step procedure has been described Section 2. Whether the two-step method will work partly depends on the link function of the model. For example, Hellerstein and Imbens (1999) only consider linear regression, which is a special case of the above two-step method. In their application μ_ℳ is the identity map. It is evident that provided the Variance-Covariance matrix of the explanatory variables is non-singular, in their case for any set of estimated sampling weights ŵ, the corresponding unique β̂ can be found. Thus in this case 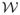= 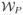⊆ 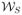_S, and the two-step estimator is guaranteed to work. However for a general link function it is not true (See, for example, Wedderburn (1976); Lauritzen (1996, Appendix D)). In Theorem 1 below we show that for large sample sizes the two-step method works in most cases.

4.2 Computational methods for the two-step procedure

In the two-step estimation procedure in Section 4.1, only the first step requires constrained maximisation. This can be achieved by following Owen (2001, Chapter 3) or Chen, Sitter, and Wu (2002). Instead of solving the primal problem for the maximising weights, both methods solve the corresponding dual problem, which is more convenient to deal with. After some algebraic manipulations (Owen, 2001) the problem transforms to finding out the Lagrangian multipliers λ_j, j = 1, 2, …, m, which minimise

$$\sum _{i=1}^{n}log({nw}_i)=-\sum _{i=1}^{n}log(1+\sum _{j=1}^m{\lambda }_j{h}_j(y_i,x_i,{\gamma }_j)),$$ (23)

subject to $\left\{1+{\sum }_{j=1}^m{\lambda }_j{h}_j(y_i,x_i,{\gamma }_j)\right\}\ge n^{-1}$ for all i = 1, 2, …, n.

Note that the dimension of the dual problem is m which is much less than the dimension of the primal problem by assumption. Also the dual problem is constrained by linear inequality constraints and thus numerically far easier to solve.

The estimated weights are given by

$${\widehat{w}}_i=\frac{1}{n}\times \frac{1}{1+{\sum }_{j=1}^m{\widehat{\lambda }}_j{h}_j(y_i,x_i,{\gamma }_j)},$$ (24)

where λ̂_j, j = 1, 2, …, m minimise the dual problem above.

Owen (2001, Chapter 3) defines a continuous and twice differentiable pseudo-logarithmic function over the real line such that the above minimisation can be performed by a modified version of Newton’s method or other standard algorithms. Chen, Sitter, and Wu (2002) discuss a modified Newton’s algorithm to minimise the dual. The former converges at worst at a linear rate. The latter is guaranteed to converge almost always, but in general has a slower speed. Both algorithms converge to weights outside Δ_n−1 if 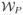is empty.

The second step consists of the usual estimation of the model parameters for the model ℳ with ŵ as the vector of sample weights. So one can use standard methods and software for estimating model parameters for a generalised linear model to perform this step (McCullagh and Nelder, 1989).

The procedure for the inner constrained maximisation in (20) which includes the score constraints, when necessary, is similar. We note that in that case the dimension of the corresponding dual problem is m + p, which is still less than the dimension of the primal problem.

5 Asymptotic properties of the estimator

In this section we investigate the asymptotic properties of the constrained estimator of the model parameters. The main emphasis will be given to the two-step estimator introduced in Section 2. In particular we discuss the case when the parametric constraints are given by the score constraints from a Generalised Linear model. The results for other estimating equations can be obtained similarly. We shall show that this estimator is consistent and asymptotically normal. Analytic expression of the asymptotic Variance-Covariance matrix will show that the standard errors of the constrained estimator of the model parameters is less than that of the unconstrained one.

5.1 Consistency and asymptotic normality of the parameter estimators

The main result of this section is stated in Theorem 1. We show that under the truth, for large samples the two-step estimator is almost always computable. Moreover, asymptotically as n → ∞, the Lagrangian multipliers minimising the dual problem in (23) tend to 0 almost surely. The theorem further establishes that the parameter estimates are strongly consistent, asymptotically normal and gives the analytic expression for their asypmtotic Variance-Covariance matrix.

In what follows we shall assume that the link function of the model ℳ is canonical. Similar results hold for non-canonical links.

Suppose we denote

$$h{(y,x,\gamma )}_{m\times 1}={(h_1(y,x,{\gamma }_1),h_2(y,x,{\gamma }_2),\dots ,h_m(y,x,{\gamma }_m))}^T,$$ (25)

$${\lambda }_{1\times m}=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m),$$ (26)

and

$$f(y,x,\beta ,\lambda )=\frac{1}{1+\lambda ·h(y,x,\gamma )}{\left(x^{(1)}(y-\mu ),\cdots ,x^{(p)}(y-\mu ),h{(y,x,\gamma )}^T\right)}^T.$$ (27)

Here μ = μ_ℳ (xβ). Note that f (y,x,β, λ) is a vector of length (p + m) and the two-step estimator is the solution of the equation system ${\sum }_{i=1}^{n}f(y_i,x_i,\beta ,\lambda )=0$. We use a setup similar to Qin and Lawless (1994) and Serfling (1980, Chapter 4.).

Theorem 1

Suppose (Y₁,X₁), (Y₂,X₂), …, (Y_n,X_n) are i.i.d. random vectors in ℝ^p+1 goverened by the model (14). Assume that the link function is μ_ℳ is canonical. Let β* be the true value of the model parameter vector. Suppose E [h (Y₁, X₁, γ)] = 0, the Jacobian matrix $\frac{\partial f(y,x,\beta ,\lambda )}{\partial (\beta ,\lambda )}$ and the Hessian $\frac{{\partial }^{2}f(y,x,\beta ,\lambda )}{{\partial }^2(\beta ,\lambda )}$ exist for all β and λ. Further suppose f (y,x,β, λ), $\frac{\partial f(y,x,\beta ,\lambda )}{\partial (\beta ,\lambda )}$ and $\frac{{\partial }^{2}f(y,x,\beta ,\lambda )}{{\partial }^2(\beta ,\lambda )}$ are elementwise bounded by integrable function in a neighbourhood nbd (β,λ) of (β*,0). Assume that E [f (Y₁,X₁, β*, 0) f^T (Y₁,X₁, β*, 0)] is positive definite and $E\left[{\frac{\partial f(Y_1,X_1,\beta ,\lambda )}{\partial (\beta ,\lambda )}|}_{(\beta ={\beta }^{★},\lambda =0)}\right]$ has full rank.

Let ${\eta }_i^{★}={\sum }_{k=1}^p{\beta }_k^{★}{X}_i^{(k)},{\mu }_i^{★}={\mu }_{ℳ}({\eta }_i^{★})$, for all i = 1,2, …, n and denote

$$h_1=h(Y_1,X_1,\gamma ),$$ (28)

$$G_{p\times p}=E[X_1^T{\mu }_{ℳ}^{\prime }({\eta }_1^{★})X_1],$$ (29)

$$G_{p\times p}^{★}=E[X_1^T{(Y_1-{\mu }_1^{★})}^2{X}_1],$$ (30)

$$K_{p\times m}=E[X_1^T(Y_1-{\mu }_1^{★})h_1^T],$$ (31)

$$H_{m\times m}=E[h_1{h}_1^T].$$ (32)

Also assume that G and H are non-singular. Then

1. $$\begin{array}{l}\mathit{almost}\mathit{surely},\mathit{the}\mathit{equation}\sum _{i=1}^{n}f(y_i,x_i,\beta ,\lambda )=0\mathit{admits}a\mathit{sequence}of\mathit{solutions}\\ ({\widehat{\beta }}_n,{\widehat{\lambda }}_n)\mathit{such}\mathit{that}({\widehat{\beta }}_n,{\widehat{\lambda }}_n)\to ({\beta }^{★},0)asn\to \infty ,\end{array}$$ (33)
2. $$\sqrt{n}\left({\widehat{\beta }}_n-{\beta }^{★}\right)\Rightarrow N(0,G^{-1}\{G^{★}-K{H}^{-1}{K}^T\}{G}^{-1}),$$ (34)
3. $$\sqrt{n}{\widehat{\lambda }}_n\Rightarrow N(0,H),$$ (35)
4. $${\widehat{\beta }}_n\mathit{and}{\widehat{\lambda }}_n\mathit{are}\mathit{asymptotically}\mathit{independent}.$$ (36)

Proof

See the Appendix

It is well known that without any population constraints the asymptotic variance co-variance matrix of $\sqrt{n}\left({\widehat{\beta }}_n-{\beta }^{★}\right)$ is given by G⁻¹G*G⁻¹. Also G⁻¹KH⁻¹K^TG⁻¹ is positive definite. Thus from (34) above it follows that the inclusion of the population constraints asymptotically reduces the standard error of the model parameters. We illustrate the finite sample properties in Section 6 below.

5.2 Estimating the asymptotic Variance-Covariance matrix

Using Theorem 1 and following Qin and Lawless (1994), the asymptotic Variance-Covariance matrix can be easily estimated from the sample. If β̂ is the estimate of the model parameters then we estimate

$${\widehat{V}}_{\mathit{asym}}=\sum _{i=1}^n{w}_{i}f\left(y_i,x_i,{\widehat{\beta }}_n,0\right)f^T\left(y_i,x_i,{\widehat{\beta }}_n,0\right)$$ (37)

$${\widehat{J}}_{\mathit{asym}}={\sum _{i=1}^n{w}_i\frac{\partial f(y_i,x_i,\beta ,\lambda )}{\partial (\beta ,\lambda )}|}_{(\beta ={\widehat{\beta }}_n,\lambda =0)}.$$ (38)

Then the estimated asymptotic Variance-Covariance matrix is given by the p × p leading principle submatrix

$$\widehat{\text{Var}}{\left({\widehat{\beta }}_n\right)}_{\mathit{asym}}=\frac{1}{n}{\left({\widehat{J}}_{\mathit{asym}}^{-1}{\widehat{V}}_{\mathit{asym}}{\widehat{J}}_{\mathit{asym}}^{-1}\right)}_{(1,2,\dots ,p)\times (1,2,\dots ,p)}.$$ (39)

Instead of using the estimated weights ŵ, one can use the asymptotic weights n⁻¹.

For small sample sizes an alternative sandwich estimator of the Variance-Covariance matrix can be constructed from Theorem 1. Suppose x is the n × p matrix of the sample observations. Let us denote

$${\widehat{\eta }}_i=\sum _{k=1}^p{\widehat{\beta }}_k{x}_i^{(k)},{\widehat{\mu }}_i={\mu }_{ℳ}({\widehat{\eta }}_i),{\widehat{\mu }}_i^{\prime }={\mu }_{ℳ}^{\prime }({\widehat{\eta }}_i),$$ (40)

$${\mathbf{D}}_{{\eta }^{\prime }}=\text{diag}[{\widehat{w}}_1{\widehat{\mu }}_1^{\prime },\dots ,{\widehat{w}}_n{\widehat{\mu }}_n^{\prime }]$$ (41)

$${\mathbf{D}}_{(y-\eta )}^{★}=\text{diag}[{({\widehat{w}}_1)}^2{\{y_1-{\widehat{\mu }}_1\}}^2,\dots ,{({\widehat{w}}_n)}^2{\{y_n-{\widehat{\mu }}_n\}}^2]$$ (42)

$${\mathbf{D}}_{(y-\eta )}=\text{diag}[{\widehat{w}}_1\{y_1-{\widehat{\mu }}_1\},\dots ,{\widehat{w}}_n\{y_n-{\widehat{\mu }}_n\}],$$ (43)

where diag[·] is a diagonal matrix with the arguments as the diagonal entries. Also let

$${\mathbf{h}}^T=[{\widehat{w}}_{1}h(y_1,x_1,\gamma )\dots ,{\widehat{w}}_{n}h(y_n,x_n,\gamma )].$$ (44)

We estimate the necessary matrices by

$${\widehat{G}}_{\mathit{sand}}={\mathbf{x}}^T{\mathbf{D}}_{{\eta }^{\prime }}\mathbf{x},{\widehat{G}}_{\mathit{sand}}^{★}={\mathbf{x}}^T{\mathbf{D}}_{(y-\eta )}^{★}\mathbf{x},{\widehat{K}}_{\mathit{sand}}={\mathbf{x}}^T{\mathbf{D}}_{(y-\eta )}\mathbf{h},{\widehat{H}}_{\mathit{sand}}={\mathbf{h}}^T\mathbf{h}.$$ (45)

Then the sandwich estimate of the asymptotic Variance-Covariance matrix of β̂_n is given by

$${\widehat{\text{Var}}}_{\mathit{sand}}\left({\widehat{\beta }}_n\right)={\widehat{G}}_{\mathit{sand}}^{-1}\left[{\widehat{G}}_{\mathit{sand}}^{★}-{\widehat{K}}_{\mathit{sand}}{\widehat{H}}_{\mathit{sand}}^{-1}{\widehat{K}}_{\mathit{sand}}^T\right]{\widehat{G}}_{\mathit{sand}}^{-1}.$$ (46)

This estimate closely approximates the Variance-Covariance matrix of β̂ obtained by inverting the Hessian at the parameter estimates. In practice we have found it produces a better estimate of the standard errors than $\widehat{\text{Var}}{\left({\widehat{\beta }}_n\right)}_{\mathit{asym}}$ when the sample sizes are small.

If the link function is non-canonical then (46) can be modified in the same way as used for quasi-likelihood (McCullagh and Nelder, 1989; Kauermann and Carroll, 2001). Specifically, the estimate is obtained by replacing x by diag $\text{diag}[{\widehat{\mu }}_1^{\prime }/V_{ℳ}({\widehat{\mu }}_1),\dots ,{\widehat{\mu }}_n^{\prime }/V_{ℳ}({\widehat{\mu }}_n)]\mathbf{x}$ in the expressions in (45) above.

6 Application to demographic hazard modelling

In the section we apply the methodology to combine survey data from the British Household Panel Survey (BHPS) (Taylor et al., 1995) with population level information from the birth registration system on the General Fertility Rate (GFR) to estimate annual birth probabilities by parity. This situation was considered by Handcock et al. (2000) using a constrained maximum likelihood framework.

The birth registration system in England and Wales collects birth data by parity only within marriage (hence we do not know the parity of unmarried women). However we will show these data can be used to improve the efficiency of estimation, from the BHPS, of annual birth probabilities of all women by parity. From the combination of birth registration numerator and population estimate denominator (Office for National Statistics, 1998) we can calculate the general fertility rate (GFR) for the years 1992 to 1996, of England and Wales, which we assume to be measured without error. The population level value of the GFR was found to be 0.06179 (Handcock et al., 2000).

Our survey data are 11, 640 person-years of women’s exposure to a birth in the BHPS between the years 1991 to 1996. We have excluded the women living in Scotland for consistency with the registration system. Births were not directly recorded in this data set. Instead we code births for women aged 15 to 44 when the women’s coresident family unit experiences an increase in the number of dependent-aged children from one year (t −1) to the next (t). The details of the construction may be found in Handcock et al. (2000). The BHPS uses an approximately equal-probability sample design so that we will assume that the weights of the samples are all equal. This simplifies the estimation and reduces the standard error of the parameter estimates.

In the data set the dependent variable Y represents the indicator of birth for a woman between times (t −1) and t and the explanatory variable X is the indicator of existence of at least one child of that woman at time (t −1).

We fit a logistic regression model to the data and constrain on the population information given by the GFR. The model is represented as

$$\text{log}-\text{odds}(Y=1\mid X=x)={\beta }_0+{\beta }_{1}x.$$ (47)

We also assume that the marginal distribution of X does not involve β₀ or β₁. Our interest is in the probabilities of a birth for a childless woman, π₀ = exp(β₀)/[1 + exp(β₀)], and for a woman with children π₁ = exp(β₀ + β₁)/[1 + exp(β₀ + β₁)].

The two score constraints corresponding to the model parameters are given by

$$\sum _{i=1}^n{w}_i\left\{y_i-\frac{e^{({\beta }_0+{\beta }_1{x}_i)}}{1+e^{({\beta }_0+{\beta }_1{x}_i)}}\right\}=\sum _{i=1}^n{w}_i\frac{y_i(1+e^{({\beta }_0+{\beta }_1{x}_i)})-e^{({\beta }_0+{\beta }_1{x}_i)}}{1+e^{({\beta }_0+{\beta }_1{x}_i)}}=0$$ (48)

$$\sum _{i=1}^n{w}_i{x}_i\left\{y_i-\frac{e^{({\beta }_0+{\beta }_1{x}_i)}}{1+e^{({\beta }_0+{\beta }_1{x}_i)}}\right\}=\sum _{i=1}^n{w}_i{x}_i\frac{y_i(1+e^{({\beta }_0+{\beta }_1{x}_i)})-e^{({\beta }_0+{\beta }_1{x}_i)}}{1+e^{({\beta }_0+{\beta }_1{x}_i)}}=0.$$ (49)

In the population we know that

$$\mathit{GFR}=E[Y]=\mathrm{0.06179.}$$ (50)

This implies the population constraint is

$$\sum _{i=1}^n{w}_i(y_i-0.06179)=0.$$ (51)

Thus from the discussion in Section 2, in order to determine the weights w_i, i = 1,2, …, n we maximise ${\sum }_{i=1}^{n}log({nw}_i)$ subject to w_i ≥ 0, for all i = 1,2, …, n, ${\sum }_{i=1}^n{w}_i=1$ and the constraints in (48), (49) and (51).

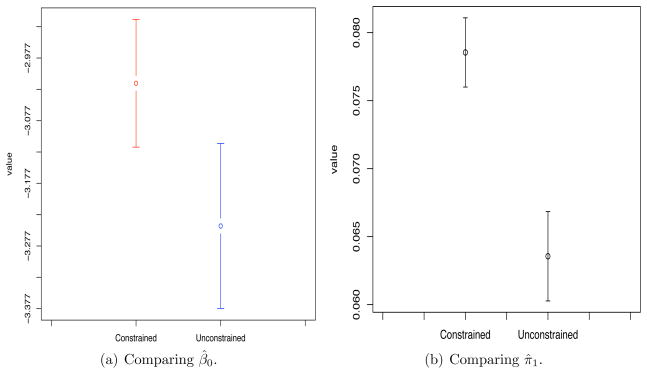
Figure 1 compares the estimates of the log-odds of a birth for a childless woman (β₀) and the probability of a birth for a woman with children (π₁). The estimated values and standard errors are shown for the procedures with and without population level constraints.

Figure 1. Comparison of the constrained and unconstrained estimates.

The error bars are one standard error above, and below, the point estimate. Panel (a): estimates of the model parameter β₀. Panel (b): estimates of the probability of a birth for a woman with children (π₁).

The estimate of the intercept parameter β₀ improves with the imposition of the population level constraints (panel a). Without the constraints the estimated value of β₀ is −3.24514 with a standard error of 0.06721. However with the constraints the estimated value increases to −3.01731 and the standard error reduces to 0.05199, a 23% reduction over the unconstrained standard error. The additional population information therefore has a large effect on the estimate.

We note that the estimate of the slope (i.e. β₁) is the same in both constrained and unconstrained cases. The estimated value of the parameter is 0.55496 with a standard error of 0.08700. Our observation of no significant reduction in the standard error of β̂₁ is because the indicator of previous birth is only indirectly constrained by the population level constraint (general fertility rate from 1992 to 1996). Note that, through its effect on the intercept parameter, the inclusion of the population level information on the pooled GFR reduces the standard errors of the estimates of the primary quantities of interest, the probabilities of a birth for a childless woman and for a woman with children (panel b). We also observe that the apparent downward bias of the unconstrained estimator is appreciably reduced.

The estimated values of the parameters and their standard errors obtained from the two step maximisation method are almost identical to those for the corresponding CMLE (results not shown). This further supports our suggestion in Section 2.4 above that moving from a maximum likelihood to an empirical likelihood framework will involve minimal cost in statistical efficiency in practical applications.

7 Discussion

In this paper we introduce a method to combine population level information with the sampled individual level information based on an empirical likelihood. On one hand our approach can be seen as an extension of the post-stratification approach using a special case of empirical likelihood (Qin and Lawless, 1994; Imbens, Spady, and Johnson, 1998). On the other hand our method extends the weighted least squares estimator of the model parameters studied in Hellerstein and Imbens (1999). The method solves a two-step nested maximisation problem where in the outer step we maximise for the parameter estimates and in the inner step sample weights are computed such that the population expectation of the dependent variable given a subset of the explanatory variables and the constraints imposed on the conditional expectation by the model are reproduced in the re-weighted sample. We further show that it is possible to simplify the nested maximization procedure of Qin and Lawless (1994) to a two-step estimator similar to Hellerstein and Imbens (1999). In the first step we find the weights satisfying only the population constraints. In the second, unconstrained estimation of the model parameters is conducted using the re-weighted sample from the first step. The asymptotic standard errors of the parameter estimates can be computed explicitly and estimated accurately by a sandwich estimator. Furthermore we introduce a description of the parameter estimates as arguments maximising the non-parametric likelihood over a subset of the simplex with appropriate dimensions.

Although potentially less efficient than the constrained maximum likelihood estimator, the empirical profile likelihood estimator in (10) has many advantages over the CMLE of (Handcock, Huovilainen, and Rendall, 2000; Handcock, Rendall, and Cheadle, 2005). The EPLE does not place constraints on the parameters and can thereby avoid non-linear constraints. The empirical likelihood based estimators use linear constraints on the weights, which are easier to solve. This ensures improvement in terms of computational stability and simplicity in implementation. Further, as the estimated sample weights can be interpreted as an estimate of the joint probability of observing a particular sample, we don’t need to specify a distribution of the explanatory variables.

Other than a more complete description within the empirical likelihood framework, our method improves upon Hellerstein and Imbens (1999) by allowing a range of linear, generalised linear and non-linear models for the association between the dependent and explanatory variables. For an example of an application in the context of a parameter dependent population level constraints see Chaudhuri, Drton, and Richardson (2005).

Since it uses a likelihood based approach, our method can be extended to Bayesian inference. Available prior information on the model parameters or the population-level constraints can be easily used together with other constraints in the estimation. Note that if this prior is not a function of the weights, the empirical profile likelihood (Qin and Lawless, 1994) does not depend on the prior. On the other hand by maximising the product of the nonparametric likelihood and the prior in (10) such information is easily incorporated in the analysis. Thus one can include expert opinions, information from a larger sample or some prior information about the constraints in the analysis.

The methodology developed in this paper has been implemented in an R package named glmc developed by the authors (Chaudhuri et al., 2006). This package performs the two-step maximisation procedure (21) and (22) and, if it fails, the nested maximisation (20) as described in Section 4. The standard error of the parameter estimates are calculated using Theorem 1 from (46). The package is available on CRAN (R Development Core Team, 2006).

There is no general algorithm to solve the constrained maximisation problem to get the EPLE. Often one needs to choose such algorithms on a case by case basis. Owen (2001) and Chen, Sitter, and Wu (2002) provide methods (both implemented in glmc) which work well for large sample sizes. For very small samples, the choice of the starting point becomes crucial and in many cases it converges outside the simplex.

We note that the two-step procedure directly applies to testing as well. In order to test the null hypothesis, f (θ) = 0 (Qin and Lawless, 1995), we take Θ = {θ : f (θ) = 0} in (9). Moreover, based on our description we conjecture that asymptotically the log-empirical likelihood ratio has a chi-squared distribution. We defer further comments on this topic.

Finally, in most cases sample points are not drawn with equal probability. Usually sampling weights accompany the sampled values. By incorporating the information contained in these sampling weights, further improvements in estimation may be achieved.

Appendix

Proof of Theorem 1

Proof

The score and the population constraints imply that ∀k = 1,2, …, p and ∀j = 1, 2, …, m

$$\sum _{i=1}^n{w}_i{x}_i^{(k)}(y_i-{\mu }_i)=\sum _{i=1}^n\frac{x_i^{(k)}(y_i-{\mu }_i)}{1+{\sum }_{j=1}^m{\lambda }_j{h}_j(y_i,x_i,{\gamma }_j)}=0.$$ (52)

$$\sum _{i=1}^n{w}_i{h}_j(y_i,x_i,{\gamma }_j)=\sum _{i=1}^n\frac{h_j(y_i,x_i,{\gamma }_j)}{1+{\sum }_{j=1}^m{\lambda }_j{h}_j(y_i,x_i,{\gamma }_j)}=0.$$ (53)

Suppose β̂ and λ̂ are the vector of estimates of the model parameters and the Lagrangian multipliers, respectively.

A Taylor series expansion of $\frac{1}{n}{\sum }_{i=1}^{n}f(y_i,x_i,\beta ,\lambda )$ around (β*, 0) gives

$$\frac{1}{n}\sum _{i=1}^{n}f(y_i,x_i,\beta ,\lambda )-\frac{1}{n}\sum _{i=1}^{n}f(y_i,x_i,{\beta }^{★},0)=\frac{1}{n}\sum _{i=1}^n\left[{\frac{\partial f(y_i,x_i,\beta ,0)}{\partial (\beta ,\lambda )}|}_{(\beta ={\beta }^{★},\lambda =0)}\right]\left[\begin{array}{c}\beta -{\beta }^{★}\\ \lambda \end{array}\right]+\frac{\zeta }{2n}[{(\beta -{\beta }^{★})}^T,{\lambda }^T]\left(\sum _{i=1}^n\mathcal{H}(y_i,x_i)\right)\left[\begin{array}{c}\beta -{\beta }^{★}\\ \lambda \end{array}\right],$$ (54)

where |ζ| ≤ 1 and ℋ(Y, X) is an integrable bound to the Hessian matrix in nbd(β*,0). The Jacobian matrix is given by

$$\frac{\partial f(y_i,x_i,\beta ,\lambda )}{\partial (\beta ,\lambda )}=\left[\begin{array}{cc}-\frac{x_i^T{x}_i{\mu }_i^{\prime }}{1+{\lambda }^{T}h(y_i,x_i,\gamma )}& \frac{h(y_i,x_i,\gamma )x_i(y_i-{\mu }_i)}{{\{1+{\lambda }^{T}h(y_i,x_i,\gamma )\}}^2}\\ 0& \frac{h(y_i,x_i,\gamma )h^T(y_i,x_i,\gamma )}{{\{1+{\lambda }^{T}h(y_i,x_i,\gamma )\}}^2}\end{array}\right]$$ (55)

The expression of the Jacobian matrix at (β*, 0) is given by

$${\frac{\partial f(y_i,x_i,\beta ,\lambda )}{\partial (\beta ,\lambda )}|}_{(\beta ={\beta }^{★},\lambda =0)}=\left[\begin{array}{cc}-x_i^T{x}_i{\mu }_i^{\prime }& h(y_i,x_i,\gamma )x_i(y_i-{\mu }_i^{★})\\ 0& h(y_i,x_i,{\gamma }_i)h^T(y_i,x_i,\gamma )\end{array}\right]$$ (56)

By assumption

$$E[f(Y_1,X_1,{\beta }^{★},0)]=0,$$ (57)

E [ℋ(Y₁, X₁)] is finite and

$$E\left[{\frac{\partial f(Y_1,X_1,\beta ,0)}{\partial (\beta ,\lambda )}|}_{(\beta ={\beta }^{★},\lambda =0)}\right]=\left[\begin{array}{cc}-G& K\\ 0& H\end{array}\right].$$ (58)

Also by the Central Limit Theorem it follows that

$$\sqrt{n}\left(\frac{1}{n}\sum _{i=1}^{n}f(y_i,x_i,{\beta }^{★},0)\right)\to N(0,V).$$ (59)

where

$$V=\text{Var}[f(Y_1,X_1,{\beta }^{★},0)]=\left[\begin{array}{cc}{G}^{★}& K\\ K^T& H\end{array}\right]$$ (60)

From this using the strong law, the continuity of f(y, x, β, λ), one can follow the description in Serfling (1980, Chapter 4.2) to show for sufficiently large n almost surely there is a sequence of solutions (β̂_n, λ̂_n) of ${\sum }_{i=1}^{n}f(y_i,x_i,\beta ,\lambda )=0$ converging to (β*,0) as n → ∞. So the strong consistency of β̂_n and λ̂_n follows.

To show the asymptotic normality we note that

$$\sum _{i=1}^{n}f\left(y_i,x_i,{\widehat{\beta }}_n,{\widehat{\lambda }}_n\right)=0.$$ (61)

Thus for large n with probability 1, (54) holds in a neighbourhood of (β*, 0). So after some rearrangement of terms it follows that for large n, with probability 1

$$\sqrt{n}\left[\begin{array}{c}{\widehat{\beta }}_n-{\beta }^{★}\\ {\widehat{\lambda }}_n\end{array}\right]+{\left[\frac{1}{n}\sum _{i=1}^n\left[{\frac{\partial f(y_i,x_i,\beta ,0)}{\partial (\beta ,\lambda )}|}_{(\beta ={\beta }^{★},\lambda =0)}\right]+\frac{\zeta }{2n}\left[{({\widehat{\beta }}_n-{\beta }^{★})}^T,{\widehat{\lambda }}_n^T\right]\sum _{i=1}^n\mathcal{H}(y_i,x_i)\right]}^{-1}\times \left[\sqrt{n}\left(\frac{1}{n}\sum _{i=1}^{n}f(y_i,x_i,{\beta }^{★},0)\right)\right]\to 0.$$ (62)

Now from this, the consistency of β̂, λ̂, (58), (59), (60) and Slutsky’s theorem it is evident that

$$\sqrt{n}\left(\begin{array}{c}{\widehat{\beta }}_n-{\beta }^{★}\\ {\widehat{\lambda }}_n\end{array}\right)\to N(0,V^{★}),$$ (63)

where

$$V^{★}={\left(\begin{array}{cc}-G& K\\ 0& H\end{array}\right)}^{-1}\left(\begin{array}{cc}{G}^{★}& K\\ K^T& H\end{array}\right){\left(\begin{array}{cc}-G& 0\\ K^T& H\end{array}\right)}^{-1}=\left(\begin{array}{cc}{G}^{-1}[G^{★}-K{H}^{-1}{K}^T]G^{-1}& 0\\ 0& H\end{array}\right).$$ (64)

From (64) the rest of the assertions of the theorem follow.